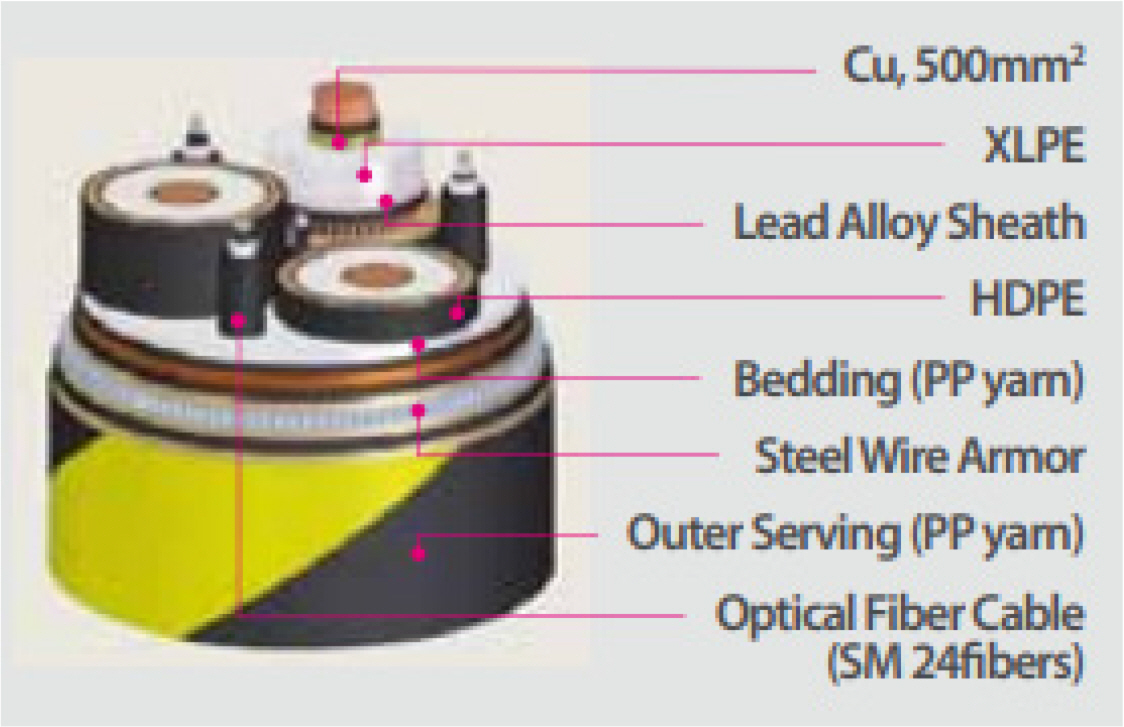
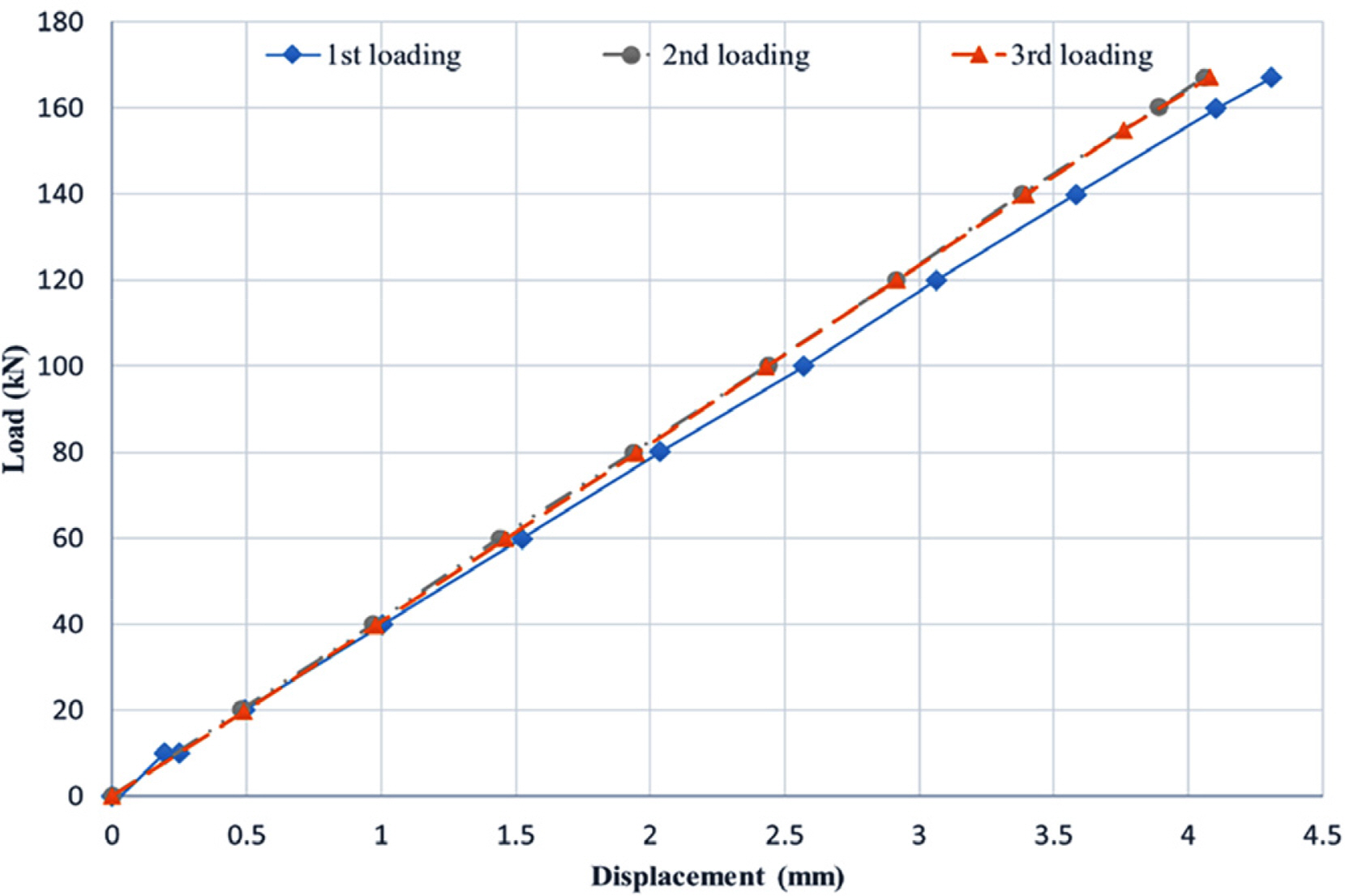
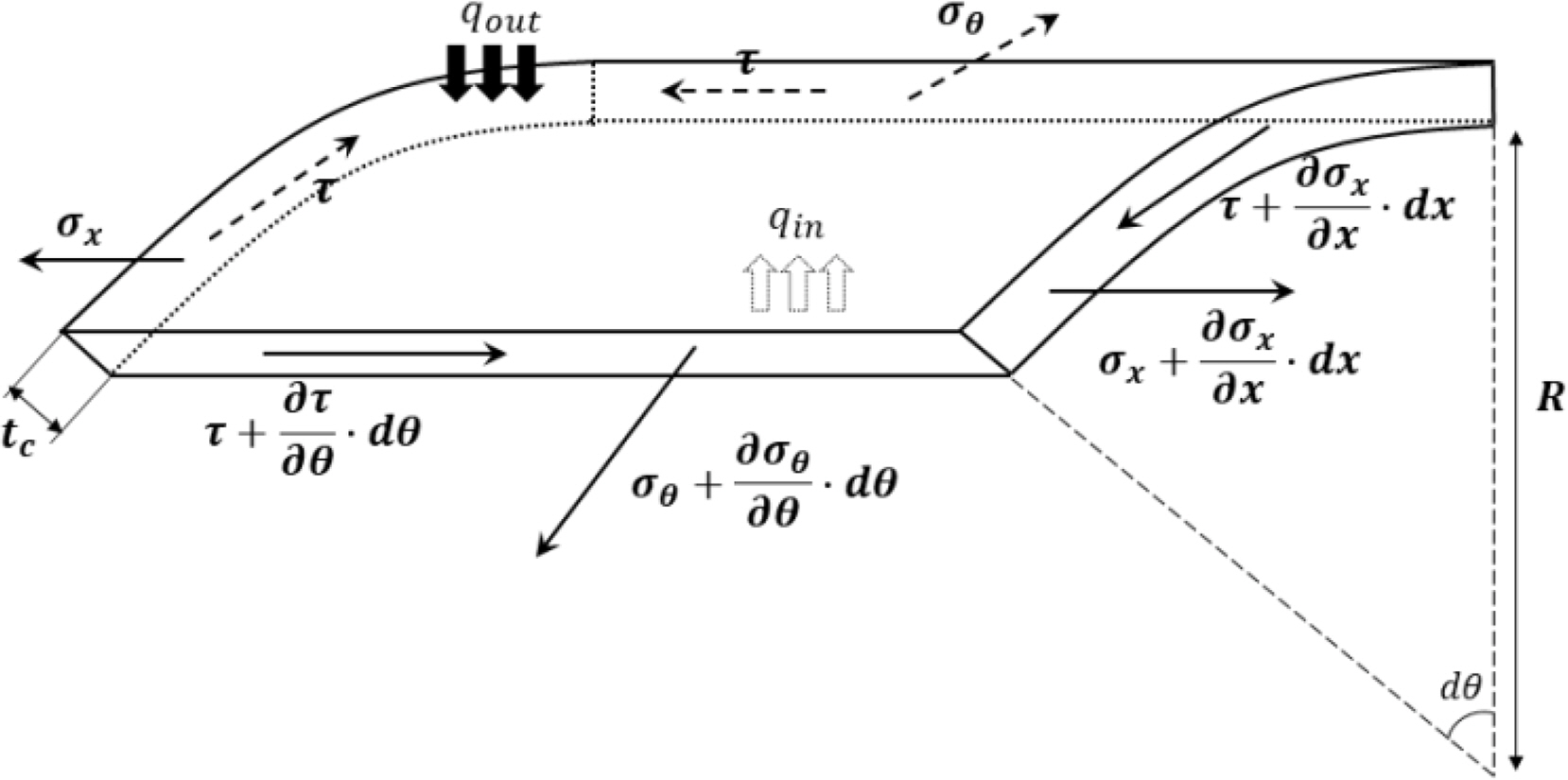
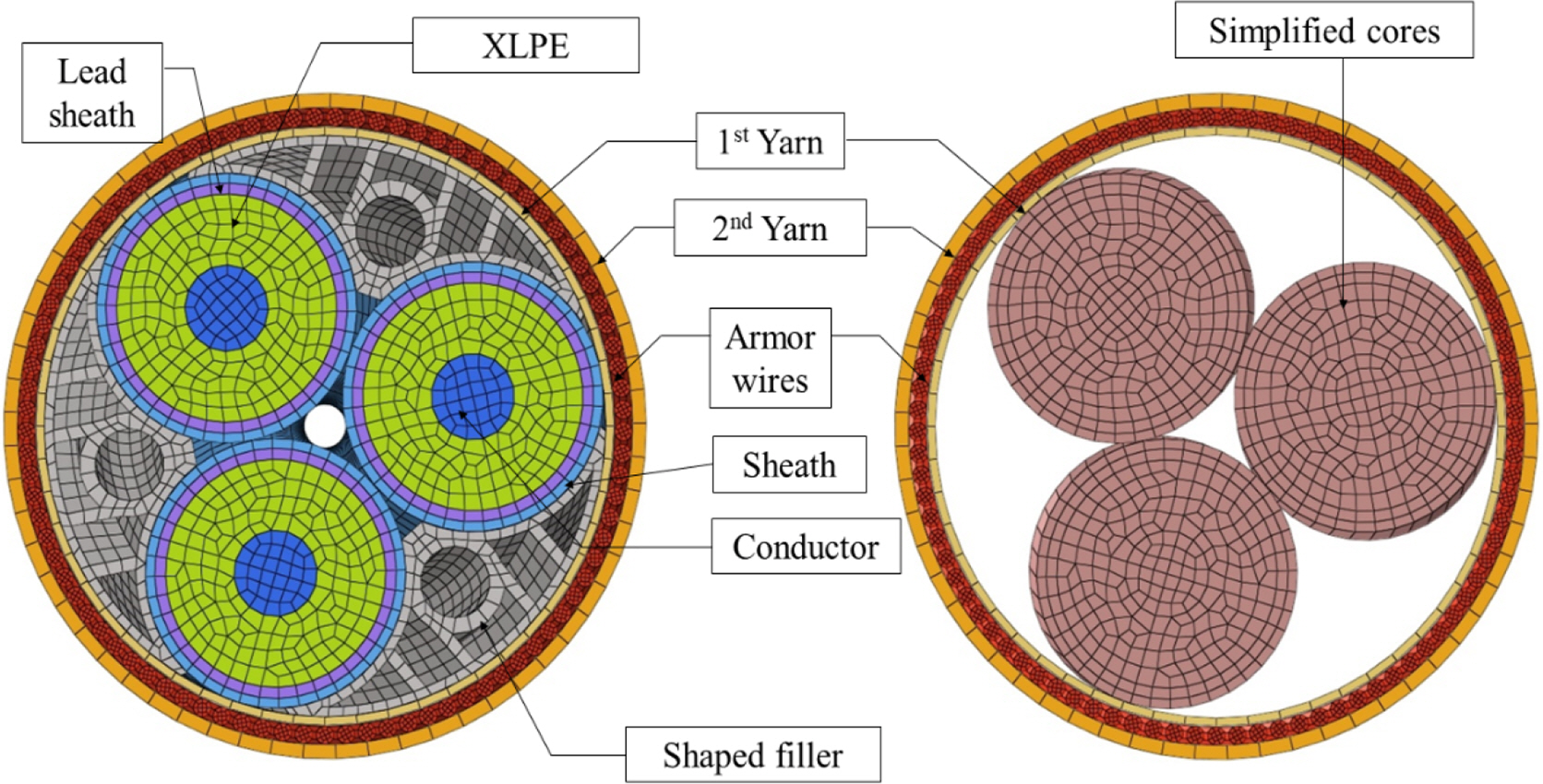
CIGRE. (2015). Recommendations for Mechanical Testing of Submarine Cables (CIGRE TB 623).
Coser, TB., Strohaecker, TR., López, FS., Bertoni, F., Wang, H., Hebert, CB., & Maioli, P. (2016). Submarine Power Cable Bending Stiffness Testing Methodology. In the 26th International Ocean and Polar Engineering Conference, OnePetro..
Delizisis, P., Dolianitis, I., Chatzipetros, D., Kanas, V., Georgallis, G., Tastavridis, K., & Angelis, E. (2021). Full Scale Axial, Bending and Torsion Stiffness Tests of a Three Core HVAC Submarine Cable.
Proceedings of International Conference on Offshore Mechanics and Arctic Engineering, V004T04A009, American Society of Mechanical Engineers.
https://doi.org/10.1115/OMAE2021-63238

Ekeberg, KI., & Dhaigude, MM. (2016). Validation of the Loxodromic Bending Assumption using High-quality Stress Measurements. In The 26th International Ocean and Polar Engineering Conference, OnePetro..
Kebadze, E. (2000). Theoretical Modelling of Unbonded Flexible Pipe Cross-sections.
Knapp, RH. (1979). Derivation of a New Stiffness Matrix for Helically Armoured Cables Considering Tension and Torsion.
International Journal for Numerical Methods in Engineering,
14(14), 515-529.
https://doi.org/10.1002/nme.1620140405

Komperød, M. (2017). Numerical Calculation of Stresses in Helical Cable Elements Subject to Cable Bending and Twisting.
Proceedings of the 58th Conference on Simulation and Modelling (SIMS 58) Reykjavik. Iceland. Linköping University Electronic Press: p 374-384.
https://doi.org/10.3384/ecp17138374

Komperød, M., Juvik, JI., Evenset, G., Slora, R., & Jordal, L. (2017). Large-Scale Tests for Identifying the Nonlinear, Temperature-Sensitive, and Frequency-Sensitive Bending Stiffness of the NordLink Cable.
In International Conference on Offshore Mechanics and Arctic Engineering, V05AT04A004. American Society of Mechanical Engineers:
https://doi.org/10.1115/OMAE2017-61103

Love, AEH. (2013). A Treatise on the Mathematical Theory of Elasticity. Cambridge University Press.
Lu, Q., Yang, Z., Yan, J., Lu, H., Chen, J., & Yue, Q. (2017). A Finite Element Model for Prediction of the Bending Stress of Umbilicals.
Journal of Offshore Mechanics and Arctic Engineering,
139(6), 061302.
https://doi.org/10.1115/1.4037065

Lutchansky, M. (1969). Axial Stresses in Armor wiress of Bent Submarine Cables.
Journal of Manufacturing Science and Engineering,
91(3), 687-691.
https://doi.org/10.1115/1.3591660

Shaw, N. (2011). Cross-section Design and Analysis of Umbilical Cable in Subsea Production System (Master Thesis).
Skeie, G., Sødahl, N., & Steinkjer, O. (2012). Efficient Fatigue Analysis of Helix Elements in Umbilicals and Flexible Risers: Theory and applications.
Journal of Applied Mathematics, 246812.
https://doi.org/10.1155/2012/246812

Tjahjanto, DD., Tyrberg, A., & Mullins, J. (2017). Bending Mechanics of Cable Cores and Fillers in a Dynamic Submarine Cable.
In International Conference on Offshore Mechanics and Arctic Engineering, V05AT04A038. American Society of Mechanical Engineers, V05AT04A038:
https://doi.org/10.1115/OMAE2017-62553

Vaz, MA., Aguiar, LAD., Estefen, SF., & Brack, M. (1998). Experimental Determination of Axial, Torsional and Bending Stiffness of Umbilical Cables. Proceedings of the 17th International Offshore & Arctic Engineering Conference, (OMAE’98), 7.