|
 |
- Search
| J. Ocean Eng. Technol. > Volume 34(3); 2020 > Article |
|
Abstract
Underwater acoustics, which is the domain that addresses phenomena related to the generation, propagation, and reception of sound waves in water, has been applied mainly in the research on the use of sound navigation and ranging (SONAR) systems for underwater communication, target detection, investigation of marine resources and environment mapping, and measurement and analysis of sound sources in water. The main objective of remote sensing based on underwater acoustics is to indirectly acquire information on underwater targets of interest using acoustic data. Meanwhile, highly advanced data-driven machine-learning techniques are being used in various ways in the processes of acquiring information from acoustic data. The related theoretical background is introduced in the first part of this paper (Yang et al., 2020). This paper reviews machine-learning applications in passive SONAR signal-processing tasks including target detection/identification and localization.
Underwater acoustics is a scientific domain that involves the study of the phenomena of sound waves in water, including their generation, propagation, and reception. Specifically, the sound navigation and ranging (SONAR) system is utilized to investigate underwater communication and target detection and to study marine resources and the environment; further, it is utilized to measure and analyze sound sources in water. The main objective of underwater acoustics-based remote sensing is the indirect acquisition of information on underwater targets of interest using acoustic data. At present, highly advanced data-driven machine-learning techniques are being applied in various ways for extracting information from acoustic data. The techniques closely related to these applications are introduced in the first part of this paper (Yang et al., 2020). This paper presents a detailed review of the applications of machine learning in underwater acoustics and passive SONAR signal processing.
Signals measured by a passive SONAR system exhibit fluctuations owing to irregular noises in the ocean. This hinders target signal detection. The conventional signal processing method for detecting target signals is based on the Neyman–Pearson criterion (Nielsen, 1991). As the probability distribution of the received signals, including the target signals, differs from that of the noise signals, the probability ratio that is set according to the presence of the target signal at the time of observation is compared with a preset value. This helps determine whether the target signal is included in the observed time period. This technique can be expanded to detect the target signal by comprehensively analyzing all the signals measured in the time domain of interest as well as signals observed at a specific time.
In general, techniques for detecting a target signal through comparison with a threshold value have a disadvantage: false alarms can occur frequently, particularly in the scenario of a low signal to-noise ratio. To overcome this problem, Komari Alaie and Farsi (2018) combined the time and frequency domain information of the measurement signals to derive an adaptive threshold for such signals. They used this threshold value to determine whether the target signal is included in the corresponding observed interval.
However, in passive SONAR, the use of a threshold to identify a target as described earlier is a detection technique that uses only the size-related features of the target signal. Shin and Kil (1996) developed a target identifier that defined and utilized the multifaceted features of a target signal in terms of various aspects to increase the accuracy of target detection. In the conventional target detection technique based on the signal size described earlier, the tendencies exhibited in the spectrogram of the observed signal are simplified, and the sum of the signal sizes corresponding to the frequency domain of interest in each time frame is used. In the study conducted by Shin and Kil, apart from these fundamental features, other features such as those related to the size/frequency statistics of the observed signal and the frequency of the target signal were integrated to utilize these as input vectors for several machine learning algorithms including neural networks. In conventional target detection, a process is required for identifying the detected target signal. However, in target identifiers that use multiple features of the target signal as mentioned in the aforementioned technique, target classification is achieved before detection (classify-before-detect method). The technique proposed by Shin and Kil delivered superior performance, compared to the performance of the conventional technique, particularly in low signal-to-noise ratio conditions.
The aforementioned studies have mainly used passive SONAR (binary classification) to determine whether the target signal is included in the observed interval. This type of classification can be extended further to the classification of various types of signals present in the ocean. Hemminger and Pao (1994) proposed a classifier that used neural networks to distinguish between six types of marine noises. In the process of detection or identification of a signal by a SONAR operator, a technique such as a short-time Fourier transform (STFT) that displays the temporal frequency variations of a signal of interest is often used in conjunction with the auditory information. With reference to this, the study conducted by Hemminger and Pao defined the features that reflected the visual information of the STFT, as follows. When the spectrum that constituted the STFT of the observed signal was compared in relation to the trend exhibited by the preceding cluster in each time frame, the STFT could be represented as a list of prototype numbers. The prototype numbers listed in this manner constituted the input vectors of the neural network. A classifier was developed according to the type of noise source to be classified. The type of noise source included in the test data was determined using a classifier that yielded the highest value among different classifier results.
While detecting a target signal using passive SONAR, a transient sound is detected for a period of time. This could be emitted by various sources such as biological sound or machinery noise. In general, a skilled SONAR operator is capable of classifying these transient sounds according to the source. Tucker and Brown (2005) extracted various features including human auditory characteristics reflected from timbre (Fig. 1) and proposed a transient sound classifier using these features. For the classification, timbre-related features that helped classify various types of sounds were selected based on the results of a classification experiment that classified various transient sounds present in underwater environments including biological and mechanical sounds. In addition, factors related to the material of the sound-generating target were explored and used as features. Finally, the features reflecting sound variability were calculated using a rhythmogram that reflected the temporal variability of transient sound (related to repeatability in the time domain). The feature vectors derived from the combination of features defined in various domains have a higher dimension than the specified data size. Among these vectors, the features that help identify the type of sound source are selected. As their study distinguished sounds included in a specific class from those in other classes, different features were selected according to the sound to be classified. These input feature vectors with reduced dimensions were combined with the k-nearest neighbors (KNN) algorithm to classify the type of sound. The classification performance obtained by combining and using features derived from various domains (including human sound perception) was superior to that obtained using statistical features of frequency variations over time that were obtained from frequency features or spectrograms of the observed signals. This was demonstrated by comparing the receiver-operating-characteristics (ROC) curve of the identifier using each feature. Finally, they concluded the following. To identify the type of transient sounds, it was most advantageous to select and use a feature that was suitable for the research purpose by integrating the sound perception features, frequency features, and statistical features.
To distinguish the types of noise sources by using machine learning, the classifiers need to learn a large amount of data. However, in practice, there is a deficiency of passive SONAR data classified by the type of noise source. Meanwhile, passive SONAR data without classification are relatively abundant. Yang et al. (2018) and Ke et al. (2018) have conducted studies utilizing unclassified SONAR data for pre-training to increase the efficiency of supervised learning. Yang et al. (2018) used the values of the final hidden layer of the competitive deep-belief network (CDBF) (designed by them) as classifier inputs. This was unlike other existing methods that use passively defined feature vectors based on the experience of experts. A large amount of data is required to automatically extract features from the input vector (e.g. spectrum) that are effective for classification. Unclassified SONAR data are used for this purpose. In CDBF, a restricted Boltzmann machine (RBM) is trained on the probability distribution of the input data. This is a type of unsupervised learning that is performed using data without class labels. Then, using the classified data, the degree of sensitivity of the unit in the hidden layer of the RBM can be calculated according to the type of the noise source. Based on this, the units of the hidden layer can be clustered. The competitive layer is placed at the rear of the hidden layer, and training is performed to increase the distinction between the clustered classes. Finally, the unit value of the competitive layer is used as the input vector of the support vector machine (SVM) to distinguish between types of ships for classification. This method has delivered a classification performance that is superior to those of methods using the Mel-frequency cepstral coefficient (MFCC), waveform, wavelet, or feature vectors based on auditory model.
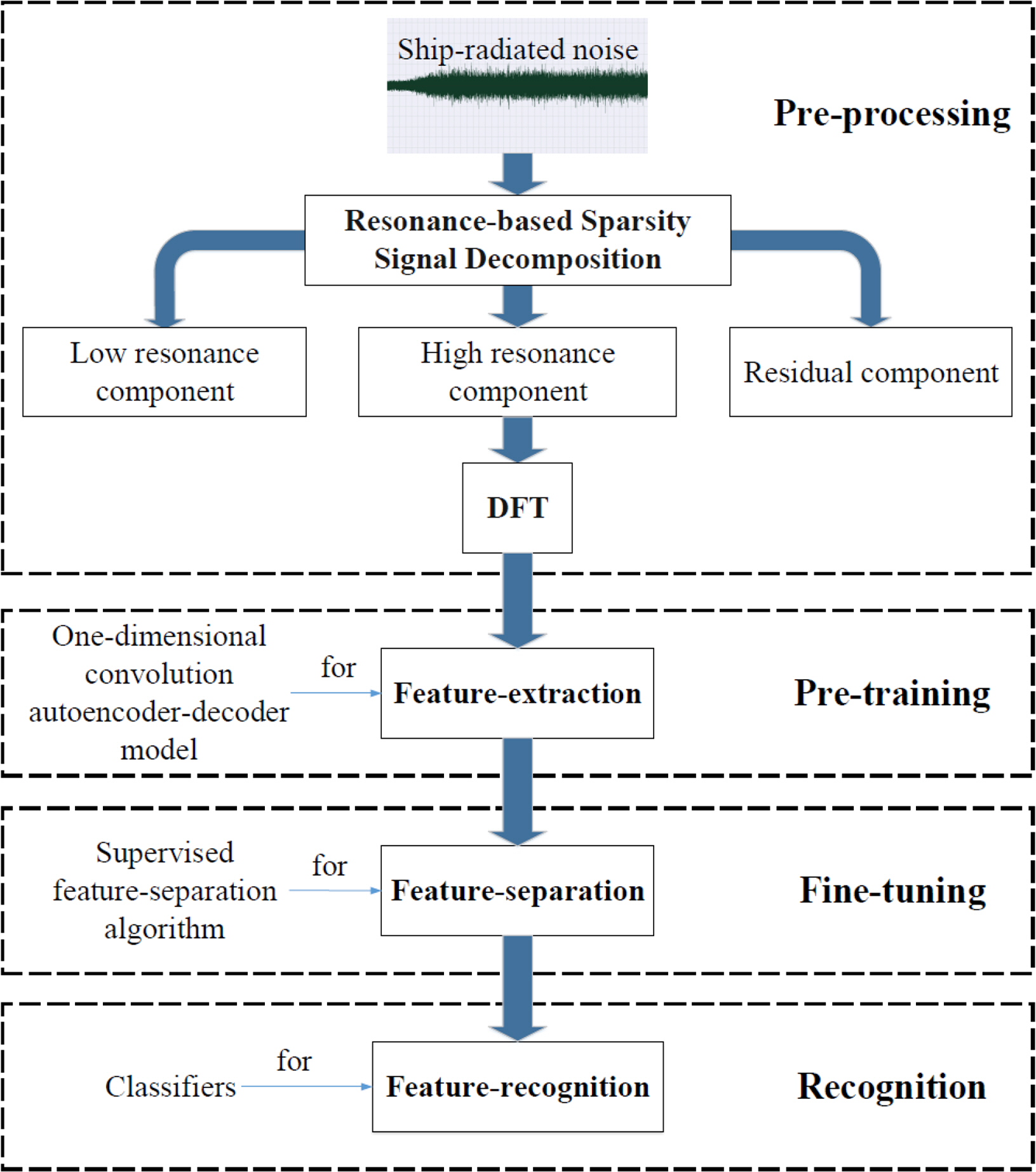
Ke et al. (2018) also used unclassified passive data to improve the accuracy of learning performed with marginal amounts of classified passive SONAR data. In their study, the following four steps were used for classifying ships: (1) pre-processing, (2) pre-training, (3) fine-tuning, and (4) classification (Fig. 2). In the pre-processing step, only the effective components for data classification were extracted from the measured time-series acoustic data through the wavelet transform. These extracted components were transformed to the frequency domain and used as a pre-training input for the subsequent step. In the pre-training step, a multi-layered autoencoder was used. High-level features for noise source classification were extracted from this encoder. In the fine-tuning step, the trained autoencoder was applied to a marginal amount of classified SONAR data. Furthermore, the training was performed such that the high-level feature vectors extracted through the feature-separation layer increased the spatial distance according to the class. The result of the fine-tuning step was used as the input to the support vector machine (SVM) in the classification step. This method delivered a better classification performance than those of the existing methods that use MFCC as the input.
Wang et al. (2019b) fused features extracted from multiple domains to identify the types of marine noise sources (four types of ship noises, marine mammal sounds, and background noise). Furthermore, they combined these with a deep neural network (DNN). Typically, MFCC is used to identify noise sources. However, it was verified in this study that the Gammatone frequency cepstral coefficient (GFCC) is more advantageous for marine noise source classification. Furthermore, the GFCC was used as a part of the feature vectors. Modified empirical mode decomposition was applied to extract the feature vectors incorporating diverse information related to complex marine noise sources, from time-series signals. At this time, the features were calculated based on the magnitude of the decomposed signals and frequency variation, which were fused with the GFCC and used as the input vectors of the DNN. The DNN had a Gaussian mixture model (GMM) in the first layer and extracted the statistical features of the feature vector rather than those of the overfit feature vector. These were used to conduct supervised learning. The performance was improved significantly compared to the results obtained from the existing noise source classification methods that combine MFCC with limited information by using a simple classifier such as a GMM.
As mentioned earlier, it has been established that the performance of a skilled SONAR operator is superior to that of the target detection process based on the traditional SONAR signal processing technique. For example, an echo signal from a metal object has a timbre that is different from that of an echo signal from a natural object, such as a rock, and humans can recognize this difference. In this regard, studies have been conducted to identify target signals from echo signals having different timbres depending on the material of the target object using active SONAR (Allen et al., 2011; Murphy and Hines, 2014; Young and Hines, 2007). Similar to these studies, Yang and Chen (2015) conducted a study wherein they tested the human capability to distinguish between artificially generated sounds and naturally occurring sounds using passive SONAR. Furthermore, they analyzed strategies for humans to recognize sounds according to the sound sources to improve the performance of the automatic identifier. In their study, experiments were performed to understand the human capabilities of auditory perception for identifying and distinguishing between artificial sounds (such as those of large ships, torpedoes, and underwater vehicles) and natural sounds (such as those from dolphins or rain), between sounds of surface ships and submarines, and between sounds from three ships. For the sound identification method used by the participants in this experiment, the following were defined and extracted from the observed signals: harmonic spectrum features associated with the tonal component of the noise source, equivalent rectangular bandwidth spectrum features associated with the timbre, and auditory cortical features associated with frequency variation characteristics over time. The features extracted over multiple domains had a high dimension. In each domain, principal component analysis (PCA) was used to reduce the dimension and then combine the features to be used as input values for machine learning. In this study, a logistic regression-based classifier was trained using the training data prepared for each class, and the performance of the classifier trained for each objective was evaluated using the test data. It was verified that the automatic target classifier was superior to the human participants in all the tasks. In particular, the performance of the automatic target classifier with feature vectors of lower dimension was better when sounds were more similar within a class or when the sounds significantly differed across classes. The automatic target classifier delivered the most inferior performance in the classification of artificial noise and natural noise and the most superior performance in the classification of noise from the three ships. In addition, they proposed a method of combining the classification experience of the human participant with the automatic target classifier for the task of artificial/natural noise classification in which the classifier delivered the most inferior classification performance. Furthermore, they verified that the classification performance of the automatic target classifier could be improved through similar combinations.
In general, a vertical/horizontal line array consisting of multiple sensors is used for target localization in underwater acoustics. In particular, when the target is located remotely, the elevation angle or the azimuthal angle (depending on the type of line array) of the target can be estimated using the time difference of arrival of the target noise incident on the line array. Hereinafter, in this review paper, the elevation angle and azimuthal angle of the target are collectively referred to as the target arrival angle. In the conventional approach for underwater acoustics, the similarity between the acoustic field actually measured in the line array and the replica field simulated according to the arrival angle with the plane wave assumption is assessed to estimate the arrival angle of the target. This angle can be estimated using the replica field that displays high similarity with the measured field (Jensen et al., 2011). This technique is highly robust against noise. However, it has a disadvantage, wherein a long line array is required to estimate the target azimuthal angle with high resolution. An adaptive beamforming method has been proposed to overcome this disadvantage. However, the adaptive beamforming method using a covariance matrix of a measured field has a disadvantage: the performance deteriorates when correlated target signals are estimated (Jensen et al., 2011).
Several techniques have recently been proposed for estimating the target arrival angle with high resolution using a limited-length line array in an environment with correlated target signals. Among these, a representative technique is compressive beamforming (Edelmann and Gaumond, 2011; Xenaki et al., 2014; Xenaki and Gerstoft, 2015). It is based on compressive sensing, which is designed to derive the solution of a (non-deterministic) linear system. In compressive sensing, the sparsest solution among the many solutions that satisfy the linear system is determined by minimizing the lo norm of signal x (Donoho, 2006). The target arrival angle in underwater acoustics can be estimated as a linear system problem. It is advantageous as the arrival angle can be estimated with high resolution using limited observation by applying compressive sensing. However, in compressive sensing with compressive beamforming, there is a trade-off between the observed data proximity and the sparsity of the estimated solution. Therefore, there is a disadvantage: the hyperparameters that determine the priority between the sparsity and data-fitting of the solution need to be adjusted passively to derive the solution that is appropriate for each scenario (Park et al., 2017). Sparse Bayesian learning (SBL), an algorithm based on machine learning, is drawing attention as an effective method to address this problem (Tipping, 2001).
SBL has been proposed for the regression of a specified data trend or classification using Bayesian inference (Tipping, 2001). Similar to compressive sensing, SBL is applied when the measured data can be represented as a linear combination of specified bases (linear system problem). In this case, it is assumed that the base size and noise in the measured data follow a normal distribution. Unlike compressive sensing (in which x is directly and deterministically derived), in SBL, x is derived by first estimating the probability distribution and then using the distribution. As mentioned earlier, the problem of evaluating the arrival angle of an underwater target can also be established as a linear system: y = Ax + n. Here, y denotes the measured data, and n denotes the noise included in each acoustic sensor of the line array. When estimating the target arrival angle using SBL, the probability distributions of x and n (i.e., the signal size and noise variance) can be extracted from the measured data. The arrival angle of the target signal incident on the line array can be evaluated using probability distribution. While performing beamforming based on SBL, the signal size and noise variance are repeatedly updated using the expectation-maximization algorithm (Tipping, 2001). The update rule used at this time is one of the key parts of SBL. However, in this review paper, rather than detailing the algorithm of SBL, we review the SBL modification method that is used to estimate the target arrival angle more robustly.
When measuring an acoustic signal in an actual experiment, the target signal is continuously recorded on the line array. Multiple measurements or multi-snapshots in the time domain can be used to obtain a reliable estimation of the arrival angle of the target signal. In particular, the target in an adjacent signal can be regarded as stationary in the underwater environments where the speed of sound waves is significantly higher than the target speed. Gerstoft et al. (2016) extended the existing SBL to utilize the stationary target signal recorded at the adjacent time. In this manner, the single measurement signal y and the corresponding target signal size x of the existing SBL were substituted with the adjacent multiple measurement signals Y = [y1, y2, …, yL] and corresponding target signal size X = [x1, x2, …, xL], respectively. Here, y1 is a signal measured at a line array at a specific time, and x1 is the corresponding target signal. In addition, in the study mentioned earlier, it was assumed that the noise had the same variance regardless of the sensor and measurement time. Gerstoft et al. (2019) extended the SBL such that these noises could have different magnitudes depending on the sensor and measurement time. In addition, they verified through a simulation that the extension was capable of robustly estimating the target arrival angle, compared to the existing method. In addition, Nannuru et al. (2019) extended the conventional SBL to account for the scenario with different matrices Af according to different frequencies. They verified the effectiveness of the extension method based on actual measurement data (SWellEx-96).
For estimating the arrival angle of a target, SBL has the advantage of automatically deriving values without the need to adjust hyperparameters separately, unlike in the case of compressive sensing. However, as the linear relationship used in SBL utilizes a replica field for a preset target signal arrival angle, a basis mismatch occurs as in compressive beamforming. This lowers its performance. To address this problem, Das (2017) proposed two methods for the off-grid sparse Bayesian arrival angle estimation algorithm and analyzed the error of each method based on the Cramer–Rao lower bound (CRLB). The first method is based on the fact that a randomly incident target signal can be expressed by the Taylor series of a replica field having the arrival angle set at equal intervals. The difference is calculated between the actual arrival angle derived using the Taylor expansion process for the incident angle and the preset arrival angle. After adding this to the estimated variable of the SBL and updating it, the proposed method is more robust against a basis mismatch than the existing method. In the second method, it is assumed that the target signal incident on the line array at an arbitrary angle can be expressed through linear interpolation of the replica field with respect to a preset arrival angle in the vicinity. The weights of the replica fields distributed at uniform angle intervals, which are used for linear interpolation, are additionally estimated by the SBL. The second method is more robust against basis mismatch than the existing SBL method. However, its performance is inferior to that of the first method. Subsequently, Das and Sejnowski (2017) extended the Taylor series-based off-grid sparse Bayesian arrival angle estimation method to include the broadband signals. This method was applied to the measured data. As shown in Fig. 3, a more reliable estimation of the target arrival angle was achieved by utilizing the common incident angle information of the target signal having various frequency components rather than using individual incident angle information.
In the case of an SBL-based beamforming technique using multiple measurements over time, the arrival angle of a target is estimated without considering the correlation of adjacent measurements. Zhang and Rao (Zhang and Rao, 2011; Zhang and Rao, 2013) extended the existing SBL technique to consider the temporal correlation of the target signal observed in the line array signal at the adjacent time. They verified that this method outperformed the other techniques.
Furthermore, in one of the techniques for estimating the target arrival angle in air, the images obtained by combining the STFT of the acoustic signal measured using the microphone array and the phase component according to the frequency in a specific time frame were used as input values for a convolutional neural network (CNN) (Chakrabarty and Habets, 2017). This technique was able to estimate the arrival angle of a signal without generating a replica field based on an understanding of the physical properties. It can also be applied to signals measured with a line array that is installed underwater. However, to date, the estimation methods of the arrival angle of an underwater target using machine learning have been developed by modifying the update rule used in SBL according to the particular scenario, with SBL as the basic framework, as described in the examples of previous studies. This is because it is challenging to obtain the underwater measurement signals necessary for learning, unlike in the case of air. However, further research is likely to be conducted in the future on the automatic extraction of the arrival angle estimation rule from the data with higher availability of the signal data necessary for learning.
In target localization, the wave propagation phenomenon in the underwater waveguide considering the sound speed profile, properties of the seafloor, and bathymetry are reflected. Furthermore, the replica field on the line array is calculated according to the location of the potential sound source. The results are compared with those of the measured field. This is called matched field processing (MFP). The research on MFP has grown rapidly because of the development of an acoustic propagation model that can simulate a real sound field in a specified marine environment. MFP is still used as a method of localizing underwater sound sources. However, there is a limitation in its use: the accuracy of the replica field is lowered when inaccurate marine environment information or an inappropriate acoustic propagation model is used (Jensen et al., 2011).
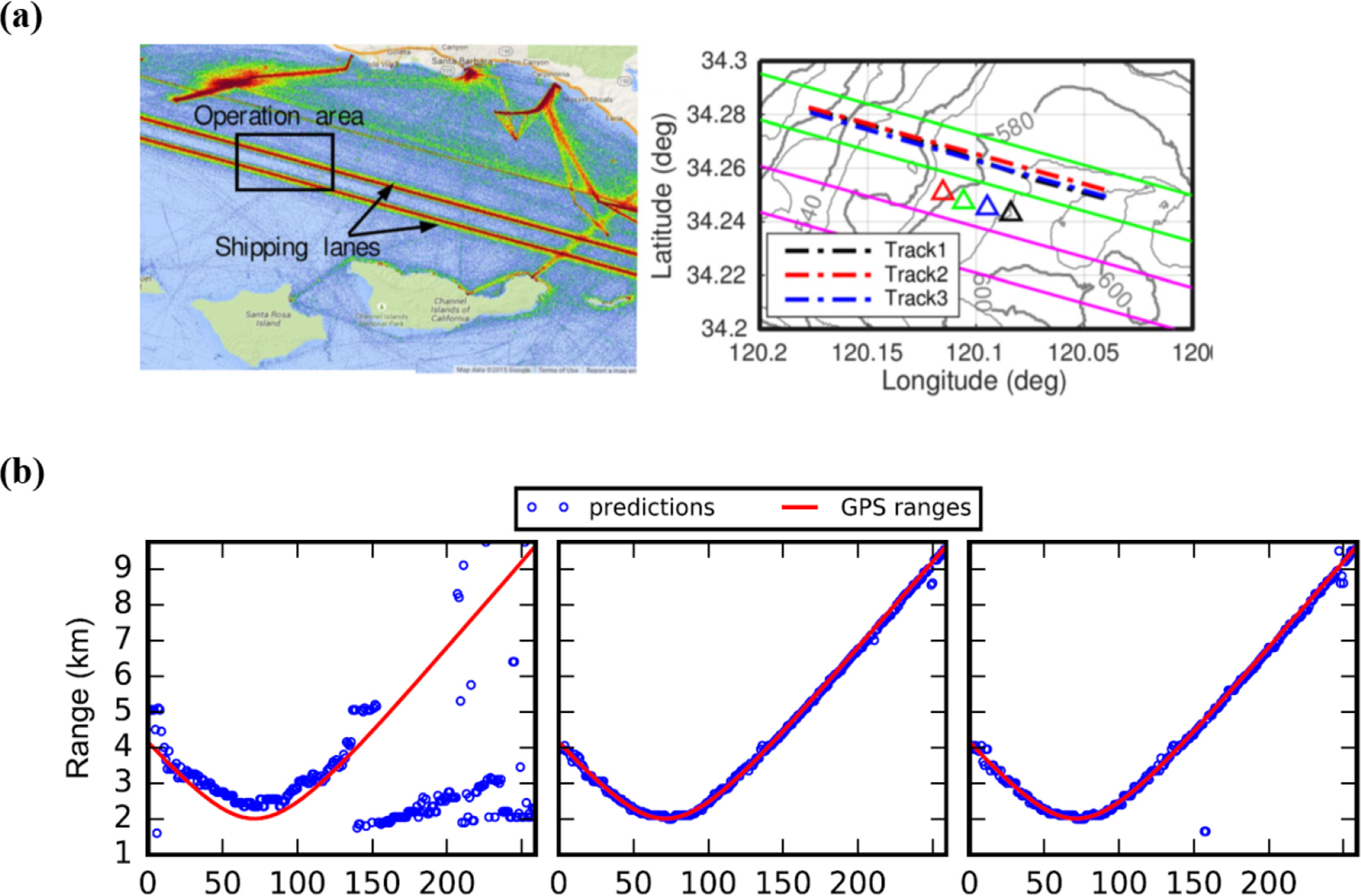
The application of machine learning to underwater sound source localization is known to have started in approximately the early 1990s (Ozard et al., 1991; Zion et al., 1991). These studies trained highly shallow feedforward neural networks (FNN) with simulation or measurement data and differentiated the range and depth information of underwater sound sources. The machine learning model used in these studies was a very simple model that considered the sum of linear weights as an output. Furthermore, in that period, there was limited understanding of how the optimal weight can be obtained using a nonlinear algorithm. This limited the amount of computation. With the development of machine learning, more advanced and improved models (compared to the initial ones) are being applied. Furthermore, an increasing number of studies are being published on the localization of underwater sound sources using data obtained directly from more complex marine environments or data simulated by models. Lefort et al. (2017) applied a regression-based localization technique for the tank experiment data and simulation data to examine whether underwater sound source localization was possible with a machine learning technique in a varying underwater channel environment. They reported on a few potential applications. In a study using in-situ measurement data, Niu et al. (2017a) directly trained the ship range estimation function with data obtained by a line array (The Santa Barbara Channel Experiment). In their study, the sound field measured by the line array and path of the ship sailing along a certain route were used as the training data, as shown in Fig. 4(a). At this time, several ships were operating on the same route, and specific ship noise and the corresponding route were used for training. Other ship noises were used for testing the performance of the proposed machine learning-based ship range estimation technique. In particular, ship noise had multiple frequency components in the low frequency band. Furthermore, the extracted vectors for each frequency were concatenated and used as the final input vector such that all the frequency components of the ship noise could be used for ship range estimation. As mentioned earlier, the GPS-based ship route was specified according to the sound field measurement time such that the range between the ship and line array for each input vector could be determined. In the case of MFP using a replica field, the performance rapidly deteriorated as the range of the ship increased. However, the machine learning-based classifier delivered superior performance even for the distant ships (Fig. 4(b)). Subsequently, Niu et al. (2017b) applied the proposed algorithm for other data (Noise09 experiment). They investigated the performance of the machine learning-based ship range estimator according to the frequency bandwidth of the ship noise or the supervised learning method (classification and regression). The method of classification with the use of multiple frequencies delivered superior results.
Furthermore, occasionally, in cases such as the operation of a passive SONAR system for military purposes, it is more important to accurately evaluate specific information, such as the depth of the target, rather than its overall spatial information. This is because the surface vessel and submarine can be distinguished according to the depth. This is another example where a simulated sound field based on an acoustic propagation model is mainly used (Conan et al., 2016; Conan et al., 2017; Liang et al., 2018). In particular, Conan et al. (Conan et al., 2017) conducted a study to distinguish the depth of a sound source by using the propagation characteristics of sound waves in a specified environment. In their study, the normal mode method was used, which is one of the representative acoustic propagation models. The depth of the sound source was extracted by converting the measurement sound field into the mode space. They verified that the sound source depth can be estimated with higher accuracy using this approach based on binary classification, compared to using MFP. In contrast, Choi et al. (Choi et al., 2019) conducted a study to formulate a rule for estimating the depth of a sound source directly from the measured data using machine learning without a physical understanding of the propagation characteristics of the waves (Choi et al., 2019). In their study, the covariance matrix of the sound field measured in the vertical line array (VLA) and the mode space covariance matrix were used as the input values for machine learning. The mode space covariance matrix is the covariance of the space vector, which is a transformation of the sound field measured in the line array into the mode space based on the normal mode method. They derived a binary classification function for classifying surface vessel and submarine noises through representative machine-learning algorithms such as random forest, SVM, FNN, and CNN. In particular, most of the combinations using real/imaginary parts of the covariance matrix as input values exhibited high accuracy. For these studies on the sound source depth classification based on machine learning, a line array measurement field was required for learning. In their study, to overcome the challenge of acquiring a sufficient amount of actual measurement acoustic data necessary for learning in an underwater environment, simulation sound field results were used that had been obtained using the normal mode method in a specified marine environment. At this time, simulated sound fields were used for training and testing that had been generated in various scenarios by varying the range and depth of the source and signal-to-noise ratio.
While estimating the ship range using a machine-learning technique, such as FNN, the classifier may be overfitted to the training data as the learning process is repeated. This may not yield superior performance on the test data. Chi et al. (2019) prevented the classifier from being overfitted to the training data by adding regularization to the test data while training on ship range estimation. As the input, they used the covariance matrix of a vectorized sound field proposed by Niu et al. (2017a). In their study, with reference to the line array, the linear relationship between the range of a ship sailing at constant speed and the measurement time was optimized for each learning process. By using the optimized linear relationship and estimated range error as a regularization of the cost function, the study verified that the method prevented the classifier from being overfitted to the training data. It also verified that the classifier exhibited superior generality, compared to the MFP or the overfitted classifier.
While estimating the location of a sound source by applying FNN, it is necessary to train the weight and bias of all the layers connecting the input and output values based on the specified learning data. Wang and Peng (2018) extracted a spread factor that determined the probability distribution of data using a generalized regression neural network based on the data and performed localization of a sound source. In this case, as in the previous study, the normalized covariance matrix of the sound field measured by a VLA was used as the input value. In addition, a supervised learning method was applied that assigned range information to all the sound fields at the training stage. Thus, their study derived an algorithm that could estimate the location of a sound source by determining a spread factor that could provide the best probabilistic description of the training data with the class information. The proposed algorithm was applied to the Swellex-96 experiment data. This revealed that the method was superior to sound source localization using FNN or MFP.
In practice, the neural network-based sound source range estimation algorithm in underwater acoustics has a limitation: the weight and bias must be trained using a limited number of sound fields because of the deficiency of data. To address this problem, Wang et al. (2019a) proposed a deep transfer learning method. In their study, a simulated sound field was generated using an acoustic propagation model under various ocean environments where the ship range was to be estimated. Then, the simulated sound field was normalized according to the line array sensor, and the frequency and sound source range was estimated based on a CNN that used the normalized field as the input image for training. In addition, a limited amount of in-situ measurement data was used to fine-tune the weight and bias of the CNN that first underwent training through a simulated sound field. This deep transfer learning method was applied to the data measured in the deep-sea environment near China. The results verified that the method outperformed the existing MFP or CNN approaches based on deep learning.
Meanwhile, the underwater MFP works similar to the beamforming technique in terms of signal processing. The exception is that in the former, the replica field calculated for the line array according to the location of the sound source is generated by reflecting the sound wave propagation in the underwater waveguide. Gemba et al. (2019) used SBL, a machine-learning algorithm, to estimate sound-source location with high resolution (depth and range from the line array). They applied the SBL-based MFP to both the simulated and actually measured sound fields and demonstrated its effectiveness. In addition, Huang et al. (2018) used a different type of DNN for the localization of a sound source. The crucial difference between the two proposed DNNs is in the presence of a direct design of features to be used for learning. In the first method using the directly designed features, the eigenvalues of the covariance matrix of the sound field observed with the line array were defined as the features, and these were combined with the neural network to localize the sound source. In particular, a time delay neural network was used to consider the temporal relationship of the measured field. Hence, the past and future (predicted) sound fields were used as the input values to estimate the present position of the measured field. In their study, regression-based supervised learning was used because the location information of the sound field used at the training stage was known, and the location of the sound source in a continuous space was derived. Accordingly, the objective function of this machine-learning technique was defined based on the distance between the estimated and actual sound-source locations. In the second method, the time-series signals measured by various sensors in the line array were used as the input values. Similar to a CNN, the filter for the sound source localization was automatically trained based on data. Furthermore, the features according to the purpose were automatically extracted and combined with an FNN to localize the sound source. Their study verified that this DNN-based sound source-localization algorithm outperformed the conventional MFP. In particular, the first method using directly designed features delivered the most superior performance, and the performance was evaluated under many scenarios. The performance of the sound source-localization algorithm based on machine learning was lowered when the ocean environment of the training data was different from that of the test data (e.g. difference in the bathymetry). This performance degradation can be reduced by training with data acquired from various environments.
As described earlier, underwater sound-source localization based on conventional MFP or machine learning uses spatially sampled sound pressure such as sound fields measured by a line array. Meanwhile, a study investigated the source localization by using the sound pressure measured by a sensor and utilizing broadband source signals with a machine-learning algorithm (Niu et al., 2019). In their study, the absolute vector of the sound pressure for each frequency was normalized and used to utilize the sound pressure measured in various frequency bands. In addition, when the magnitude of the sound source was frequency dependent, to reduce the effect of the sound source magnitude on the sound source localization, the above process was repeated at predetermined frequency-band intervals. This information was derived from the measured sound pressure and then applied to a DNN. The training for range information exploration was conducted by dividing into two stages depending on the range interval. Furthermore, an acoustic propagation model was used to generate large amount of acoustic data that was necessary for the training in two stages. This sound source-localization algorithm was applied to the data measured in the Yellow Sea. It delivered superior localization performance, compared to the performance of MFP.
In this paper, we have reviewed the history and evolution of passive SONAR applications from the studies employing conventional techniques to the research employing recent machine-learning techniques for target detection, classification, and localization.
In a passive SONAR system, target detection/classification uses and integrates multiple features from time, frequency, and other domains to overcome the limitations of the probability distribution analysis and threshold comparison-based techniques for signals that contain both the target signal and noise. The information of the target is extracted from the measured signals. The target identifier models are of various types in terms of use, ranging from simple binary classifiers to models imitating human sound perception capabilities and deep learning models capable of multiple classifications. These models are combined with conventional theoretical models. In addition, these complement each other in terms of the sound sources, environmental characteristics, and research objectives for continuous development. Various techniques are used for localization in passive SONAR systems, ranging from the conventional localization techniques represented by array signal processing and MFP to classification and regression models using compressive sensing, SBL, and machine- learning techniques based on measurement data. However, the satisfactory performance of these machine-learning techniques can be ensured only when sufficient quality data are secured. Therefore, methods are applied for simultaneously using the actual measurement data and data generated from the acoustic models. Although this paper describes techniques for utilizing machine learning only for passive SONAR systems, these techniques can be directly applied to active SONAR systems. This aspect as well as the passive SONAR system for detecting and classifying target signals will be discussed in the future.
Notes
Author ORCIDs and Contributions
Fig. 1
Overview of the training (a) and testing (b) procedures. During training, three kinds of features are computed for each example in the training set. During testing, the feature vectors for each transient class are computed, and a classifier is used to determine the confidence value for each class model. The class with the highest confidence value is considered as the label of the test example (Tucker and Brown, 2005).
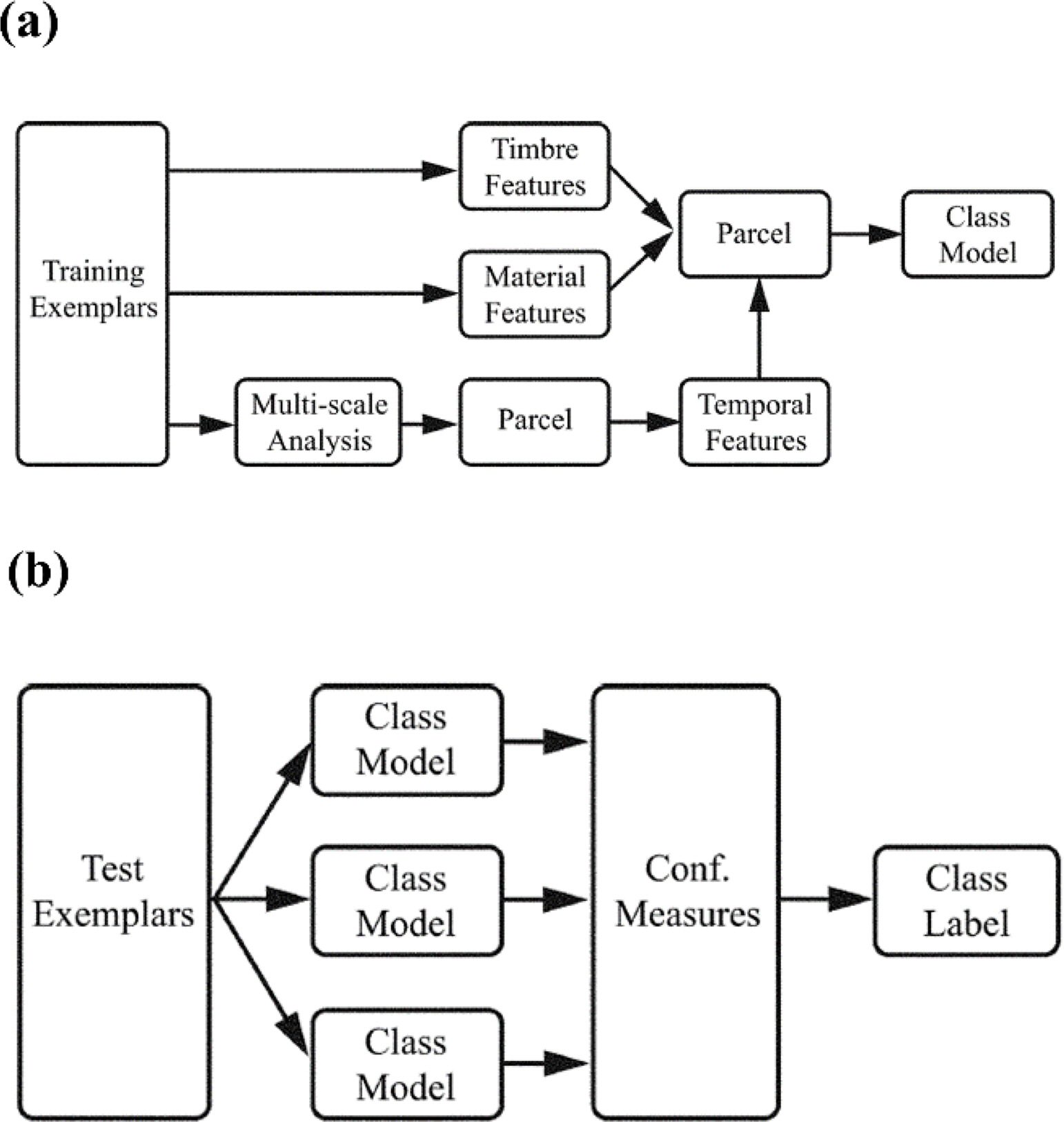
Fig. 3
Comparing the conventional beamforming (CBF) spectra (denoted in blue) from two frequency bins [(a) 2625 Hz and (b) 2725 Hz] and the incoherent average of the CBF spectra from all frequency bins (c) with the estimated spectrum [denoted in dotted black in (a), (b), and (c)] by the proposed wideband direction-of-arrival estimation algorithm (Das and Sejnowski, 2017).
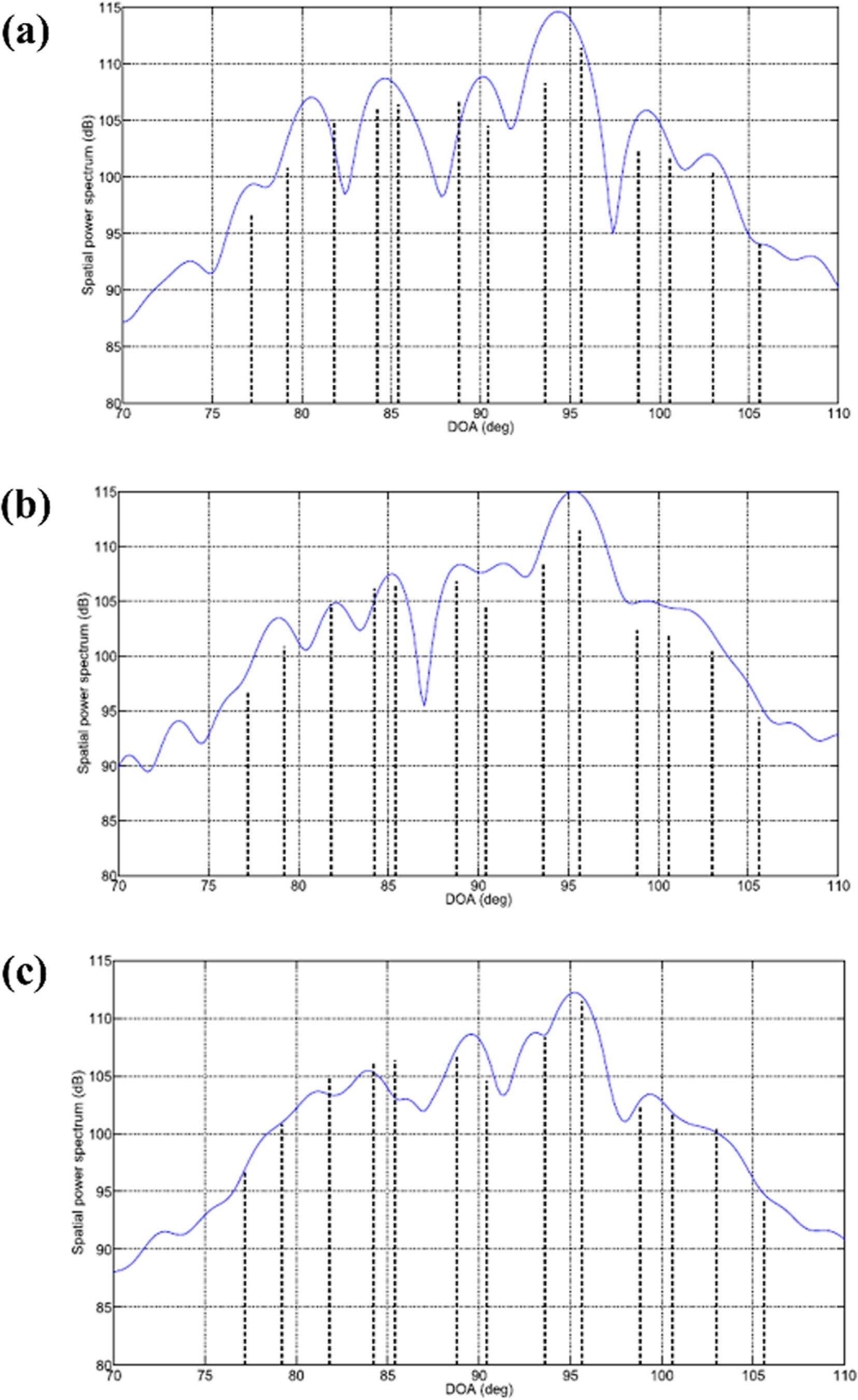
Fig. 4
(a) Operation area and two shipping lanes in Santa Barbara Basin and the experiment geometry with three cargo ships transiting the operation area. The vertical line arrays are denoted by triangles. (b) Localization results with frequency band 53–200 Hz by Bartlett MFP (left); SVM classifier (middle); and FNN classifier (right) (Niu et al., 2017a).
References
Allen, N., Hines, PC., & Young, VW. (2011). Performances of Human Listeners and an Automatic Aural Classifier in Discriminating between Sonar Target Echoes and Clutter. The Journal of the Acoustical Society of America, 130(3), 1287-1298. https://doi.org/10.1121/1.3614549


Chakrabarty, S., & Habets, EA. (2017). Broadband DOA Estimation Using Convolutional Neural Networks Trained with Noise Signals. Paper Presented at the 2017 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA). https://doi.org/10.1109/WASPAA.2017.8170010

Chi, J., Li, X., Wang, H., Gao, D., & Gerstoft, P. (2019). Sound Source Ranging Using a Feed-forward Neural Network with Fitting-based Early Stopping. The Journal of the Acoustical Society of America, 146(3), EL258-EL264 https://doi.org/10.1121/1.5126115.


Choi, J., Choo, Y., & Lee, K. (2019). Acoustic Classification of Surface and Underwater Vessels in the Ocean Using Supervised Machine Learning. Sensors, 19(16), 3492. https://doi.org/10.3390/s19163492



Conan, E., Bonnel, J., Chonavel, T., & Nicolas, B. (2016). Source Depth Discrimination with a Vertical Line Array. The Journal of the Acoustical Society of America. 140(5), EL434-EL440. https://doi.org/10.1121/1.4967506


Conan, E., Bonnel, J., Nicolas, B., & Chonavel, T. (2017). Using the Trapped Energy Ratio for Source Depth Discrimination with a Horizontal Line Array: Theory and Experimental Results. The Journal of the Acoustical Society of America, 142(5), 2776-2786. https://doi.org/10.1121/1.5009449


Das, A. (2017). Theoretical and Experimental Comparison of Off-grid Sparse Bayesian Direction-of-arrival Estimation Algorithms. IEEE Access, 5, 18075-18087. https://doi.org/10.1109/ACCESS.2017.2747153

Das, A., & Sejnowski, TJ. (2017). Narrowband and Wideband Off-grid Direction-of-arrival Estimation via Sparse Bayesian Learning. IEEE Journal of Oceanic Engineering, 43(1), 108-118. https://doi.org/10.1109/JOE.2017.2660278

Donoho, DL. (2006). Compressed Sensing. IEEE Transactions on Information theory, 52(4), 1289-1306. https://doi.org/10.1109/TIT.2006.871582

Edelmann, GF., & Gaumond, CF. (2011). Beamforming Using Compressive Sensing. The Journal of the Acoustical Society of America, 130(4), EL232-EL237. https://doi.org/10.1121/1.3632046


Gemba, KL., Nannuru, S., & Gerstoft, P. (2019). Robust Ocean Acoustic Localization with Sparse Bayesian Learning. IEEE Journal of Selected Topics in Signal Processing, 13(1), 49-60. https://doi.org/10.1109/JSTSP.2019.2900912

Gerstoft, P., Mecklenbräuker, CF., Xenaki, A., & Nannuru, S. (2016). Multisnapshot Sparse Bayesian Learning for DOA. IEEE Signal Processing Letters, 23(10), 1469-1473. https://doi.org/10.1109/LSP.2016.2598550

Gerstoft, P., Nannuru, S., Mecklenbräuker, CF., & Leus, G. (2019). DOA Estimation in Heteroscedastic Noise. Signal Processing, 161, 63-73. https://doi.org/10.1016/j.sigpro.2019.03.014

Hemminger, TL., & Pao, Y-H. (1994). Detection and Classification of Underwater Acoustic Transients Using Neural Networks. IEEE Transactions on Neural Networks, 5(5), 712-718. https://doi.org/10.1109/72.317723


Huang, Z., Xu, J., Gong, Z., Wang, H., & Yan, Y. (2018). Source Localization Using Deep Neural Networks in a Shallow Water Environment. The Journal of the Acoustical Society of America, 143(5), 2922-2932. https://doi.org/10.1121/1.5036725


Jensen, FB., Kuperman, WA., Porter, MB., & Schmidt, H. (2011). Computational Ocean Acoustics. Springer Science & Business Media.
Ke, X., Yuan, F., & Cheng, E. (2018). Underwater Acoustic Target Recognition Based on Supervised Feature-Separation Algorithm. Sensors, 18(12), 4318. https://doi.org/10.3390/s18124318



Komari Alaie, H., & Farsi, H. (2018). Passive Sonar Target Detection Using Statistical Classifier and Adaptive Threshold. Applied Sciences, 8(1), 61. https://doi.org/10.3390/app8010061

Lefort, R., Real, G., & Dremeau, A. (2017). Direct Regressions for Underwater Acoustic Source Localization in Fluctuating Oceans. Applied Acoustics, 116, 303-310. https://doi.org/10.1016/j.apacoust.2016.10.005

Liang, G., Zhang, Y., Zhang, G., Feng, J., & Zheng, C. (2018). Depth Discrimination for Low-Frequency Sources Using a Horizontal Line Array of Acoustic Vector Sensors Based on Mode Extraction. Sensors, 18(11), 3692. https://doi.org/10.3390/s18113692



Murphy, SM., & Hines, PC. (2014). Examining the Robustness of Automated Aural Classification of Active Sonar Echoes. The Journal of the Acoustical Society of America, 135(2), 626-636. https://doi.org/10.1121/1.4861922


Nannuru, S., Gemba, KL., Gerstoft, P., Hodgkiss, WS., & Mecklenbräuker, CF. (2019). Sparse Bayesian Learning with Multiple Dictionaries. Signal Processing, 159, 159-170. https://doi.org/10.1016/j.sigpro.2019.02.003

Nielsen, RO. (1991). Sonar Signal Processing. Artech House.
Niu, H., Gong, Z., Ozanich, E., Gerstoft, P., Wang, H., & Li, Z. (2019). Deep-learning Source Localization Using Multi-Frequency Magnitude-only Data. The Journal of the Acoustical Society of America, 146(1), 211-222. https://doi.org/10.1121/1.5116016


Niu, H., Ozanich, E., & Gerstoft, P. (2017a). Ship Localization in Santa Barbara Channel Using Machine Learning Classifiers. The Journal of the Acoustical Society of America, 142(5), EL455-EL460. https://doi.org/10.1121/1.5010064


Niu, H., Reeves, E., & Gerstoft, P. (2017b). Source Localization in an Ocean Waveguide Using Supervised Machine Learning. The Journal of the Acoustical Society of America, 142(3), 1176-1188. https://doi.org/10.1121/1.5000165


Ozard, JM., Zakarauskas, P., & Ko, P. (1991). An Artificial Neural Network for Range and Depth Discrimination in Matched Field Processing. The Journal of the Acoustical Society of America, 90(5), 2658-2663. https://doi.org/10.1121/1.401860

Park, Y., Seong, W., & Choo, Y. (2017). Compressive Time Delay Estimation off the Grid. The Journal of the Acoustical Society of America. 141(6), EL585-EL591. https://doi.org/10.1121/1.4985612


Shin, FB., & Kil, DH. (1996). Full-spectrum Signal Processing Using a Classify-before-detect Paradigm. The Journal of the Acoustical Society of America, 99(4), 2188-2197. https://doi.org/10.1121/1.415407

Tipping, ME. (2001). Sparse Bayesian Learning and the Relevance Vector Machine. Journal of Machine Learning Research, 1, Jun. 211-244.
Tucker, S., & Brown, GJ. (2005). Classification of Transient Sonar Sounds Using Perceptually Motivated Features. IEEE Journal of Oceanic Engineering, 30(3), 588-600. https://doi.org/10.1109/JOE.2005.850910

Wang, W., Ni, H., Su, L., Hu, T., Ren, Q., Gerstoft, P., & Ma, L. (2019a). Deep Transfer Learning for Source Ranging: Deep-sea Experiment Results. The Journal of the Acoustical Society of America, 146(4), EL317-EL322. https://doi.org/10.1121/1.5126923


Wang, X., Liu, A., Zhang, Y., & Xue, F. (2019b). Underwater Acoustic Target Recognition: A Combination of Multi-Dimensional Fusion Features and Modified Deep Neural Network. Remote Sensing, 11(16), 1888. https://doi.org/10.3390/rs11161888

Wang, Y., & Peng, H. (2018). Underwater Acoustic Source Localization Using Generalized Regression Neural Network. The Journal of the Acoustical Society of America, 143(4), 2321-2331. https://doi.org/10.1121/1.5032311


Xenaki, A., & Gerstoft, P. (2015). Grid-free Compressive Beamforming. The Journal of the Acoustical Society of America, 137(4), 1923-1935. https://doi.org/10.1121/1.4916269


Xenaki, A., Gerstoft, P., & Mosegaard, K. (2014). Compressive Beamforming. The Journal of the Acoustical Society of America, 136(1), 260-271. https://doi.org/10.1121/1.4883360


Yang, H., Lee, K., Choo, Y., & Kim, K. (2020). Underwater Acoustic Research Trends with Machine Learning: General Background. Journal of Ocean Engineering and Technology, 34(2), 147-154. https://doi.org/10.26748/2020.015


Yang, H., Shen, S., Yao, X., Sheng, M., & Wang, C. (2018). Competitive Deep-belief Networks for Underwater Acoustic Target recognition. Sensors, 18(4), 952. https://doi.org/10.3390/s18040952



Yang, L., & Chen, K. (2015). Performance and Strategy Comparisons of Human Listeners and Logistic Regression in Discriminating Underwater Targets. The Journal of the Acoustical Society of America, 138(5), 3138-3147. https://doi.org/10.1121/1.4935390


Young, VW., & Hines, PC. (2007). Perception-based Automatic Classification of Impulsive-source Active Sonar Echoes. The Journal of the Acoustical Society of America, 122(3), 1502-1517. https://doi.org/10.1121/1.2767001


Zhang, Z., & Rao, BD. (2011). Sparse Signal Recovery with Temporally Correlated Source Vectors Using Sparse Bayesian Learning. IEEE Journal of Selected Topics in Signal Processing, 5(5), 912-926. https://doi.org/10.1109/JSTSP.2011.2159773

Zhang, Z., & Rao, BD. (2013). Extension of SBL Algorithms for the Recovery of Block Sparse Signals with Intra-block Correlation. IEEE Transactions on Signal Processing, 61(8), 2009-2015. https://doi.org/10.1109/TSP.2013.2241055

Zion, B., Beran, M., Chin, S., & Howard, JJ. (1991). A Neural Network Approach to Source Localization. The Journal of the Acoustical Society of America, 90(4), 2081-2090. https://doi.org/10.1121/1.401635

- TOOLS
-
METRICS

-
- 22 Crossref
- Scopus
- 7,393 View
- 519 Download
- Related articles in JOET
-
Underwater Acoustic Research Trends with Machine Learning: General Background2020 April;34(2)