|
 |
- Search
| J. Ocean Eng. Technol. > Volume 35(3); 2021 > Article |
|
Abstract
Current industrial practices and approaches are simplified and do not describe the actual behavior of plated elements of offshore topside structures for safety design due to fires. Therefore, it is better to make up for the defective methods with integrated fire safety design methods based on fire resistance characteristics such as residual strength capacity. This study numerically investigates the residual strength of steel stiffened panels exposed to hydrocarbon jet fire. A series of nonlinear finite element analyses (FEAs) were carried out with varying probabilistic selected exposures in terms of the jet fire location, side, area, and duration. These were used to assess the effects of exposed fire on the residual strength of a steel stiffened panel on a ship-shaped offshore structure. A probabilistic approach with a feasible fire location was used to determine credible fire scenarios in association with thermal structural responses. Heat transfer analysis was performed to obtain the steel temperature, and then the residual strength was obtained for the credible fire scenarios under compressive axial loading using nonlinear FEA code. The results were used to derive closed-form expressions to predict the residual strength of steel stiffened panels with various exposure to jet fire characteristics. The results could be used to assess the sustainability of structures at risk of exposure to fire accidents in offshore installations.
Ships and ship-shaped offshore installations can be exposed to hydrocarbon fires and explosions. These dangers have serious consequences for human health, structural safety, and the surrounding environment (Czujko, 2001; HSE, 2000). Current industrial practices develop an initial design prediction to prevent and mitigate the escalation of accidental events, which requires appropriate understanding of related design methods and effectiveness. The safety concerns are reflected in current regulations and guidelines for qualitative or quantitative fire and explosion risk analysis (QRA) and risk management (Vinnem, 2007; NORSOK, 2010; Nolan, 1996; Paik and Czujko, 2011; Seo et al., 2017).
In current fire safety design (Franssen and Real, 2010; Purkiss, 2006), the fire scenario of steel structures is generally considered as fire heat exposed to the surface of structural members with the same intensity. For the thermal structural response, heat intensities are assumed to remain the same throughout the exposed fire duration. However, this method tends to be simplified and does not describe the actual behavior, which accompanies time, space characteristics, radiation, and convection. The outcome of these assumptions results in time-release changes of flammable materials in fire accidents. Current industrial practices in fire safety design methods consist of various applicable of international/national regulations, standards, and guidance. Therefore, it is better to make up for the defective methods with integrated fire safety design methods based on fire resistance characteristics such as the residual strength capacity. An essential integrated fire safety design method requires fire computational fluid dynamics (CFD) simulations and thermal finite element analysis (FEA) simulation (Paik et al., 2010; Shetty et al., 1998).
For these reasons, previous researchers have suggested procedures or guidance for fire risk analysis that consist of probabilistic-based fire accidental design loads, fire CFD analyses, and nonlinear FE analyses. Applications for ships and offshore installations have also been suggested and examined (Soares et al., 1998, Paik et al., 2013; Kim et al., 2013; Salem et al., 2016). Most of the methodologies assumed only one-dimensional steel structures because the structures consist of primary structural strength members (beams, columns, etc.). However, ship-shaped offshore structures and the topsides of an offshore installation include living quarters, process modules, drilling modules, etc., which are mostly assembled or welded steel plates with primary structural strength members. Therefore, their structural layout and arrangement have to be considered regarding functional, performance, and safety requirements for the design philosophy.
The most common fire accident case in offshore platforms is when a pressurized leak gas causes a jet fire. The main constituent is hydrocarbon gas materials in offshore installations, which can lead to various fire characteristics. Therefore, it is necessary to study the jet fire load characteristics with flammable hydrocarbon material in topside process modules of platforms (Sun et al., 2017). However, current approaches and studies of fire exposure areas and fire duration only consider major fire accidents (Fig. 1(a)) in safety design and management, but minor fire accidents (Fig. 1(b)) should also be considered for structural sustainability in operating conditions.
Current industrial practices and approaches provide only limited information on plated elements of offshore topside structures for safety design and assessment of sustainability due to fires. Therefore, the effect of residual strength capacity and the thermal response behavior of plated structures during a fire should be identified. This study looks at the residual strength of plated panels under fire load by numerical analysis using a nonlinear finite element method (FEM). The results were used to derive closed-form expressions to predict the residual strength of steel stiffened panels with various exposures to jet fire areas and times.
Fig. 2 shows the proposed approach for determining residual strength and fire damage index in this study. Credible scenarios for all possible exposed fire scenarios for a target structure were selected using probabilistically characterized variables that affect the structural damage. A fire damage index in a credible scenario is identified as a phenomenological fire exposure characteristic, such as location and time. The residual strength (ultimate strength) capacity of stiffened panel structures in a fire scenario can be analyzed by appropriate numerical tools. The proposed procedure was conducted for each of the selected credible scenarios in realistic fire accidents, and a diagram can show the reduction or sustainable structural strength (residual strength) and the fireŌĆÖs effect on the damage index. This diagram serves as a first-cut design evaluation and is used to identify the acceptance criteria for ships and offshore installationsŌĆÖ safety design against fire accidental damage.
Once an objectŌĆÖs structural topology has been defined with geometrical and material properties, the type of fire load should be identified. Fire is a complex chain reaction where fuel is combined with oxygen, generating heat, smoke, and light. Most hydrocarbon fires can be divided into jet fires and pool fires for health, structural safety, and environmental safety requirements for a design philosophy. A jet fire occurs when a flammable liquid or gas is ignited after its release from a pressurized, punctured vessel or pipe and is a turbulent diffusion flame resulting from the combustion of a hydrocarbon fuel continuously released with some significant momentum in a particular direction. A pool fire occurs when a flammable liquid leaks from a vessel or pipeline to form a fluid reservoir, which then ignites. Common characteristics of a hydrocarbon jet fire are a turbulent flame, a high heat flux, and the capability of eroding a material that it impacts. Pool fires are turbulent diffusions, burning above an upward-facing, vaporizing liquid fuel. The vaporizing fuel has almost zero or low initial momentum. The fire load can be obtained by performing a CFD analysis or using a profile specified in the regulations, such as hydrocarbon fire and pool fire regulations (ISO, 1999). Fig. 3 shows the general profiles for hydrocarbon and pool fires.
After determining the type of fire load, the damage parameters that affect the residual ultimate strength should be characterized. The location and exposed areas of fire damage were the basic parameters used in this study. The other parameters depend on the type of damage. For example, gas temperature is a critical parameter of fire damage when calculating the residual ultimate strength of structures. CFD may be performed to calculate a more accurate damage index. CFD simulation results, such as temperature, time, and heat flux etc., may give damage parameters to calculate the residual ultimate strength of structures.
The fire damage scenarios were established via sampling techniques based on characterized damaged parameters, which were calculated using the probability density function. A small number of fire damage scenarios were selected based on scenario sampling methods, such as the Latin hypercube sampling method (LHS), etc. It was necessary to consider as many damage scenarios as possible to develop an R-D diagram that could reflect a smaller interval of random variables in a wider range of damage extent.
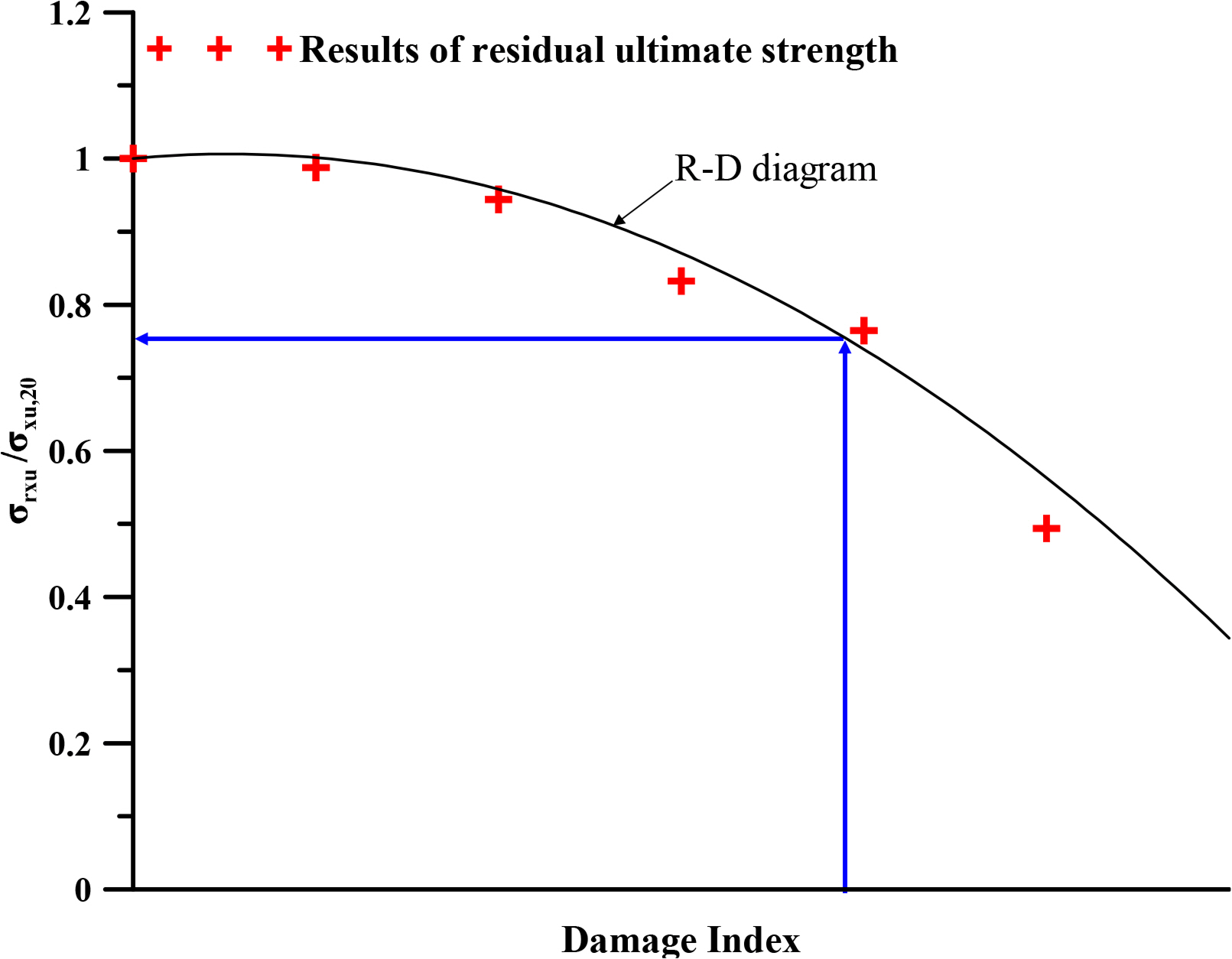
After selecting the fire damage scenarios, the fire damage index can be defined in the form of an R-D diagram. A residual strength analysis was performed for each selected fire damage scenario. The fire damage index (r/b) was determined by the ratio of the flame radius (r) and the breadth of the plate (b). Candidate methods (numerical, analytical, and experimental methods) are able to calculate the residual strength. In this study, numerical methods were most commonly applied to structural analysis as they have been found to be the most efficient (Kim et al., 2014). Once the fire damage index and the ultimate strength were simulated for the selected fire damage scenarios, the diagram was expressed in form of Fig. 4. R-D diagrams can be used to predict the residual strength with fire exposure damage.
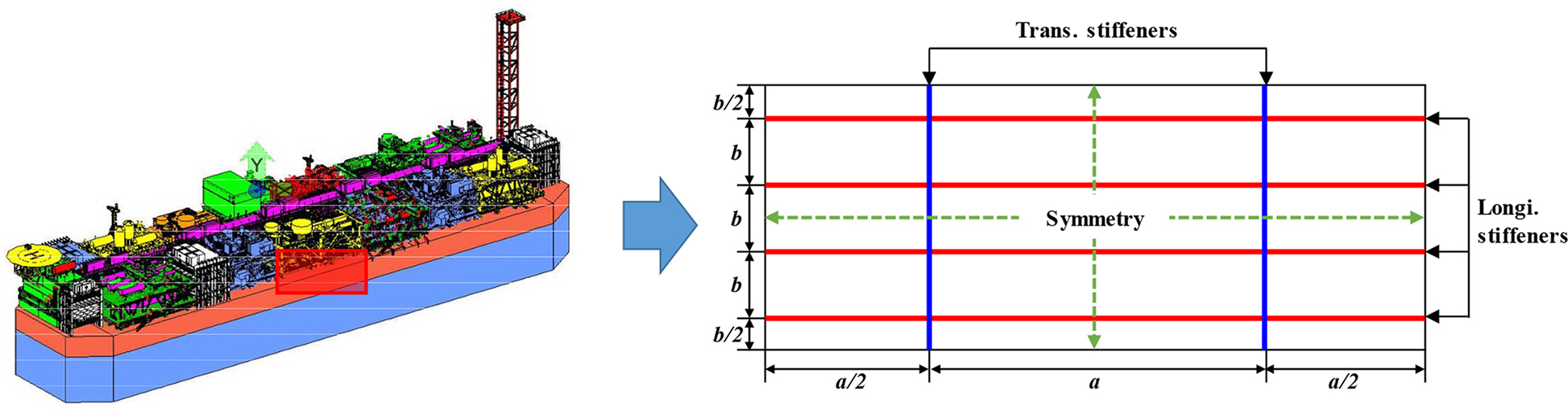
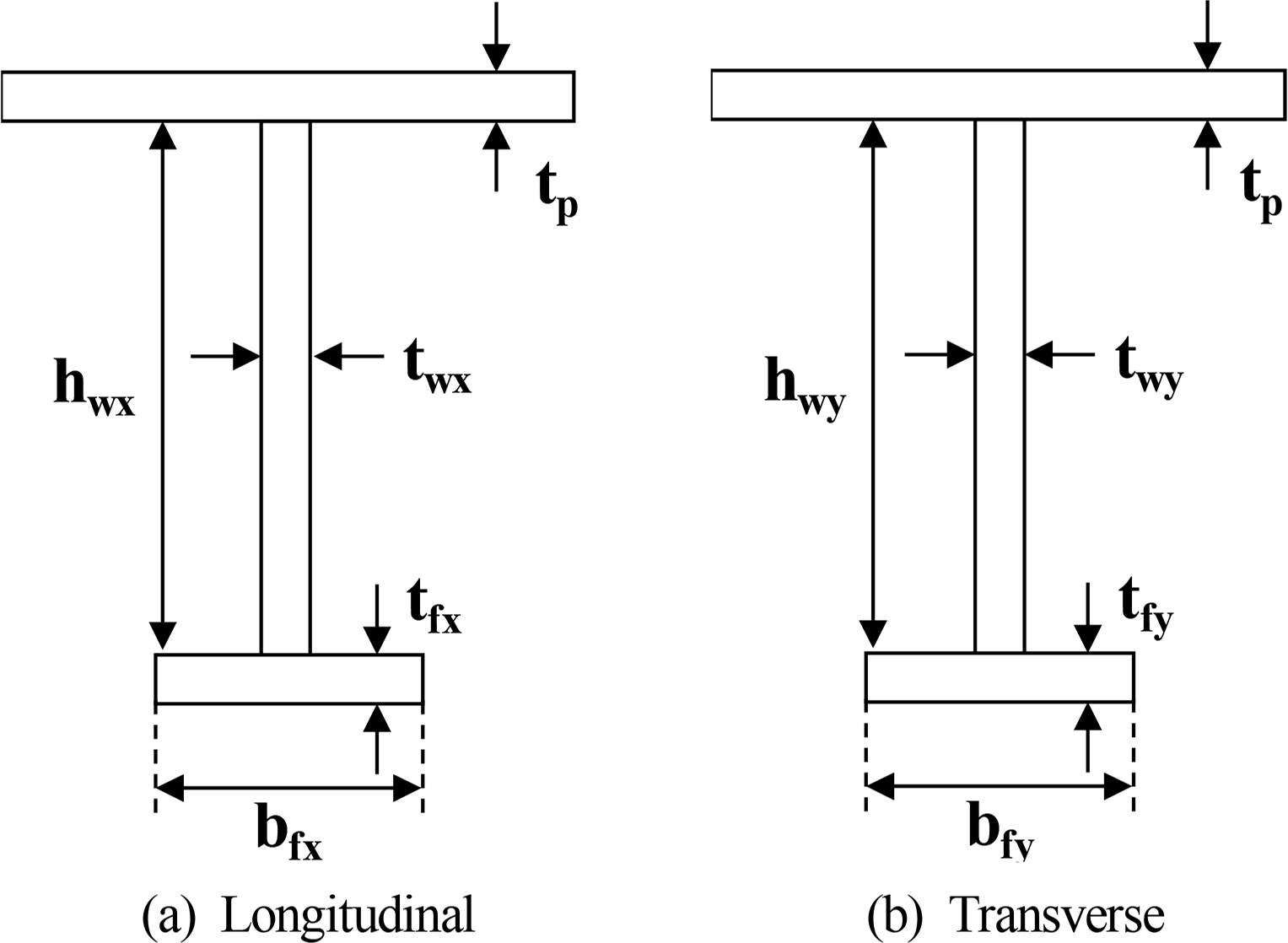
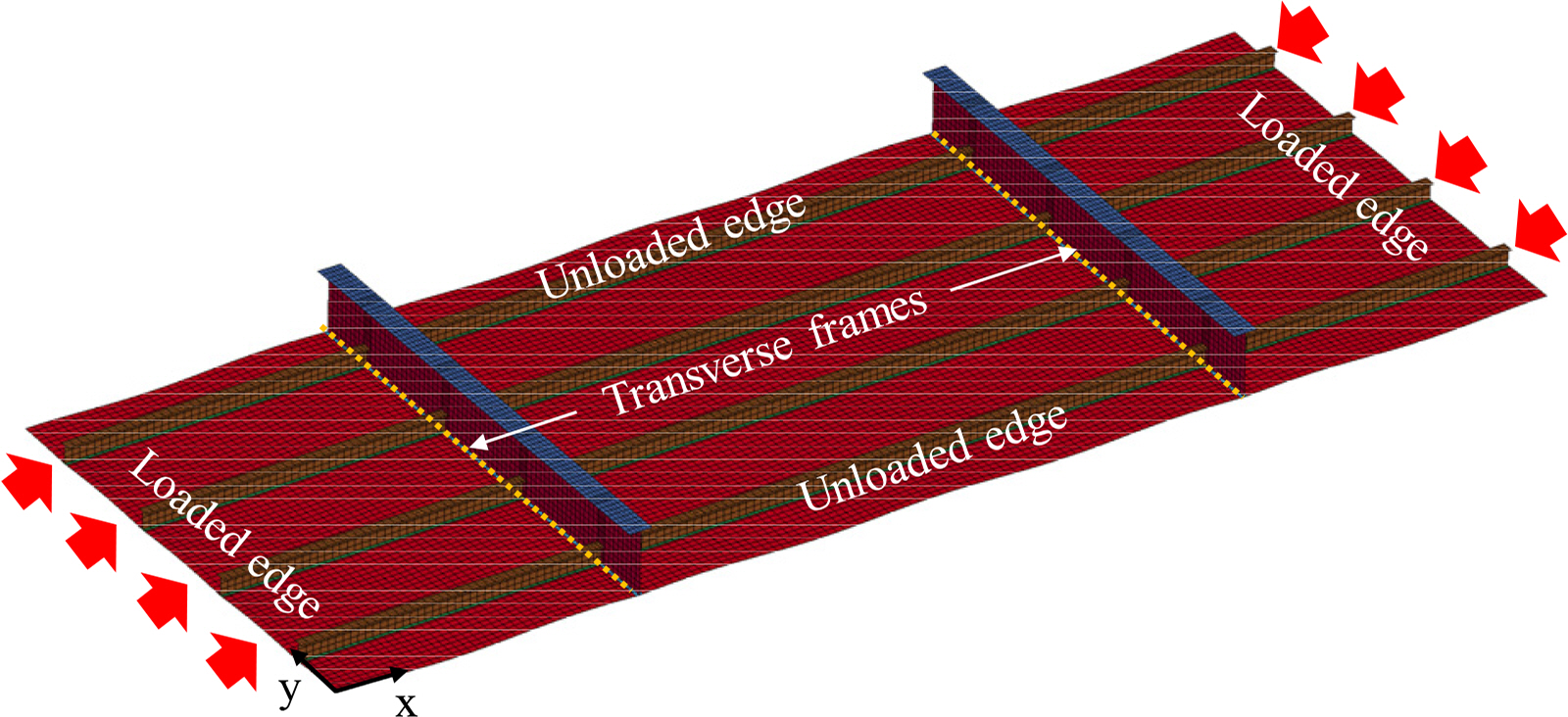
Fig. 5 shows a floating, production, storage and offloading (FPSO) structure, which is one type of ship-shaped offshore installation. Steel stiffened panels were used to construct part of the deck of the FPSO. It was supported by girders and frames along the longitudinal and transverse edges. The spacing of the stiffeners was a = 4000 mm between the transverse stiffeners and b = 800 mm between the longitudinal stiffeners. This study considered T-bars as both longitudinal and transverse stiffeners. Fig. 6 and Table 1 show the cross sections of the longitudinal and transverse stiffeners (Paik and Thayaballi, 2003).
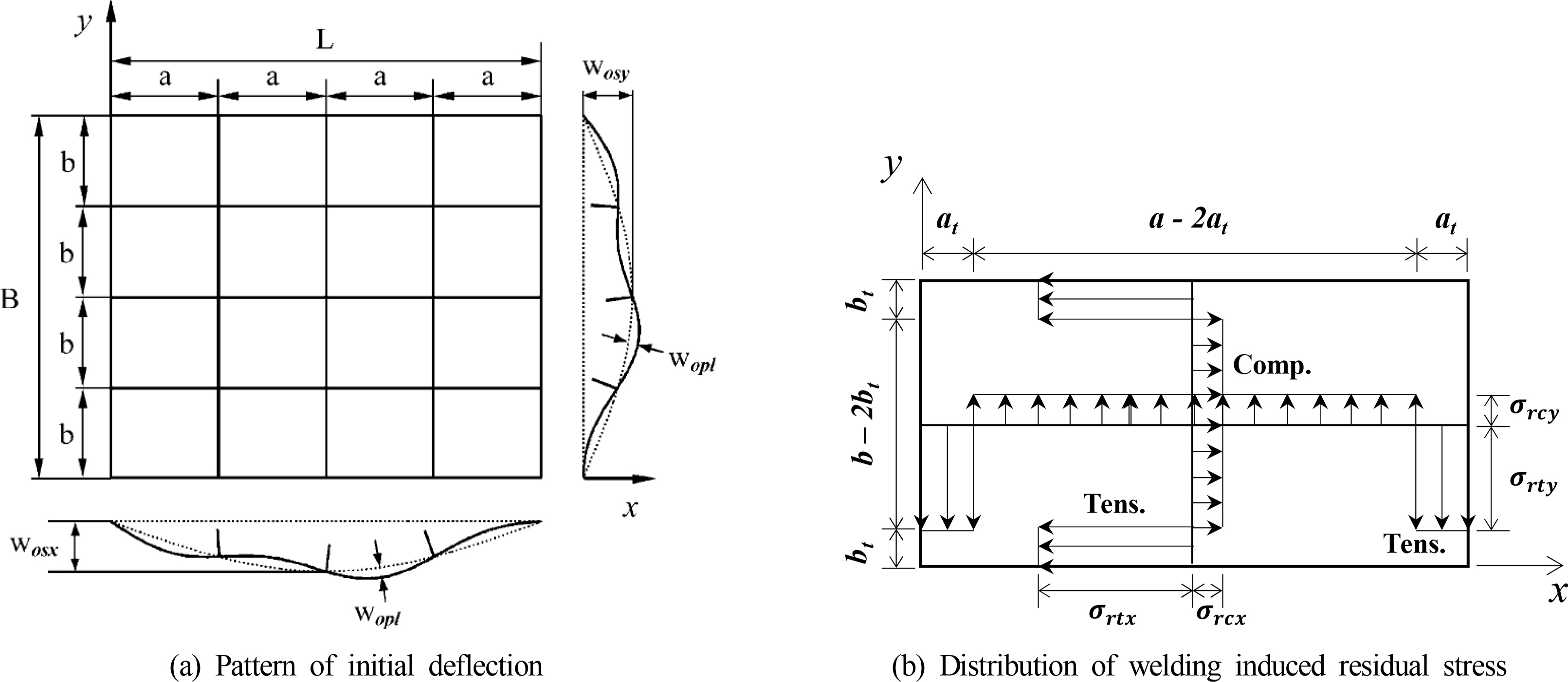
The stiffened plate panel was modeled using shell elements to perform the heat transfer analysis and nonlinear structural response analysis. The mesh size was 45 mm, and the number of four-noded shell elements was 17 in between the longitudinal stiffeners (Hughes and Paik, 2010). The stiffened plate panels are considered to have welding-induced initial deflections (in Fig. 7(a)). The initial deflections are denoted by wopl for plating between stiffeners and wosx and wosy for x- and y-stiffeners, respectively. The stiffened plate panel may also have welding-induced residual stresses. Fig. 7(b) shows the typical idealization of residual stresses in plating between stiffeners. The simplified residual stresses are considered uniform compressive residual stresses, which are denoted by Žārsx and Žārsy for x- and y-stiffeners, respectively. In this study, both initial deflection and residual stress were considered.
The fire damage parameters for the calculation of the fire damage index can be defined as follows:
In general, fire profiles can be obtained through numerical, analytical, and experimental methods. The jet and pool fire curves shown in Fig. 3 were obtained by analytical methods. With the numerical method, the temperature-time profile was calculated using CFD programs. The temperature-time profile could also be obtained by measuring the gas temperature in experiments. In this study, jet fire was calculated by the analytical method and used as the fire type. The fire duration, position, and radius of the flame were primary parameters to calculate the extent of fire damage.
A total of 120 scenarios were selected to calculate the fire damage index, and the range of each parameter was probabilistically defined. The fire duration was classified into six groups with 10 min. per group, and the probability density of each group was equal. Table 2 shows the probability of fire duration. The direction of the side exposed to fires affects the temperature and strength of structures. In this study, it was assumed that the plate was only exposed to fire as shown in Fig. 8.
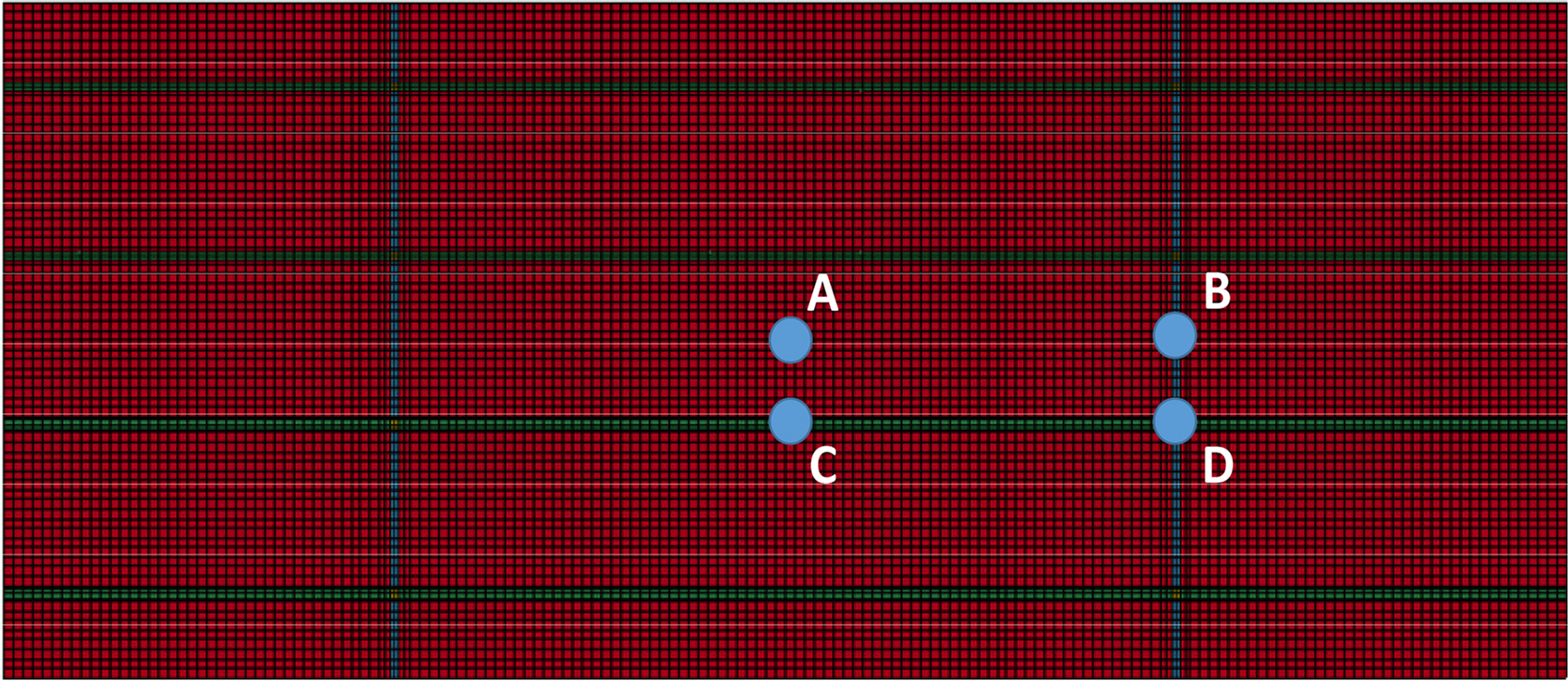
Fig. 9 shows the position of the flame center, and Table 3 represents the probability of fire position. The fire position was classified into four groups as follows:
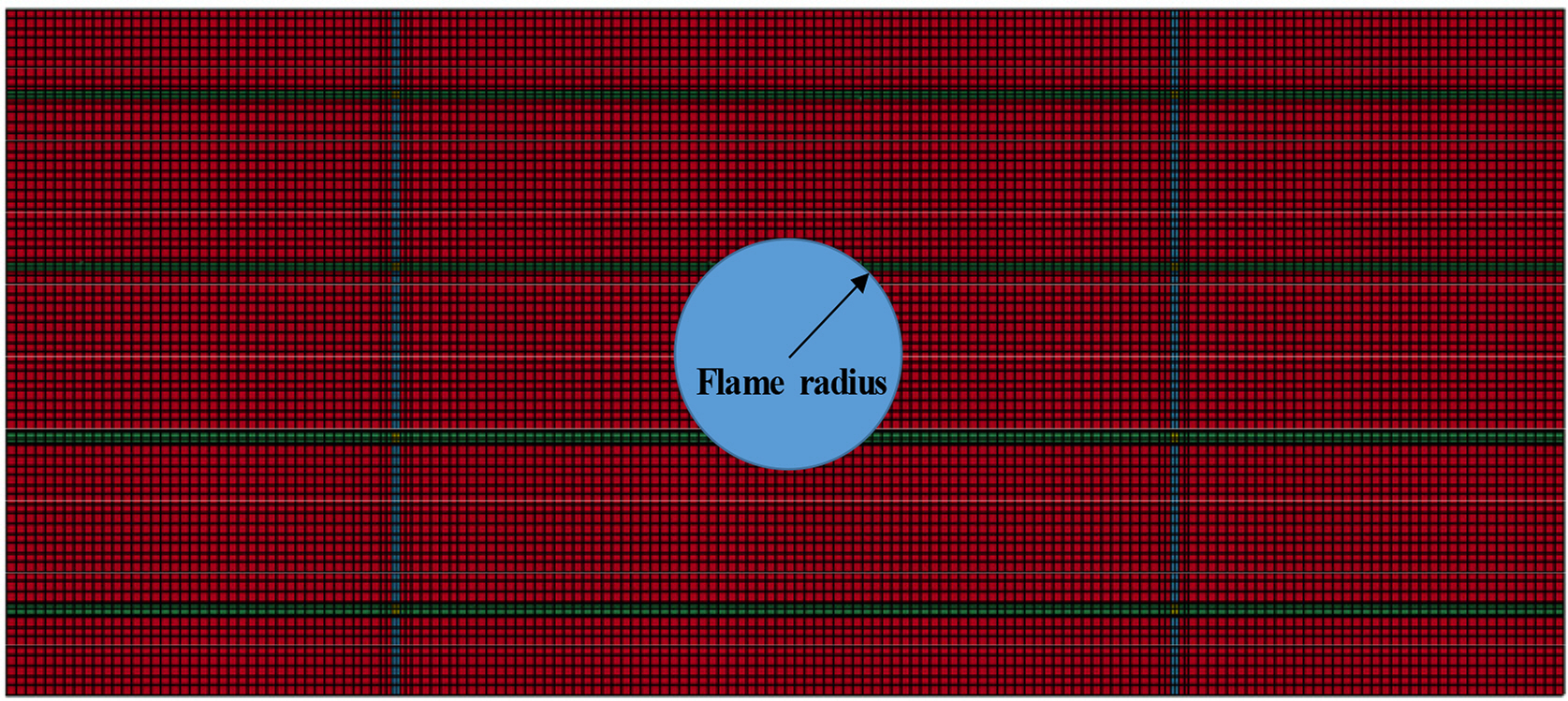
As the shape of flames resembles circles, the shape of the fire was assumed to be circular. The probabilistic characteristics of the fire area were identified based on the radius of the flame. Fig. 10 and Table 4 show the shape and probability of the fire area. Table A1 lists 120 representative fire damage scenarios using the four major parameters that were considered. The selected scenarios included all of the variables for each parameter.
The fire damage index for selected scenarios was calculated using LS-DYNA code, which uses shell elements to model the structures (ANSYS, 2018). The gas temperature did not determine the temperature of the exposed steel because of the effects of radiation and convection. Thus, a heat transfer analysis needed to be carried out to identify the steel temperature while considering the effects of radiation and convection (Kim et al., 2013).
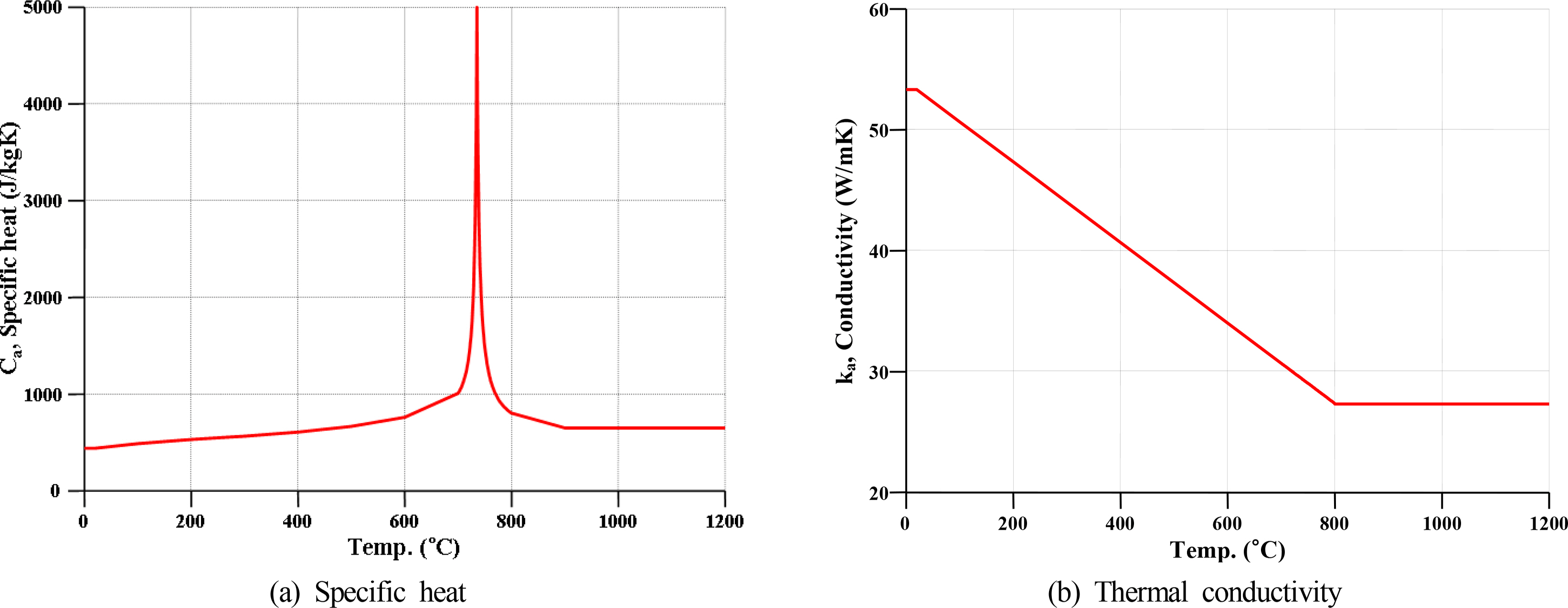
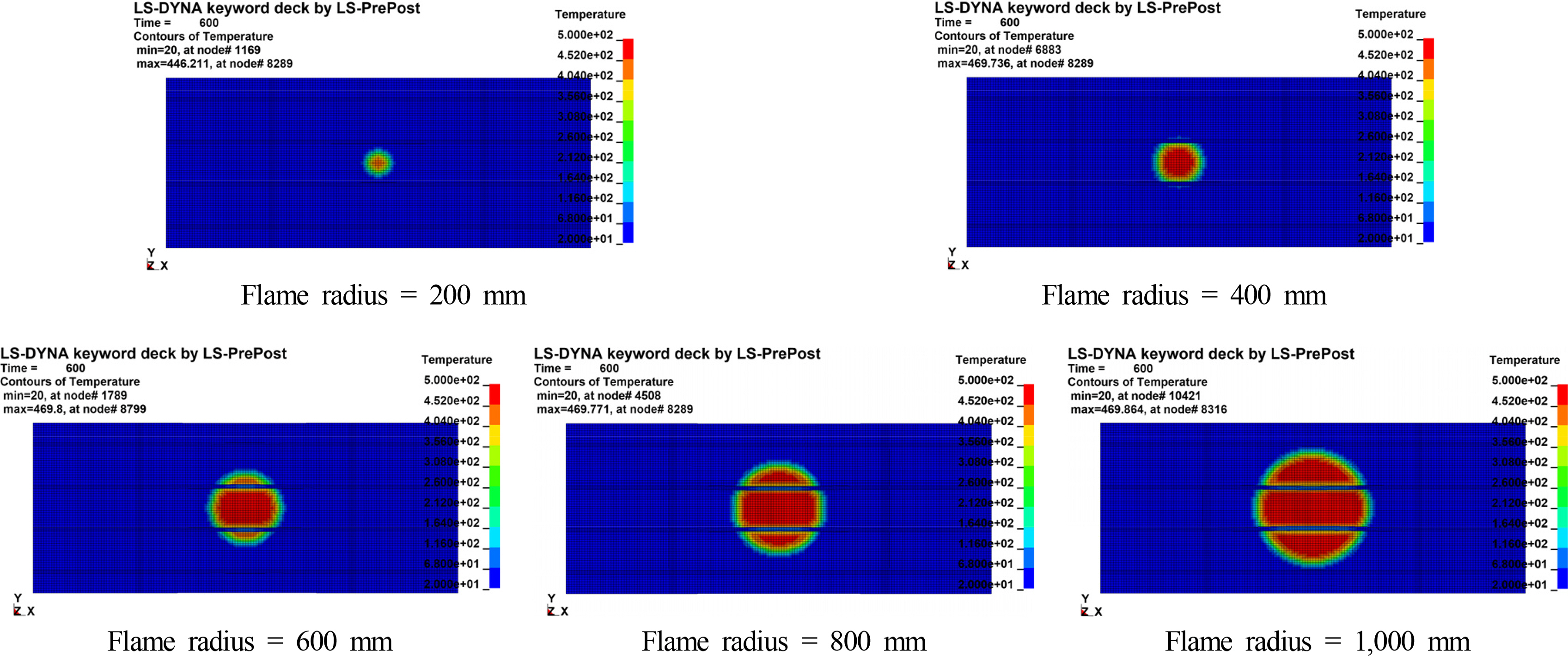
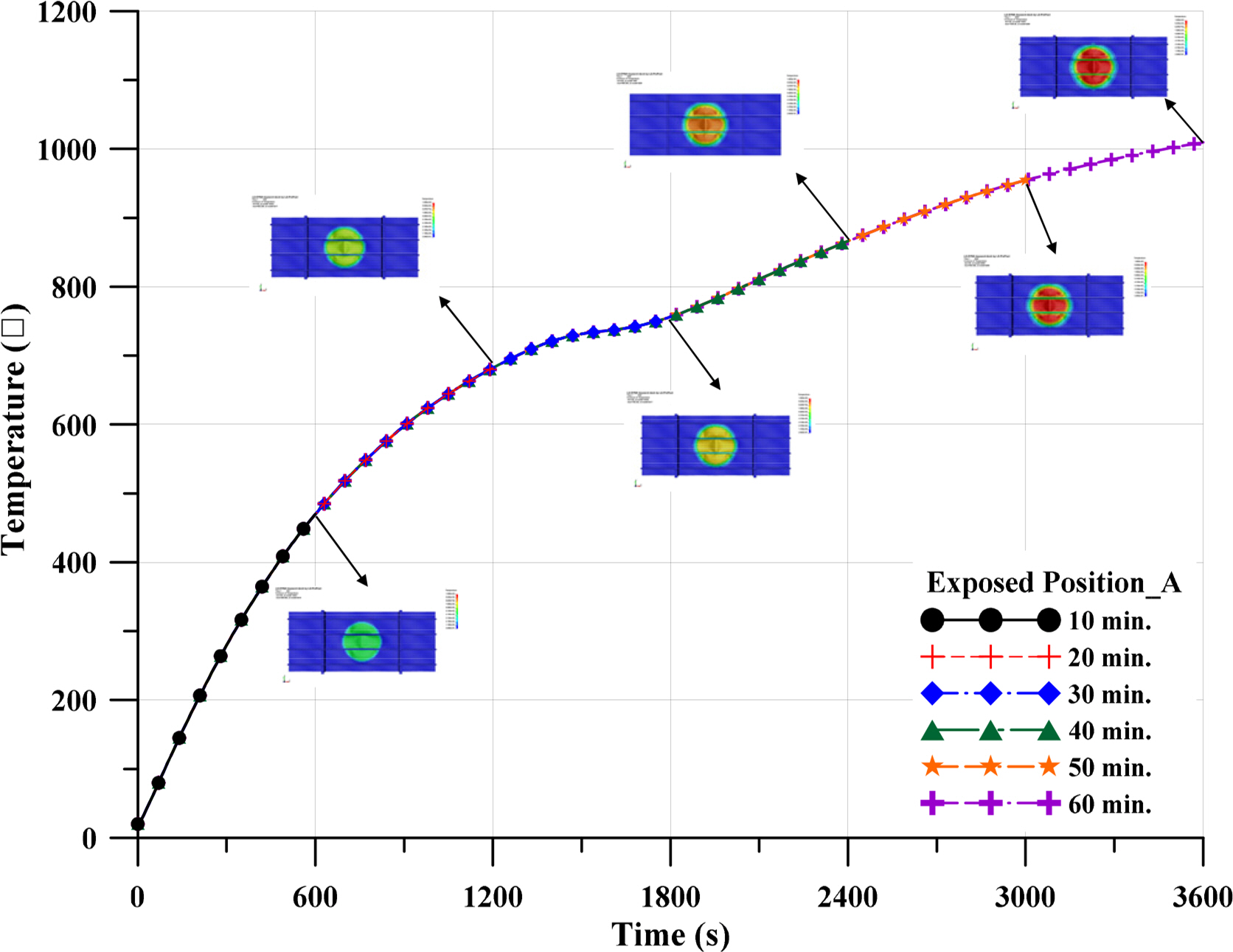
Fig. 11 shows the heat transfer analysis method conceptually. The applied method conducts the heat flux and temperature between the gas (Tg) and surface (Ts1) of the steel structural element with an exposed side. Radiation, convection, and heat loss should be considered for the unexposed side. In the case of shell elements in LS-DYNA, the temperature was uniform (Ts1 = Ts2) in the steel thickness direction. In this study, the coefficient of convection was hc = 25 W/m2K, and the emissivity of carbon steel was ╬Ąs = 0.7 (Franssen and Real, 2010). The temperature-dependent specific heat and thermal conductivity of carbon steel shown in Fig. 12 were considered to result in an accurate heat transfer analysis. Fig. 13 shows a typical temperature distribution of fire position A after 10 minutes.
The residual strength analysis was performed using LS-DYNA with the shell element models that were used for the heat transfer analysis to calculate the residual ultimate strength. To perform the residual ultimate strength analysis under fire conditions, the mechanical properties related to temperature changes needed to be applied properly. This study used the elastic perfectly plastic material model according to the steel temperature. The strength of steel should be taken as 0.2% of the proof strength, and the section modulus and the cross-sectional effective area can be determined with EN 1993-1-5 (2006) and the mechanical properties at 20┬░C.
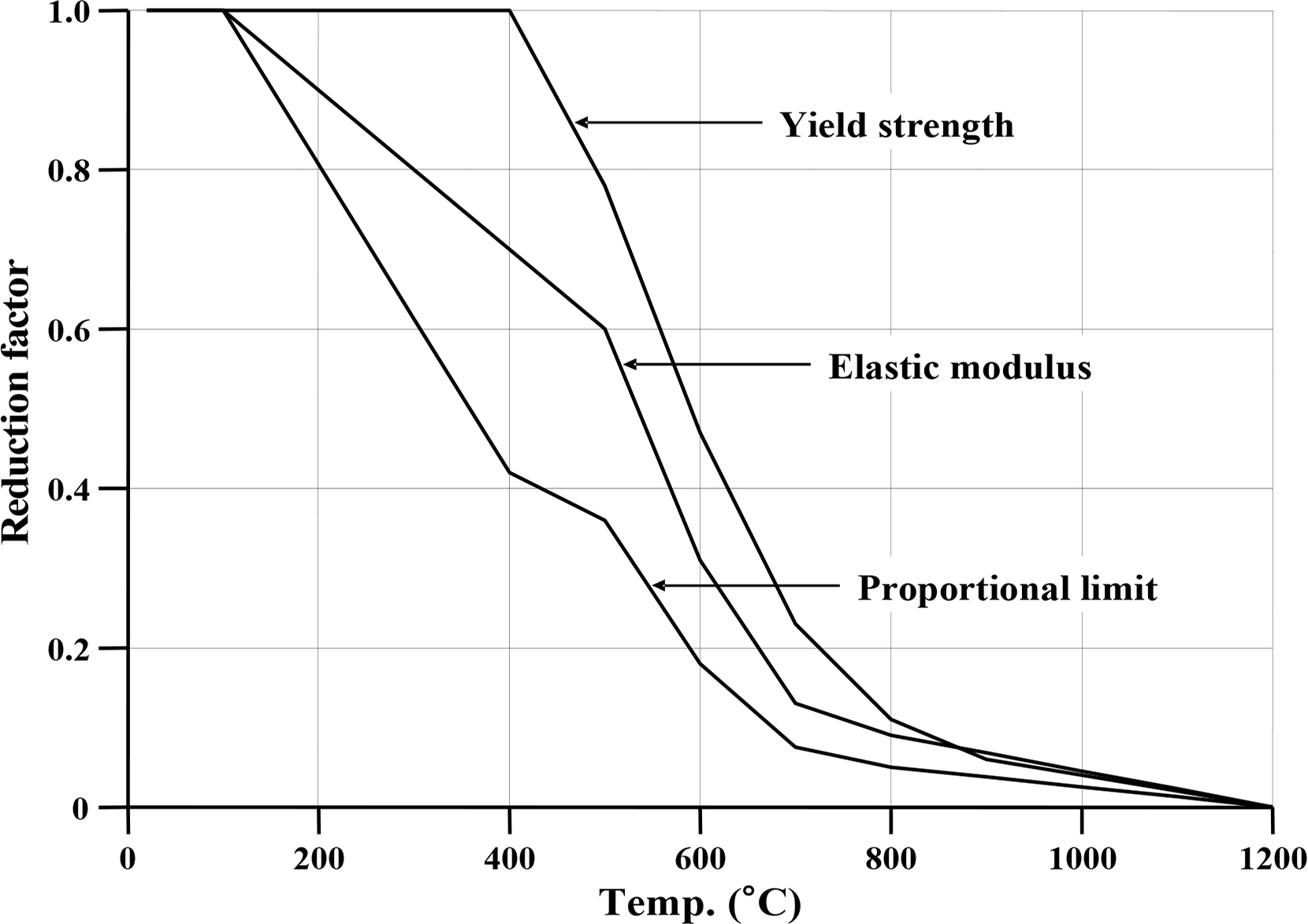
Fig. 14 shows the relation between the characteristics of the yield stress and elastic modulus of carbon steel and temperature increments. The yield stress and elastic modulus of the steel stiffened panel at 20┬░C were 240 MPa and 200 GPa, respectively, and the Poisson ratio was 0.3. The residual strength analysis considered a reduction factor for the stress-strain relationship of carbon steel at elevated steel temperatures. Fig. 15 and Table 5 show the boundary conditions and loading conditions. A uniaxial compressive load in the longitudinal direction was applied, and the mechanical load was applied after the thermal load, as shown in Fig. 16.
Fig. 17 shows the steel temperature versus exposure time of position A at various time durations. As shown in the figure, when the fire duration is more than 40 minutes, the steel temperature distribution of the stiffened panel does not reach steady state, but it can be confirmed that the temperature rises slowly. Fig. 18 shows the typical ultimate strength behavior of the steel stiffened panel under axial compression at various time durations among 120 selected fire damage scenarios. As expected, the ultimate strength was lower when the radius of the flame was widened. The overall lateral deflection shape of the plate along the longitudinal direction tended to be similar to the initial applied imperfection mode shape. This finding could help to identify the effect of fire damage on the compressive ultimate strength of the steel stiffened panel.
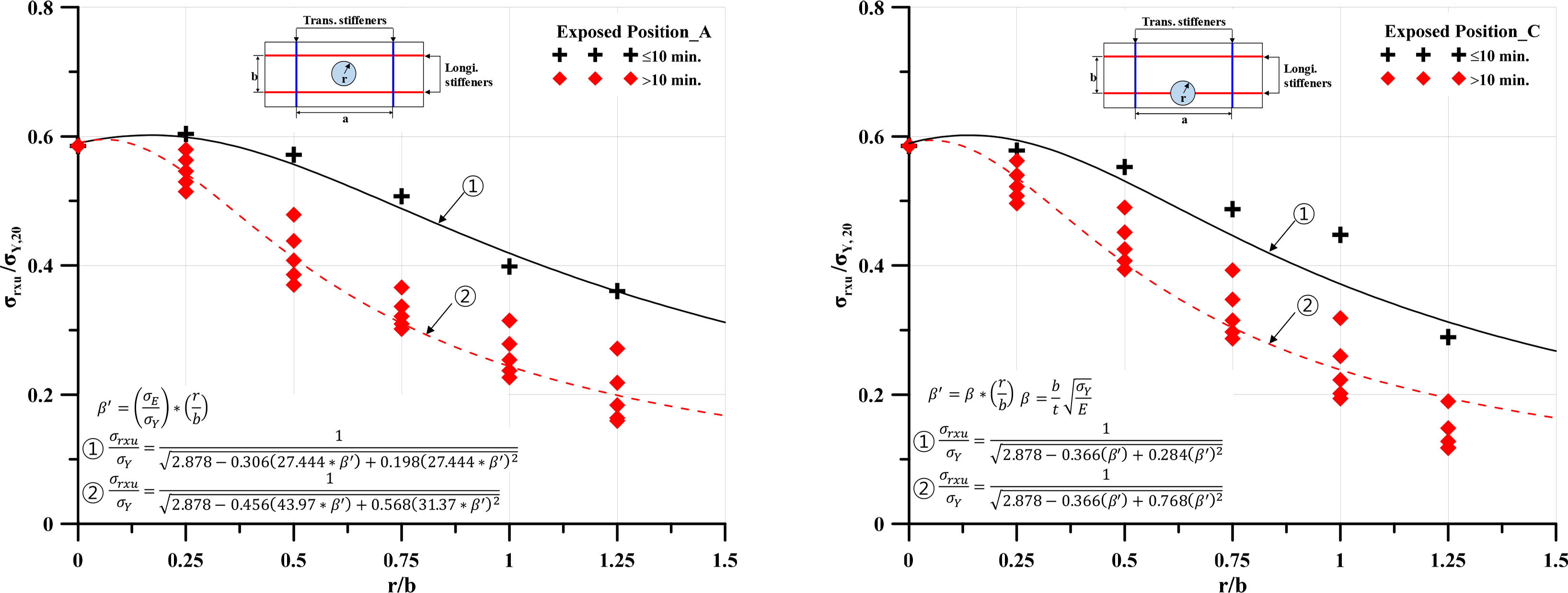
Fig. 19 shows the variation of the residual ultimate strength reduction factor of the steel stiffened panel under longitudinal axial compression with different sizes and locations of the area exposed to fire, which was obtained by FEA. The R-D diagram was developed using the residual ultimate strength reduction factor. In this study, R-D diagrams were developed based on the yield stress and ultimate strength at ambient temperature.
R-D formulae are proposed to estimate the ultimate strength of a stiffened panel under a compressive axial load at each fire position. In design practice, it is considered that Positions A to D can be determined as critical fire positions. Positions B and D are both on webs of a large transverse frame. These fire positions tend to have conservative residual strength compared to Positions A and C. Therefore, the formulae were derived from a numerical database of 120 cases, the elastic buckling strength, and the plate slenderness ratio.
The design formulae were derived using the least squares method based on the FEA results. The fire duration was divided at 10 min. for formulations. The residual ultimate strength ( Žārxu) under a compressive axial load at fire position A was formulated as follows:
For fire position C, the design formulae of residual ultimate strength were derived as follows:
where,
k = Buckling coefficient (It can be approximated to k = 4)
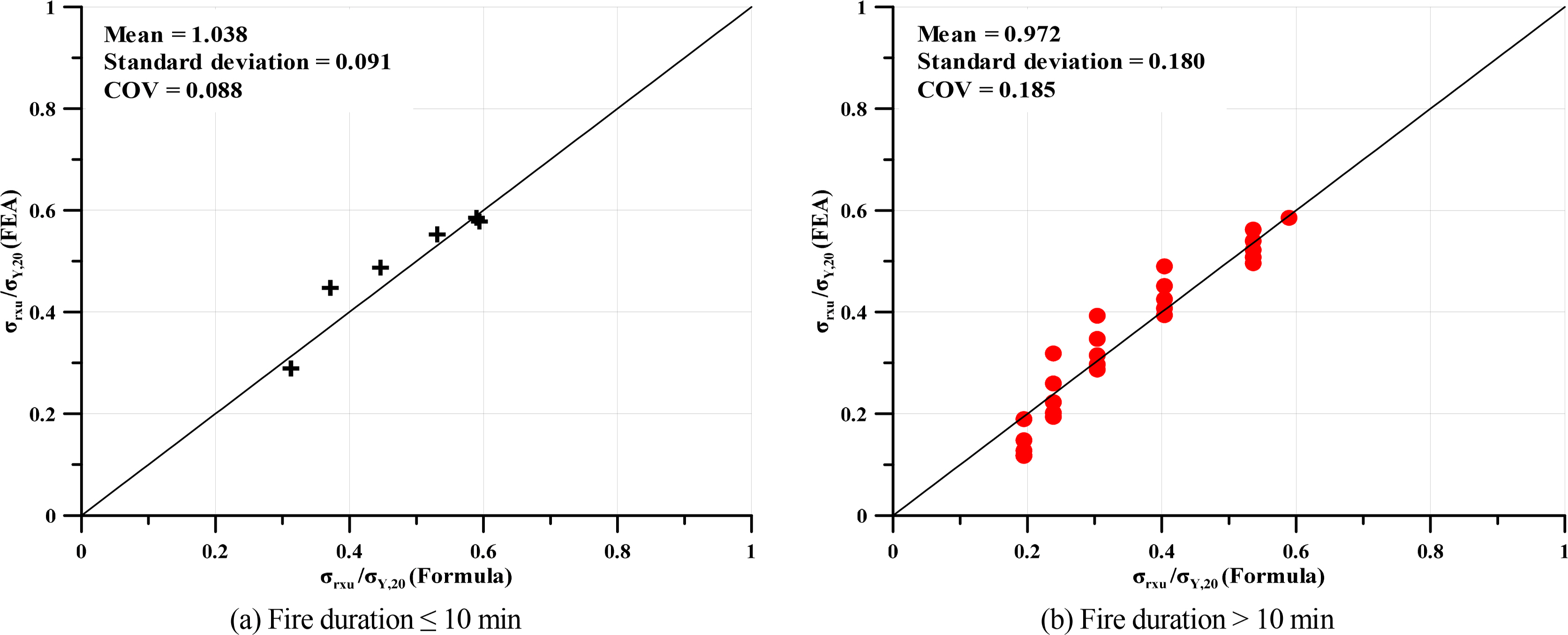
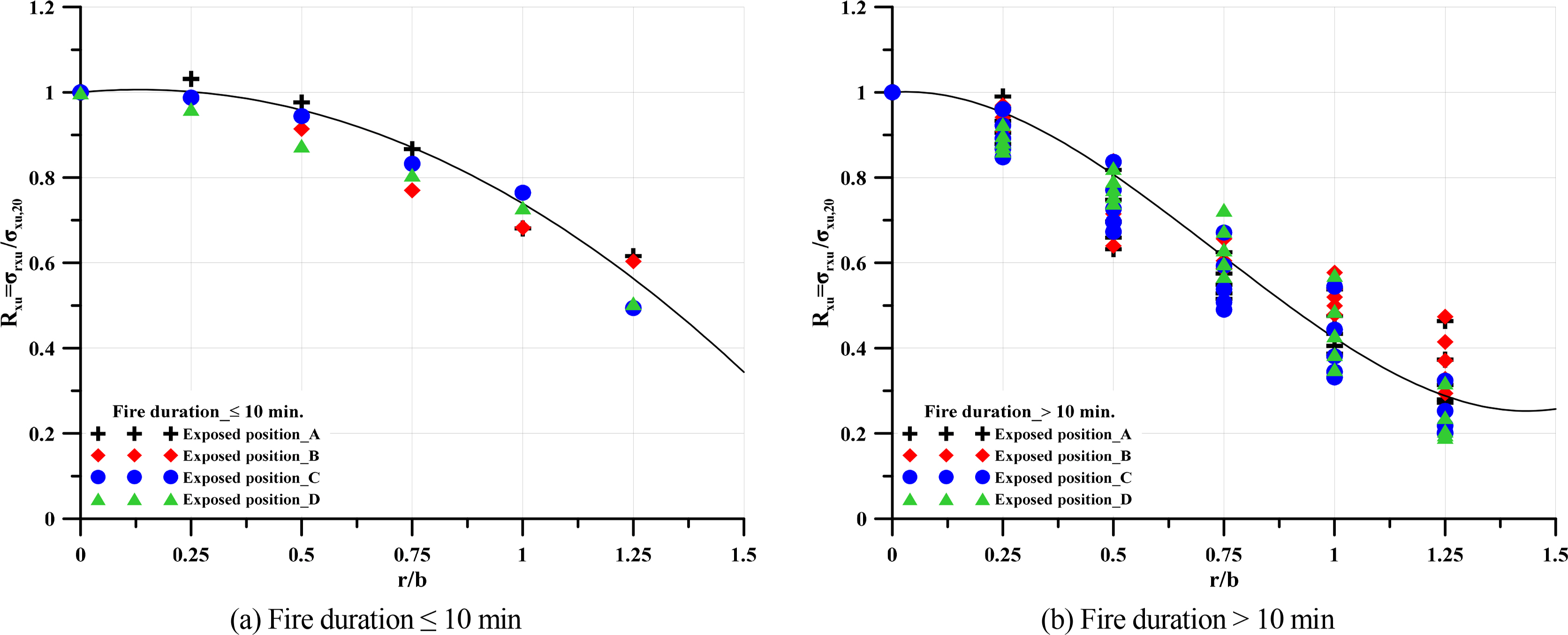
The accuracy of the present formulae calculated against the ratio of the flame radius and the breadth of the plate was checked by comparison with the FEA results at fire position A, as shown in Fig. 20. The mean, standard deviation, and coefficient of variation values for the design formulae in Eqs. (1)ŌĆō(2) were 0.985 and 0.977, 0.028 and 0.120, and 0.029 and 0.123, respectively. Likewise, the values for the design formulae in Eqs. (3)ŌĆō(4) were 1.038 and 0.972, 0.091 and 0.180, and 0.088 and 0.185, respectively.
A residual ultimate strength reduction factor (Rxu) is proposed to estimate the ultimate strength of a steel stiffened plate panel under longitudinal axial compression with varying area and duration of fire exposure. The residual ultimate strength reduction factor can be defined by a polynomial equation in terms of flame radius and plate aspect ratio as follows:
where
A polynomial equation is among the most frequently used empirical equations for fitting functions (Kim et al., 2019). The polynomial equation has well-known and understood properties. Also, a polynomial equation is computationally easy to use and has moderate flexibility of shapes. However, polynomial models have poor extrapolatory properties. Polynomials may provide good fits within the range of data, but they will frequently deteriorate rapidly outside the range of the data. Fig. 21 shows the accuracy of Eq. (5) by comparison to the FEA results, and Fig. 22 indicates the mean, standard deviation, and COV.
This study presented methods for the development and application of an R-D diagram. As a first step, fire damage parameters were characterized. The selected parameters were the fire duration, fire position, and fire area. Heat transfer analysis was carried out to identify the fire damage index for selected fire damage scenarios. Subsequently, an ultimate strength analysis was performed for a steel stiffened panel under longitudinal axial compression. The R-D diagram was developed using the residual ultimate strength reduction factor based on the yield stress and ultimate strength at ambient temperature. However, the empirical formula in this study has the following limitations:
The final goal of this study is to develop an empirical equation that can calculate the residual ultimate strength that can be applied to all types of stiffened panels and load types. To develop the equation, the following plan will be carried out:
From the obtained R-D diagram, the residual strength of the structure under fire conditions in offshore installations could be easily predicted.
Funding
This research was a part of the project titled, ŌĆ£Development of guidance for prevent of leak and mitigation of consequence in hydrogen shipsŌĆØ, which is funded by the Ministry of Oceans and Fisheries and was supported by the Global Advanced Engineer Education Program for Future Ocean Structures (P0012646), which is funded by the Ministry of Trade, Industry and Energy.
Fig.┬Ā2.
Proposed method for the development of residual strength versus damage index diagram (R-D diagram)
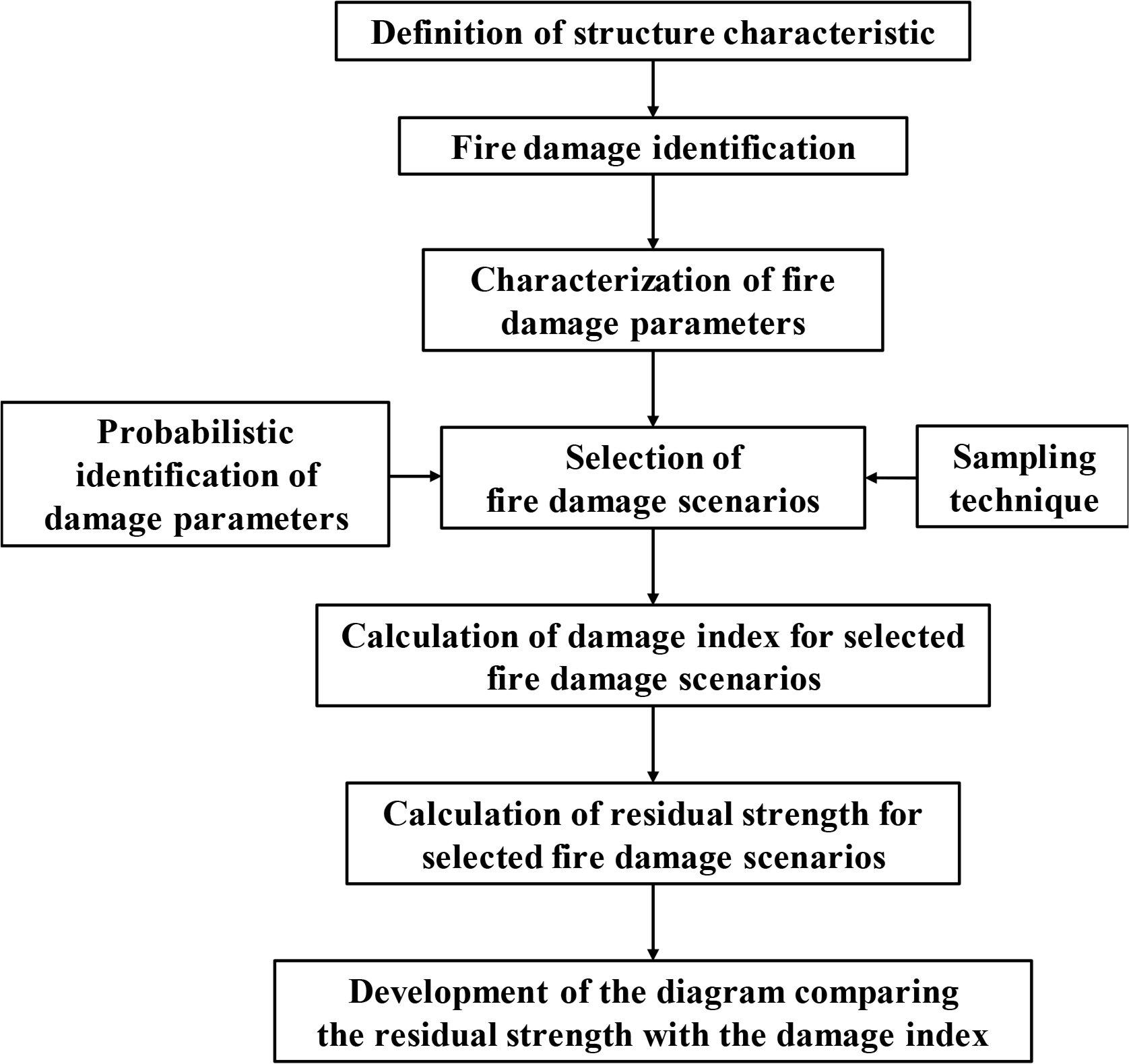
Fig.┬Ā3.
The time versus gas temperature profile for hydrocarbon (EN 1991-1-2, 2002) and pool (ISO, 1999) fires
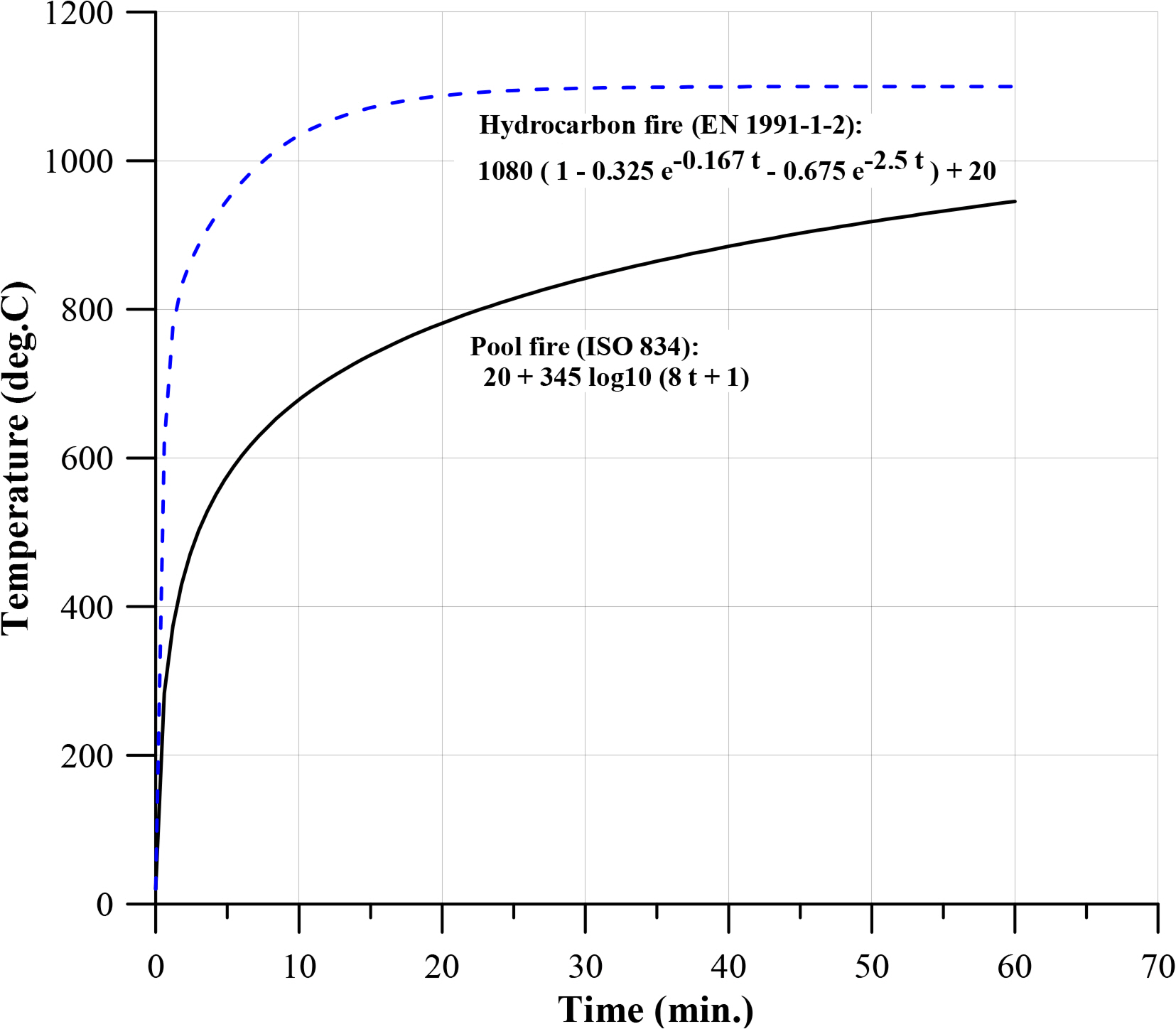
Fig.┬Ā18.
Typical ultimate strength behavior of steel stiffened panel after 10 and 60 minutes of fire exposure (Position A)

Fig.┬Ā19.
Variation of the ultimate strength reduction factor of the steel stiffened panel under longitudinal axial compression with different sizes and locations of the area exposed to fire: (a) Fire position A, (b) Fire position B, (c) Fire position C, and (d) Fire position D
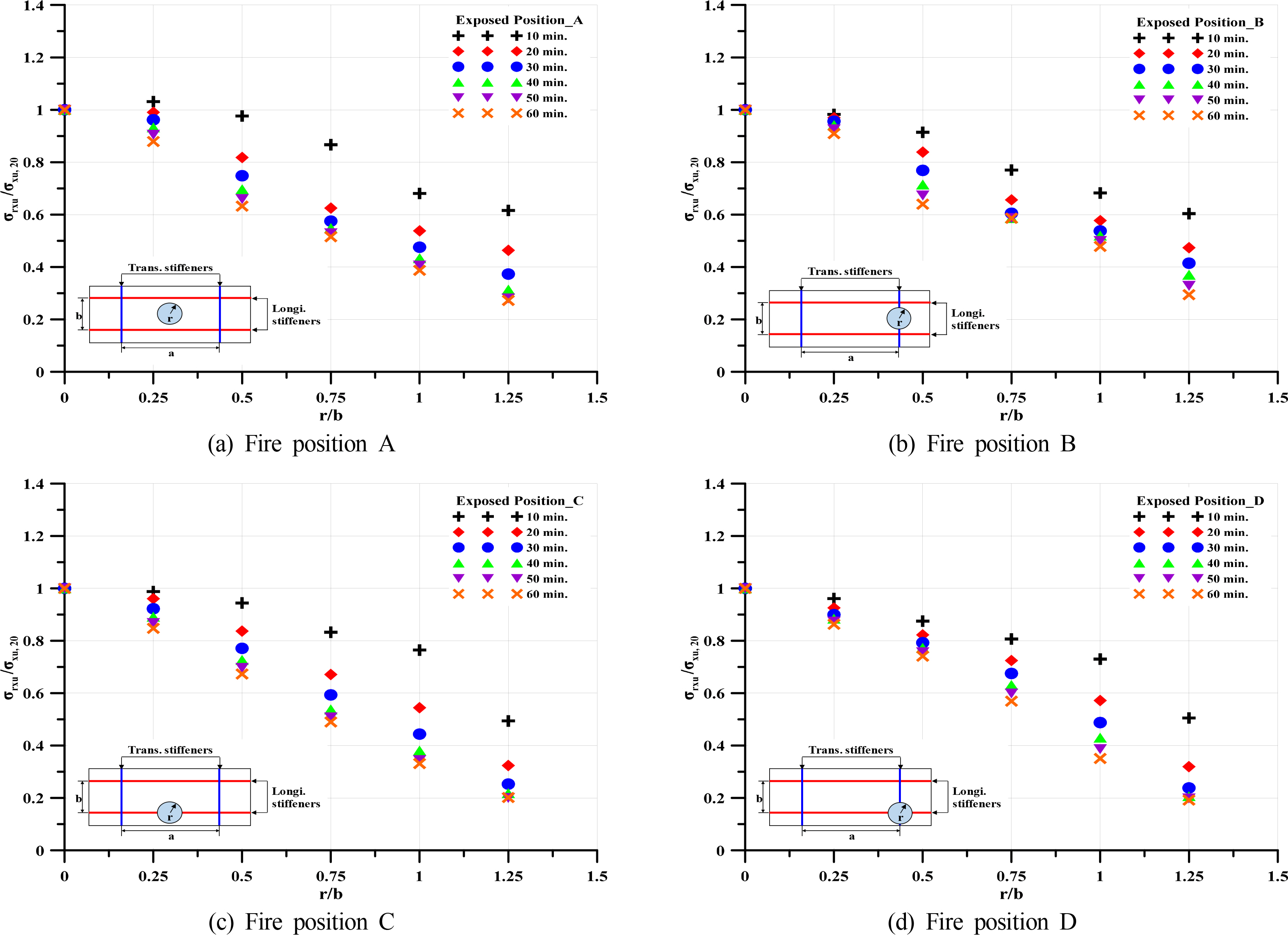
Fig.┬Ā21.
Accuracy of the residual ultimate strength reduction factor: (a) fire duration Ōēż 10 min and (b) fire duration > 10 min
Table┬Ā1.
Principal dimensions of plate girders and stiffeners.
| Longitudinal | (x-direction) | Transverse | (y-direction) |
|---|---|---|---|
| tp (mm) | 6 | tp (mm) | 6 |
| hwx (mm) | 125 | hwy (mm) | 430 |
| twxx (mm) | 7 | twy(mm) | 12 |
| bfx (mm) | 75 | bfy (mm) | 150 |
| bfx (mm) | 7 | tfy (mm) | 15 |
Table┬Ā2.
Probability of fire duration
| Duration time (min) | Probability (%) |
|---|---|
| 10 | 16.667 |
| 20 | 16.667 |
| 30 | 16.667 |
| 40 | 16.667 |
| 50 | 16.667 |
| 60 | 16.667 |
| Total | 100 |
Table┬Ā4.
Probability of fire area
| Fire radius r | Radius-breadth ratio (r/b) |
|---|---|
| 200 | 0.25 |
| 400 | 0.50 |
| 600 | 0.75 |
| 800 | 1.00 |
| 1000 | 1.25 |
| Total | - |
Table┬Ā5.
Boundary conditions (U = translational degree of freedom, R= rotational degree of freedom)
References
ANSYS Inc. (2018). UserŌĆÖs Manual for ANSYS/LS-DYNA 18.1, ANSYS Inc.
Czujko, J. (2001). Design of Offshore Facilities to Resist Gas Explosion Hazard. Oslo, Norway. CorrOcean ASA.
EN 1991-1-2. (2002). Eurocode 1: Actions on Structures. Part 1-2: General Actions-Actions on Strcutres Exposed to Fire, Brussels, Belgium. CEN.

EN 1993-1-5. (2006). Eurocode 3: Design of Steel Structures. Part 1.5: Plated Strcutral Element, Brussels, Belgium. CEN.

Franssen, JM., & Real, PV. (2010). Fire Design of Steel Structures, ECCS Eurocode Design Manuals. Berlin. Ernst & Sohn.
HSE. (2000). Offshore Hydrocarbon Releases Statistics and Analysis, Offshore Technology Report OTO 2000 112, London. Health & Safety Excutive.
Hughes, O., & Paik, JK. (2010). Ship Structural Analysis and Design. New Jersey, USA. The Society of Naval Architects and Marine Engineers.
ISO. (1999). Fire-Resistance Tests-Elements of Building Construction - Part 1: General Requirements (ISO 834-1).
Kim, DK., Kim, BJ., Seo, JK., Kim, HB., Zhang, X., & Paik, JK. (2014). Time-dependent Residual Ultimate Longitudinal Strength ŌĆō Grounding Damage Index (R-D) Diagram. Ocean Engineering, 76, 163-171.
https://doi.org/10.1016/j.oceaneng.2013.06.023

Kim, DK., Lim, HL., & Yu, SY. (2019). Ultimate Strength Prediction of T-bar Stiffened Panel Under Longitudinal Compression by Data Processing: A Refined Empirical Formulation. Ocean Engineering, 192, 106522.
https://doi.org/10.1016/j.oceaneng.2019.106522

Kim, JH., Kim, DC., Kim, CK., Islam, S., Park, SI., & Paik, JK. (2013). A Study on Methods for Fire Load Application with Passive Fire Protection Effects. Ocean Engineering, 70, 177-187.
https://doi.org/10.1016/j.oceaneng.2013.05.017

Nolan, DP. (1996). Handbook of Fire and Explosion Protection Engineering Principles for Oil, Gas, Chemical, and Related Facilities. New Jersey, USA. Noyes Publications.
NORSOK. (2010). Norwegian Standards ŌĆō Risk and Emergency Preparedness Assessment (Z-013), NORSOK.
Paik, JK., & Czujko, J. (2011). Assessment of Hydrocarbon Explosion and Fire Risks in Offshore Installations: Recent Advances and Future Trends. The IES Journal Part A: Civil & Structural Engineering, 4(3), 167-179.
https://doi.org/10.1080/s19373260.2011.593345

Paik, JK., & Thayaballi, AK. (2003). Ultimate Limit State Design of Steel-plated Structures. Chichester. John Wiley & Sons.
Paik, JK., Czujko, J., Kim, JH., Park, SI., Islam, MDS., & Lee, DH. (2013). A New Procedure for the Nonlinear Structural Response Analysis of Offshore Installations in Fires. Transaction of Society of Naval Architects and Marine Engineers, 121, 224-250.

Paik, JK., Kim, BJ., Jeong, JS., Kim, SH., Jang, YS., Kim, GS., & Czujko, J. (2010). CFD Simulations of Gas Explosion and Fire Actions. Ships and Offshore Structures, 5, 3-12.
https://doi.org/10.1080/17445300902872028

Purkiss, JA. (2007). Fire Safety Engineering Design of Structures. Second Edition New York, USA. Elsevier.
Salem, AM., Dabess, EM., Banawan, AA., & Leheta, HW. (2016). Fire Safety Design of Nilefloating Hotels. Ships and Offshore Structures, 11, 482-500.
https://doi.org/10.1080/17445302.2015.1027564

Seo, JK., Lee, SE., & Park, JS. (2017). A Method for Determining Fire Accidental Loads and Its Application to Thermal Response Analysis for Optimal Design of Offshore Thin-walled Structures. Fire Safety Journal, 92, 107-121.
https://doi.org/10.1016/j.firesaf.2017.05.022

Shetty, NK., Soares, CG., Thoft-Christensen, P., & Jensen, FM. (1998). Fire Safety Assessment and Optimal Design of Passive Fire Protection for Offshore Structures. Reliability Engineering & System Safety, 61(1ŌĆō2), 139-149.
https://doi.org/10.1016/S0951-8320(97)00124-5

Soares, CG., Gordo, JM., & Teixeira, AP. (1998). Elasto-plastic Behaviour of Plates Subjected to Heat Loads. Journal of Constructional Streel Research, 45(2), 179-198.
https://doi.org/10.1016/S0143-974X(97)00062-X

Sun, L., Yan, H., Liu, S., & Bai, Y. (2017). Load Characteristics in Process Modules of Offshore Platforms Under Jet Fire: The Numerical Study. Journal of Loss Prevention in the Process Industries, 47, 29-40.
https://doi.org/10.1016/j.jlp.2017.02.018

Vinnem, JE. (2007). Offshore Risk Assessment: Principles, Modelling and Applications of QRA Studies. London. Springer.
APPENDICES
Appendix
Table A1 Results and fire damage scenarios
- TOOLS
-
METRICS

-
- 7 Crossref
- Scopus
- 3,165 View
- 81 Download
- Related article in JOET