1. Introduction
2. Large-Scale Experimental Setup
3. Numerical Model
3.1 Numerical Model Setup
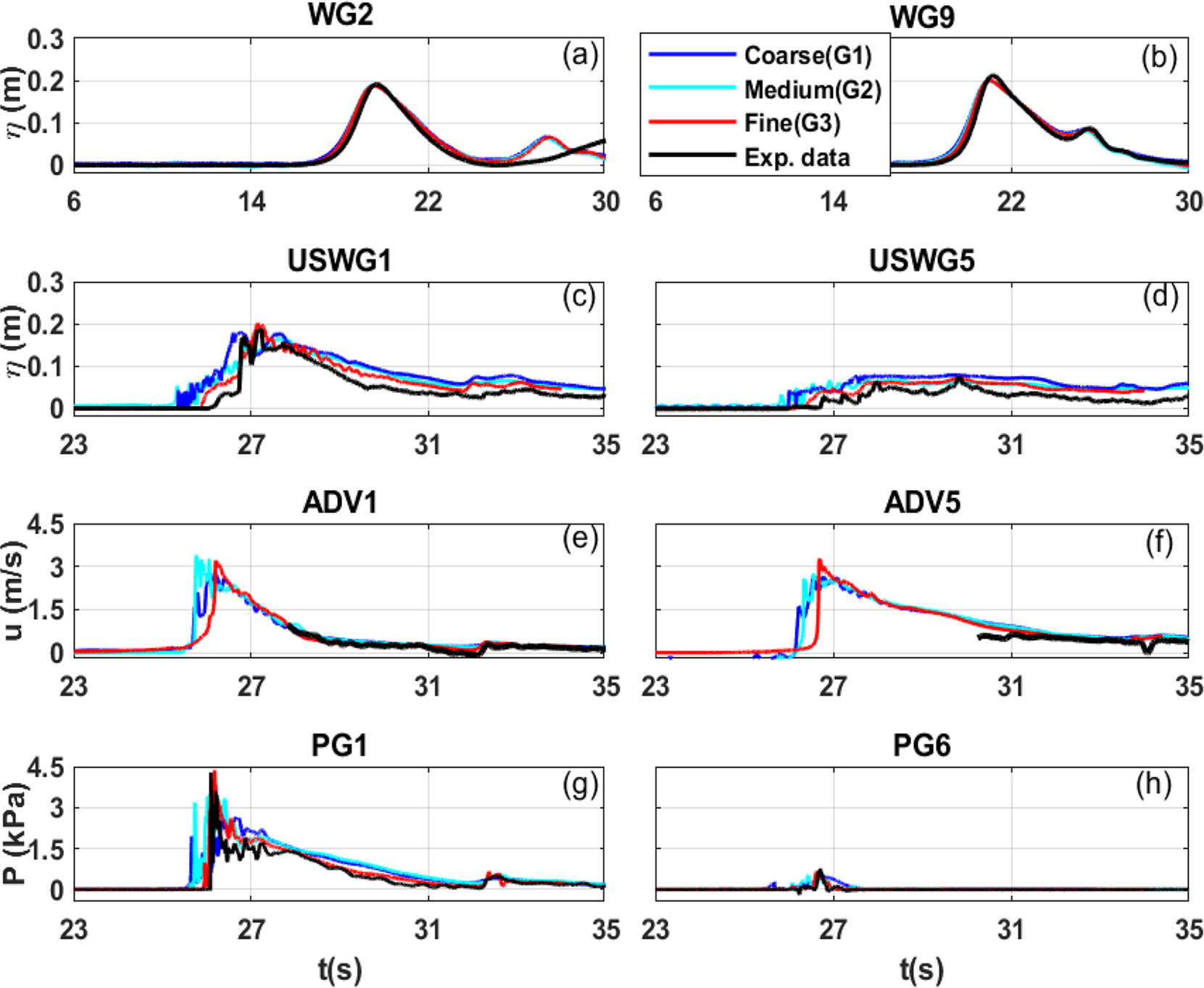
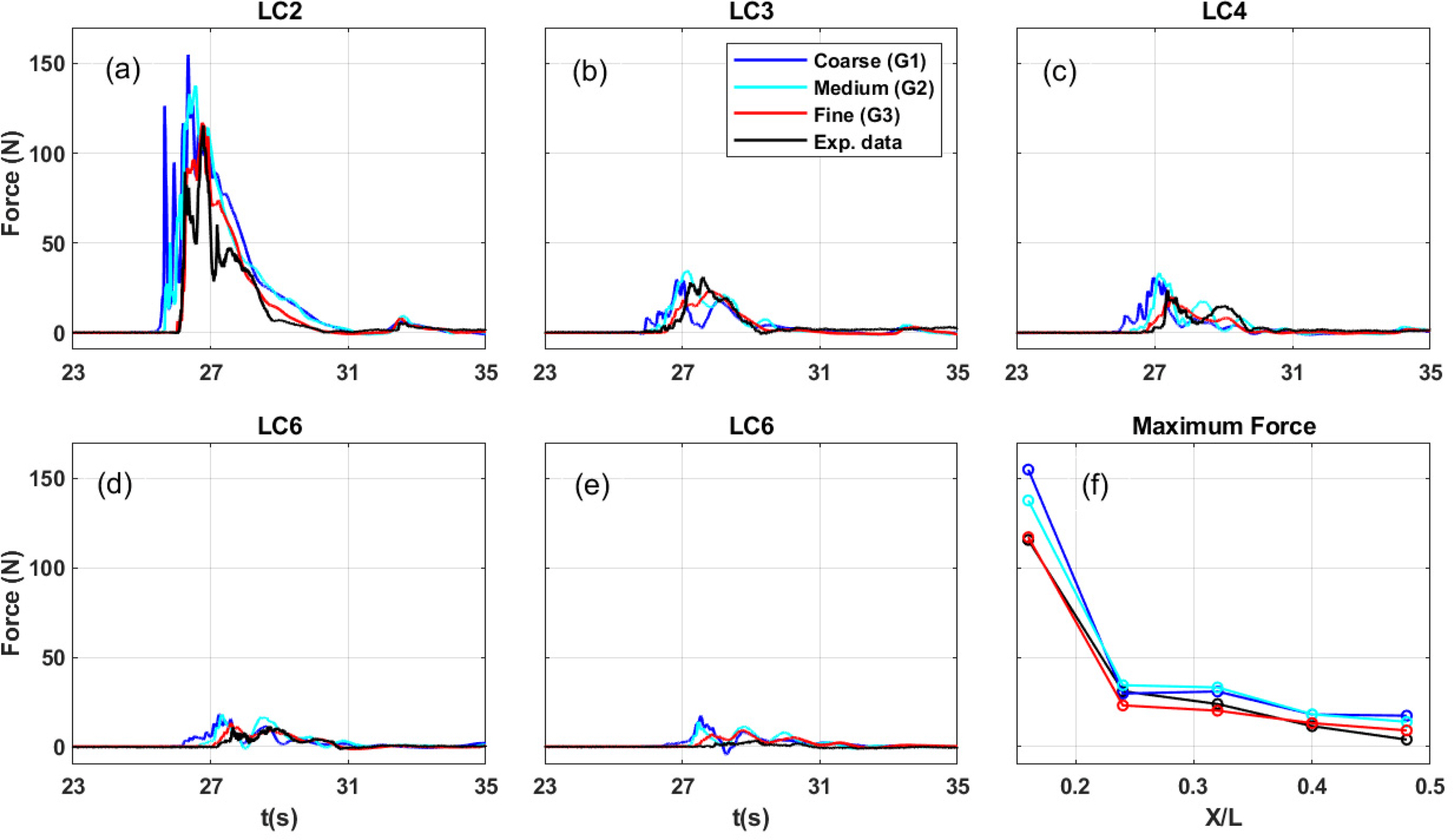
3.2 Numerical Model Validation
4. Results and Discussion
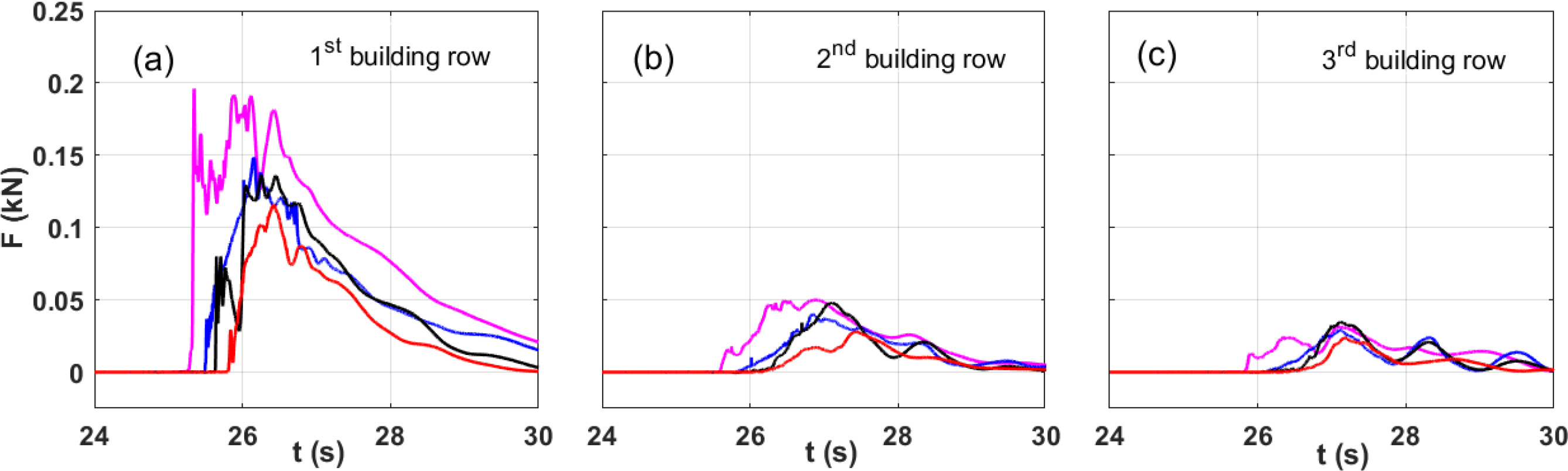
4.1 Hydrodynamic Characteristics and Loadings in the Constructed Environment
4.2 Effects of Incident Wave Heights
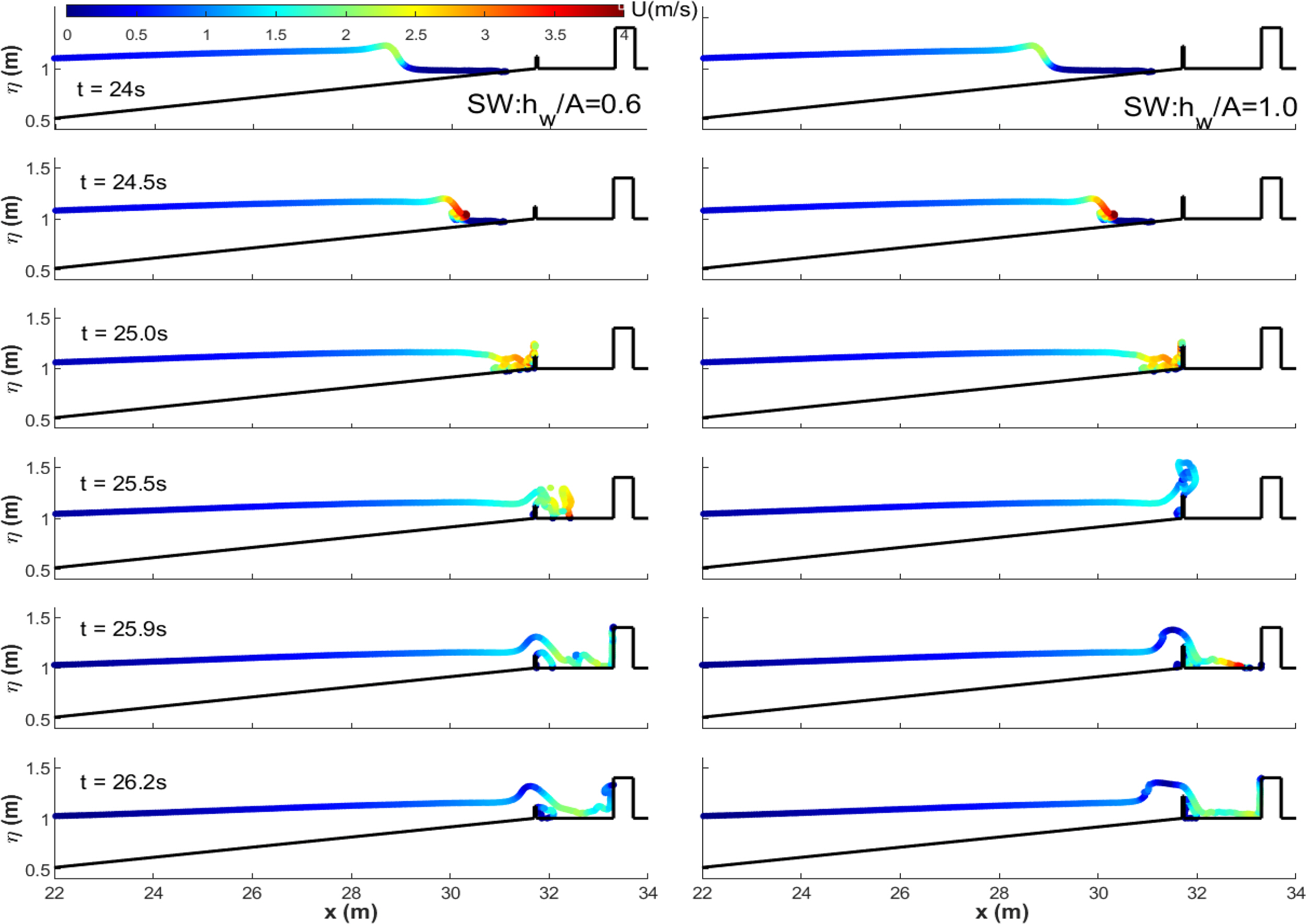
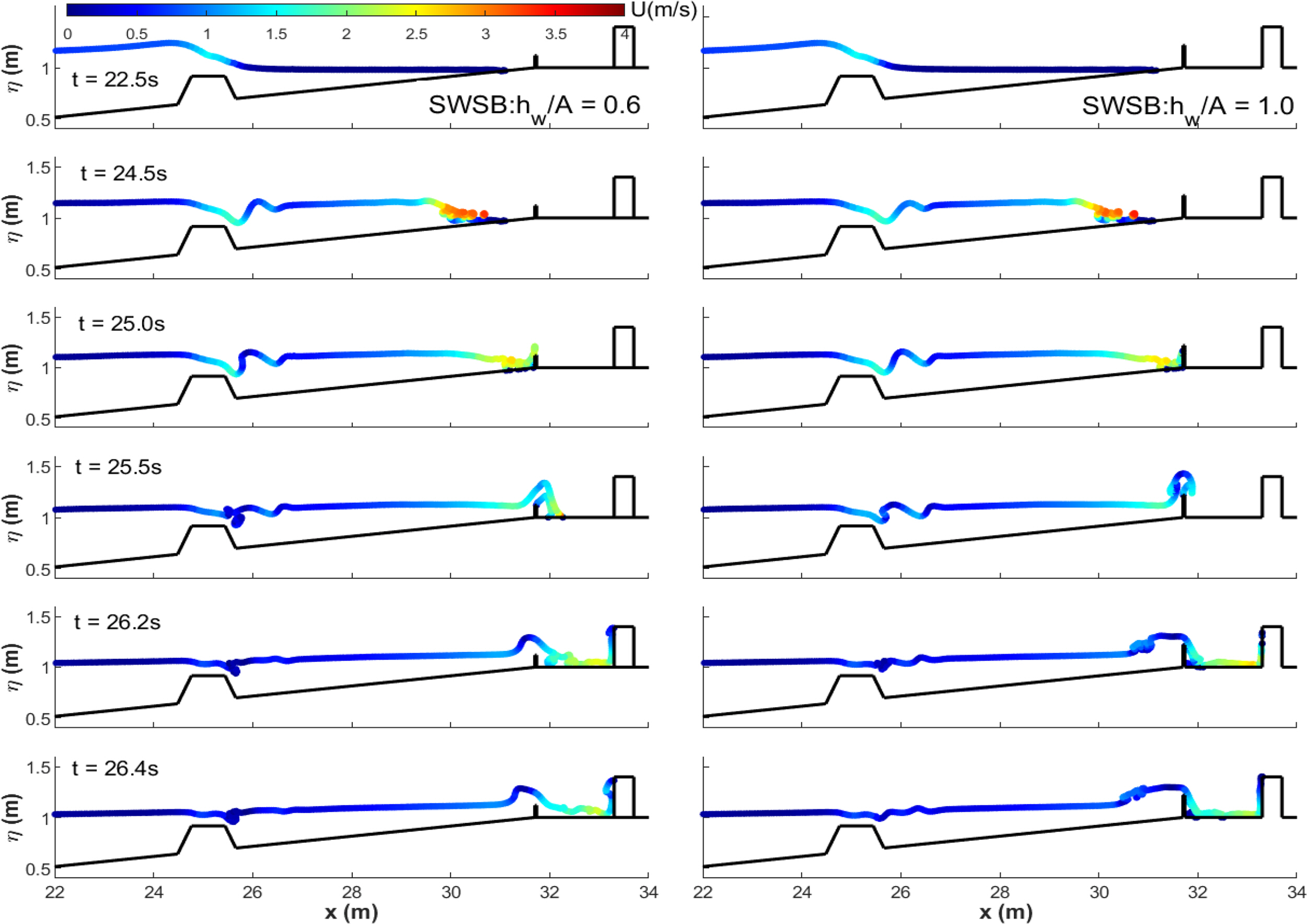
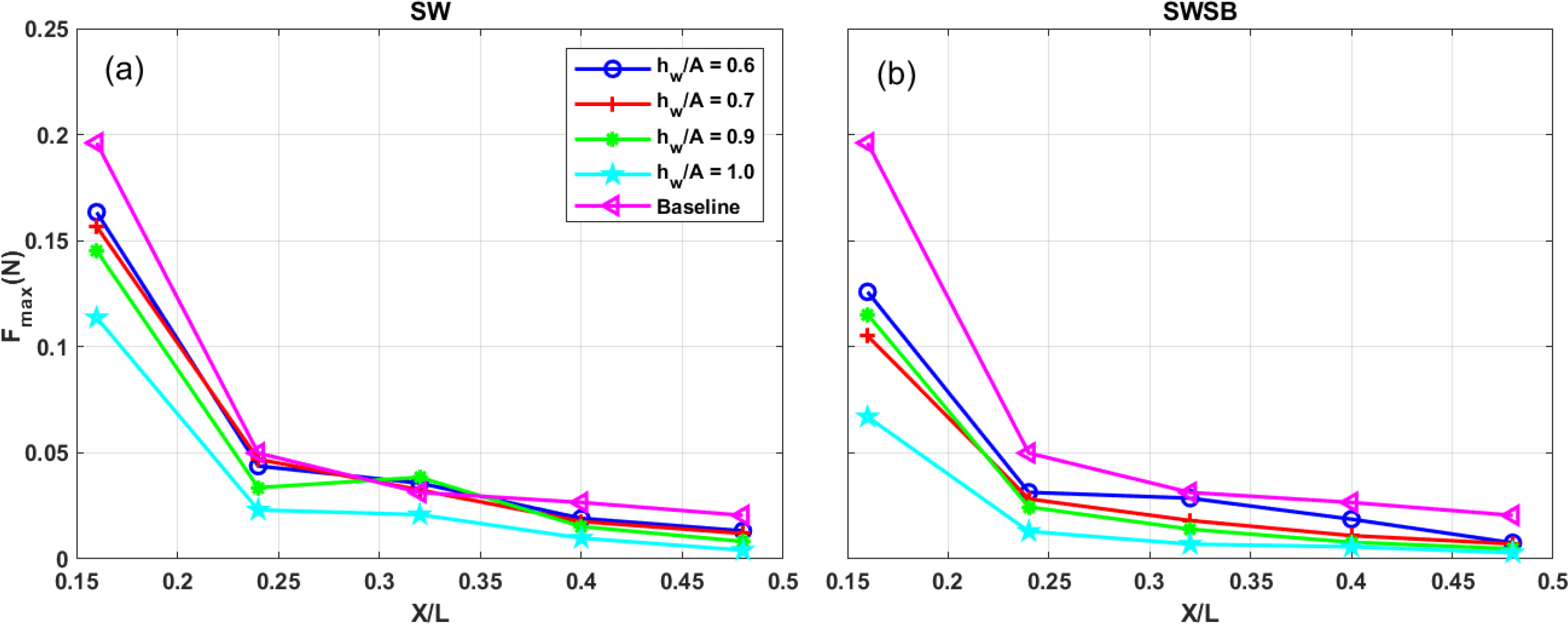
4.3 Effects of Seawall Heights
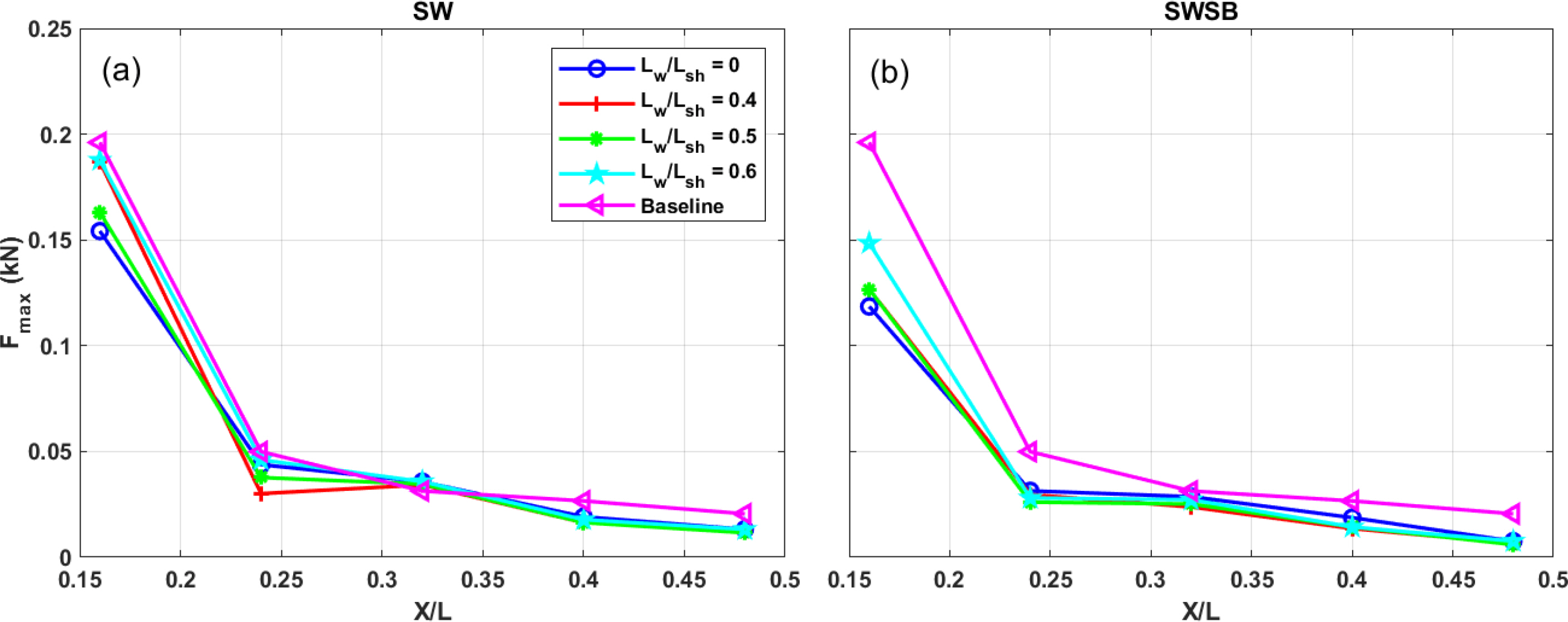
4.4 Effects of Seawall Positions
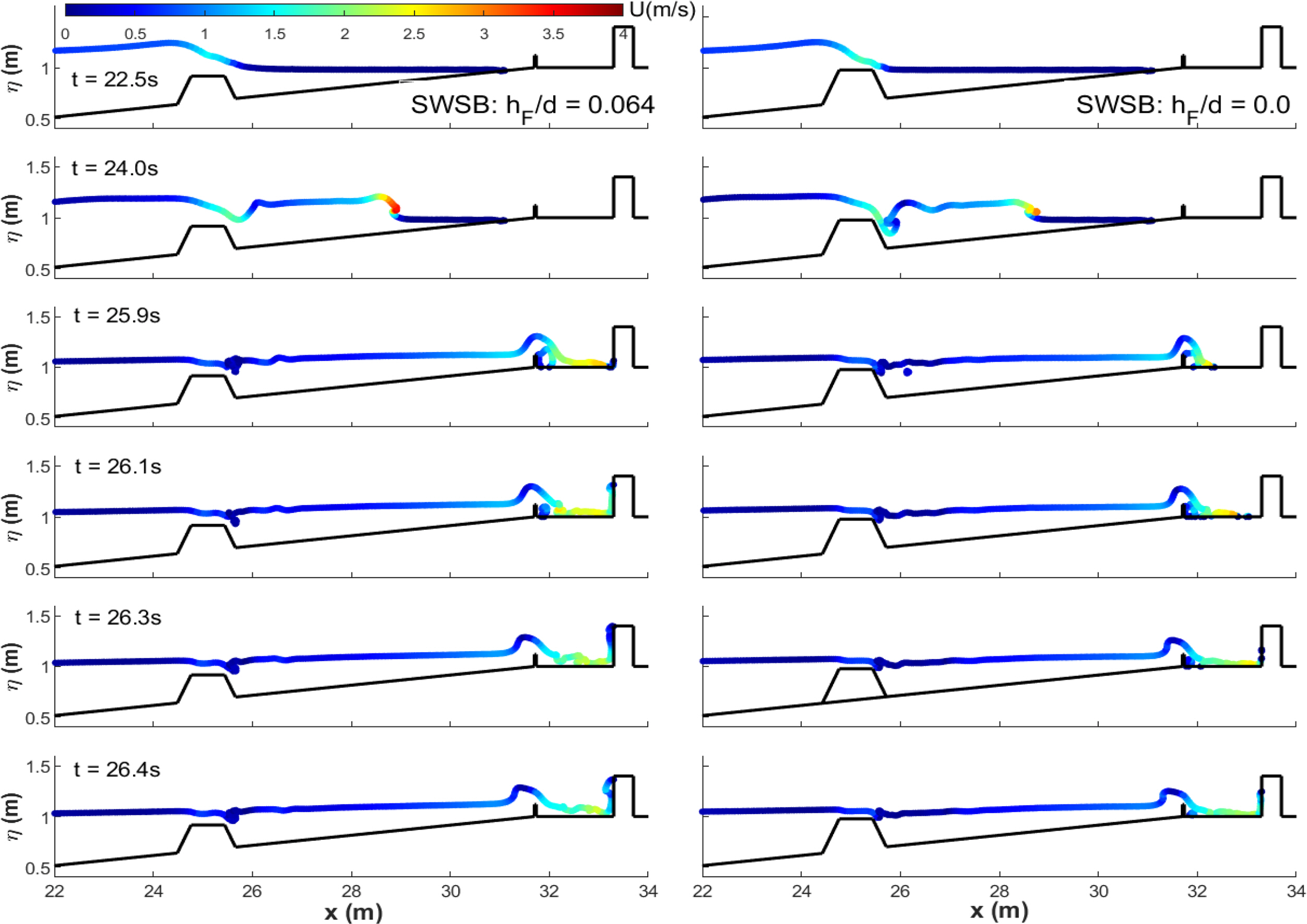
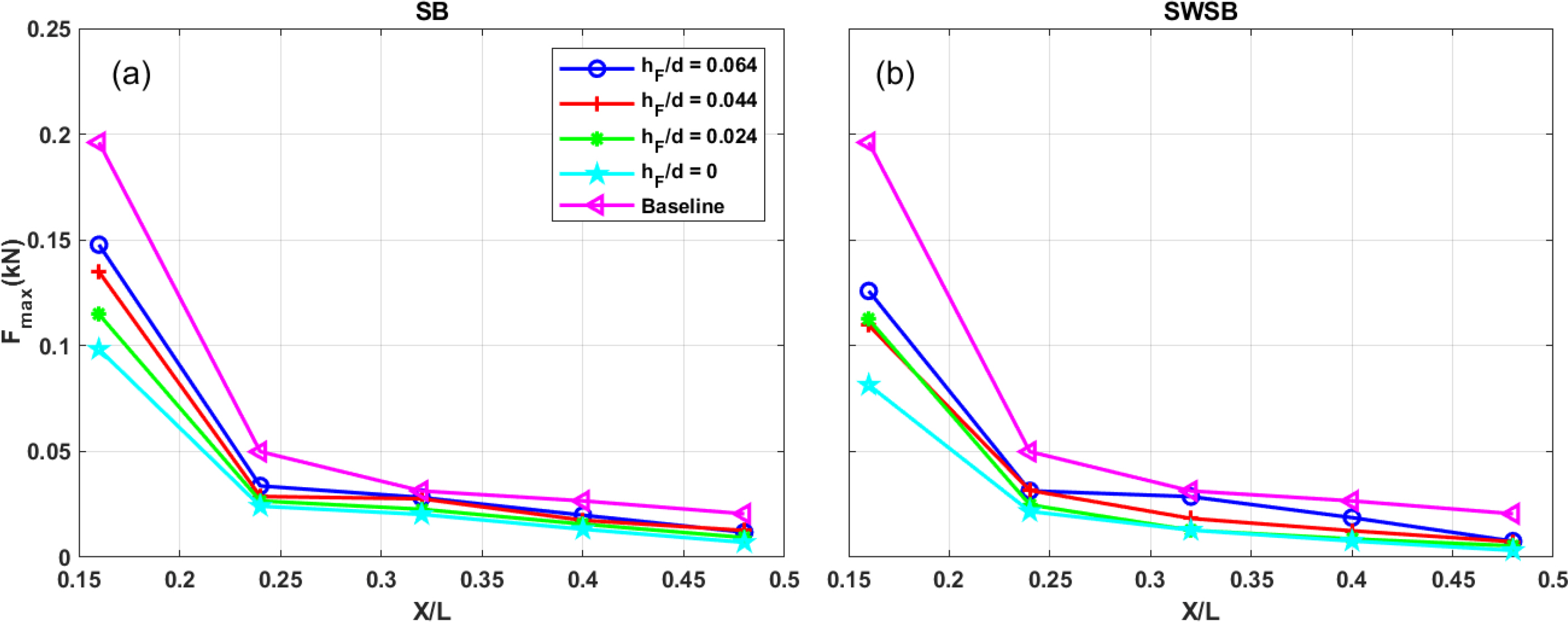
4.5 Effects of Submerged Breakwater Freeboards
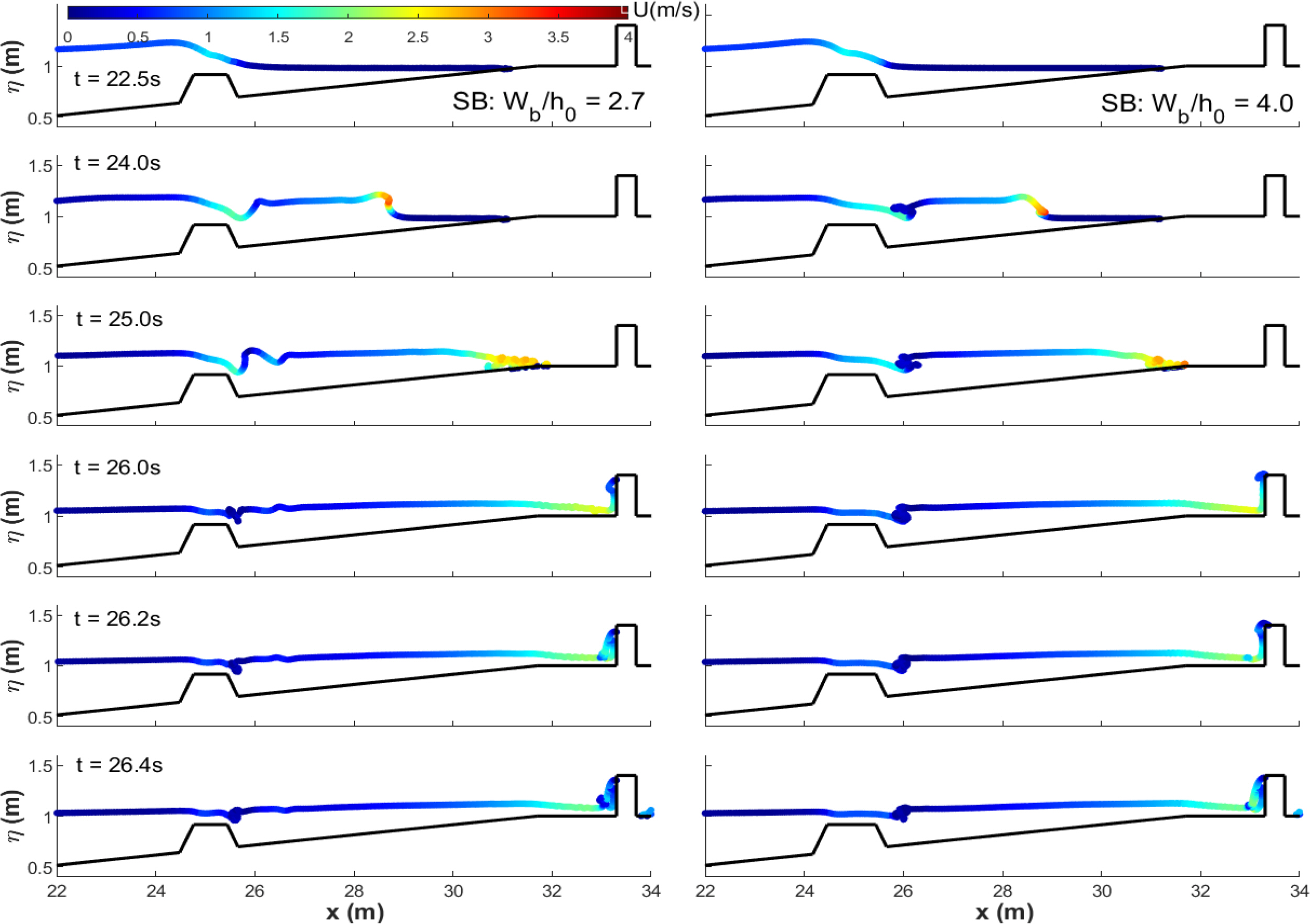
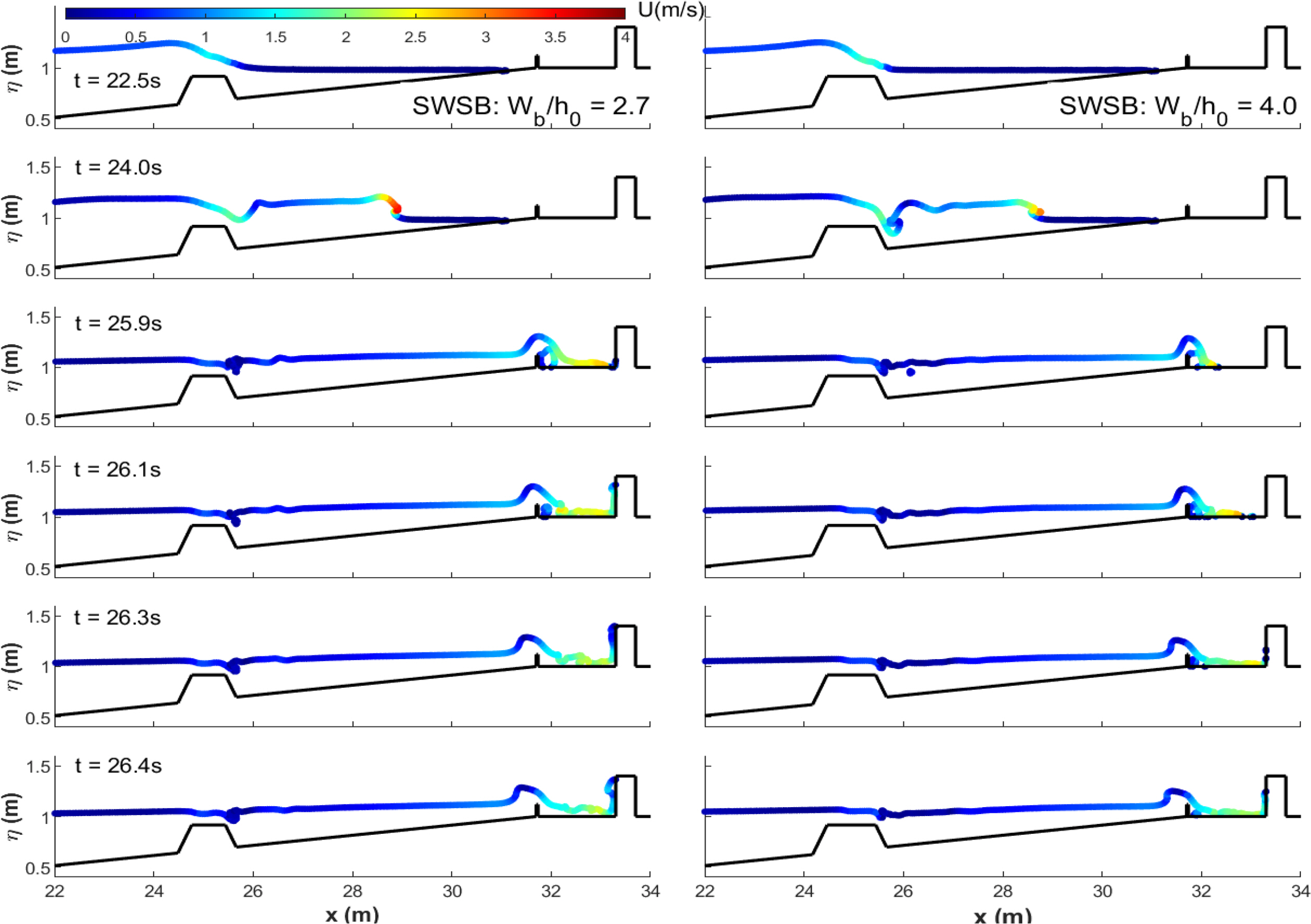
4.6 Effects of Submerged Breakwater Crest Widths
5. Conclusions
In general, installing a submerged breakwater and seawall can greatly reduce the intensity of tsunami-like wave-induced overland flow impacts on coastal communities. While the baseline and SB configurations generated relatively symmetric flow propagating in the constructed environment, SW induced a large turbulent wave splash with high velocities in the built environment. Combined structural configurations significantly reduced cross-shore velocities, inundation depths, and maximum horizontal forces on the inland buildings.
The maximum flow depth and horizontal force linearly increased with the amplitude of incident waves. The presence of both a seawall and submerged breakwater significantly reduced flow depths and forces by a maximum of 64% and 84% relative to the baseline in the four wave conditions, respectively.
The maximum force dramatically decreased with increasing seawall height. The maximum force reductions ranged from 15% to 45% for the SW configuration at different heights in the first building row, but with the additional of a submerged breakwater (SWSB), the rate of maximum force reduction only increased by 20% compared to the SW configuration.
A low-lying seawall located closer to the first building row induced larger wave overtopping that directly impacted the front face of the first building rows, amplifying the maximum force by up to 25% for the seawall position of Lw/Lsh = 0.6 compared to the seawall at the shoreline at Lw/Lsh = 0.
Effects of crest widths of submerged breakwaters on reducing maximum forces were very limited. The SB-only and SWSB configurations resulted in reductions of 25% and 38% of maximum baseline forces in the first building array, respectively.
The freeboard of submerged breakwaters greatly influenced hydrodynamics and maximum forces in the constructed environment. Lower freeboard significantly dissipated tsunami-like wave energies, generating lower turbulent bore impacts on vertical buildings. A submerged breakwater with its crest at the still water level can reduce baseline forces by 50% and 70% for the SB-only and SWSB configurations.