|
 |
- Search
| J. Ocean Eng. Technol. > Volume 34(5); 2020 > Article |
|
Abstract
As regulations concerning ship vibration and noise are becoming stricter, considerable attention is being drawn to prediction technologies for ship vibration and noise. In particular, the resonance and lock-in phenomena caused by vortex-induced vibration (VIV) have become considerably important with increases in the speed and the size of ships and ocean structures, which are known to cause structural problems. This study extends the fluid-structure interaction (FSI) analysis method to predict resonances and lock-in phenomena of high modes and VIV of ship rudders. Numerical stability is secured in underwater conditions by implementing added mass, added damping, and added stiffness by applying the potential theory to structural analysis. An expanded governing equation is developed by implementing displacements and twist angles of high modes. The lock-in velocity range and resonant frequencies of ship rudders obtained using the developed FSI method agree well with the experimental results and the analytic solution. A comparison with local vibration guidelines published by Lloyd’s Register shows that predictions of resonances and lock-in phenomena of high modes are necessary in the shipbuilding industry due to the possible risks like fatigue failure.
As the regulations related to ship vibration and noise have recently become stricter, prediction technology for ship vibration and noise has become important. In particular, with an increase in the risk of vortex-induced vibration (VIV) arising from the growing trend of building large and high-speed ships, various studies are actively being conducted to address this issue. VIV refers to the structural vibration caused by the periodic vortex shedding in the wake of the bluff body. It mainly occurs in ship rudders and propellers, as well as in submarine sails. Structural problems caused by VIV also occur in offshore risers (Jung et al., 2019; Son et al., 2019).
When the vortex shedding frequency approaches the structure’s natural frequency, resonance occurs in which the structure vibrates severely into the natural frequency component. At the same time, lock-in occurs in which the vortex shedding frequency shifts to the natural frequency due to the structure’s resonance. As the amplitude of VIV is highest when resonance and lock-in occurs, the prediction and control of VIV is essential in cases of resonance and lock-in phenomena in terms of the ship’s structural stability.
To predict VIV, there are methods for conducting experiments by building a model ship and performing analytical fluid-structure interaction (FSI) analysis. FSI analysis is an analysis methodology that obtains the response of a structure (fluid) by a fluid (structure). Research on FSI analysis has been actively carried out since 1970 (Felippa et al, 2001). FSI analysis can largely be classified into the monolithic method and the partitioned method. In the monolithic method, fluid and structure calculations are performed using a single matrix equation. This method has the advantage of being mathematically rigorous; however, it has a disadvantage in that the complexity of the analysis becomes high because of the large-scale system. In the partitioned method, fluid and structure calculations are performed using separate governing equations, and then the two results are integrated through boundary conditions at every time step. It is an analysis method that is easy to develop because it utilizes currently available computational fluid dynamics (CFD) and structural analysis programs, although it is less mathematically rigorous than the monolithic method. The partitioned method is classified into a tight (or strong) coupling method and a loose (or weak) coupling method. The tight-coupling method determines the degree of convergence of the results within one time step and performs subiterations. It has the advantage of high accuracy, but has the disadvantage of high computational cost. The loose-coupling method performs only one CFD analysis and one structural analysis within one time step without the subiteration process. It has the advantage of low computational cost but has the disadvantage of relatively low accuracy. In particular, FSI analysis based on the loose-coupling method has limitations in an underwater environment where the added mass effect is strong.
Campbell (2010) and Lee (2014) performed a 3D FSI analysis using the tight-coupling method for a hydrofoil and derived analysis results that favorably matched the experimental results. However, to predict the VIV of various ship rudders at design stage, there is a need for an FSI analysis method that can sufficiently reflect the added mass effect of an underwater environment while lowering the computational cost. By applying the empirical equation for the fluid force developed by Munch et al. (2010) to the aeroelastic analysis model used to predict the flutter of aircraft wings, Young et al. (2012) developed a hybrid algorithm, which is an FSI analysis algorithm that considers the fluid added mass. They predicted vortex-induced twisting vibration of the hydrofoil using this algorithm. In particular, by performing analysis of the hydrofoil model, which the fluid added mass has a significant impact on, they verified the effectiveness of the hybrid algorithm compared with the tight-coupling and loose-coupling methods in terms of convergence and accuracy. Chae (2015) established the bend-twist (BT) FSI analysis procedure by integrating the hybrid algorithm with CFD and verified the analysis results of the NACA0015 hydrofoil using the experimental results. The BT FSI analysis has a considerable advantage in terms of the computational cost because it uses a 2D CFD analysis without subiterations to obtain the VIV of the hydrofoil with the same wing cross-section in the span direction. However, there is a disadvantage in that it reflects only the effects of the first bending and twisting mode.
In this study, we develop a high-mode BT FSI analysis method by extending the BT FSI analysis method of Chae (2015) to analytically implement the high-mode resonance and lock-in phenomena of ship rudders with low computational cost. We perform a high-mode BT FSI analysis on a hydrofoil, which is similar to the shape of a ship rudder, and predict the VIV for the flow velocity. We verify and analyze vibration by comparing the experimental results, analytic solutions, and analysis results.
A ship rudder is regarded as a continuum with infinite degrees of freedom. Unlike the equation of motion of an object with a finite number of degrees of freedom, the Lagrange equation based on the variational approach is required to derive the equation of motion of a continuum structure. The vibration of a continuum structure for an external force can be obtained using the Lagrange equation as follows:
where T, Γ, U, W, and qj refer to kinetic energy, energy dissipation term, potential energy, work, and the jth degree of freedom displacement function, respectively.
The ship rudder can be assumed as a one-dimensional continuum structure. In addition, as the bending and twisting modes predominantly influence the ship rudder, the deformation z of the structure can be assumed as a function of time t and space x, as follows:
where Sfj and Sgj are the jth mode bending and twisting shape functions, respectively; and dj and θj are the jth mode bending- and twisting-mode coefficients, respectively. When the deformation of the structure is defined in this way, T and U are expressed as follows:
where μ, EI and s refer to structural linear density, flexural rigidity, and span length, respectively. When Eqs. (3) and (4) are applied to Eq. (1), the motion equation in the form of a matrix is obtained, as follows:
where M, C, K and F refer to structural mass matrix, structural damping matrix, structural elastic matrix, and external force vector, respectively.
The fluid force and moment exerted on the vibrating wing cross-section should consider the static fluid force and moment variation according to the angle of attack and the amplitude reduction and phase shift due to unsteadiness. The amplitude reduction and phase shift due to unsteadiness depend on the dimensionless frequency k of the wing cross-section, which is expressed by the Theodorsen function C(k) as
where
H 1 2 ( k ) H 0 2 ( k )
Theodorsen (1949) derived the fluid force and moment LT, TT exerted on the thin wing cross-section in flow velocities based on the potential method as follows:
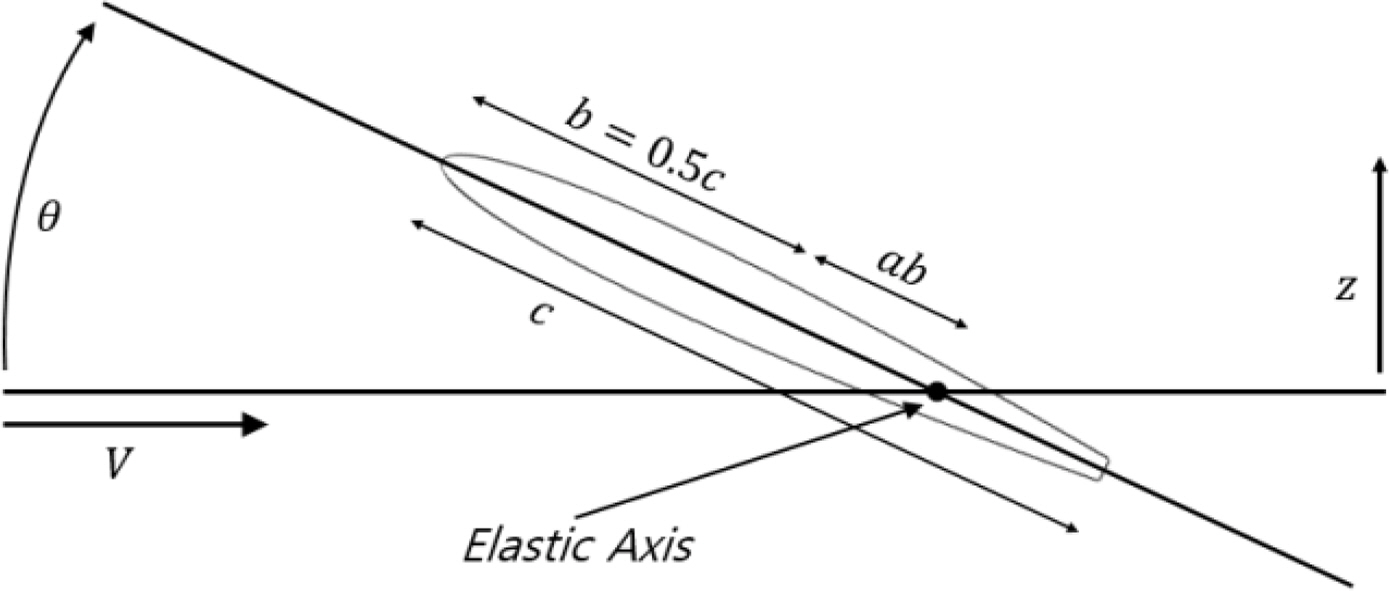
where ρf refers to the fluid density; a is the dimensionless distance from the midpoint of the chord to the elastic axis of the wing cross-section; b is half the chord length; and V, d and θ refer to the flow velocity, bending displacement, and twisting angle, respectively. The upward direction of d and LT is positive, and the counterclockwise direction of θ and TT is positive. A schematic diagram of a, b, c and V, and the directions of d and θ in the wing cross-section is shown in Fig. 1.
The potential method is based on the assumption of incompressible, inviscid and irrotational condition. In this study, we focused on predicting VIV when vortex shedding occurs in the wake of ship rudders. As vortex shedding occurs due to the viscosity and boundary layer of the fluid, it is theoretically impossible to predict the vortex strength and vortex shedding frequency based on the potential method. Therefore, CFD considering viscosity is essential for deriving the vortex-induced fluid force and moment. Chae (2015) developed a BT FSI analysis method for deriving the VIV of the hydrofoil using CFD. By considering only the first bending- and twisting-mode vibration of the hydrofoil, the bending displacement and twisting angle of the hydrofoil can be assumed, as in Eq. (9).
The equation of motion Eq. (10) is obtained applying Eq. (9) to the Lagrange equation Eq. (1) described in Section 2.1, as follows:
Here,
where xθ, rθ, ωb1, ωt1, ξ and Ip refer to the distance from the elastic axis to the center of gravity, the radius of gyration, the first bending-mode natural frequency, the first twisting-mode natural frequency, the damping coefficient, and the polar moment of inertia, respectively; Sff11 is the value obtained by integrating the square of the first bending-mode shape function Sf1 from 0 to s. In the same way, Sgg11, Sf″f″11 and Sfg11 are the values obtained by integrating the square of Sg1, Sf″1 and Sf1Sg1 from 0 to s, respectively. The loose-coupling method can perform the FSI analysis using Eq. (10) as the governing equation and applying the boundary conditions in Eq. (11) at the fluid-structure boundary interface.
where νm, σs, σf and n refer to the mesh movement velocity, structural stress, fluid stress, and normal vector, respectively
FCFD includes the inviscid force FT = [Sff11LT, Sgg11TT]T based on the potential method. When the fluid density is much smaller than the structural density, the effect of the inviscid force of FCFD is inconsiderable. Therefore, it is appropriate to perform the FSI analysis using the loose-coupling method based on Eq. (10). However, in an underwater environment, since the fluid density is quite high, the effect of the inviscid force by the added mass, added damping, and added stiffness is relatively considerable. Therefore, it is inappropriate to use Eq. (10) as the governing equation. Chae (2015) used Eq. (12), where the inviscid force term is excluded on both sides of Eq. (10), as the governing equation for the BT FSI analysis, to reflect the effect of the inviscid force in an underwater environment without subiterations in the partitioned method.
While the FSI described in Eq. (12) in the previous section has the advantage of favorably reflecting the effect of the inviscid force by the added mass, etc., without subiteration in an underwater environment, it also has a disadvantage in that it cannot realize resonance and lock-in phenomena caused by high bending- and twisting-mode vibration by taking into account only the first bending- and twisting-mode vibration. Therefore, in this study, we extend the governing equation for the FSI analysis to take into account high bending- and twisting-mode vibration. First, we extend the equation for the bending displacement and twisting angle, yielding
If the governing equation for FSI analysis that considers high bending-and twisting-mode vibrations is obtained by applying Eq. (13) to Eq. (1) and Eqs. (7) – (8), the equation can be written in the form of a matrix equation of size 2n × 2n for the nth mode. The derived matrix equation has regularity; thus, it can be generalized to a matrix pattern of size 2 × 2. The governing equation for the FSI analysis is expressed for a relatively simple second mode as follows:
Here,
i,j = 1,2
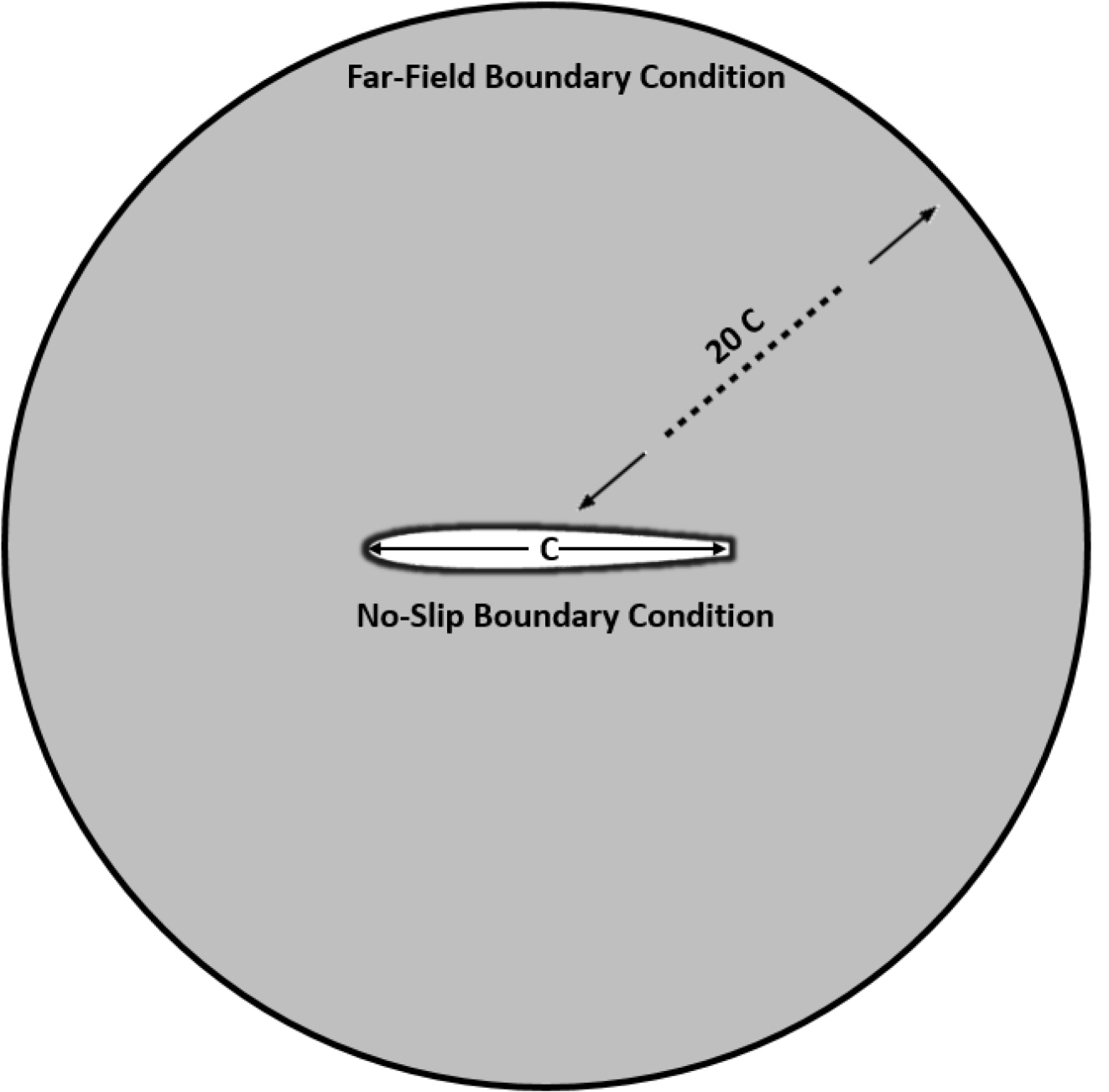
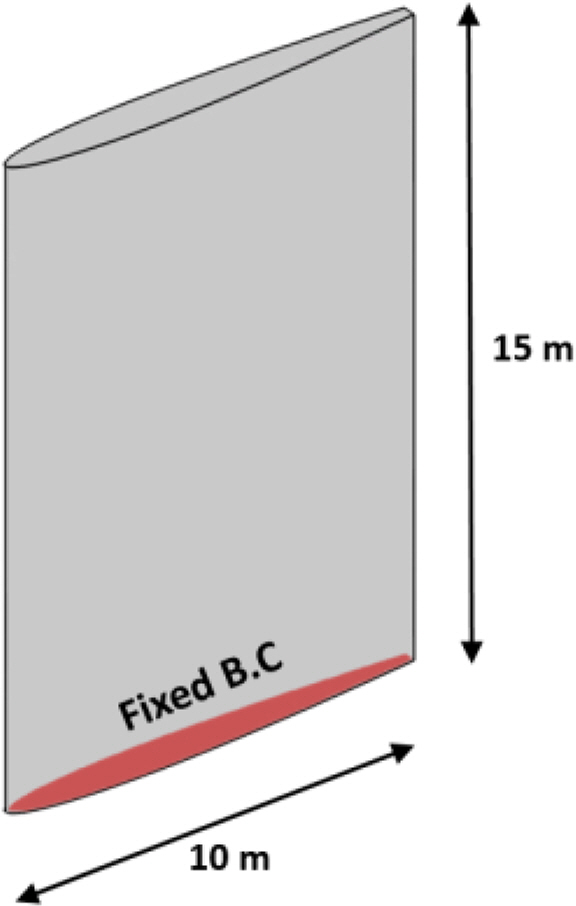
In the process of FSI analysis, we performed the CFD analysis of the hydrofoil by first identifying the reliability of the CFD analysis. In this analysis, we used OpenFOAM, an open-source CFD program. The CFD solver is based on the Reynolds-averaged Navier-Stokes (RANS) governing equation. The k− ω shear stress transport (k − ω SST) model combining the k − ω model and the k − ∊ model was used as the turbulence model (Kim et al., 2017). The detailed analysis settings are listed in Table 1. For comparison with the experimental results, the same cross-section shape as that of the test object of Ausoni (2009) and Zobeiri (2012) was used as the hydrofoil shape for analysis. The wing cross-section shape to be analyzed is shown in Fig. 2. It is the same as NACA0009; however, it is cut so that the end thickness is 3.22% of the chord length. The chord length of the hydrofoil for analysis is 0.1 m. For comparison with the experimental results (Ausoni, 2009; Zobeiri, 2012), we performed the CFD analysis for a total of 17 flow velocities ranging from 10 m/s to 26 m/s at an interval of 1 m/s. Considering the underwater environment, we set the medium density to 1000 kg/m3 and the kinematic viscosity to 1e−6 m2/s. The analysis domain is a circle with a radius of 20 times the chord length, where the elastic axis of the analysis object is set to be at the origin. The analysis domain and boundary conditions are shown in Fig. 3, and the analysis mesh is shown in Fig. 4. The number of meshes is approximately 100,000, and the dimensionless number y+ value related to the thickness of the mesh closest to the wall is approximately 1. By assuming a far-field condition, we applied freestream velocity and freestream pressure boundary conditions to the outer boundary of the analysis domain and applied a no-slip boundary condition to the wing surface. We used 5e−7 s as the time step, so that the maximum value of the Courant-Friedrichs-Lewy (CFL) number related to analysis stability did not exceed 1.
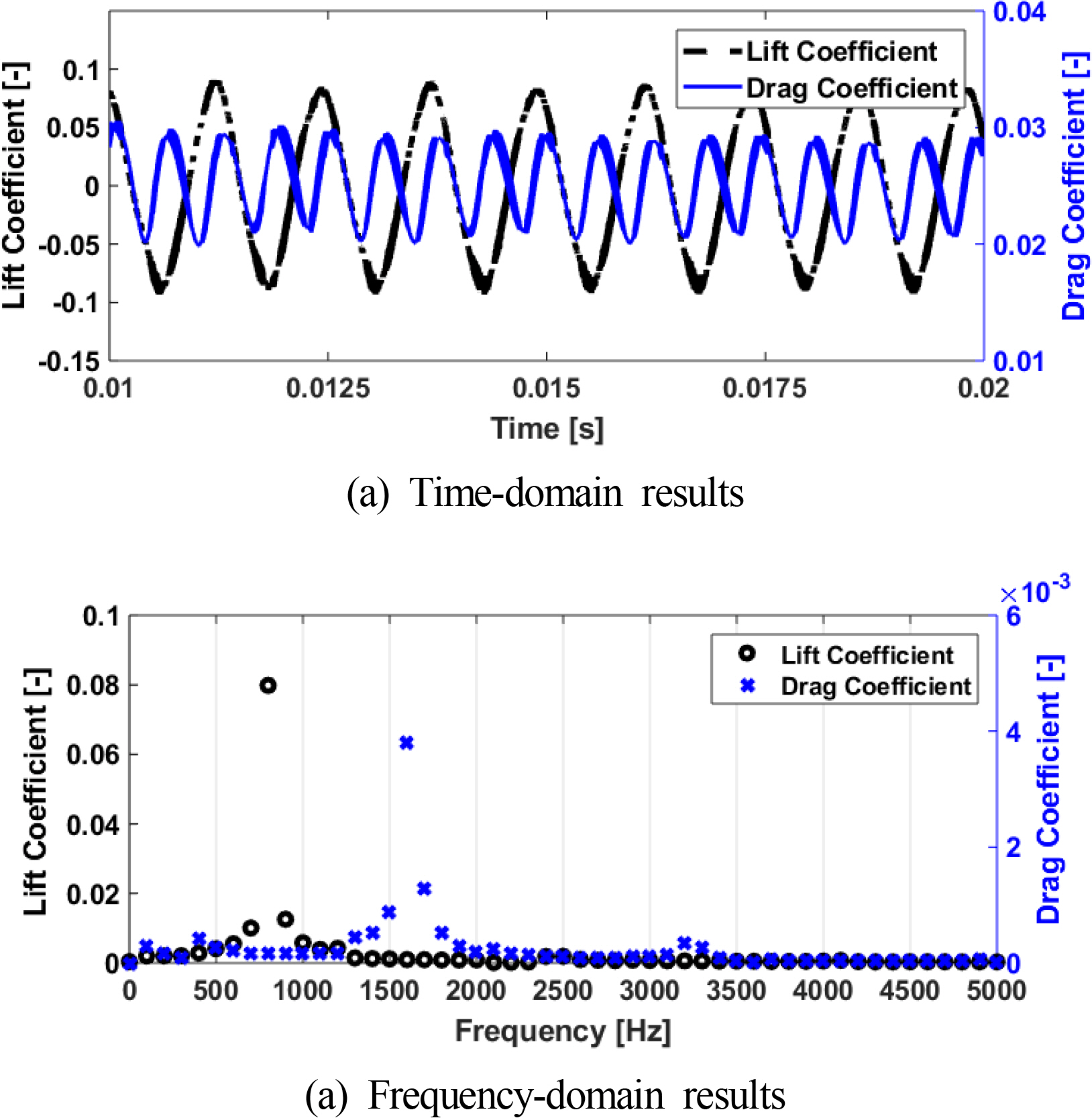
The CFD analysis result of the flow field around the hydrofoil is shown in Fig. 5, which confirms vortex shedding in the wake. The analysis results of drag and lift coefficients are shown in Fig. 6. Vibration characteristics of one dominant peak component are observed. In particular, the peak frequency of the drag coefficient is twice the peak frequency of the lift coefficient, which is attributed to the characteristics of vortex shedding that occurs alternately on both sides (Blevins, 2001). A comparison of the mean values of the drag and lift coefficients obtained using the experiment and the CFD analysis is shown in Table 2. For the drag coefficient, the analysis results differ from the experimental results by approximately 4% (Zobeiri, 2012); this is attributed to the difference in the 3D effect between the experimental and analysis results (Mittal and Balachandar, 1995). In addition, since this analysis model has a symmetrical shape with an angle of attack of 0°, the lift coefficient was approximately 0 in the experimental and analysis results. The Strouhal number of the hydrofoil for the flow velocity between the experimental and analysis results is shown in Fig. 7. The Strouhal number is a dimensionless number for the vortex shedding frequency f, and is defined as fD/V. Assuming that there is no resonance and lock-in, when D is set as the thickness between separation points, the Strouhal number is approximately 0.2 for a wide range of the Reynolds number regardless of the cross-section shape (Sarpkaya, 1979). The experimental results (Ausoni, 2009) show that the Strouhal number changes at the flow velocities of 10–14 m/s. This is because the vortex shedding frequency at these flow velocities is close to the structure’s natural frequency, thus causing resonance and lock-in phenomena. At the flow velocity after 14 m/s, the Strouhal number test result shows that it has a constant value of 0.23, and the Strouhal number derived by the CFD analysis (model scale, x) under the same Reynolds number has a constant value of approximately 0.24 in the entire flow velocity range, which is similar to the experimental results. We verified the reliability of this CFD analysis procedure by confirming that the lift coefficient, drag coefficient, and Strouhal number derived by the CFD analysis matches the experimental results.
To identify the characteristics of the fluid force frequency of the ship rudder, we performed the CFD analysis for each flow velocity on the model scale shape, enlarged 100 times, and represented the Strouhal number in Fig. 7 (ship scale, square). Despite a 100 times difference in the Reynolds number, the Strouhal number was approximately 0.22 in the entire flow velocity range, which is similar to the experimental and model scale analysis results and also matches Sarpkaya’s results (1979).
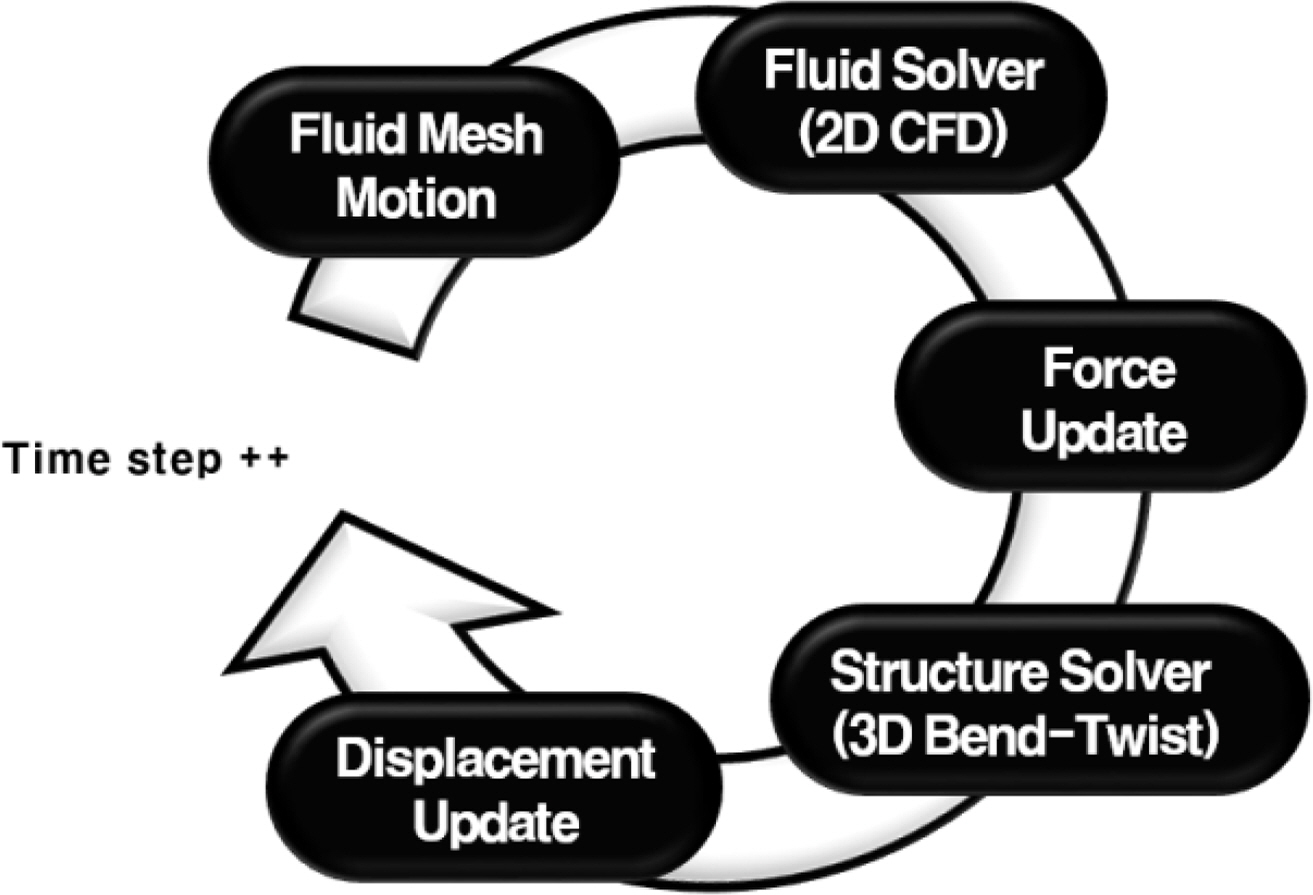
The high-mode BT FSI analysis procedure is shown in Fig. 8. For the CFD analysis, we used OpenFOAM, as in Section 3.1. The pimpleDyMFoam solver suitable for the analysis with mesh movement was used. The detailed analysis settings are listed in Table 3. The equation of motion Eq. (14) was used as the governing equation for the bending-twisting structural analysis.
To simulate the ship rudder, we set the analysis target to the model scale shape, enlarged 100 times, and created the CFD analysis using the same procedure as in Section 3.1. We applied freestream velocity and freestream pressure boundary conditions to the outer boundary of the analysis mesh domain and applied moving wall velocity boundary conditions to the wing surface, which satisfied Eq. (11). We used 2e−5 s as the time step, so that the maximum value of the CFL number related to analysis stability did not exceed 1.
The structural parameter values required for the FSI analysis are shown in Table 4; ρs, EI, ξ, μ, and the center of gravity were derived for the shape, as seen in Fig. 9, and the material properties were derived for the steel structural model. Fixed boundary conditions were applied at the end of the model for the simulation of the ship rudder. The bending-mode natural frequency fB, and the twisting-mode natural frequency fT were derived using the 3D finite element method (FEM) to analyze the vibration for the structural model. When the twisting mode occurs, the position where the deformation was minimal was set as the elastic axis, and rθ was derived based on this. The values related to the twisting-mode shape function were derived using the Euler-Bernoulli cantilever analytic solution (Abu-Hilal, 2003), and the first and second bending- and twisting-mode shape functions are shown in Fig. 10. It is expected that resonance and lock-in phenomena will occur in the first twisting mode and the second bending mode within the flow velocity range of this analysis; thus, we performed the BT FSI analysis considering the second mode as well.
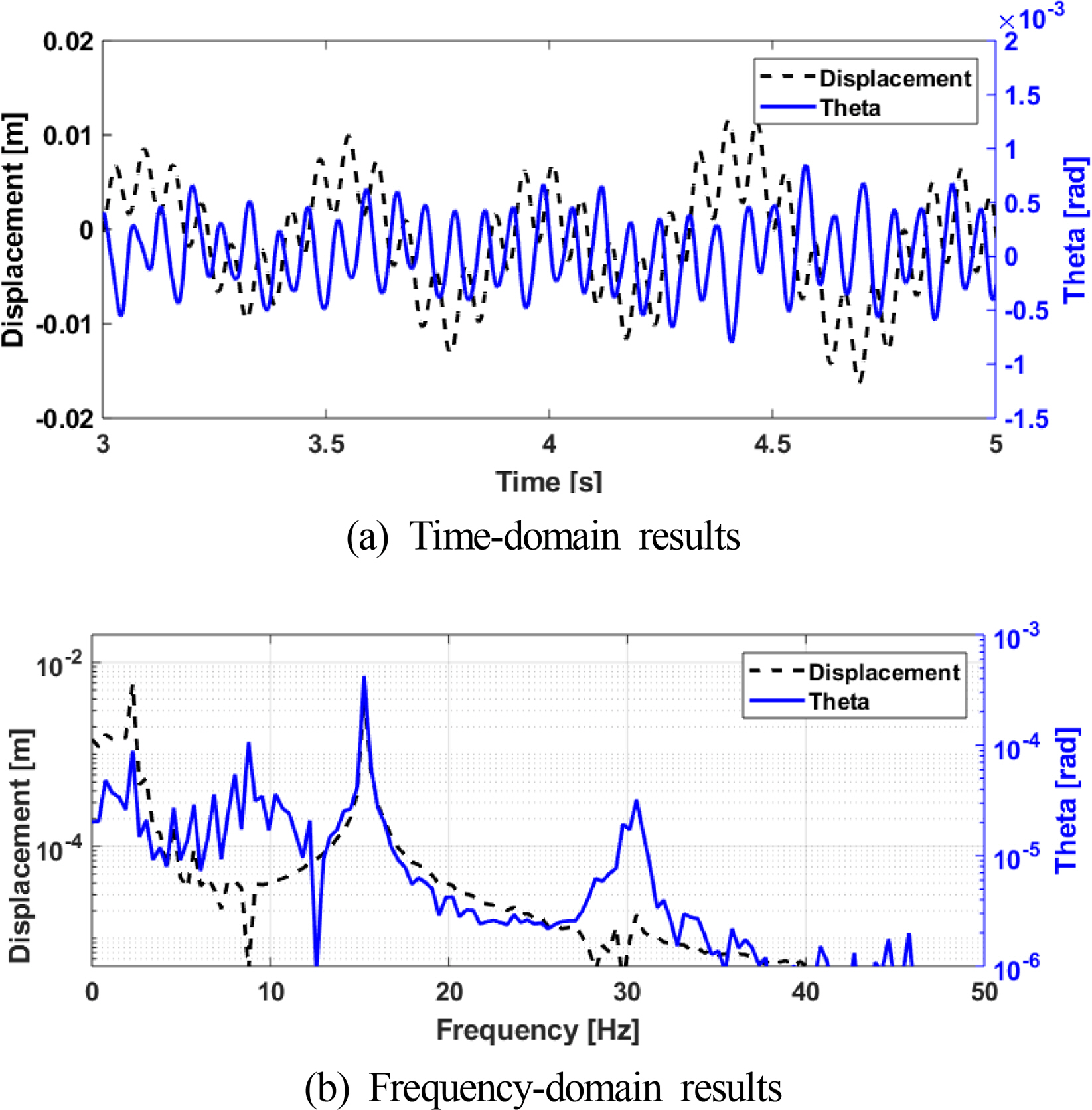
The vibration displacement and angle derived by the BT FSI analysis at a Reynolds number of 2.3e8 are shown in Fig. 11, and periodic vibration is observed in the figure. In particular, peak responses are observed in both the vortex shedding frequency component and the underwater natural frequency component. The VIV frequency for each flow velocity derived by high-mode BT FSI analysis of the hydrofoil is shown in Table 5. Overall, the VIV frequency tends to increase with an increase in the flow velocity. This is because the Strouhal number has a constant value in a wide range of the Reynolds number. We confirmed lock-in phenomena in which the VIV frequency was maintained at a constant value at flow velocities of 13–14 m/s and 23–24 m/s. We obtained the underwater natural frequency for the analysis target using the analytic solution of a cantilever (Ausoni, 2009), and compared this with the lock-in frequencies, as displayed in Table 6. The frequencies favorably matched the first twisting-mode underwater natural frequency and the second bending-mode underwater natural frequency, respectively, which confirm that 13–14 m/s was the first twisting-mode resonance and lock-in region; 23–24 m/s is the second bending-mode resonance and lock-in region. The underwater natural frequency is inversely proportional to the scale and the Strouhal number has a constant value in a wide range of the Reynolds number. Therefore, if the shape is the same, the lock-in velocity at which vortex shedding occurs at the underwater natural frequency, even when the scale is different, is the same as in Eq. 15 (Ausoni, 2009).
Here, Vlock, St and fw are the lock-in velocity, Strouhal number, and underwater natural frequency, respectively. Using this, the 1/100 scale model experimental results (Zobeiri, 2012) were compared with the lock-in velocity. The lock-in velocity (11–13 m/s) obtained as a result of the experiment and the lock-in velocity (11–13 m/s) obtained as a result of the high-mode BT FSI analysis were similar, which verifies the reliability of this analysis in terms of the frequency.
To examine the structural stability of ship rudders with the VIV responses derived through the analysis performed in this study, we referred to the local vibration guidance suggested by Lloyd’s Register (Lloyd’s Register, 2006). As seen in Fig. 12, the results of the VIV displacement derived using the high-mode BT FSI analysis are displayed in the ship’s local vibration guidance graph. The VIV responses displacement and frequency are shown in Table 5 and Table 7, respectively. An x in red indicates the displacement when lock-in occurs, and a circle in blue indicates the displacement in other situations. In the frequency range of interest (5–100 Hz), the red shaded area indicates the area where the risk due to vibration is expected to be high, and the other areas are shown as the blue shaded areas. The VIV responses in the lock-off condition was expected to cause a high risk at some flow velocities close to the second bending mode. The VIV responses in the first twisting mode and the second bending mode lock-in condition was expected to cause a high risk in terms of local vibration.
In this study, we performed high-mode BT FSI analysis on the hydrofoil to predict the VIV responses in the wake of ship rudders. In particular, the conventional BT FSI analysis method that considers only the first bending- and twisting-mode vibration was extended into the high mode to numerically predict the resonance and lock-in phenomena caused by the high mode. The results of the high-mode BT FSI analysis were verified in terms of the frequency by comparing the analysis results and the experimental results for the analysis target based on the NACA0009 hydrofoil cross-section.
The experimental results and the FSI analysis results confirmed that the vortex shedding frequency generally tends to increase with an increase in the flow velocity, and that the vibration increases and simultaneously the vortex shedding frequency shifts to the structure’s natural frequency as the vortex shedding frequency approaches the structure’s natural frequency. When the VIV displacement derived from the FSI analysis results was analyzed based on the local vibration guidance published by Lloyd’s Register, it was expected that there would be a strong possibility of structural defects occurring due to resonance and lock-in phenomena. Therefore, we confirmed that there was a need for technology to predict the resonant and lock-in phenomena, including the high mode.
We suggest the following two directions for future research. First, to structurally simulate the actual ship’s rudder, research on the mode characteristics of the cantilevered structure, including the web structure and rudder stock, must be conducted. Second, research on methods for high-mode BT FSI analysis is necessary when non-uniform flow instead of uniform flow enters as incoming flow. Studies based on these two topics can help further develop technology to predict the VIV of ship rudders in actual ship operation, and this analysis model is expected to facilitate a safety review process when designing an actual ship.
Acknowledgements
This research was conducted with the support of Seoul National University BK21, Education and Research Center for Creative Offshore Plant Engineers. It was also supported by the Research Institute of Marine Systems Engineering (RIMSE) and the Research Foundation (2019R1F1A1062914).
Fig. 7.
Comparison of Strouhal number for various flow velocities for CFD results and experimental results

Fig. 12.
FSI analysis results of vortex-induced vibration displacements with local vibration guidance published by Lloyd’s Register
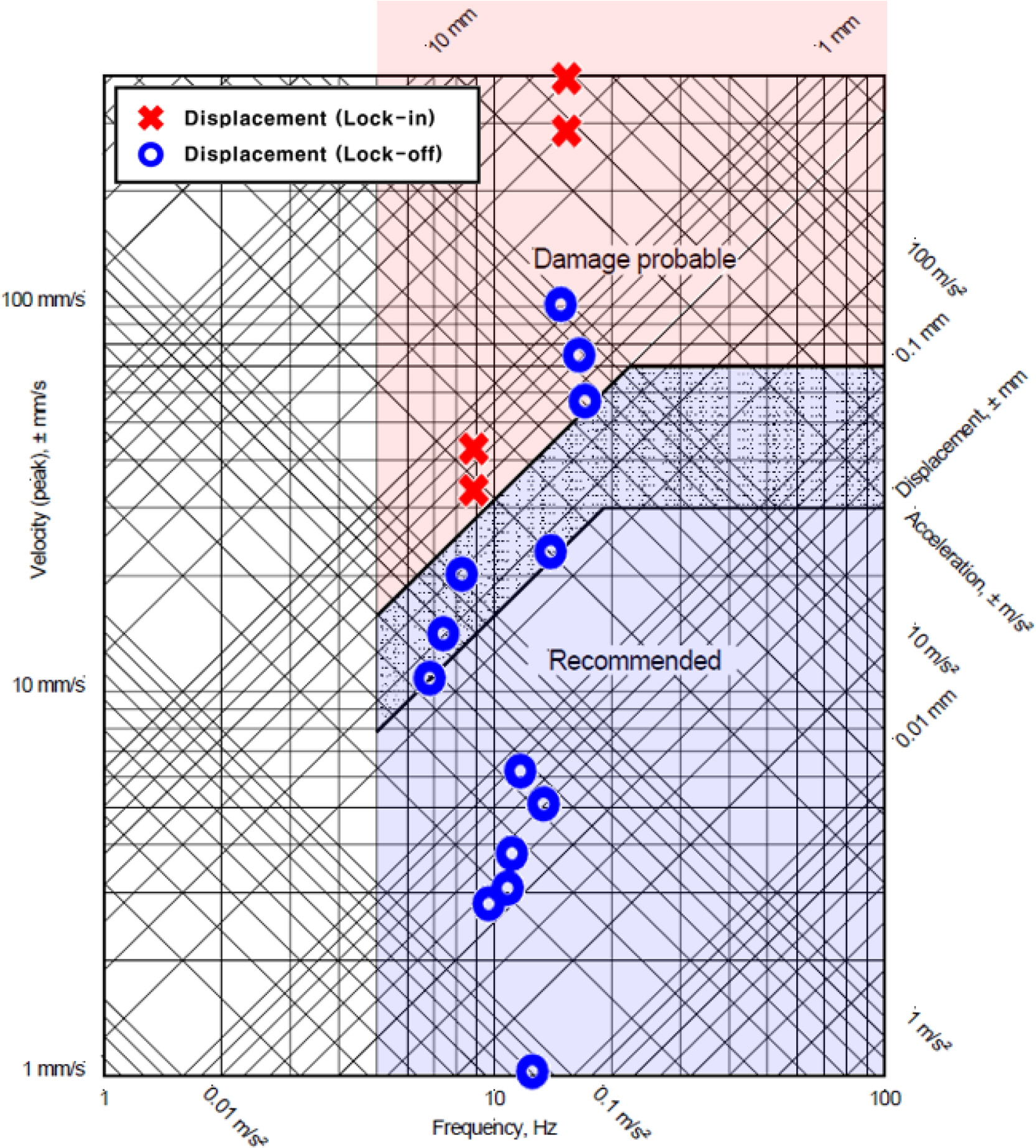
Table 1.
Detailed CFD solver setting
| Solver platform | OpenFOAM 4.x |
| Solver | pimpleFoam |
| Solver algorithm | PIMPLE1 algorithm |
| Turbulence model | RANS, k− ω SST |
| Time derivative schemes | Backward (transient, second order implicit) |
| Gradient schemes | Gauss linear |
| Velocity FV solver | Symmetric Gauss-Seidel |
| Pressure FV solver | PCG2 |
Table 2.
Comparison of mean value of lift and drag coefficient between CFD and experimental results at Re = 1.1e6
| At Re = 1.1e6 | Experiment | CFD |
|---|---|---|
| Drag Coefficient (CD) | 0.0240 | 0.0243 |
| Lift Coefficient (CL) | 0 | −0.0019 |
Table 3.
Detailed CFD solver settings for high-mode BT FSI analysis
Table 4.
Structural input parameters for second-mode BT FSI analysis
Table 5.
Vortex-induced vibration frequency for various flow velocities using high-mode BT FSI analysis
Table 6.
Comparison between FSI analysis lock-in frequency and solution of analytic underwater natural frequency
| Analytic solution | FSI analysis | |
|---|---|---|
| 1st Twisting/1st Lock-in freq (Hz) | 8.46 | 8.86 |
| 2nd Bending/2nd Lock-in freq (Hz) | 15.81 | 15.43 |
Table 7.
Vortex-induced vibration displacement for various flow velocities using high-mode BT FSI analysis
References
Abu-Hilal, M. (2003). Forced Vibration of Euler-Bernoulli Beams by Means of Dynamic Green Functions. Journal of Sound and Vibration, 267(2), 191-207.
https://doi.org/10.1016/S0022-460X(03)00178-0

Ausoni, P. (2009). Turbulent Vortex Shedding from a Blunt Trailing Edge Hydrofoil (Ph.D. Thesis). EPFL, Lausanne; Swiss.
Blevins, RD. (2001). Flow-induced vibration. 2nd ed Florida, USA. Krieger Publishing.
Campbell, RL. (2010). Fluid-structure Interaction and Inverse Design Simulations for Flexible Turbomachinery (PhD Thesis). The Pennsylvania State University; University Park, USA.
Chae, EJ. (2015). Dynamic Response and Stability of Flexible Hydrofoils in Incompressible and Viscous Flow (PhD Thesis). The University of Michigan; Ann Arbor, USA.
Felippa, CA., Park, KC., & Farhat, C. (2001). Partitioned Analysis of Coupled Mechanical Systems. Computer Methods in Applied Mechanics and Engineering, 190(24–25), 3247-3270.
https://doi.org/10.1016/S0045-7825(00)00391-1

Jung, JH., Jeong, K L., Gill, JH., & Jung, D. (2019). Large Eddy Simulation of Free Motion of Marine Riser using OpenFOAM. Journal of Ocean Engineering and Technology, 33(5), 387-393.
https://doi.org/10.26748/KSOE.2019.074


Kim, JI., Park, IR., Kim, KS., & Ahn, JW. (2017). Numerical Analysis of Non-Cavitating and Cavitating Performance of a SVA Potsdam Propeller. Journal of the Society of Naval Architects of Korea, 54(3), 215-226.
https://doi.org/10.3744/SNAK.2017.54.3.215


Lee, AH. (2014). Fluid-Structure Interaction of Large Amplitude Structure Vibrations and Moderately High Reynolds Number Turbulent Flows (PhD Thesis). The Pennsylvania State University; University Park, USA.
Lloyd’s Register. (2006). Ship Vibration and Noise Guidance Notes, London, United Kingdom. Lloyd’s Register.
Mittal, R., & Balachandar, S. (1995). Effect of Three-dimensionality on the Lift and Drag of Nominally Two-dimensional Cylinders. Physics of Fluids, 7(8), 1841-1865.
https://doi.org/10.1063/1.868500

Münch, C., Ausoni, P., Braun, O., Farhat, M., & Avellan, F. (2010). Fluid-structure Coupling for an Oscillating Hydrofoil. Journal of Fluids and Structures, 26(6), 1018-1033.
https://doi.org/10.1016/j.jfluidstructs.2010.07.002

Sarpkaya, T. (1979). Vortex-Induced Oscillations: A Selective Review. Journal of Applied Mechanics, 46(2), 241-258.
https://doi.org/10.1115/1.3424537


Son, HA., Lee, SS., & Cho, SR. (2019). Effects of Flow Acceleration on Drag Force and Wake Field of 2D Circular Cylinder. Journal of the Society of Naval Architects of Korea, 56(6), 507-514.
https://doi.org/10.3744/SNAK.2019.56.6.507.

Theodorsen, T. (1949). General Theory of Aerodynamic Instability and the Mechanism of Flutter. Washington, DC, USA. National Advisory Committee for Aeronautics.
Young, YL., Chae, EJ., & Akcabay, DT. (2012). Hybrid Algorithm for Modeling of Fluid-structure Interaction in Incompressible, Viscous flows. Acta Mechanica Sinica, 28(4), 1030-1041.
https://doi.org/10.1007/s10409-012-0118-3


Zobeiri, A. (2012). Effect of Hydrofoil Trailing Edge Geometry on the Wake Dynamics (Ph.D. Thesis). EPFL, Lausanne; Swiss.
- TOOLS
-
METRICS

-
- 1 Crossref
- Scopus
- 2,755 View
- 279 Download
- Related articles in JOET
-
A Study on the Internet Based Cooperation-Design system for Ship Design2001 November;15(4)
A Study on the Prediction of Wave Deformation Model1995 December;9(2)
Numerical Study on Wave-Induced Motion Response of Tension Leg Platform in Waves2014 December;28(6)
Study on Coning Motion Test for Submerged Body2015 December;29(6)
A Preliminary Study on the Ice-induced Fatigue in Ice-going Ships2016 ;30(4)