|
 |
- Search
| J. Ocean Eng. Technol. > Volume 33(5); 2019 > Article |
|
Abstract
Because offshore structures are affected by various environmental loads, the risk of damage is high. As a result of ever-changing ocean environmental loads, damage to offshore structures is expected to differ from year to year. However, in previous studies, it was assumed that a relatively short period of load acts repeatedly during the design life of a structure. In this study, the residual life of an offshore wind turbine support structure was evaluated in consideration of the timing uncertainty of the ocean environmental load. Sampling points for the wind velocity, wave height, and wave period were generated using a central composites design, and a transfer function was constructed from the numerical analysis results. A simulation was performed using the joint probability model of ocean environmental loads. The stress time history was calculated by entering the load samples generated by the simulation into the transfer function. The damage to the structure was calculated using the rain-flow counting method, Goodman equation, Miner’s rule, and S-N curve. The results confirmed that the wind speed generated at a specific time could not represent the wind speed that could occur during the design life of the structure.
해상풍력발전기는 육상용과는 다르게 풍 하중뿐만 아니라 수심 및 해저지반 등과 같은 환경적 요인과 조류 및 파랑 등이 바람과 함께 복합적으로 작용한다. 복합하중은 지역에 따라 다르며, 해상풍력발전기를 구성하는 다양한 요소 중 지지구조물에서 복합하중의 대부분을 부담한다. 이러한 지지구조물은 전체 시스템 중에서 제작 및 시공에 소요되는 비용도 만만치 않으므로 안전과 비용 측면에서 하중의 예측 및 평가는 필수적이고 중요한 과정이다. 구조물에 작용하는 하중은 해양환경에 노출된 구조물의 수명에 직접적인 영향을 주는데, 크기가 작은 복합하중이 지속적으로 가해질 경우 취약한 부재에 손상이 발생되어 제 기능을 발휘하지 못할 수 있다. 이러한 지지구조물의 피로 손상에 대한 설계 방법은 다양한 설계기준에 제시되어 있고 (AISC 2005; API 2007; DNV 2011; IEC 2005; IEC 2009), 여러 연구자들에 의해 피로 평가에 대한 연구가 수행되었다. Dong et al.(2011)은 주파수영역에서 각 부재별 응력전달함수를 구하여 피로 손상에 대해 평가하였고, 나아가 신뢰성해석을 통해 확률론적 평가를 수행하였다(Dong et al., 2012). Yeter et al.(2014)와 Yeter et al.(2015)은 응력스펙트럼 밀도함수에서 IFFT(Inverse fast fourier transform) 방법을 사용하여 응력시간이력을 계산함으로써 피로해석 및 신뢰성해석을 수행하였다. Kelma and Schaumann (2015)은 재킷형식 지지구조물의 K-조인트에서 발생되는 응력범위에 대해 Peak over threshold(POT) 기법을 적용하여 높은 응력범위의 확률분포를 추정하고 피로손상에 미치는 영향에 대해 분석하였다. 선행 연구를 비롯한 많은 해상구조물의 손상 평가는 특정 응력수준에 대해 수행되거나 재료에 대한 불확실성만을 고려하며, 하중의 경우 일반적으로 단기간 하중이 설계 수명 동안 반복적으로 가해진다는 가정에 기반을 둔다. 그러나 지구의 바람 및 파랑에 대한 다양한 연구에서 수십 년 동안 평균 및 극치가 증가했을 가능성이 있음을 보여주며(Thomas et al., 2008; Tokinaga and Xie, 2011; McVicar et al., 2012; Young et al., 2012), 매년 상이한 분포 형태를 갖는 하중은 구조물의 수명에 직접적인 영향을 주기 때문에 특정 기간의 하중이 반복된다는 가정은 매우 위험한 제한사항임을 판단할 수 있다. 본 연구는 위와 같은 가정에서 발생할 수 있는 문제를 수치적 분석결과를 통해 제기하고, 효율적인 해결 방안을 찾기 위해 수행되었다. 결정론적 방법과 시뮬레이션 기법을 활용한 확률론적 방법의 피로수명을 계산하여 비교하였으며, 확률론적 방법을 이용하여 환경요인의 발생 시기에 따른 기대수명을 산정하였다.
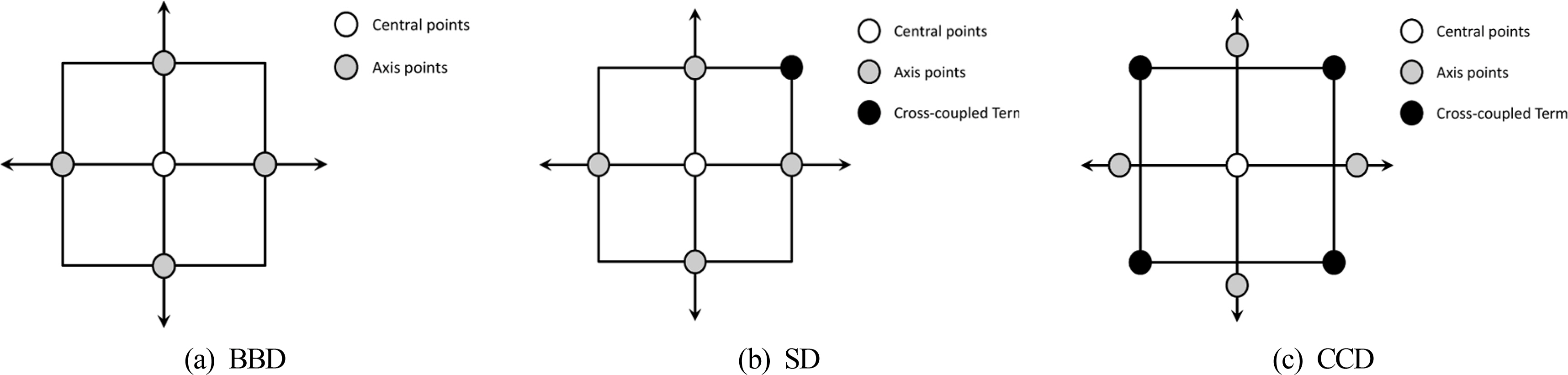
동적해석은 일정시간까지 각 시간간격에 대해 반복적인 해석이 요구되므로 정적해석에 비해 많은 시간이 소요된다. 특히 해상풍력터빈은 20년 이상의 설계수명을 갖는 구조물이므로 이 시간 동안 동적해석을 수행하는 것은 현실적인 어려움이 따른다. 이 경우 정적해석을 기반으로 정의된 회귀모델을 응답 산정에 활용하여 소요 시간문제를 해결할 수 있다. 회귀모델은 응답면 기법(Response surface method)을 이용하여 정의할 수 있다. 구조해석을 통해 얻을 수 있는 응답은 음함수 형태를 나타내게 되는데, 이러한 경우 응답면 기법을 이용하여 양함수 형태로의 근사화가 가능하다(Schuëller et al., 1989; Raymond and Douglas, 2002). 먼저 입력 변수의 발생이 가능한 범위를 결정하여 해당범위 내에서 표본점(Sample points)을 선택하고, 각 표본점에 대해 해석을 수행하여 응답을 산출하면 최소자승법(Least square method)을 이용하여 응답면 구성에 사용되는 계수를 얻을 수 있다. 주로 사용되는 표본점 산정 방법은 Fig. 1과 같이 BBD (Bucher-bourgund design), SD(Saturated design), CCD(Central composite design) 등이 있다(Bucher and Bourgund, 1987; Haldar and Mahadevan, 2000; Box and Wilson, 1951). BBD 방법의 경우 연성항이 제외되기 때문에 구성된 응답면이 많은 오차를 수반할 수 있다는 단점이 있고, CCD 방법은 연성항을 충분히 고려하지만 다량의 표본점으로 인해 해석에 많은 시간이 된다. SD 방법은 부분적으로 연성항을 고려함으로써 효율적이나, 고려되지 않는 연성항으로 인해 오차를 가질 수 있다. 이에 높은 정확도를 보이는 CCD 방법을 연구에 이용하였다.
3가지 입력 변수(Xi)에 대한 응답면 구성은 식 (1)의 계수 b를 계산함으로써 이루어진다.
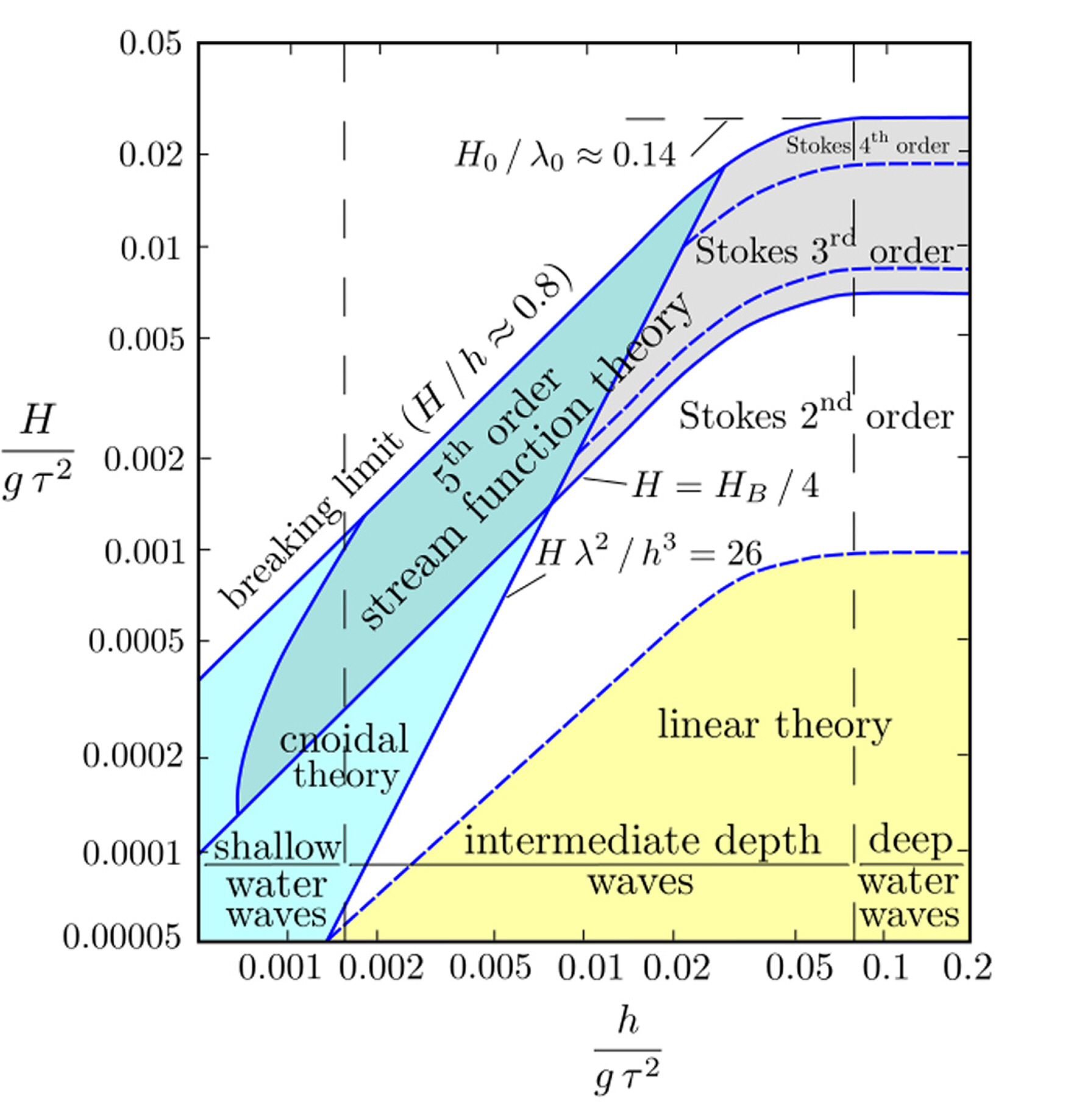
해상구조물의 설계 시 사용되는 파랑이론은 설계 해역의 환경정보(수심, 파고, 주기)로부터 Fig. 2를 통해 결정된다. 선박 또는 해양구조물 설계 단계에서 주로 사용되는 파랑이론은 선형이론으로써 수직기둥에 작용하는 파랑하중은 식 (2)의 모리슨(Morison) 방정식에 의해 계산할 수 있다(Morison et al., 1950). 본 논문에서 사용된 구조물과 같이 임의의 방향으로 경사진 부재는 유체입자의 속도 및 가속도를 경사부재의 수직 및 평행 방향으로 나누어 모리슨 방정식의 수직 성분만을 사용하는 방법이 주로 사용된다(Kim and Lee, 2015).
여기서, CD, CI, ρw, un, ∂un/∂t는 각각 항력계수, 관성력계수, 해수의 밀도, 물 입자의 수직성분 속도와 가속도를 의미한다.
부재의 연결이 용접으로 이루어진 해양구조물은 기하학적 형상에 의해 응력집중 현상이 발생된다. 용접 부재는 응력집중 현상에 의해 공칭응력보다 높은 Hot spot 응력이 발생하고, 지속적으로 작용하는 하중에 매우 취약한 것으로 알려져 있다. 이미 다양한 연구로부터 용접부의 형상계수 및 기하형상에 대한 영향 함수를 사용하여 응력집중계수(Stress concentration factor, SCF)의 산정식이 제안되었으나, 모델이 동일할 경우에도 응력집중계수는 상이하게 산정되고 Joint의 형상이 복잡한 경우에는 적용이 어려운 문제가 있다(Kuang et al., 1975; DNV, 2013; Lee, 2016). 따라서 본 연구에서는 식 (3)과 같이 상세모델링을 통해 계산된 Hot spot 응력(σh)과 공칭응력(σn)의 비를 해석에 활용하였다. 다만, 상세모델링을 통해 응력집중계수를 추정하는 경우 하중의 종류 및 방향에 따라 다양하게 계산될 수 있으므로 사용 시 이를 유의해야한다.
난류(Turbulence)는 풍속의 변화를 야기하는 요소로 터빈의 출력 및 안전성의 변동을 유발하며, 난류의 크기를 일컫는 난류강도(Turbulence intensity)에 따라 풍속의 불규칙성을 표현할 수 있다. 난류강도는 측정된 풍속 자료로부터 계산될 수 있으나, 터빈의 등급에 따라 제안된 난류강도를 이용하여 풍속의 시간이력을 얻을 수 있는 바람장(Wind field)을 생성할 수 있다. 본 연구에서는 International Electro-technical Commission(IEC) 61400-1 (IEC, 2005)에서 제안한 다음의 난류강도 계산식을 풍하중 생성에 활용하였다.
여기서, Vhub는 풍력발전기 허브 위치에서의 풍속을 의미하고, Iref는 풍속이 15 m/s인 경우 난류강도의 기댓값으로 풍력터빈의 등급에 따라 상이하며, 본 연구에서는 A등급으로 가정하여 0.16의 기댓값을 사용하였다.
해상풍력발전기에 작용하는 해양 환경하중은 바람, 파랑, 조류 등 다양하며, IEC 61400-3(IEC, 2009)의 Design load cases(DLC)에서는 피로해석 시 바람과 파랑의 결합 확률모델을 사용하도록 제시하고 있다. Johannessen et al.(2001)은 북해에서의 평균 풍속, 유의 파고, 피크 주기의 결합 확률모델을 제안하고 있으며, 본 연구에서는 해석에 사용하고자 하는 대상 구조물 설치지역의 해양 환경자료와 Johannessen et al.(2001)에 의해 제안된 확률모델을 이용하여 피로해석을 수행하고자 한다. 풍속 V가 주어진 경우 유의파고에 대한 조건부 확률분포는 2-파라미터 와이블 분포로 형상계수 kh와 척도계수 qh는 다음의 식 (5)와 같이 계산할 수 있으며, 식을 구성하는 ak, bk, aq, bq는 와이블 분포의 파라미터 계산에 사용되는 상수로, 구조물 설치 지역의 해양 환경자료와 회귀분석을 통해 계산할 수 있다.
피로해석에 사용되는 일반적인 사이클 집계(Cycle counting) 방법은 레인플로우 사이클 집계(Rainflow cycle counting)로, 시간이력이 다양한 지붕모양을 형성한다는 상상에서 유래하여 개선되어왔다(Matsuishi and Endo, 1968; Rychlik, 1987). 사이클 집계로부터 응력진폭, 평균응력 그리고 이에 상응하는 사이클 횟수가 출력되며, 이 세 가지 인자로 구성된 행렬을 마르코프 행렬(Markov matrix)라 한다. 마르코프 행렬을 이용할 경우 방대한 시간이력에 비해 자료의 양이 줄고 응답의 진폭에 대해 재구성할 수 있으나, 응답이 갖는 순차적 정보가 제거된다는 단점이 있다. 본 연구에서의 손상 계산은 순차적 정보가 요구되지 않으므로 마르코프 행렬을 피로해석에 활용하였다. Table 1은 마르코프 행렬의 예로, 임의의 외력 조건에 대해 계산된 응력 시간이력을 이용하여 산정한 것이다.
현실에서 발생하는 평균응력은 0이 아닌 경우가 대부분이나, 피로 손상을 계산할 때는 평균응력이 0인 완전 역전 조건(응력비 R = σmin/σmax = -1)에서 수행된다. 평균응력이 증가할수록 응력비는 양의 방향으로 커지고 피로한도가 증가하게 된다. 또한 다양한 사이클의 평균응력이 상이하면, 동일한 진폭을 갖더라도 응력범위의 임계치가 다를 수 있다. 때문에 효율적인 계산을 할 수 있는 응력범위 임계치의 보편화 방법이 주로 사용되는데, Goodman(1899)은 식 (8)과 같이 Goodman 방정식을 고안하였다. 식의 σa, σe, σm, σu는 각각 응력진폭, 등가응력진폭, 평균응력, 인장강도를 의미한다.
피로에 대한 정량화는 Miner(1945)에 의해 처음으로 시도되어 현재까지도 많은 연구자들에 의해 사용되고 있는 방법이다. 피로에 의한 구조물의 파괴는 다양한 복합하중에 의해 부재가 한계점까지 도달했을 때 발생되는데, 이때의 손상은 최대응력이 피로한도를 초과하는 경우에만 발생된다는 가정이 있다. 피로한도보다 낮은 응력도 손상에 영향을 미칠 수 있으나, 복잡한 하중의 처리 방법에서 발생되는 다양한 문제의 극복에는 어려움이 있다. 때문에 상기의 결함을 갖는데도 불구하고 여전히 Miner의 선형손상법칙이 사용되고 있으며, 이는 다음과 같이 표현된다. 여기서 nT, ni, Ni는 각각 전체 응력 사이클의 횟수, i번째 응력범위에 대해 발생된 사이클 횟수, i번째 응력범위에 대한 S-N 곡선의 수명을 의미한다.
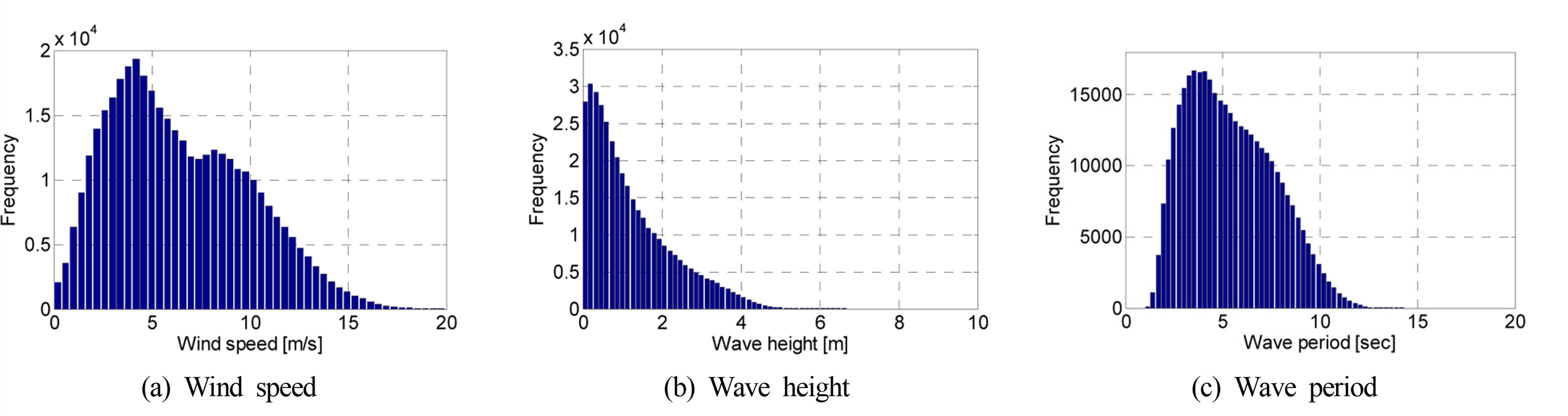
국내 지역적 특성에 부합하는 확률모델의 구성을 위해서는 장기간 관측된 자료(풍속, 파고, 주기)로부터 모델을 구성하는 계수 값을 추정해야 한다. 그러나 국내의 경우 풍력터빈의 설계 수명 이상의 기간 동안 관측된 자료는 존재하지 않으므로 MOF (2005)의 25년간 후측(Hindcast) 자료를 연구에 활용하였다. 자료의 위치는 구조물의 설치 위치에 가장 근접한 군산항 부근이다. 풍속 자료는 1시간 평균값으로 해수면 기준 10m 높이에서 산출된 것이며, 멱법칙(Power law)을 이용하여 터빈의 허브 위치에 대한 풍속으로 변환하였다.
IEC 61400-3(IEC, 2009)에는 피로 해석 시 평균풍속 및 유의파고와 더불어 피크주기를 사용하도록 제시되어있다. 그러나 보유한 자료는 유의주기이므로 Goda and Takagi(2000)가 제안한 다음의 식 (11)을 이용하여 피크주기로 변환하였다. 여기서 γ는 피크증대계수(Peak enhancement factor)를 의미한다.
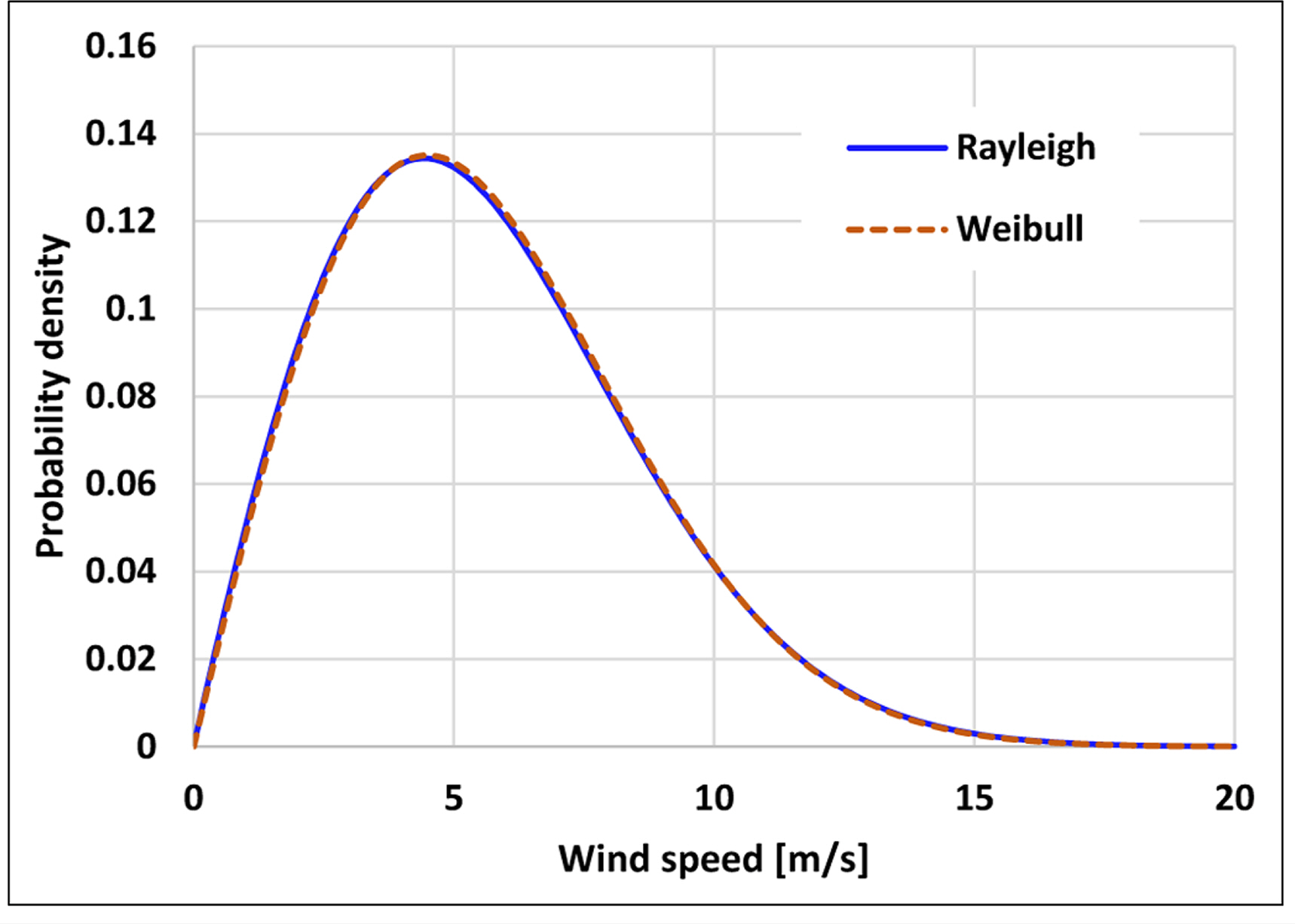
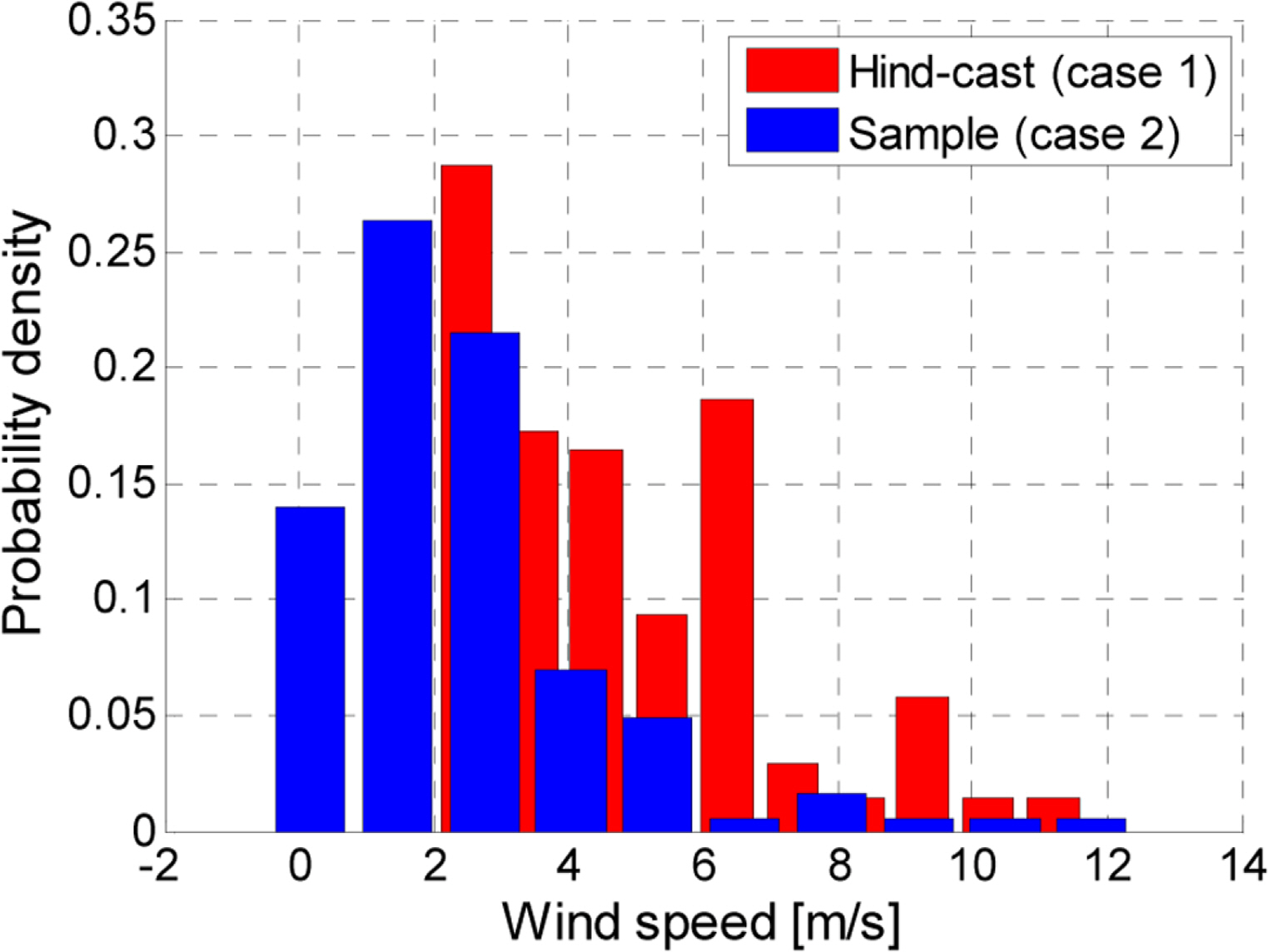
확률론적 피로수명 평가를 위해 수행되는 시뮬레이션에는 앞서 언급한 확률모델이 이용되고, 정해진 풍속에 의해 파고와 주기가 결정되므로 풍속자료에 적합한 이론적 분포를 선정해야한다. 일반적으로 풍속의 확률분포는 와이블 분포와 함께 레일리(Rayleigh) 분포가 사용되고 있으며(Manwell et al., 2002; IEC, 2005; Ucar and Balo, 2010), 상기의 Johannessen et al.(2001)이 제안한 확률모델에서도 와이블 분포가 사용되었다. 레일리 분포는 와이블 분포의 형상 파라미터를 상수(2.0)로 고정한 경우로, 평균풍속을 척도 파라미터로 취급할 수 있어 간편하다. 파라미터를 추정하는 방법으로는 모멘트법(Method of moments), 최우도법(Method of maximum likelihood) 등이 있으며, 본 연구에서는 표본크기가 충분히 클 때 가장 효율적인 방법으로 평가되는 최우도법을 이용하여 상기의 두 가지 이론적 분포의 파라미터를 추정하였다(Jeong et al., 2008). 풍속 자료로부터 추정된 확률 밀도함수는 Fig. 3에 도시하였고, 육안으로 구별하기 어려울 정도의 흡사한 형상을 띄는 것을 확인하였다. 따라서 평균풍속을 파라미터로 활용할 수 있는 레일리 분포를 풍속의 확률분포로 선정하였다. 레일리 분포의 확률밀도함수는 식 (12)와 같고, 평균풍속 V ¯ σ = V ¯ / π / 2
해상풍력발전기의 피로에 대해서는 IEC 61400-3(IEC, 2009)에서 DLC를 이용하여 평가하도록 제시되어 있다. 다양한 DLC는 터빈의 상태와 각종 하중의 조건 등을 구분하여 해석을 수행하도록 정리한 것으로 발전상태, 고장 발생 시 발전상태, 가동 시작상태 등 다양한 조건이 포함되어 있으나, 하중에 대한 해상풍력터빈 설계의 경우 크게 두 가지로 구분할 수 있다. 1년 이하의 회기주기를 갖는 정상하중조건은 일반적으로 피로하중해석에 적용되고, 50년 회기주기의 극한하중조건은 설계 풍속 및 파랑의 극한 조건을 고려한다. 본 연구의 목적 상 터빈은 설계수명 동안 고장이나 급정지 상태가 발생하지 않는다는 가정 하에 발전 상태의 조건인 DLC 1.2를 해석 조건으로 활용하였다. DLC 1.2에 대한 간략한 정보는 Table 3에 나타내었다. 여기서, 바람조건의 경우 후측 자료의 확률분포 및 시뮬레이션 기법을 이용하므로 Cut-in, Cut-out의 범위에 제한을 두지 않는다.
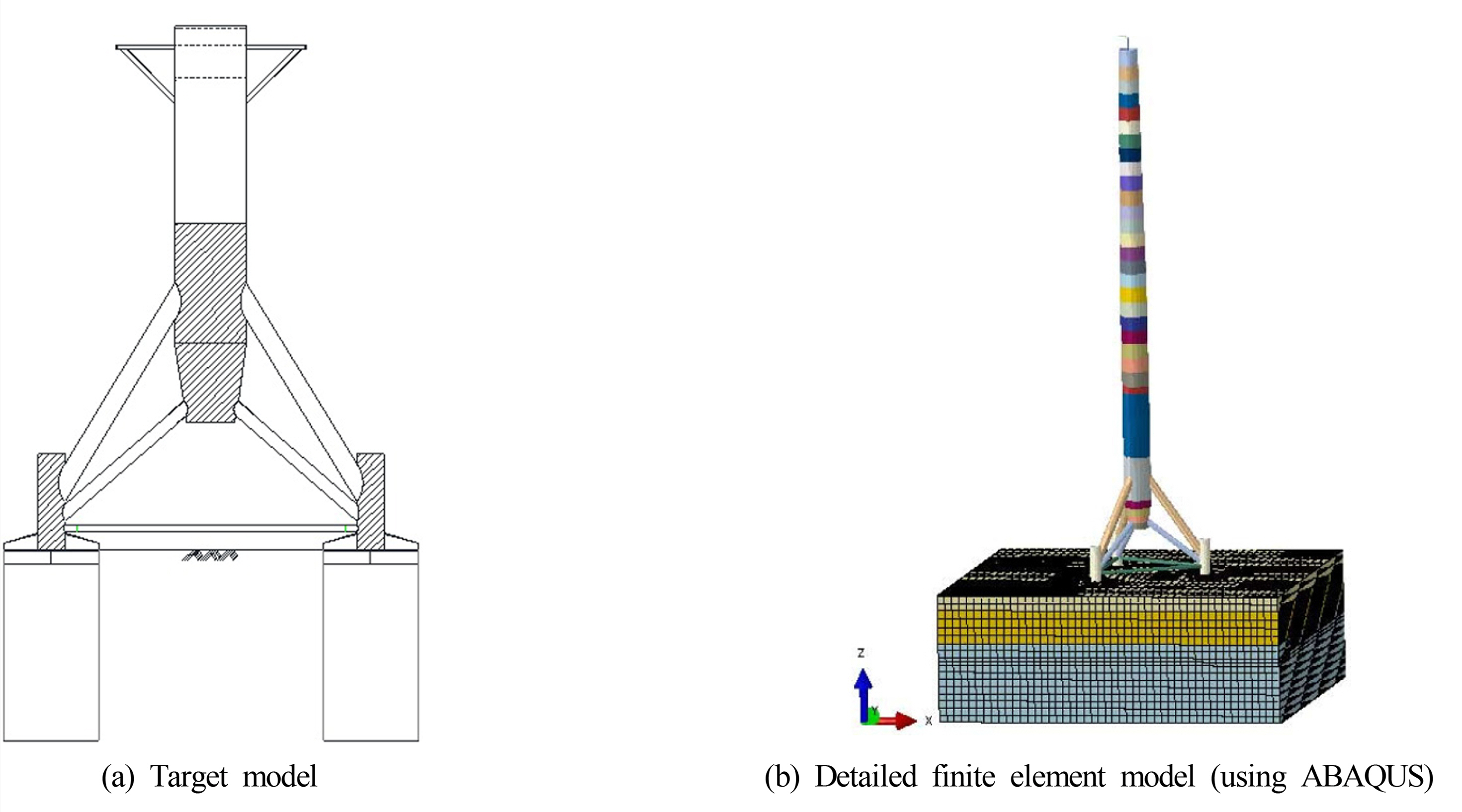
본 연구에서 활용한 구조물은 3MW 급 해상풍력발전기로 Fig. 4(a)와 같이 Tripod 형식의 지지구조이며 기본 제원은 Table 4에 나타내었다. 기초는 석션 버켓 형식을 적용하여 내부의 유체를 외부로 강제 배출시킬 때 발생하는 내⋅외부 압력차를 이용하여 설치한다. 석션 버켓의 기초를 갖는 터빈은 지반과 버켓의 상호작용에 의해 지지력이 결정되므로 설계지반정수의 산정이 중요한 과정이다. 본 연구에서는 설치 대상지인 군산 남방파제 인근의 착저식 콘 관입시험 및 지반조사 결과를 토대로 Table 5와 같이 각 층의 설계지반정수를 결정하였다.
앞서 정의된 설계지반정수는 구조물과 지반의 상호작용 효과를 나타낼 수 있는 스프링계수 계산에 사용되었다. Fig. 4(b)와 같이 ABAQUS(2013)를 이용하여 단일 석션 버켓의 상세모델을 구성하고, 단계적 하중을 입력하여 버켓의 수평력, 수직력, 모멘트 응답을 산출하였다. 하중-응답 관계로부터 지반 대표 강성행렬을 산정함으로써 Table 6과 같이 스프링계수가 계산되었다.
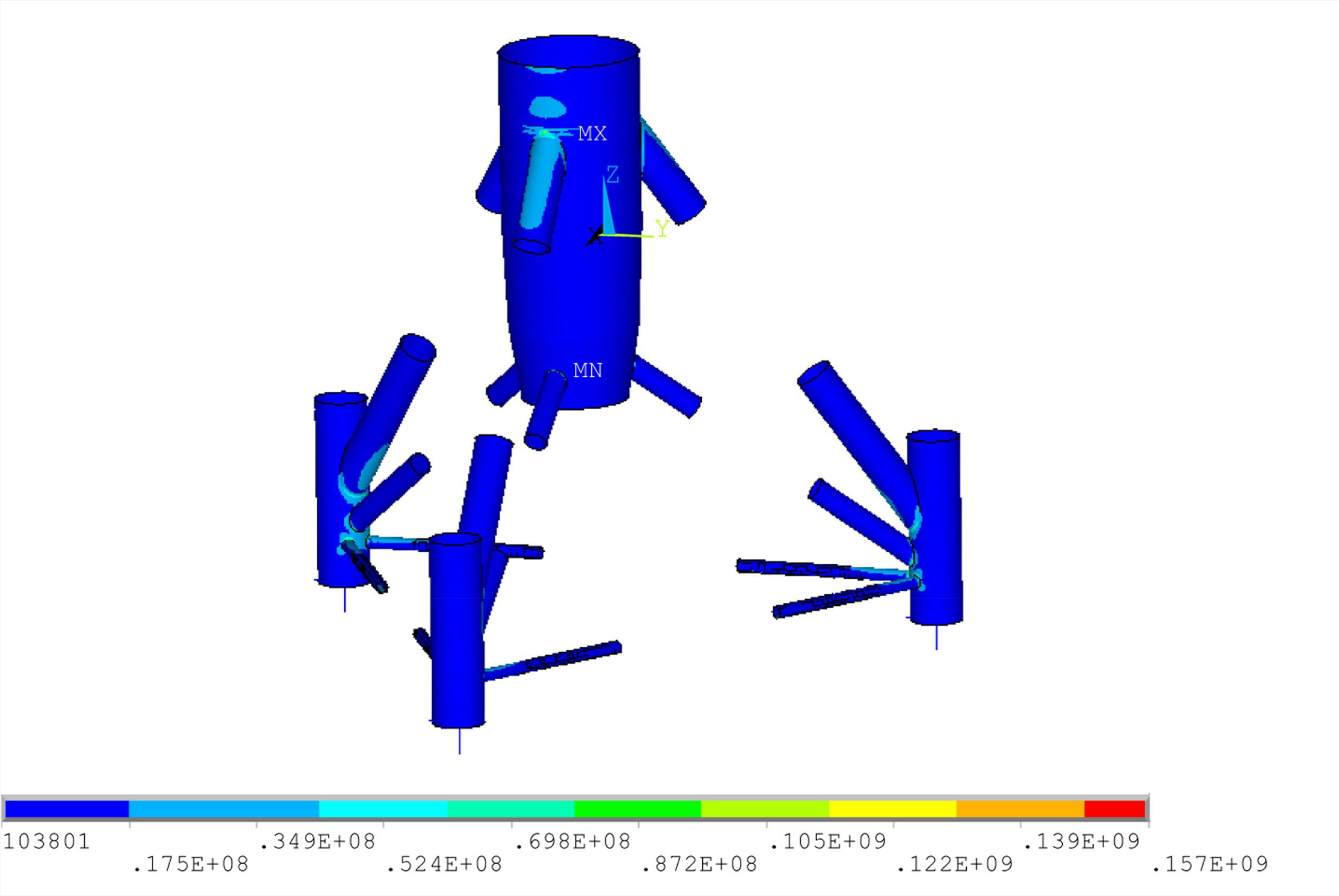
해상풍력터빈의 하부 조인트와 같이 복잡한 형상을 갖는 부재는 유한요소 상세모델로부터 응답이 산출되어야 하나, 상세 모델의 구조해석은 요구되는 해석시간이 많아 효율적이지 못하다. 따라서 취약 부재의 위치를 선별하여 응력집중계수를 산정하고, 보다 단순화된 유한요소모델로부터 얻은 응답에 적용하는 방법을 이용하였다. 로터(Rotor)와 너셀(Nacelle)을 포함한 상부구조물은 집중질량으로 처리하였고, 해석에 적용된 하중의 크기는 각 환경요인들의 평균값을 이용하였다. 상세모델의 취약 부재는 Fig. 5와 같이 TP(Transition piece) 하단의 조인트로, 상세모델과 보 요소를 이용한 모델에 대해 계산된 응력으로부터 응력집중계수는 7.25로 산정되었다. 모델링 및 구조해석에는 범용 유한요소해석 프로그램인 ANSYS(2010)를 사용하였다.
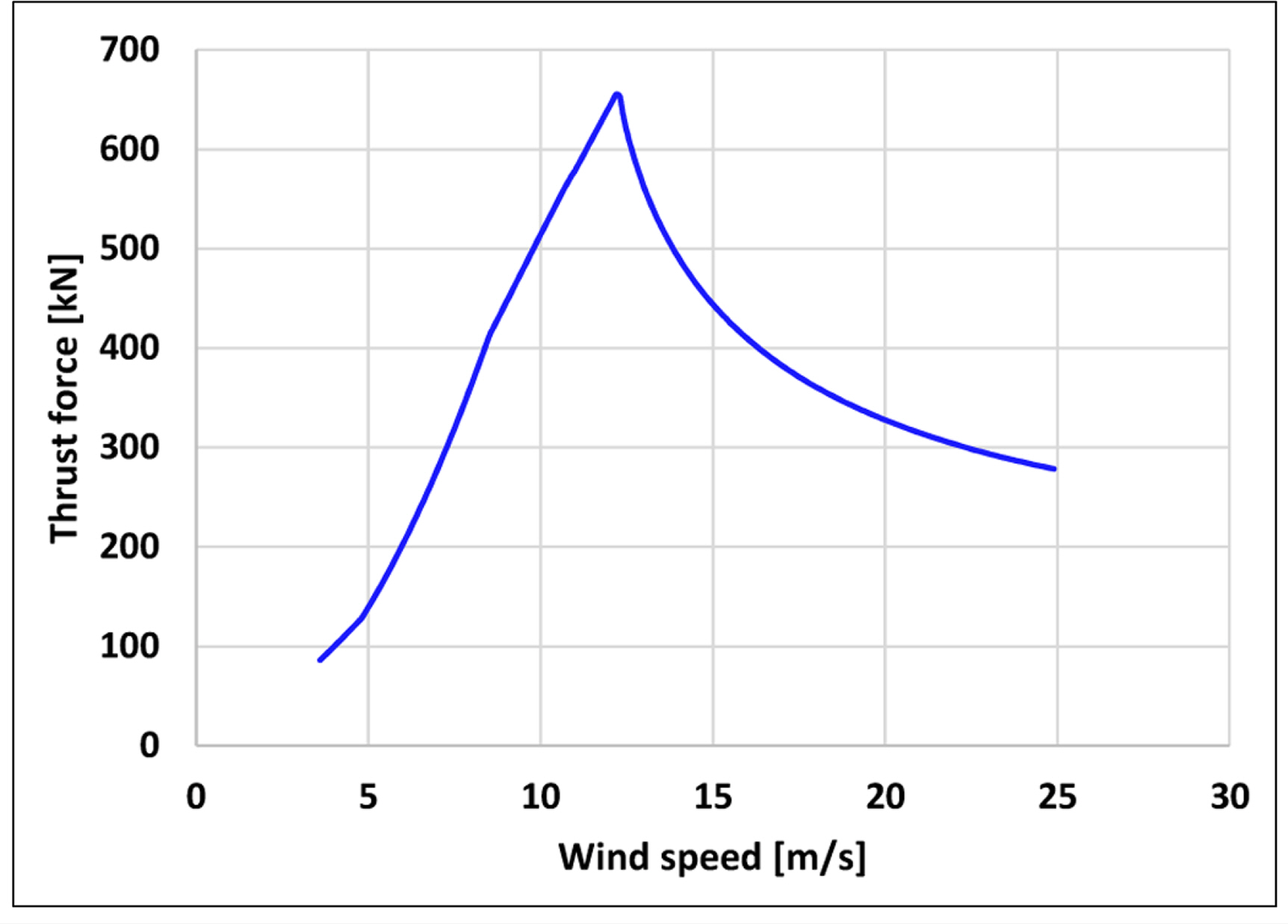
회귀모델의 독립변수 중 하나인 바람에 의한 하중은 풍력발전기 설계 프로그램인 GH-Bladed(Bossanyi, 2010)를 통해 평균풍속별 추력을 Fig. 6과 같이 산정해두고, 각 표본점에 해당되는 풍속에 대한 추력을 유한요소모델에 입력함으로써 고려할 수 있다. 설계 해역의 환경정보로부터 선형(Linear/airy) 파랑이론이 결정되어 부재에 작용하는 유체입자의 속도와 가속도를 계산하고, 모리슨 방정식을 이용하여 정적 파력을 계산하였다.
식 (1)과 같이 사전에 정의된 다항함수의 회귀계수를 산정하기 위해 각 표본점을 이용하여 파력 및 추력을 계산하고, 이를 유한요소모델에 입력하여 구조해석을 수행하였다. CCD 기법을 활용하여 선정된 표본점으로부터 응답을 산정하고 회귀모델을 구성하였다. 입력 자료와 회귀모델의 결정계수는 0.9999로 산정되어 매우 적합한 것이 확인되었다. Fig. 7은 구성된 회귀계수 산정에 사용된 표본점과 응답면 결과로, Fig. 7(a)는 3가지 표본점 구성인자(풍속, 파고, 파주기) 중 풍속과 파고에 대한 응력, Fig. 7(b)는 풍속과 파주기에 대한 응력을 도시한 그림이다.
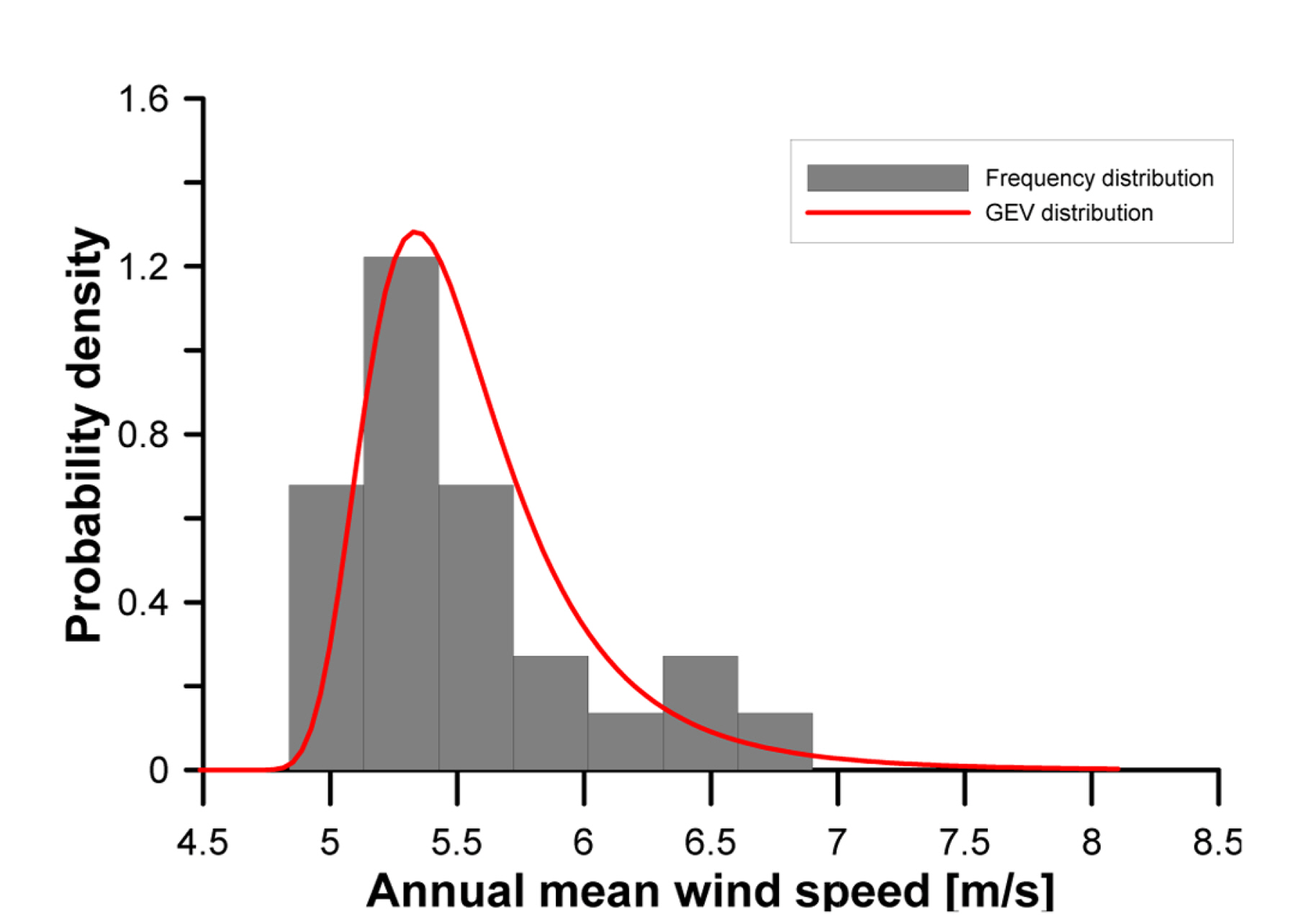
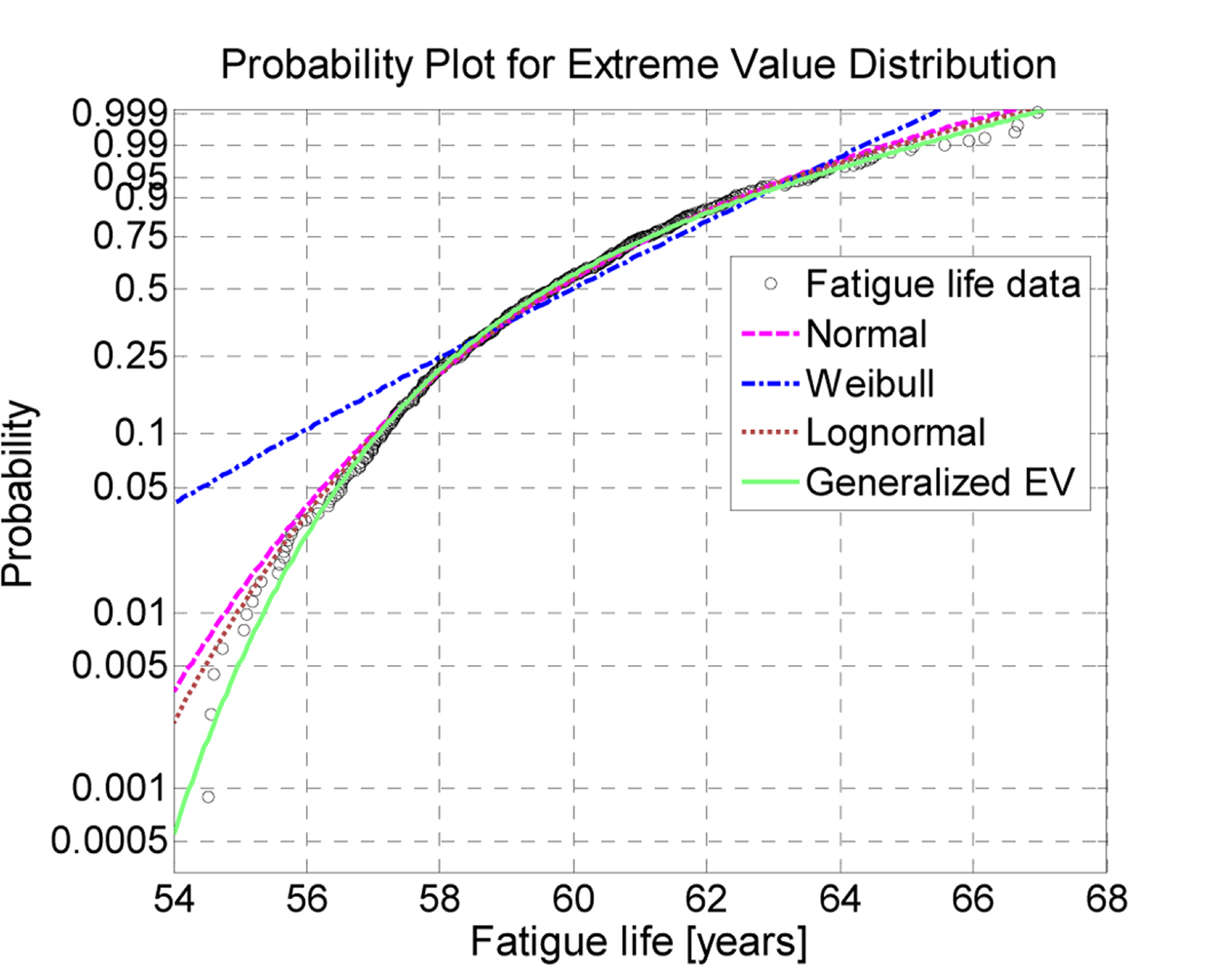
환경요인 추출 과정은 다음과 같다. 연평균 풍속자료로부터 적합한 이론적 분포와 파라미터를 추정하고, 추정된 분포에서 연평균 풍속을 추출한다. 연평균 풍속의 경험적 분포에는 일반화된 극치(Generalized extreme value, GEV)분포가 적합한 것으로 확인되었다. 기존의 극치분포는 Type Ⅰ, Ⅱ, Ⅲ 중 하나를 선정하여 적용하였으나(Fisher and Tippett 1928), 분포 형식을 선정하는 과정에서의 불확실성을 산정하는 것이 매우 어렵다는 제한 사항이 존재한다(Coles et al, 2001). Jenkinson(1955)은 상기 세가지 극치분포 선정에서 오는 불확실성을 일반화된 극치분포를 제안함으로써 보완하였으며, 제안된 분포함수는 다음과 같다.
여기서 ξ, α, κ는 각각 위치모수(Location parameter), 척도모수(Scale parameter), 형상모수(Shape parameter)를 의미한다. Fig. 8에는 연평균 풍속에 대한 빈도분포 및 GEV 분포를 도시하였다.
추출된 연평균 풍속은 식 (13)의 레일리 분포에서 파라미터로 사용되는데, 해당 분포에서는 일 최대풍속이 추출된다. 일 평균풍속과 일 최대풍속의 관계에 대해 회귀를 통해 사전에 정의하고, 추출된 일 최대풍속은 일 평균풍속으로 변환된다. 마찬가지로 일 평균풍속은 1시간 평균풍속에 대한 레일리 분포의 파라미터로 사용되며, 여기서는 1시간 평균풍속이 추출된다.
해양구조물의 피로손상을 계산하기 위해서는 충분한 양의 사이클 수가 요구되나, 보유한 자료는 1시간 간격으로써 이를 충족할 수 없다. 충분히 작은 시간간격의 풍속 시계열은 바람장(Wind filed)을 생성하여 얻을 수 있다. 본 연구에서는 바람장 생성 시 풍력발전기 설계 프로그램인 GH-Bladed(Bossanyi, 2010)의 난류특성 모델인 von Karman 스펙트럼을 이용하였으며, 입력값으로 공간의 크기, 추출된 1시간 평균풍속, 난류강도, 지속시간 등을 정의하였다. 생성된 시계열의 시간간격은 0.25초이다.
연구 과정에 대한 이해를 돕기 위해 사례 2에서 사용된 방법과 일련의 과정들을 종합적으로 정리하여 Fig. 10과 같이 흐름도에 나타내었다.
후측 시계열 자료를 직접 해석에 사용하는 사례 1과 상기 언급된 식 (5)-(7)의 확률모델과 식 (1)의 회귀모델을 이용하는 사례 2로 구분하여 피로해석을 수행하였다. 사례 1은 환경요인의 시계열 자료를 이용하여 시간이력해석을 수행하고, 해석 결과인 응답 시간이력으로부터 피로수명을 계산한다. 사례 2는 레일리 분포에서 추출된 풍속을 식 (5)-(7)의 확률모델에 입력하여 파고와 주기를 산출한다. 산출된 환경요인을 회귀모델에 입력하여 응답 시간이력을 계산하고, 피로해석을 수행한다. 사례 1은 결정론적 방법으로써 사례 2의 확률론적 방법과 비교가 가능하고, 응답 산출 시 직접적인 시간이력해석이 수행되므로 회귀모델의 검증에도 활용이 가능하다. 그러나 사례 1의 경우 장기간 시간이력 해석을 수행하는 것은 많은 소요시간이 요구되므로, 각 사례의 해석에는 6일간의 시계열 자료가 사용되었다. 사례 2의 시뮬레이션 기법을 이용하여 지지구조물의 피로수명을 계산하면 매 회마다 상이한 결과가 발생하므로 약 500회 반복계산을 통해 결과를 누적하였다. 누적결과는 많은 연구에서 활용되는 네 가지 이론적 분포인 정규(Normal), 대수정규(Log-normal), 일반화된 극치(Generalized extreme value), 와이블(Weibull) 분포와 대조하여 육안으로 관찰하고(Figs. 11-12), Table 8과 같이 KolmogorovSmirnov(K-S) 적합도 검정을 통해 수치적인 판단도 함께 수행하였다. 피로수명의 분포는 대수정규분포가 가장 적합한 것으로 판단되며, 기대수명은 약 60년, 변동계수는 0.0614로 나타났다. 여기서 변동계수는 표준편차를 평균으로 나눈 값이며, 단위에 관계없이 자료의 변동성을 표현하는 표준화된 척도이다. 두 사례의 피로수명, 상대오차, 피로수명의 확률분포, 변동계수, 그리고 설계수명 25년을 기준으로 산정된 파괴확률을 Table 9에 나타내었다. 수명을 비교해보면 사례 2의 기대수명이 사례 1의 피로수명 보다 약 2년 높게 나타났다. 그 이유로 수명 계산에 사용된 각 사례별 풍속 자료의 상이함을 들 수 있다. 사례 1의 경우 사용된 풍속 시계열은 비교적 높은 풍속이 발생하는 시기(1979년 1월)의 자료이며, 이를 하중해석 및 응답해석에 직접적으로 사용한다. 반면, 사례 2는 추정된 확률분포로부터 풍속을 추출하여 사용하였다. 풍속의 경험적 분포와 이론적 분포가 동일하다면 충분히 많은 양의 추출된 풍속 분포는 경험적 분포와 흡사한 형상을 가질 것이다. 그러나 추정된 이론적 분포는 경험적 분포와 완벽히 일치하지 않으며, 분포로부터 추출되는 값은 매 회 상이한 크기를 갖게 된다. 그러므로 Fig. 13과 같이 사례 1의 경우보다 사례 2에서 비교적 낮은 크기의 풍속이 추출됨에 따라 수명의 차이가 발생한 것으로 판단된다.
기존 연구의 제한사항이 갖는 문제점을 본 연구에서 제안한 확률론적 해석기법을 이용하여 분석하였다. 특정 시기의 단기간 자료를 이용하는 방법을 재현하고자 후측 자료로부터 매년 6개월 분량의 풍속을 취하여 확률분포를 추정하였다. 기대수명의 산정 과정은 상기의 사례 2와 동일하나, 사례 2에서 500회 반복계산을 수행했을 때 100회 이상이 될 경우 근사 수렴되었으므로 약 120회의 반복계산을 수행하였다. Fig. 14는 각 연도별 하중이 가해졌을 때의 기대수명이므로 최대 및 최소 수명 값은 각각 33년(1991년도)과 12년(2000년도)으로 나타났으며, 변동계수는 0.2168로 산정되었다. 일반적으로 풍력터빈의 구조응답에는 풍속이 가장 큰 기여도를 보이며, 상기와 같은 기대수명 차이의 주된 원인 역시 풍속으로 판단된다. 이를 확인하기 위해 회귀모델의 입력변수로 사용된 풍속에 대해 연별 평균값을 계산하여 함께 도시하였다. 그림으로부터 기대수명은 연별 평균 풍속의 크기에 반대되는 경향을 보이는 것을 알 수 있고, 예상대로 연별 기대수명의 경향은 풍속의 영향임이 확인되었다.
본 연구에서는 풍속, 파고, 주기의 발생 시기에 따른 통계적 특성의 차이와 같이 관측 자료로 표현되지 못하는 해양 환경요인의 변동성이 해상풍력발전기 지지구조물의 피로수명에 미치는 영향을 분석하였다. 결정론적 방법(사례 1)과 확률론적 방법 (사례 2)을 이용하여 피로해석을 수행하였으며, 확률론적 방법은 피로수명 결과에 적합한 이론적 분포를 추정함으로써 파괴 확률(설계수명 보다 작은 수명이 발생될 확률)을 산정할 수 있었다. 또한 지지구조물의 연별 기대수명과 산정된 기대수명에 대한 변동성으로부터 하중의 시기적 불확실성이 수명에 미치는 영향을 확인할 수 있었다. 본 연구의 제안방법은 유지보수 주기를 결정하는데 사용될 수 있고, 이는 생애주기 비용(Life cycle cost, LCC) 또는 균등화된 발전비용(Levelized cost of electricity, LCOE) 측면에서 활용가치를 기대해볼 수 있다. 더불어 지지구조물의 해체 시기 및 사용연한 연장의 결정 등에서도 그 활용성이 기대된다.
후기
이 논문은 한국연구재단(No. 2016R1D1A3B03933885)과 산업통상자원부(MOTIE) 및 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(No. 20183010025200).
Table 1.
Markov Matrix
| Stress amplitude | |||||||
|---|---|---|---|---|---|---|---|
| 0.3509 | 1.0528 | 1.7546 | ⋯ | 16.4936 | 17.1954 | ||
| Mean stress | −1.3694 | 48 | 3 | 1 | 0 | 0 | |
| 1.3455 | 31 | 6 | 1 | 0 | 0 | ||
| 4.0604 | 25 | 8 | 2 | 0 | 0 | ||
| ⋮ | ⋱ | ||||||
| 61.0732 | 25 | 5 | 0 | 0 | 0 | ||
| 63.7881 | 7 | 0 | 0 | 0 | 0 | ||
Table 2.
Basic design S-N curve
| log10 (kl) S in MPa | m | Condition | |
|---|---|---|---|
| Welded Joints [WJ] | 12.48 | 3.0 | for N < 107 |
| 16.13 | 5.0 | for N > 107 |
Table 3.
Design load case 1.2
| Design situation | Wind condition | Waves | Wind & wave directionality | Sea currents |
|---|---|---|---|---|
| Power production | NTM Vin < Vhub < Vout | NSS Joint prob. distribution of Hs, Tp, Vhub | COD, MUL | No currents |
Table 4.
Specification and environmental condition of offshore wind turbine
Table 5.
Dynamic soil design constant at Gunsan south breakwater
Table 6.
Spring coefficients
| dx | dy | dz | θx | θy | θz | |
|---|---|---|---|---|---|---|
| Fx | 4.78E+8 | 0 | 0 | 0 | −4.01E+9 | 0 |
| Fy | 0 | 4.78E+8 | 0 | 4.01E+9 | 0 | 0 |
| Fz | 0 | 0 | 4.95E+8 | 0 | 0 | 0 |
| Mx | 0 | 4.01E+9 | 0 | 4.83E+10 | 0 | 0 |
| My | −4.01E+9 | 0 | 0 | 0 | 4.83E+10 | 0 |
| Mz | 0 | 0 | 0 | 0 | 0 | 3.29E+7 |
Table 7.
The coefficients used in the probabilistic model
Table 8.
Goodness of fit test (K-S)
| Distribution | Critical value (Dnα) | Maximum difference (Dn) | P-value |
|---|---|---|---|
| Normal | 0.0569 | 0.0283 | 0.7469 |
| Log-normal | 0.0171 | 0.9958 | |
| Generalized extreme value | 0.0204 | 0.9699 | |
| Weibull (2-parmeters) | 0.0785 | 0.0018 |
Table 9.
Characteristic for fatigue life and relative error
References
ABAQUS. (2013). Standard User’s Manual – Version 6.13 Dassault Systemes Simulia Corp.
American Institute of Steel Construction (AISC). (2005). Specification for Structural Steel Buildings, AISC, 360-05.
American Petroleum Institute (API),. (2007). Recommended Practice for Planning, Design and Constructing Fixed Offshore Platforms Working Stress Design. API Publishing Services.
ANSYS. (2010). ANSYS User’s Manual - Version 12.1.
Bossanyi, EA. (2010). GH-Bladed Version 4.0 User Manual. Garrad Hassan and Partners Limited Document, 2..
Box, J., & Wilson, W. (1951). Central Composites Design. Journal of the Royal Statistical Society, 1, 1-35.
Bucher, CG., & Bourgund, U. (1987). Efficient use of Response Surface Methods. Universität Innsbruck, Institut für Mechanik.
Coles, S., Bawa, J., Trenner, L., & Dorazio, P. (2001). An Introduction to Statistical Modeling of Extreme Values. Springer: London. doi.org/10.1007/978-1-4471-3675-0
Det Norske Veritas (DNV). (2011). Fatigue Design of Offshore Steel Structures. RP-C203..
Det Norske Veritas (DNV). (2013). Design of offshore wind turbine structures. DNV-OS-J101..
Dong, W., Moan, T., & Gao, Z. (2011). Long-Term Fatigue Analysis of Multi-Planner Tubular Joints for Jacket-Type Offshore Wind Turbine in Time Domain. Engineering Structures, 33(6), 2002-2014. https://doi.org/10.1016/j.engstruct.2011.02.037

Dong, W., Moan, T., & Gao, Z. (2012). Fatigue Reliability Analysis of the Jacket Support Structure for Offshore Wind Turbine considering the Effect of Corrosion and Inspection. Reliability Engineering and System Safety, 106, 11-27. https://doi.org/10.1016/j.ress.2012.06.011

Fisher, RA., & Tippett, LHC. (1928). Limiting Forms of the Frequency Distribution of the Largest or Smallest Member of a Sample. Mathematical Proceedings of the Cambridge Philosophical Society, 24(2), 180-190. https://doi.org/10.1017/S0305004100015681

Goda, Y., & Takagi, H. (2000). A Reliability Design Method of Caisson Breakwaters with Optimal Wave Heights. Coastal Engineering Journal, 42(4), 357-387. https://doi.org/10.1142/S0578563400000183

Goodman, J. (1899). Mechanics Applied to Engineering. Longman, Green and Company: London.
Haldar, A., & Mahadevan, S. (2000). Reliability Assessment using Stochastic Finite Element. John Wiley: New York.
International Electro-Technical Commission (EIC). (2005). Wind Turbines-Part 1: Design Requirements, IEC, Geneva.
International Electro-Technical Commission (EIC). (2009). Wind Turbines-Part 3: Design Requirements for Offshore Wind Turbines, IEC, Geneva.
Jenkinson, AF. (1955). The Frequency Distribution of the Annual Maximum (or Minimum) Values of Meteorological Elements. Quarterly Journal of the Royal Meteorological Society, 81(348), 158-171. https://doi.org/10.1002/qj.49708134804

Jeong, ST., Kim, JD., Ko, DH., & Yoon, GL. (2008). Parameter Estimation and Analysis of Extreme Highest Tide Level in Marginal Seas Around Korea. Journal of Korean Society of Coastal and Ocean Engineers, 20(5), 482-490.
Johannessen, K., Meling, TS., & Hayer, S. (2001). Joint Distribution for Wind and Waves in the Northern North Sea. In the Eleventh International Offshore and Polar Engineering Conference, International Society of Offshore and Polar Engineers Stavanger Norway.
Kelma, S., & Schaumann, P. (2015). Probabilistic Fatigue Analysis of Jacket Support Structures for Offshore Wind Turbines Exemplified on Tubular Joints. Energy Procedia, 80, 151-158. https://doi.org/10.1016/j.egypro.2015.11.417

Kim, DH., & Lee, SG. (2015). Reliability Analysis of Offshore Wind Turbine Support Structures under Extreme Ocean Environmental Loads. Renewable Energy, 79, 161-166. https://doi.org/10.1016/j.renene.2014.11.052

Kuang, JG., Potvin, AB., & Leick, RD. (1975). Stress Concentration in Tubular Joints. Proceedings of Offshore Technology Conference.

Le Méhauté, B. (2013). An Introduction to Hydrodynamics and Water Waves. Springer Science & Business Media: Berlin.
Lee, SG. (2016). Reliability Analysis of Offshore Wind Turbine Support Structure Considering Dynamic Response Characteristics. Ph. D., Kunsan National University, Thesis Korea.
Manwell, JF., McGowan, JG., & Rogers, AL. (2002). Wind Energy Explained: Theory, Design and Application. John Wiley & Sons.
Matsuishi, M., & Endo, T. (1968). Fatigue of Metals Subjected to Varying Stress. Japan Society of Mechanical Engineers, Fukuoka, Japan, 68(2), 37-40.
McVicar, TR., Roderick, ML., Donohue, RJ., Li, LT., Van Niel, TG., Thomas, A., Grieser, J., Jhajharia, D., Himri, Y., Mahowald, NM., Mescherskaya, AV., Kruger, AC., Rehman, S., & Dinpashoh, Y. (2012). Global Review and Synthesis of Trends in Observed Terrestrial Near-Surface Wind Speeds: Implications for Evaporation. Journal of Hydrology, 416-417 182-205. https://doi.org/10.1016/j.jhydrol.2011.10.024

Miner, MA. (1945). Cumulative Fatigue Damage. Journal of Applied Mechanics, 12(3), A159-A164.
Ministry of Oceans and Fisheries (MOF). (2005). Estimation Report of Deep-sea Design Wave in the Whole Sea Area (II), Korea Institute of Ocean Science & Technology (KIOST).
Morison, JR., Johnson, JW., & Schaaf, SA. (1950). The Force Exerted by Surface Waves on Piles. Journal of Petroleum Technology, 2(05), 149-154. https://doi.org/10.2118/950149-G

Raymond, HM., & Douglas, CM. (2002). Response Surface Methodology: Process and Product Optimization using Designed Experiments. John Wiley & Sons: New York.
Rychlik, I. (1987). A New Definition of the Rainflow Cycle Counting Method. International Journal of Fatigue, 9(2), 119-121. https://doi.org/10.1016/0142-1123(87)90054-5

Schuëller, GI., Bucher, CG., Bourgund, U., & Ouypornprasert, W. (1989). On Efficient Computational Schemes to Calculate Structural Failure Probabilities. Probabilistic Engineering Mechanics, 4(1), 10-18. https://doi.org/10.1016/0266-8920(89)90003-9

Thomas, BR., Kent, EC., Swail, VR., & Berry, DI. (2008). Trends in Ship Wind Speeds Adjusted for Observation Method and Height. International Journal of Climatology: A Journal of the Royal Meteorological Society, 28(6), 747-763. https://doi.org/10.1002/joc.1570

Tokinaga, H., & Xie, SP. (2011). Wave-and Anemometer-Based Sea Surface Wind (WASWind) for Climate Change Analysis. Journal of Climate, 24(1), 267-285. https://doi.org/10.1175/2010JCLI3789.1

Ucar, A., & Balo, F. (2010). Assessment of Wind Power Potential for Turbine Installation in Coastal Areas of Turkey. Renewable and Sustainable Energy Reviews, 14(7), 1901-1912. https://doi.org/10.1016/j.rser.2010.03.021

Yeter, B., Garbatov, Y., & Soares, CG. (2015). Fatigue Damage Assessment of Fixed Offshore Wind Turbine Tripod Support Structures. Engineering Structures, 101, 518-528. https://doi.org/10.1016/j.engstruct.2015.07.038

Yeter, B., Garbatov, Y., & Soares, C.G.. (2014). Fatigue Reliability Assessment of an Offshore Supporting Structure Maritime Technology and Engineering,. CRC Press: p 689-700.
Young, IR., Vinoth, J., Zieger, S., & Babanin, AV. (2012). Investigation of Trends in Extreme Value Wave Height and Wind Speed. Journal of Geophysical Research: Oceans. 117(C11), https://doi.org/10.1029/2011JC007753

- TOOLS
-
METRICS

-
- 1 Crossref
- Scopus
- 9,941 View
- 113 Download
- Related articles in JOET
-
Seismic Reliability Analysis of Offshore Wind Turbine Support Structure2015 October;29(5)