|
 |
- Search
| J. Ocean Eng. Technol. > Volume 33(4); 2019 > Article |
|
Abstract
The magnitude of the roll motion of a floating structure depends on the roll damping acting on the body. In other words, the roll damping of a floating structure must be accurately obtained in order to precisely evaluate the roll motion. Various methods are used to evaluate the roll damping of a floating structure, such as the linear potential theory, computational fluid dynamics (CFD), and model tests. However, it is difficult to evaluate the roll motion of a floating structure with appendages such as a bilge keel and riser slot due to the limitation of ignoring the viscous effects in the linear potential theory. Among these methods, a model test based on a free decay test and harmonic excited roll motion (HERM) is known to be the most reliable method to estimate the roll damping of the floating structures. In this study, model tests using free decay and HERM techniques were performed in the Ocean Engineering Basin (OEB) of KRISO with various types of midship sections. The roll damping results were estimated based on post-processing methods using both techniques, and the roll damping results were compared.
해상 유전 개발의 경제성 확보를 위해 오일 메이저 및 국영석유회사는 저유가 시대에 맞는 저비용 해양플랜트 개발의 필요성을 제기하고 있다. 특히, 깊은 수심 및 인프라가 부족한 해역에 주로 투입되는 선박형 부유식 해양구조물인 FPSO(Floating production storage offloading)의 효율적인 설계 및 개발이 대표적이다.
부유식 해양구조물 설계의 가장 기본이 되는 정보는 대상 부유체의 파랑 중 동적 거동, 상대 파고 및 가속도 정보이다. 특히, 부유체의 6자유도 운동 중 횡동요(Roll)는 폭 방향 및 수직 방향으로의 가속도를 유발하는 중요한 인자로 부유체 선체 및 상부의 트러스 구조에 하중을 발생시킨다. 또한 해양구조물의 상부 공정 설비는 동적 거동 중에 구조 안정성을 확보하여야 할 뿐만 아니라 요구되는 공정 처리 기능을 원활히 수행해야하므로 부유체의 동적 거동 및 가속도 정보는 공정 설비 설계 시 중요하게 다뤄져야 한다. 따라서 해양구조물의 구조적 안정성을 확보하고 선체 및 상부 처리시설의 최적 설계를 위해서는 투입 환경 조건에서 해양구조물의 동적 거동을 정확하게 추정하고 평가해야 한다. 특히, 점성에 의한 감쇠 영향을 많이 받는 횡동요를 정확하게 평가해야 폭 방향 및 수직 방향 가속도를 엄밀하게 추정할 수 있다.
횡동요 감쇠에 대한 연구는 경험식을 바탕으로 상선의 감쇠계수 추정을 비롯하여 모형 시험 및 CFD(Computational fluid dynamics) 해석 기법 등에 대한 연구가 지속적으로 진행되었다. 경험식을 통한 횡동요 감쇠 계수 추정법은 일반적인 상선의 선형에 대해 횡동요 감쇠를 선체 양력 성분, 마찰 성분, 빌지킬 성분 등으로 세분화하여 각기 성분의 감쇠 영향을 추정한 후 이를 합하여 전체 횡동요 감쇠를 추정하는 방법이다(Ikeda et al., 1976; Ikeda et al., 1978).
모형 시험을 통한 횡동요 감쇠 계수 추정 기법으로는 자유 감쇠, 가진 운동을 통한 감쇠, 가진 횡모멘트를 통한 감쇠 추정법이 있다. 이중 자유 감쇠 추정법은 대상 부유체를 일정한 횡각도를 준 후 구속을 풀어 자유 감쇠하는 시계열을 계측하고 이를 분석하는 추정 기법으로 시험 절차가 간단하여 널리 활용되고 있다. 가진 운동이나 가진 횡모멘트를 활용한 감쇠 추정 기법은 가진을 위한 별도의 장치가 필요로 하다는 단점이 있으나 특정 횡동요 각도, 다양한 횡동요 주기, 파랑 및 선속 조건에서의 감쇠 계수를 추정할 수 있다는 장점이 있다. Handschel et al.(2015)은 횡동요 자유 감쇠 실험뿐만 아니라 Blume(1979)이 제안한 회전 무게추에 의한 횡동요 가진 개념을 도입하여 Post panamax containership의 횡동요 감쇠 계수를 추정 연구를 수행하였다. Oliva-Remola et al.(2018)은 내부에서 이동하는 무게추를 이용한 가진운동을 통해 횡동요 감소 계수 실험을 수행하였으며 자유 감쇠 실험 결과와 비교하였다. 또한 가진 운동을 포함한 횡동요 거동을 수학적 모델로 구성하여 해석하여 모형 시험 결과와 비교하였다.
Park et al.(2017)은 감쇠 계수 추정 모형 시험을 위해 폭방향으로 정현파의 신호로 이동하는 무게추를 활용한 횡동요 가진 장치를 설계하였으며 가진 장치를 이용한 모형 시험 결과로부터 횡동요 감쇠 계수 추정하는 후처리 기법을 검토하였다. 제작된 가진 장치를 30k LNG-BS(LNG-bunkering shuttle)에 적용하여 모형 시험을 수행하였고 추정한 횡동요 감쇠 계수를 자유감쇠 실험 결과와 비교하였다(Park et al., 2018).
모형 시험 및 CFD를 이용한 횡동요 감쇠 추정 기법과 시계열의 해석에 대해서는 29차 ITTC stability in waves committee의 ‘Terms of reference’ 항목으로 심도 있게 다루어지고 있으며 횡동요 감쇠 추정에 대한 가이드라인 개선을 위해 지속적인 연구가 필요하다고 언급하였다.
횡동요 감쇠 계수는 모형 시험의 결과인 시간에 따른 횡동요 및 횡모멘트의 시계열을 분석하여 추정할 수 있으며 식 (1)은 횡동요 운동방정식을 나타낸다.
여기서 I는 관성 모멘트, Ia는 부가 관성 모멘트, C1은 선형 횡동요 감쇠계수, C2는 비선형 횡동요 감쇠계수, K는 횡 복원력, M(t)는 외력항으로 가진 횡 모멘트를 각각 나타낸다. 또한, ϕ ¨ ϕ ˙
여기서 Md는 무게추 무게, Ld는 중심축으로부터 무게추 최대 이동 거리, g는 중력가속도, ω는 무게추의 왕복 주파수를 나타낸다.
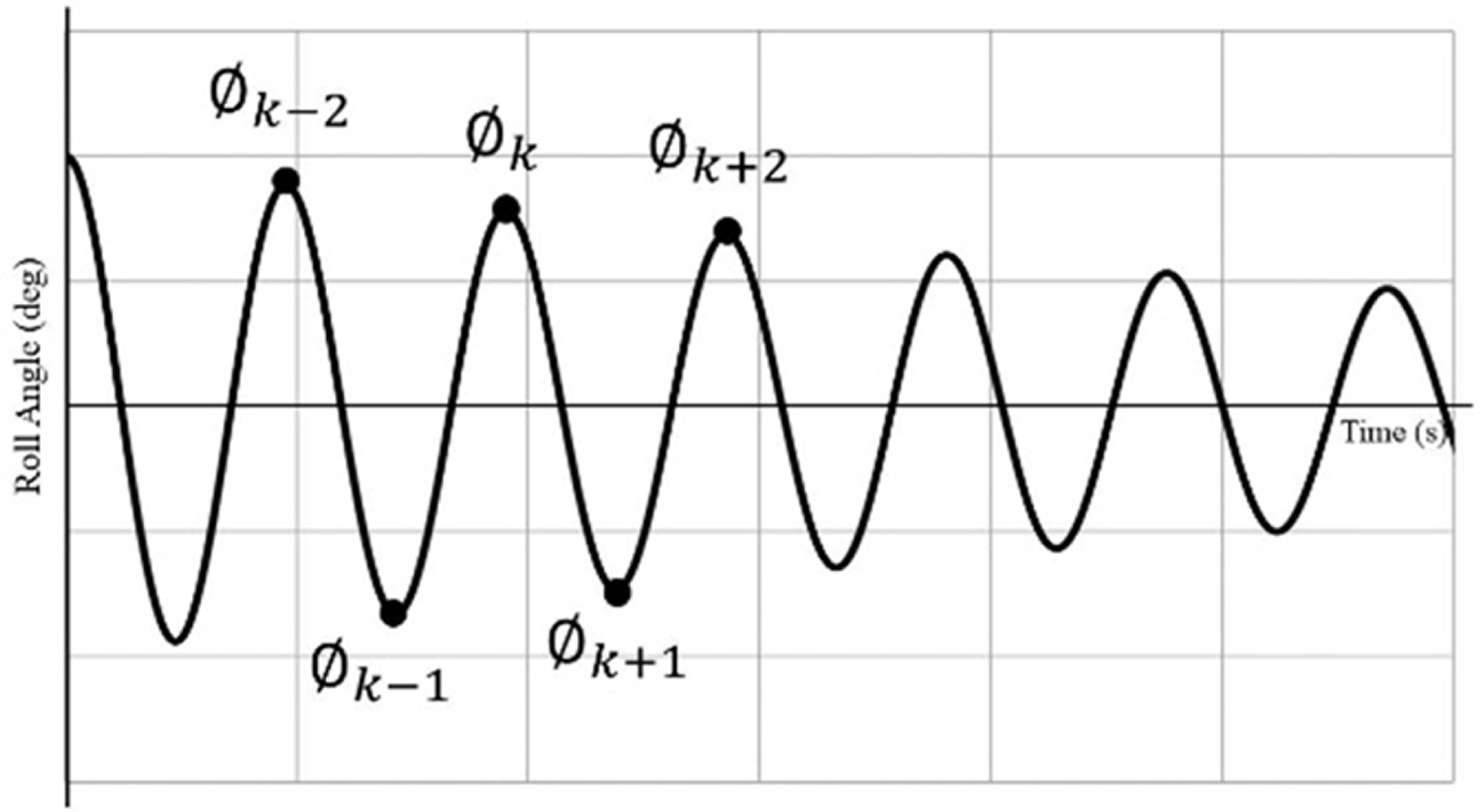
자유 감쇠 모형 시험은 Fig. 1과 같이 대상 부유체를 일정한 각도로 횡동요를 발생시킨 후 구속을 풀어 시간에 따른 횡동요 시계열을 계측한다. 계측된 시계열의 형태는 첫 횡동요를 시작으로 점차 줄어 최종적으로 0도로 수렴하게 되며 이때 시계열에 나타나는 각 주기의 최고, 최저점들을 이용하여 감쇠를 추정한다.
대수감쇠율 기법(Logarithmic decrement)은 횡동요의 연속된 각 주기의 최고 또는 최저점들의 대수감쇠 비를 통해 횡동요 감쇠 계수를 추정한다. 대수감쇠율 기법은 비선형 감쇠의 영향을 등가의 선형 감쇠로 간주하여 횡동요 감쇠를 선형 감쇠로 추정하는 방법과 비선형 감쇠 영향을 반영하여 선형, 비선형 감쇠를 구하는 방법으로 나눌 수 있다. 상대감쇠율 기법(Relative decrement)은 횡동요의 선형 및 비선형 감쇠를 최고점 또는 최저점의 상대 감소량을 통해 이용하여 추정한다. 한 주기 동안 횡동요 변화값 및 평균값의 관계를 Extinction coefficient 또는 Decay coefficient로 나타내며 Himeno(1981)는 에너지 보존 법칙에 통해 Decay coefficient로부터 선형, 비선형 횡동요 감쇠 계수를 추정하였다.
가진 운동을 통한 횡동요 감쇠 추정법은 한 주기 동안 주어진 횡동요 에너지가 횡동요 감쇠로 인한 에너지 소실과 같다는 관계를 이용하며 비선형 감쇠의 영향이 포함된 등가의 선형 감쇠결과로 나타난다.
가진된 횡동요는 감쇠 조건에 따라 가해진 횡동요 모멘트와 위상차를 가진다. Motion and moment phase shift 방법은 가진 장치에 의한 횡동요 모멘트, 가진된 횡동요 크기, 위상차를 이용하여 횡동요 감쇠를 추정한다. Lissajous curve를 이용한 추정법은 횡동요 모멘트와 발생한 횡동요의 관계를 이용한다. 주기운동의 경우 닫힌 영역을 가지며 내부 영역의 면적이 한 주기동안 소실된 에너지를 의미하므로 이를 이용하여 감쇠를 추정한다. 가진 장치에 의해 가해진 횡동요 모멘트는 설정된 주기 및 크기로 발생하며 Fourier polynomial approximation을 통해 표현될 수 있다. 특히, 횡동요 공진 주기에 해당하는 횡동요 모멘트가 가해진 경우에는 횡동요와 90도의 위상차를 나타낸다. 한 주기 동안 소실되는 에너지는 Fourier polynomial 계수의 함수로 간단히 표현되고 이를 통해 횡동요 감쇠를 추정한다.
본 연구에서는 가진 운동 모형 시험에 대해 Lissajous curve 기법을 이용하여 등가의 선형 감쇠 결과를 도출하였다. 식 (5)는 횡동요 한 주기 동안 감쇠에 의해 소실된 에너지를 나타내며 식 (6)은 Lissajous curve의 닫힌 영역의 면적에 해당하는 에너지를 나타낸다. 식 (5)와 식 (6)이 같으므로 횡동요 크기 ϕa에서의 등가 선형 횡동요 감쇠는 식 (7)로 구할 수 있다.
여기서 ϕa는 가진된 횡동요 크기, ω는 횡동요 주파수, Ce(ϕa)는 횡동요 크기 ϕa에서의 등가 선형 횡동요 감쇠, M은 가진 횡 모멘트를 나타낸다.
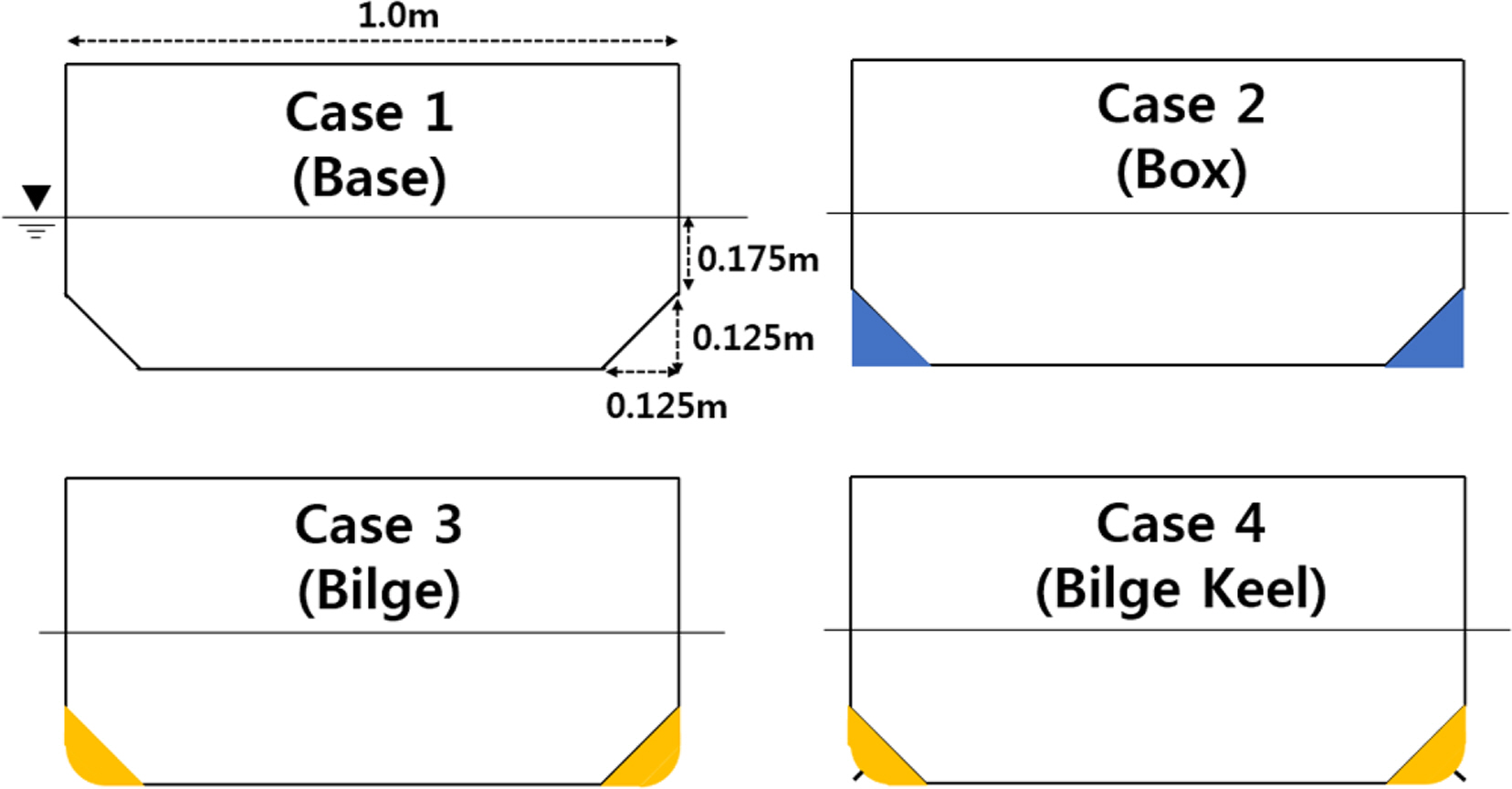
본 연구에서는 선박형 부유체의 다양한 중앙 단면 형상의 횡동요 감쇠 계수를 검토하기 위해 Fig. 2와 같이 3종류의 중앙단면과 빌지킬이 부착된 모델을 대상으로 모형 시험을 수행하였다.
Case 1을 기본 중앙단면으로 하였으며 선체 양 하단부에 길이 방향으로 추가적인 형상 구조물을 설치하여 중앙 단면에 변화를 주었다.
모형 시험에 사용된 모형선(Case 1)을 Fig. 3에 나타내었으며 각 Case의 모델 제원을 Table 1에 나타내었다. Case 4는 Case 3 선형에 빌지킬을 추가로 부착하였다. Case 1, 2 및 3의 횡동요 공진 주기는 설계값을 이용하여 포텐셜 기반의 In-house 프로그램인 AdFLOW(Advanced analysis system for floating body in waves using higher-order element method)를 통해 계산하였으며 Case 4의 횡동요 공진주기는 자유 감쇠 모형 시험 결과로부터 얻었다. 설계 횡동요 공진주기와 모형 시험에서 구현된 횡동요 공진 주기는 4.1장의 Table 5에 비교하였다.
가진 운동 장치는 Park et al.(2017)이 제시한 설계 기법을 활용하여 대상 모델의 횡동요를 원하는 크기로 가진시킬 수 있는 사양으로 제작되었다. 제작된 가진 장치는 Fig. 4와 같이 모형선의 중앙부, 데크 상단에 장착하였고 횡동요 모멘트는 무게추, 이동 거리 및 이동 주기의 조합으로 구현된다. 실험에 사용된 가진 장치의 제원은 Table 2에 정리하였다. 본 실험에서는 무게추 26.5kg을 사용하였으며 주기 및 이동 거리는 각 실험 케이스별로 요구되는 횡동요가 발생하도록 구성하였다.
횡동요 감쇠 계수 추정을 위해 자유 감쇠 및 가진 운동 감쇠모형 시험은 선박해양플랜트연구소 해양공학수조에서 수행되었다. 모형의 무게 분포를 조정하여 Table 1의 제원을 만족하는 GM(Metacentric height) 및 횡동요 공진 주기를 갖도록 설정하였다. 자유 감쇠 및 가진 운동 감쇠 모형 시험이 동일한 무게 조건에서 수행될 수 있도록 가진 장치 및 무게추를 모형선 데크 상부에 미리 장착하여 무게 분포를 조정하였으며 자유 감쇠 시험 시에는 무게추를 선체 중앙에 고정하여 모형 시험을 수행하였다.
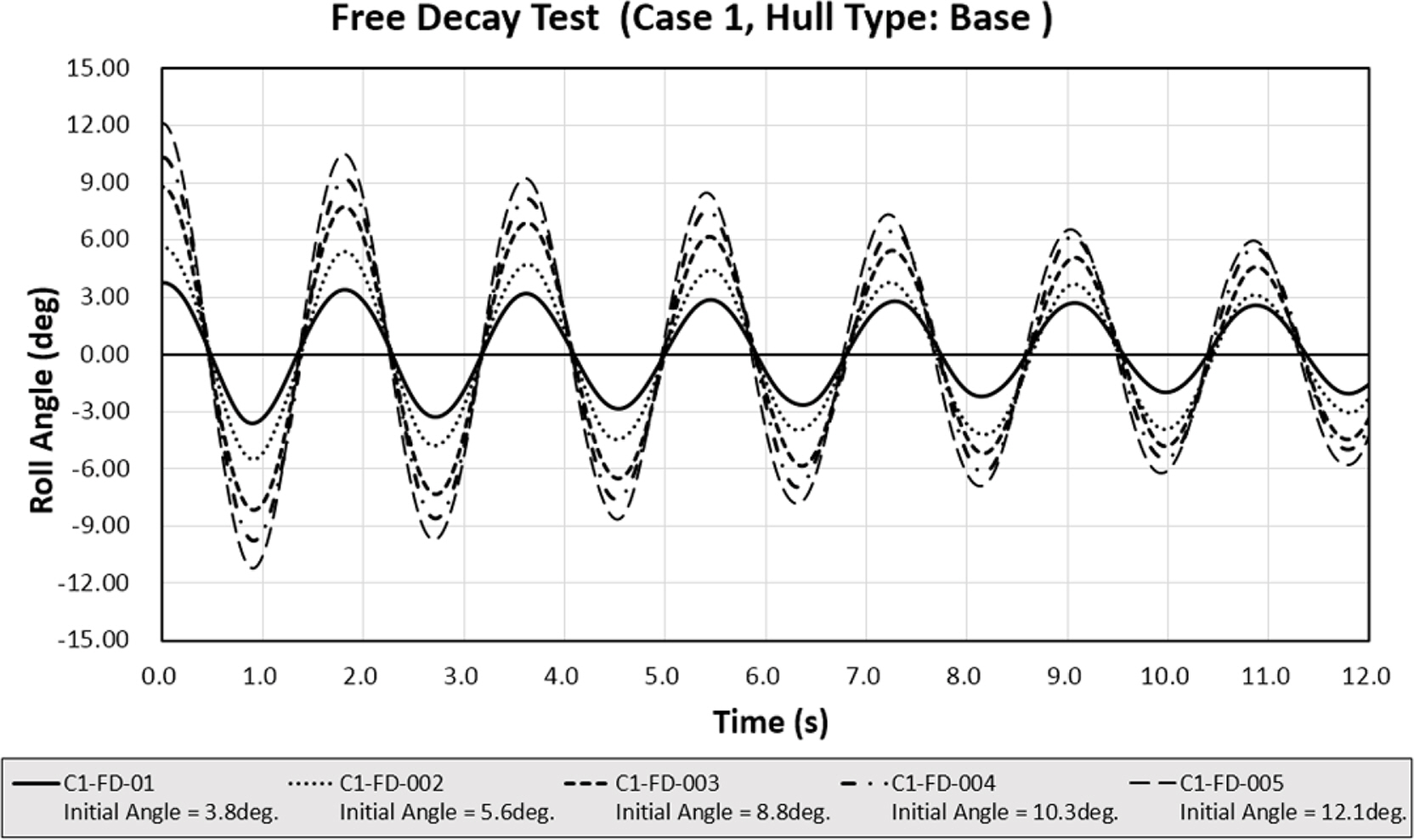
모형 시험은 각 Case별로 각기 다른 5개의 횡동요 각도에 대해 자유 감쇠 실험을 수행하였다. 자유 감쇠 모형시험에서는 초기 각도를 달리하여 시험 케이스를 구성하였고 가진 운동 감쇠모형 시험은 횡동요 공진주기에서 무게추의 이동 거리를 조정하면서 적정 횡동요가 발생하도록 구성하였다. 모형 시험 구성에 대한 예시로 Case 1에 대한 모형 시험 조건을 Table 3 및 Table 4에 나타내었다. 다만, Case 4의 경우에는 횡동요 공진 주기가 1.87초이므로 무게추의 왕복 주기를 횡동요 공진 주기에 해당하는 1.87초로 설정하였다.
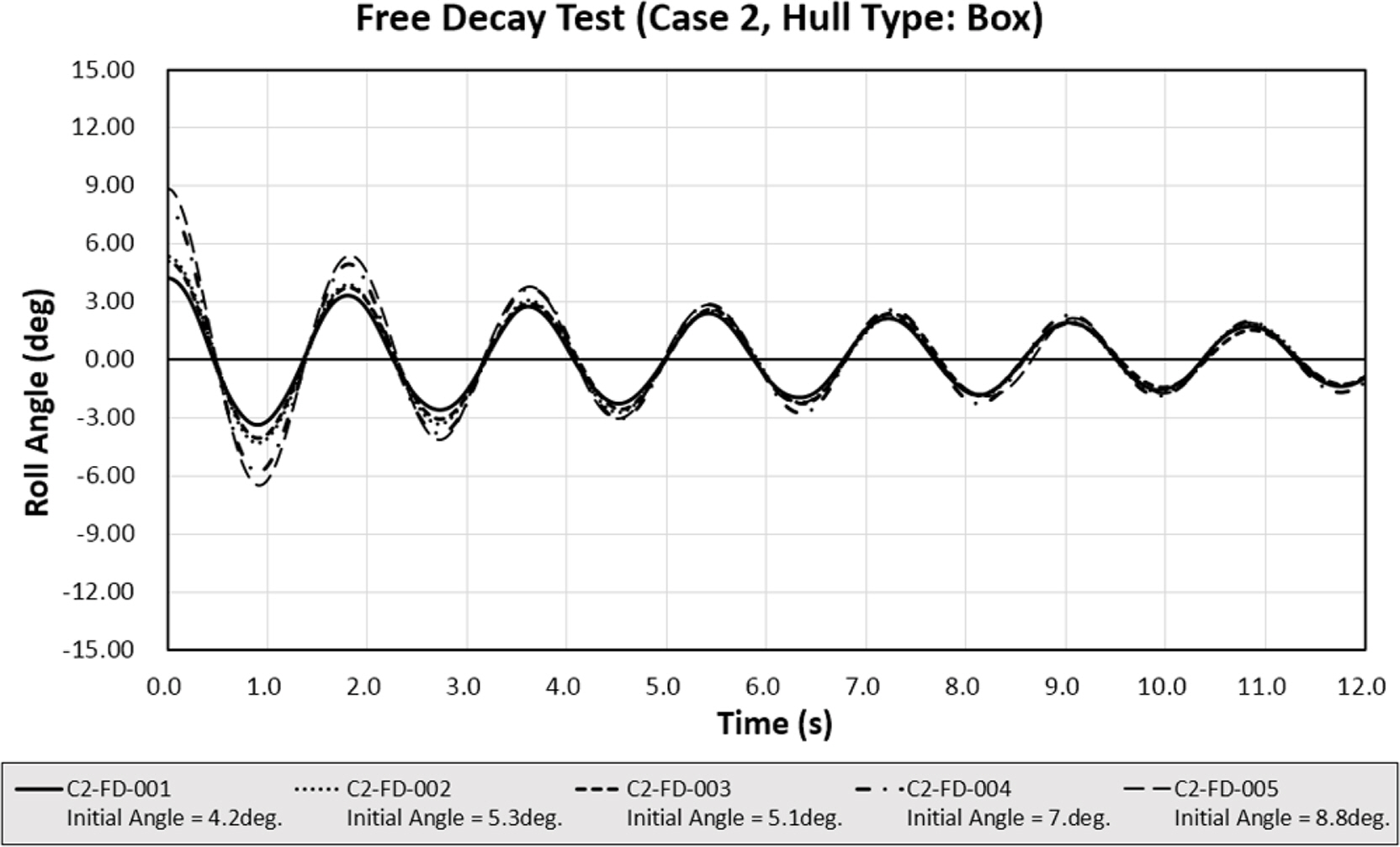
자유 감쇠 모형 시험은 Table 3과 같이 각 Case별로 총 5개의 초기 각도 조건에 대해서 실험을 수행하였으며 각 실험 Case의 자유 감쇠 시험 시계열을 Figs. 5-8에 도시하였다. 또한 Fig. 9는 Case 1~3의 경우 초기 횡동요 각도 조건이 약 8.8도, Case 4의 경우에는 초기 횡동요 각도 조건이 약 8.0도인 실험의 시간에 따른 횡동요 시계열을 나타낸 것으로 각 Case의 횡동요의 감소 형태를 파악할 수 있다. 실험 모델은 Table 1에 정리되어 있는 횡동요 공진 주기를 갖도록 구성되었으며 목표 횡동요 공진 주기와 자유 감쇠 모형 시험 계측 결과를 통해 얻은 횡동요 공진 주기 결과를 Table 5에 비교하였다.
Case 4의 경우에는 횡동요 공진 주기가 약 1.87초로 약 4% 증가하는 것으로 나타났으며 이는 Case 4는 빌지킬을 부착한 것이 이외에는 Case 3과 동일한 무게 분포를 가지고 있으므로 공진 주기 증가는 빌지킬에 의한 영향으로 판단된다.
자유 감쇠 추정 기법은 횡동요의 크기가 연속적 변화하는 과정에서의 추정 결과를 도출한다. 그러나 횡동요 감쇠 결과는 특정 횡동요 값에서의 결과로 나타나므로 추정된 감쇠 결과가 어느 횡동요 값에 대응하는지 검토가 필요하다. 예를 들어 추정된 횡동요 감쇠 결과가 자유 감쇠의 초기 횡동요 값에 대응하는지, 선택된 피크 횡동요 값의 평균에 대응하는지에 따라 횡동요 감쇠 추정 결과는 다르게 나타난다. 대응되는 횡동요 값의 적합성을 검토하기 위해 자유 감쇠 시계열 내 선택된 구간의 전체 피크를 적용한 횡동요 감쇠 추정 결과와 특정 횡동요 값이라 근사할 수 있는 인접한 두 개의 피크만을 이용한 횡동요 감쇠 추정 결과 비교하였다.
특정 횡동요에서 감쇠값을 검토를 위해 Case 4(C4-FD-005)를 대상으로 인접한 두 개의 횡동요 크기만은 이용하여 순차적으로 횡동요 감쇠를 추정한 결과와 선택 구간 전체를 대상으로 횡동요 감쇠를 추정한 결과를 Fig. 10에 나타내었다. 또한 Fig. 11에는 Case 4 실험에 대해 연속된 최고, 최저점을 이용하여 순차적으로 횡동요 감쇠를 추정한 결과와 선형 추세선을 표식 및 점선으로 각각 표시하였다. 또한 Case 4 자유 감쇠 실험의 횡동요 감쇠 추정 결과를 횡동요 평균값에 대해 Fig. 11에 함께 나타내었다. Fig. 11에 의하면 선형 추세선과 횡동요 평균에 대한 횡동용 감쇠 결과가 유사한 경향을 보여주고 있다. 이를 통해 선택 구간에서의 횡동요 감쇠 추정 결과를 횡동요 평균값에 대응하여 나타낸 결과가가 특정 횡동요 크기에서의 감쇠 결과와 유사한 값을 보여 준다고 판단할 수 있다.
Fig. 12는 자유 감쇠 실험 시계열의 선택된 구간 내 횡동요 크기를 이용하여 대수감쇠율 기법으로 선형 감쇠 결과를 도출한 결과로 횡동요 평균값에 대해 임계 횡동요 감쇠값과 횡동요 감쇠 계수의 비율인 상대 감쇠로 표현하였다. 상대 감쇠 크기는 횡동요 각도가 커짐에 따라 증가하는 경향을 보이며 선체 하부의 형태 및 빌지킬의 유무에 따른 횡동요 감쇠가 크게 영향을 받는 것으로 나타났다.
Case 1과 Case는 3은 약 1%에서 2% 사이의 상대 감쇠값을 가지며 횡동요 각도에 크게 영향을 받지 않는 것으로 나타났다. Case 2는 선체 하부의 엣지 효과로 횡동요 상대 감쇠값이 횡동요 각도에 따라 약 3%에서 6%로 나타났다. Case 4는 Case3 조건에 빌지킬을 부착한 것으로 횡동요 상대 감쇠값이 횡동요 각도 조건에 따라 약 4.5%에서 6.5%까지 추정되었다.
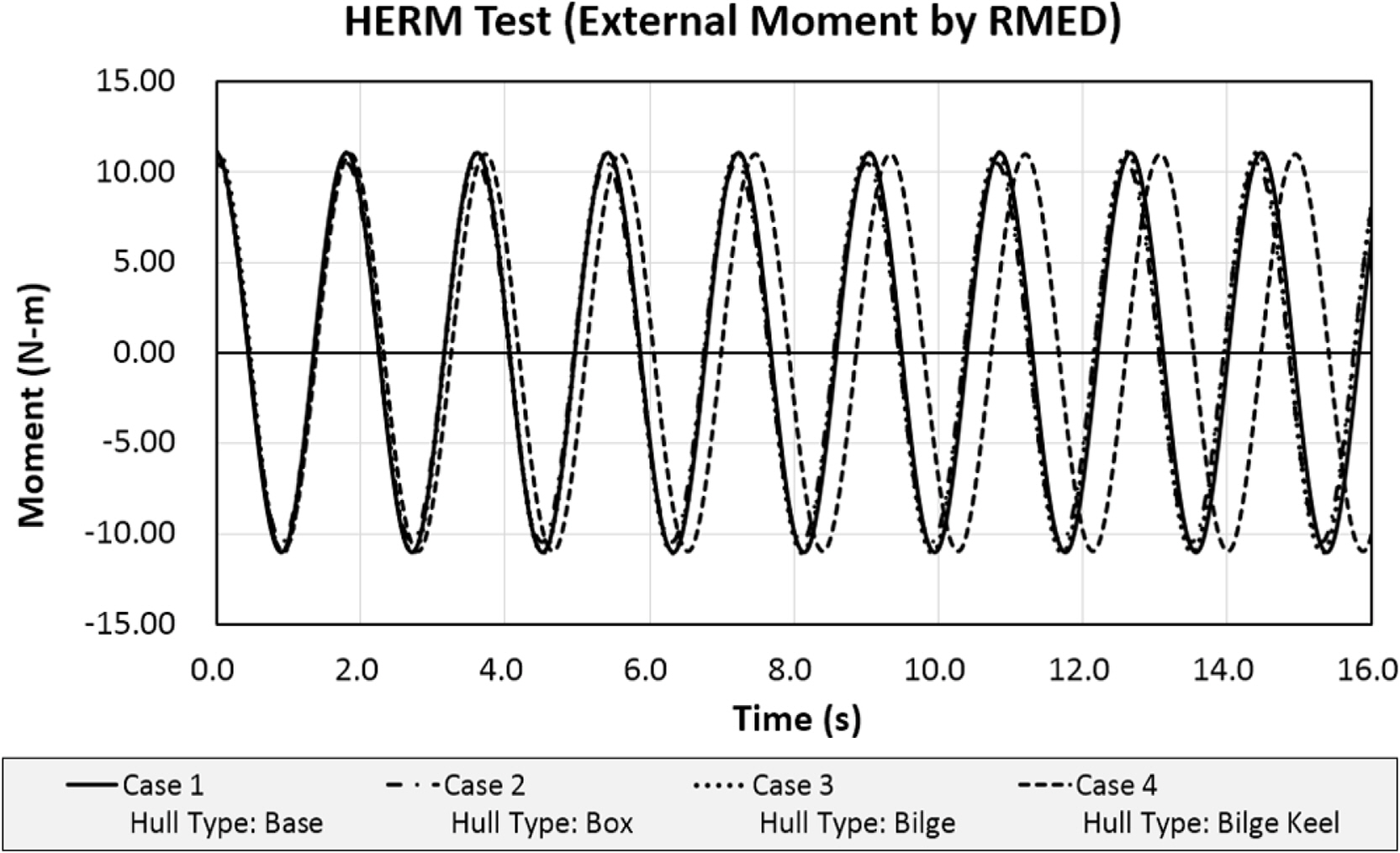
가진 운동을 통한 감쇠 추정 모형 시험은 Table 4 조건을 기반으로 하되 가진 장치의 무게추 이동 거리 조건에 따라 실험이 조건이 추가되었다. Fig. 13은 동일한 크기의 횡동요 가진 모멘트가 적용된 실험 조건이며 자유 감쇠 실험을 통해 얻은 공진주가가 적용되었다. Fig. 14는 Fig. 13의 횡동요 가진 모멘트가 가해졌을 때 각 Case의 횡동요 시계열을 나타낸 것이다. 가해진 횡동요 모멘트의 주기가 횡동요 공진 주기와 같으므로 모멘트와 횡동요의 위상차는 약 90도를 보이고 있으며 각각의 Case별로 중앙 단면 특성 및 빌지킬 유무에 따라 각기 다른 횡동요 결과를 보여준다.
완만한 빌지 반경을 가지는 Case 3은 약 12.7도의 횡동요로 가장 큰 값을 보여주며 Case 1이 약 10.8도의 횡동요로 거동하였다. Case 2는 선체 하부의 엣지 효과로 횡동요가 약 5도 발생하였으며 빌지킬이 부착된 Case 4는 약 3.6도의 횡동요 결과를 나타내었다.
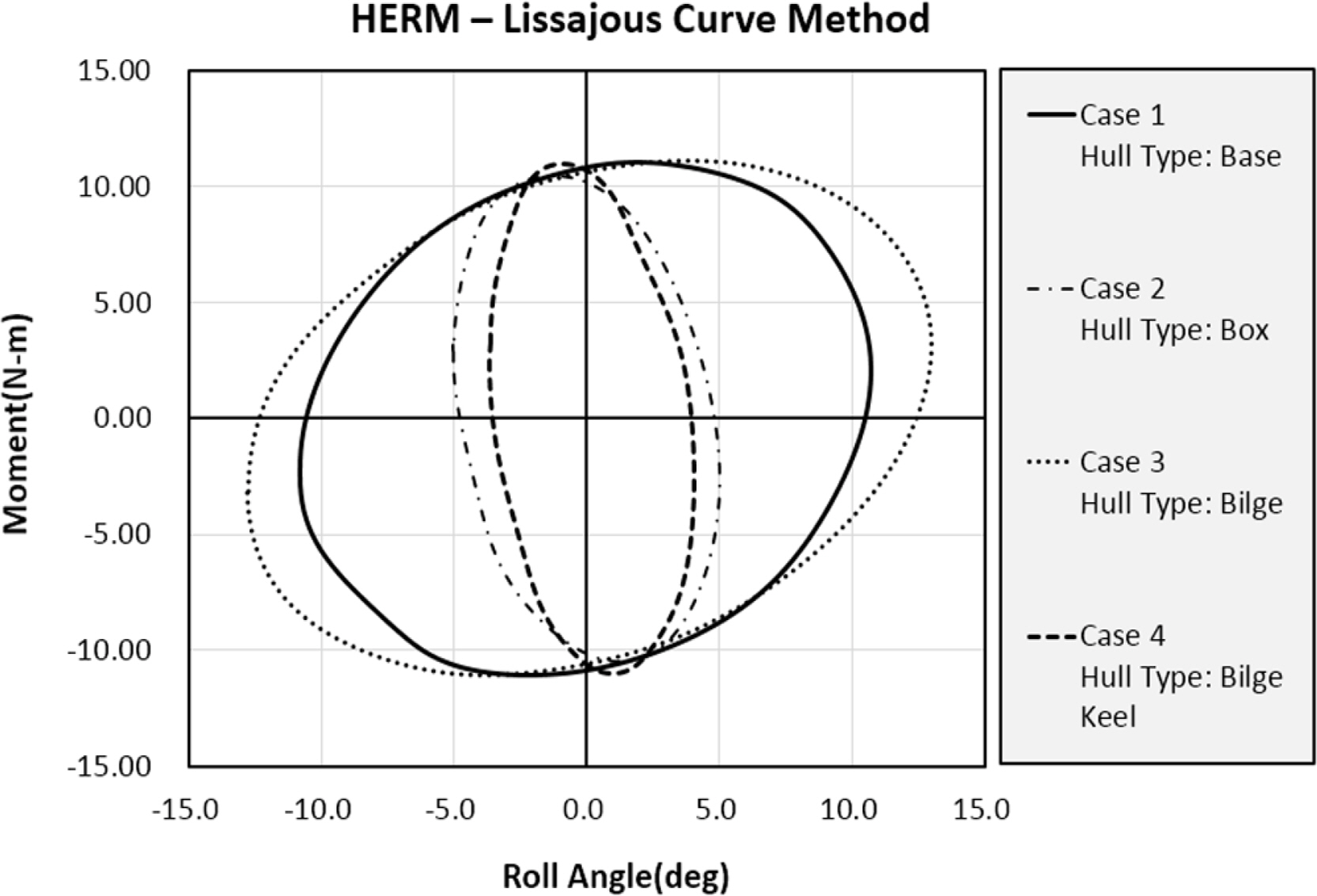
Fig. 15는 Fig. 13과 Fig. 14의 시험 결과에 대한 Lissajous Curve를 나타낸다. Lissajous curve 내부 영역의 면적이 한 주기동안 소실된 에너지를 의미하므로 이를 이용하여 식 (7)과 같이 횡동요 감쇠값을 추정할 수 있다.
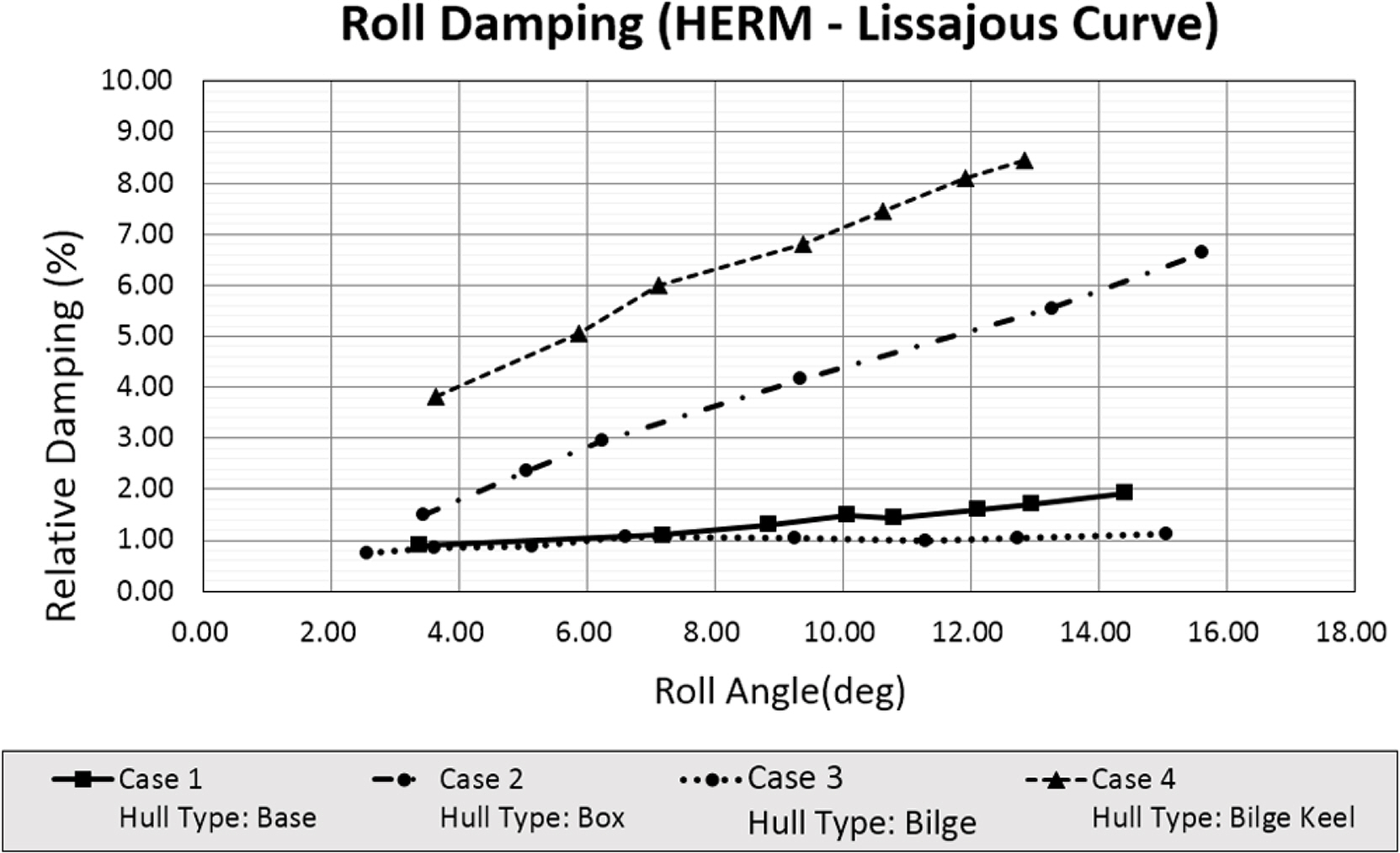
Fig. 16은 각 Case 및 가진 조건별로 감쇠 계수를 추정한 결과이다. Case 1은 약 1%에서 2% 사이의 상대 감쇠값을 가지며 Case 3은 약 1%의 상대 감쇠값으로 두 Case 모두 횡동요 각도에 크게 영향을 받지 않는 것으로 나타났다. Case 2는 선체 하부의 엣지 효과로 횡동요 상대 감쇠값이 횡동요 각도에 따라 약 1.5%에서 6.8%로 증가한다. Case 4는 Case3 조건에 빌지킬을 부착한 것으로 횡동요 상대 감쇠값이 횡동요 각도 조건에 따라 약 4.0%에서 8.5%까지 나타났다.
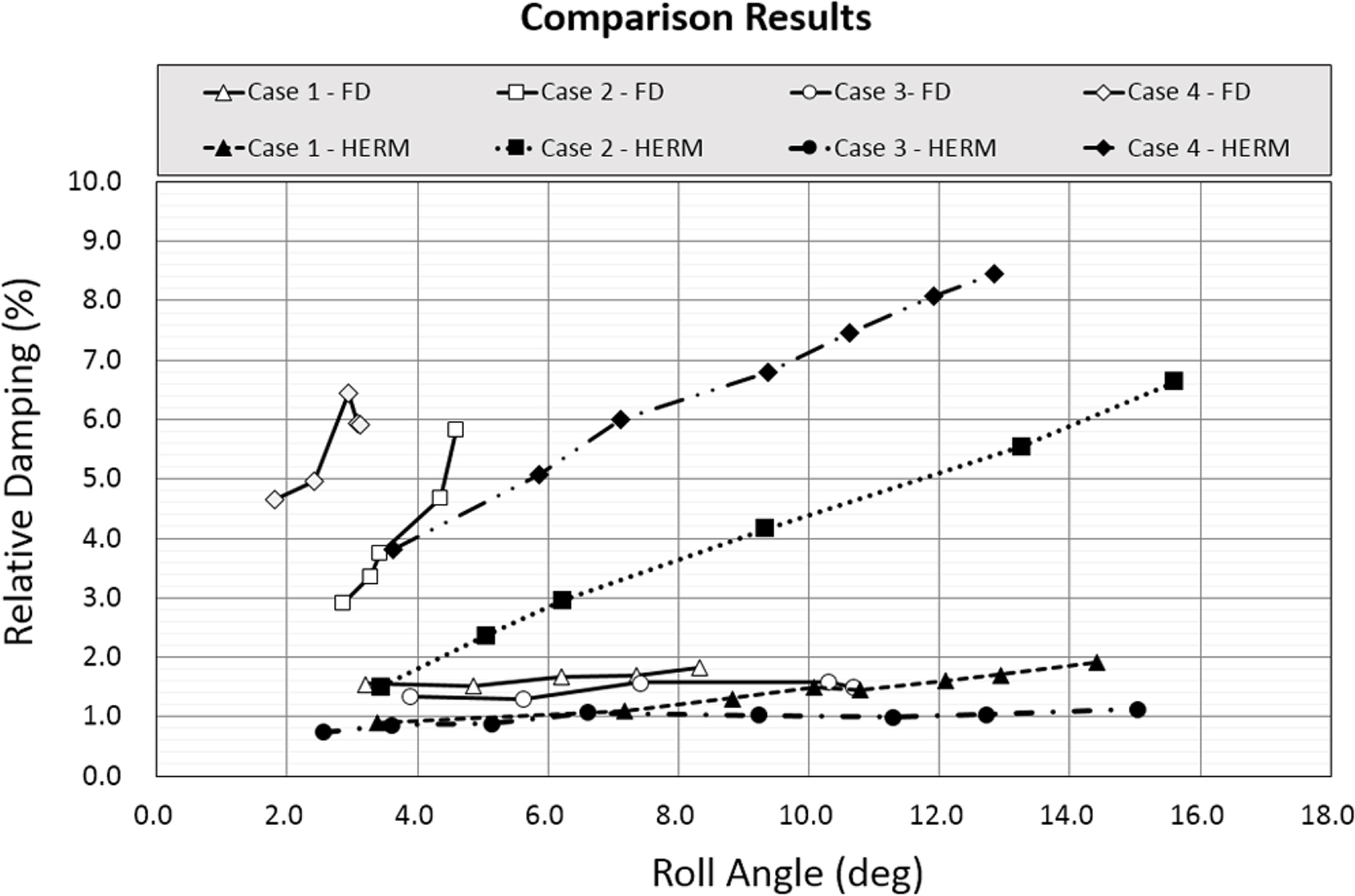
본 연구에서는 자유 감쇠 모형 시험과 가진 운동 모형 시험을 통해 각각 추정기법을 적용하여 대상 Case 별 횡동요 감쇠 계수를 추정하여 비교하였다. Fig. 17에 자유 감쇠 모형시험과 가진 운동 모형 시험의 횡동요 감쇠 추정 결과를 함께 표시하였다. Case 1과 Case 3의 경우에는 선형 특성 상 횡동요 상대 감쇠값이 2% 내외로 작으며 자유 감쇠 추정 기법과 가진 운동 감쇠 추정 기법 간 차이가 크지 않다.
Case 2와 Case 4의 경우 두 모형 시험 기법에 의한 결과가 차이를 보이고 있으며 전반적으로 자유 감쇠 모형 시험을 통한 횡동요 감쇠값이 크다. 이는 모형 시험 기법의 특성 및 감쇠 추정 기법의 차이로 부터 기인한 것으로 추정한다.
자유 감쇠 시험은 부유체가 특정 횡동요 각도를 유지한 정적 상태를 초기 조건으로 두고 시험을 수행하므로 시험 기간 동안 선체 주위의 유체가 충분히 교란되지 않은 상태에서의 횡동요 감쇠값을 추정한다. 반면, 가진 운동 모형 시험을 이용한 추정기법은 가진 장치에 의해 가해진 모멘트에 의해 횡동요가 일정 각도로 수렴한 이후의 시계열을 이용하므로 선체 주위 유동은 충분히 교란된 상태라 볼 수 있다. 이는 Case 3과 Case 4의 결과 비교에서 확인할 수 있다. Case 3은 빌지킬이 없는 선형이므로 횡동요에 의해 발생하는 유체 교란이 상대적으로 미비하며 횡동요 감쇠에 작용하는 영향이 작다. 결과적으로 Case 3의 횡동요 감쇠 결과는 두 모형 시험 기법의 차이가 크지 않다. 반면 빌지킬이 부착되어 선체 주위의 유체 교란이 중요한 Case 4의 경우에는 횡동요 감쇠 결과가 모형 시험 기법에 따라 큰 차이를 보인다.
자유 감쇠 모형 시험을 이용한 횡동요 추정 기법은 초기 횡동요 크기를 시작으로 점차 감소하는 형태의 연속적인 횡동요 거동 중의 횡동요 감쇠를 추정한다. 따라서 4.1장에서 살펴본 바와 같이 자유 감쇠 모형 시험의 경우 선택 구간에서의 횡동요 크기를 이용한 감쇠 추정 결과는 횡동요 평균값에 대응하여 나타나는 것이 유효하다. 반면, 가진 장치를 이용한 횡동요 감쇠 추정 기법은 가진 장치에 의한 모멘트로 인해 발생하는 횡동요 값을 통해 감쇠 결과 추정하므로 특정 횡동요 값의 횡동요 감쇠를 직접적으로 확인할 수 있는 장점이 있다.
본 연구에서는 3종류의 중앙 단면과 빌지 곡률을 가지는 중앙단면에 빌지킬이 부착된 모델을 대상으로 자유 감쇠 및 가진 운동 감쇠 모형 시험을 수행하였다. 자유 감쇠 모형 시험 결과는 대수감쇠율 기법을 통해 횡동요 상대 감쇠 계수 값을 추정하였으며 가진 운동 모형시험 결과는 Lissajous curve 기법을 이용하여 등가의 선형 감쇠를 구한 후 상대 감쇠 계수 값으로 나타내었다.
기본 선형인 Case 1과 빌지 반경을 가지는 Case 3은 횡동요 각도 조건에서 전반적으로 1%~2%내외의 상대 감쇠 결과를 보여주었으며 모형 시험 기법 간 큰 차이를 보이지 않았다. 반면, 선체 하부가 엣지 형태인 Case 2와 빌지킬이 부착된 Case 4는 횡동요 각도가 증가함에 따라 횡동요 감쇠값이 크게 증가하였다. Case 4는 Case 3과 동일 선형 조건에 빌지킬만 추가로 부착된 경우로 빌지킬이 횡동요 저감에 상당히 효율적인 수단임을 확인할 수 있다.
자유 감쇠와 가진 운동 감쇠의 횡동요 감쇠 추정 결과를 비교하면 각진 형태 선체 및 빌지킬이 부착되어 선체 주위 유체 교란 및 횡동요 감쇠가 크게 나타는 경우에는 전반적으로 자유 감쇠 모형 시험에 의한 횡동요 감쇠 추정 결과 가진 운동을 통한 감쇠 추정 결과 대비 크게 나타났다. 이는 두 모형 시험 기법의 특성 및 감쇠 추정 기법 간 차이에 의한 것으로 보이며 향후 CFD 및 파랑 중 동적 거동 수치 해석 등을 통해 두 모형 시험 및 추정 기법의 특성을 엄밀하게 검토할 예정이다.
후기
본 논문은 해양수산부 국가개발사업인 ‘심해공학수조 운영을 위한 연구 인프라 구축 및 심해플랜트 Pre-FEED 원천핵심기술 개발’및 선박해양플랜트연구소 주요사업 ‘심해공학수조 기반 표준 해양구조물 성능평가 기술 개발’로 수행된 연구결과입니다(PMS3850, PES3200).
Fig. 8.
Free decay time series with 5 different initial roll angle for Case 4, hull type: bilge keel
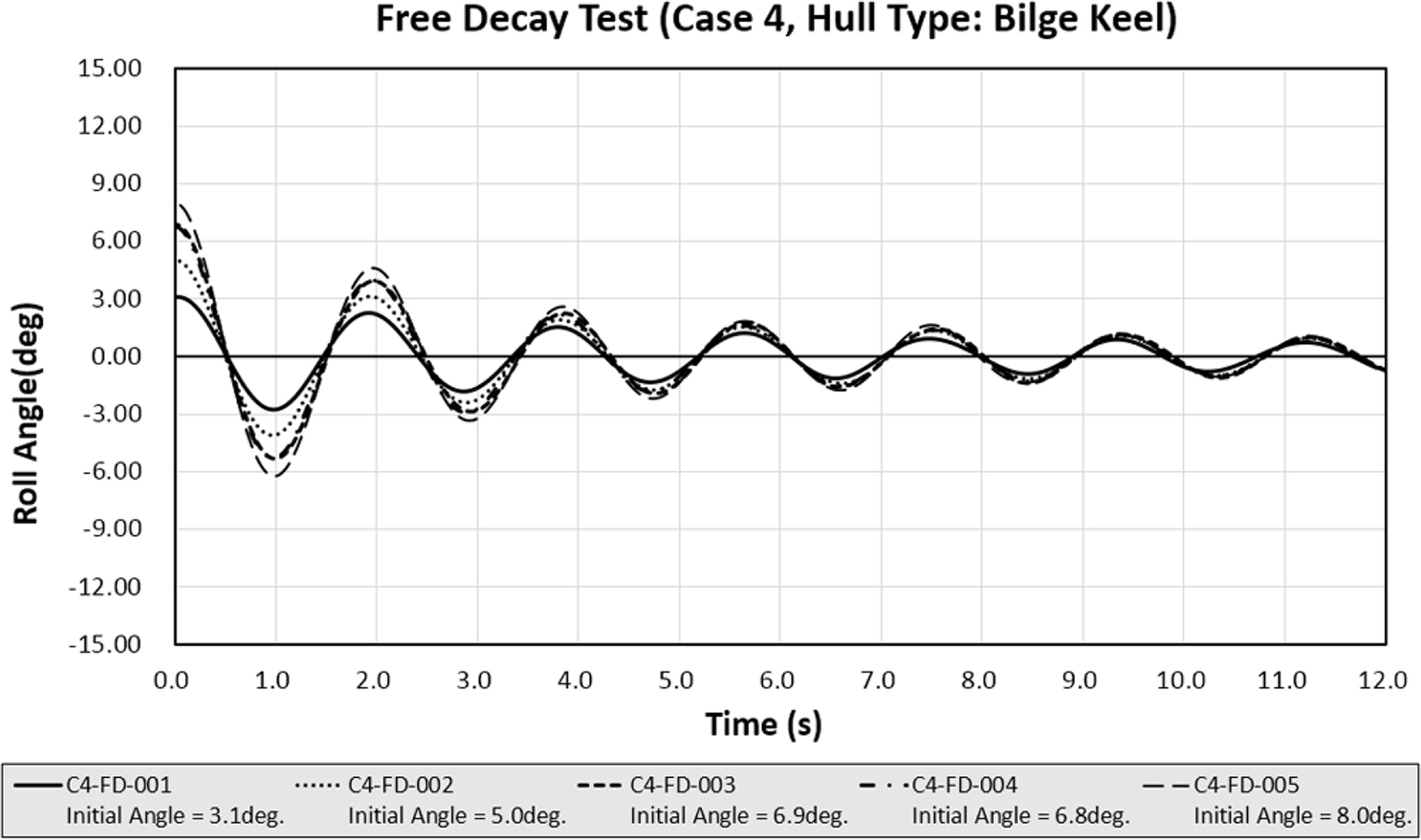
Fig. 9.
Comparison of free decay time series with approximately 8.8degree initial angle for Case 1, 2, 3 and 8.0 degree initial roll angle for Case 4
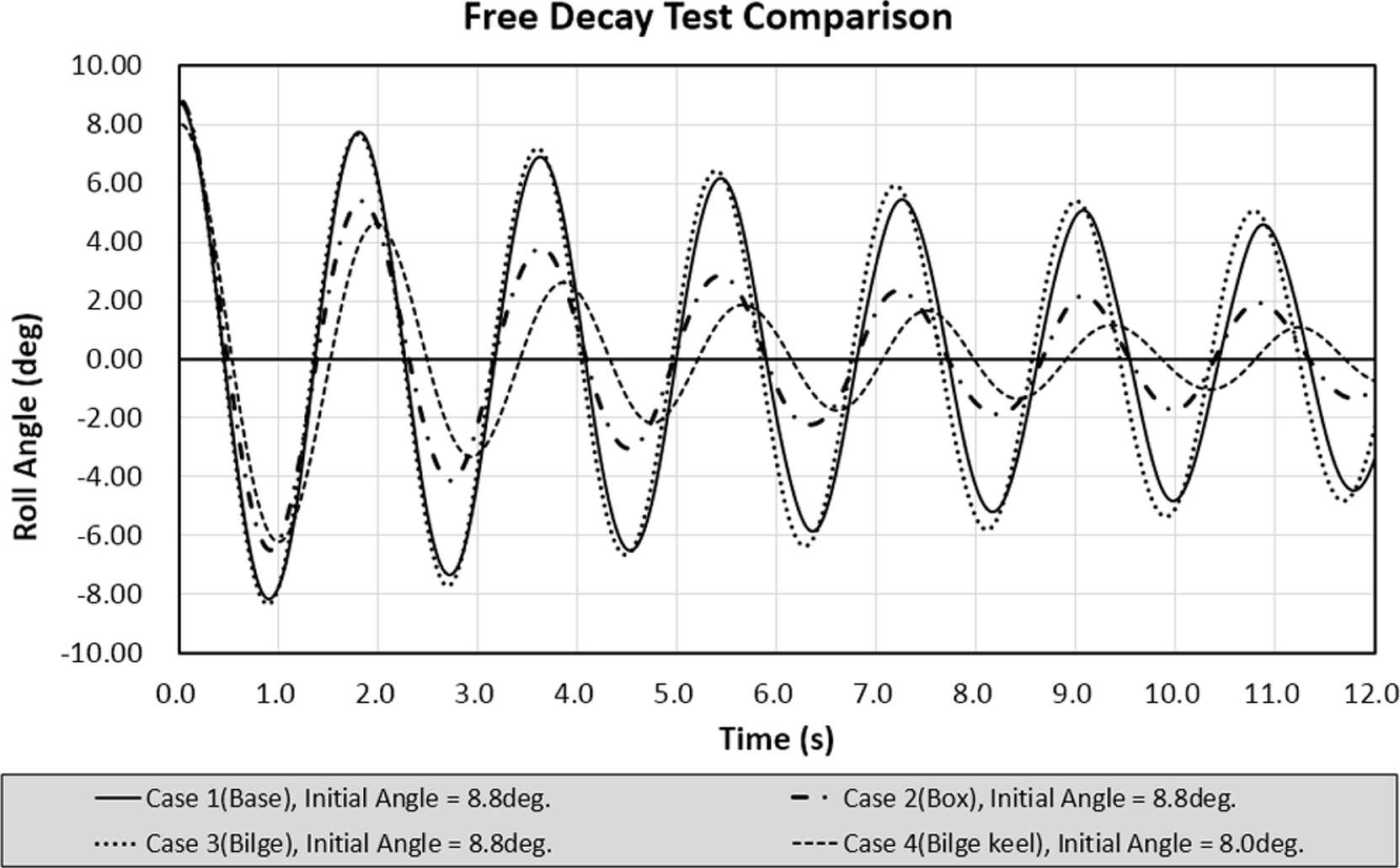
Fig. 10.
Comparison of logarithmic slopes between adjacent two peaks and total peaks for Case 4 (C4-FD-005)
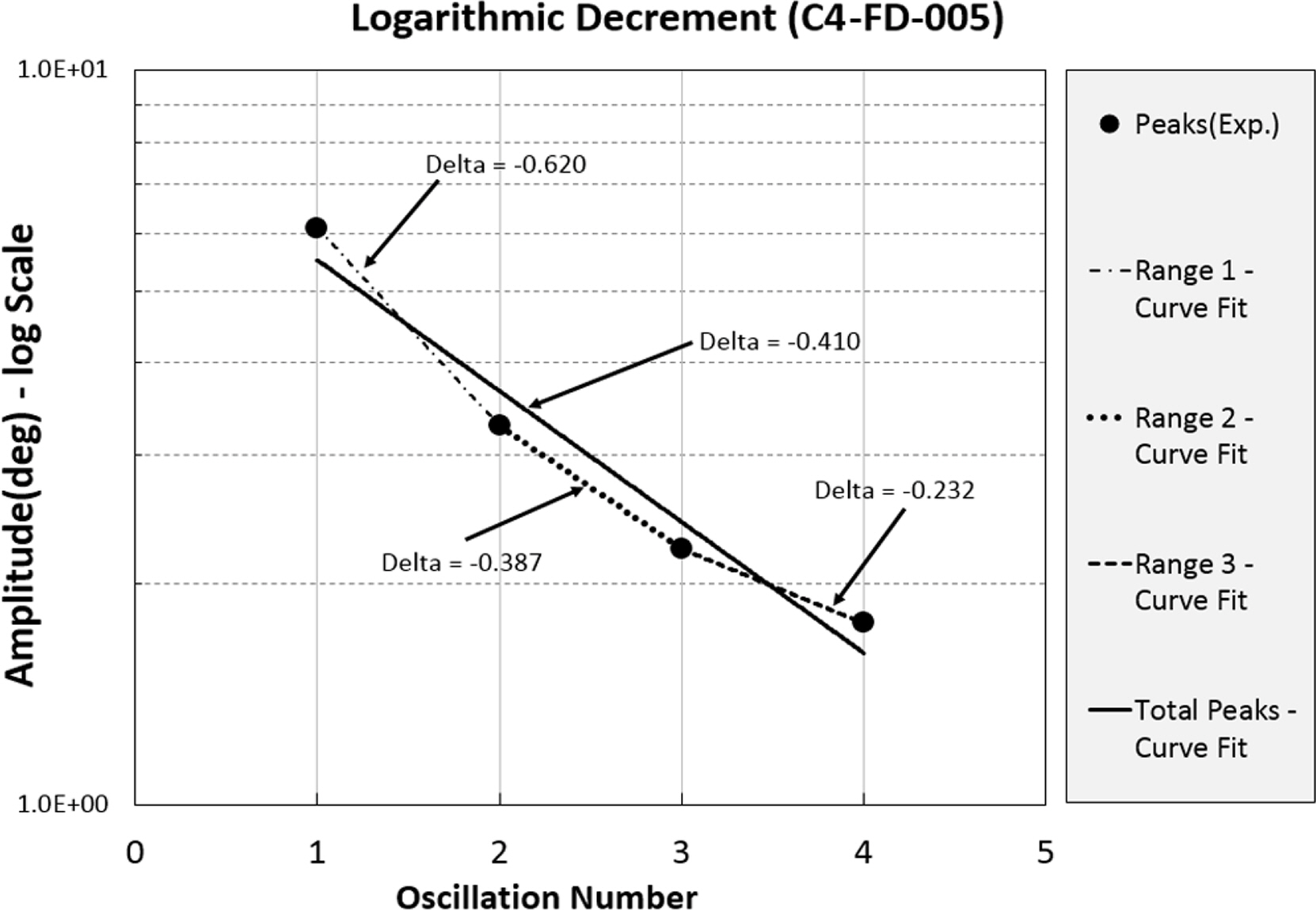
Fig. 11.
Comparison of relative damping of using adjacent two peaks, linear curve and total peaks for Case 4
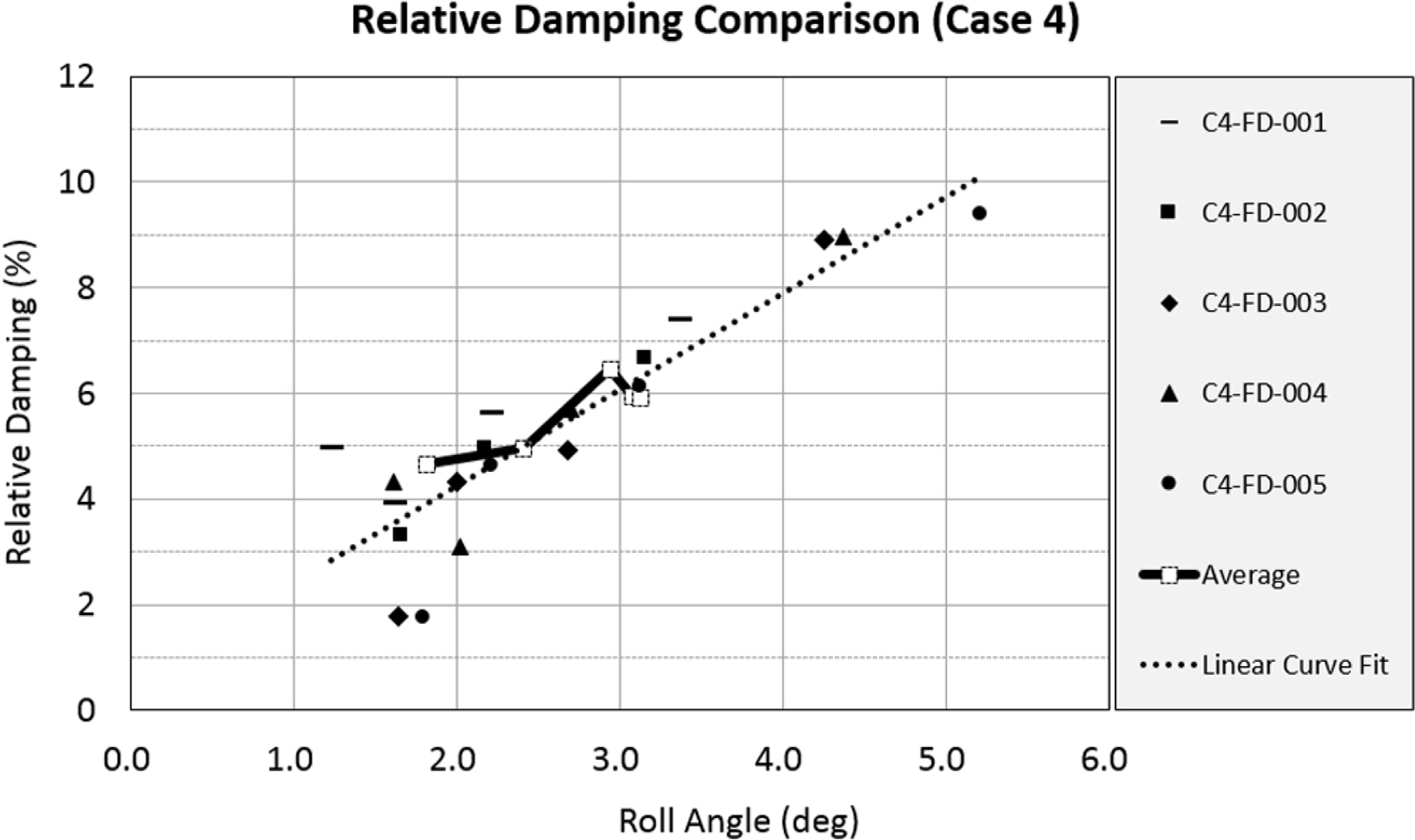
Table 1.
Particulars of test models
Table 2.
Specification of roll motion excitation device
Table 3.
Model test matrix of free decay tests for Case 1
| Test ID | Initial roll angle (deg) for free decay test |
|---|---|
| C1-FD-001 | ∼ 3.0 |
| C1-FD-002 | ∼ 6.0 |
| C1-FD-003 | ∼ 9.0 |
| C1-FD-004 | ∼ 12.0 |
| C1-FD-005 | ∼ 15.0 |
References
Blume, P. (1979). Experimentelle Bestimmung von Koeffizienten der Wirksamen Rolldämpfung und Ihrer Anwendung zur Abschätzung Extremer Rollwinkel. Ship Technology Research, Schiffstechnik, 26, 3-23.
Himeno, Y. (1981). Prediction of Ship Roll Damping - State of the Art. University of Michigan: p 239.
Ikeda, Y., Himeno, Y., & Tanaka, N. (1976). On Roll Damping Force of Ship: Effects of Friction of Hull and Normal Force of Bilge Keels. Journal of the Kansai Society of Naval Architects, Japan, 161, 41-49.
Ikeda, Y., Himeno, Y., & Tanaka, N. (1978). A Prediction Method for Ship Roll Damping.. Report of Department of Naval Architecture University of Osaka Prefecture: p 00405.
Oliva-Remola, A., Bulian, G., & Perez-Rojas, L. (2018). Estimation of Damping through Internally Excited Roll Tests. Ocean Engineering, 160, 490-506.

Park, B., Jung, J., Park, I., Jung, D., Cho, S., & Sung, H. (2017). Study on Estimation Methods of Roll Damping Coefficients for 30k LNG-BS Using Designed Excitation Device for Harmonic Roll Motion. Proceedings of Fall Conference of the Korean Society of Ocean Engineers, 86-90. https://doi.org/10.1016/j.oceaneng.2018.04.052

Park, B., Jung, J., Jung, D., Park, I., Cho, S., & Sung, H. (2018). Study on the Estimation Methods of Roll Damping Coefficients Using Designed Excitation Device for Harmonic Roll Motion.. Proceedings of ISOPE 2018. Sapporo, Japan..
Handschel, S., Feder, D., & Abdel-Maksoud, M. (2015). Estimation of Ship Roll Damping - a Comparison of the Decay and the Harmonic Excited Roll Motion Technique for a Post Panamax Container Ship.. Proceedings of the 12th International Conference on the Stability of Ships and Ocean Vehicles Glasgow, UK: 475-488.
- TOOLS
-
METRICS

-
- 2 Crossref
- Scopus
- 7,184 View
- 153 Download
- Related articles in JOET
-
Experimental Study on Reducing Motion of Circular Cylinder in Currents2019 August;33(4)
Experimental Study on Reducing Lateral Force on Circular Cylinder Using Strings2018 August;32(4)
An Experimental Study on the Appendage Development of the Incinerating Vessel1999 February;13(1)