|
 |
- Search
| J. Ocean Eng. Technol. > Volume 32(4); 2018 > Article |
|
Abstract
Recently, it was predicted that the size of offshore markets will grow as gas prices edge up. This paper presents experimental results for using strings as a suppression device on a circular cylinder and discusses the various data. A test model was used to investigate the role of strings by varying the thickness of the strings used to suppress a cylinder’s lateral force taking into account the effect of turbulence promoted. A substantial amount of experimental data were taken from experiments performed on cylinders at Reynolds number up to a maximum value of 105. The suppression of vortex shedding and a lateral force reduction of up to 70% were observed for the cylinder with strings.
최근 계속되는 유가상승과 해양 개발사업의 발달로 인해 해양플랜트 발주물량이 지속적으로 늘어날 것이라 전망된다. 이에 석유와 가스를 시추하는데 필요한 Umbilical, Riser, Spar 등과 같은 원형실린더 형상 구조물의 수요 또한 증가할 것이라 예측된다. 이러한 원형실린더 형상 구조물은 횡단면이 둥근 형상을 가지며 일정한 유속이 가해지면 주기적으로 비대칭적인 Vortex shedding 현상이 발생하게 된다(Park, 2017). Vortex shedding 현상으로 원형실린더 형상 구조물은 지속적으로 진동을 수반하게 되고, 이를 VIV(Vortex induced vibration)라 한다. VIV 응답은 비선형적인 운동특성을 가지며, 원형실린더 형상 구조물에 반복적인 하중을 유발하여 구조적 피로손상을 발생시키는 원인이 된다. 따라서 VIV 응답은 원형실린더 형상 구조물을 설계할 때 주요 고려대상이 된다. 뿐만 아니라 원형실린더 형상 구조물의 fn(Natural frequency)과 fs(Vortex shedding frequency)의 비가 1에 근접할수록 VIV 응답이 커지고 fn과 fs 의 비가 1이 될 경우 공진응답의 일종인 Lock-in 현상이 발생하게 된다.
이러한 VIV 현상을 감소시키기 위하여 Strake, Streamlined fairing 등의 저감장치가 사용되고 있다. 그러나 Strake의 경우 제작 및 조립이 용이하지 않고, 구조물의 무게를 증가시키는 단점이 있으며, Streamlined fairing의 경우는 고가의 시공비가 발생하는 단점이 있다.
관련 주요연구로 VIV 현상에 대한 분석을 한 Jung and Yoon(2015)은 Reynolds number(Re)가 와류 감쇠에 미치는 영향에 대해 분석하고 나선형 해양구조물 주위 유동에 대한 연구를 하였고, Kim(2010)은 Riser의 VIV 현상의 수치해석 방법에 대해 연구를 하였다. Son(2010)은 실린더에 필름을 부착하여 와동으로 인한 영향을 줄이는 실험을 진행하였다. 그러나 최근 국내에서 Son(2010)의 연구 외에는 VIV 저감에 관한 모형실험은 활발하지 않다.
본 연구에서는 기존의 VIV 저감장치의 단점을 보완하기 위해 String 타입의 저감장치를 고안하였다. String이 설치된 원형실린더의 항력 및 수평력의 감소효과를 검증하기 위해 회류수조(CWC, Circulating water channel)에서 모형실험을 실시하였다. 또한 String의 유무, 굵기 및 설치 위치를 변화시켜 VIV 저감 효율을 비교분석하였다.
본 실험에서는 원형실린더가 균일 흐름 중에 있을 때 작용하는 항력과 수평력을 측정 하다. 흐름방향으로 작용하는 힘을 항력이라 하고, 흐름에 수직된 방향의 힘을 수평력이라 한다. 실린더에 작용하는 양·항력은 아래와 같다.
항력계수(CD)는 Re에 따라 변하고 Re는 동점성계수와 유속, 직경에 따라 변하며 다음과 같다.
와류로 인한 항력과 수평력의 크기를 비교하기 위해 무차원계수를 사용하였다. 실린더가 발생시킨 와류의 주기를 분석하기 위하여 무차원계수인 Strouhal number(St)를 사용하였고 유속을 일반화하기 위해 감속 속도(Vr, Reduced velocity)를 사용하였다. 와 Vr 의 식은 아래와 같다.
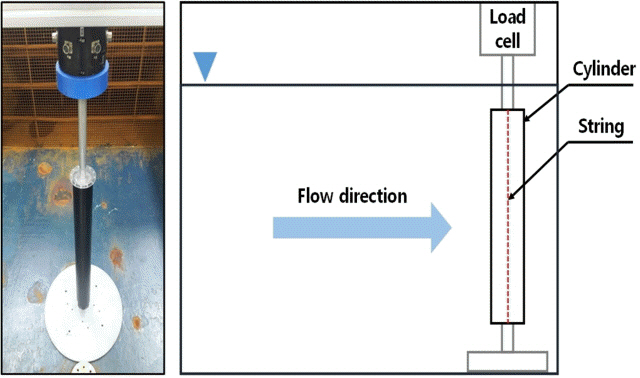
Fig. 1은 모형실험이 실시된 회류수조와 6분력계를 나타낸 사진이다. 회류수조의 크기는 1.8×1.2×4.0m (B×D×L)이며 측정수심은 0.915m이다. 원형 실린더에 작용하는 항력과 수평력을 측정하기 위하여 6분력계를 사용하였으며 힘의 측정범위는 ±100N이다.
원형실린더의 길이는 0.75m로 제작되었고, 지름은 벽면효과(Wall effect)를 고려하여 0.075m로 설정하였으며, 구조물은 양단지지의 형태로 구속하였다. 실린더의 자유수면 효과(Free surface effect)를 없애고자 직경이 작은 봉으로 실린더를 연결하였고, 작은 봉에 작용하는 양·항력은 전체 힘의 약 4%로 미소하다 가정하고 힘을 계측하였다. Fig. 2는 설치된 실린더의 모습과 모식도를 나타낸 그림이다.
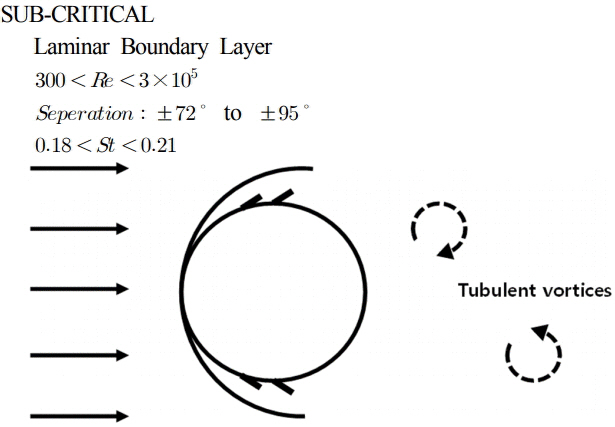
Fig. 3은 특정 Re범위에서 원형실린더 형상 구조물에 작용하는 와류(Gustafsson, 2012)에 관한 그림이고 본 실험에 사용된 속도와 무차원 값의 범위는 Table 1에 제시하였다.
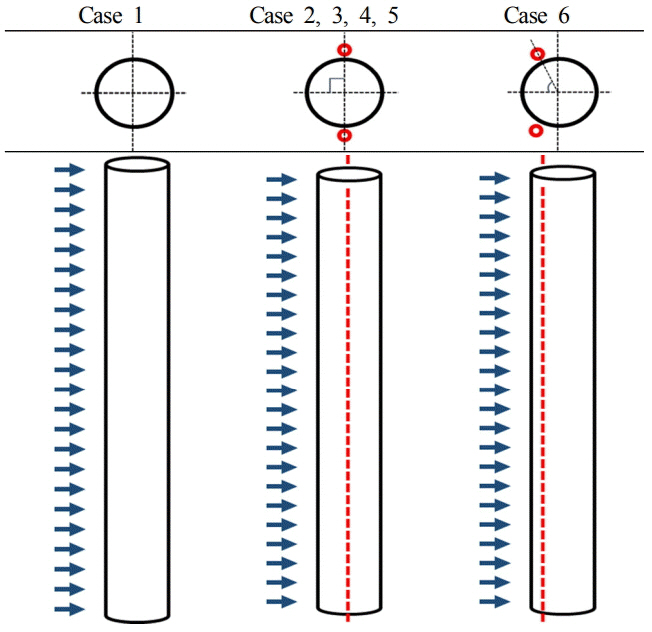
String은 니켈 재질로, 중심으로부터 1.1×DCylinder떨어진 거리에 설치하였고, 설치되었을 때 진동수는 40Hz로 설정하였다. 실험 계측 시간은 각 유속별로 180초이고, 균일류를 얻기 위하여 계측 전 60초간의 대기시간을 가졌다. 뿐만 아니라 신뢰성을 확보하기 위하여 Case별로 동일 유속에서 3회 반복 실험을 실시하였다.
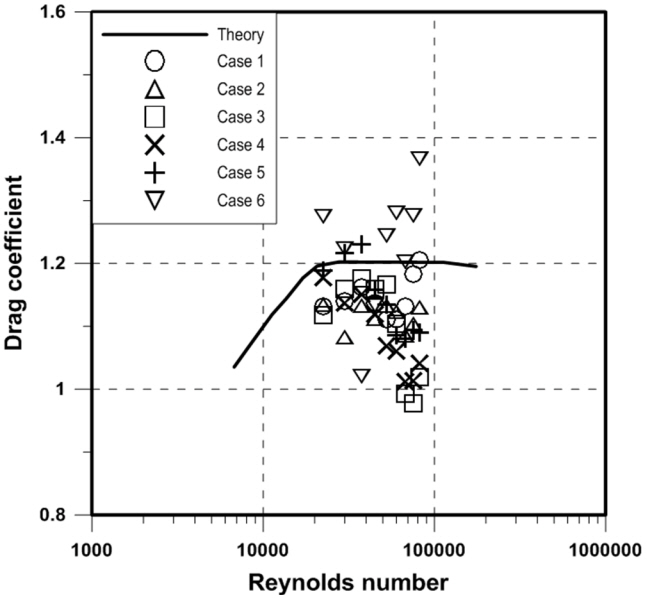
Fig. 5에서는 Re변화에 따른 CD 의 이론값(Blevins, 2001)은 실선으로 나타내었고, 각 Case의 실험 결과 값을 점으로 표시하여 비교한 것이다. Case 1의 경우 이론값과 실험 결과 값이 비교적 잘 일치하는 것을 볼 수 있고 String을 흐름 수직된 방향에 설치한 경우 이론값에 비해 계수 값의 크기가 줄어들고, String을 전방으로 설치한 경우엔 커졌음을 볼 수 있다.
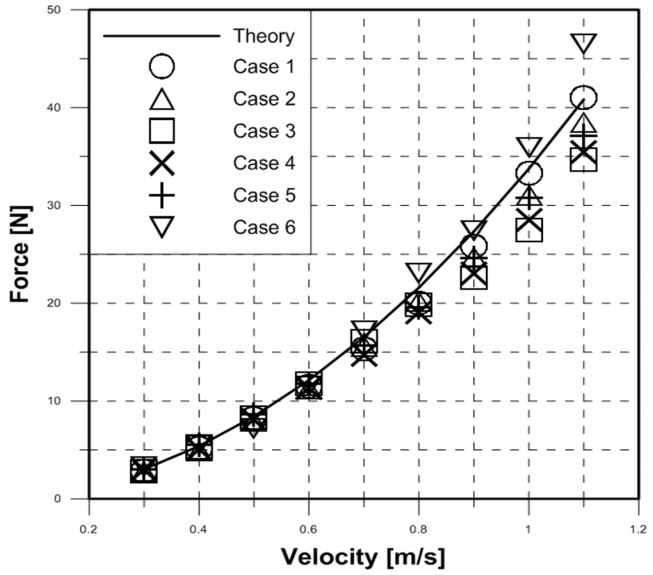
유속의 변화에 따라 원형실린더에 작용하는 항력값을 이론식과 비교하여 Fig. 6에 도시하였고, Table 3은 각 Case별 유속변화에 따른 항력값을 나타내었다. Case 2에서 Case 6까지 결과값은 이론보다 작게 계측되었다. 이는 String의 떨림으로 인해 난류가 유발되어 원형실린더 전·후방의 압력차가 감소(Jo et al., 2008)하여 발생한 현상으로 분석된다. 그러나 Case 2 ~ Case 5의 결과를 바탕으로 String의 굵기에 따른 항력값의 차이는 없었으나, Case 6의 결과를 바탕으로 String의 설치위치를 전방으로 이동시켰을 때에는 항력값을 증가시키는 현상이 발생하였음을 알 수 있었다.
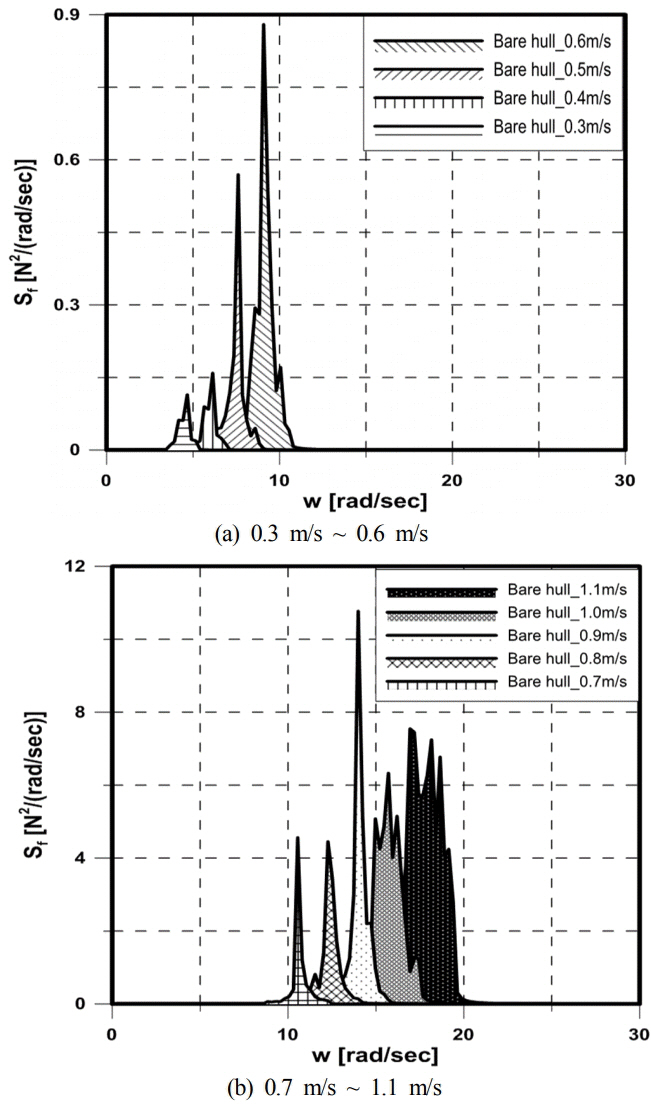
Fig. 7은 Case 1의 수평력 스펙트럼을 각 유속별로 비교하여 보여주고 있다. Fig. 7(a)는 유속이 증가할수록 원형실린더에서 와류가 떨어져 나가는 주기가 짧아지면서 fs가 커지는 것으로 판단된다. Fig. 7(b)은 0.9m/s에서의 최댓값이 다른 유속보다 훨씬 크게 나타났으며, 이는 특정 fs의 밀도가 높아져 발생한 것으로 분석된다.
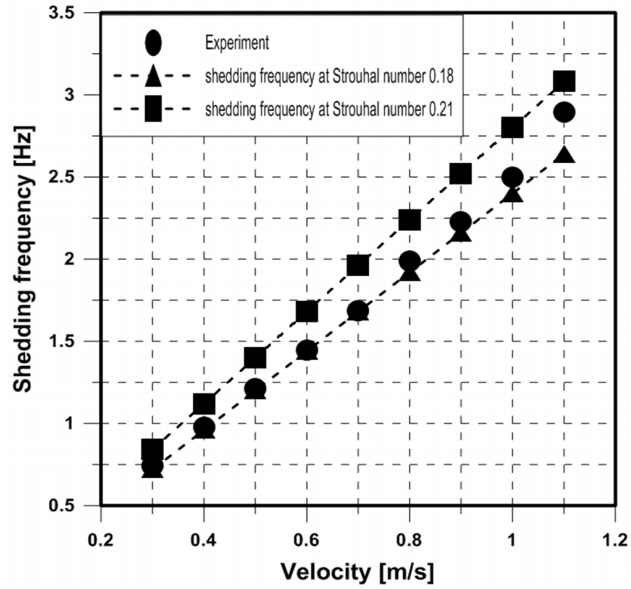
Fig. 8은 VIV 현상이 활발하게 발생하는 St의 범위(Achenbach and Heinecke, 1981)를 fs로 변환하여 유속별로 나타낸 그림이고, Table 4는 Fig. 8의 fs값을 나타냈다. 그림에서 볼 수 있듯이 실험결과가 이론값의 범위 내에 속해져 있다는 것을 확인할 수 있었다.
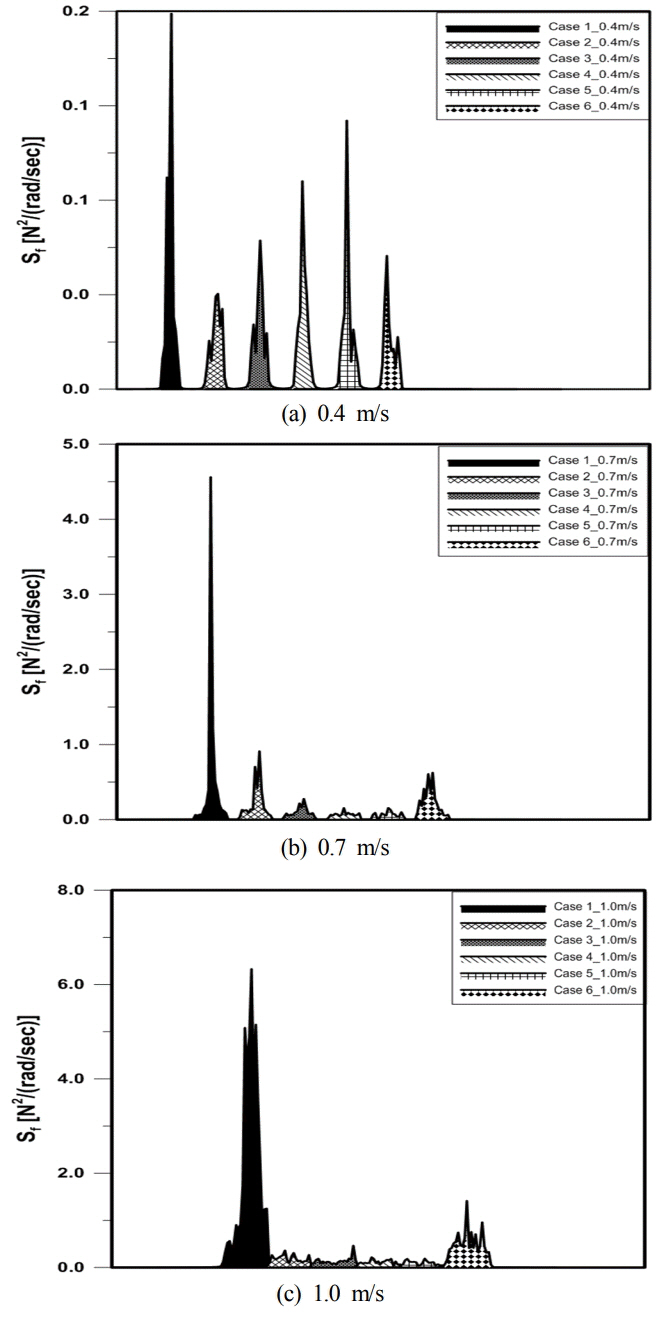
Fig. 9는 대표적인 유속에서 Case별 수평력 스펙트럼을 비교한 그림이다. 제시된 유속에서 Case별 fs는 동일하지만, 면적을 비교하기 위하여 Case별로 스펙트럼을 축 평행 이동시켜 나타내었다. 스펙트럼의 면적은 힘의 크기를 나타내며, 모든 스펙트럼에서 Case 2 ~ Case 5의 면적이 Case 1 보다 작은 것을 확인할 수 있다. 그리고 유속이 0.4m/s에서 1.0m/s로 증가할수록 수평력 저감성능이 큰 것을 확인 할 수 있었다. 이는 유속이 높아질수록 String으로 인한 주변 유체의 난류 강도가 커져 발생한 현상으로 분석된다.
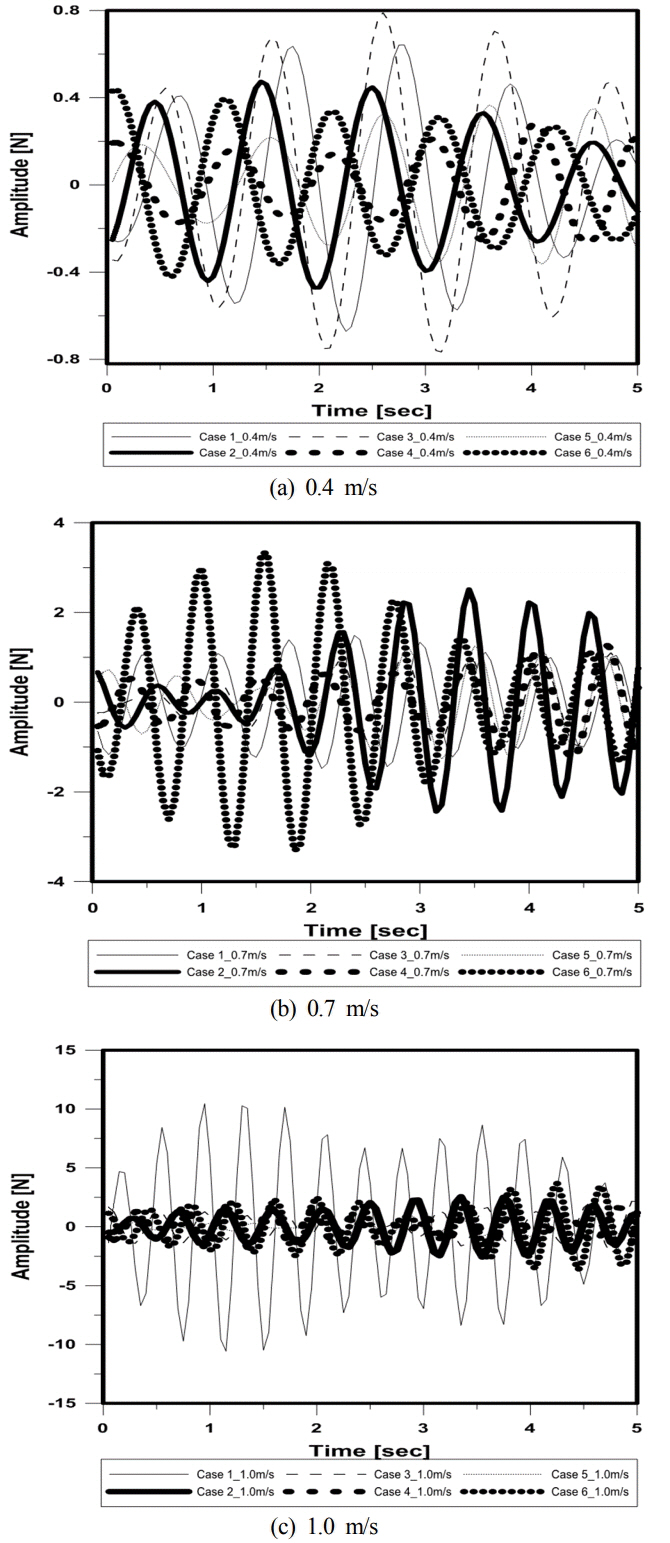
Fig. 10은 세 가지 유속에서 Case별 시계열 그래프로 수평력의 진폭을 비교한 결과이다. 진폭을 비교한 결과 Case 1이 나머지 Case보다 수평력이 큰 것을 확인할 수 있었으며, 유속이 0.4m/s에서 1.0m/s로 증가할수록 진폭의 크기가 확연하게 줄어드는 것을 확인할 수 있었다.
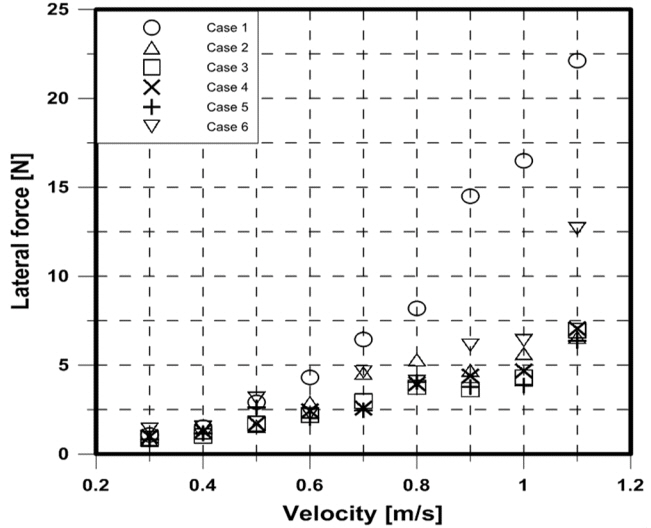
Fig. 11은 x축을 유속으로 y축을 수평력으로 나타낸 그래프이다. 수평력은 진폭의 평균값으로 계산하여 나타내었다.
Case 2 ~ Case 5의 경우 Case 1보다 수평력의 크기가 작아진 것을 확인할 수 있었다. 그렇지만 String 굵기 변화에 따른 수평력 저감 성능은 큰 차이를 보이고 있지 않다. 그리고 설치위치를 전방으로 이동시킨 Case 6의 경우 수평력 저감성능은 있지만, 저감성능에 관한 전반적인 변화 양상을 추정할 수 없었다.
이에 Table 5에서는 각 Case의 VIV 저감성능을 수치로 제시하였다. Case 1에 비해 Case 2 ~ Case 5는 유속이 증가할수록 저감성능이 커지는 것을 확인할 수 있었다. 그렇지만 유속 0.8m/s이하에서는 수평력 저감성능이 뚜렷한 양상을 보이지 않았으며, 유속 0.9m/s이상의 범위에서는 최소 70%의 저감성능을 가지고 있었다. 이는 유속이 높아짐에 따라 Sring의 fs가 커지고 난류강도가 커짐과 동시에 Shedding의 폭이 줄어들어 이러한 경향이 나왔다고 판단된다. Case 6의 경우는 Case 2 ~ Case 5의 저감성능과는 다른 양상을 보여주었다. 이는 String이 전방에 설치된 경우에는 수평력 감소에 긍정적인 영향을 주지 못한다는 것을 알 수 있었다.
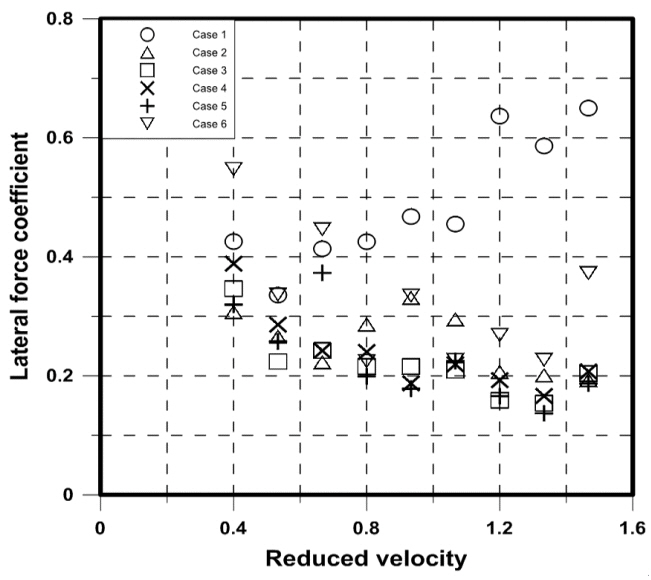
Fig. 12는 x축을 Vr 로 y축은 수평력 계수(CL)로 나타낸 그래프이다. Case 1은 Vr이 증가할수록 CL이 증가하는 경향을 보여준다. 그리고 Case 2 ~ Case 5는 String의 떨림으로 인하여 유속이 증가할수록 CL이 작아지는 현상이 발생함을 알 수 있다. 하지만 Case 6의 경우는 뚜렷한 경향을 띄지 않고 있음을 알 수 있었다.
본 연구에서는 모형실험을 통해 String을 이용한 저감장치의 수평력 저감성능에 대한 연구를 수행하였고, 실험결과를 비교함으로써 String을 이용한 저감장치가 원형실린더 VIV 현상에 미치는 영향을 고찰 하였다. 본 연구로부터 다음과 같은 결론을 얻었다.
(1) 항력의 경우 String의 위치를 변화시킨 Case 6을 제외한 모든 경우에서 String을 부착하지 않은 Case 1에 비해 실린더 전·후방에서의 압력차가 줄어들어 항력이 작게 측정되었다.
(2) 원형실린더 형상의 구조물에 부착된 String은 난류를 유발하였고, 이러한 난류의 영향으로 String을 부착하지 않은 Case 1에 비해 String을 부착한 모든 경우에서 수평력이 감소하였다.
(3) 본 실험조건에서 String 굵기의 변화는 수평력 감소효과에 영향을 미치지 않으며, 설치위치가 흐름 전방인 Case 6 보다 흐름의 수직방향에 설치된 Case 2 ~ Case 5의 수평력 감소효과가 더 크게 나타났다.
(4) Vr 이 1.2이상인 영역에서 String이 부착된 경우 수평력은 String을 부착하지 않은 Case 1에 비해 약 77% 감소하였다. 그러나 Vr 이 1.067이하인 영역에서는 비교적 저유속구간으로, String에 의한 감소효과가 크지 않았다.
(5) 설치 위치를 변화시킨 Case 6을 제외한 모든 경우에서 유속이 증가할수록 항력 및 수평력 저감성능은 크게 작용한다.
향후 Strake와 Streamlined fairing이 부착된 원형실린더 형상 구조물과 수평력 저감성능의 비교연구가 필요하며, 구조적 피로손상과 관련하여 VIV 현상으로 인한 원형실린더 형상 구조물의 응답에 대한 추가연구가 필요하다.
Table 1.
Experimental conditions
| V [m/s] | Vr | Re | CD |
|---|---|---|---|
| 0.3 | 0.40 | 22,500 | |
| 0.4 | 0.53 | 30,000 | |
| 0.5 | 0.67 | 37,500 | |
| 0.6 | 0.80 | 45,000 | |
| 0.7 | 0.93 | 52,500 | 1.2 |
| 0.8 | 1.07 | 60,000 | |
| 0.9 | 1.20 | 67,500 | |
| 1.0 | 1.33 | 75,000 | |
| 1.1 | 1.47 | 82,500 |
Table 2.
Experimental Cases
| Case | DString / DCylinder | Position |
|---|---|---|
| Case 1 | - | - |
| Case 2 | 0.007 | 90° |
| Case 3 | 0.011 | 90° |
| Case 4 | 0.013 | 90° |
| Case 5 | 0.017 | 90° |
| Case 6 | 0.017 | 60° |
Table 3.
Comparison of drag force [N]
References
Achenbach, E., & Heinecke, E. (1981). On Vortex Shedding from Smooth and Rough Cylinders in the Range of Reynolds Numbers 6×103 to 5×106. Journal of Fluid Mechanics, 109, 239-251.

Blevins, RD. (2001). Flow-Induced Vibration. 2nd Edition Van Nostrand Reinhold: New York, USA.
Gustafsson, A. (2012). Analysis of Vortex-Induced Vibrations of Risers. (M.Sc Thesis). Chalmers University of Technology; Sweden.
Jo, HJ., Doh, DG., Kang, SH., Shin, DR., & Son, MS. (2008). Reducing Method of Lateral Force on the Cylinder Using Experiments.. Proceedings of 2008 Joint Conference of Korea Association of Ocean Science and Technology Societies 2481-2484.
Jung, JH., & Yoon, HS. (2015). Reynolds Number Effects on Flow Over Twisted Offshore Structure with Drag Reduction and Vortex Suppression. Journal of Ocean Engineering and Technology, 29(1), 9-15.

Kim, WJ. (2010). Numerical Simulation and Signal Analysis Method for Vortex-Induced Vibration of Flexible Risers. (Ph.D. Thesis). Mokpo National University; Korea.
Park, CY. (2017). Experimental Investigation of Vortex- and Wake-Induced Vibration of Tandem Cylinders. (M.Sc Thesis). Korea Maritime and Ocean University; Korea.
Son, MS. (2010). Experiment Study about Decrease Law of Lift Force Acting on Cylinder. (M.Sc Thesis). Korea Maritime and Ocean University; Korea.
- TOOLS
-
METRICS

-
- 2 Crossref
- Scopus
- 5,157 View
- 93 Download
- Related articles in JOET
-
Experimental Study on Reducing Motion of Circular Cylinder in Currents2019 August;33(4)
Numerical Study on Sheet Metal Forming Analysis Using the One-Step Forming1999 May;13(2)
An Experimental Study on Slamming Phenomenon by Forced Impact2007 February;21(1)