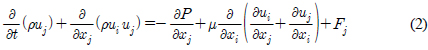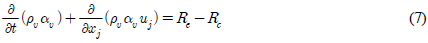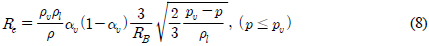3.2 ьИШь╣ШэХ┤ьДЭ ъ▓░ъ│╝
ъ│╡ыПЩьЭШ ы░ЬьГЭьаХыПДыКФ ыЛдьЭМ ьЛЭ (11)ыбЬ ьаХьЭШыРЬ ь║Ры╣ДэЕМьЭ┤ьЕШьИШ(╧Г)ые╝ ьВмьЪйэХШьЧм эПЙъ░АэХШьШАыЛд. ьЧмъ╕░ьДЬ pтИЮьЩА VтИЮыКФ ьЬаьЮЕьЬаыПЩьЭШ ьХХыаеъ│╝ ьЖНыПДые╝ ыВШэГАыВ╕ыЛд. ъ│ДьВ░ьЭА ь║Ры╣ДэЕМьЭ┤ьЕШэД░ыДР ьЛЬэЧШьб░ъ▒┤ъ│╝ ыПЩьЭ╝эХШъ▓М Rn=1.6├Ч105ьЧРьДЬ ьХХыаеьЭД ыВоь╢░ъ░Аый░ ьИШэЦЙэХШьШАъ│а, ыаИьЭ┤ыЖАьжИьИШ(Rn)ыКФ ыЛдьЭМ ьЛЭ (12)ыбЬ ьаХьЭШэХШый░, ьЧмъ╕░ьДЬ dыКФ ьРРъ╕░ьЭШ эПн, ╬╜ыКФ ыПЩьаРьД▒ ъ│ДьИШые╝ ыВШэГАыВ╕ыЛд.
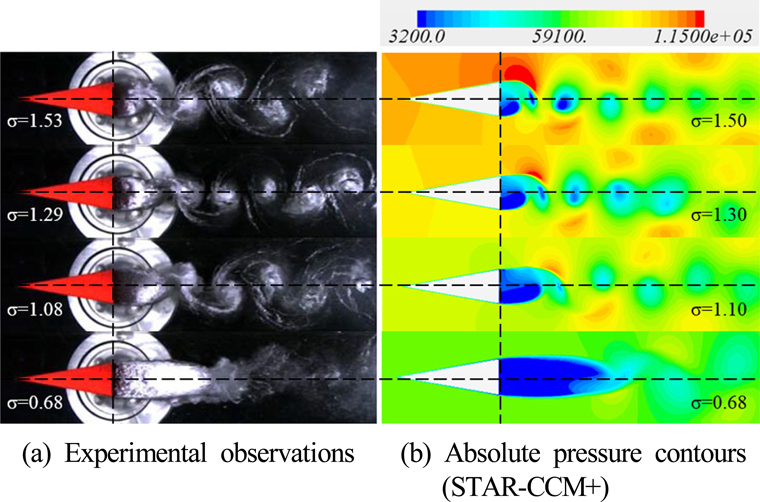
Fig. 2ыКФ ь║Ры╣ДэЕМьЭ┤ьЕШьИШъ░А ыВоьХДьзРьЧР ыФ░ыЭ╝ ьРРъ╕░ьЭШ эЫДыеШьЧРьДЬ ъ│╡ыПЩьЭ┤ ьД▒ьЮеэХШыКФ ыкиьК╡ьЭД ы│┤ьЧмьдАыЛд. ь╢йыВиыМАэХЩъ╡Р ь║Ры╣ДэЕМьЭ┤ьЕШэД░ыДР ъ┤Аь╕б ъ▓░ъ│╝ьЩА ьИШь╣ШэХ┤ьДЭьЭД эЖ╡эХЬ ьаИыМАьХХыае(Absolute pressure) ы╢ДэПмые╝ ыПЩьЭ╝эХЬ ь║Ры╣ДэЕМьЭ┤ьЕШьИШ ьб░ъ▒┤ьЧРьДЬ ы╣Дъ╡РэХШьШАьЭД ыХМ ы░ЬьГЭэХШыКФ ъ│╡ыПЩьЭШ эШХьГБьЭ┤ ы╣Дъ╡РьаБ ьЮШ ьЭ╝ь╣ШэХиьЭД эЩХьЭ╕эХа ьИШ ьЮИыЛд.
Fig.┬а2
Comparison of wake cavitating flow
ы░ЬьГЭэХЬ ъ│╡ыПЩьЭШ эШХьГБ ы░П эК╣ьД▒ьЭД ы│┤ыЛд ый┤ы░АэХШъ▓М ъ▓АьжЭэХШъ╕░ ьЬДэХШьЧм ьИШь╣ШэХ┤ьДЭьЭД эЖ╡эХ┤ ъ│ДьВ░эХЬ ъ│╡ыПЩьЭШ ъ╕╕ьЭ┤ьЩА ьРРъ╕░ьЧР ьЮСьЪйэХШыКФ эХныае эК╣ьД▒ьЭД ьЛдэЧШ(
Jeong and Ahn, 2016) ы░П ы╣ДьаРьД▒ эХ┤ьДЭы▓Х(
Kim et al., 2013)ьЭД эЖ╡эХ┤ ьЦ╗ьЭА ъ▓░ъ│╝ьЩА ы╣Дъ╡РэХШьЧм эПЙъ░АэХШьШАыЛд.
Fig. 3ъ│╝
Fig. 4ьЭШ ы╣Дъ╡Р ъ▓░ъ│╝ые╝ эЖ╡эХ┤ ь║Ры╣ДэЕМьЭ┤ьЕШьИШьЧР ыФ░ыЭ╝ ы░ЬьГЭэХЬ ъ│╡ыПЩьЭШ ым┤ь░иьЫР ъ╕╕ьЭ┤(
l/
d)ьЩА ьРРъ╕░ьЧР ьЮСьЪйэХШыКФ эХныае ъ│ДьИШ(
CD)ъ░А эХ┤ыЛ╣ ъ▓░ъ│╝ьЩА ьЮШ ьЭ╝ь╣ШэХиьЭД ьХМ ьИШ ьЮИыЛд. эК╣эЮИ, ы│╕ ьЧ░ъ╡мьЧРьДЬыКФ ьРРъ╕░ эЫДыеШьЧРьДЬ ы░ЬьГЭэХШыКФ ьЩАыеШьЭШ ьг╝ъ╕░ьаБьЭ╕ ъ▒░ыПЩ эК╣ьД▒ьЭД ьЧДы░АэХШъ▓М эПЙъ░АэХШъ│аьЮРэХШьШАыЛд. 2ь░иьЫР ьРРъ╕░ьЭШ эЫДыеШьЧРьДЬ эШХьД▒ыРШыКФ ьЬаыПЩьЮеьЭА
Fig. 5ьЧР ыВШэГАыВЬы░ФьЩА ъ░ЩьЭ┤ ъ░Аъ╣МьЪ┤ эЫДыеШ(Near wake)ьЩА ыи╝ эЫДыеШ(Far wake) ьШБьЧньЬ╝ыбЬ ъ╡мы╢ДыРШый░, ъ╖╕ ьВмьЭ┤ьЧР ь▓ЬьЭ┤ьШБьЧньЬ╝ыбЬ ъ╡мы╢ДэХа ьИШ ьЮИыЛд. ьРРъ╕░ ыБЭыЛиьЧРьДЬ ы░ХыжмыРШыКФ ьЩАыеШыКФ ьЖНыПДъ░А ъ░АьЖНыРиьЧР ыФ░ыЭ╝ ьЭ╝ы░ШьаБьЬ╝ыбЬ ь▓ЬьЭ┤ъ╡мъ░ДьЭД ъ▒░ь╣Шый┤ьДЬ ьЩАыеШьЭШ ьдСьЛмьЧРьДЬ ь║Ры╣ДэЕМьЭ┤ьЕШьЭ┤ ы░ЬьГЭэХШъ▓М ыРШый░, ыи╝ эЫДыеШ ьШБьЧньЧРьДЬ ьЮШ ьХМыадьзД Karman ьЩАыеШьЭШ ы░ЬьГЭьЭД ьХ╝ъ╕░эХЬыЛд(
Franc and Michel, 2004). ыШРэХЬ ь║Ры╣ДэЕМьЭ┤ьЕШьИШъ░А ыЖТьЭД ыХМ, ьжЙ ъ│╡ыПЩьЭШ ъ╕╕ьЭ┤ъ░А ьззьЭА ьб░ъ▒┤ьЧРьДЬыКФ ьРРъ╕░ эПньЭШ 1ы░░ ьЭ┤ьаДьЭШ ъ░Аъ╣МьЪ┤ эЫДыеШ ьШБьЧньЧРьДЬ Karman ьЩАыеШьЩА ьг╝ъ╕░ьаБ эК╣ьД▒ьЭ┤ ыЛдые╕ ъ╡мьЖН ьЩАыеШ(Restricted vortex)ъ░А ьб┤ьЮмэХЬыЛд.
Fig.┬а3
Comparison of the cavity length according to the cavitation number

Fig.┬а4
Comparison of the drag coefficient according to the cavitation number
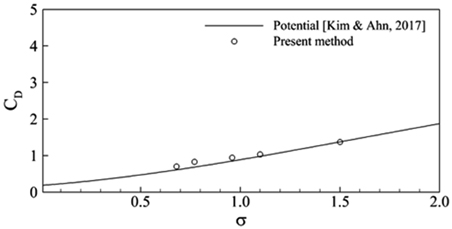
Fig.┬а5
Typical structure of the cavitating wake

ыи╝ьаА ыи╝ эЫДыеШ ьШБьЧньЧРьДЬ ы░ЬьГЭэХШыКФ Karman ьЩАыеШьЭШ ьг╝ъ╕░ьаБ эК╣ьД▒ьЭД ьВ┤эО┤ы│┤ъ╕░ ьЬДэХШьЧм ь║Ры╣ДэЕМьЭ┤ьЕШьИШ
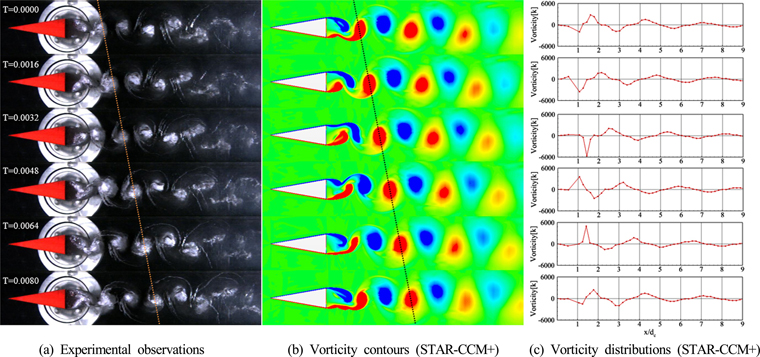
╧Г=1.30ьЭ╝ ыХМ, ьЛЬъ░ДьЧР ыФ░ыЭ╝ ыВШэГАыВШыКФ 2ь░иьЫР ьРРъ╕░ эЫДыеШ ьЬаыПЩ эК╣ьД▒ьЭД ьВ┤эО┤ы│┤ьХШыЛд. ьИШь╣ШэХ┤ьДЭьЭД эЖ╡эХ┤ ьЩАыПД(Vorticity
k, min тИТ600/s, max 600/s) ы╢ДэПмые╝ эЩХьЭ╕эХЬ ъ▓░ъ│╝(
Fig. 6(b)), Karman ы│┤эЕНьКдьЭШ ы░ХыжмыРШыКФ ьг╝ъ╕░ъ░А 0.008sыбЬ ыВШэГАыВмьЬ╝ый░ ьЭ┤ыКФ ыПЩьЭ╝эХЬ ьб░ъ▒┤ьЭШ ьЛдэЧШъ▓░ъ│╝(
Fig. 6(a))ьЩА ы╣Дъ╡РэХШьШАьЭД ыХМ эХ┤ыЛ╣ ьг╝ъ╕░ъ░А ьЭ╝ь╣ШэХЬыЛд. ыШРэХЬ, ьРРъ╕░ьЭШ ьдСьЛмьДаьЭД ыФ░ыЭ╝ ь╢Фь╢ЬэХЬ ьЩАыПДьЭШ ьД╕ъ╕░ ы╢ДэПмъ░А эХ┤ыЛ╣ ьг╝ъ╕░ьЩА ьЭ╝ь╣ШэХШъ▓М ы░Шы│╡ыРиьЭД эЩХьЭ╕эХШьШАыЛд(
Fig. 6(c)).
Fig.┬а6
Periodic motion of the Karman vortex street in the far wake region (cal. ╧Г=1.30, exp. ╧Г=1.29)
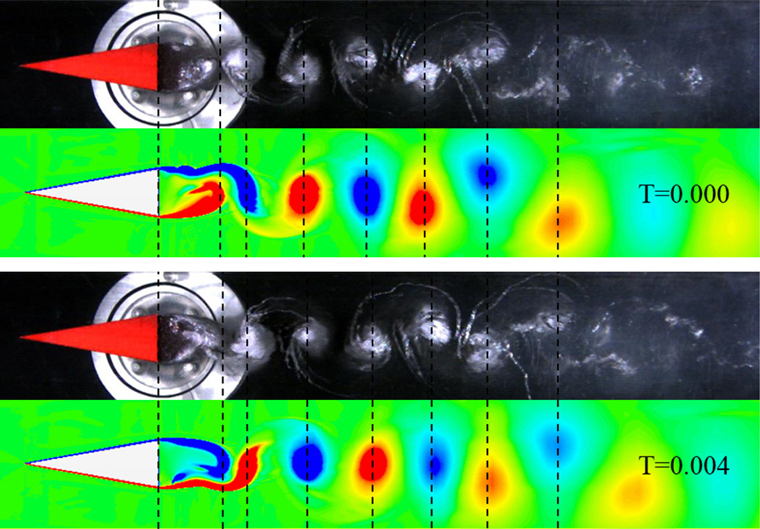
ы│┤ыЛд ый┤ы░АэХЬ ы╣Дъ╡Рые╝ ьЬДэХШьЧм ъ╕░ьдАьЭ┤ ыРШыКФ
T=0.000ь┤ИьЩА ьг╝ъ╕░ьЭШ ьаИы░ШьЭ╕
T=0.004ь┤ИьЭ╝ ыХМьЭШ ьИШь╣ШэХ┤ьДЭ ъ▓░ъ│╝ ьдС ьЩАыПД(Vorticity
k, min тИТ600/s, max 600/s) ы╢ДэПмые╝ ьЛдэЧШ ъ▓░ъ│╝ьЩА ы╣Дъ╡РэХШьШАьЭД ыХМ, ъ░Б ьЛЬъ░Ды│Д Karman ьЩАыеШьЭШ ы░Хыжм ьЬДь╣ШьЩА ъ│╡ыПЩьЭШ эШХьГБьЭ┤ ьЮШ ьЭ╝ь╣ШэХШыКФ ъ▓ГьЭД эЩХьЭ╕эХа ьИШ ьЮИыЛд(
Fig. 7).
Fig.┬а7
Comparison of periodic motion of the Karman vortex (cal. ╧Г=1.30, exp. ╧Г=1.29)
ъ│╡ыПЩьЭШ ьД▒ьЮеьЭА ыи╝ эЫДыеШьЧРьДЬ ы░ЬьГЭэХШыКФ Karman ьЩАыеШьЭШ эШХьГБьЧРыПД ьШБэЦеьЭД ып╕ь╣ЬыЛд. ыПЩьЭ╝эХЬ ы░йэЦеьЬ╝ыбЬ эЪМьаДэХШыКФ Karman ьЩАыеШ ьВмьЭ┤ьЭШ ьИШэПЙ ъ▒░ыжмые╝
A, ьИШьзБъ▒░ыжмые╝
BыЭ╝ъ│а эХа ыХМ(
Fig. 5 ь░╕ьб░), ь║Ры╣ДэЕМьЭ┤ьЕШьИШ ы│АэЩФьЧР ыФ░ые╕ ыСР ъ▒░ыжмьЭШ ы╣Д(
B/
A)ые╝ эПЙъ░АэХШьШАыЛд(
Fig. 8). ь║Ры╣ДэЕМьЭ┤ьЕШьИШъ░А ъ░РьЖМэХиьЧР ыФ░ыЭ╝ ьЩАыеШ ъ░ДьЭШ ьИШьзБъ▒░ыжмыКФ ъ░РьЖМэХШъ│а ьИШэПЙъ▒░ыжмыКФ ьжЭъ░АэХШьЧм ъ▒░ыжмы╣ДыКФ ь╡ЬыМА 75%ъ╣МьзА ъ░РьЖМэХШыКФ ъ▓ГьЭД ьХМ ьИШ ьЮИьЬ╝ый░, ьЛдэЧШ ъ▓░ъ│╝ьЩА ы╣Дъ╡РэХШьЧм ьЮШ ьЭ╝ь╣ШэХиьЭД эЩХьЭ╕эХШьШАыЛд.
Fig.┬а8
Geometric characteristic of the vortex street

ыЛдьЭМьЬ╝ыбЬ ъ░Аъ╣МьЪ┤ эЫДыеШ ьШБьЧньЧРьДЬ ы░ЬьГЭэХШыКФ ъ╡мьЖН ьЩАыеШьЭШ ьг╝ъ╕░ьаБ эК╣ьД▒ьЭД ьВ┤эО┤ы│┤ъ╕░ ьЬДэХШьЧм ьХЮьДЬьЩА ыПЩьЭ╝эХЬ ь║Ры╣ДэЕМьЭ┤ьЕШьИШ
╧Г=1.30ьЭ╝ ыХМ, ьЛЬъ░ДьЧР ыФ░ыЭ╝ ыВШэГАыВШыКФ 2ь░иьЫР ьРРъ╕░ эЫДыеШ ьЬаыПЩ эК╣ьД▒ьЭД ьВ┤эО┤ы│┤ьХШыЛд.
Fig. 9ыКФ ьЩ╝ьк╜ы╢АэД░ ьЩАыПД(Vorticity k, min тИТ600/s, max 600/s), ьХХыае(Absolute total pressure, min 3200Pa, max 1.15├Ч10
5Pa), ьИШьжЭъ╕░ ь▓┤ьаБы╢ДьЬи(Vapor volume fraction, min 0, max 1)ьЭД ы│┤ьЧмьг╝ый░, ьХХыаеъ│╝ ьИШьжЭъ╕░ ь▓┤ьаБы╢ДьЬи ы╢ДэПмъ░А ы░Шы│╡ыРиьЭД эЖ╡эХ┤ ъ╡мьЖН ьЩАыеШьЭШ ьг╝ъ╕░ъ░А
T=0.04ьЮДьЭД эЩХьЭ╕эХШьШАыЛд. эХ┤ыЛ╣ ъ│ДьВ░ ьб░ъ▒┤ьЭШ ъ▓╜ьЪ░ ьЩ╝ьк╜ ьЩАыПД ы╢ДэПмьЧРьДЬ эЩХьЭ╕эХа ьИШ ьЮИыУпьЭ┤ ъ╡мьЖН ьЩАыеШьЭШ эХЬ ьг╝ъ╕░(
T=0.04) ьХИьЧР Karman ьЩАыеШьЭШ ьг╝ъ╕░(
T=0.008)ъ░А 5ы▓И ы░Шы│╡ыРиьЭД эЩХьЭ╕эХа ьИШ ьЮИыЛд. ыЛдызМ ьИШь╣ШэХ┤ьДЭьЭД эЖ╡эХЬ ьИШьжЭъ╕░ ь▓┤ьаБы╢ДьЬи ы╢ДэПмьЩА ьЛдэЧШьЧРьДЬ ы░ЬьГЭэХЬ ъ│╡ыПЩьЭШ эШХьГБьЭД ы╣Дъ╡РэХШьШАьЭД ыХМ ьИШь╣ШэХ┤ьДЭ ъ▓░ъ│╝ыКФ ьРРъ╕░ эЫДыеШыбЬ ыЦиьЦ┤ьа╕ ыВШъ░АыКФ ы│┤эЕНьКд ьдСьЛмьЧРьДЬ ы░ЬьГЭэХШыКФ ъ│╡ыПЩьЭД ыкиьВмэХШьзАыКФ ык╗эХШъ│а ьЮИыКФыН░, эД░ыДР ыВ┤ы╢А ьХХыае ы░П ьЖНыПДьЮеьЭА ьЬаьВмэХШъ▓М ыкиьВмыРиьЭД ъ│аыадэХШьШАьЭД ыХМ ь║Ры╣ДэЕМьЭ┤ьЕШ ыкиыН╕ьЧРьДЬьЭШ ьзИыЯЙ ьЖРьЛдьЧР ыМАэХЬ ы│┤ыЛд ый┤ы░АэХЬ ъ│аыадъ░А ыНФ эХДьЪФэХа ъ▓ГьЬ╝ыбЬ ы│┤ьЭ╕ыЛд.
Fig.┬а9
Periodic motion of the restricted vortex in the near wake region (╧Г=1.30)

ыШРэХЬ ьРРъ╕░ьЭШ ьдСьЛмьДаьЭД ыФ░ыЭ╝ ь╢Фь╢ЬэХЬ ьЩАыПДьЭШ ьД╕ъ╕░ ы╢ДэПмые╝ ьВ┤эО┤ы│┤ьХШьЭД ыХМ(
Fig. 10), эХЬьг╝ъ╕░ъ░А ы░Шы│╡ыРШыКФ
T=0.000ъ│╝
T=0.040ьЭШ ъ▓░ъ│╝ъ░А ьРРъ╕░ эПньЭШ 1ы░░ыРШыКФ ыПЩьЭ╝эХЬ ьзАьаРьЧРьДЬ ьЩАыПДьЭШ ь╡ЬыМАь╣Шые╝ ъ░ЦыКФ ъ▓ГьЭД эЩХьЭ╕эХа ьИШ ьЮИьЬ╝ый░, ъ│ДьВ░ыРЬ ъ░Бъ░БьЭШ ъ▓░ъ│╝ъ░А Karman ьЩАыеШъ░А ы░Шы│╡ыРШыКФ ьг╝ъ╕░ьЭ┤ыпАыбЬ эЫДыеШьШБьЧн ьаДы░ШьЧР ъ▒╕ь╣Ь ьЩАыПД ы╢ДэПмъ░А ыПЩьЭ╝эХиьЭД эЩХьЭ╕эХа ьИШ ьЮИыЛд.
Fig.┬а10
Vorticity distributions along the center line of a wedge- shaped submerged body (╧Г=1.30)
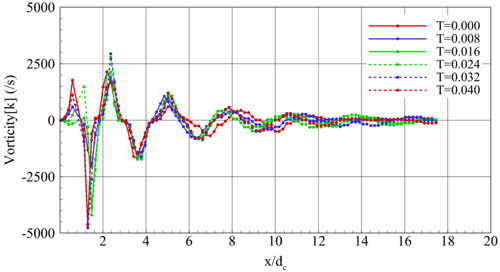
Fig. 11ьЭА ъ╡мьЖН ьЩАыеШьЩА ы░Хыжм ьЩАыеШьЭШ эК╣ьД▒ьЭД ы│┤ыЛд ый┤ы░АэХШъ▓М эПЙъ░АэХШъ╕░ ьЬДэХ┤ ьДЬыбЬ ыЛдые╕ ь║Ры╣ДэЕМьЭ┤ьЕШьИШ ьб░ъ▒┤ьЧРьДЬ ы░ЬьГЭэХШыКФ ы│АыПЩьХХыаеьЭД ы╢ДьДЭэХШьЧм ьг╝ъ╕░ьаБьЭ╕ эК╣ьД▒ьЭД ы╣Дъ╡РэХШьШАыЛд.
Fig. 11(a)ьЩА ъ░ЩьЭ┤ ьРРъ╕░ьЭШ ыБЭыЛиьЭ┤ ьЬДь╣ШэХЬ ъ┤Аь╕бь░╜ ьГБы╢АьЧРьДЬ ъ│Дь╕быРЬ ы│АыПЩьХХыаеьЭД
Fig, 11(b)ьЩА ъ░ЩьЭ┤ ъ│аьЖН эС╕ыжмьЧР ы│АэЩШ(FFT, fast Fourier transform)ьЭД эЖ╡эХ┤ ьг╝эММьИШьШБьЧньЭШ ьЖМьЭМьИШьдА(Sound pressure level, SPL)ьЬ╝ыбЬ ы│АэЩШэХШьЧм ыВШэГАыВ┤ьЧИыЛд. ьИШь╣ШэХ┤ьДЭ ъ▓░ъ│╝ ыШРэХЬ ьЛдэЧШъ│╝ ъ░ЩьЭА ьЬДь╣ШьЧРьДЬьЭШ ы│АыПЩьХХыае ъ░ТьЭД ьг╝эММьИШьШБьЧньЭШ ьЖМьЭМьИШьдАьЬ╝ыбЬ ы│АэЩФэХШьЧм ы╣Дъ╡РэХШьШАыЛд. ъ╖╕ ъ▓░ъ│╝ ьГБыМАьаБьЬ╝ыбЬ ыВоьЭА ьг╝эММьИШьЩА ыЖТьЭА ьг╝эММьИШ эК╣ьД▒ьЭ┤ ыкЕэЩХэХШъ▓М ы╢ДыжмыРШьЦ┤ ыВШэГАыВШыКФ ъ▓ГьЭД эЩХьЭ╕эХа ьИШ ьЮИыЛд. ь║Ры╣ДэЕМьЭ┤ьЕШ ьИШъ░А ыВоьХДьзИьИШыбЭ ыи╝ эЫДыеШьШБьЧньЧРьДЬ ы░ЬьГЭэХШыКФ Karman ьЩАыеШьЭШ ы░Хыжм ьг╝ъ╕░ыКФ ьззьХДьзАый░, ьжЙ ьг╝эММьИШыКФ ь╗дьзАый░, ъ░Аъ╣МьЪ┤ эЫДыеШьШБьЧньЧРьДЬ ы░ЬьГЭэХШыКФ ъ╡мьЖН ьЩАыеШыКФ ъ│╡ыПЩьЭШ ъ╕╕ьЭ┤ъ░А ьжЭъ░АэХиьЧР ыФ░ыЭ╝ ьг╝ъ╕░ъ░А ь╗дьзАъ╕░ ыХМым╕ьЭ┤ый░, ьИШь╣ШэХ┤ьДЭ ъ▓░ъ│╝ ыШРэХЬ ьЭ┤ыЯмэХЬ эК╣ьД▒ьЭД ьЮШ ы│┤ьЧмьг╝ъ│а ьЮИыЛд. ьЭ┤ыЯмэХЬ ьг╝эММьИШ эК╣ьД▒ьЭД ый┤ы░АэЮИ ы╣Дъ╡РэХШъ╕░ ьЬДэХ┤ ыЛдьЭМ ьЛЭ (13)ьЬ╝ыбЬ ьаХьЭШыРШыКФ StrouhalьИШ(
St)ые╝ ьВмьЪйэХШьЧм ы╣Дъ│╡ыПЩ ьГБэГЬьЭШ эЫДыеШьЩА ъ│╡ыПЩ ьГБэГЬьЭШ эЫДыеШьЧРьДЬ ы░ЬьГЭэХШыКФ ьг╝эММьИШ эК╣ьД▒ьЭД эПЙъ░АэХШьШАыЛд.
Fig.┬а11
Sound pressure level in the frequency domain

ьЧмъ╕░ьДЬ
fыКФ ьг╝эММьИШ,
dыКФ ьРРъ╕░ьЭШ эПн,
VтИЮ ыКФ ьЬаыПЩьЖНыПДьЭ┤ыЛд.
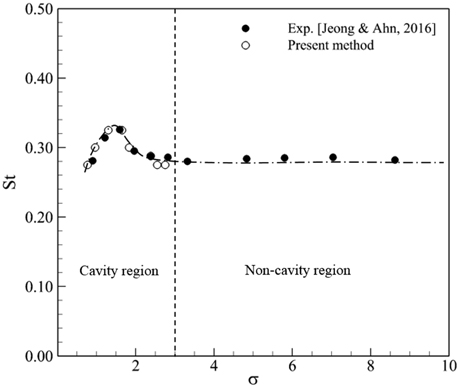
Fig. 12ыКФ ь║Ры╣ДэЕМьЭ┤ьЕШьИШьЧР ыФ░ыЭ╝ ыВШэГАыВШыКФ Karman ьЩАыеШьЭШ ьг╝эММьИШ эК╣ьД▒ьЭД StrouhalьИШыбЬ ыВШэГАыВ╕ ъ▓░ъ│╝ыбЬ, ы╣Дъ│╡ыПЩ ьГБэГЬьЭ╝ ыХМьЭШ StrouhalьИШыКФ ьХ╜ 0.28ыбЬ ьЭ╝ьаХэХШъ▓М ьЬаьзАыРШыЛдъ░А ь║Ры╣ДэЕМьЭ┤ьЕШьЭ┤ ы░ЬьГЭэХШый┤ ъ╖╕ ъ░ТьЭА ьХ╜ 18% ьаХыПД ьжЭъ░АэХШьШАыЛдъ░А ыЛдьЛЬ ъ░РьЖМэХШыКФ ъ▓ГьЭД эЩХьЭ╕эХа ьИШ ьЮИыЛд. ъ╖╕ ь╡ЬыМАъ░ТьЭА ь║Ры╣ДэЕМьЭ┤ьЕШьИШ(
╧Г) 1.29ьЧРьДЬ ыВШэГАыВмьЬ╝ый░, ьЭ┤ыХМ ъ╡мьЖН ьЩАыеШьЧРьДЬ ьГЭьД▒ыРЬ ъ│╡ыПЩьЭШ ъ╕╕ьЭ┤ъ░А ьРРъ╕░ьЭШ эПн(
d)ъ│╝ ьЭ╝ь╣ШэХиьЭД эЩХьЭ╕эХШьШАыЛд. ьЭ┤эЫД ь║Ры╣ДэЕМьЭ┤ьЕШьИШъ░А ыВоьХДьзРьЧР ыФ░ыЭ╝ Karman ьЩАыеШьЭШ ы░Хыжм ьг╝эММьИШыКФ ы╣Дъ│╡ыПЩ ьГБэГЬьЩА ъ░ЩьХДьзАыКФ ъ▓ГьЭД ьХМ ьИШ ьЮИыЛд. ы╣Дъ│╡ыПЩ ьГБэГЬьЧРьДЬыКФ ьЬаьЖН ы│АэЩФьЧР ьГБъ┤АьЧЖьЭ┤ ьЭ╝ьаХэХШъ▓М ьЬаьзАыРШыКФ Karman ьЩАыеШьЭШ StrouhalьИШыКФ ъ│╡ыПЩьЭ┤ ы░ЬьГЭэХШый┤ьДЬ ъ╡мьЖН ьЩАыеШьШБьЧньЧРьДЬ ы░ЬьГЭэХШыКФ ъ│╡ыПЩьЭШ ьШБэЦеьЬ╝ыбЬ ьжЭъ░АэХШыКФ эК╣ьД▒ьЭД эЩХьЭ╕ эХШьШАыЛд. ьжЙ, ьЭ╝ы░ШьаБьЬ╝ыбЬ ьЮШ ьХМыадьа╕ ьЮИыКФ ы░ФьЩА ъ░ЩьЭ┤ ы╣Дъ│╡ыПЩ ьГБэГЬьЧРьДЬыКФ ьЬаьЖН ы│АэЩФьЧР ьГБъ┤АьЧЖьЭ┤ ьЭ╝ьаХэХШъ▓М ыВШэГАыВШыКФ Karman ьЩАыеШьЭШ ы░Хыжм ьг╝эММьИШ эК╣ьД▒ьЭА ъ│╡ыПЩьЧР ьЭШэХ┤ эБ░ ьШБэЦеьЭД ы░ЫьЬ╝ый░ ым┤ьЧЗы│┤ыЛд ъ╡мьЖН ьЩАыеШьЭШ ьД▒ьЮеъ│╝ ы░АьаСэХЬ ъ┤АыаиьЭ┤ ьЮИьЭМьЭД ьХМ ьИШ ьЮИыЛд.
Fig.┬а12
Strouhal number versus cavitation number