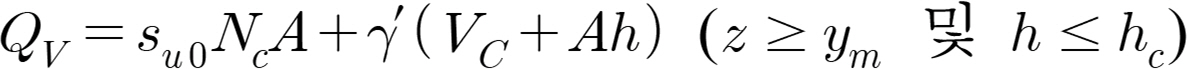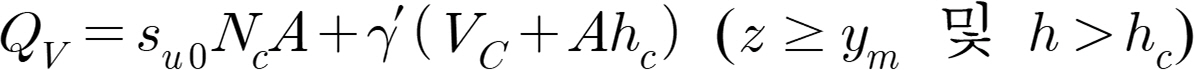1. Introduction
2. Methodology
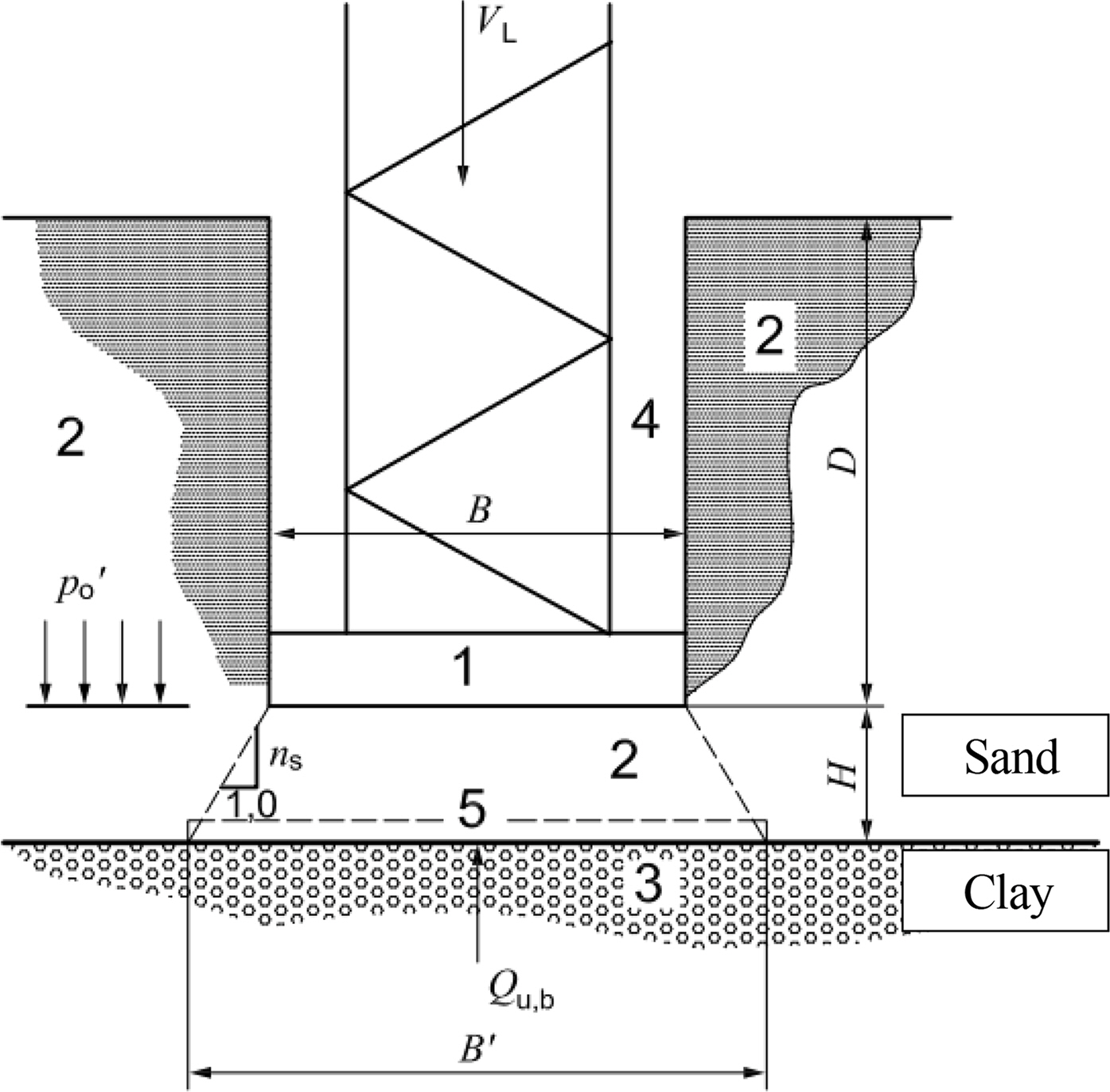
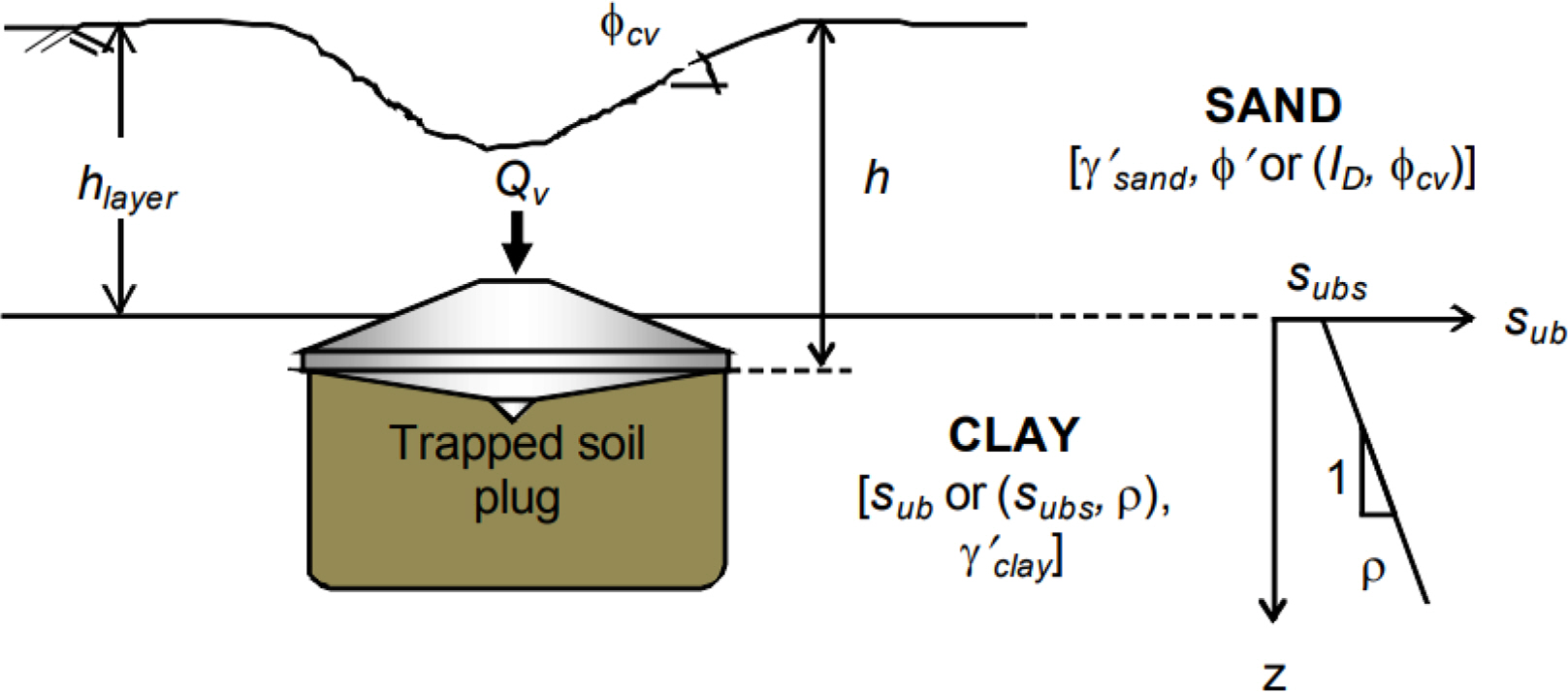
2.1 BS EN ISO 19905-1(2016) Method
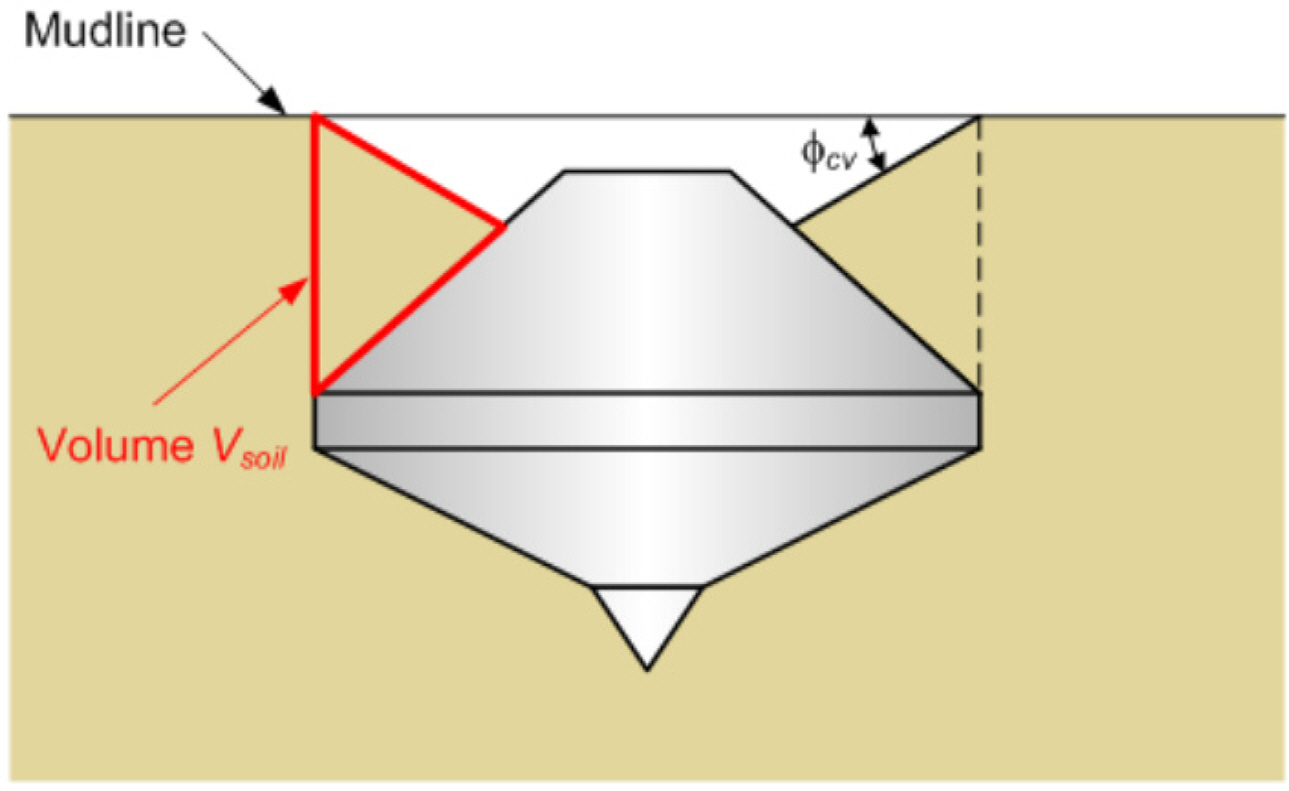
2.2 InSafeJIP Report (2011) Method
2.3 Centrifuge Model Test
3. Centrifuge Model Test for Foundation Installation
3.1 Centrifuge Test Condition
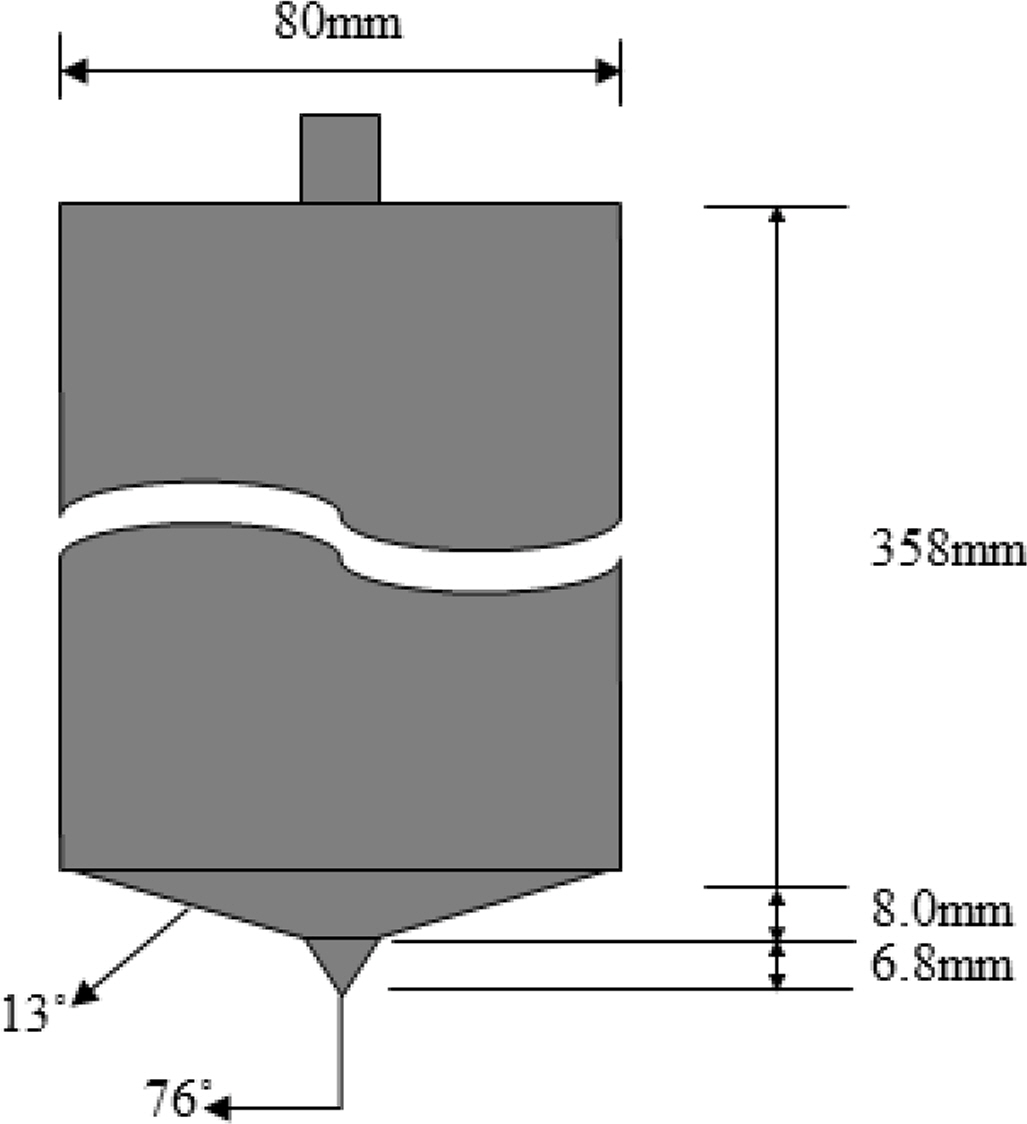
3.1.1 Model spudcan
3.1.2 Model soil
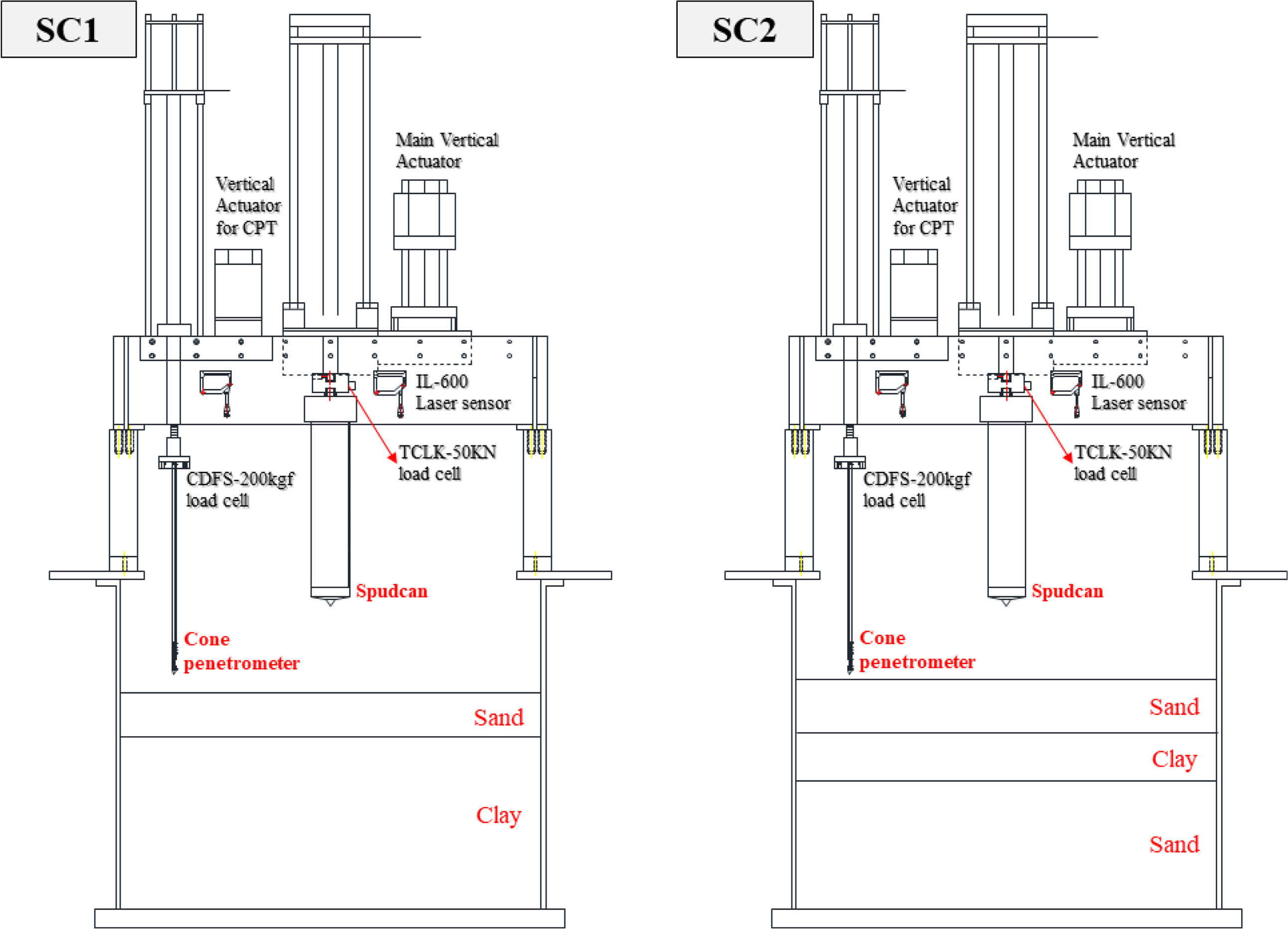
3.2 Testing System
3.2.1 Geotechnical centrifuge
3.2.2 Vertical load control equipment
3.2.3 Miniature cone penetration test (CPT)
4. Test Results
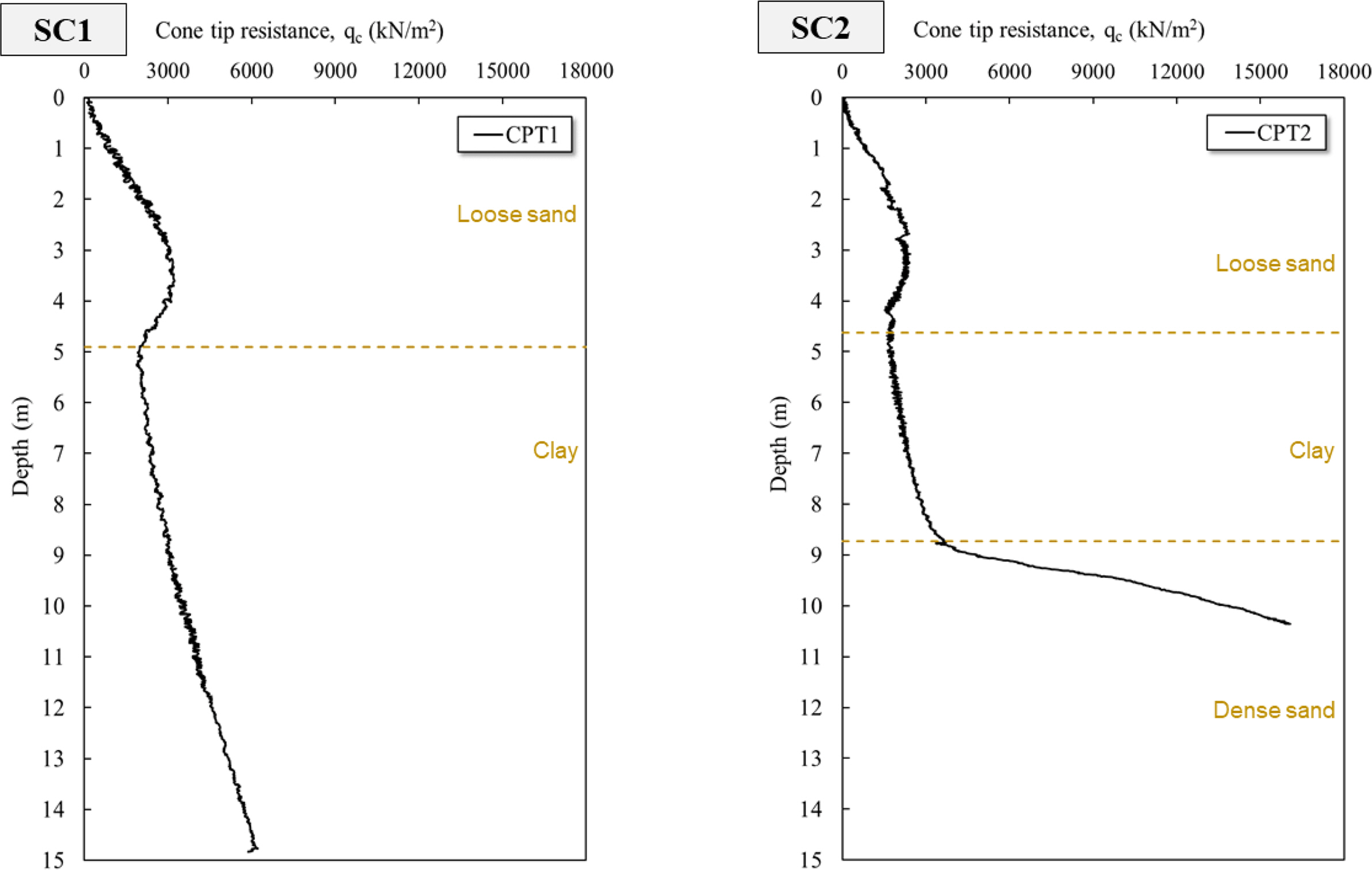
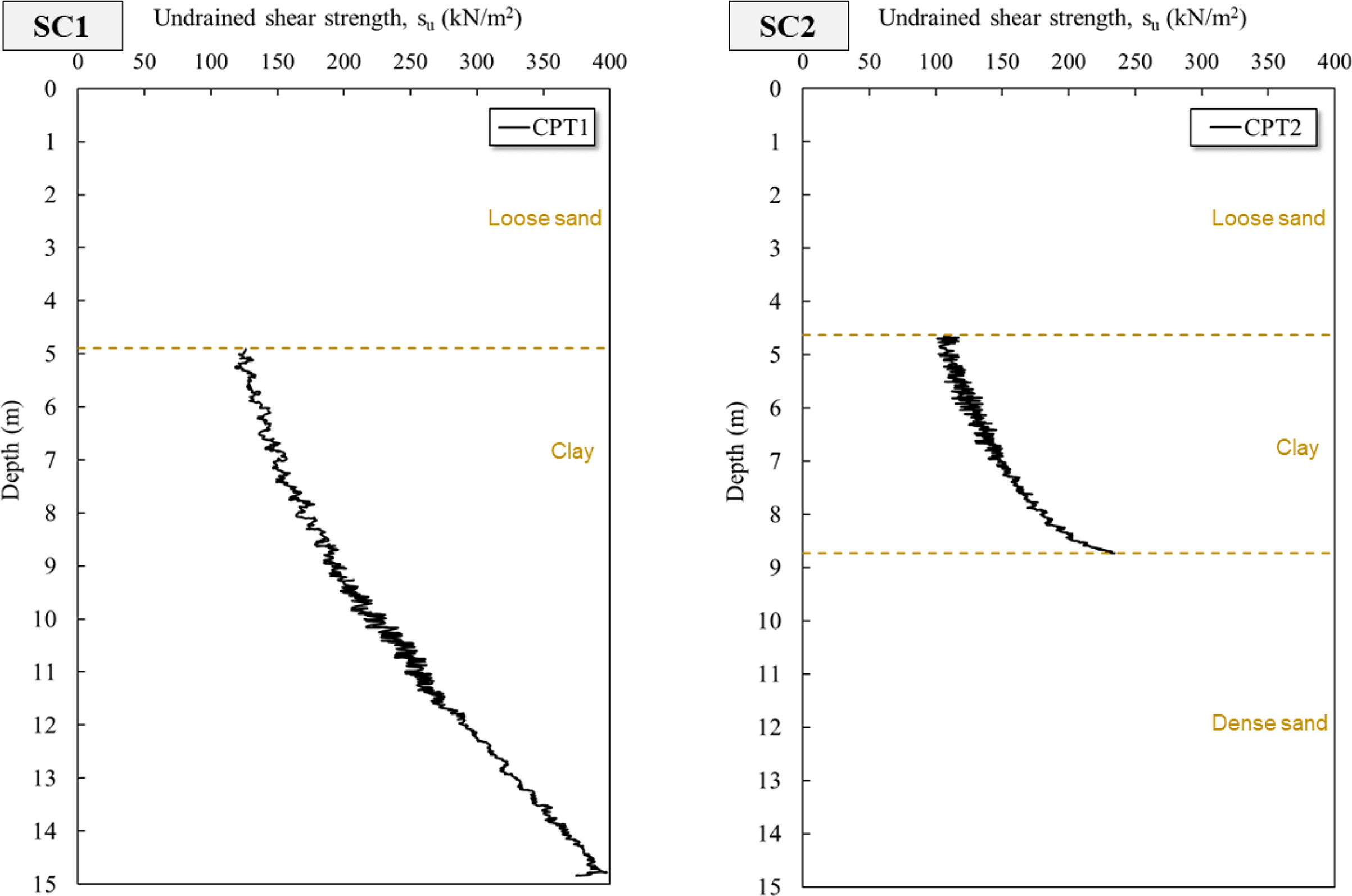
4.1 Cone Penetration
4.2 Spudcan Penetration
5. Discussion
6. Conclusions
In centrifuge model tests on the vertical penetration of a jack-up spudcan, while the spudcan was penetrating the upper loose sand layer, the vertical bearing resistance tended to decrease before penetrating the lower clay layer as the spudcan approached the sand-clay interface. This decrease in vertical bearing resistance is likely caused by the penetration of the sand plug trapped beneath the spudcan into the lower clay layer earlier than the actual spudcan. On the other hand, vertical bearing resistance increased again as the spudcan penetrated the clay layer. in the case of such soil conditions for installing of the offshore wind jack-up substructure, the punch-through effect is not expected to occur predominantly, but fast running is expected to occur at depths where vertical bearing resistance decreases. Fast running refers to the phenomenon in which the spudcan penetrates the soil rapidly and uncontrollably without penetration resistance increase and sinks deep into the soil at depths where vertical bearing resistance decreases during the installation of the jack-up spudcan. In addition, a squeezing effect is possibly expected when there is a stronger soil layer (dense sand) beneath a clay layer; that is a hard soil stratum underlying a weak soil layer causes an increase in the vertical bearing resistance as the spudcan approaches the interface between weaker and stronger soil strata.
The analysis results obtained using the ISO method (2016) showed a similar trend to the centrifuge model test regarding the vertical bearing resistance. In particular, the vertical bearing resistance in the upper loose sand layer was similar to the test data, but the punch-through phenomenon showing a decrease in vertical bearing resistance was not observed. In addition, in the soil condition of sand over clay, the estimates obtained using the ISO formula did not show a decrease in load arising from the impact of a high undrained shear strength of more than 100 kPa. In the soil condition of clay-over-dense sand, which is the condition of weak soil over a stronger stratum soil, the increase in vertical bearing resistance due to the squeezing effect was not prominent compared to the test results. In addition, the ISO method does not provide a method for calculating the vertical bearing resistance of a spudcan in multi-layered soils with three or more layers. Thus, when the ISO method is used to calculate the vertical bearing resistance in such soil conditions, a multi-layered soil with three or more strata is assumed to be a single sand–soil layer, so this method tends to predict very large vertical bearing resistances in such cases.
The InSafeJIP method (Osbone et al., 2011) showed a vertical bearing resistance pattern similar to that of the ISO (2016) method, but the estimated vertical bearing resistance obtained using the InSafeJIP method was more than two times larger than the value obtained using the ISO method in the upper sand layer in the soil condition of under loose sand over clay. In particular, because the InSafeJIP method predicted an excessively high vertical bearing resistance from the initial stage of penetration, it is considered more appropriate also to analyze the vertical bearing capacity under the condition of a single-layer sand soil when estimating vertical bearing resistance at the initial stage of penetration and predict vertical bearing resistance at a shallow depth by using the lower limit value. In addition, an analysis using the InSafeJIP method resulted in a more prominent punch-through effect than the centrifuge model test and ISO method. In the InSafeJIP method, the dense sand layer, which is the lowest layer among the loose sand-clay-dense layers, was assumed to be a single-layer sand soil, which is similar with the ISO method. On the other hand, the estimate by the InSafeJIP method was considerably lower than the value obtained by the ISO method because of the difference in the bearing capacity factors utilized in both methods, and it was even somewhat lower than the test result.
The measured vertical bearing resistances of a spudcan of the centrifuge model test differed in absolute value from the estimates calculated by theoretical formulas. Regarding the overall pattern of estimates, however, the ISO (ISO, 2016) and InSafeJIP methods (Osbone et al., 2011) predicted a penetration behavior that essentially matched the test data. On the other hand, in the case of a strong sand layer, compared to the test results, the InSafeJIP method predicted a smaller vertical bearing resistance, and the ISO predicted a very high vertical bearing resistance. When calculating the vertical bearing resistance of a spudcan using such theoretical equations, the geotechnical properties of friction angle and undrained shear strength of soils significantly impact the calculation of the bearing capacity factors for both clay and sand layers. Therefore, the cone penetration tests (CPT) and laboratory testing using site specimen should also be carried out to estimate the shear strength parameters of soils and comprehensively evaluate the vertical bearing resistance of a spudcan at the stage of a site investigation when designing offshore wind turbines.