|
 |
- Search
| J. Ocean Eng. Technol. > Volume 37(3); 2023 > Article |
|
Abstract
This paper intends to introduce the applicability of HydroQus to a problem of a tanker collision against a semi-submersible type floating offshore wind turbine (FOWT). HydroQus is a plug-in based on potential flow theory that generates interactive hydroforces in a commercial Finite element analysis (FEA) code Abaqus/Explicit. Frequency response analyses were conducted for a 10MW capacity FOWT to obtain hydrostatic and hydrodynamic constants. The tanker was modeled with rigid elements, while elastic-plastic elements were used for the FOWT. Mooring chains were modeled to implement station keeping ability of the FOWT. Two types of fracture models were considered: constant failure strain model and combined failure strain model HC-LN model composed of Hosford-Coulomb (HC) model & localized necking (LN) model. The damage extents were evaluated by hydroforces and failure strain models. The largest equivalent plastic strain observed in the cases where both restoring force and radiation force were considered. Stress triaxiality and damage indicator analysis showed that the application of HC-LN model was suitable. It could be stated that applications of suitable failure strain model and hydrodynamics into the collision simulations were of importance.
Along with the continuous upsizing of offshore wind turbine (OWT) units to reduce the cost of power generation, commercial farms are also becoming larger. As commercial farms become larger, ships must be allowed to pass through them, increasing the likelihood of collisions with OWTs. A cargo ship collided with an OWT at a 330 MW commercial wind farm in Germany (Jasmina, 2023). Furthermore, collisions can lead to significant damage to floating OWTs (FOWTs), such as structural damage and loss of stability due to flooding, while ships can cause economic and environmental losses such as cargo loss and oil spills, as well as loss of life. To prepare for this, the Det Norske Veritas (DNV) offshore standard (DNV, 2013) provides design guidance for accidental ship collisions.
Dai et al. (2013) studied the collision of a fixed wind turbine with a monopile substructure and a 230-ton vessel and provided suggestions for collision risk reduction. Moulas et al. (2017) studied the collision of an OWT with a 4,000-ton ship on monopile and jacket substructures. They considered different ship speeds and collision angles, but environmental loads such as wind and wave loads were not considered. Bela et al. (2017) performed a collision analysis between a 5,000-ton vessel and an OWT with a monopile substructure. The effects of ship speed, wind load, and soil stiffness on the collision were analyzed, but hydrodynamic forces acting on the ship were not considered.
Echeverry et al. (2019) performed a collision analysis of a spar-type FOWT and Márquez et al. (2022) studied the collision of a reinforced concrete barge-type FOWT with a 3,000-ton ship. Both studies used MCOL to consider hydrodynamic forces, but did not consider wave and wind loads. Zhang and Hu (2022) studied the collision of a spar-type FOWT with a 4,000-ton ship. User subroutines were used in LS-DYNA (LSTC, 2023) to implement aerodynamics and hydrodynamics. The drag force on the rotor area was calculated and the wind thrust load was applied as a point load to the center of the rotor. Since it was difficult to accurately model the initial mooring layout, instead of directly modeling the mooring lines, the linearized restoring matrix proposed by Jonkman (2007) was applied.
This study aims to address the collision of a 10 MW semi-submersible FOWT with a 5,000 ton ship using Abaqus/Explicit (Simulia, 2021). In order to generate fluid forces in Abaqus, either arbitrary Lagrangina Eulerian (ALE) or coupled Eulerian Lagrangian (CEL) must be utilized. However, the adoption of ALE or CEL requires too long computational time, so in this study, HydroQus developed by Han (2022) and Yoon et al. (2023) is used to perform the collision analysis of ship and FOWT. HydroQus is a plug-in of the commercial finite element analysis (FEA) code Abaqus that generates real-time hydrodynamic forces. HydroQus calculates hydrodynamic forces such as radiation force, wave excitation force, as well as restoring force acting on the FOWT in real time. Yoon et al. (2023) verified the accuracy of HydroQus and performed a collision analysis between a ship and an iceberg. The mooring of the FOWT was modeled using beam elements and joint elements. The HC-LN model, a synthesis of the Hosford-Coulomb (HC) model and the localized necking (LN) model, was used to accurately predict the structural damage caused by the collision. A user subroutine developed by Cerik et al. (2019) was applied to implement the HC-LN model in Abaqus.
According to Newton's second law, the governing equation of motion for a floating body can be expressed as Eq. (1). Mij is the mass of a floating body, and üj is the acceleration of a floating body. The subscript i and j represent 6 degrees of freedom, 1 = surge, 2 = sway, 3 = heave, 4 = roll, 5 = pitch, and 6 = yaw. The restoring force
F i r e s F i r a d F i w v F i m r F i c o l
For modeling the mooring lines, the catenary equations presented in the studies of Masciola et al. (2013) and Jonkman (2007) were used, and are given by Eqs. (7)–(14). l and h denote the vertical and horizontal positions of the fairlead, respectively. H and V are the horizontal and vertical forces at the fairlead. EA, W, and L are the properties of the mooring line: axial stiffness, weight per unit length, and unstretched length. CB is the friction coefficient between seabed and mooring line and LB is the laid length on seabed. By calculating Eq. (10) and Eq. (11), the location along the line segment s is derived, which are used to model mooring lines.
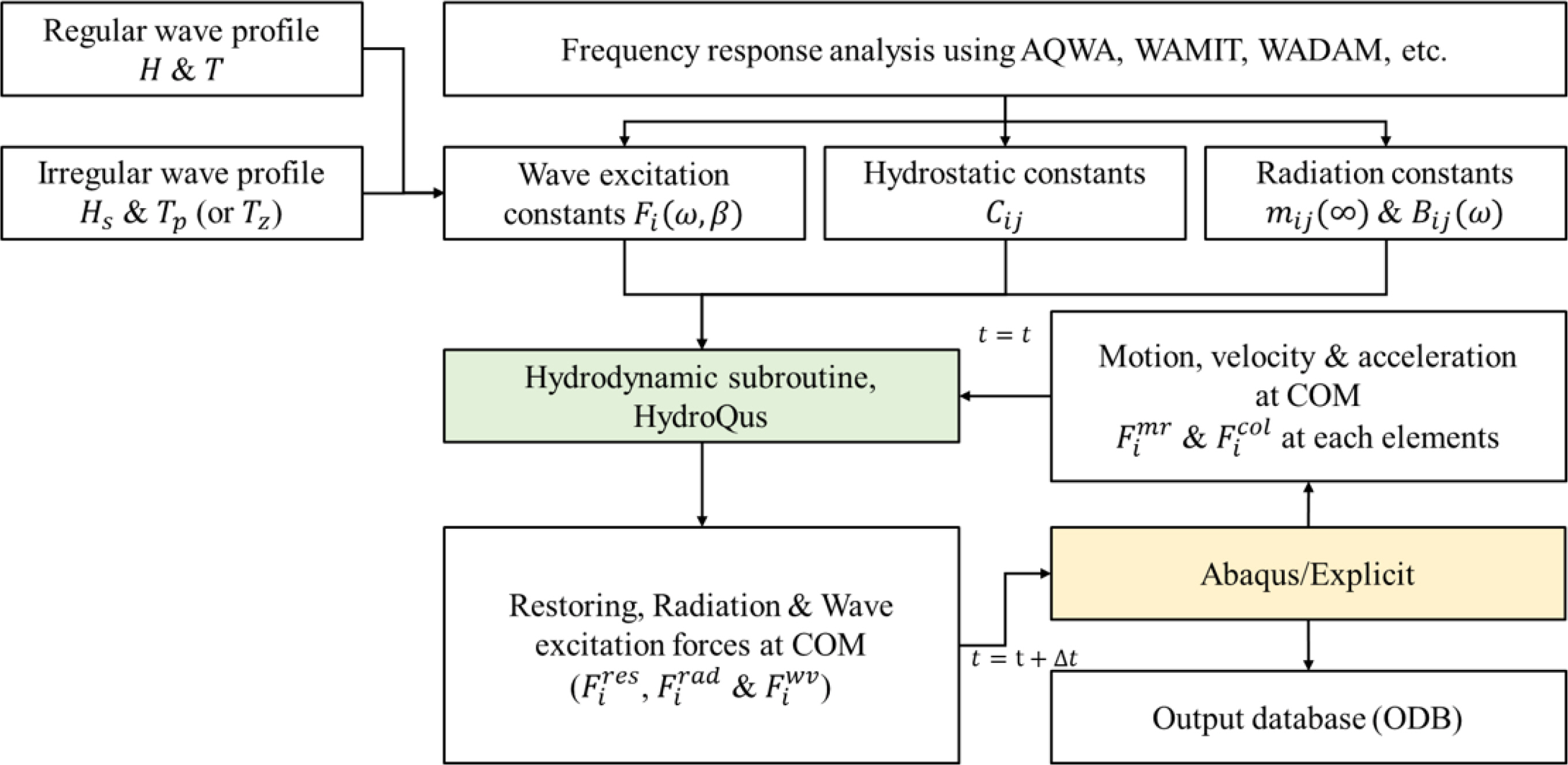
Abaqus is a commercial FEA code that includes a variety of material constitutive equations and a robust contact algorithm. However, Abaqus is not capable of generating hydrodynamic forces based on potential flow theory on its own. To solve this problem, the authors of this paper developed HydroQus, a hydrodynamic plug-in compatible with Abaqus/Explicit. HydroQus can generate linear or nonlinear restoring forces, radiation forces, and 1st and 2nd order wave excitation forces. The hydrodynamic coefficients used in the calculations must be obtained in advance from a frequency response analysis. For the wave excitation force calculation, the wave height H (or significant wave height Hs ) and wave period T (or peak period Tp) must be defined. HydroQus calculates the hydrodynamic forces using the displacement, velocity, and acceleration at the center of mass (CoM) of the FOWT at t= t1 (current time) in Abaqus and gives them to Abaqus/Explicit. Abaqus solves the equations of motion for the FOWT and the ship, respectively, using the hydrodynamic forces. During this process, Abaqus is responsible for generating the drag-based mooring tension forces and collision forces. The displacements, velocities, and accelerations at the CoM obtained by solving the equations of motion are fed back to HydroQus and used to generate the hydrodynamic forces at t= t2 (next time). This procedure is summarized in Fig. 1.
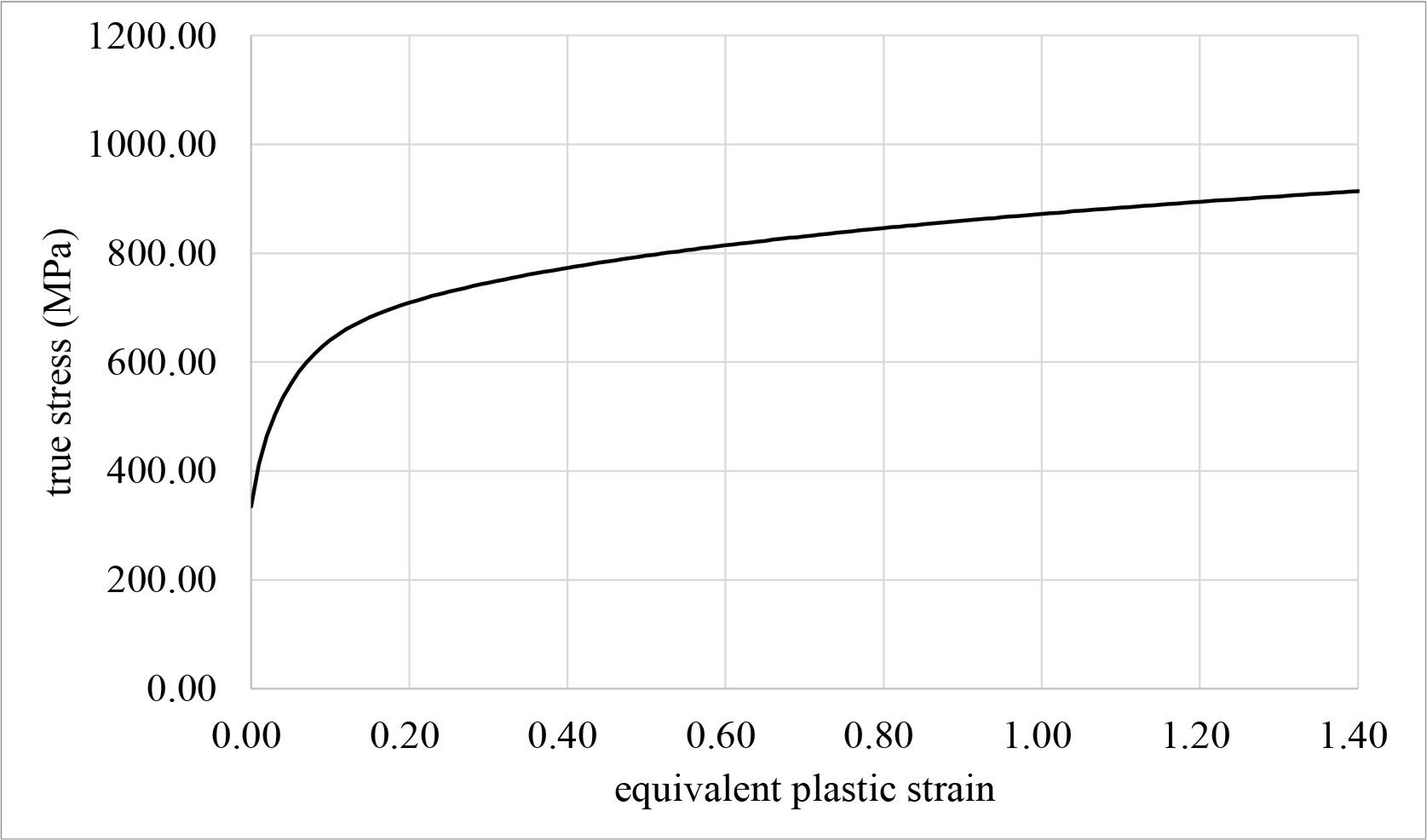
To accurately represent the hardening behavior after onset of necking, the combined Swift-Voce hardening model proposed by Sung et al. (2010) is applied in this study. The Swift-Voce hardening law is given by Eq. (15), where α is the weighting factor between Swift law and Voce law. The Swift law and Voce law are given by Eq. (16) and Eq. (17), respectively. Cerik and Choung (2020) derived A, ∊0, n, k0, Q, and β through tensile tests and numerical analyses.
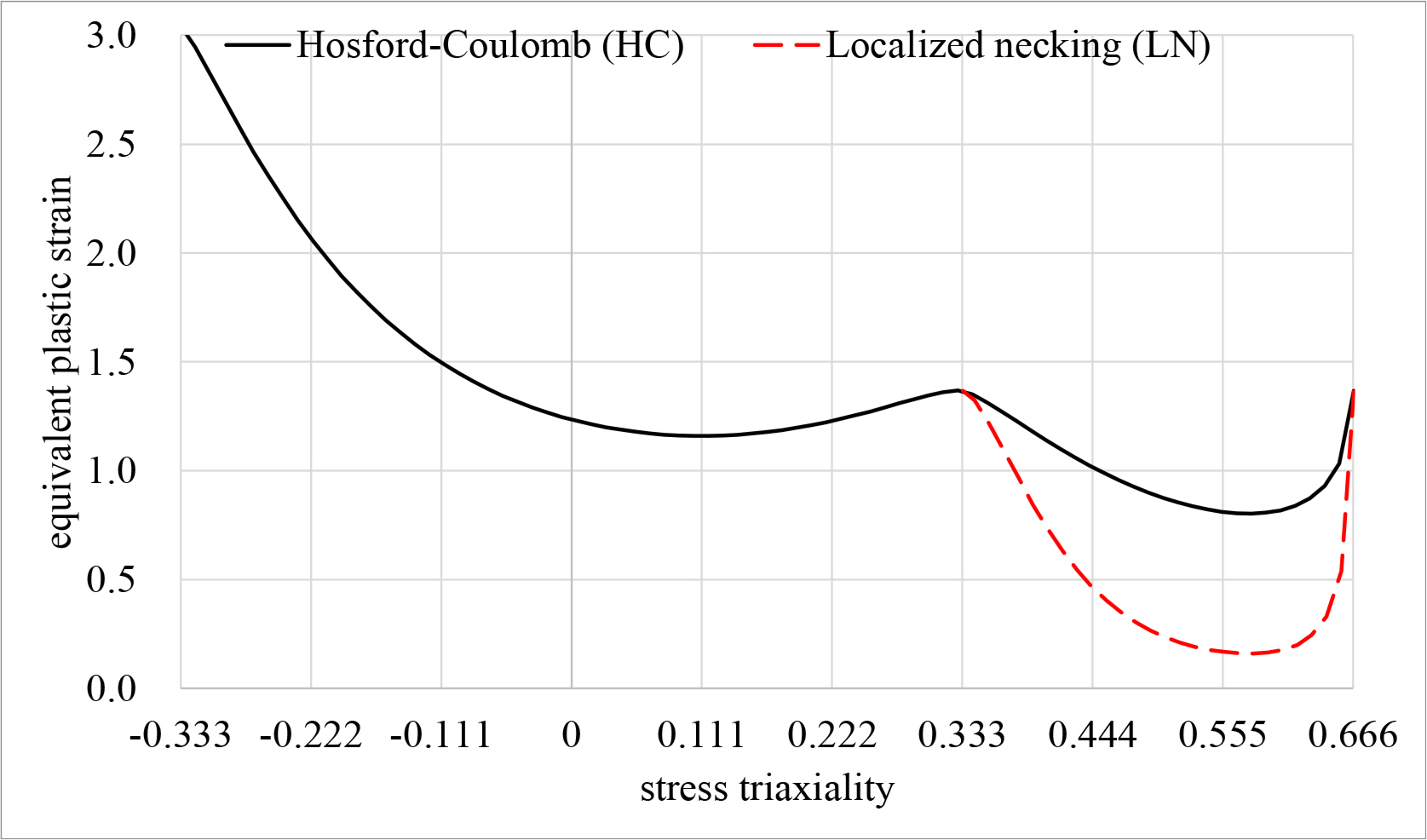
The fracture strain in the HC model proposed by Mohr and Marcadet (2015) is given by Eq. (18). Where η is the stress triaxiality and θ̄ is the Lode angle. From Eq. (18) and Eq. (19)a is the load angle sensitivity, b is the fracture strain modulus, c is the stress triaxiality sensitivity, and nf is the transformation exponent. The load angle parameter functions f1, f2 and f3 are calculated through Eqs. (20)–(22). To consider the stress path effect, the damage indicator D in Eq. (23) is introduced. It is assumed that fracture initiates when the damage indicator reaches 1.0.
The LN fracture strain model proposed by Pack and Mohr (2017) is given by Eq. (24). Where d is the Hosford exponent and pf is the transformation exponent. Stress triaxiality functions g1 and g2 are calculated using Eq. (25) and Eq. (26). A necking indicator N is introduced to consider the stress path effect (see Eq. (27)). Fracture is considered to occur when N reaches 1.0.
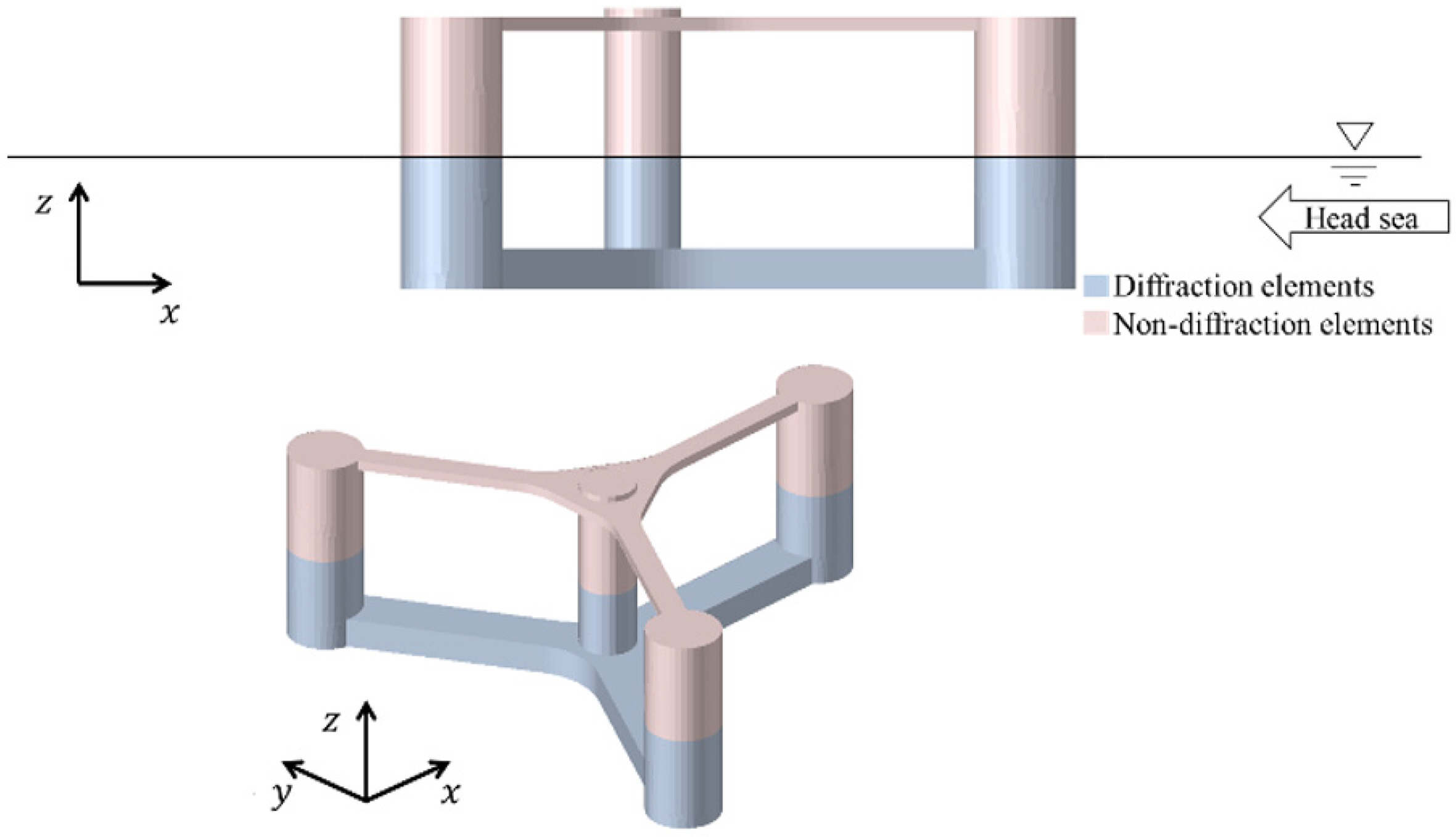
Fig. 2 is the model of FOWT used for the frequency response analysis. The frequency response analysis model consisted of approximately 5,500 diffraction elements and 4,500 non-diffraction elements. Tower and RNA were not included in the model, but were included in the mass information. Table 1 shows the mass information of the FOWT.
Frequency response analysis was performed using Aqwa (Ansys, 2022). The results of frequency response analysis in head sea condition are shown in Fig. 3 which includes the heave and pitch motion response amplitude operators (RAOs). The corresponding radiation coefficients for surge, sway, heave, roll, pitch and yaw motions are shown in Figs. 3(b)–3(g). It can be seen that the added masses nearly converged to a certain value as the frequency increased. The wave damping coefficients also nearly converged to zero as the frequency increased. Fig. 3(h) shows the 1st order wave excitation force RAOs in the heave and pitch directions.
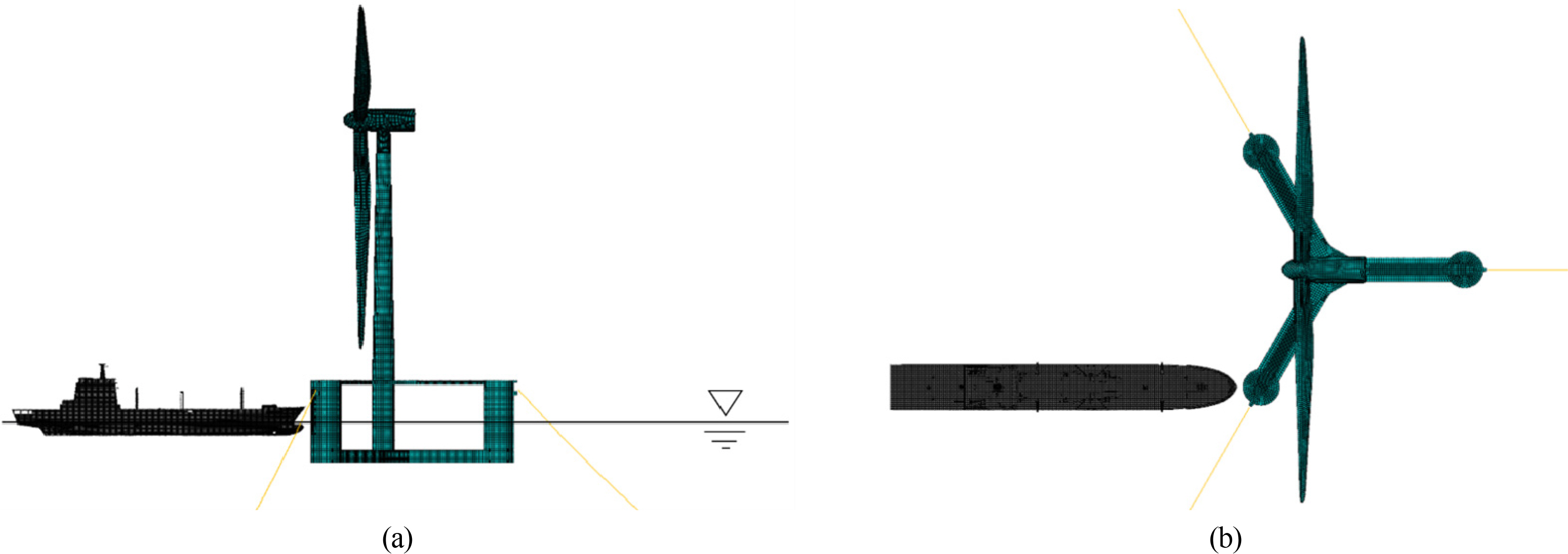
The tanker used in the collision simulations is shown in Fig. 4. In this study, the tanker was assumed to be a rigid body of R3D3 and R3D4 shell elements, while a MASS element, and a ROTARYI element were used to represent the mass. The main dimensions and masses of the ship are shown in Table 2.
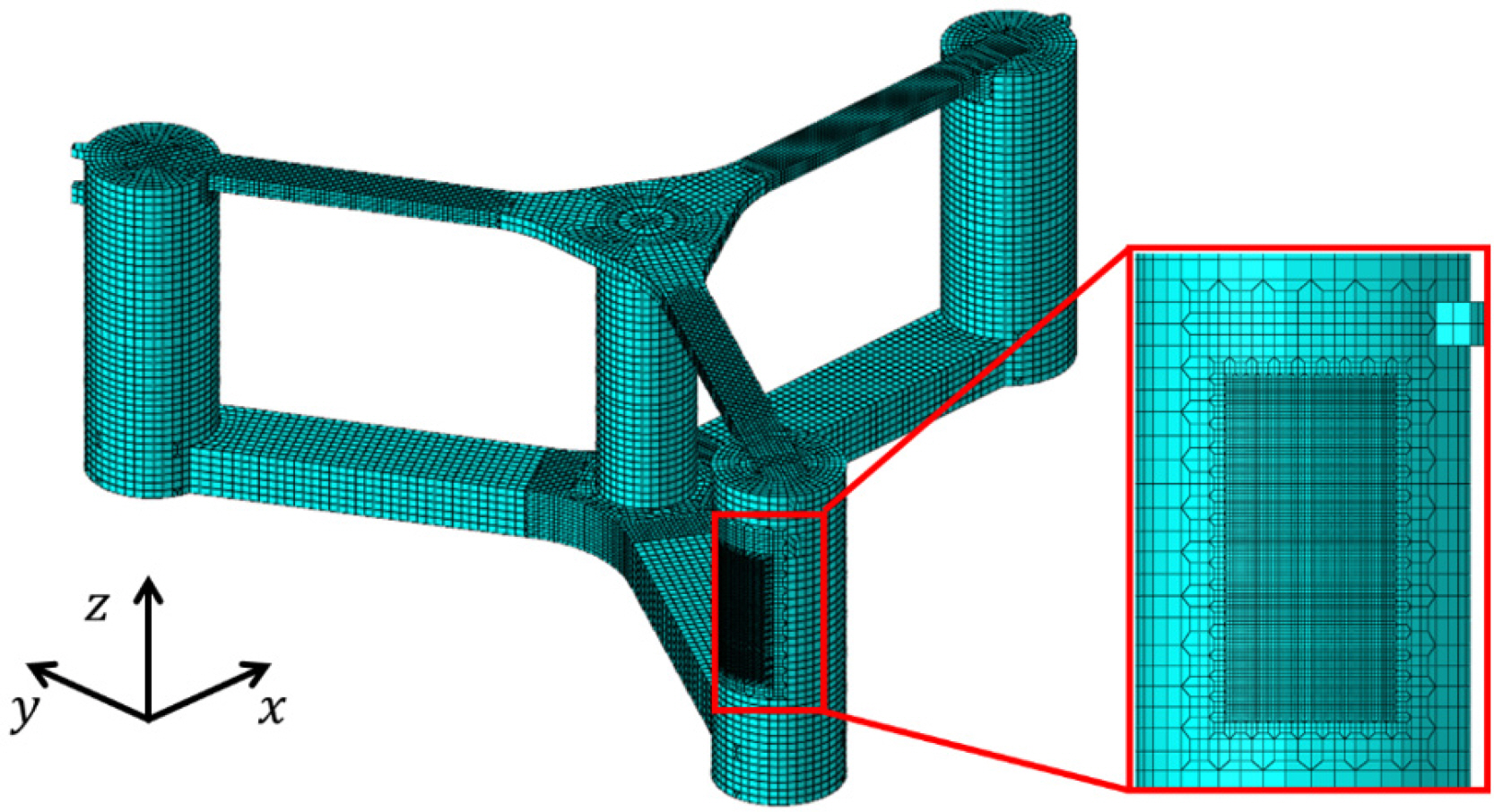
The FOWT was modeled with shell elements S3R and S4R. The element size was the longitudinal stiffener spacing, but the element size was reduced to 1/8 of the longitudinal stiffener spacing in the area where collisions were expected. The FEA model of the FOWT is summarized in Fig. 5 and Table 3.
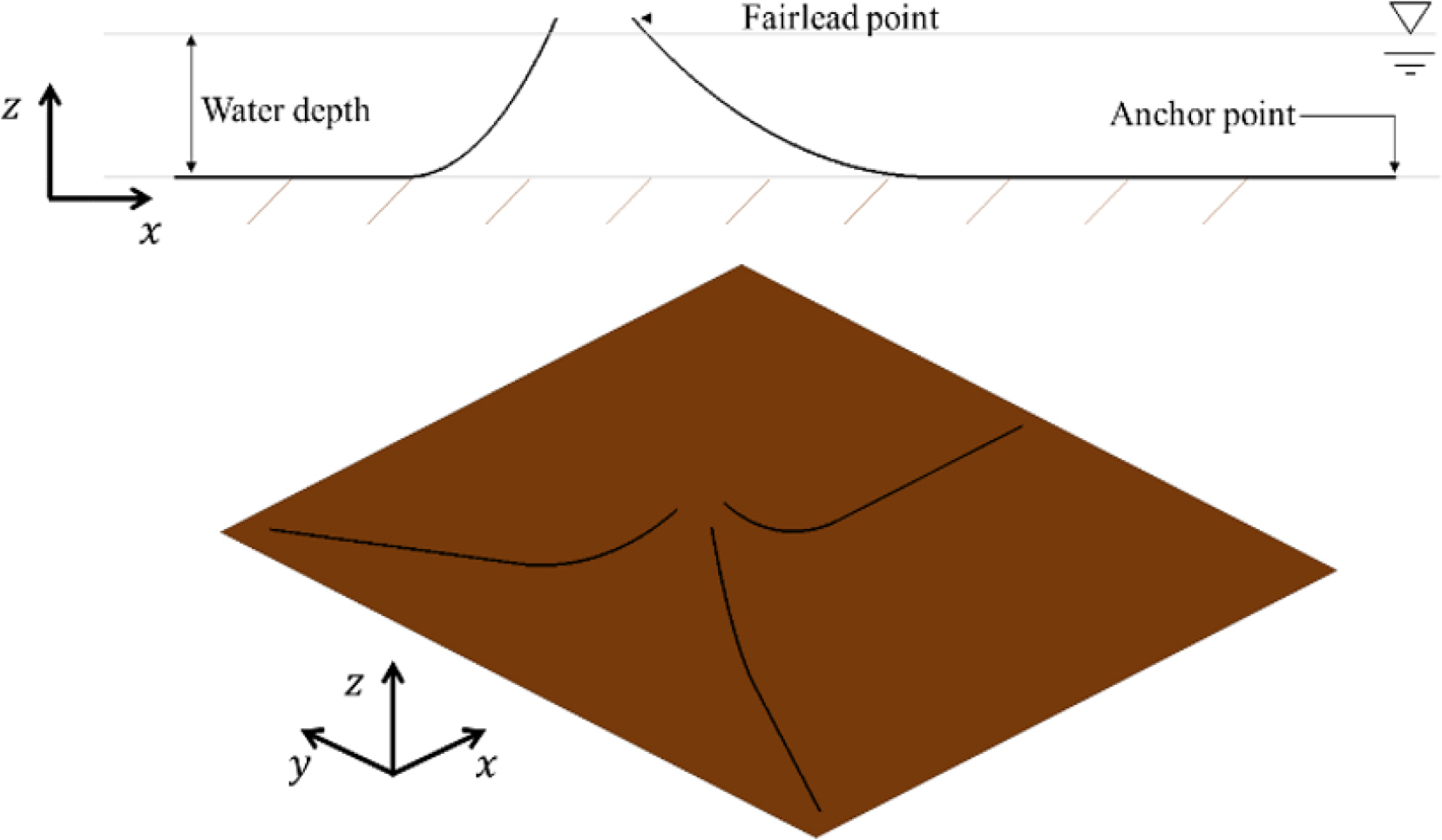
The initial layout of the mooring lines was determined using the catenary equation. The mooring lines were modeled using beam element (B31) and joint element (UJOINT) connecting the beam elements to allow rotation. The seabed was modeled as a rigid element. The modeled seabed and mooring lines layout is shown in Fig. 6. Table 4 presents the modeling information of seabed and mooring line.
The DTU 10 MW wind turbine (Borg et al., 2015) released by the LIFES50+ project was used to model the tower and RNA (see Table 5). Fig. 7 shows the FEA model of the complete FOWT including mooring lines, floating body, tower, and RNA.
In this study, the floating body of the FOWT is made of AH36 steel for ship structures. In this study, the combined Swift-Voce hardening law was used to define the flow stress of this steel. The material constants of the combined Swift-Voce hardening law were determined based on the tensile test results by Park et al. (2020) (see Fig. 8). They also conducted a series of fracture tests. Their results were used in this study to obtain the fracture strain locus as shown in Fig. 9.
The objective of this study is unfolded into two. The first objective is to determine the impact of hydrodynamic forces on structural damage in a FOWT-tanker collision. Therefore, the cases were divided into those before and after considering hydrostatic restoring force and radiation force in the collision simulations. The second objective is to determine the impact of the fracture model on the structural damage assessment. For this purpose, the cases were divided into those with the HC-LN fracture model applied and those defined by a constant failure strain ∊f. In this case, ∊f was assumed to be 0.2, which has been the most widely used failure strain. Six cases were generated, which are summarized in Table 6. In all cases, the initial forward velocity of the tanker was assumed to be 5 knots (9.26 km/h). The collision analysis model is shown in Fig. 10.
The equivalent plastic strain is an important measure for determining the extent of damage. The equivalent plastic strain distribution just after the collision process is finished are shown in Fig. 11. Comparing the corresponding cases before and after considering hydrostatic force and hydrodynamic force (for example, comparing Case1-1, Case2-1 and Case3-1, or Case1-2, Case2-2, and Case3-2), there are no significant differences in the equivalent plastic strain distributions and maximum equivalent plastic strains. When comparing the constant failure strain model with the HC = LN model (e.g., Case1-1 and Case1-2), constant failure strain model shows similar damage extents as the HC-LN model, although the maximum equivalent plastic strains were developed up to 0.2 with the constant failure strain model.
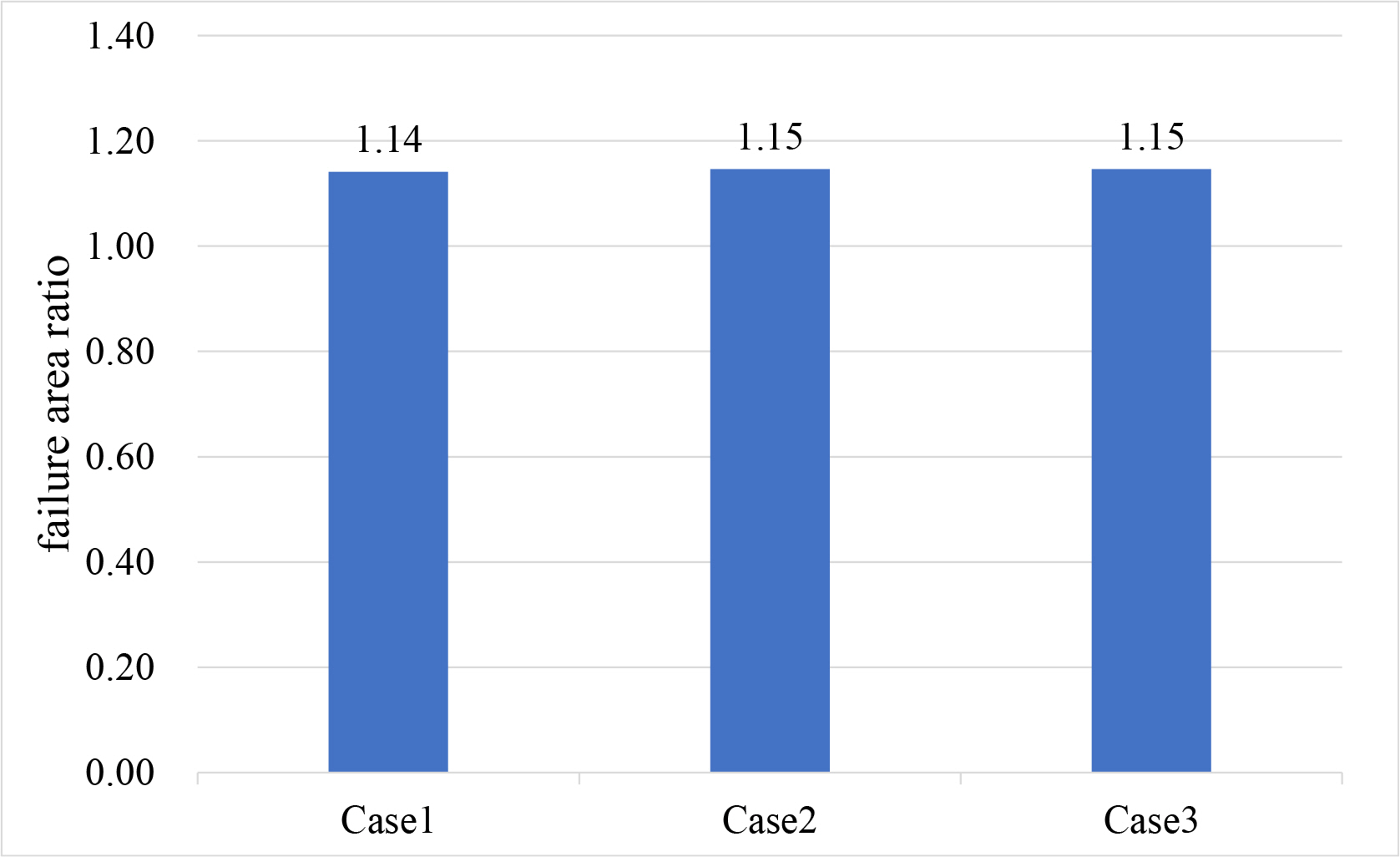
In this study, the damage extent is defined as the failed area of the side shell. The ratio of the damage extent with constant failure strain model divided by that with HC-LN model is shown in Fig. 12. In all cases, this ratio exceeds 1.0, which means that the constant failure strain model predicts larger damage extents than the HC-LN model.
The stress triaxiality and damage indicators of Case3-2 were analyzed as an example. The stress triaxiality immediately after the collision occurred is shown in Fig. 13(a). It can be seen from Fig. 13(a) that the stress triaxiality in the collision area corresponds to the biaxial tension. A stress path at a fracture initiation location was formed with this stress triaxiality and the necking damage was accumulated. After the collision was completely terminated, the necking indicator and ductile fracture damage indicator are shown in Fig. 13(b)–(c), respectively. As expected, we can see that the LN necking damage indicator was developed much larger than the HC damage indicator.
The authors of this study developed HydroQus, a hydrodynamic plug-in that can calculate hydroforces such as hydrostatic restoring force and hydrodynamic radiation/wave excitation forces. Using HydroQus to implement the hydrodynamic forces acting on the FOWT, a FOWT-tanker collision analysis was performed. Two different fracture models (constant failure strain model and HC-LC model) were applied to the collision simulations with and without the application of hydroforces to reasonably determine the damage extents.
The effect of hydroforces on the damage extents from the collision was relatively limited. This was presumed to be due to the fact that the collision occurs in a very short instant. A comparison of the failure areas caused by the collision showed that the constant failure strain model predicted larger fractures by about 15% compared to the HC-LC model. Since the size of the failure determines the speed and amount of flooding, a more scientific and reasonable failure model was required for the FOWT's impact analysis. The analysis of stress triaxiality and damage indicators confirmed that the use of the HC-LN model was justified.
The pitch motion of the ship generated by the waves changes the direction and magnitude of the impact force and should be considered in the future. The impact of ship hydrodynamics on collision simulations needs to be considered in the future. The ability of moorings to constrain the FOWT needs to be evaluated, as modeling moorings requires special effort.
Conflict of Interest
Joonmo Choung serves as an editor in chief of the Journal of Ocean Engineering and Technology, but he had no role in the decision to publish this article. No potential conflict of interest relevant to this article was reported.
Funding
This research was supported by the Korea Energy Technology Evaluation and Planning funded by the Ministry of Trade, Industry and Energy of Korea (No. 20213000000030) and Korea Environmental Industry & Technology Institute funded by Korea Ministry of Environment (No. 146836).
Fig. 3.
Frequency response analysis results: (a) Motion RAOs; (b) Radiation coefficients in surge direction; (c) Radiation coefficients in sway direction; (d) Radiation coefficients in heave direction; (e) Radiation coefficients in roll direction; (f) Radiation coefficients in pitch direction; (g) Radiation coefficients in yaw direction; (h) Wave excitation forces
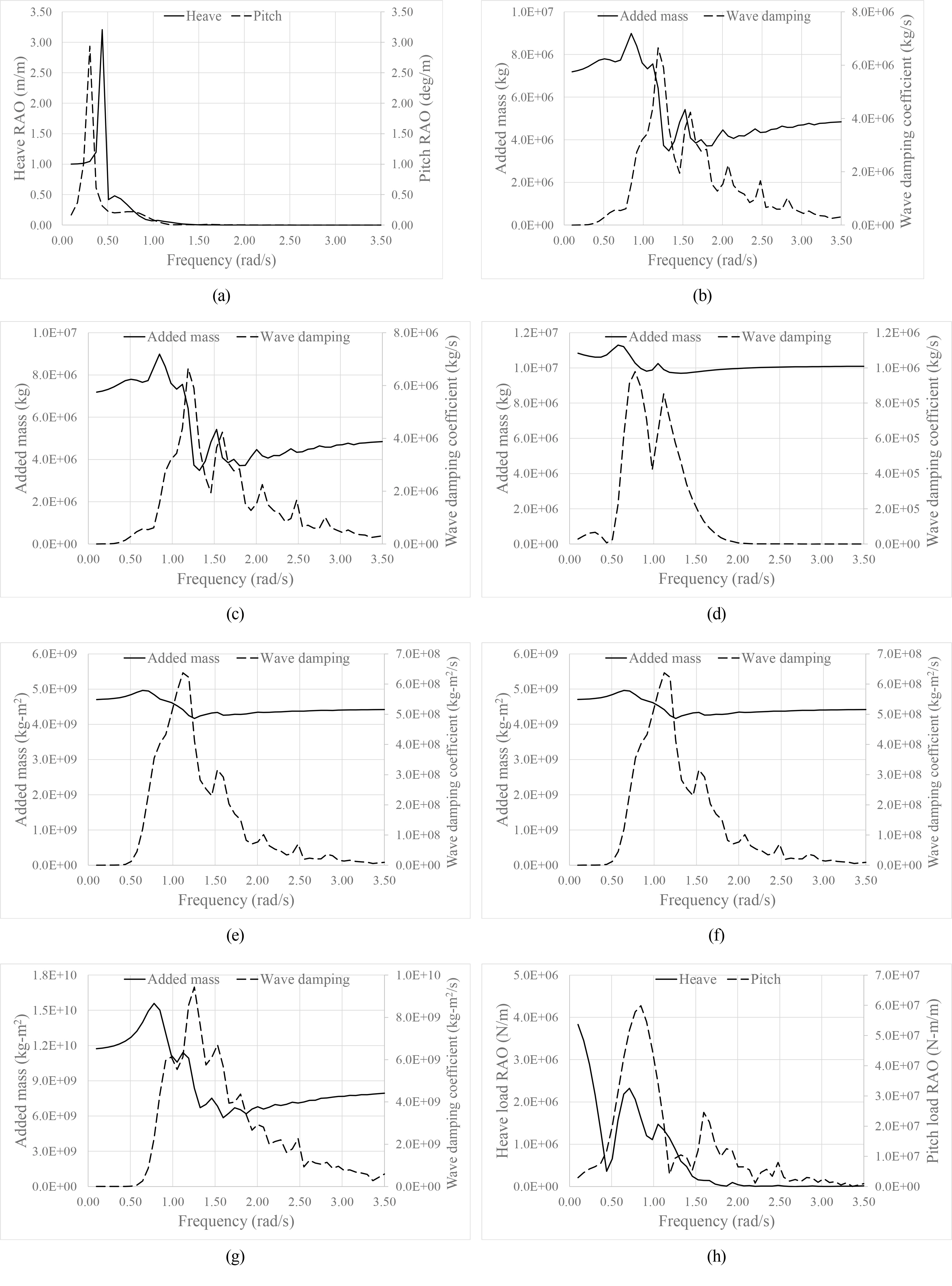
Fig. 11.
Equivalent plastic strain distribution: (a) Case1-1 & Case1-2; (b) Case2-1 & Case2-2; (c) Case3-1 & Case3-2

Fig. 13.
Stress triaxiality, LN necking indicator and HC damage indicator of Case3-2; (a) Stress triaxiality; (b) LN necking indicator; (c) HC damage indicator
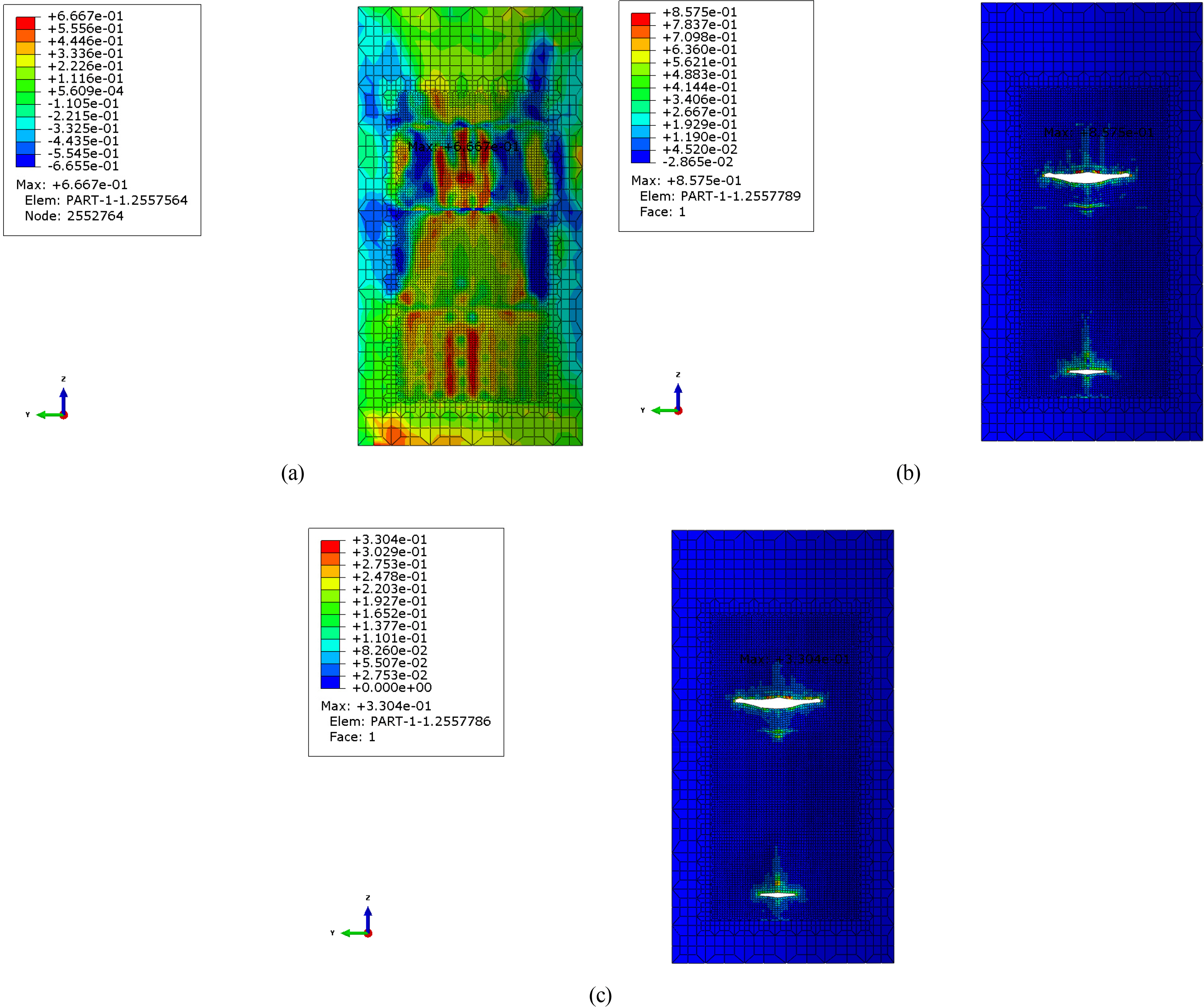
Table 1.
Principal dimensions and mass information of the FOWT
Table 2.
Modeling information of tanker
Table 3.
Modeling information of floater
Table 4.
Modeling information for mooring system
References
Ansys. (2022). Ansys User Manual, Ansys.
Bela, A., Le Sourne, H., Buldgen, L., & Rigo, P. (2017). Ship collision analysis on offshore wind turbine monopile foundations. Marine Structures, 51, 220-241.
https://doi.org/10.1016/j.marstruc.2016.10.009

Borg, M., Mirzaei, M., & Brendmose, H. (2015). D1.2 Wind turbine models for the design. DTU, Public LIFES50 D, 1..
Cerik, B. C., & Choung, J. (2020). Ductile fracture behavior of mild and high-ytnsile strength shipbuilding steels. Applied Sciences, 10(20), 7034.
https://doi.org/10.3390/app10207034

Cerik, B. C., Ringsberg, J. W., & Choung, J. (2019). Revisiting MARSTRUCT benchmark study on side-shell collision with a combined localized necking and stress-state dependent ductile fracture model. Ocean Engineering, 187, 106173.
https://doi.org/10.1016/j.oceaneng.2019.106173

Dai, L., Ehlers, S., Rausand, M., & Utne, I. B. (2013). Risk of collision between service vessels and offshore wind turbines. Reliability Engineering & System Safety, 109, 18-31.
https://doi.org/10.1016/j.ress.2012.07.008

Det Norske Veritas (DNV). (2013). Design of offshore wind turbine structures, (DNV-OS-J101).
Echeverry, S., Márquez, L., Rigo, Ph., & Sourne, H. L. (2019). Numerical crashworthiness analysis of a spar floating offshore wind turbine impacted by a ship. In: Soares C. Guedes, ed. Developments in the collision and grounding of ships and offshore structures. 1st ed. p 85-95 CRC Press:
https://doi.org/10.1201/9781003002420-11

Han, D. H. (2022). Development of a fluid-structure interaction technique for marine structures using non-viscous hydro-forces and explicit finite element method. [Doctoral dissertation, Inha University; ]. https://inha.dcollection.net/public_resource/pdf/200000598213_20230605182419.pdf
Jasmina, O. M. (2023) April 27. Cargo ship strikes turbine at Orsted’s Gode Wind 1 offshore wind farm, suffers massive damage. Offshore Energy. https://www.offshore-energy.biz/cargo-ship-strikes-orsteds-gode-wind-1-offshore-wind-farm-suffers-massive-damage/
Jonkman, J. M. (2007). Dynamics modeling and loads analysis of an offshore floating wind turbine. (NREL/TP-500-41958, 921803). https://doi.org/10.2172/921803
Márquez, L., Le Sourne, H., & Rigo, P. (2022). Mechanical model for the analysis of ship collisions against reinforced concrete floaters of offshore wind turbines. Ocean Engineering, 261, 111987.
https://doi.org/10.1016/j.oceaneng.2022.111987

Masciola, M., Jonkman, J., & Robertson, A. (2013). Implementation of a multisegmented, quasi-static cable model. (ISOPE-I-13-127).
Mohr, D., & Marcadet, S. J. (2015). Micromechanically-motivated phenomenological Hosford–Coulomb model for predicting ductile fracture initiation at low stress triaxialities. International Journal of Solids and Structures, 67–68, 40-55.
https://doi.org/10.1016/j.ijsolstr.2015.02.024

Moulas, D., Shafiee, M., & Mehmanparast, A. (2017). Damage analysis of ship collisions with offshore wind turbine foundations. Ocean Engineering, 143, 149-162.
https://doi.org/10.1016/j.oceaneng.2017.04.050

Pack, K., & Mohr, D. (2017). Combined necking & fracture model to predict ductile failure with shell finite elements. Engineering Fracture Mechanics, 182, 32-51.
https://doi.org/10.1016/j.engfracmech.2017.06.025

Park, S.-J., Cerik, B. C., & Choung, J. (2020). Comparative study on ductile fracture prediction of high-tensile strength marine structural steels. Ships and Offshore Structures, 15(sup1), S208-S219.
https://doi.org/10.1080/17445302.2020.1743552

Simulia. (2021). Abaqus user manual, Dassault Systemes Simulia Corp.
Sung, J. H., Kim, J. H., & Wagoner, R. H. (2010). A plastic constitutive equation incorporating strain, strain-rate, and temperature. International Journal of Plasticity, 26(12), 1746-1771.
https://doi.org/10.1016/j.ijplas.2010.02.005

Yoon, D. H., Jeong, S. -Y., & Choung, J. (2023). Collision simulations between an icebreaker and an iceberg considering ship hydrodynamics. Ocean Engineering, 279, 114333.
https://doi.org/10.1016/j.oceaneng.2023.114333

Zhang, Y., & Hu, Z. (2022). An aero-hydro coupled method for investigating ship collision against a floating offshore wind turbine. Marine Structures, 83, 103177.
https://doi.org/10.1016/j.marstruc.2022.103177

- TOOLS
-
METRICS

-
- 1 Crossref
- Scopus
- 1,642 View
- 132 Download