Adam, F., Myland, T., Dahlhaus, F., & Großmann, J. (2014) November. Gicon®-TLP for wind turbines—the path of development.
In the 1st International Conference on Renewable Energies Offshore (RENEW), 24-26.

Ansys. (2016). ANSYS aqwa theory manual, release 18.2, ANSYS, Canonsburg.
Bae, Y.H., & Kim, M.H. (2013). Rotor-floater-tether coupled dynamics including second-order sum–frequency wave loads for a mono-column-TLP-type FOWT (floating offshore wind turbine).
Ocean Engineering,
61, 109-122.
https://doi.org/10.1016/j.oceaneng.2013.01.010

Chung, W.C., Pestana, G.R., & Kim, M. (2021). Structural health monitoring for TLP-FOWT (floating offshore wind turbine) tendon using sensors.
Applied Ocean Research,
113, 102740.
https://doi.org/10.1016/j.apor.2021.102740

Ghafari, H.R., Neisi, A., Ghassemi, H., & Iranmanesh, M. (2021). Power production of the hybrid Wavestar point absorber mounted around the Hywind spar platform and its dynamic response.
Journal of Renewable and Sustainable Energy,
13(3), 033308.
https://doi.org/10.1063/5.0046590

Global Wind Energy Council Global. (2019). Wind Report 2018, Global Wind Energy Council.
Hansen, R.H., Kramer, M.M., & Vidal, E. (2013). Discrete displacement hydraulic power take-off system for the wavestar wave energy converter.
Energies,
6(8), 4001-4044.
https://doi.org/10.3390/en6084001

Jonkman, J. (2010). Definition of the floating system for phase IV of OC3 (No. NREL/TP-500-47535). National Renewable Energy Lab.
Jonkman, J., Butterfield, S., Musial, W., & Scott, G. (2009). Definition of a 5-MW reference wind turbine for offshore system development (No. NREL/TP-500-38060). National Renewable Energy Lab.
Jonkman, J. M., & Buhl, M.L Jr. (2005). Fast user’s guide-updated august 2005 (No. NREL/TP-500-38230). National Renewable Energy Lab.
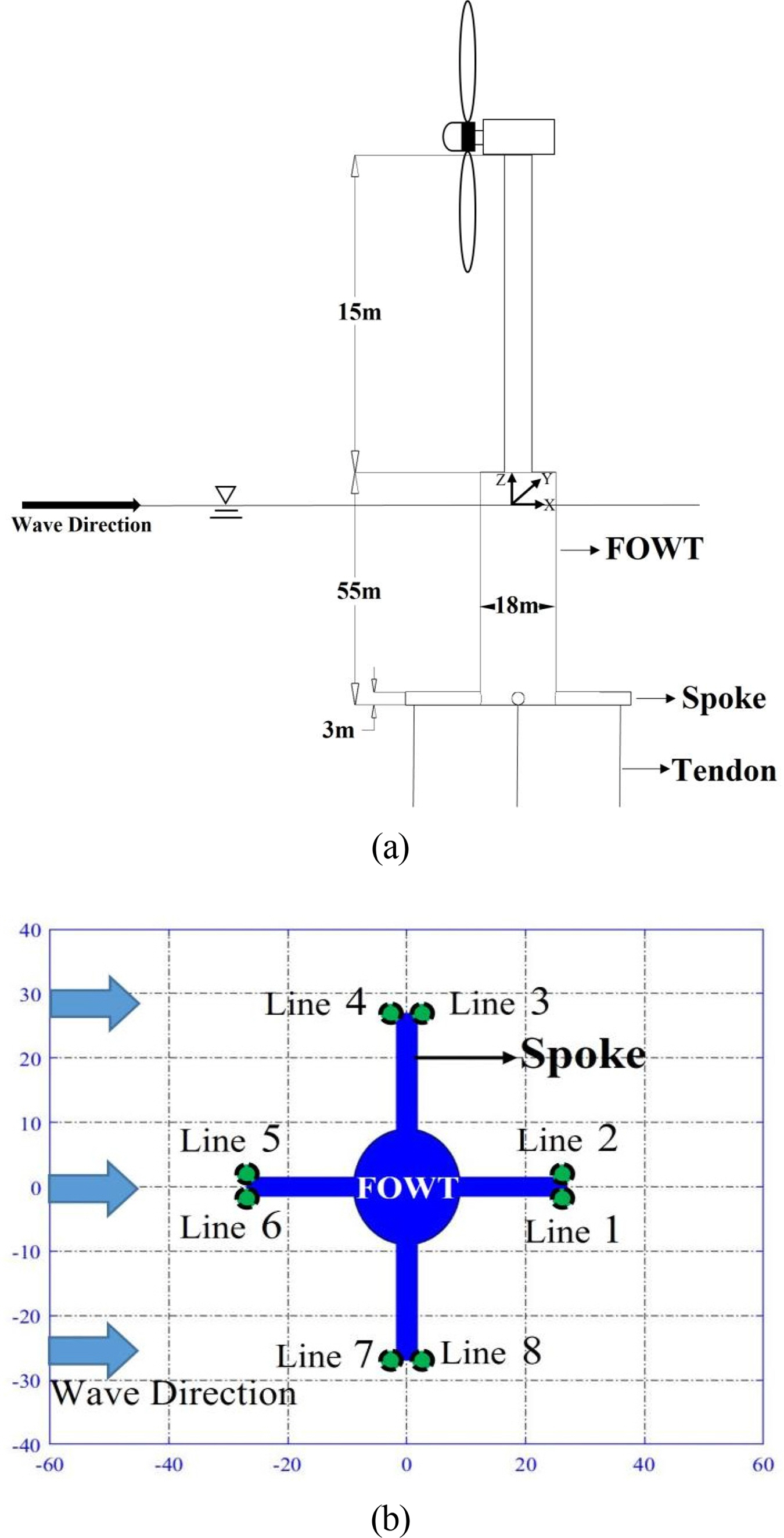
Kim, H., Kim, I., Kim, Y.Y., Youn, D., & Han, S. (2016). Simulation and experimental Study of A TLP type floating wind turbine with spoke platform.
Journal of Advanced Research in Ocean Engineering,
2(4), 179-191.
https://doi.org/10.5574/JAROE.2016.2.4.179

Kim, K.H., Lee, K., Sohn, J.M., Park, S., Choi, J.S., & Hong, K. (2015). Conceptual design of large semi-submersible platform for wave-offshore wind hybrid power generation.
Journal of the Korean Society for Marine Environment & Energy,
18(3), 223-232.
https://doi.org/10.7846/JKOSMEE.2015.18.3.223

Kim, M.H. (1993). Second-harmonic vertical wave loads on arrays of deep-draft circular cylinders in monochromatic uni-and multi-directional waves.
Applied ocean research,
15(5), 245-262.
https://doi.org/10.1016/0141-1187(93)90014-O

Kim, M.H., & Yue, D.K. (1989). The complete second-order diffraction solution for an axisymmetric body Part 1. Monochromatic incident waves.
Journal of Fluid Mechanics,
200, 235-264.
https://doi.org/10.1017/S0022112089000649

Kim, S.J., Koo, W.C., & Kim, M.H. (2021). The effects of geometrical buoy shape with nonlinear Froude-Krylov force on a heaving buoy point absorber.
International Journal of Naval Architecture and Ocean Engineering,
13, 86-101.
https://doi.org/10.1016/j.ijnaoe.2021.01.008

Lee, H., Cho, I.H., Kim, K.H., & Hong, K. (2016). Interaction analysis on deployment of multiple wave energy converters in a floating hybrid power generation platform.
Journal of the Korean Society for Marine Environment & Energy,
19(3), 185-193.
https://doi.org/10.7846/JKOSMEE.2016.19.3.185

Matha, D., Fischer, T., Kuhn, M., & Jonkman, J. (2010). Model development and loads analysis of a wind turbine on a floating offshore tension leg platform (No. NREL/CP-500-46725), National Renewable Energy Lab.
Muliawan, M.J., Karimirad, M., & Moan, T. (2013). Dynamic response and power performance of a combined spar-type floating wind turbine and coaxial floating wave energy converter.
Renewable Energy,
50, 47-57.
https://doi.org/10.1016/j.renene.2012.05.025

Oguz, E., Clelland, D., Day, A. H., Incecik, A., López, J.A., Sánchez, G., & Almeria, G.G. (2018). Experimental and numerical analysis of a TLP floating offshore wind turbine.
Ocean Engineering,
147, 591-605.
https://doi.org/10.1016/j.oceaneng.2017.10.052

Park, S., Kim, K.H., & Hong, K. (2018). Conceptual design of motion reduction device for floating wave-offshore wind hybrid power generation platform.
Journal of Ocean Engineering and Technology,
32(1), 9-20.
https://doi.org/10.26748/KSOE.2018.2.32.1.009

Pantusa, D., Francone, A., & Tomasicchio, G.R. (2020). Floating offshore renewable energy farms. A life-cycle cost analysis at Brindisi, Italy.
Energies,
13(22), 6150.
https://doi.org/10.3390/en13226150

Ran, Z. (2000). Coupled dynamic analysis of floating structures in waves and currents (Publication No. 9994319) [Doctoral dissertation, Texas A&M University]. ProQuest Dissertations Publishing.
Robertson, A., Jonkman, J., Masciola, M., Song, H., Goupee, A., Coulling, A., & Luan, C. (2014). Definition of the semi submersible floating system for phase II of OC4 (No. NREL/TP-5000-60601). National Renewable Energy Lab.
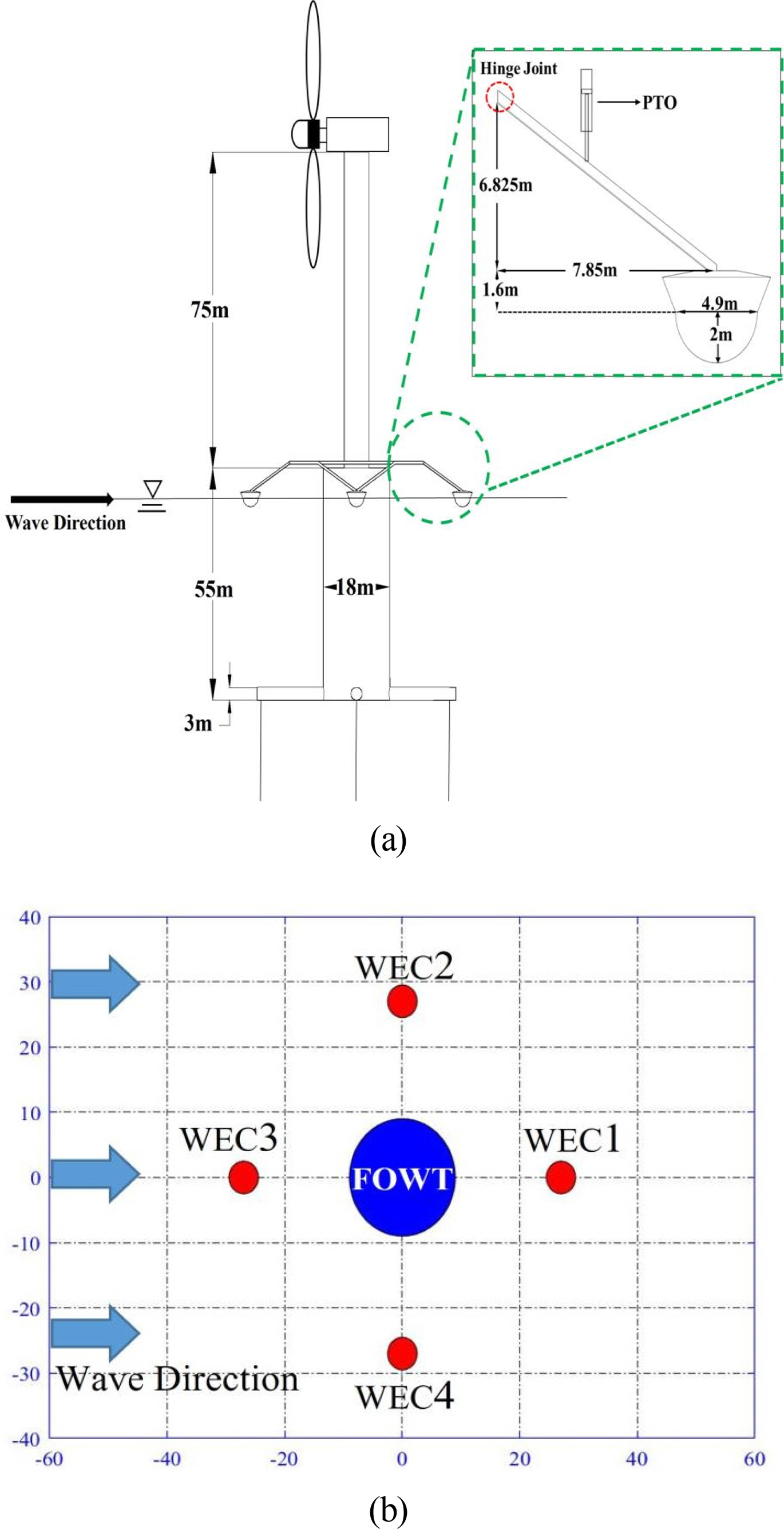
Si, Y., Chen, Z., Zeng, W., Sun, J., Zhang, D., Ma, X., & Qian, P. (2021). The influence of power-take-off control on the dynamic response and power output of combined semi-submersible floating wind turbine and point-absorber wave energy converters.
Ocean Engineering,
227, 108835.
https://doi.org/10.1016/j.oceaneng.2021.108835

Tsouroukdissian, A.R., Park, S., Pourazarm, P., Cava, W.L., Lackner, M., Lee, S., & Cross-Whiter, J. (2016). Smart novel semi-active tuned mass damper for fixed-bottom and floating offshore wind [Conference presentation]. Offshore Technology Conference 2016 Houston, Texas, USA:
https://doi.org/10.4043/26922-MS

Ullah, S., Branquinho, R., Mateus, T., Martins, R., Fortunato, E., Rasheed, T., & Sher, F. (2020). Solution combustion synthesis of transparent conducting thin films for sustainable photovoltaic applications.
Sustainability,
12(24), 10423.
https://doi.org/10.3390/su122410423

Yang, J., Teng, B., Gou, Y., Chen, L., & Jin, R. (2020). Half-wave frequency response phenomenon of a tightly moored submerged sphere under monochromatic wave action simulated by using the body-exact approach.
Applied Ocean Research,
103, 102317.
https://doi.org/10.1016/j.apor.2020.102317