|
 |
- Search
| J. Ocean Eng. Technol. > Volume 36(4); 2022 > Article |
|
Abstract
This study reviews the recent development and research results of a fixed oscillating water column (OWC) wave energy converter (WEC). The OWC WEC can be divided into fixed and floating types based on the installation location and movement of the structure. In this article, the study on a stationary OWC WEC, which is close to commercialization through the accumulation of long-term research achievements, is divided into five research categories with a focus on primary energy conversion research. These research categories include potential-flow-based numerical analysis, wave tank experiments, computational fluid dynamics analyses toward investigation of fluid viscous effects, U-shaped OWC studies that can amplify water surface displacement in the OWC chamber, and studies on OWC prototypes that have been installed and operated in real sea environments. This review will provide an overview of recent research on the stationary OWC WEC and basic information for further detailed studies on the OWC.
There have been a growing interest and developmental effort toward environment-friendly renewable energy owing to climate change and environmental pollution. The development of eco-friendly energy cannot be further delayed, in which global R&D efforts and cooperation are urgently required. Marine energy, one of the well-known eco-friendly energy resources, can be classified into wave energy, offshore wind energy, tidal current energy, and ocean thermal energy. In particular, wave energy is a highly promising energy source, considering its high energy density, overall amount of energy, and future potential. Several methods have been developed to convert wave energy to electrical energy; these methods can be classified into movable body, wave overtopping, or oscillating water column (OWC) depending on the primary energy conversion type. Among these, OWC-type energy conversion involves the displacement of the water level inside a chamber, as the incident wave flows into an energy converter, and subsequently, the airflow inside the chamber can rotate special air turbines, e.g., Wells turbine or impulse turbine, installed on a nozzle to convert energy. Such energy conversion method possesses the advantages of easy maintenance and repair of an energy conversion system and no direct contact with incident waves, as the major energy conversion system, e.g., power take-off (PTO), is located outside the water surface.
A fixed OWC wave energy converter (WEC) has been actively researched worldwide and produced extensive research achievements among various wave energy conversion methods, while being closest to commercialization. Therefore, a necessity has arisen to organize the R&D achievements with regard to an OWC WEC and provide basic information. To this end, this study has generally organized the achievements and various research content of a fixed OWC WEC in various countries. However, as it is impossible to organize and discuss all the research achievements, this study focused on the primary energy conversion of various OWC structures. The results of secondary energy conversion, e.g., PTO system, will be introduced in future studies. We expect that the readers will gather basic information for detailed and precise R&D on an OWC WEC based on the research achievements organized in this study.
The concept of an OWC WEC was first described in 1947; however, this specific term first appeared in a paper published in 1978 (Masuda and Miyazaki, 1978; Evans, 1978; Falcão and Henriques, 2016). Prior to 1978, such type of WECs has been referred to as the Masuda device. The OWC WEC has been most widely studied, and numerous prototype structures have been installed in real sea environments.
The OWC WEC can be divided into fixed and floating types. In this paper, the research achievements and results of the primary energy conversion of a fixed OWC WEC are divided into the following five categories: potential flow analysis, relevant wave tank experiments, computational fluid dynamics (CFD) analyses assuming viscous fluids, U-shaped OWC (U-OWC) studies that can amplify free surface displacement in a chamber, and study results of OWC prototypes that have been installed and operated in real sea environments.
A floating-type OWC WEC includes single and multiple air chambers and a backward bent duct buoy (BBDB), which possesses a relatively high energy conversion efficiency owing to its unique structure. The R&D achievements and study results of the floating-type OWC WEC will be comprehensively reviewed in future studies.
The dynamic analysis of a fixed OWC WEC is based on a potential flow assumption that considers inviscid, incompressible, and irrotational fluids. Incident waves flowing into a chamber generate a vortex, which is the effect of fluid viscosity, in a skirt-shaped structure at the inlet of an OWC, thus causing energy attenuation. However, a potential flow analysis can be conducted under the assumption that the actual energy loss caused by fluid viscosity is not significant compared to the entire incident energy amount. Accordingly, the overall performance of an OWC and extraction energy efficiency can be calculated.
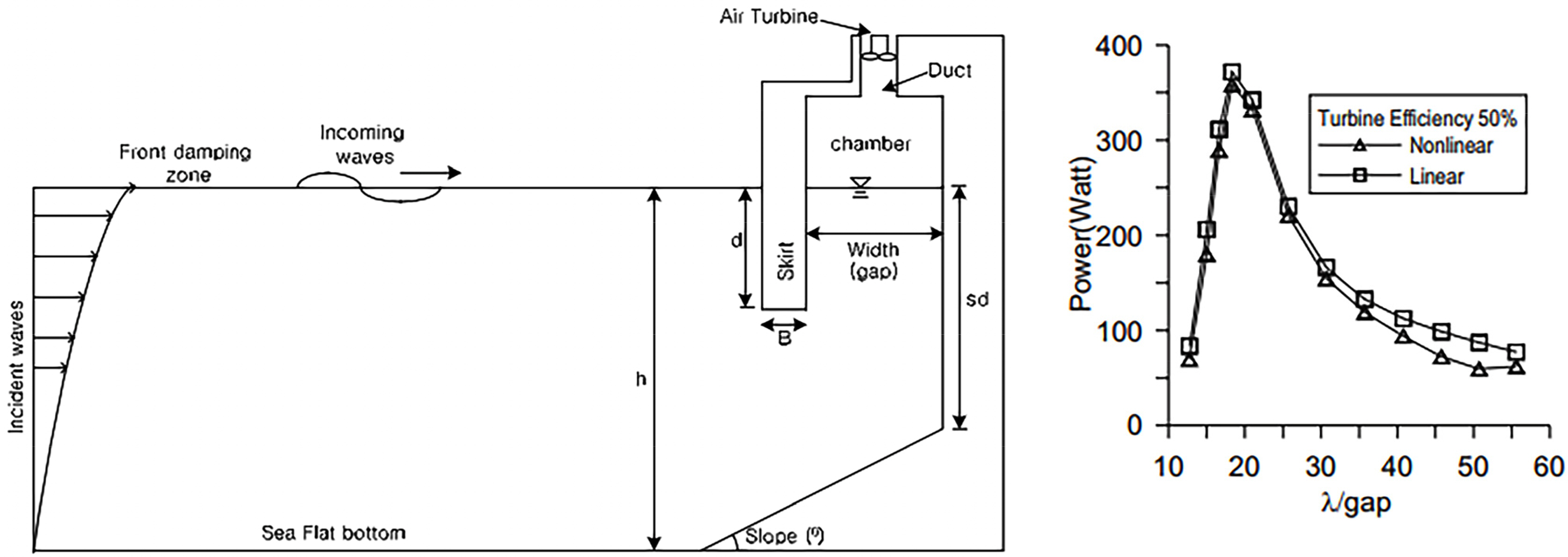
The potential flow analysis involves generally a boundary element method (BEM) to solve boundary integral equations at fluid boundaries. Delauré and Lewis (2003) used the first-order mixed distribution panel method to analyze a three-dimensional fixed OWC device under regular and irregular wave conditions and confirmed its accuracy based on a comparison with the experimental results of irregular waves at a scale of 1:36. Josset and Clément (2007) analyzed fluid dynamic problems by uncoupling the internal chamber flow and exterior structure considered for the numerical analysis of an OWC in the time domain and solved the fluid dynamic problem of an OWC exterior structure, which requires long computation time. Thus, they developed a numerical analysis tool that is useful in each step of a plant project, starting from the pre-conception to plant monitoring of an OWC. In addition, numerical simulation results confirmed that productivity can be improved by 15.5% by replacing the Wells turbine of a fixed 400-kW OWC WEC located on the Pico Island of Portugal. Koo and Kim (2010) developed a fully nonlinear numerical wave tank capable of expressing free surface displacement using the mixed Eulerian–Lagrangian (MEL) method and simulated nonlinear wave motions of free surface inside a chamber (Fig. 1). Furthermore, a damping coefficient proportional to the average vertical velocity of the free surface was substituted in boundary conditions in order to implement the energy loss of a chamber skirt caused by fluid viscosity when incident waves flowed inside the chamber. Through this, more accurate results were obtained by adding energy loss due to viscosity to the potential flow analysis assuming an inviscid fluid. The maximum extractable energy was computed by calculating the available wave energy according to the volume ratio between the chamber and duct. Liu et al. (2010) also considered the MEL method and studied the interaction between incident waves and structures using the desingularized boundary integral equation method (DBIEM), which distributes the source outside the boundary of the fluid computational domain. Kim et al. (2021a) calculated the pneumatic damping coefficient, which has a similar meaning to the coefficient that converts the air pressure in a chamber into electrical energy, as a theoretical solution, and applied it to a two-dimensional numerical wave tank to obtain the energy extraction efficiency of an OWC. Such method differs from the method where the air damping coefficient is determined by comparing with previous experimental results or using a trial-and-error method.
Several studies on the high-order boundary element method (HOBEM), which can better simulate the nonlinearity of each element than the constant panel method (CPM), have been reported. Ning et al. (2015) developed a fully nonlinear 2D numerical wave tank in the time domain using the HOBEM, which can improve the efficiency and accuracy of numerical computation results by modeling the CPM of the corners or edge shapes of OWC structures. Wang et al. (2018) compared the numerical analysis results according to nonlinearity and viscosity terms to analyze the effects of nonlinearity and viscosity on fluid dynamic efficiency. Fluid dynamic efficiency improved considering nonlinearity and viscosity when the amplitude of incident waves was small; however, the efficiency decreased when the amplitude of the incident waves increased, as the transmission of the second-order harmonic wave component weakened owing to strong nonlinearity.
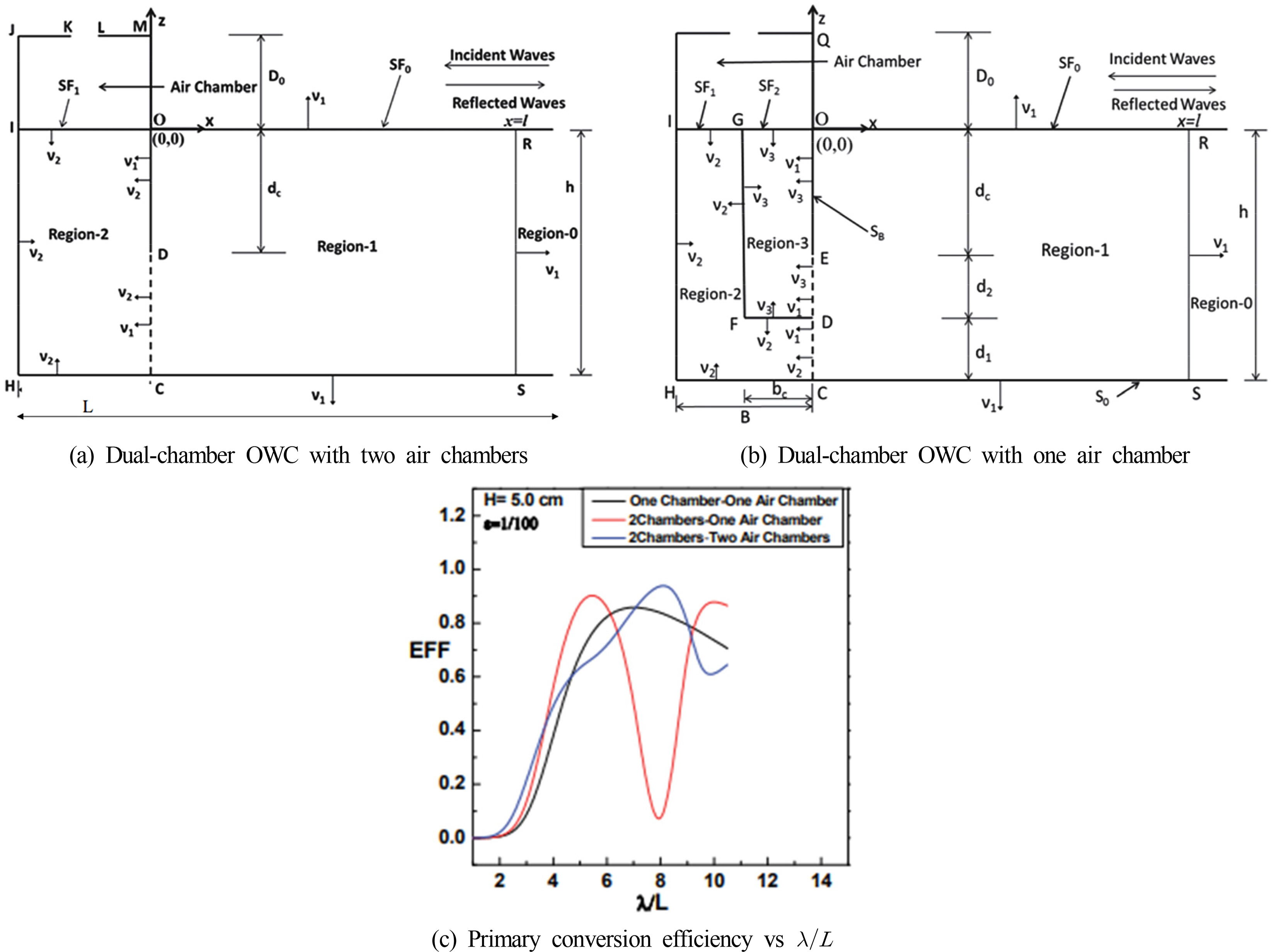
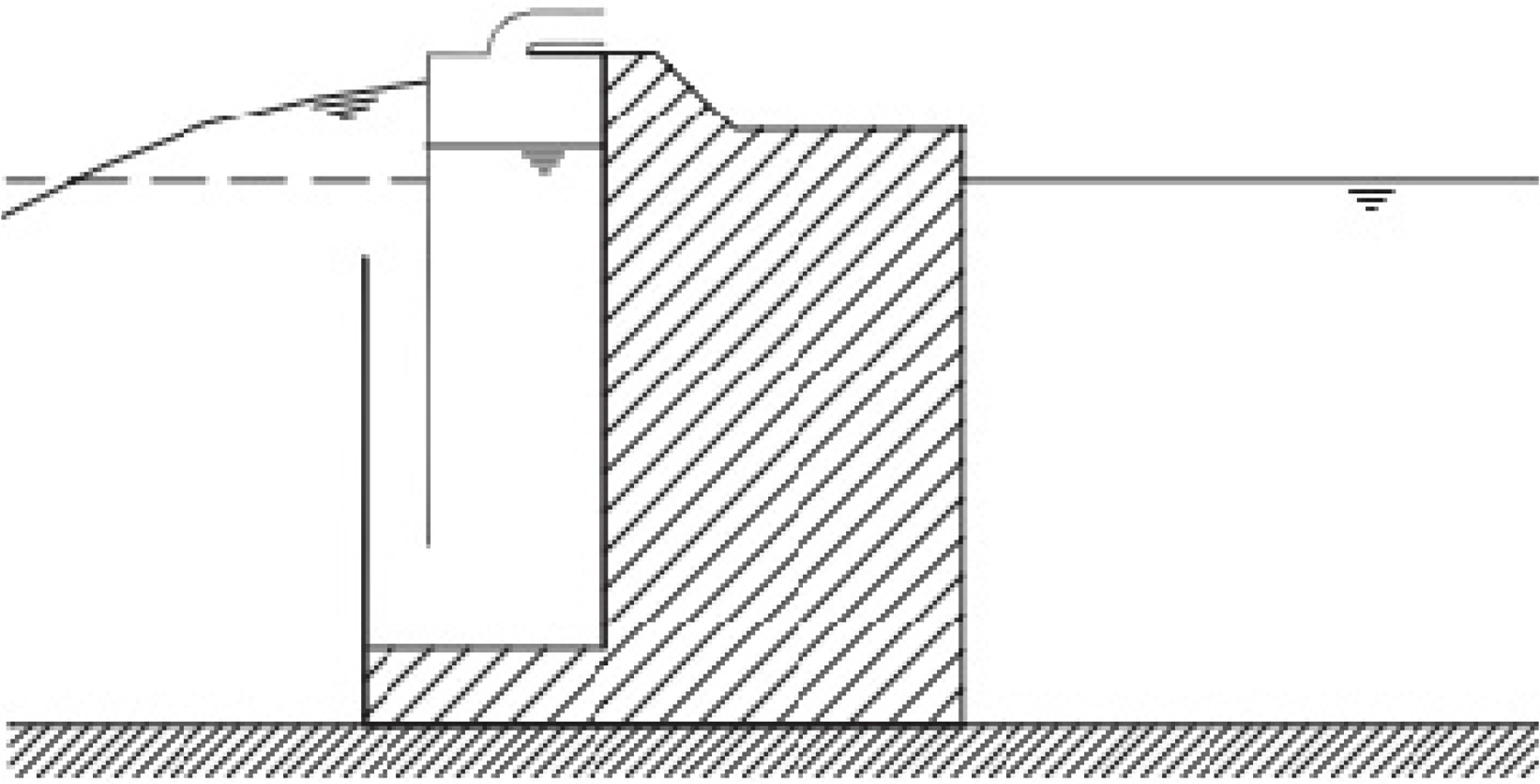
Studies have been conducted on applying a dual chamber or changing the sea floor to improve the energy conversion efficiency of an OWC device. Rezanejad et al. (2013) analyzed the effects of stepped sea bottom on the OWC efficiency (Fig. 2). Two methods were used to solve the boundary value problem (BVP) of the computational domain: the matched eigenfunction expansion method and the boundary integral equation method (BIEM) satisfying boundary conditions. The performance of a device is not significantly affected if a sea floor step is positioned inside a chamber, whereas the performance improves if a sea floor step is positioned outside the chamber. The performance of a device improves when the peak frequency decreases owing to a decrease in the water depth. An OWC can achieve relatively high efficiency if the OWC structure and step are designed, so that the second and third resonance occurs near the first resonance frequency. Moreover, it was confirmed that the horizontal distance between the OWC skirt and step edge needs to be closer to 1/4 of the incident wavelength to maximize the effects of the third resonance mechanism. In a subsequent study, it was confirmed that the efficiency of a dual chamber drastically improved in a wide frequency band in relation to that of a single chamber on a stepped sea floor (Rezanejad et al., 2015). The performance could have improved if at least one sea floor step was positioned outside the chamber. The performance improved when one step was located inside and outside the chamber; however, it was smaller than when two steps were positioned outside the chamber. The viscosity effect inducing vortex shedding near the step, which was ignored, can be considered for a more realistic prediction. Koirala et al. (2015) measured primary conversion efficiency by comparing the following cases using a 2D numerical model in the frequency domain: a dual chamber comprising two air chambers and a dual chamber comprising one air chamber (Fig. 3). The pneumatic pressure inside the chambers, reflection coefficient, and primary conversion and coupling efficiencies of each chamber were calculated using the BIEM. The dual-chamber OWC comprising two air chambers exhibited higher energy efficiency in a long wave region than the single-chamber OWC under the same physical conditions. Furthermore, the dual chamber comprising one air chamber exhibited two peak values on the primary conversion efficiency curve, and the primary conversion efficiency was extremely low when the wavelength (λ) was eight times the OWC length (L).
Several studies on an inclined OWC, which can be installed by linking with a breakwater, were conducted. With regard to the hydrodynamic problem of the OWC chamber, Kim et al. (2020) used the finite element method to perform a time domain analysis based on the linear potential flow theory. They confirmed that the energy conversion efficiency of the OWC chamber demonstrates a nonlinear response based on the incident wave height with regard to hydrodynamic performance. Kim et al. (2021b) reviewed the validity of applying a linear decomposition method (radiation and scattering problems) and calculating turbine–chamber interactions based on linear air pressure drop characteristics and confirmed that the results matched the irregular wave simulation results. Yang et al. (2021) compared the experimental results of a 2D fully nonlinear numerical wave tank to calculate the wave height inside the chamber considering the chamber width and changes in the chamber skirt draft and further computed the maximum amount of extractable wave energy by calculating the energy components of a WEC system (Fig. 4). Table 1 provides the comparisons of the potential-flow-based numerical analysis methods for OWC mentioned in this section and the shape of the OWC chamber.
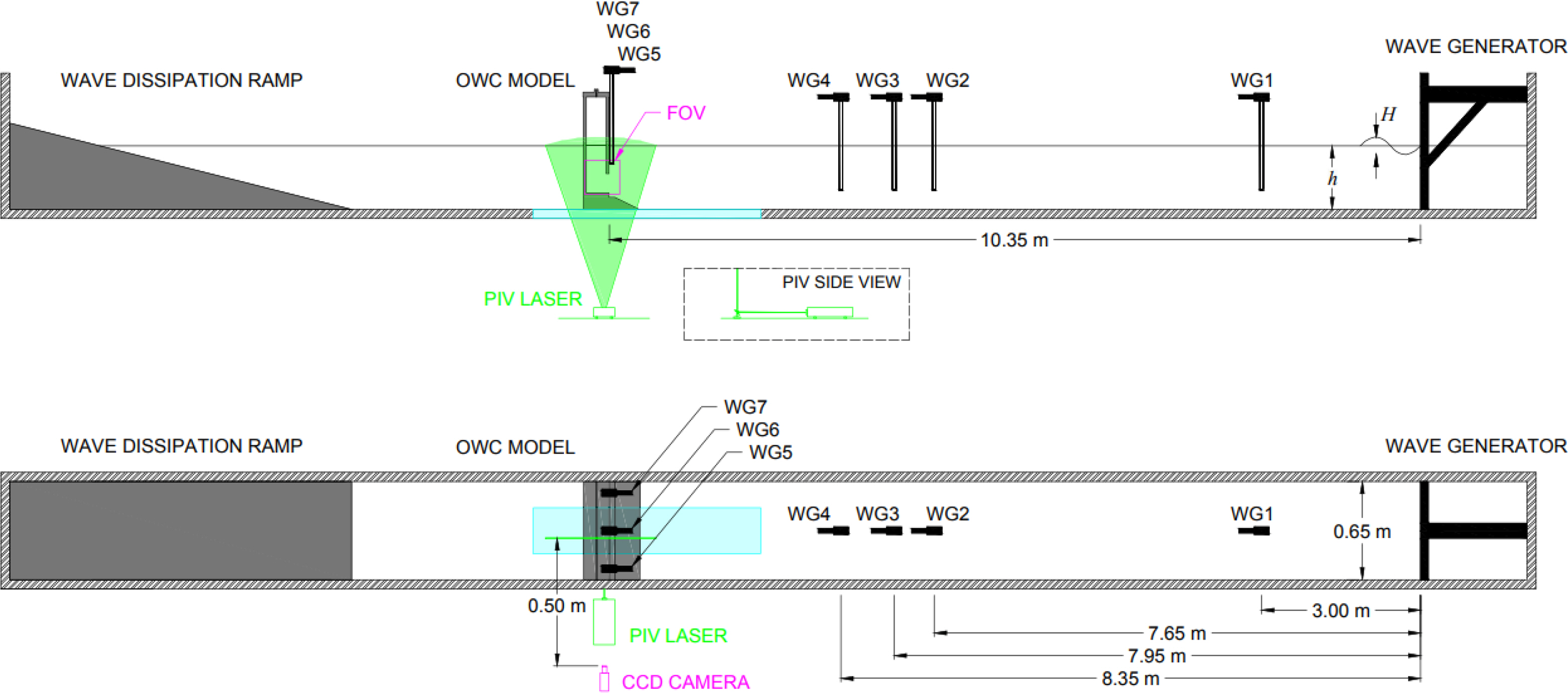
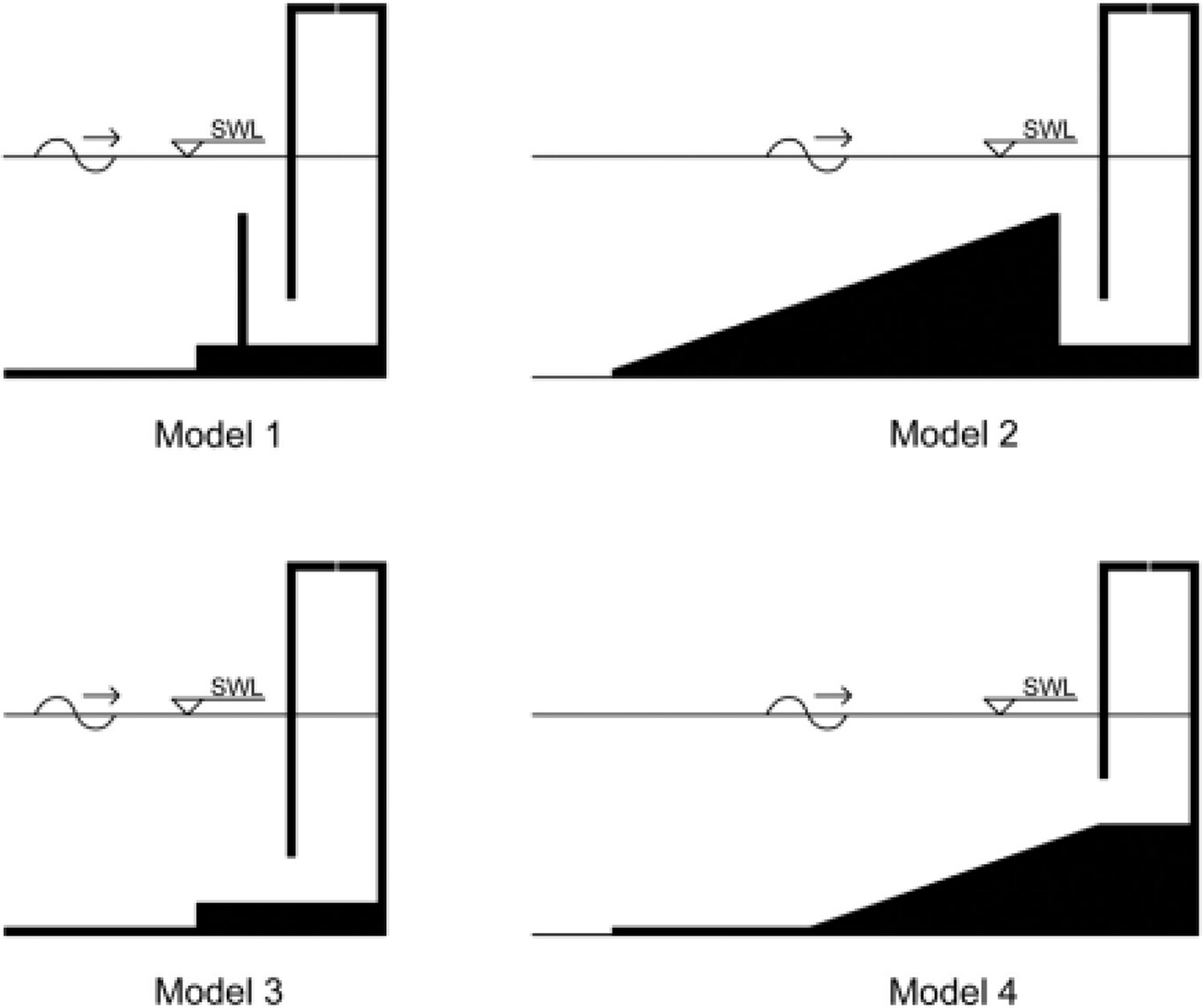
Various wave tank experiments were conducted to test the performance of OWC and verify the numerical analysis results of a fixed OWC WEC. To verify the OWC numerical model (theoretical solution using the wave Green function) installed on the coast with an arbitrary topography, Wang et al. (2002) conducted an experiment for OWC models at a scale of 1:12, considering different seabed slopes in a wave tank (length: 32.0 m, width: 18.0 m, and depth: 1.0 m) under a regular wave condition. Gouaud et al. (2010) installed an OWC on an underwater three-dimensional mound (UTDM) in a large-scale ocean engineering basin and conducted an experiment considering regular and irregular wave conditions. They confirmed a significant increase in the capture–width ratio caused by the concentrated waves on the mound. Therefore, it was confirmed that the use of UTDM would result in economical efficiency by amplifying the energy flux at the inlet of the OWC. Koo et al. (2012) installed a fixed OWC WEC model on a 2D wave basin and measured the water surface displacement inside the chamber according to the incident wave frequency. Moreover, they examined the maximum water surface displacement depending on structural changes, i.e., chamber skirt draft and seabed slope angle, to identify the effects of different shapes. Allsop et al. (2014) tested a large-scale OWC model (approximately 1:5–1:9 model scale) in a wave tank to measure wave energy, water column movement, air pressure, and airflow according to the size of an orifice size. Accordingly, calibration data needed for a CFD model were expected. The scale effect for wave energy and performance was examined by comparing the results based on a small-scale model test. Viviano et al. (2018) compared the results of a small-scale experiment conducted in a random incident wave condition with those of a large-scale experiment (Allsop et al., 2014) and analyzed the scale effect for water column movement, reflected waves, and external force applied to an outer front wall. Moreover, they investigated the air compression effect through a small-scale experiment. Ning et al. (2016) conducted an OWC wave tank experiment to measure the water surface displacement inside a chamber according to the shape coefficient of structures and compared the results with previous numerical results (Ning et al., 2015). They verified that the surface displacement inside a chamber is significantly affected by incident wavelength and chamber width ratio, whereas the seabed slope is relatively less influential. In addition, the seiching phenomenon (maximum amplitude at both ends of a chamber and 0 amplitude in the center) occurs when the hydrodynamic efficiency is close to 0 and the wavelength (λ) is twice the chamber width (B). López et al. (2015) measured flow characteristics, i.e., water particle velocity, vorticity, kinetic energy, and turbulence kinetic energy, using particle imaging velocimetry (PIV) based on a phase-averaging procedure to analyze the effects of turbine damping and tidal level on the OWC device (Fig. 5). Thus, it was confirmed that the damping coefficient by the turbine is a major factor affecting the energy extraction efficiency.
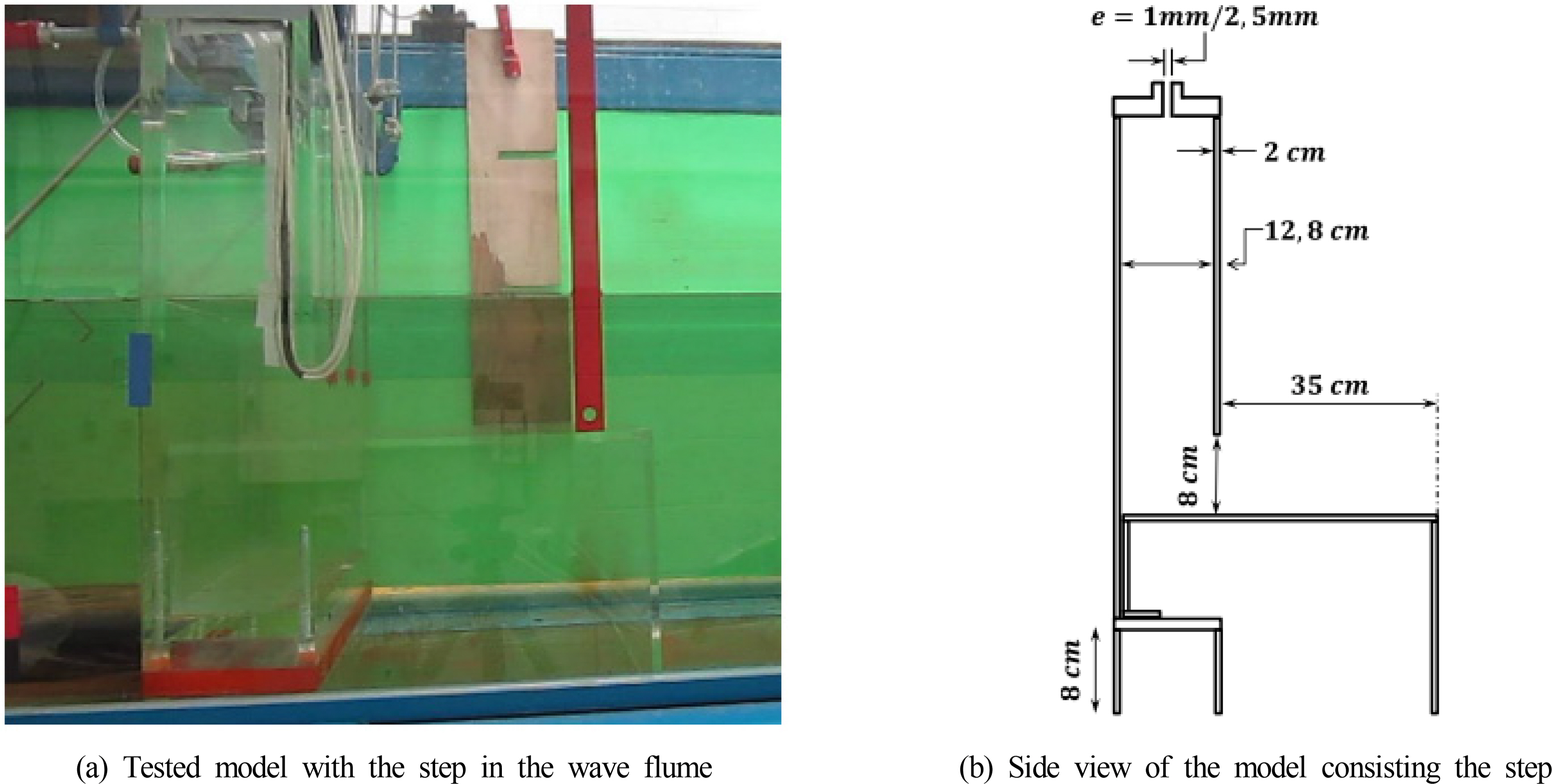
Rezanejad et al. (2017) conducted a wave tank experiment for an OWC device placed on a stepped floor terrain and reported that the efficiency of an OWC is significantly affected by the incident wave period and turbine damping coefficient. A subsequent study (Rezanejad and Guedes Soares, 2018) confirmed that the frequency bandwidth with regard to OWC efficiency can be substantially improved when a dual-mass concept is applied and verified through an experiment that the performance improvement of an OWC device in a stepped sea floor condition corresponds to the implementation of a dual-mass system (Fig. 6).
Dizadji and Sajadian (2011) conducted a 2D wave tank experiment (16.0 m × 0.7 m × 0.5 m) for an inclined OWC model to identify the effects of each shape coefficient of the structure, including the inclination angle (30°–60°), and selected an optimization model for maximum energy extraction, reporting 32% efficiency. Park et al. (2018b) evaluated the performance of a conventional type chamber with a right-angle OWC skirt and a sloped-type chamber based on a 2D wave basin (40.0 m × 0.6 m × 1.0 m) experiment and reported that the sloped-type chamber demonstrated excellent energy extraction performance and could be installed by linking with breakwater (Fig. 7). Furthermore, Lim et al. (2021) calculated a wave load applied to the OWC structure combined with sloped breakwater through CFD simulation and verified the stability of the WEC structures through a 2D physical model experiment (50.0 m × 1.2 m × 1.5 m).
Ikoma et al. (2019) conducted a wave tank experiment for an OWC WEC (Projecting Wall-OWC model), in which a projecting wall for improving energy efficiency is installed on a double-dissipating caisson. The experiment confirmed that the water surface displacement and air pressure inside a chamber were significantly affected by the wave height. Furthermore, the use of the double-dissipating caisson was advantageous for the primary energy conversion of 80% or higher.
Owing to advancements in computer processing capabilities, a CFD analysis, which includes Navier–Stokes equations that can consider fluid viscosity within the computation domain as governing equations, is being actively used to predict the performance of an OWC WEC. The CFD model possesses the advantage of being able to consider strong nonlinearity, complex viscous effects, turbulence, and vortex. For example, the loss of incident wave energy can be estimated by applying the fluid viscosity effect generated in a specific shape region of a structure when incident waves enter the chamber. However, computational modeling is difficult, calculation time may drastically increase with the number of grids, and the experimental verification of the results is required. Open-source codes, e.g., REEF3D and OpenFOAM, or commercial CFD codes, e.g., Fluent and Star-CCM+, are generally used. Several studies that used REEF3D and OpenFOAM have been reported. Kamath et al. (2015) studied the PTO damping effect for a 2D OWC chamber using a REEF3D-based numerical model with incompressible Reynolds-averaged Navier–Stokes (RANS) (Fig. 8). They confirmed that the PTO damping coefficient, which is required to achieve the maximum hydrodynamic efficiency, increases with the incident wavelength and the hydrodynamic efficiency is influenced by incident wavelength, wave height, and PTO damping. Rajan et al. (2019) performed a numerical analysis based on the floor slope of an OWC device, PTO damping effect, and incident wave conditions and further analyzed the hydrodynamic efficiency by calculating chamber pressure, free surface velocity, and free surface rise.
Iturrioz et al. (2015) modeled a fixed detached OWC using OpenFOAM and verified the model using the experimental data (IHCantabria’s OpenFOAM: IHFOAM) for free surface displacement, pheumatic pressure, and air veolcity. IHFOAM, which is used to fit interaction between waves and structures, was proposed by Higuera et al. (2013). Furthermore, actual wave conditions were simulated using active wave absorption at the boundary and the simulation speed was increased by reducing the computational domain. Vyzikas et al. (2017b) compared the results of the multiphase RANS numerical model with the COAST experimental results of Plymouth University (UK) to simulate the interaction of the OWC under regular and irregular wave conditions.
Studies are actively being conducted using Fluent and Star-CCM+, which are commercial CFD codes. The results of conducting studies on OWC using Fluent are mentioned hereafter. Marjani et al. (2008) performed a simulation on flow characteristics inside a chamber by modeling a chamber and impulse turbine. Teixeira et al. (2013) investigated the optimal performance of an OWC installed onshore based on the relationship between chamber shape and turbine characteristics; the Fluinco model, which handles incompressible flow problems based on the Navier–Stokes equations, was used with the two-step semi-implicit Taylor–Galerkin method. Similar results were obtained by comparing the flow variables acquired from Fluinco with the results of a commercial model—Fluent. Luo et al. (2014) developed a 2D fully nonlinear CFD model and analyzed the efficiency of a fixed OWC equipped with a linear PTO. They confirmed that the optimal pneumatic damping coefficient of an OWC is dependent on the incident wave height, and the hydrodynamic extraction of an OWC device rather decreases as the wave height increases in the nonlinear wave condition. Therefore, the hydrodynamic system of an OWC is fully nonlinear, which cannot be accurately represented with the superposition of linear responses.
The following studies used Star-CCM+. López et al. (2014) implemented a 2D numerical model based on the RANS equations and the volume of fluid (VOF) technique for the analysis of the turbine and chamber and verified the calculation results by comparing them with the wave tank experimental results. The damping coefficients of various turbines were computed using the verified numerical model, and the OWC efficiency was calculated under regular and irregular wave conditions. Moreover, López et al. (2016) developed a method for determining a damping coefficient that optimizes the OWC performance using a 2D RANS-VOF numerical model. The comprehensive performance of an OWC was calculated by determining the optimal turbine damping coefficient for the impulse turbine model in a real sea environment (A Guarda Port in Spain). Elhanafi et al. (2016) verified the numerical model by comparing the water surface displacement inside a chamber of the OWC with the wave tank experiment results using the fully nonlinear 2D RANS model and confirmed that the PTO damping coefficient and increase in the wave height play key roles in the generation of the vortex at the chamber inlet. In a subsequent study (Elhanafi et al., 2017), the RANS-VOF numerical model was used to investigate the effects of air compression on the OWC performance in the models, whose size scale ranged from 1:50 to actual size. Dai et al. (2019) compared the experimental results of two small- and large-wave tanks with the CFD calculation results to identify whether the hydrodynamic scale effect can be reproduced based on the CFD analysis and confirmed that the Reynolds number has a major impact.
Several studies on a multi-chamber OWC or the alteration in sea floors have been reported. Rezanejad et al. (2019) created sea floor stepped bottom at the chamber front to improve the efficiency of an OWC device using OpenFOAM and compared the results with the wave tank experiment for verification. Energy extraction and flow pattern characteristics around the floor step were presented based on the CFD analysis results. Mohapatra and Sahoo (2020) analyzed the effects of sea floor steps on the hydrodynamic performance of the OWC using Fluent. A PTO device was modeled using a porous zone to demonstrate the characteristics of an actual air turbine. The performance of an OWC was improved when the floor step was present, which corresponds to the results of one of the previous studies (Rezanejad et al., 2013) conducted using the BIEM. Shalby et al. (2019) developed an incompressible 3D CFD model for simulating a fixed multi-chamber OWC using Star-CCM+ and compared its results with the results of a wave tank experiment conducted at a 1:25 scale. A PTO system possessing an intermediate level of damping has the maximum Capture width ratio (CWR) in most periods excluding long waves.
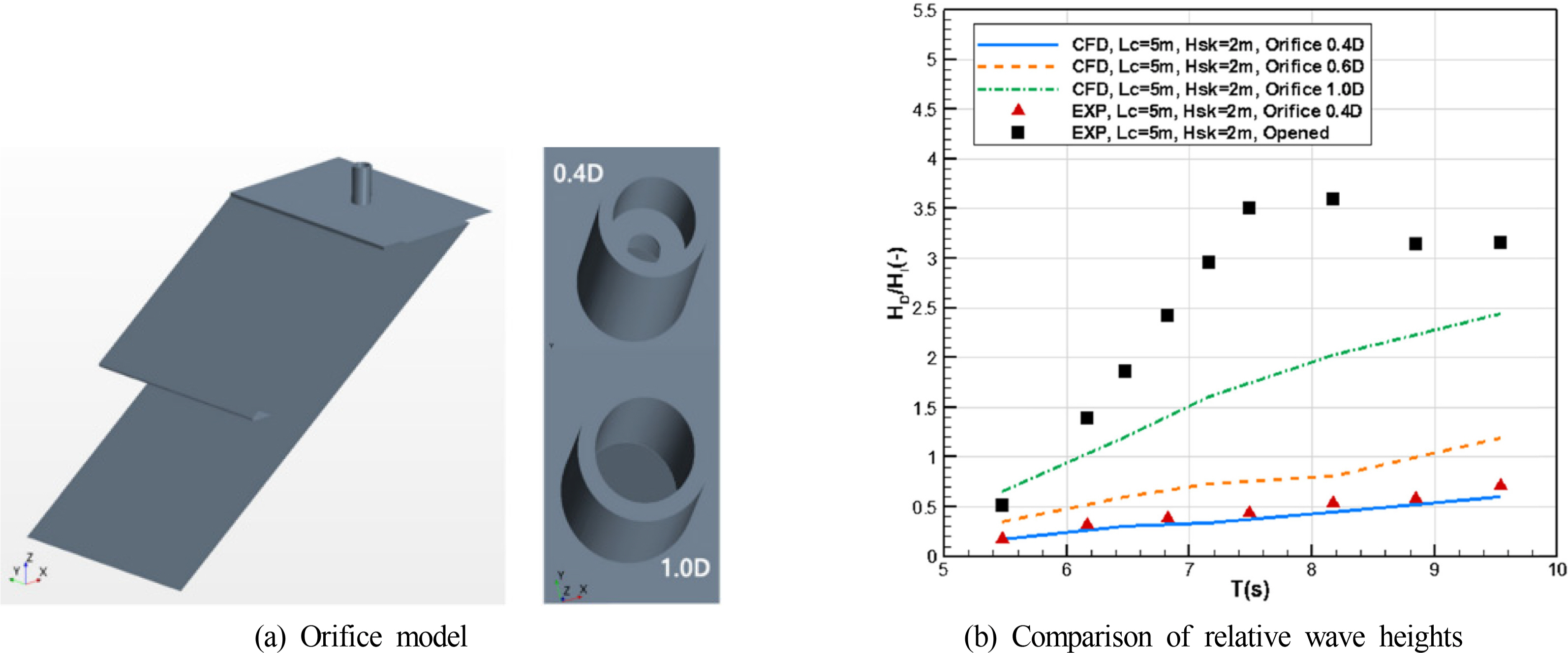
Mahnamfar and Altunkaynak (2017) created a model considering various inclined angles (30°–47°) using FLOW 3D and compared the results with those of the wave tank experiment based on the Nash–Sutcliffe coefficient of efficiency as a performance evaluation measure. Park et al. (2018a) verified the reliability of the CFD analysis method by comparing the open chamber of an inclined OWC and the chamber model comprising an orifice against the 2D wave tank experiment results using Star-CCM+ (Fig. 9). The turbine effect was considered for the model with an orifice, and therefore, the wave elevation inside the chamber was decreased. Gaspar et al. (2020) used Fluent to compare a vertical chamber and a 40°-inclined chamber of OWC. The PTO system considered the Wells turbine, and the incident wave generation scheme considering active absorption was applied. The numerical analysis demonstrated that run-up/-down and sloshing occurred more evidently and the energy efficiency was higher in peak periods inside the inclined chamber. In a vertical chamber condition, the changes in energy extraction efficiency according to incident wave periods were not significantly high.
Liu et al. (2009a; 2009b) verified the integrated analysis of the interaction among the OWC, air chamber, and impulse turbine using an orifice model through CFD. A numerical wave tank was built based on the two-phase VOF model for generating 3D incident waves. The parameters affecting the energy conversion efficiency and performance of the WEC system, e.g., incident wave period, wave height, water depth, and duct diameter, were examined, and the results were compared with the results of the experiment conducted using a 50 m x 0.8 m x 1.2 m (length, width, and depth) wave tank. Bouali and Larbi (2017) used the commercially available CFX program to develop a numerical wave tank of the 3D fully nonlinear RANS-VOF model and developed the sequential optimization procedure for major parameters, e.g., PTO damping, structural characteristics, and incident wave conditions for the optimization of an OWC. Zhang et al. (2012) developed a numerical technique based on the 2D two-phase model using the level-set immersed boundary method to analyze the water surface displacement and pneumatic pressure of the flow field inside the chamber. Table 2 provides the comparison of CFD codes and OWC model types used in the previous studies mentioned in this paper.
Studies have been actively conducted on U-OWC, in which a U-shaped U-OWC is developed by installing a structure in front of the chamber for enhancing energy extraction efficiency and water surface displacement inside the OWC chamber. The concept of the U-OWC was first proposed by Boccotti (2003). Boccotti (2007a) compared U-OWC and conventional OWC and confirmed that the amplitude of pressure variation inside the chamber increases while the natural period of water surface displacement inside the chamber extends in the U-OWC. Then, it was confirmed that the performance of U-OWC is outstanding under small- and large-wave conditions. Boccotti (2007b) performed a theoretical analysis of the OWC installed on the caisson breakwater (Fig. 10). Boccotti et al. (2007) conducted an experiment on U-OWC for a 1:10 scaled model on the east coast of the Strait of Messina and compared the results with the theoretical results of Boccotti (2007b).
Strati et al. (2016) introduced the first real-sea-area U-OWC prototype (2.7 MW) installed at the Civitavecchia Port in Rome, Italy, and studied the optimization of the extraction performance of the U-OWC equipped with the Wells turbine by controlling the turbine under various incident wave conditions (Fig. 11). Arena et al. (2013a) compared the wave conditions of Civitavecchia (Rome) and Pantelleria (Sicily), which are two Italian coasts suitable for installing a U-OWC prototype. In 2012, Arena et al. (2013b) explained the construction process and design of the U-OWC breakwater installed at the Civitavecchia Port.
Vyzikas et al. (2017a) compared the energy extraction efficiency by applying geometric revisions to the conventional vertical OWC and U-OWC proposed by Boccotti (2003) to propose an OWC having various sloped attachments (Fig. 12). Thus, it was confirmed that the performance of U-OWC was better than the conventional vertical OWC. Malara and Arena (2013) proposed a modeling process for a wave field that interacts with the U-OWC under random incident wave conditions based on a linear wave theory. The drawbacks of existing theoretical modeling were resolved, and a hydrodynamic memory effect, which was disregarded in the previous modeling process was included. Malara et al. (2017) attempted to verify the reliability of a mathematical model based on the unsteady Bernoulli equation to estimate the response of the U-OWC in the time domain. For such reason, an experiment was conducted at the Reggio Calabria coast in Italy, and the results were compared with numerical analysis results. Through this study, the Darcy-Weisbach-based chamber head loss model, which is traditionally used in a steady flow analysis, has a problem of over-prediction than the experiment. To overcome this limitation, the use of an instantaneous acceleration-based model including an abnormal head loss proportional to water column inertia was proposed. Ashlin et al. (2019) performed the response analysis of water surface displacement inside the U-OWC chamber using REEF3D, which is described as a 2D CFD numerical wave tank model. The RANS equations, k-omega turbulence model, and level-set free surface method were used. The calculation results matched those measured through wave tank experiments.
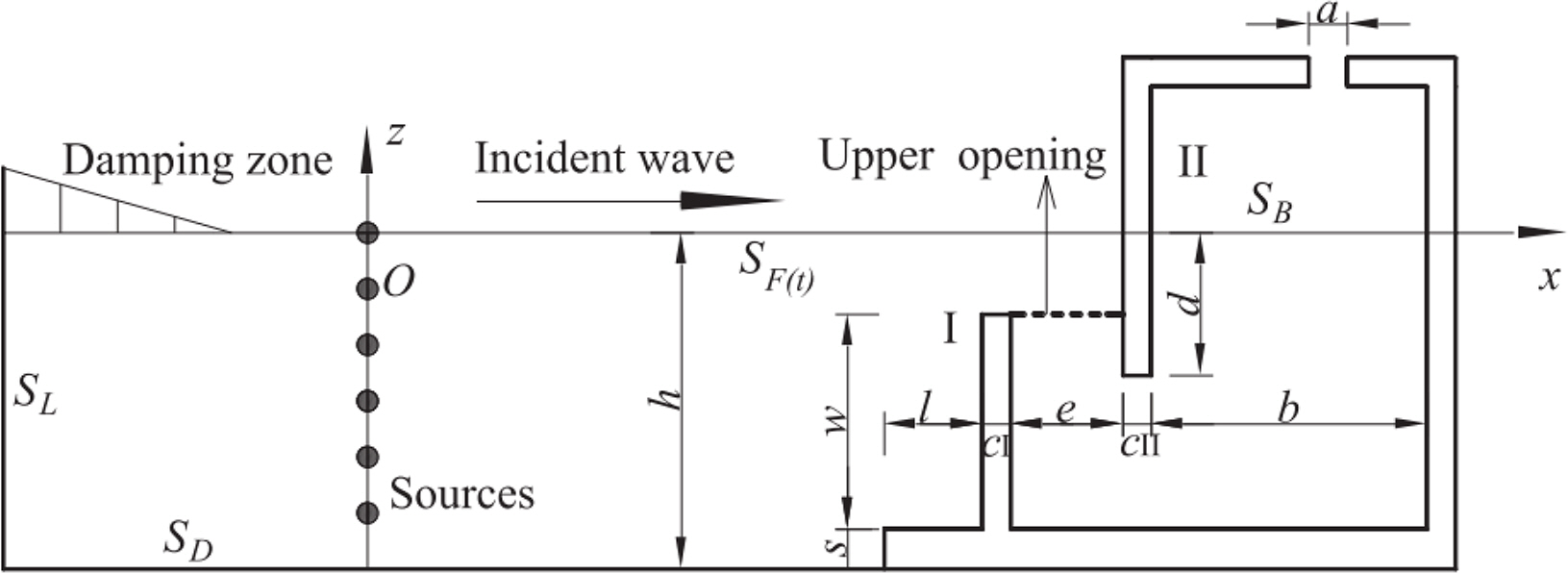
Ning et al. (2020) applied the U-OWC using a 2D fully nonlinear numerical model based on a high-order BEM and performed a geometric parameter analysis of structures, i.e., the height and width of a vertical duct in the time domain (Fig. 13). The calculation results agreed well with the published experimental results, in which the pneumatic pressure inside the chamber and hydrodynamic efficiency (I in Fig. 13) increased as the submerged vertical duct height and wall thickness increased. However, the efficiency gradually diminished as the wall thickness increased. Belibassakis et al. (2020) examined the performance of an OWC considering the interaction between the sea floor terrain of the installation area and incident waves using the BEM. The resonance period of the OWC chamber was adjusted by installing an additional vertical wall in front of the OWC, and the effects of other parameters, e.g., chamber size and depth changes. were explained. Furthermore, the possibility of installing an OWC at a coastal port in Romania with sufficient wave energy was confirmed. Tsai et al. (2018) calculated the OWC model linked with fixed breakwater using Fluent and verified the results by comparing them with the experimental results. They installed a perforated wall at the front section of an OWC to create a U-type flow for improving the energy extraction efficiency of an OWC and further proposed a new model capable of reducing a wave force applied to the skirt-shaped structure of an OWC.
Various studies on the verification of numerical analysis and experimental results for a fixed OWC WEC model and the establishment, installation, and operation of real-sea area models have been reported. First, Falnes (1993) installed the prototype of an initial OWC at Toftestallen in Norway (Fig. 14).
In 1999, Falcão (2000) installed a 400-kW OWC WEC operated using the Wells turbine on the coast of Pico Island in Portugal (Fig. 15). Two ducts were installed and connected in a series with a turbine for better stability.
Moreover, in 1999, Heath et al. (2000) installed a 500-kW land-installed marine power energy transmitter (LIMPET) OWC on Islay Island (Scotland) and reported the operation results (Fig. 16). LIMPET, which succeeds the 75-kW OWC prototype installed in the UK near the Islay Island, Scotland, in 1991 by Queen’s University of Belfast (QUB), was constructed to solve various problems arising prior to commercial development. LIMPET includes a rectangular inclined OWC having the maximum output of 500 kW, which induces air flows generated through two contra-rotating Wells turbines connected to a 250-kW induction generator.
Zhang et al. (2009) investigated the wave energy technology development in China and reported the wave energy development outlook (Fig. 17). In particular, a 100-kW OWC demonstration plant operated on the Zhelang coast in Shanwei, Guangdong, which was the only large-scale project that was integrated with the power grid in China at that time.
Torre-Enciso et al. (2009) reported the processes from the establishment of the breakwater-linked OWC concept in the Mutriku Port in northern Spain to project completion (Fig. 18). The Mutriku wave energy plant comprises 16 chambers, in which each upper opening is connected to a turbo generator set with a rate capacity of 18.5 kW, thus generating a total output of 296 kW. This plant was the first multi-chamber facility, and the first commercial project in which a technical company sold an energy converter to investors for commercial operations.
Kihara et al. (2019) installed a prototype of a projecting-wall OWC (PW-OWC) at the Sakata Port in Japan. The characteristics of the impulse turbine in constant airflow (Q) were identified, and the turbine size was found to be independent of the constant airflow (Q) and pressure difference (dP).
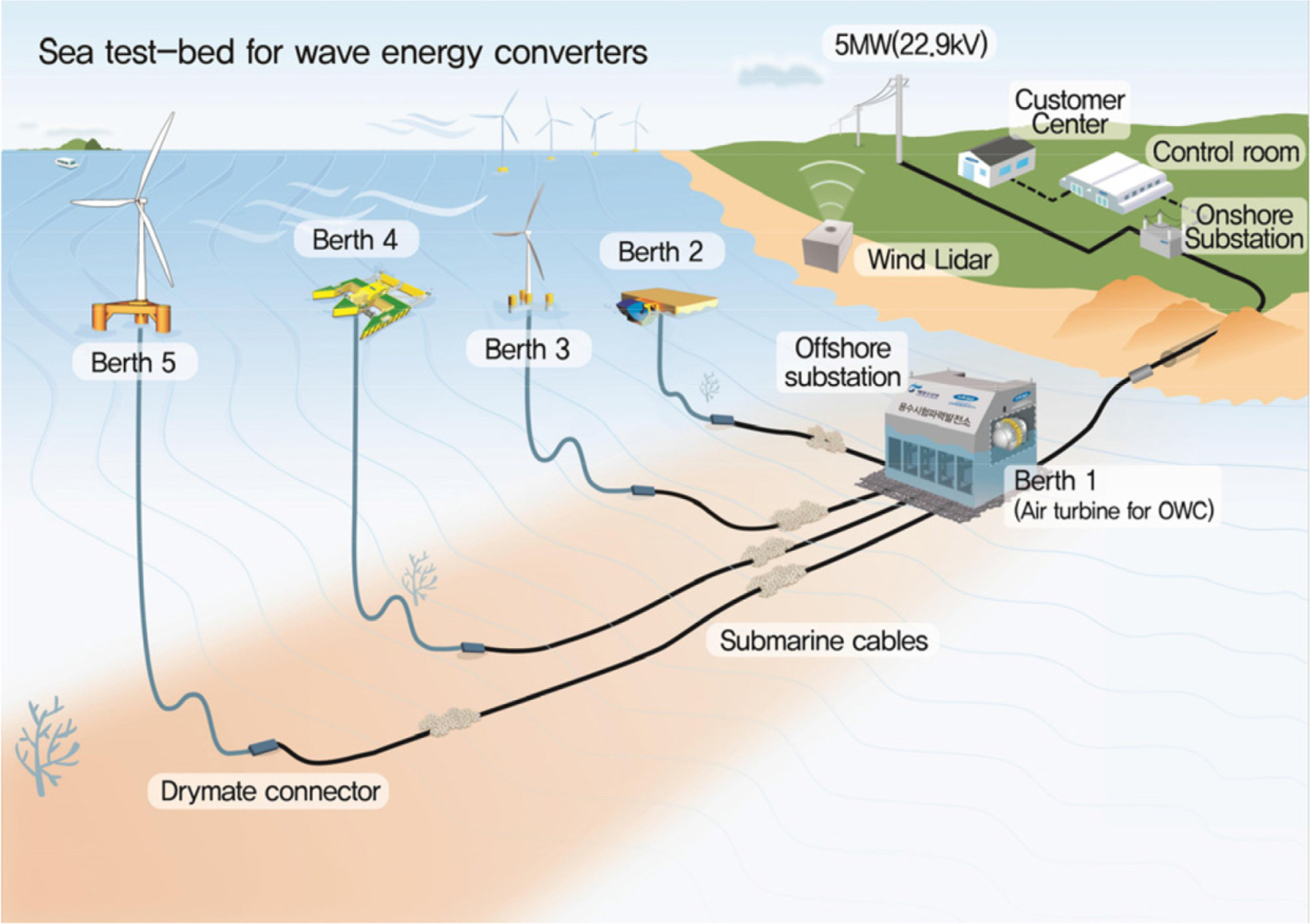
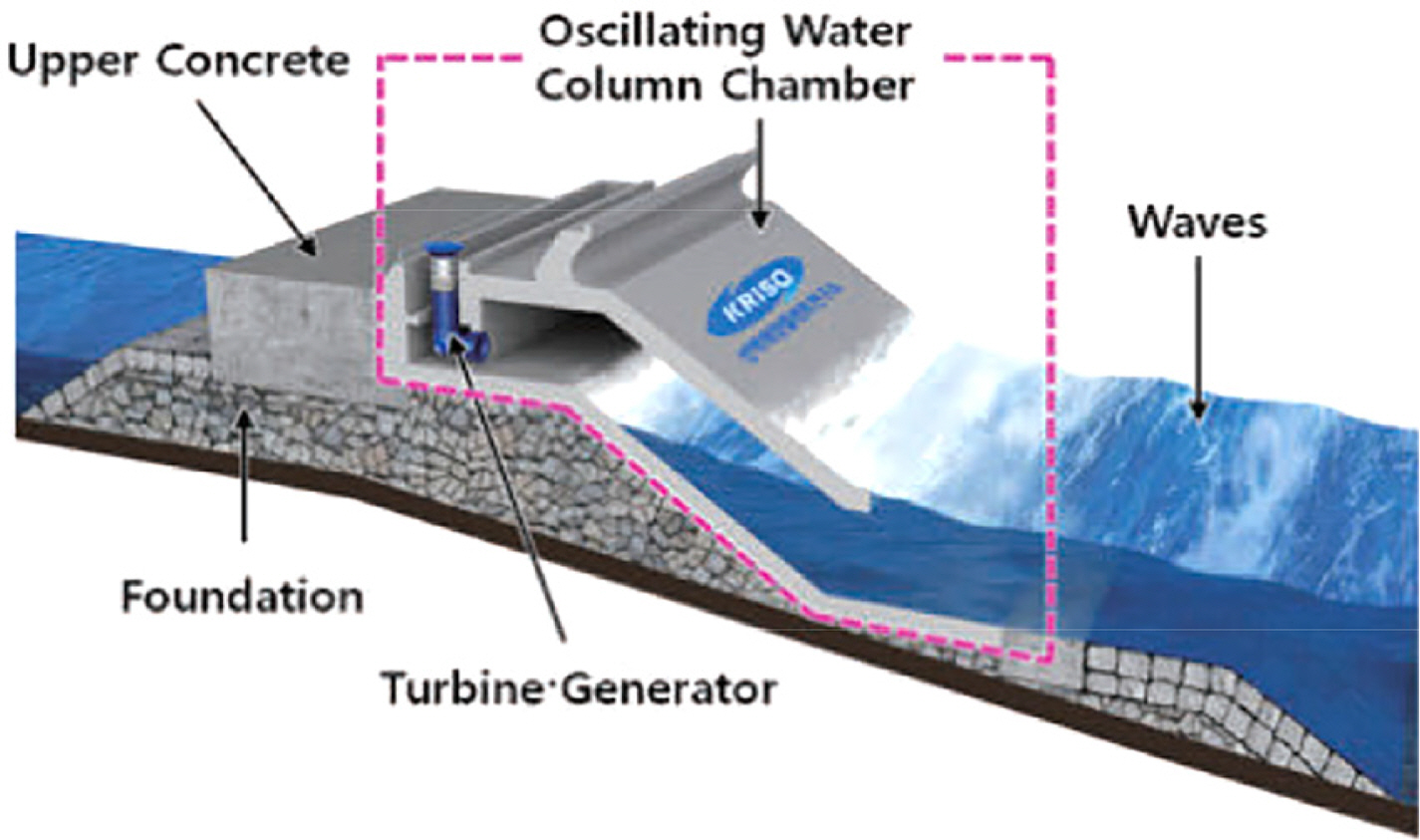
Research and experiments are actively conducted on real-sea WECs in Korea. Choi et al. (2018) reported that power is generated through a test operation of a 500-kW water wave energy plant, which is a pilot plant (before the construction of a prototype) (Fig. 19). Moreover, Supervisory Control and Data Acquisition (SCADA) comprising marine monitoring, facility monitoring, and environmental monitoring systems is in operation. The marine monitoring system controls ships, and the facility monitoring system remotely controls the electrical and mechanical devices of a marine substation. The environmental monitoring system collects weather and marine data.
Lim et al. (2021) reviewed the method for estimating a wave load applied to the front part of an OWC linked with breakwater, which will be installed at Mok-ri Port in Chujado Island, Jeju, Korea (Fig. 20). A wave load applied to the OWC structure installed at the front part of the inclined breakwater was estimated based on the port and fishing port design standards; the CFD-based numerical results were compared with the results of the wave pressure calculations or 2D model experimental results to examine the stability of the structure. Meanwhile, a 30-kW OWC WEC linked with breakwater in Chujado Island is associated with an energy storage system to be used in the island area, and the pilot operation of the prototype will continue until 2027.
This study focused on the primary energy conversion of a fixed OWC WEC and explained current R&D achievements in five research categories: (1) potential flow-based numerical analysis, (2) wave tank experiments, (3) CFD analyses considering fluid viscous effects, (4) U-OWC studies that can amplify water surface displacement in the OWC chamber, and (5) studies on OWC prototypes that have been installed and operated in real sea environments. Hence, the research achievements proposed in this study will provide basic research informations for researchers planning to conduct detailed research on an OWC WEC. However, there are research achievements that have been omitted or missing owing to time and space constraints to investigate and describe all the related studies. In particular, the secondary energy conversion of a WEC will be further discussed in future studies. Therefore, readers are advised to keep this in mind while reviewing the content of this paper.
Conflict of Interest
Weoncheol Koo serves as an editor of the Journal of Ocean Engineering and Technology but has no role in the decision to publish this article. No potential conflict of interest relevant to this article was reported.
Notes
This research was funded and conducted under 「the Competency Development Program for Industry Specialists」 of the Korean Ministry of Trade, Industry and Energy (MOTIE), operated by Korean Institute for Advancement of Technology (KIAT) (No. P0012646, HRD program for Global Advanced Engineer Education Program for Future Ocean Structures).
Fig. 4.
Schematic of a sloped OWC system and comparison of each energy component (Yang et al., 2021)
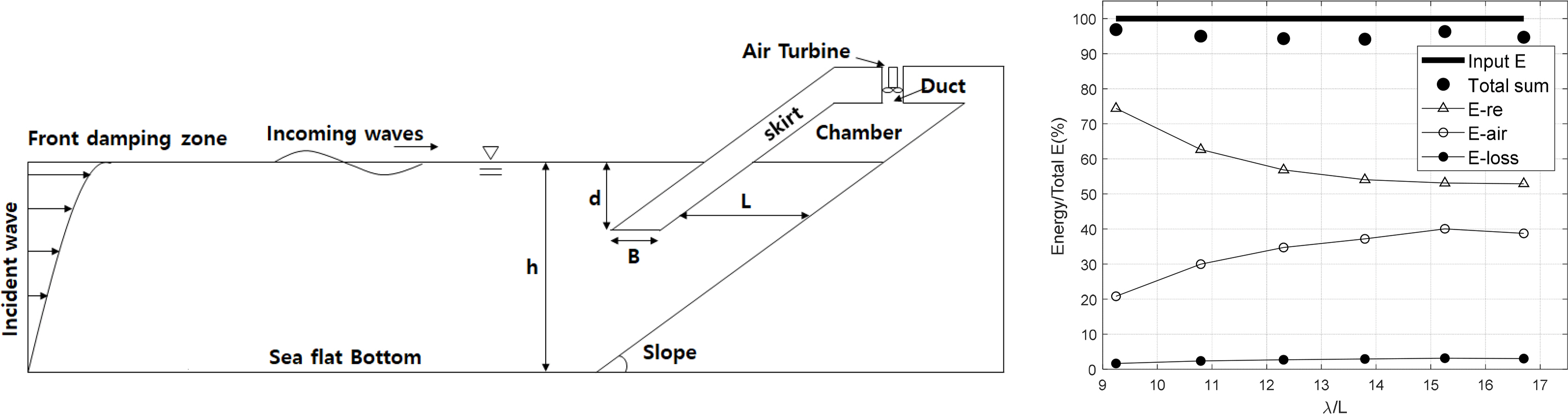
Fig. 7.
Experimental models installed in the 2D wave flume and measured relative wave heights (Park et al., 2018b)

Fig. 8.
List of damping values and hydrodynamic efficiency with a constant wave height H = 0.06 (Kamath et al., 2015)
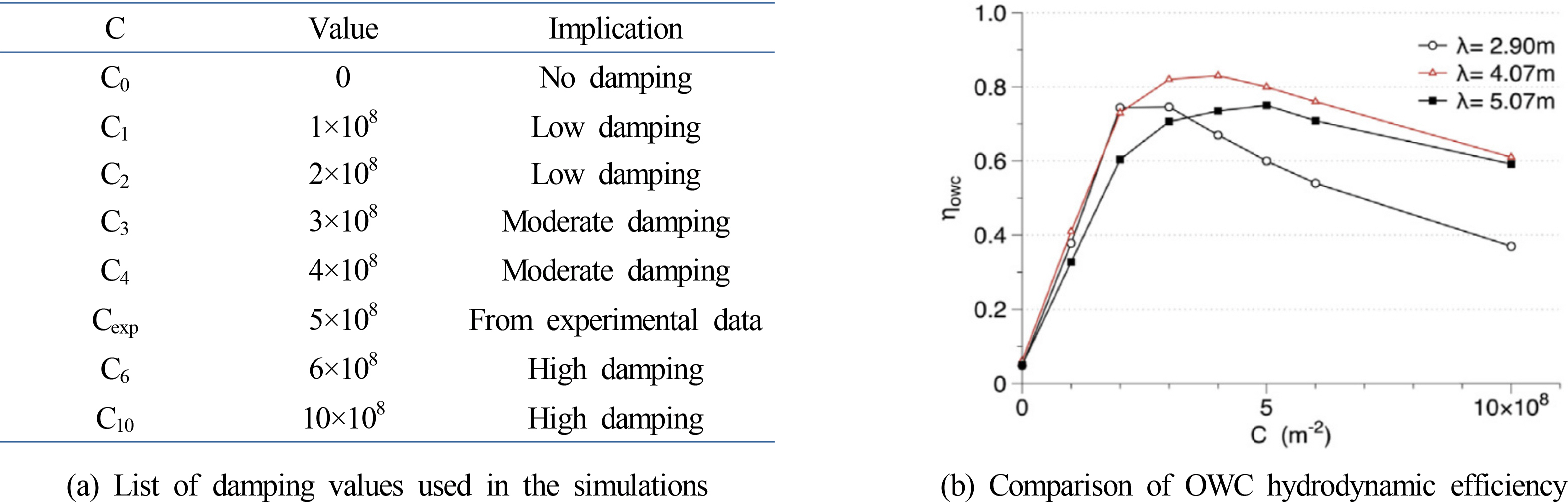
Fig. 16.
5500 KW OWC (LIMPET) installed on the coast of the Scottish island of Islay (Heath et al., 2000)

Table 1.
Comparisons of the reference(Potential flow)
| Reference | Computational method | Chamber type |
|---|---|---|
| Koo and Kim (2010) | BEM | Vertical chamber |
| Kim et al. (2021a) | BEM | Vertical chamber |
| Liu et al. (2010) | DBIEM | Vertical chamber |
| Ning et al. (2015) | HOBEM | Vertical chamber |
| Wang et al. (2018) | HOBEM | Vertical chamber |
| Rezanejad et al. (2013) | Matched eigenfunction expansion, BIEM | Stepped sea bottom |
| Rezanejad et al. (2015) | Matched eigenfunction expansion, BIEM | Stepped sea bottom, Dual-chamber |
| Koirala et al. (2015) | BEM | Dual-chamber |
| Kim et al. (2020) | FEM | Sloped chamber |
| Kim et al. (2021b) | FEM | Sloped chamber |
| Yang et al. (2021) | BEM | Sloped chamber |
Table 2.
Comparison among previous studies with regard to the CFD analysis
| Reference | CFD code | OWC Type |
|---|---|---|
| Kamath et al. (2015) | REEF3D | Vertical chamber |
| Iturrioz et al. (2015) | OpenFOAM | Vertical chamber |
| Teixeira et al. (2013) | Fluent | Vertical chamber |
| López et al. (2014) | Star-CCM+ | Vertical chamber |
| Rezanejad et al. (2019) | OpenFOAM | Stepped sea bottom |
| Mohapatra and sahoo (2020) | Fluent | Stepped sea bottom |
| shalby et al. (2019) | Star-CCM+ | Multi-chamber |
| Mahnamfar and Altunkaynak (2017) | FLOW 3D | Sloped chamber |
| Park et al. (2018a) | Star-CCM+ | Sloped chamber |
| Gaspar et al. (2020) | Fluent | Sloped chamber |
References
Allsop, W., Bruce, T., Alderson, J., Ferrante, V., Russo, V., Vicinanza, D., & Kudella, M. (2014). Large Scale Tests on a Generalised Oscillating Water Column Wave Energy Converter. Proceedings of the Hydralab IV Joint User Meeting. Lisbon.
Arena, F., Fiamma, V., Laface, V., Malara, G., Romolo, A., Viviano, A., & Carillo, A. (2013a). Installing U-OWC Devices Along the Italian Coasts. Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering. Nantes: France. V008T09A061. https://doi.org/10.1115/OMAE2013-10928

Arena, F., Malara, G., Romolo, A., & Ascanelli, A. (2013b). On Design and Building of a U-OWC Wave Energy Converter in the Mediterranean Sea: A Case Study. Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering. Nantes: France. V008T09A102. https://doi.org/10.1115/OMAE2013-11593

Ashlin, SJ., Sannasiraj, S.A., Sundar, V.., Malara, G.., Arena, F., & Romolo, A. (2019). Numerical Validation of Hydrodynamic Characteristics of Open-sea U-type Oscillating Water Column Wave Energy Converter. Advances in Renewable Energies Offshore - Proceedings of the 3rd International Conference on Renewable Energies Offshore. London. p 569-577.
Belibassakis, K., Magkouris, A., & Rusu, E. (2020). A BEM for the Hydrodynamic Analysis of Oscillating Water Column Systems in Variable Bathymetry. Energies, 13(13), 3403.
https://doi.org/10.3390/en13133403

Boccotti, P. (2003). On a New Wave Energy Absorber. Ocean Engineering, 30, 1191-1200.
https://doi.org/10.1016/S0029-8018(02)00102-6

Boccotti, P. (2007a). Comparison Between a U-OWC and a Conventional OWC. Ocean Engineering, 34(5‒6), 799-805.
https://doi.org/10.1016/j.oceaneng.2006.04.005

Boccotti, P. (2007b). Caisson Breakwaters Embodying an OWC with a Small Opening-Part I: Theory. Ocean Engineering, 34(5‒6), 806-819.
https://doi.org/10.1016/j.oceaneng.2006.04.006

Boccotti, P., Filianoti, P., Fiamma, V., & Arena, F. (2007). Caisson Breakwaters Embodying an OWC with a Small Opening-Part II: A Small-scale Field Experiment. Ocean Engineering, 34, 820-841.
https://doi.org/10.1016/j.oceaneng.2006.04.016

Bouali, B., & Larbi, S. (2017). Sequential Optimization and Performance Prediction of an Oscillating Water Column Wave Energy Converter. Ocean Engineering, 131, 162-173.
https://doi.org/10.1016/j.oceaneng.2017.01.004

Choi, JS., Lee, J., Lim, CH., Ko, TK., Park, JY., Kim, K., & Cho, IH. (2018). Status for Development of the Open Sea Test Site for Wave Energy Converters in Korea. Retrieved April 2022 from https://tethys-engineering.pnnl.gov/sites/default/files/publications/AWTEC2018-446.pdf
Dai, S., Day, S., Yuan, Z., & Wang, H. (2019). Investigation on the Hydrodynamic Scaling Effect of an OWC Type Wave Energy Device Using Experiment and CFD Simulation. Renewable Energy, 142(2019), 184-194.
https://doi.org/10.1016/j.renene.2019.04.066

Delauré, YMC., & Lewis, A. (2003). 3D hydrodynamic Modelling of Fixed Oscillating Water Column Wave Power Plant by a Boundary Element Methods. Ocean Engineering, 30, 309-330.
https://doi.org/10.1016/S0029-8018(02)00032-X

Dizadji, N., & Sajadian, SE. (2011). Modeling and Optimization of the Chamber of OWC System. Energy, 36(5), 2260-2366.
https://doi.org/10.1016/j.energy.2011.01.010

Elhanafi, A., Fleming, A., Macfarlane, G., & Leong, Z. (2016). Numerical Energy Balance Analysis for an Onshore Oscillating Water Column-wave Energy Converter. Energy, 116, 539-557.
https://doi.org/10.1016/j.energy.2016.09.118

Elhanafi, A., Gregor, M., Fleming, A., & Leong, Z. (2017). Scaling and Air Compressibility Effects on a Three-dimensional Offshore Stationary OWC Wave Energy Converter. Applied Energy, 189, 1-20.
https://doi.org/10.1016/j.apenergy.2016.11.095

Evans, DV. (1978). The Oscillating Water Column Wave-energy Device. IMA Journal of Applied Mathematics, 22, 4 423-433.
https://doi.org/10.1093/imamat/22.4.423

Falcão, A.F.O., & Henriques, JCC. (2016). Oscillating-water-column Wave Energy Converters and Air Turbines: A Review. Renewable Energy, 85, 1391-1424.
https://doi.org/10.1016/j.renene.2015.07.086

Falcão, AFO. (2000). The Shoreline OWC Wave Power Plant at the Azores. Proceedings of the 4th European Wave Energy Conference. Aalborg Denmark. p 42-47.
Falnes, J. (1993). Research and Development in Ocean-Wave Energy in Norway. In Proceedings of the International Symposium on Ocean Energy Development. Hokkaido: Japan. p 27-39.
Gaspar, LA., Teixeira, PRF., & Didier, E. (2020). Numerical Analysis of the Performance of Two Onshore Oscillating Water Column Wave Energy Converters at Different Chamber Wall Slopes. Ocean Engineering, 201, 107119.
https://doi.org/10.1016/j.oceaneng.2020.107119

Gouaud, F., Rey, V., Piazzola, J., & Van Hooff, R. (2010). Experimental Study of the Hydrodynamic Performance of an Onshore Wave Power Device in the Presence of an Underwater Mound. Coastal Engineering, 57(11–12), 996-1005.
https://doi.org/10.1016/j.coastaleng.2010.06.003

Heath, T., Whittaker, TJT., & Boake, CB. (2000). The Design, Construction and Operation of the LIMPET Wave Energy Converter (Islay, Scotland). Proceedings of the 4th European Wave Energy Conference. Aalborg Denmark. p 49-55.
Higuera, P., Lara, JL., & Losada, IJ. (2013). Realistic Wave Generation and Active Wave Absorption for Navier–Stokes Models: Application to OpenFOAM®. Coastal Engineering, 71, 102-118.
https://doi.org/10.1016/j.coastaleng.2012.07.002

Ikoma, T., Masuda, K., Eto, H., & Shibuya, S. (2019). Basic Characteristics of the Primary Conversion of an Oscillating Water Column Type Wave Energy Converter Installed on a Wave-Dissipating Double Caisson. Journal of Offshore Mechnics and Arctic Engineering, 141(6), 061902.
https://doi.org/10.1115/1.4042943

Iturrioz, A., Guanche, R., Lara, JL., Vidal, C., & Losada, IJ. (2015). Validation of OpenFOAM® for Oscillating Water Column Three-dimensional Modeling. Ocean Engineering, 107, 222-236.
https://doi.org/10.1016/j.oceaneng.2015.07.051

Josset, C., & Clément, AH. (2007). A Time-Domain Numerical Simulator for Oscillating Water Column Wave Power Plants. Renewable Energy, 32, 1379-1402.
https://doi.org/10.1016/j.renene.2006.04.016

Kamath, A., Bihs, H., & Arntsen Ф, A. (2015). Numerical Modeling of Power Take-off Damping in an Oscillating Water Column Device. International Journal of Marine Energy, 10, 1-16.
https://doi.org/10.1016/j.ijome.2015.01.001

Kihara, K., Hosokawa, Y., Masuda, K., & Ikoma, T. (2019). A Practical Estimation Method of PTO and a Sea Test of a PW-OWC Type Wec Using a Wave Dissipating Double Caisson. Advances in Renewable Energies Offshore. London. p 531-538.
Kim, DM., Min, EH., & Koo, W. (2021a). Numerical Study on the Optimal Shape and Performance of an Oscillating Water Column Using Analytic Air Damping Coefficients and Numerical Wave Tank. Journal of The Korean Society for Marine Environment & Energy, 24(1), 1-8.
https://doi.org/110.7846/JKOSMEE.2021.24.1.1

Kim, J.-S.., Nam, B.W.., Kim, K.-H.., Park, S.., Shin, S.H.., & Hong, K. (2020). A Numerical Study on Hydrodynamic Performance of an Inclined OWC Wave Energy Converter with Nonlinear Turbine–Chamber Interaction Based on 3D Potential Flow. Journal of Marine Science and Engineering, 8, 176.
https://doi.org/10.3390/jmse8030176

Kim, J.-S., Kim, K.-H., Park, J., Park, S., & Shin, SH. (2021b). A Numerical Study on Hydrodynamic Energy Conversions of OWC-WEC with the Linear Decomposition Method under Irregular Waves. Energies, 14(6), 1522.
https://doi.org/10.3390/en14061522

Koirala, P., Nagata, S., Imai, Y., Murakami, T., & Setoguchi, T. (2015). Numerical Analysis of Primary Conversion Efficiency of Oscillating Water Columns with Multiple Chambers. Procedia Engineering, 105, 568-600.
https://doi.org/10.1016/j.proeng.2015.05.036

Koo, W., & Kim, MH. (2010). Nonlinear Time-Domain Simulation of a Land-Based Oscillating Water Column. Journal of Waterway, Port, Coastal, and Ocean Engineering, 136(5), 276-285.
https://doi.org/10.1061/(ASCE)WW.1943-5460.0000051

Koo, W., Kwon, JS., Kim, JD., Kim, SJ., Kim, MW., & Choi, MK. (2012). Experimental Study of Shape Parameter of Land-Based OWC Wave Energy Converter. Journal of Ocean Engineering and Technology, 26(3), 33. ‒38. https://doi.org/10.5574/KSOE.2012.26.3.033

Lim, CH., Shin, S., Park, S., Kim, KH., Oh, JH., Kim, GY., & Nam, JS. (2021). A Study on the Estimation of the Wave Load on the Structure of wave Energy Converter connected to Rubble-Mound Breakwater. Journal of the Korean Society for Marine Environment & Energy, 24(4), 179-190.
https://doi.org/10.7846/JKOSMEE.2021.24.4.179

Lim, CH., Shin, S., Park, S., Kim, KH., Oh, JH., Kim, GY., & Nam, JS. (2021). A study on the Estimation of the Wave Load on the Structure of wave Energy Converter connected to Rubble-Mound Breakwater. Journal of the Korean Society for Marine Environment & Energy, 24(4), 179-190.
https://doi.org/10.7846/JKOSMEE.2021.24.4.179

Liu, C., Huang, Z., Keung, ALW., & Geng, N. (2010). A Numerical Study of Wave Energy Converter in the Form of an Oscillating Water Column Based on a Mixed Eulerian-Lagrangian Formulation. Proceedings of the ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, China. p 589-596.
https://doi.org/10.1115/OMAE2010-21056

Liu, Z., Hyun, BS., Hong, KY., & Lee, Y. (2009a). Investigation on Integrated System of Chamber and Turbine for OWC Wave Energy Convertor. Proceedings of 19th International Offshore and Polar Engineering Conference. Osaka: Japan. ISOPE-I-09-050.
Liu, Z., Shi, H., & Hyun, B. (2009b). Practical Design and Investigation of the Breakwater OWC Facility in China. Proceedings of the 8th European Wave and Tidal Energy Conference. Uppsala: Sweden. p 304-308.
López, I., Castro, A., & Iglesias, G. (2015). Hydrodynamic Performance of an Oscillating Water Column Wave Energy Converter by Means of Particle Imaging Velocimetry. Energy, 83, 89-103.
https://doi.org/10.1016/j.energy.2015.01.119

López, I., Pereiras, B., Castro, F., & Iglesias, G. (2014). Optimization of Turbine-Induced Damping for an OWC Wave Energy Converter Using a RANS-VOF Numerical Model. Applied Energy, 127, 105-114.
https://doi.org/10.1016/j.apenergy.2014.04.020

López, I., Pereiras, B., Castro, F., & Iglesias, G. (2016). Holistic Performance Analysis and Turbine-Induced Damping for an OWC Wave Energy Converter. Renewable Energy, 85, 1155-1163.
https://doi.org/10.1016/j.renene.2015.07.075

Luo, Y., Nader, JR., Cooper, P., & Zhu, SP. (2014). Nonlinear 2D Analysis of the Efficiency of Fixed Oscillating Water Column Wave Energy Converters. Renewable Energy, 64, 255-265.
https://doi.org/10.1016/j.renene.2013.11.007

Mahnamfar, F., & Altunkaynak, A. (2017). Comparison of Numerical and Experimental Analyses for Optimizing the Geometry of OWC Systems. Ocean Engineering, 130, 10-24.
https://doi.org/10.1016/j.oceaneng.2016.11.054

Malara, G., & Arena, F. (2013). Analytical Modelling of an U-Oscillating Water Column and Performance in Random Waves. Renewable Energy, 60, 116-126.
https://doi.org/10.1016/j.renene.2013.04.016

Malara, G., Romolo, A., Fiamma, V., & Arena, F. (2017). On the Modelling of Water Column Oscillations in U-OWC Energy Harvesters. Renewable Energy, 101, 964-972.
https://doi.org/10.1016/j.renene.2016.09.051

Marjani, AE., Ruiz, RC., Rodriguez, MA., & Santos, MTP. (2008). Numerical Modelling in Wave Energy Conversion Systems. Energy, 33, 1246-1253.
https://doi.org/10.1016/j.energy.2008.02.018

Masuda, Y., & Miyazaki, T. (1978). Wave Power Electric Generation Study in Japan. Proceedings of International Symposium on Wave and Tidal Energy. Canterbury; England: B6-85-B6-92.
Mohapatra, P., & Sahoo, T. (2020). Hydrodynamic Performance Analysis of a Shore Fixed Oscillating Water Column Wave Energy Converter in the Presence of Bottom Variations. Journal of Engineering for the Maritime Environment, 234(1), 37-47.
https://doi.org/10.1177/1475090219864833

Ning, DZ., Guo, BM., Wang, RQ., Vyzikas, T., & Greaves, D. (2020). Geometrical Investigation of a U-Shaped Oscillating Water Column Wave Energy Device. Applied Ocean Research, 97, 102-105.
https://doi.org/10.1016/j.apor.2020.102105

Ning, DZ., shi, J., Zou, QP., & Teng, B. (2015). Investigation of Hydrodynamic Performance of an OWC (Oscillating Water Column) Wave Energy Device Using a Fully Nonlinear HOBEM (Higher-Order Boundary Element Method). Energy, 83, 177-188.
https://doi.org/10.1016/j.energy.2015.02.012

Ning, DZ., Wang, RQ., Zou, QP., & Teng, B. (2016). An Experimental Investigation of Hydrodynamics of a Fixed OWC Wave Energy Converter. Applied Energy, 168, 636-648.
https://doi.org/10.1016/j.apenergy.2016.01.107

Park, JY., Baek, H., Shim, H., & Choi, JS. (2020). Preliminary Investigation for Feasibility of Wave Energy Converters and the Surrounding Sea as Test-Site for Marine Equipment. Journal of Ocean Engineering and Technology. 34(5), 351-360.
https://doi.org/10.26748/KSOE.2020.011

Park, S., Kim, KH., Nam, BW., Kim, JS., & Hong, K. (2018a). A Study on the Performance Evaluation of the OWC WEC Applicable to Breakwaters using CFD. The Korean Society for Marine Environment & Energy, 21(4), 317-327.

Park, S., Nam, BW., Kim, KH., & Hong, K. (2018b). Parametric Study on Oscillating Water Column Wave Energy Converter Applicable to Breakwater. Journal of Advanced Research in Ocean Engineering, 4(2), 66-77.
http://dx.doi.org/10.5574/JAROE.2018.4.2.066
Rajan, SN., Karmakar, D., & Guedes Soares, C. (2019). Influence of Damping on an Oscillating Water Column WEC Integrated with a Breakwater. Advances in Renewable Energies Offshore -Proceedings of the 3rd International Conference on Renewable Energies Offshore. London. p 579-587.
Rezanejad, K., & Guedes Soares, C. (2018). Enhancing the Primary Efficiency of an Oscillating Water Column Wave Energy Converter Based on a Dual-mass System Analogy. Renewable Energy, 123, 730-747.
https://doi.org/10.1016/j.renene.2018.02.084

Rezanejad, K., Bhattacharjee, J., & Guedes Soares, C. (2013). Stepped Sea Bottom Effects on the Efficiency of Nearshore Oscillating Water Column Device. Ocean Engineering, 701, 25-38.
https://doi.org/10.1016/j.oceaneng.2013.05.029

Rezanejad, K., Bhattacharjee, J., & Guedes Soares, C. (2015). Analytical and Numerical Study of Dual-Chamber Oscillating Water Columns on Stepped Bottom. Renewable Energy, 75, 272-282.
https://doi.org/10.1016/j.renene.2014.09.050

Rezanejad, K., Gadelho, JFM., & Soares, CG. (2019). Hydrodynamic Analysis of an Oscillating Water Column Wave Energy Converter in the Stepped Bottom Condition Using CFD. Renewable Energy, 135, 1241-1259.
https://doi.org/10.1016/j.renene.2018.09.034

Rezanejad, K., Guedes Soares, C., López, I., & Carballo, R. (2017). Experimental and Numerical Investigation of the Hydrodynamic Performance of an Oscillating Water Column Wave Energy Converter. Renewable Energy, 106, 1-16.
https://doi.org/10.1016/j.renene.2017.01.003

Shalby, M., Elhanafi, A., Walker, P., & Dorrell, DG. (2019). CFD Modelling of a Small-Scale Fixed Multi-chamber OWC Device. Applied Ocean Research, 88, 37-47.
https://doi.org/10.1016/j.apor.2019.04.003

Strati, FM., Malara, G., & Arena, F. (2016). Performance Optimization of a U-Oscillating-Water-Column Wave Energy Harvester. Renewable Energy, 99, 1019-1028.
https://doi.org/10.1016/j.renene.2016.07.080

Teixeira, PRF., Davyt, D.P., Didier, E., & Ramalhais, R. (2013). Numerical Simulation of an Oscillating Water Column Device Using a Code Based on Navier-Stokes Equations. Energy, 61(2013), 513-530.
https://doi.org/10.1016/j.energy.2013.08.062

Torre-Enciso, Y., Ortubia, I., López de Aguileta, LI., & Marqués, J. (2009). Mutriku Wave Power Plant: from the Thinking out to the Reality. Proceedings of 8th European Wave and Tidal Energy Conference. Uppsala: Sweden. p 319-329.
Tsai, CP., Ko, DH., & Chen, YC. (2018). Investigation on Performance of a Modified Breakwater-Integrated OWC Wave Energy Converter. Sustainability, 10(3), 643.
https://doi.org/10.3390/su10030643

Viviano, A., Naty, S., & Foti, E. (2018). Scale Effects in Physical Modelling of a Generalized OWC. Ocean Engineering, 162, 248-258.
https://doi.org/10.1016/j.oceaneng.2018.05.019

Vyzikas, T., Deshoulieres, S., Barton, M., Giroux, O., Greaves, D., & Simmonds, D. (2017a). Experimental Investigation of Different Geometries of Fixed Oscillating Water Column Devices for Wave Energy Generation. Renewable Energy. 104: p 248-258.
https://doi.org/10.1016/j.renene.2016.11.061

Vyzikas, T., Deshoulières, S., Giroux, O., Barton, M., & Greaves, D. (2017b). Numerical study of Fixed Oscillating Water Column with RANS-type Two-phase CFD Model. Renewable Energy, 102, 294-305.
https://doi.org/10.1016/j.renene.2016.10.044

Wang, DJ., Katory, M., & Li, YS. (2002). Analytical and Experimental Investigation on the Hydrodynamic Performance of Onshore Wave-power Devices. Ocean Engineering, 29(8), 871-885.
https://doi.org/10.1016/S0029-8018(01)00058-0

Wang, RQ., Ning, DZ., Zhang, CW., Zou, QP., & Liu, Z. (2018). Nonlinear and Viscous Effects on the Hydrodynamic Performance of a Fixed OWC Wave Energy Converter. Coastal Engineering, 131, 42-50.
https://doi.org/10.1016/j.coastaleng.2017.10.012

Yang, HJ., Min, EH., & Koo, W. (2021). Numerical Analysis of Wave Energy Extraction Performance According to the Body Shape and Scale of the Breakwater-integrated Sloped OWC. Journal of Ocean Engineering and Technology, 35(4), 296-304.
https://doi.org/10.26748/KSOE.2021.020

Zhang, D., Li, W., & Lin, Y. (2009). Wave Energy in China: Current Status and Perspectives. Renewable Energy, 34(10), 2089-2092.
https://doi.org/10.1016/j.renene.2009.03.014

Zhang, Y., Zou, QP., & Greaves, D. (2012). Air-Water Two-Phase Flow Modeling of Hydrodynamic Performance of an Oscillating Water Column Device. Renewable Energy, 41, 159-170.
https://doi.org/10.1016/j.renene.2011.10.011

- TOOLS
-
METRICS

-
- 1 Crossref
- Scopus
- 3,481 View
- 163 Download
- Related article in JOET
-
Experimental Study of Shape Parameter of Land-based OWC Wave Energy Converter2012 June;26(3)