Nomenclature
O ŌĆō xyz: Earth-fixed coordinate
o ŌĆō xbybzb: Body-fixed coordinate
U: Vehicle speed (m/s)
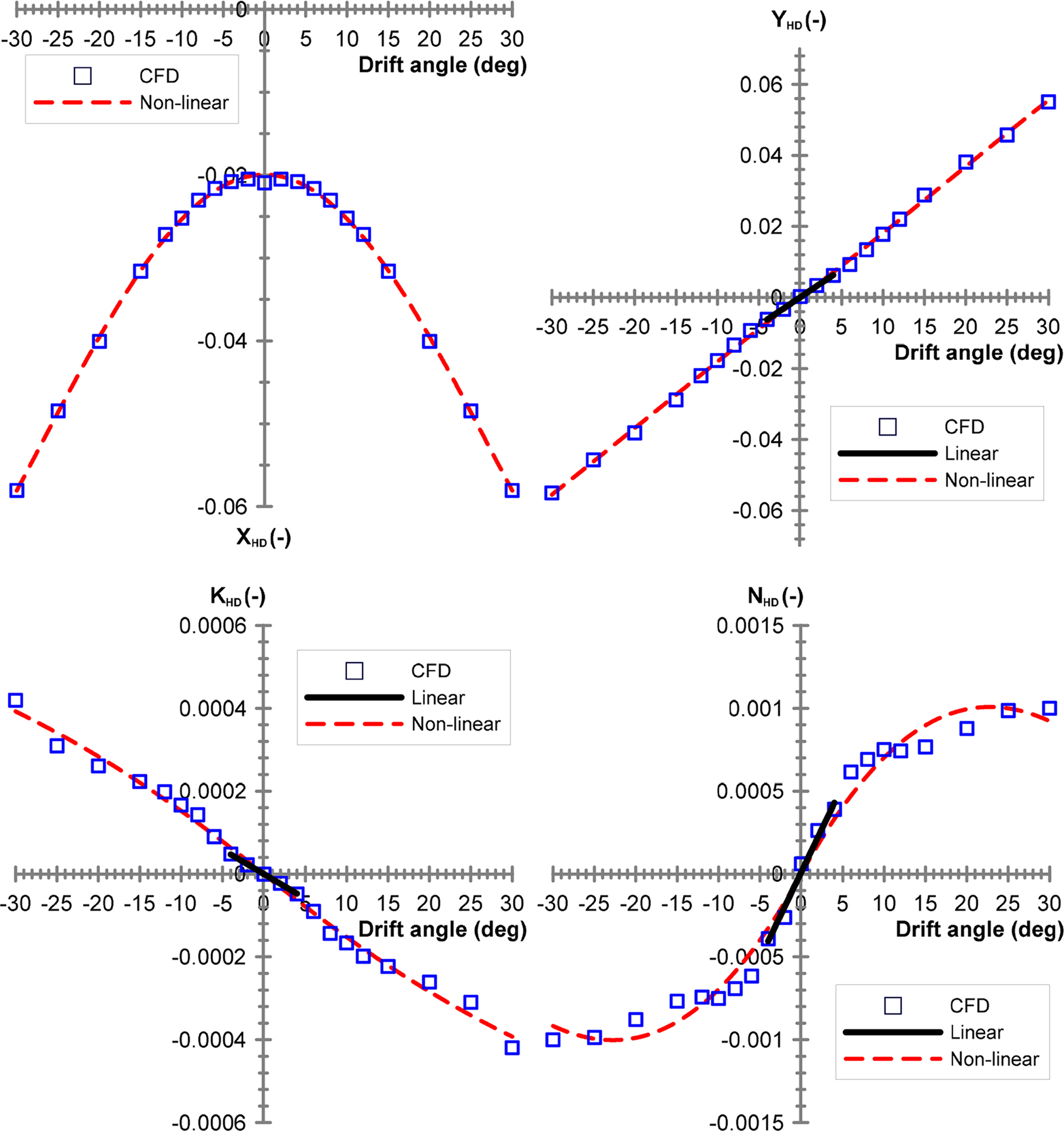
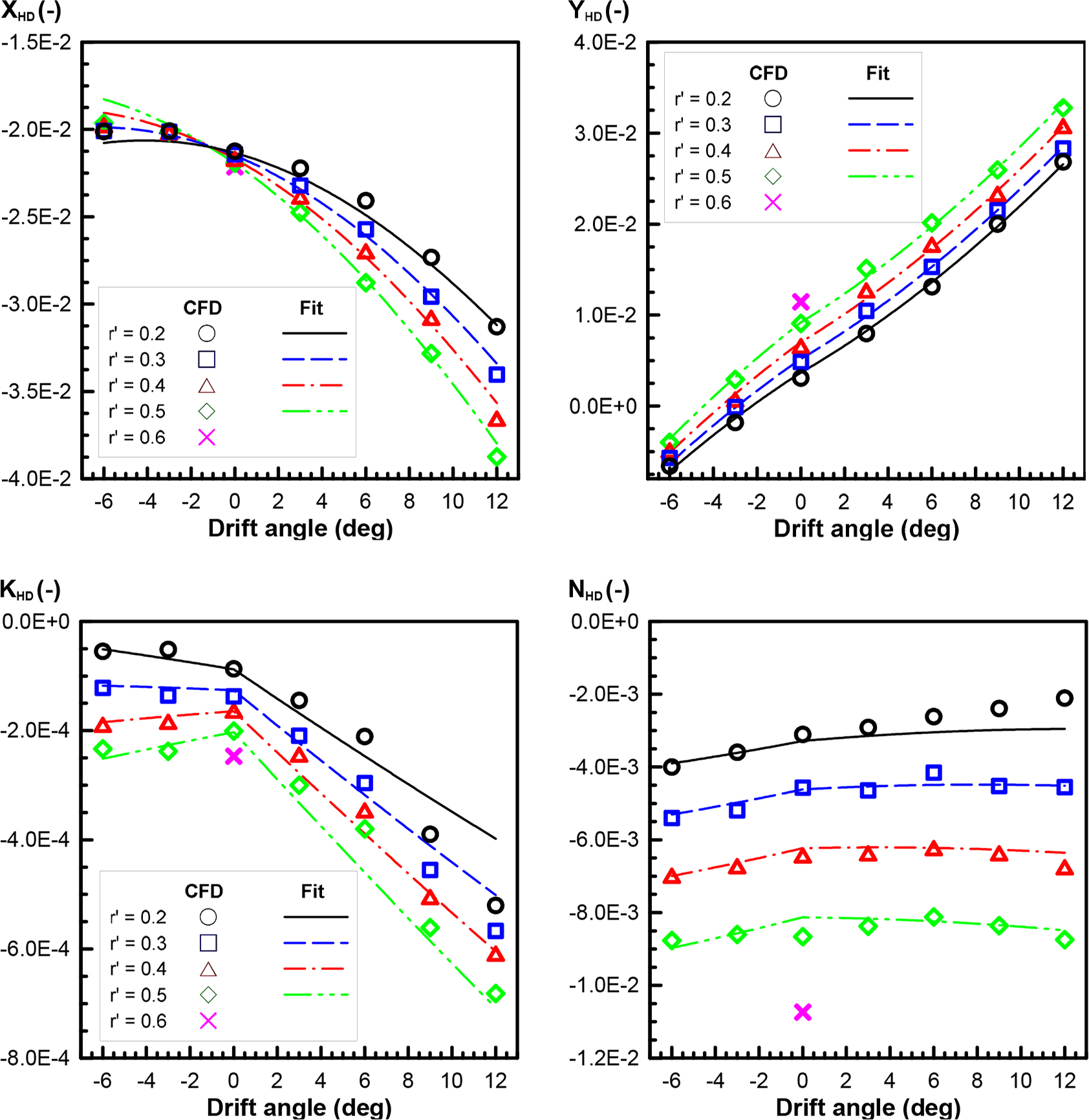
╬▓: Drift angle (deg)
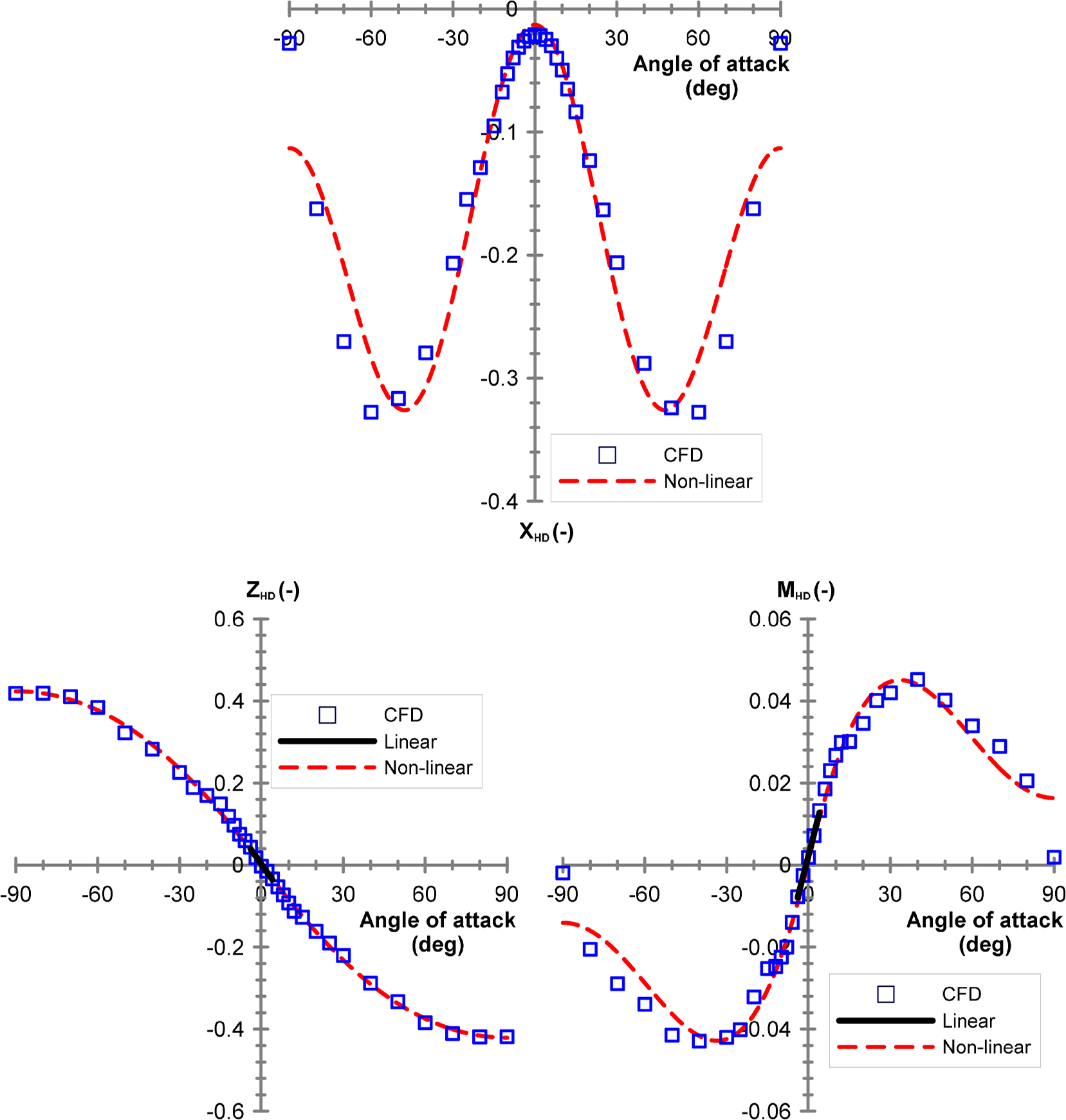
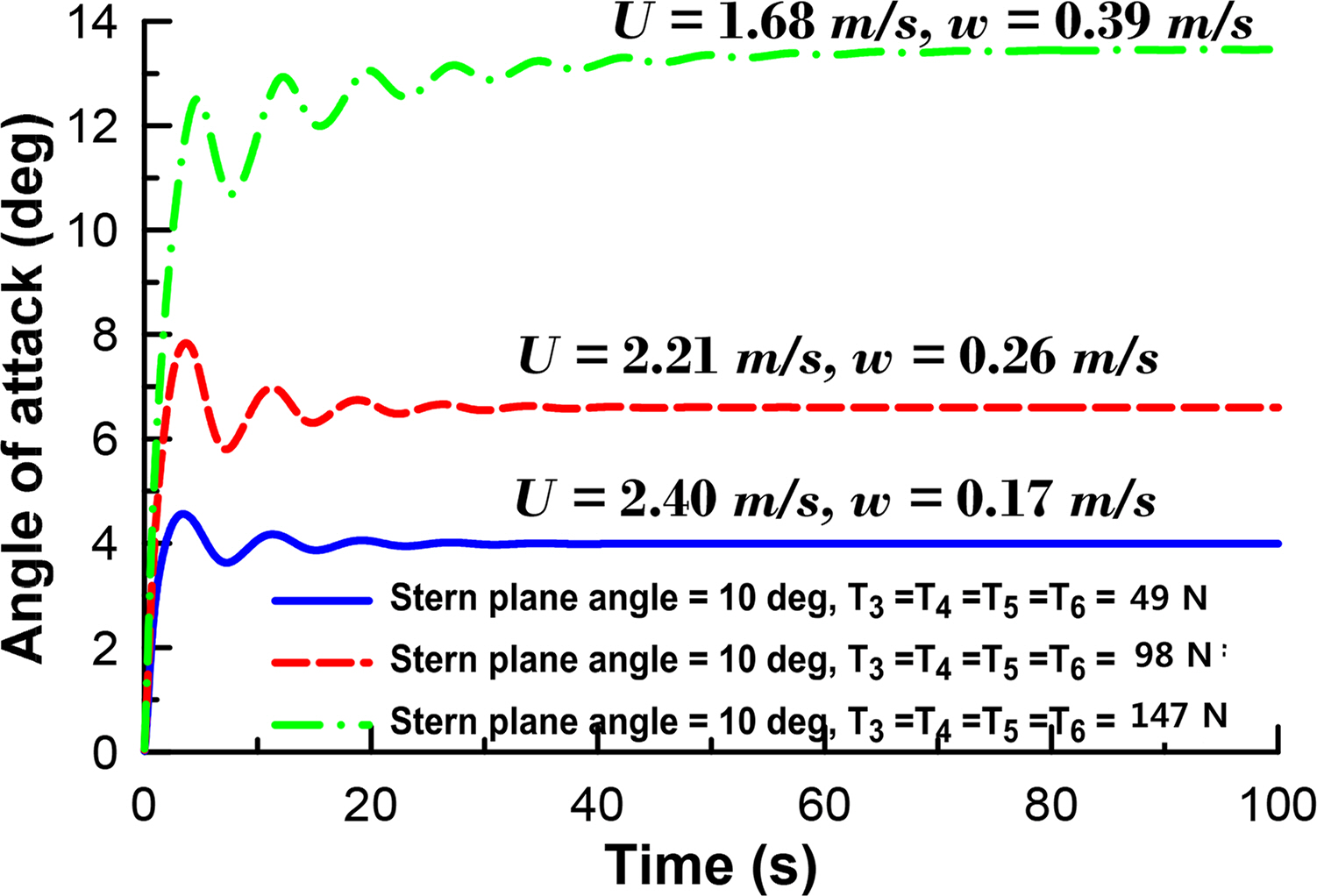
╬▒: Angle of attack (deg)
u: Surge (axial) velocity (m/s)
v: Sway (lateral) velocity (m/s)
w: Heave (vertical) velocity (m/s)
p: Roll rate (deg/s)
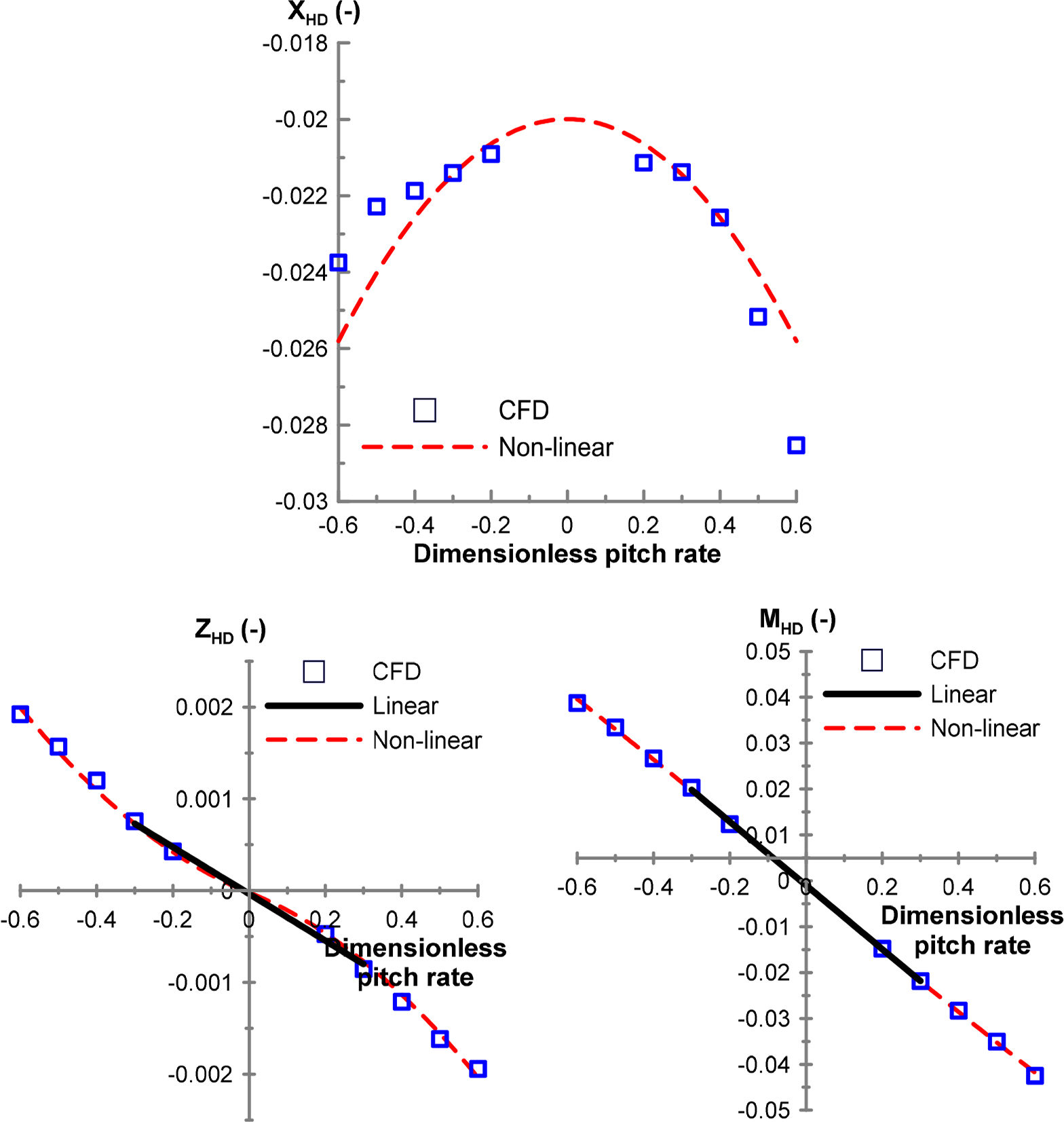
q: Pitch rate (deg/s)
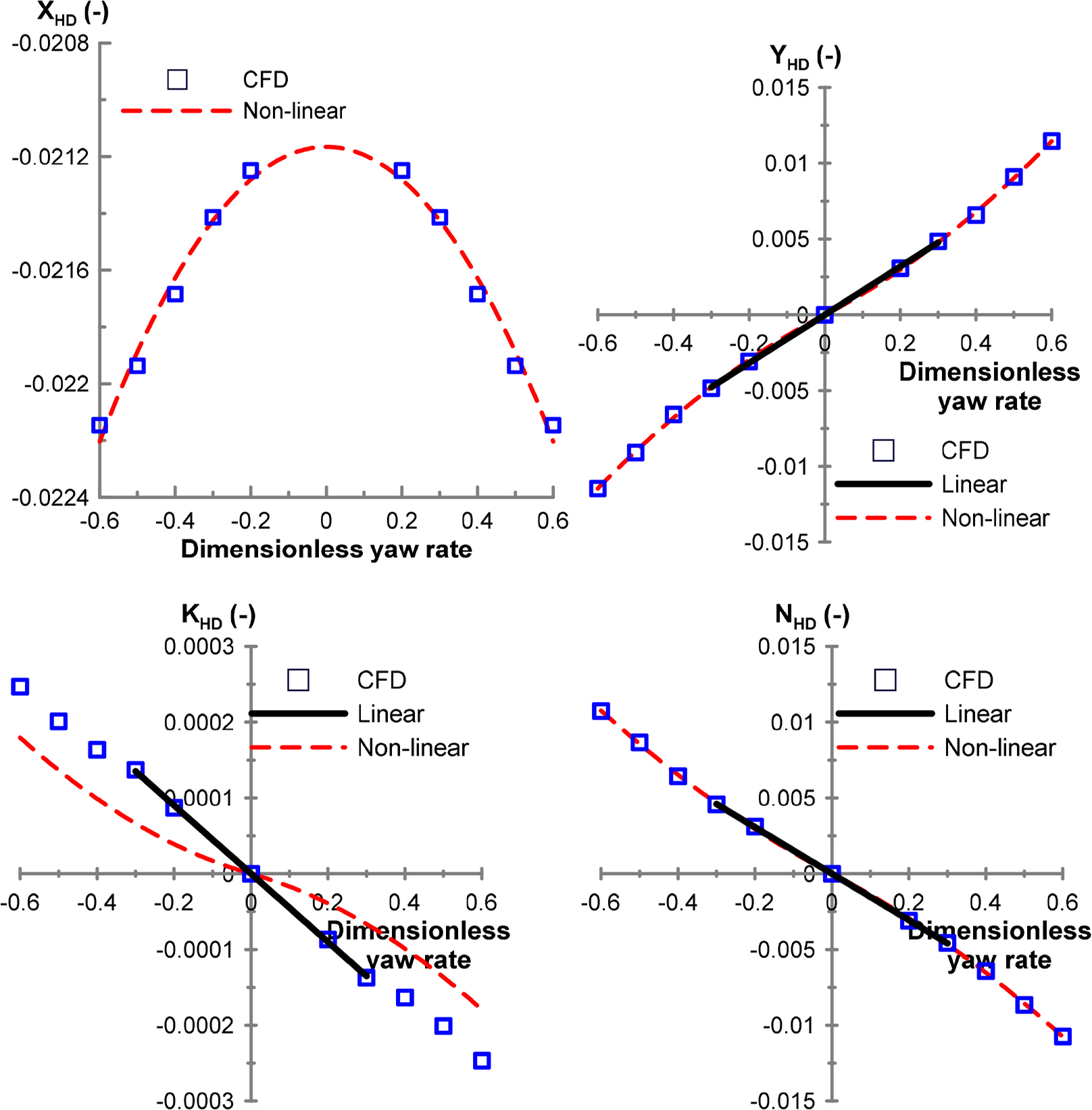
r: Yaw rate (deg/s)
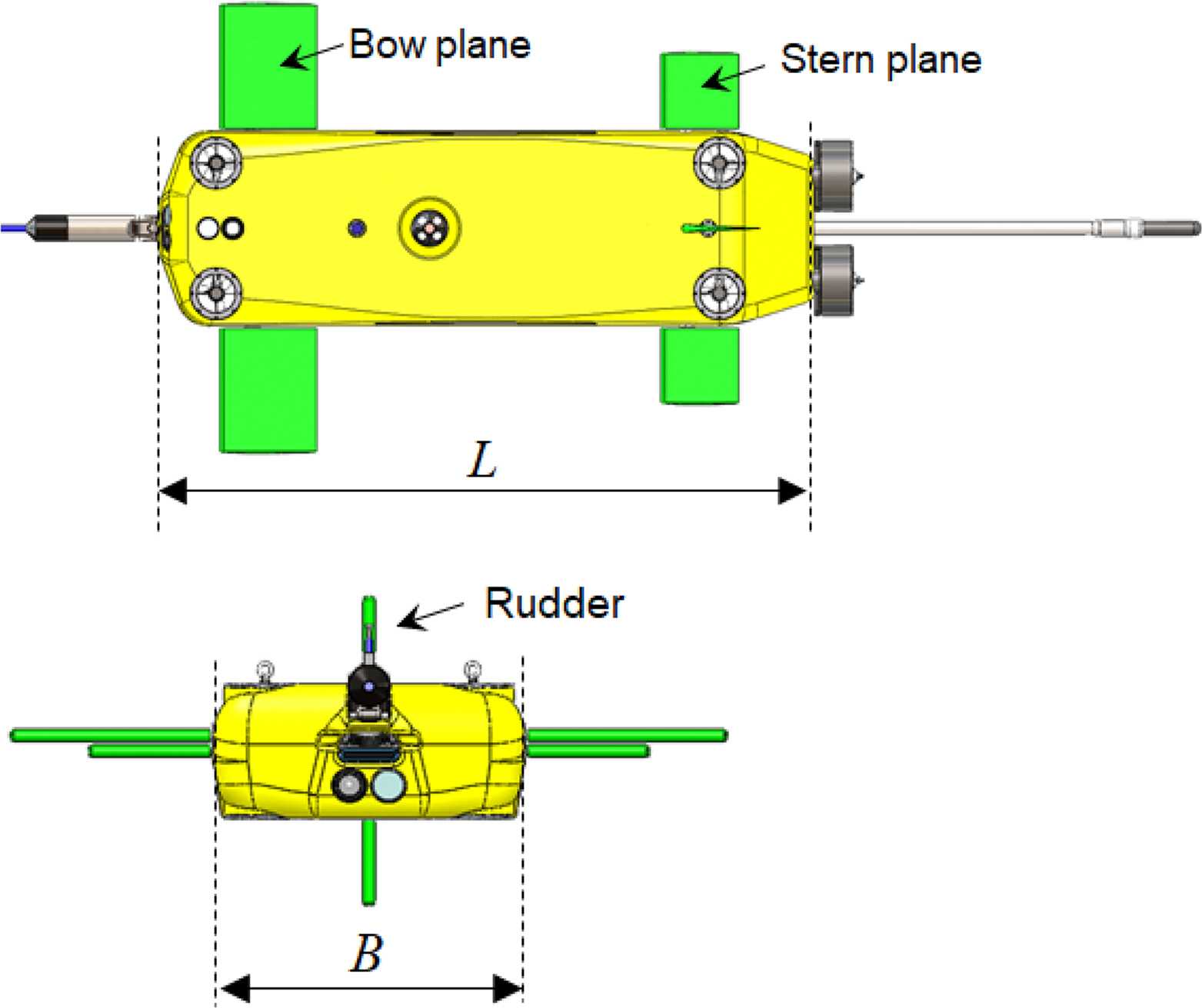
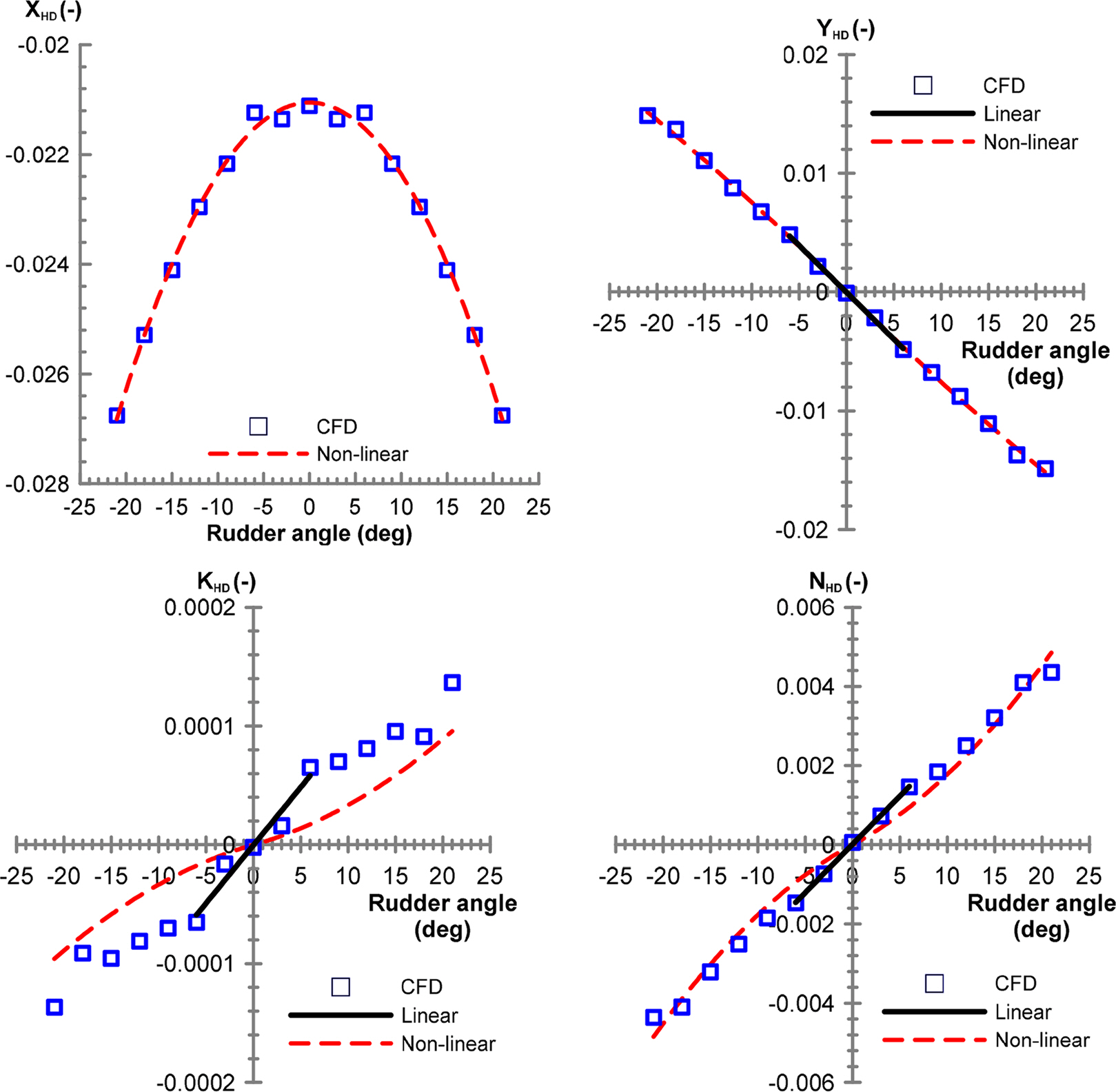
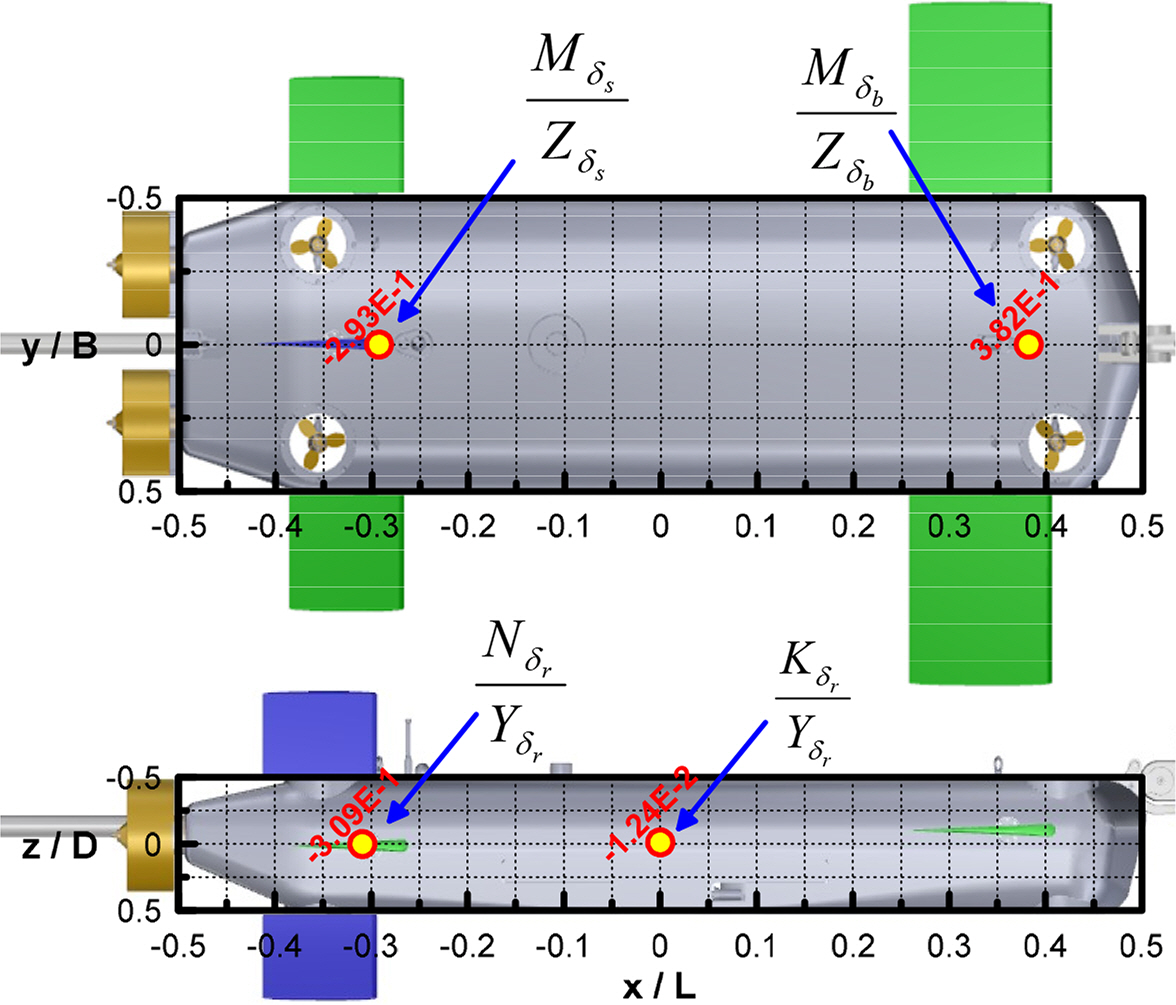
╬┤r: Rudder angle (deg)
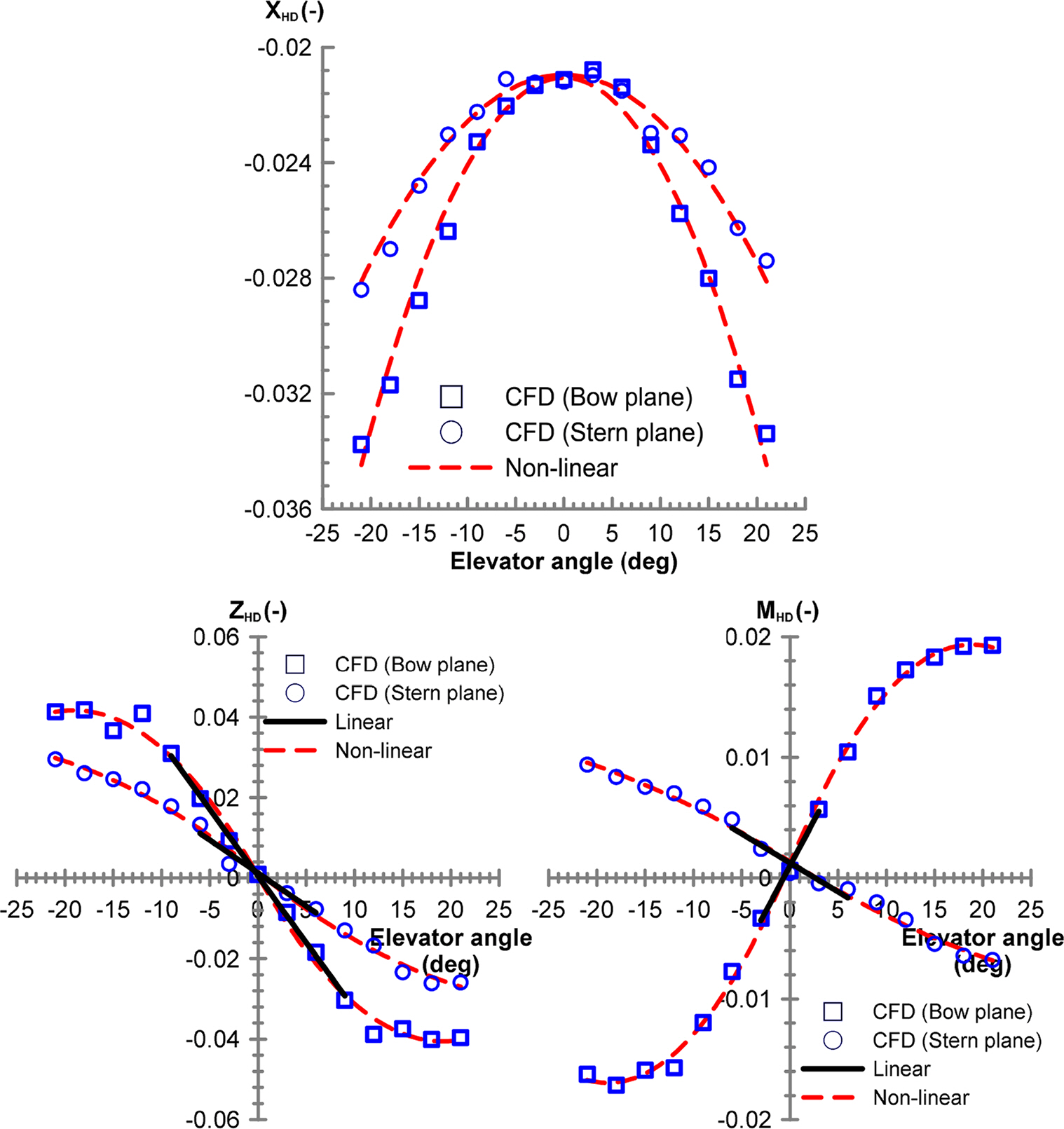
╬┤b: Bow plane angle (deg)
╬┤s: Stern plane angle (deg)
Xu╠ć: Derivative of XHD with respect to u╠ć
Xu: Derivative of XHD with respect to u
Xu|u|: Derivative of XHD with respect to u|u|
X╬┤b|╬┤b|: Derivative of XC with respect to ╬┤b|╬┤b|
X╬┤s|╬┤s|: Derivative of XC with respect to ╬┤s|╬┤s|
X╬┤r|╬┤r|: Derivative of XC with respect to ╬┤r|╬┤r|
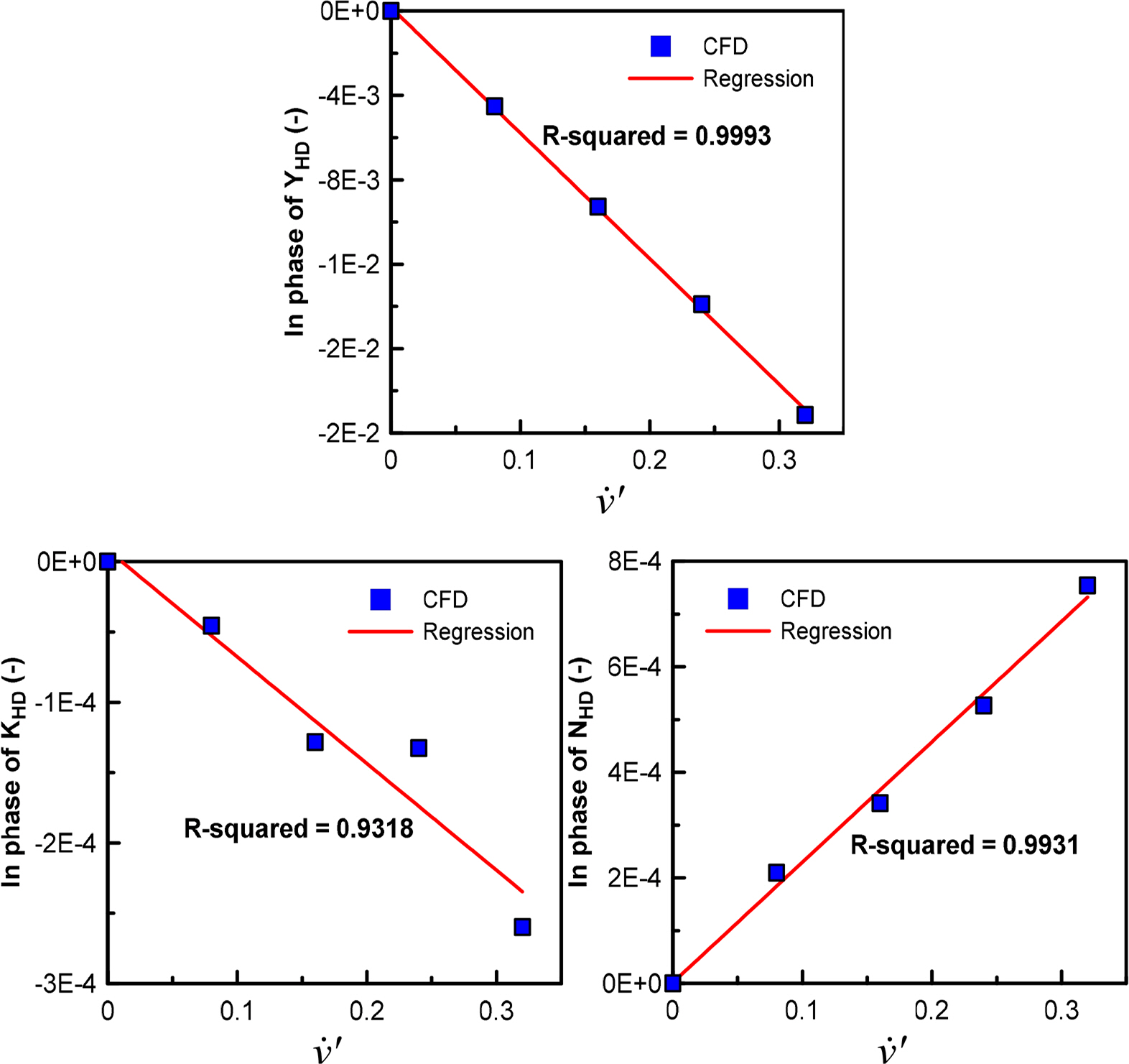
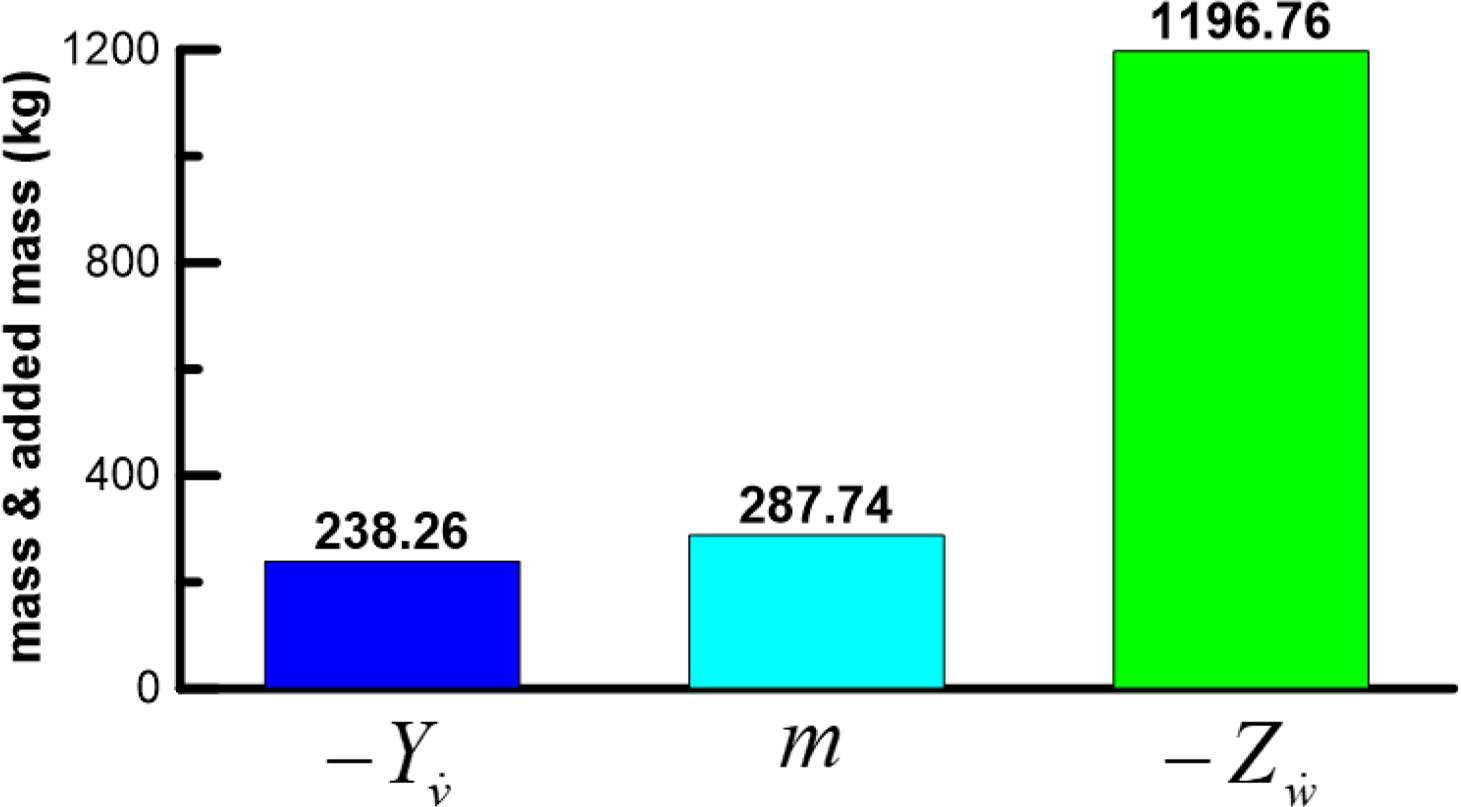
Yv╠ć: Derivative of YHD with respect to v╠ć
Yp╠ć: Derivative of YHD with respect to p╠ć
Yr╠ć: Derivative of YHD with respect to r╠ć
Yv: Derivative of YHD with respect to v
Yp: Derivative of YHD with respect to p
Yr: Derivative of YHD with respect to r
Y╬┤r: Derivative of YC with respect to ╬┤r
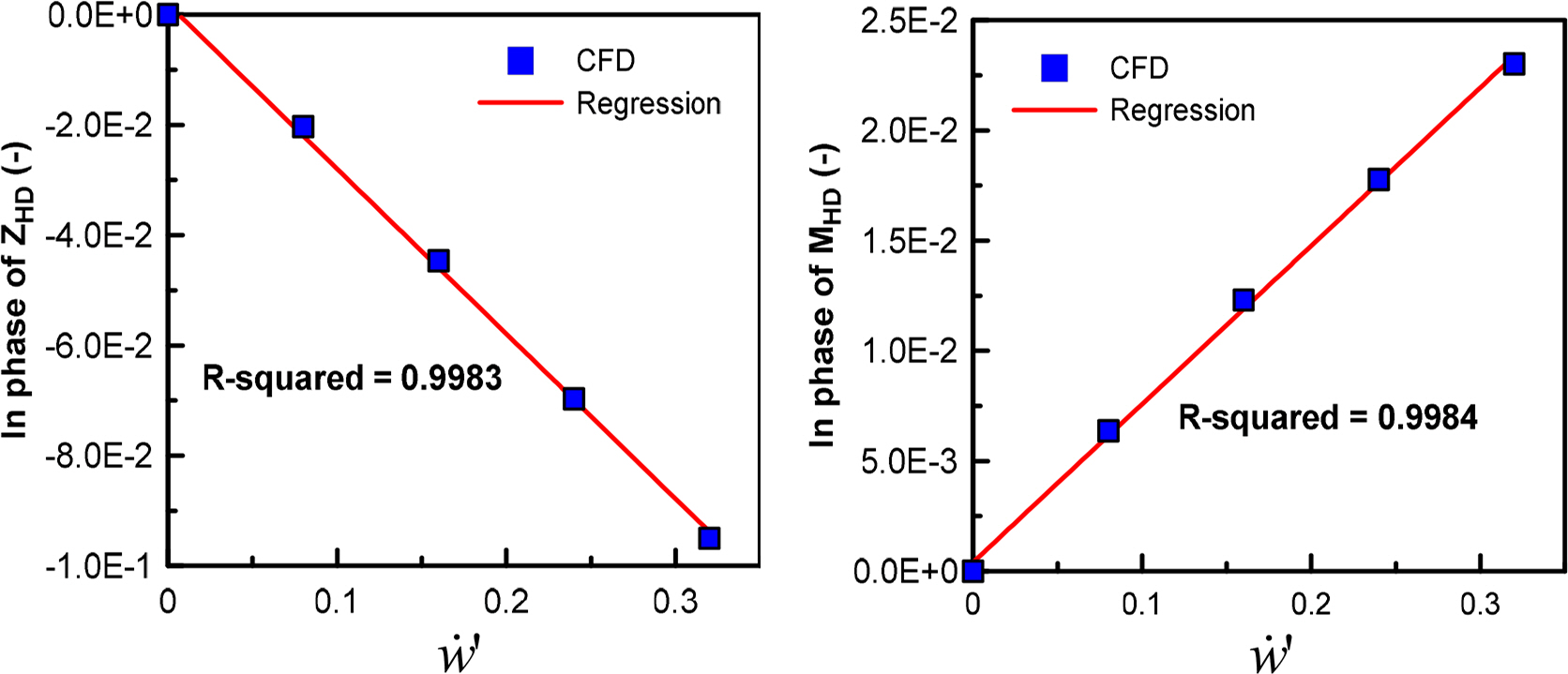
Zw╠ć: Derivative of ZHD with respect to w╠ć
Zq╠ć: Derivative of ZHD with respect to q╠ć
Zw: Derivative of ZHD with respect to w
Zq: Derivative of ZHD with respect to q
Z╬┤b: Derivative of ZC with respect to ╬┤b
Z╬┤s: Derivative of ZC with respect to ╬┤s
Kv╠ć: Derivative of KHD with respect to v╠ć
Kp╠ć: Derivative of KHD with respect to p╠ć
Kr╠ć: Derivative of KHD with respect to r╠ć
Kv: Derivative of KHD with respect to v
Kp: Derivative of KHD with respect to p
Kr: Derivative of KHD with respect to r
K╬┤r: Derivative of KC with respect to ╬┤r
Mw╠ć: Derivative of MHD with respect to w╠ć
Mq╠ć: Derivative of MHD with respect to q╠ć
Mw: Derivative of MHD with respect to w
Mq: Derivative of MHD with respect to q
M╬┤b: Derivative of MC with respect to ╬┤b
M╬┤s: Derivative of MC with respect to ╬┤s
Nv╠ć: Derivative of NHD with respect to v╠ć
Np╠ć: Derivative of NHD with respect to p╠ć
Nr╠ć: Derivative of NHD with respect to r╠ć
Nv: Derivative of NHD with respect to v
Np: Derivative of NHD with respect to p
Nr: Derivative of NHD with respect to r
N╬┤r: Derivative of NC with respect to ╬┤r