|
 |
- Search
| J. Ocean Eng. Technol. > Volume 35(3); 2021 > Article |
|
Abstract
The maneuvering performance of a ship on the actual sea is very different from that in calm water due to wave-induced motion. Enhancement of a ship’s maneuverability in waves at the design stage is an important way to ensure that the ship navigates safely. This paper focuses on the maneuvering prediction of a Russian trawler in wind and irregular waves. First, a unified seakeeping and maneuvering analysis of a Russian trawler is proposed. The hydrodynamic forces acting on the hull in calm water were estimated using empirical formulas based on a database containing information on several fishing vessels. A simulation of the standard maneuvering of the Russian trawler was conducted in calm water, which was checked using the International Maritime Organization (IMO) standards for ship maneuvering. Second, a unified model of seakeeping and maneuvering that considers the effect of wind and waves is proposed. The wave forces were estimated by a three-dimensional (3D) panel program (ANSYS-AQWA) and used as a database when simulating the ship maneuvering in wind and irregular waves. The wind forces and moments acting on the Russian trawler are estimated using empirical formulas based on a database of wind-tunnel test results. Third, standard maneuvering of a Russian trawler was conducted in various directions under wind and irregular wave conditions. Finally, the influence of wind and wave directions on the drifting distance and drifting angle of the ship as it turns in a circle was found. North wind has a dominant influence on the turning trajectory of the trawler.
The maneuvering performance of a ship on the actual sea is very different from that in calm water due to wave-induced motion. It is crucial to account for the ship’s maneuverability in waves at the design stage. Numerous prior studies have investigated the maneuverability of ships in waves. According to the International Towing Tank Conference (ITTC) (ITTC, 2011), there are four methods of predicting the movements of a ship maneuvering in waves: experiments, two-time scale, unified theory, and contract for difference (CFD) methods.
Yasukawa (2006) proposed a method of estimating the hydrodynamic force components, including added mass, wave damping, and wave excitation forces. In his study, the basic motion equations were divided into two groups, high-frequency induced motion problems, and low-frequency maneuvering problems. Yasukawa (2006, 2008) performed a free-running model test in regular waves using the SR108 container ship. The experiment was conducted with various wavelengths in head sea and beam sea conditions. Skejic and Faltinsen (2007, 2008) presented a seakeeping and maneuvering analysis of two ships. They focused on overtaking and replenishment maneuvers between two ships.
Seo et al. (2011) applied linear and nonlinear ship motion analysis to analyze ship-maneuvering performance in high-amplitude waves. The maneuvering performance of the S-175 container ship was discussed with regard to wave slope. Also, the wave drift force was calculated using the direct pressure integration method. Skejic (2013) presented a maneuvering simulation of ships in a seaway and discussed the significant role of unified maneuvering and seakeeping. Zhang et al. (2017) proposed a method for predicting ship maneuvering in regular waves of the S-175 container ship. Wang and Wan (2018) used a CFD solver called naoe-FOAM-SJTU to analyze a ship’s maneuverability in waves.
Previous studies only focused on the influence of regular waves on the ship’s maneuverability. However, the ocean waves are actually irregular waves, so it is really necessary to study the effect of the irregular waves on the maneuvering performance of the ship, especially when designing a trawler. This paper proposes a unified model of seakeeping and maneuvering, which is used to predict the maneuverability of a Russian trawler in wind and waves. In this study, ANSYS-AQWA was utilized to estimate wave drift forces and moments. In addition, the wind forces and moments acting on the Russian trawler were estimated using empirical formulas, which are based on a database containing wind tunnel test data.
Standard maneuvers of the Russian trawler were conducted in calm water, wind, and irregular wave conditions, and the effect of the operation scenario on turning trajectories are discussed. Previous studies have not investigated the operation conditions of this vessel. In this study, the operation conditions of the trawler in the Sea of Okhotsk were investigated to determine the wave and wind conditions for operation conditions. The ship’s maneuverability in different seasons was checked with changes in the wind and wave directions.
In order to predict a ship’s maneuvering performance in wind and waves, two right-handed coordinate systems were adopted, including a body-fixed coordinate system Oxy and an earth-fixed coordinate system Ox0y0, as shown in Fig. 1. The body-fixed coordinate system advances with the ship’s forward speed U and rotates with rotation speed r. In addition, δ, ψ, μ, β, and ψA are the rudder angle, heading angle, incident wave direction, drift angle, and incident wind direction, respectively. The ship’s position is expressed with respect to the earth-fixed coordinate system.
Two types of hydrodynamic models are commonly used to predict the maneuverability of a ship: the Abkowitz model and Maneuvering Modeling Group (MMG) model. In this study, the MMG model for maneuvering motion in 3DOF was applied, which is described by Eq. (1). u and v are the velocity components in the x-axis and y-axis direction, respectively. u̇ and v̇ are the surge acceleration and sway acceleration, respectively. ṙ, Izz, m, and xG are the angular acceleration, the moment of inertia about the z axis, the ship’s mass, and the longitudinal position of the ship’s center of gravity, respectively. X and Y are the hydrodynamic forces, and N is the moment around the z-axis. The subscripts H, P, and R denote the hydrodynamic forces due to the hull, propeller, and rudder in calm water, respectively. The subscripts W and A denote the hydrodynamic forces induced by waves and wind, respectively.
In this study, the mathematical model of hydrodynamic forces suggested by Yoshimura and Ma (2003) was used to predict the ship’s maneuvering performance in calm water. They proposed empirical formulas to predict the hydrodynamic derivatives are based on a database of hydrodynamic derivatives containing information on several fishing vessels, including a recent European wide-beam vessel. XH, YH, and NH are modeled as functions of the non-dimensional sway velocity and non-dimensional yaw rate using Eq. (2). u′ and v′ are non-dimensional velocity components in the x-axis and y-axis directions, respectively. r′ is the non-dimensional yaw rate, and X0 is the ship resistance. X′vv, X′rr, X′vr, X′vvvv, Y′v, Y′r, Y′vvv, Y′vvr, Y′vrr, Y′rrr, N′v, N′r, N′vvv, N′vvr, N′vrr, and N′rrr are the hydrodynamic derivatives of the polynomials and are estimated based on empirical formulas for fishing vessels suggested by Yoshimura and Ma (2003).
The rudder force and moment can be estimated through a combination of the interaction factor and the rudder normal force using Eq. (3). FN, aH, and tR are the rudder’s normal force, the rudder’s force increase factor, and the steering resistance deduction factor, respectively. The rudder’s normal force is expressed in Eq. (4). xR and xH are the longitudinal position of the rudder and the additional lateral force component, respectively.
where vR and uR are the lateral and longitudinal inflow velocities induced on the rudder by propeller rotation, respectively. Λ and AR are the rudder aspect ratio and the rudder area. fα represents the rudder lift gradient coefficient, and UR represents the resultant inflow velocity to the rudder. η denotes the ratio of the propeller diameter to the rudder span. ∊ represents the ratio of the wake fraction at the rudder position to that of the propeller position. κ represents the interaction between the propeller and rudder.
αR denotes the effective inflow angle to the rudder. βR represents the effective inflow angle to the rudder, and γR represents the flow straightening coefficient. l′R is an experimental constant that is used to express vR accurately. wP represents the wave coefficient at propeller position. The interaction force coefficients tR, aH, l′R, and ∊ can be obtained from Yoshimura and Ma’s empirical formulas for fishing vessels.
The longitudinal force of the propeller XP can be estimated using Eq. (5). tP, ρ, and DP are the thrust deduction factor, the water density, and the diameter of the propeller, respectively. For simplicity, the thrust deduction factor tP is assumed to be constant at any given propeller load. KT is the thrust coefficient, which can be expressed as the 3rd polynomial of the propeller advance ratio JP using Eq. (6). k0, k1, k2, and k3 are coefficients representing KT.
where
T = ρ n P 2 D P 4 K T ( J P )
The steady wave-induced forces in irregular waves can be estimated using Eq. (7). H1/3 and g denote the significant wave height and the gravity acceleration, respectively. C̄XW, C̄YW, and C̄NW denote the average value of the steady wave-induced force and moment coefficients in irregular waves estimated using Eq. (8). C̄XW, C̄YW and C̄NW are estimated based on the short-term prediction technique by Yasukawa et al. (2017). These coefficients are stored in files in databases and used when simulating the ship’s maneuverability in irregular waves. Sζζ (ω) and G(θ) denote the wave spectrum and the wave direction distribution function, respectively. The ITTC spectrum is used as the wave spectrum Sζζ (ω). The cosine-squared spreading function is used as the wave direction distribution function (θ). CXW (ω, χ), CYW (ω, χ), and CNW (ω, χ) denote the wave-induced steady force and moment coefficient in regular waves expressed as a function of the wave frequency ω and the wave direction χ.
The hydrodynamic forces due to wind can be obtained using the empirical formula presented by Kitamura et al. (2017), which is based on a wind tunnel test and is shown in Eq. (9). LOA is the overall length of the ship, AF is the frontal projected area, AL is the lateral projected area, and C is the distance from mid-ship to the centroid of AL . HC is the height of centroid of AL from the calm water level. CXLI, CALF, CCF, and CYLI are coefficients of the multiple regression formulae. The hydrodynamic coefficients due to wind can be estimated using Eq. (10).
In order to investigate the ship maneuverability, a Russian trawler designed by Deahea Ship Design Corporation was selected. Fig. 2 shows the geometry of the Russian trawler. The principal dimensions are listed in Table 1.
The standard maneuvers of the trawler in calm water are conducted with constant propeller revolution. The propeller revolution is selected to produce a speed of 12 knots (6.17 m/s) when the trawler vessel moves forward in calm water. The propeller speed was 4.384 revolutions per second. Simulations of the ship turning in a circle were conducted in wind and irregular waves based on the operation conditions in the Sea of Okhotsk.
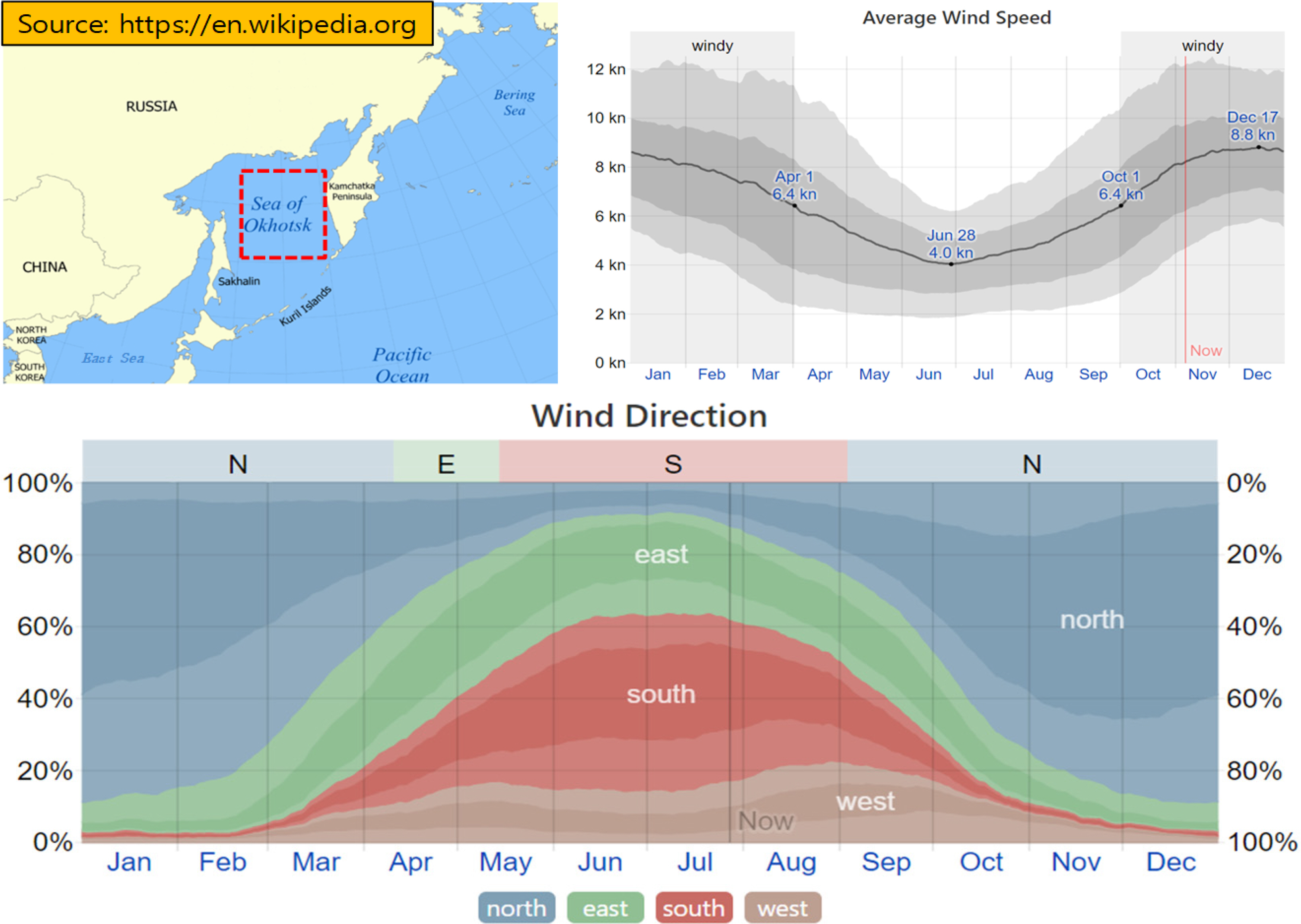
The maximum wind speed was selected for the simulation according to the wind direction in Table 2. East wind is defined using the period of April to May, South wind is defined using the period of May to September, and North wind is defined using the period of September to April of the following year. The maximum wind speed is the time selection value that is equivalent to each wind direction. The wind direction and average wind speed at 10 m above the ground in the Sea of Okhotsk were obtained from the Weather Spark website. The wind speed and wind direction change dramatically depending on seasonal variation. Fig. 3 shows the wind direction and wind speed in the Sea of Okhotsk. A comparison of the wind speed and wind direction in various seasons is presented in Table 2.
The hydrodynamic coefficients of the trawler were estimated based on the empirical formulas presented by Yoshimura and Ma (2003). The hydrodynamic coefficients of the trawler are listed in Table 3. The interaction coefficients among the hull, propeller, and rudder were also estimated based on Yoshimura and Ma’s empirical formulas and are listed in Table 4.
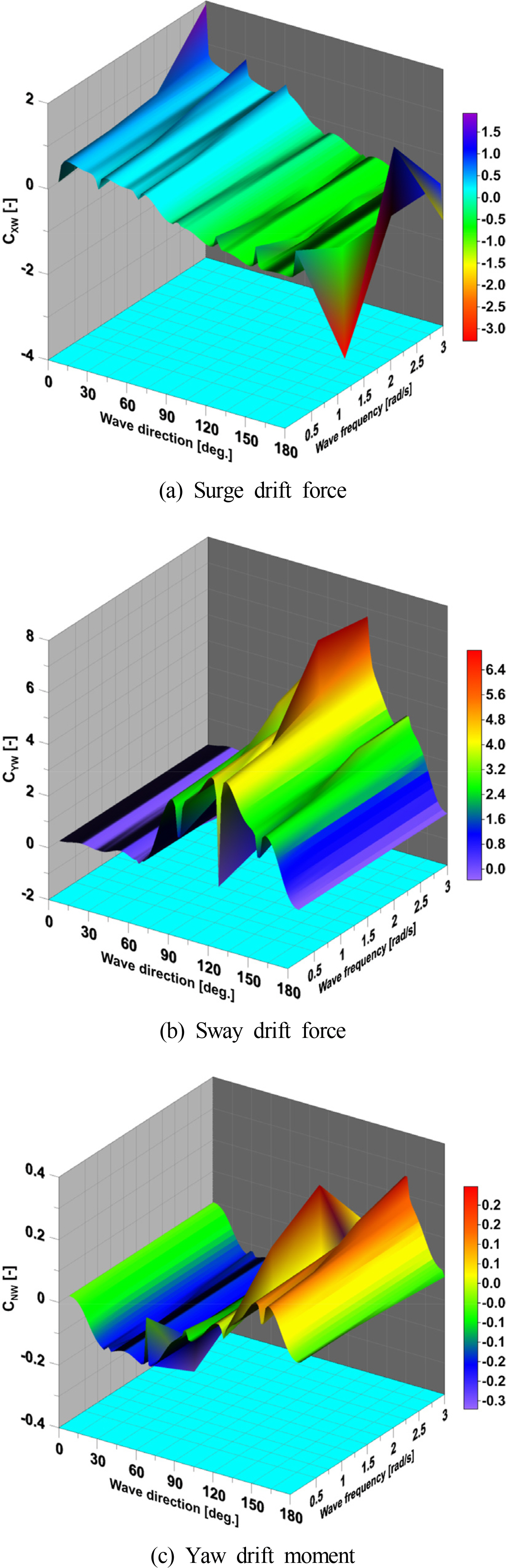
Fig. 4 shows the wave drift forces and moment in various wave directions and wave frequencies. The surge drift force has a similar tendency to the overall trend of the surge drift force in the head sea. The maximum value of surge drift force occurs at low wave frequencies, where the wavelength is greater than the ship’s length. The wavelength is greater than the length of the vessel when the wave frequency is smaller than 1.35 rad/s. The surge drift force decreases gradually with an increase in the wave frequency and wave direction and almost disappears in following sea.
The maximum value of the sway drift force occurs at high wave frequency and in oblique sea, especially at a wave direction of 120 degrees. The sway drift force decreases gradually as the wave frequency decreases and it almost disappears in the head sea and the following sea. At wave directions of 180 degrees and 0 degrees, a small value of the sway drift force is observed without a distinct peak. The maximum value of yaw drift moment occurs in oblique sea, especially at wave directions of 150 degrees and 60 degrees. The yaw drift moment increases significantly at high wave frequency, while it decreases gradually as the wave frequency decreases and almost disappears in the head sea and the following sea.
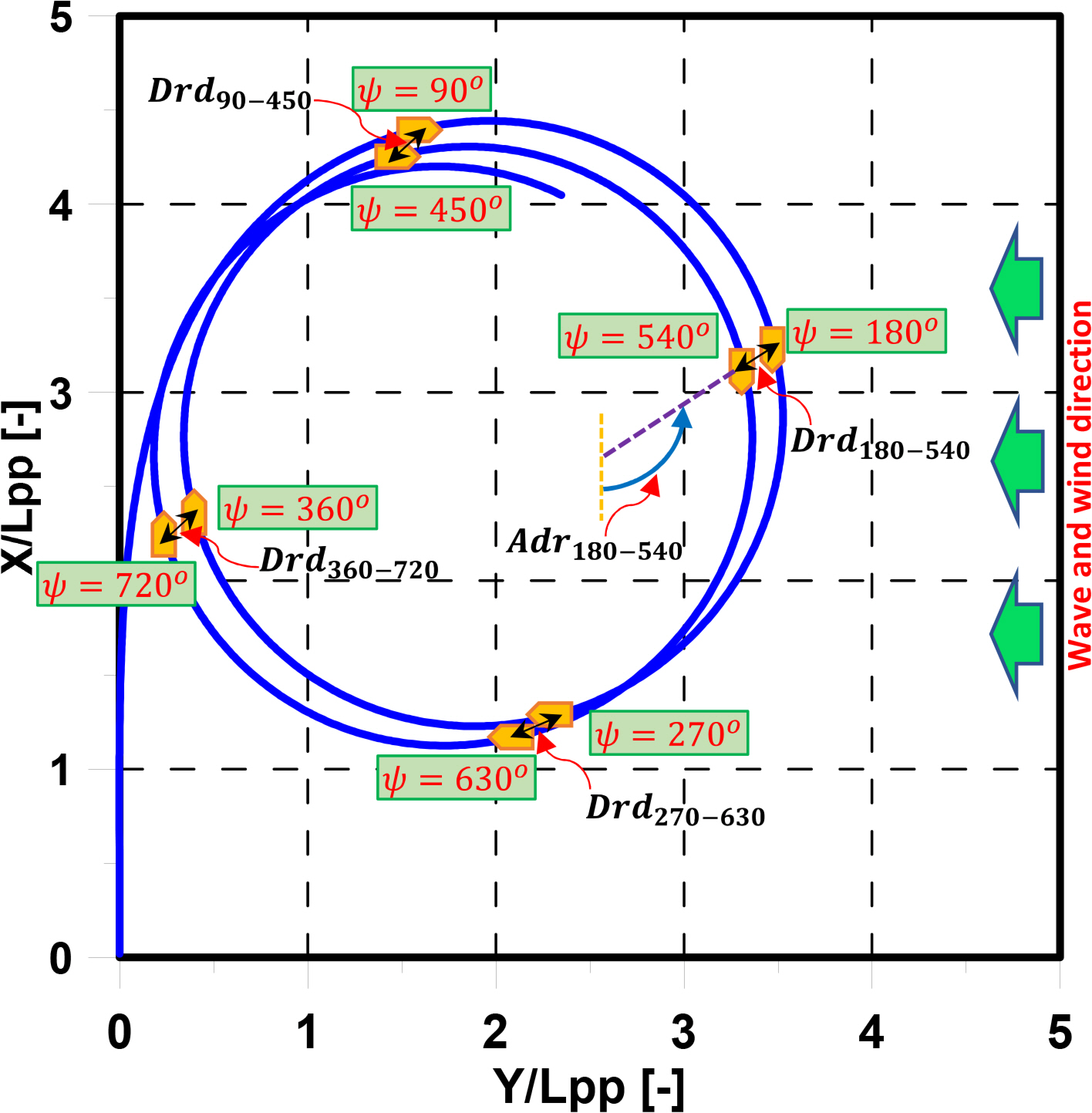
To analyze the turning trajectories in irregular wave and wind conditions, we applied the drifting distance and the drifting angle suggested by Kim et al. (2019). The drifting distance Drd is the distance between lines that are perpendicular to the tangent to the turning trajectory, as shown in Fig. 4. For example, Drd90 − 450 represents the magnitude of the vector between two points corresponding to heading angles of 90 degrees and 450 degrees.
The drifting angle Adr is the angle between the tangential line of the turning trajectory and the ship’s approach direction in the x direction, as shown in Fig. 5. For instance, Adr90 − 450 represents the angle between the ship’s approach direction in the x direction and the tangential line of two points corresponding to heading angles of 90 degrees and 450 degrees. The relative drift angle Rdr is the angle between the drifting angle and the wave propagation direction, which can be estimated using Eq. (11). δ is the rudder angle, χ is the wave propagation direction, and Adris the drifting angle. The relative drifting distance Rdr is suggested by Kim et al. (2019) to describe the ship’s turning trajectory in waves.
The predicted turning trajectory of the trawler in calm water is shown in Fig. 6(a). The surge velocity, sway velocity, and yaw rate of the turning circle in calm water are shown in Figs. 6(b), 6(c), and 6(d), respectively. The results of the advance and the tactical diameter of the trawler are compared to the standards of the International Maritime Organization (IMO) for ship maneuverability, as shown in Table 5. Therefore, the turning ability of the trawler in calm water is confirmed and satisfied with the value proposed by the IMO’s standards.
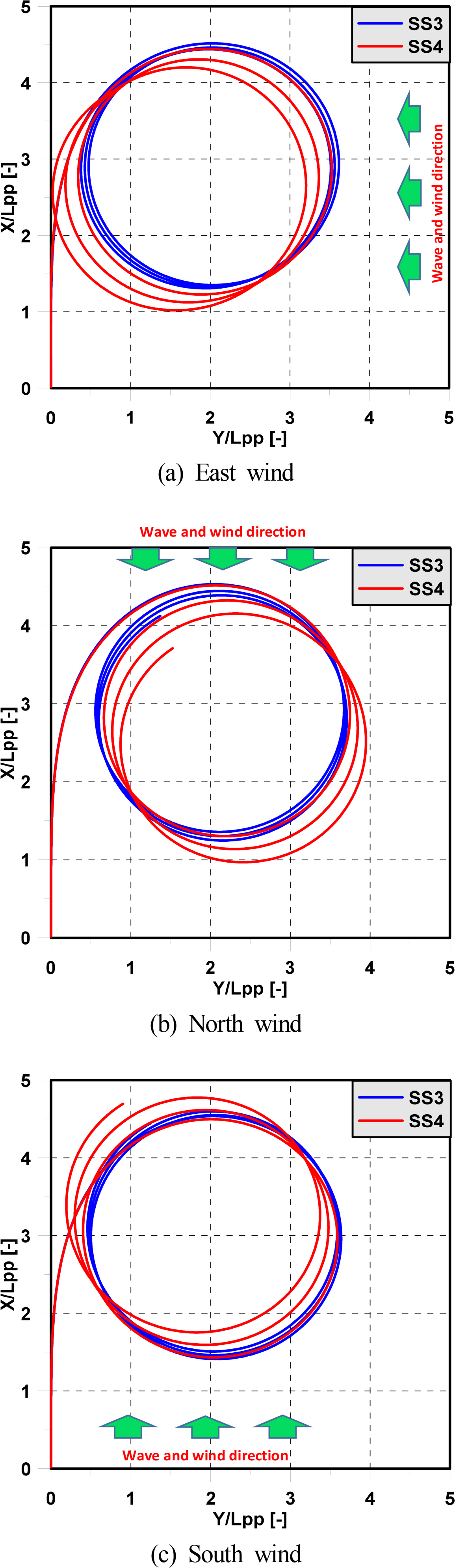
In order to investigate the effect of the operation scenario, we simulated the movements of the trawler as it turns in a circle in wind and irregular waves. The wave direction is similar to the wind direction. The maximum wind speed was selected in this simulation. Fig. 7 shows the turning trajectories of the trawler in the operation scenario for various wind directions. It can be seen that the wind direction and significant wave height have dominant effects on the turning trajectories of the trawler.
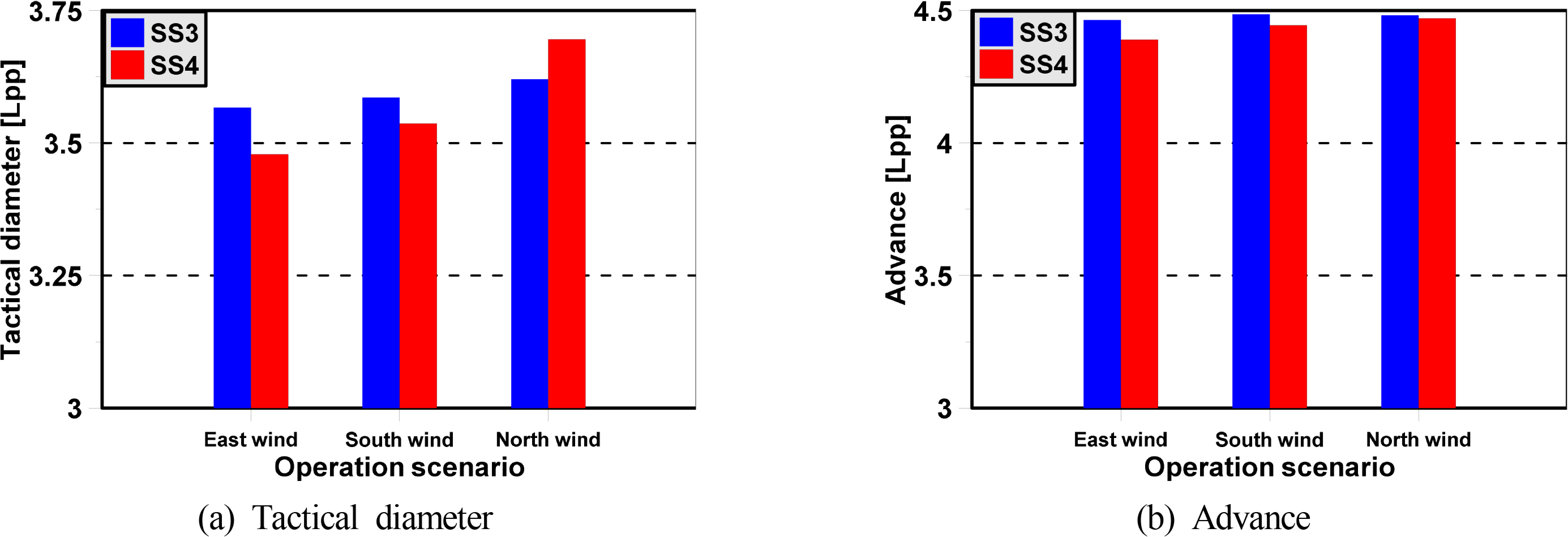
The direction of the wind and waves slightly influences the advance of the trawler, while it significantly affects the tactical diameter, as shown in Fig. 8. This happens because the ship turns at the initial stage until the heading angle is 90 degrees, and the ship’s trajectory changes slightly. During the initial turning, the hydrodynamic forces induced by the rudder produce a surge acceleration, sway acceleration, and yaw acceleration. There is a gradual increase in the hydrodynamic forces and moment acting on the ship hull, which consist of an acceleration-dependent term and velocity-dependent term.
When the ship turns at times less than 50 s, the hydrodynamic forces and moment are changed by the motion induced by wind and waves, as shown in Fig. 9. However, these hydrodynamic forces are very small in comparison to the hydrodynamic forces caused by the acceleration in the initial turning. Therefore, the ship’s trajectory changes very slightly at the early stages of turning. This is the reason why the advance is relatively similar when the ship turns in various wind and wave directions.
The changing of the hydrodynamic forces and moment changed by the motion induced by wind and waves for North wind (green line) can be divided into 4 phases: A, B, C, and D. Phase A is related to the occurrence of the maximum value of the sway and yaw moment changed by the motion induced by wind and waves. These hydrodynamic forces occur when the incident wave direction is 90 degrees, as shown in Fig. 9. Phase B involves the occurrence of the maximum surge force changed by the motion induced by wind and waves at the incident wave direction of 180 degrees or the incident wind direction of 0 degrees, as seen in Fig. 9. In this case, the sway force and yaw moment changed by the motion induced by wind and waves are approximately zero.
Phase C is similar to phase A and causes a large sway force and yaw moment changed by the motion induced by wind and waves when the incident wave direction reaches 90 degrees. At the time of phase C, the speed of the ship has reached steady turning, and the effects of the acceleration changes are small. Likewise, phase D is similar to phase B and causes the greatest reduction in surge force changed by the motion induced by wind and waves, even though the sway and yaw moment changed by the motion induced by wind and waves are close to zero.
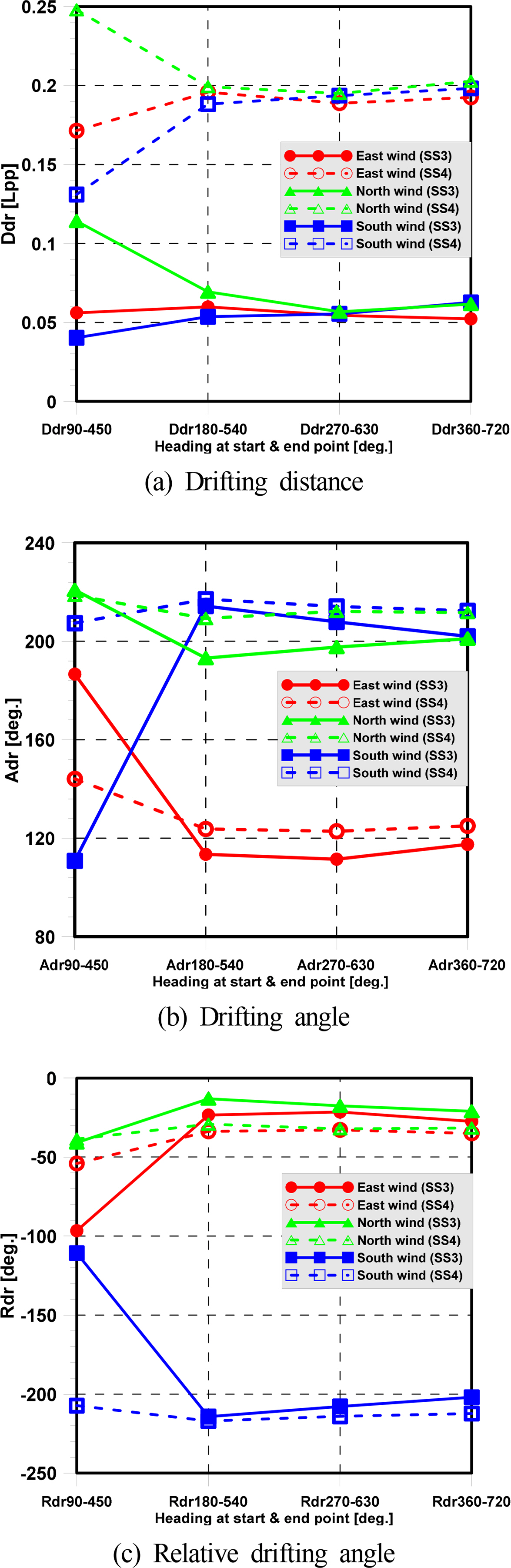
Fig. 10 shows the drifting distance and drifting direction for various wind directions. It is evident that the North wind has the dominant influence on the turning trajectory of the trawler. In particular, when the ship moves in the North wind, the value of the drifting distance is bigger than that of the East or South winds, as shown in Fig. 10. The South wind has the smallest influence on the drifting distance. The drifting direction is approximately parallel to the wind and wave-propagation direction. This happens because the North wind causes a change of the wave direction relative to ships in the 90-degree direction and 180 degrees earlier than East wind and South winds.
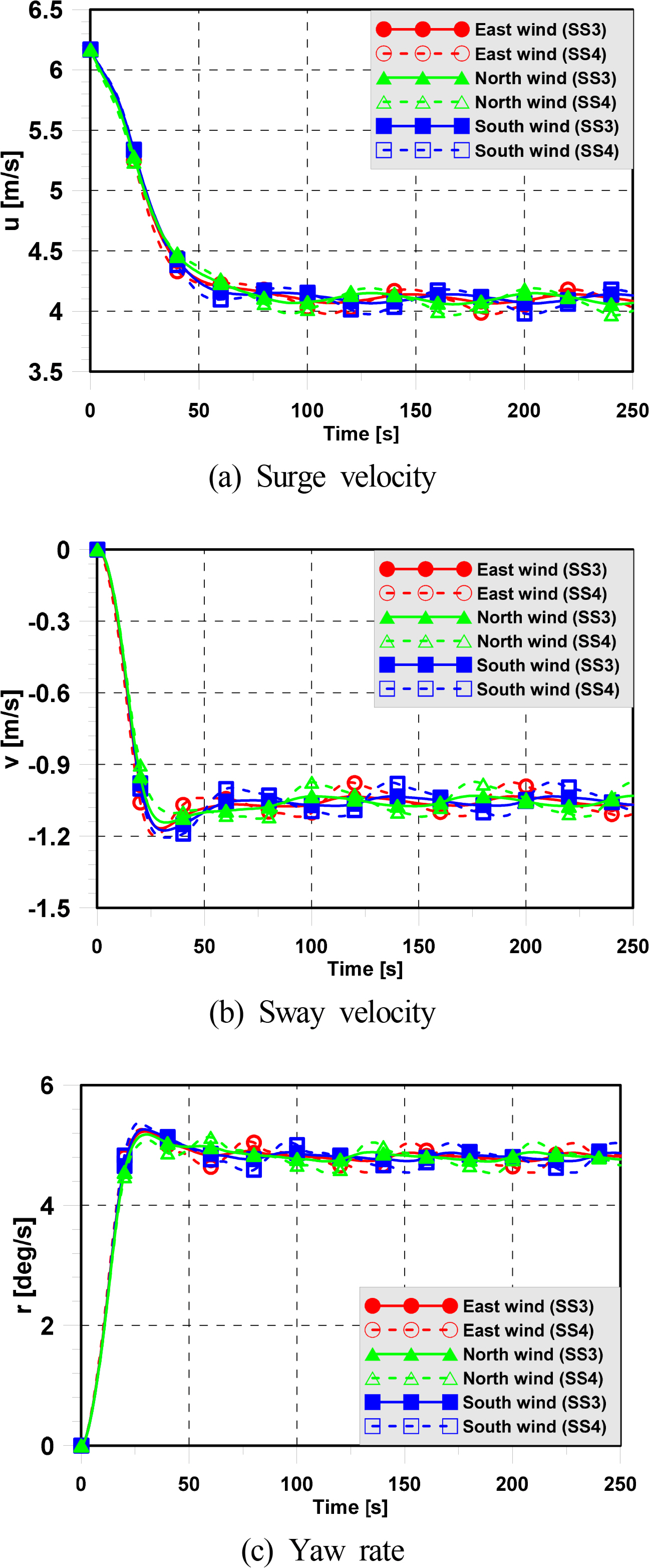
This is the reason why the ship turning in North wind causes the largest drifting distance. It is also why the ship’s tactical diameter in the North wind is the largest, as shown in Fig. 8. The ship enters the steady turning phases after 50 s due to the hydrodynamic force and moment acting on the hull and the control force and moment due to rudder and propeller reaching equilibrium. However, the surge velocity, sway velocity, and yaw rate oscillate in wind and irregular waves due to the hydrodynamic forces changed by the motion induced by wind and waves. This makes the ship’s trajectory change dramatically after initial turning.
Fig. 11 shows the maneuvering motion including the surge velocity, sway velocity, and yaw rate with various wind directions and the significant wave heights. It can be seen that the approach surge velocities with various wind directions are similar to the approach surge velocities in calm water, while the sway velocity and yaw rate oscillate in wind and irregular waves. Although the speed at the beginning of a turn differs greatly depending on the wind direction, the histories of speed variations in various wind directions become similar during steady turns, as shown in Fig. 11. For this reason, the drifting distance and drift angle are quite different during the initial circle, but these values become similar after the second and third circles. The results of the relative drifting angle reveal the difference between the propagation direction and the drifting angle, and the drifting direction is similar to the wind and wave propagation direction when the ship reaches the second and third circles.
In this paper, the movements of a trawler as it turned in circles in calm water, wind, and irregular waves were simulated using a unified model of seakeeping and maneuvering. Our concluding remarks are as follows. First, the operation scenario of the trawler in the Sea of Okhotsk was analyzed. The hydrodynamic coefficients of the trawler were estimated using empirical formulas. The hydrodynamic forces due to wind and irregular waves were estimated, and the wave drift forces and moment in irregular waves are estimated by applying a short-term prediction technique.
Second, the standard maneuvering parameters in calm water satisfy the criteria of the IMO standards for a ship’s maneuverability. The direction of the wind and waves slightly influences the advance of the trawler, while it significantly affects the tactical diameter because the ship’s trajectory changes slightly at the initial stage. Finally, the North wind has a dominant effect on the tactical diameter and the turning trajectories of the trawler. The North wind causes the largest drifting distance. Moreover, the drifting distance and drifting angle become similar after the second and third circles, although these values are quite different at the beginning of the first turn.
Funding
This research was supported by the programs, “Development of design and construction method of 36 m class trawlers for fishing in the Far East Waters for the support of Russia export.” Which is funded by the Ministry of Trade, Industry and Energy (MOTIE, Korea), and “Development of Autonomous Ship Technology (2019-2020, Development of autonomous system having intelligent navigation decision making function),” which is funded by the Ministry of Oceans and Fisheries (MOF, Korea).
Table 1.
Principal dimensions of the Russian trawler
Table 2.
Operation scenario in the Sea of Okhotsk
| Item | Apr.–May | May–Sep. | Sep.–Apr |
|---|---|---|---|
| Wind direction | East wind (38%) | South wind (50%) | North wind (89%) |
| Average wind speed (m/s) | 2.1 | 3.3 | |
| Maximum wind speed (m/s) | 5.1 | 5.1 | 6.2 |
Table 3.
Hydrodynamic coefficients
Table 4.
Interaction coefficients
| Interaction coefficients | Value | Interaction coefficients | Value |
|---|---|---|---|
| 1− tR | 0.853 | γR | 0.458 |
| aH | 0.048 | ∊ | 0.995 |
| x′H | −0.450 | κ | 0.428 |
| l′R | −0.936 | - | - |
Table 5.
Maneuver parameters in turning circle in calm water
| Item | Trawler | IMO standard |
|---|---|---|
| Advance (Lpp)(1) | 4.496 | 4.5 |
| Tactical diameter (Lpp) | 3.600 | 5.0 |
References
International Towing Tank Conference (ITTC)
. (2011). Final Report and Recommendation to the 26th ITTC. Proceedings of 26th International Towing Tank Conference, Rio de Janeiro, Brazil.
Kim, DJ., Yun, K., Park, JY., Yeo, DJ., & Kim, YG. (2019). Experiment Investigation on Turning Characteristics of KVLCC2 Tanker in Regular Waves. Ocean Engineering, 175, 197-206.
https://doi.org/10.1016/j.oceaneng.2019.02.011

Kitamura, F., Ueno, M., Fujiwara, T., & Sogihara, N. (2017). Estimation of Above Water Structural Parameters and Wind load on Ships. Ship and Offshore Structures, 12(8), 1100-1108.
https://doi.org/10.1080/17445302.2017.1316556

Skejic, R., & Faltinsen, OM. (2007). A Unified Seakeeping and Maneuvering Analysis of Two Interacting Ships. Proceedings of the 2nd International Conference on Marine Research and Transportation. 209-218.
Skejic, R., & Faltinsen, OM. (2008). A Unified Seakeeping and Maneuvering Analysis of Ships in Regular Waves. Journal of Marine Science and Technology, 13, 371-394.
https://doi.org/10.1007/s00773-008-0025-2

Seo, MG., Kim, YH., & Kim, KH. (2011). Effects on Nonlinear Ship Motion on Ship Maneuvering in Large Amplitude Waves. Journal of the Society of Naval Architects of Korea, 48(6), 516-527.
https://doi.org/10.3744/SNAK.2011.48.6.516

Skejic, R. (2013). Ships Maneuvering Simulations in a Seaway – How Close Are We to Reality? Proceedings of International Workshop on Next Generation Nautical Traffic Models, 2013, 91-101.
Wang, JH., & Wan, DC. (2018). CFD Investigations of Ship Maneuvering in Waves Using Naoe-FOAM-SJTU Solver. Journal of Marine Science and Application, 17, 443-458.
https://doi.org/10.1007/s11804-018-0042-4

Weather Spark. (2020). Average Weather in Okhotsk. Retrieved December 2020 from https://weatherspark.com/y/144221/Average-Weather-in-Okhotsk-Russia-Year-Round
Yasukawa, H. (2008). Simulations of Ship Maneuvering in Waves (2nd Report: Zig-Zag and Stopping Maneuvers). Journal of the Japan Society of Naval Architects and Ocean Engineers, 7, 163-170.
https://doi.org/10.2534/jjasnaoe.7.163

Yasukawa, H. (2006). Simulations of Ship Maneuvering in Wave (1st Report: Turning Motion). Journal of the Japan Society of Naval Architects and Ocean Engineers, 4, 127-136.
https://doi.org/10.2534/jjasnaoe.4.127

Yasukawa, H., Zaky, M., Yonemasu, I., & Miyake, R. (2017). Effect of Engine Output on Maneuverability of a VLCC2 in Still Water and Adverse Weather Conditions. Journal of Marine Science and Technology, 22, 574-586.
https://doi.org/10.1007/s00773-017-0435-0

Yoshimura, Y., & Ma, N. (2003). Manoeuvering Prediction of Fishing Vessels. Proceeding of MARSIM’03 Conference. Kanazawa: Japan. p 1-11.
Zhang, W., Zou, Z.J.., & Deng, D.H. (2017). A Study on Prediction of Ship Maneuvering in Regular Waves. Ocean Engineering, 137, 367-381.
https://doi.org/10.1016/j.oceaneng.2017.03.046

- TOOLS
-
METRICS

-
- 1 Crossref
- Scopus
- 4,386 View
- 101 Download