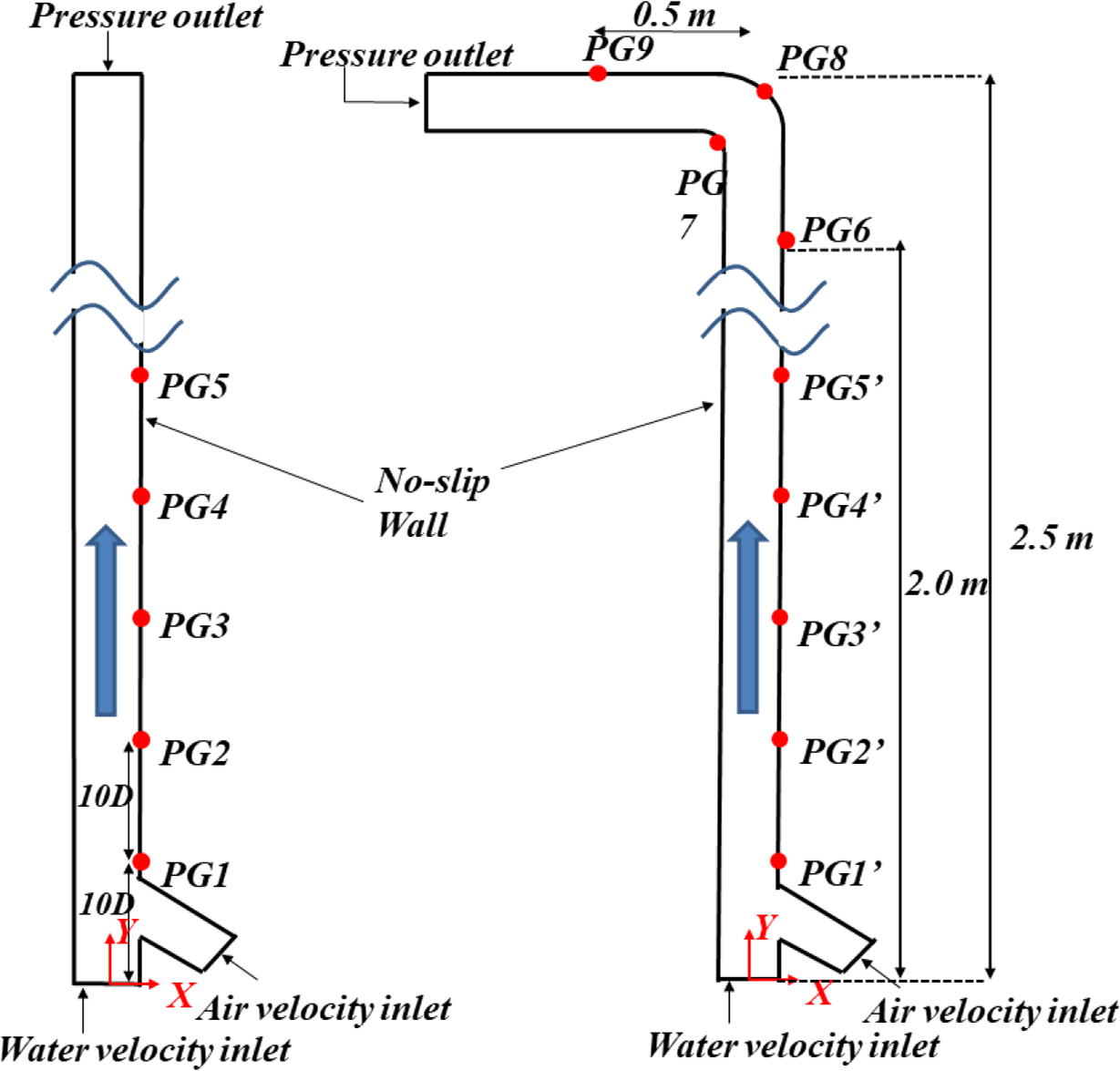
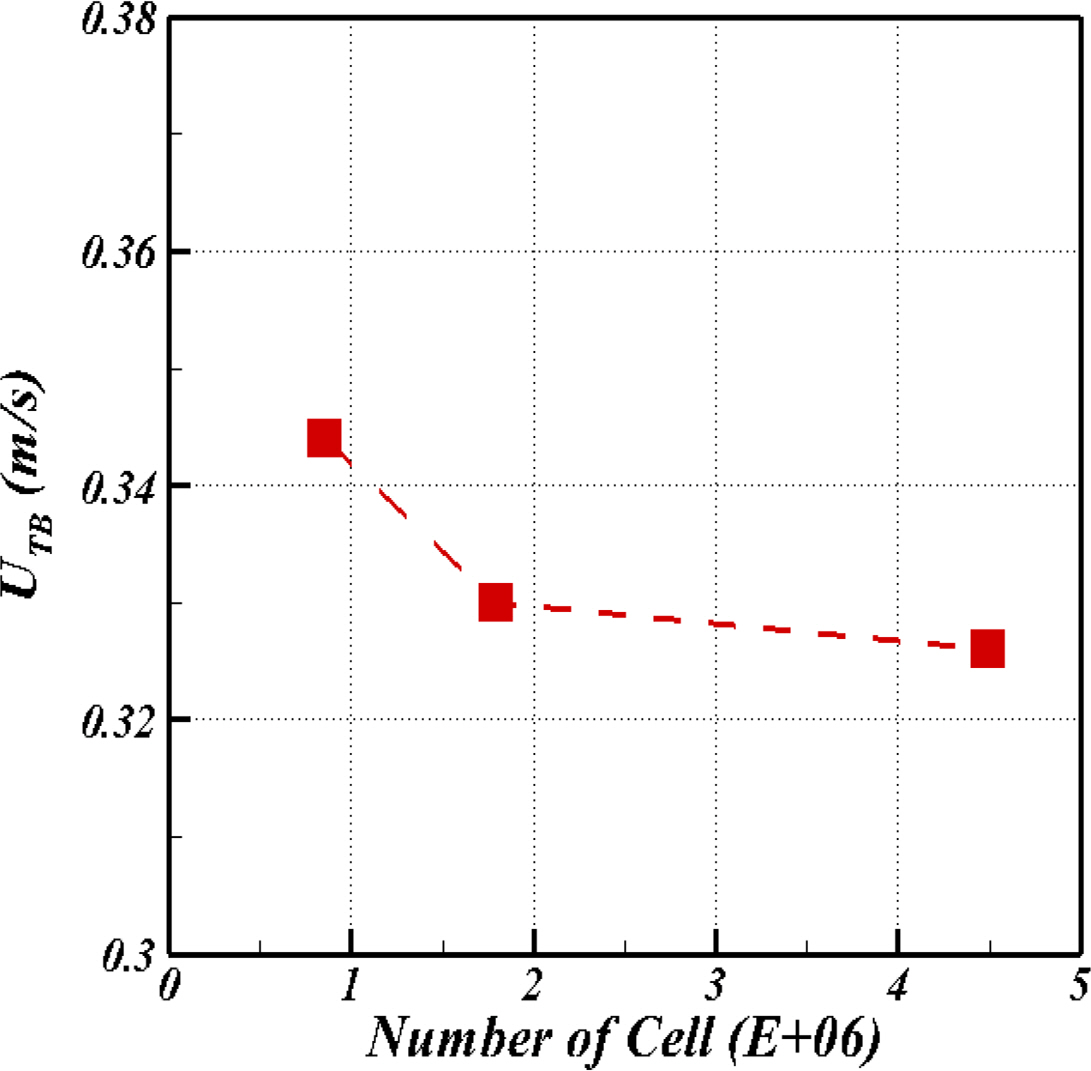
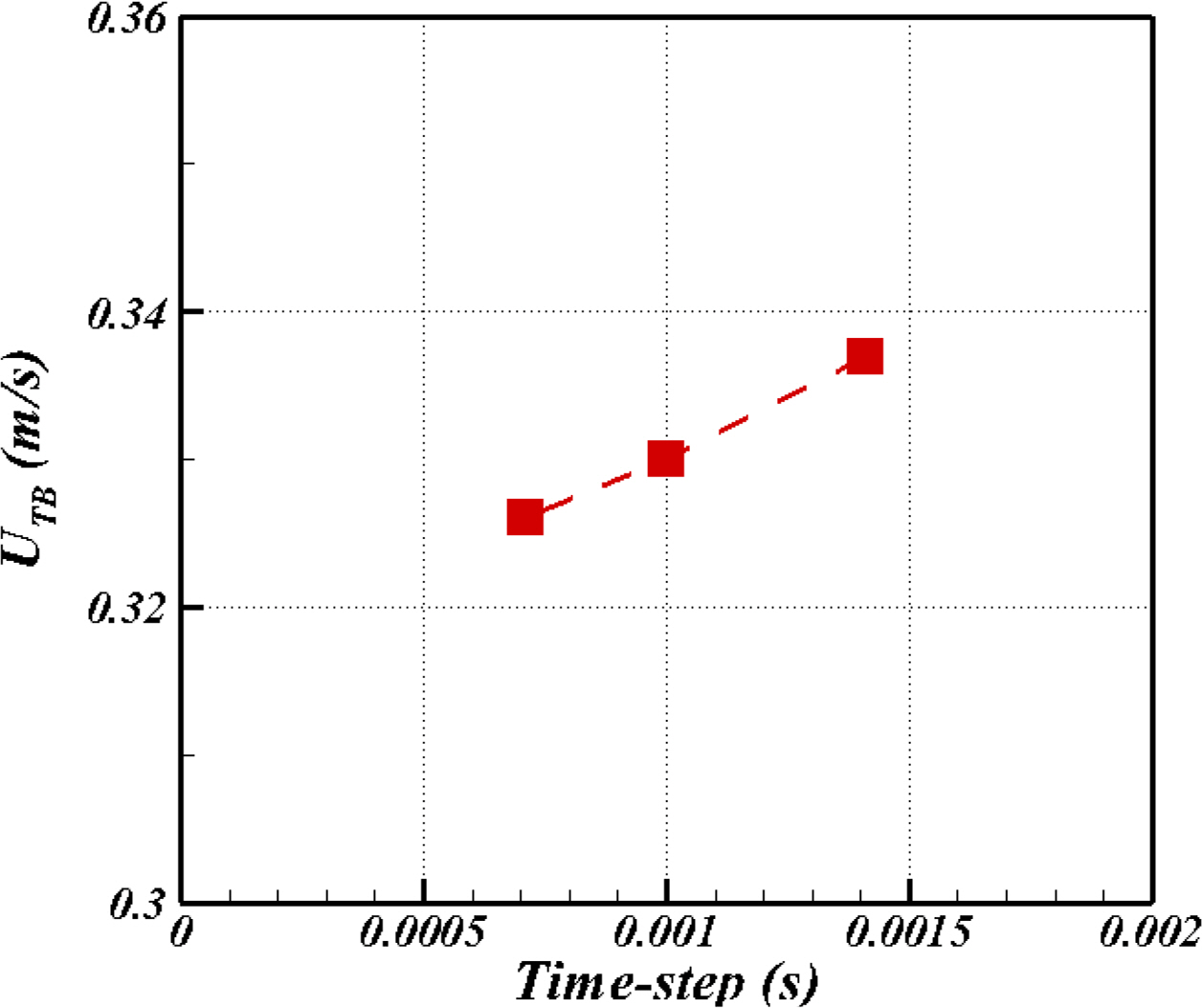
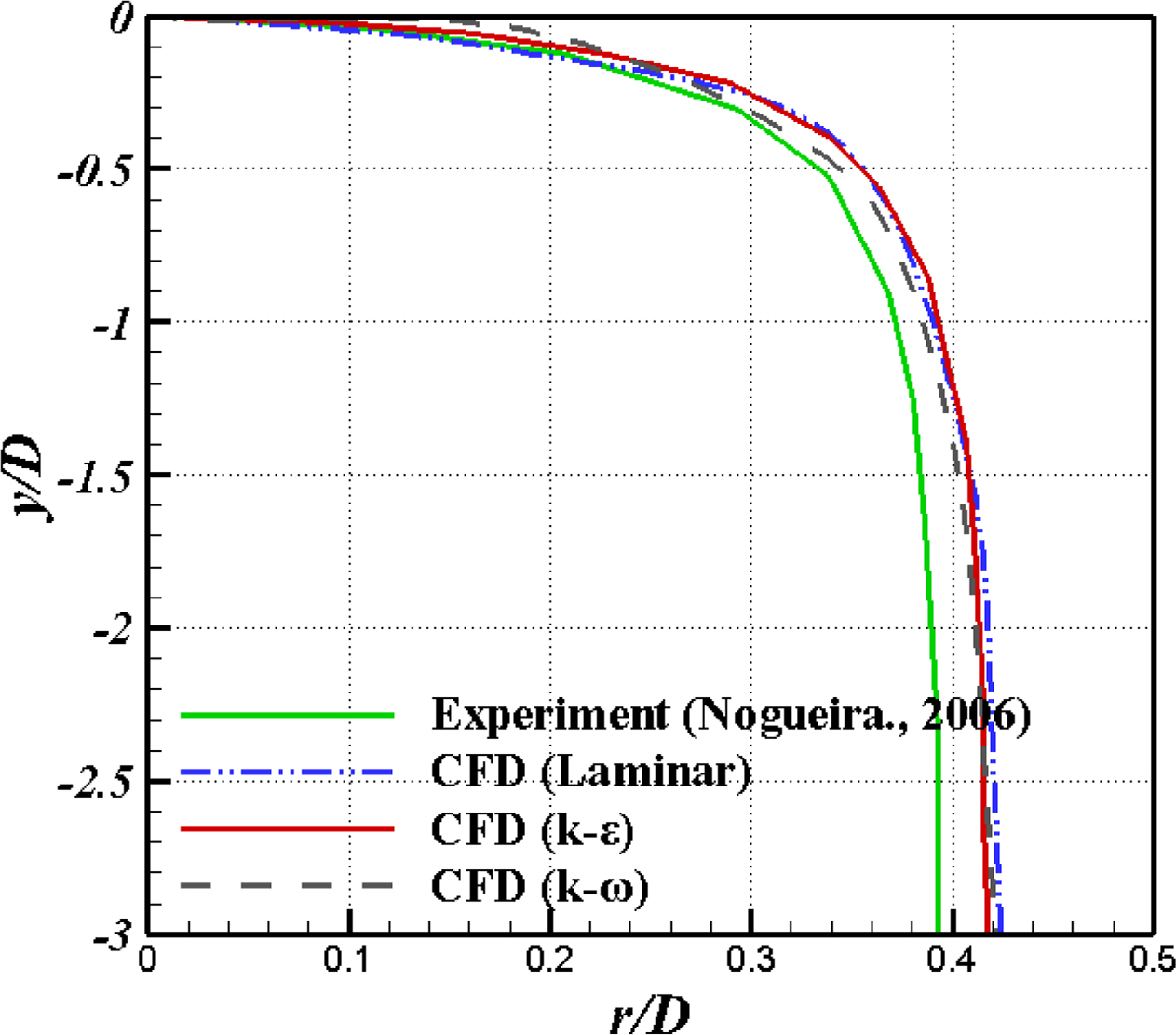
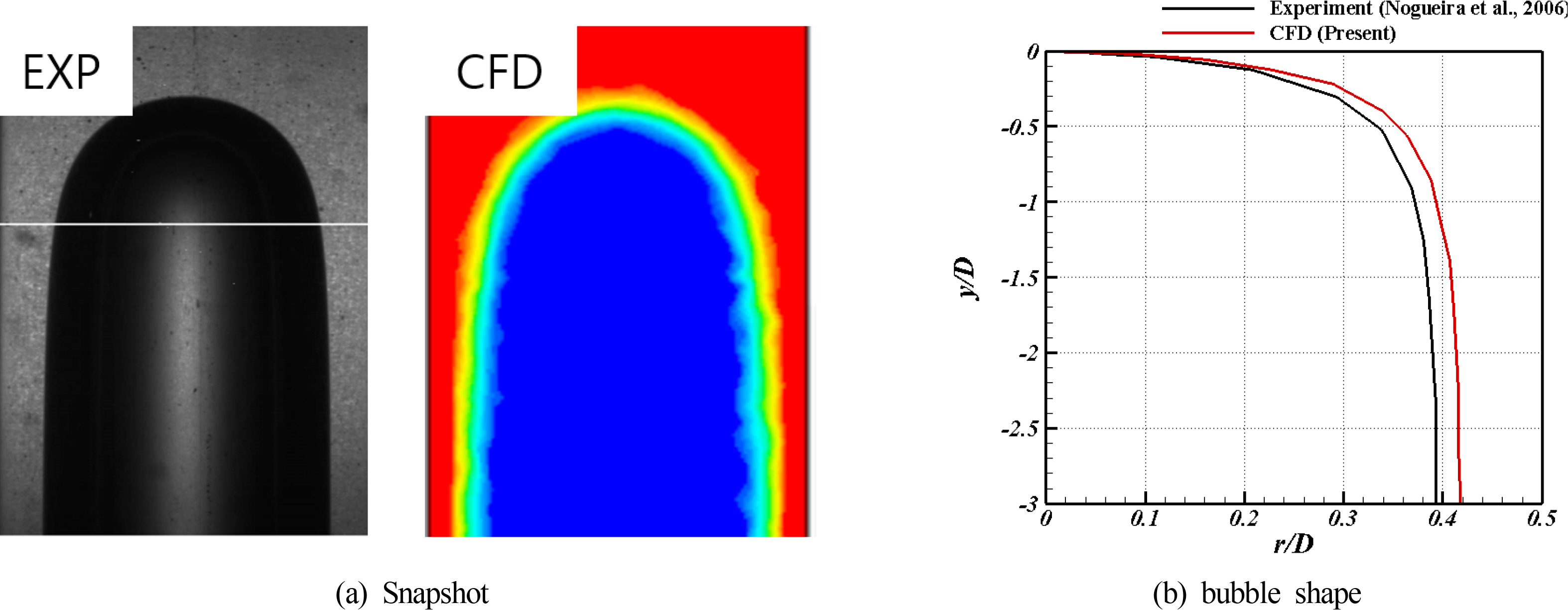
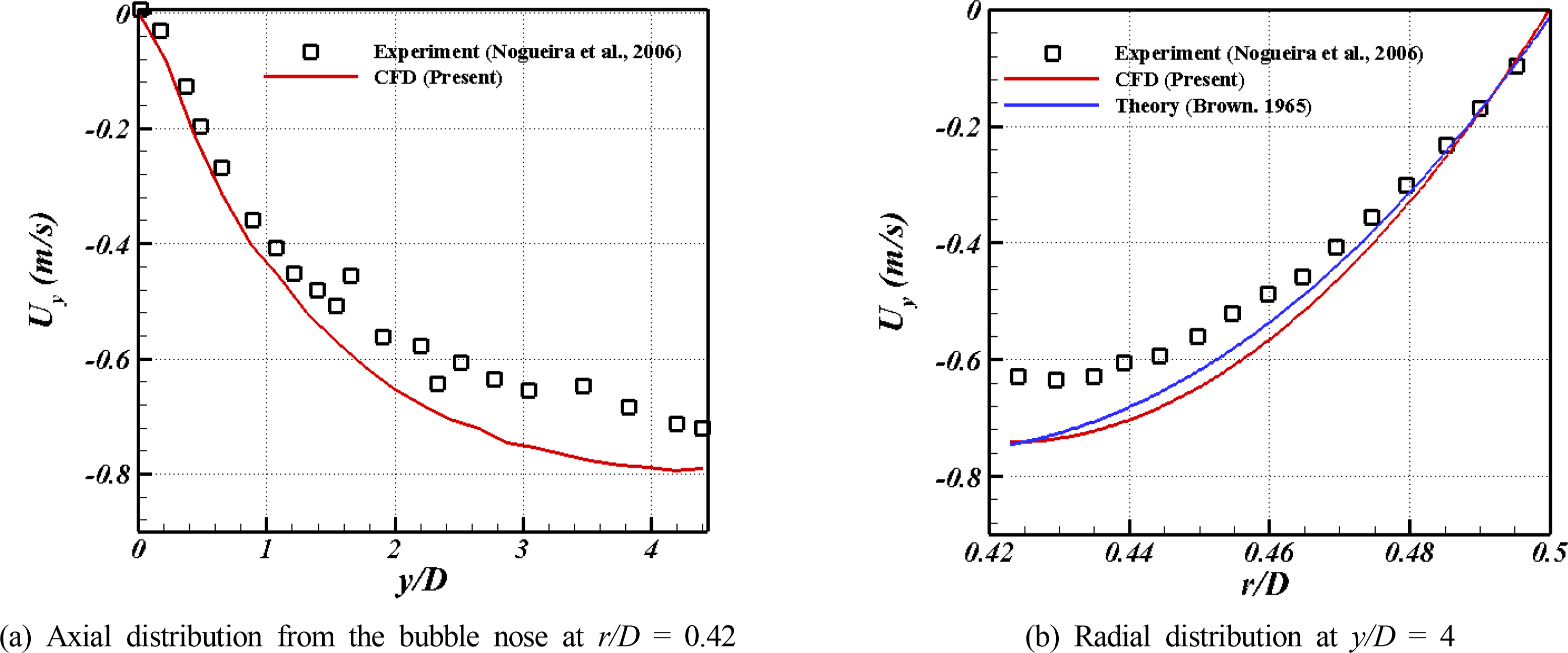
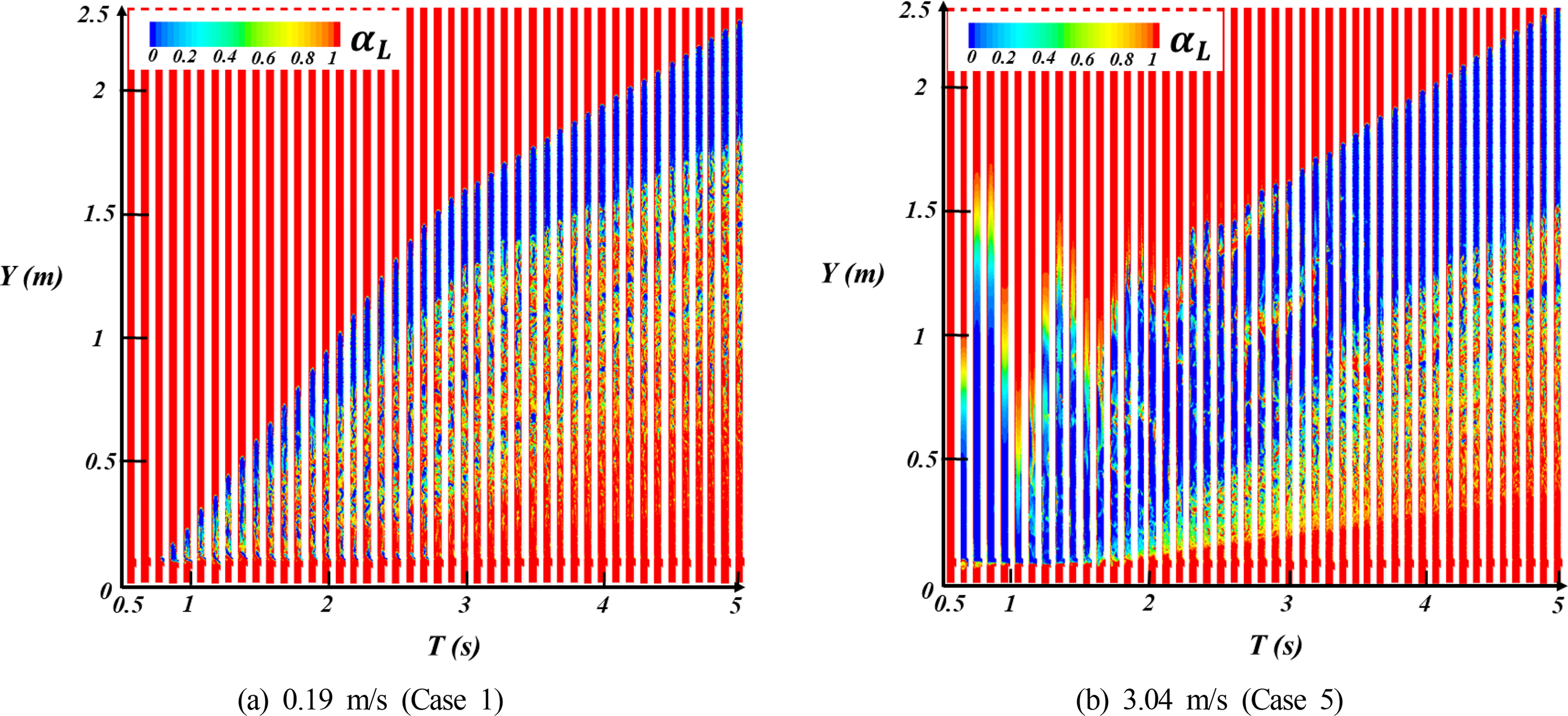
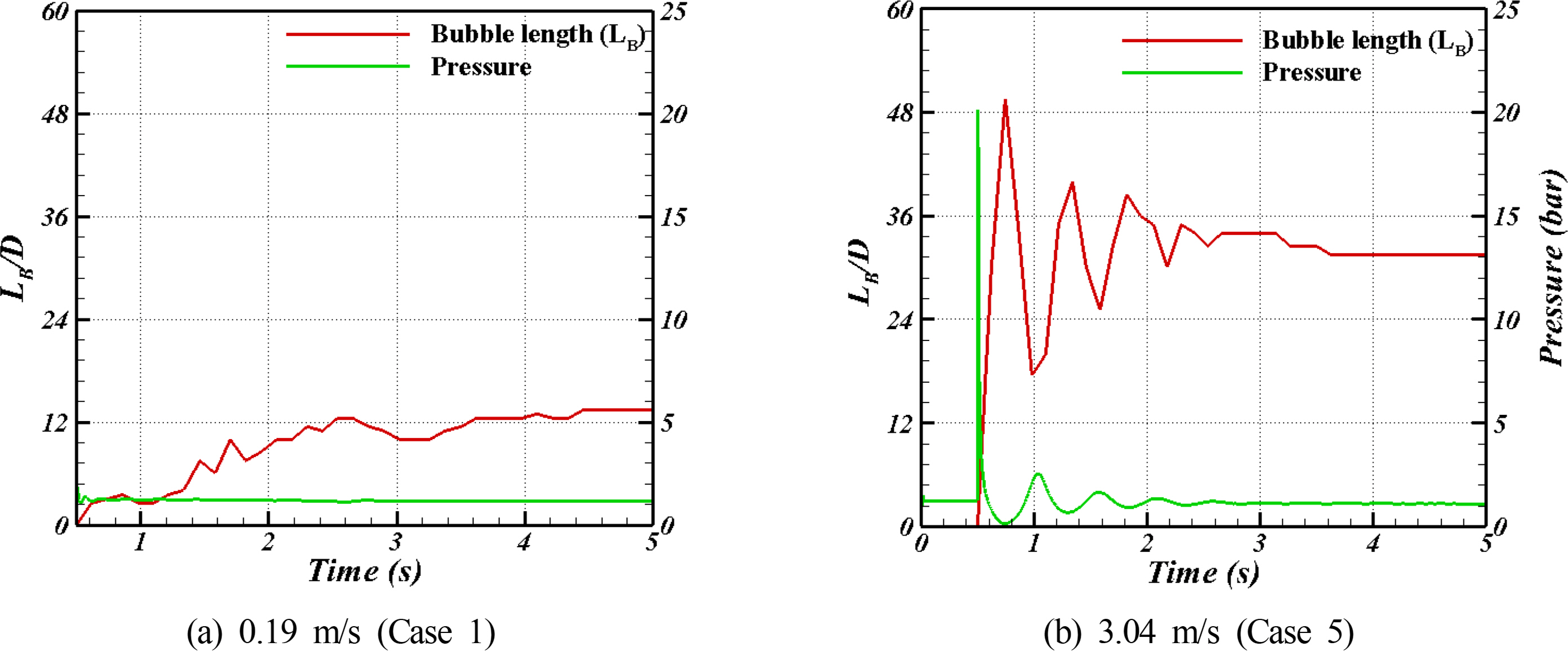
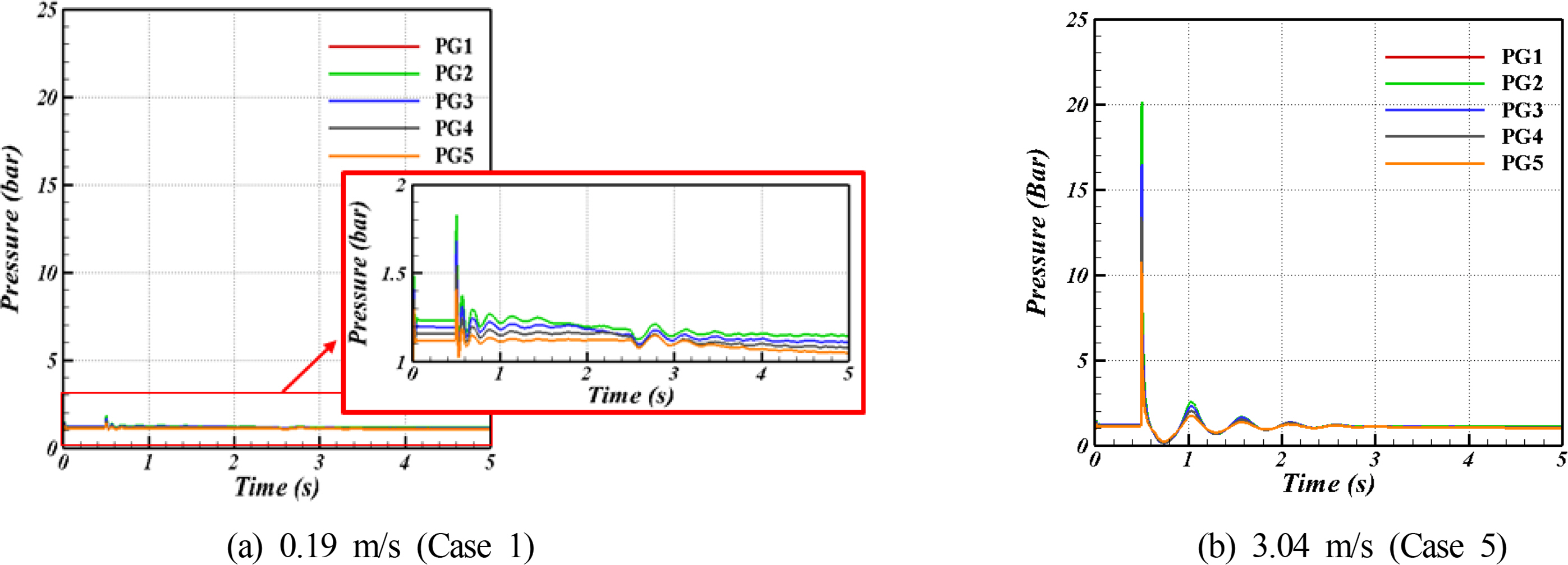
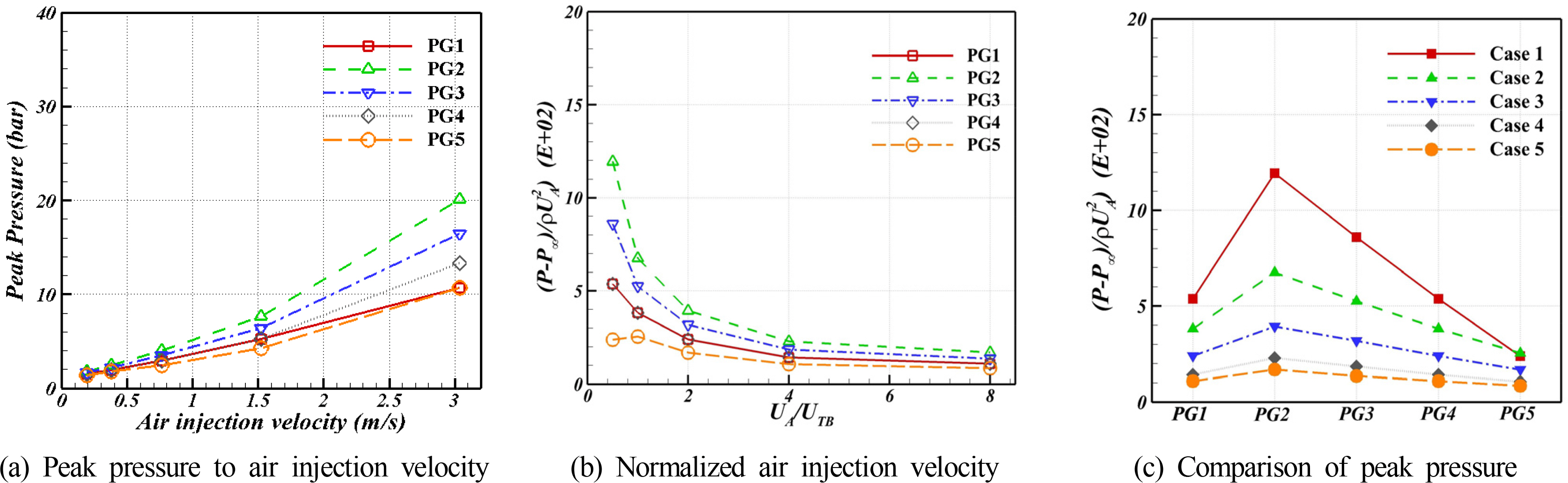
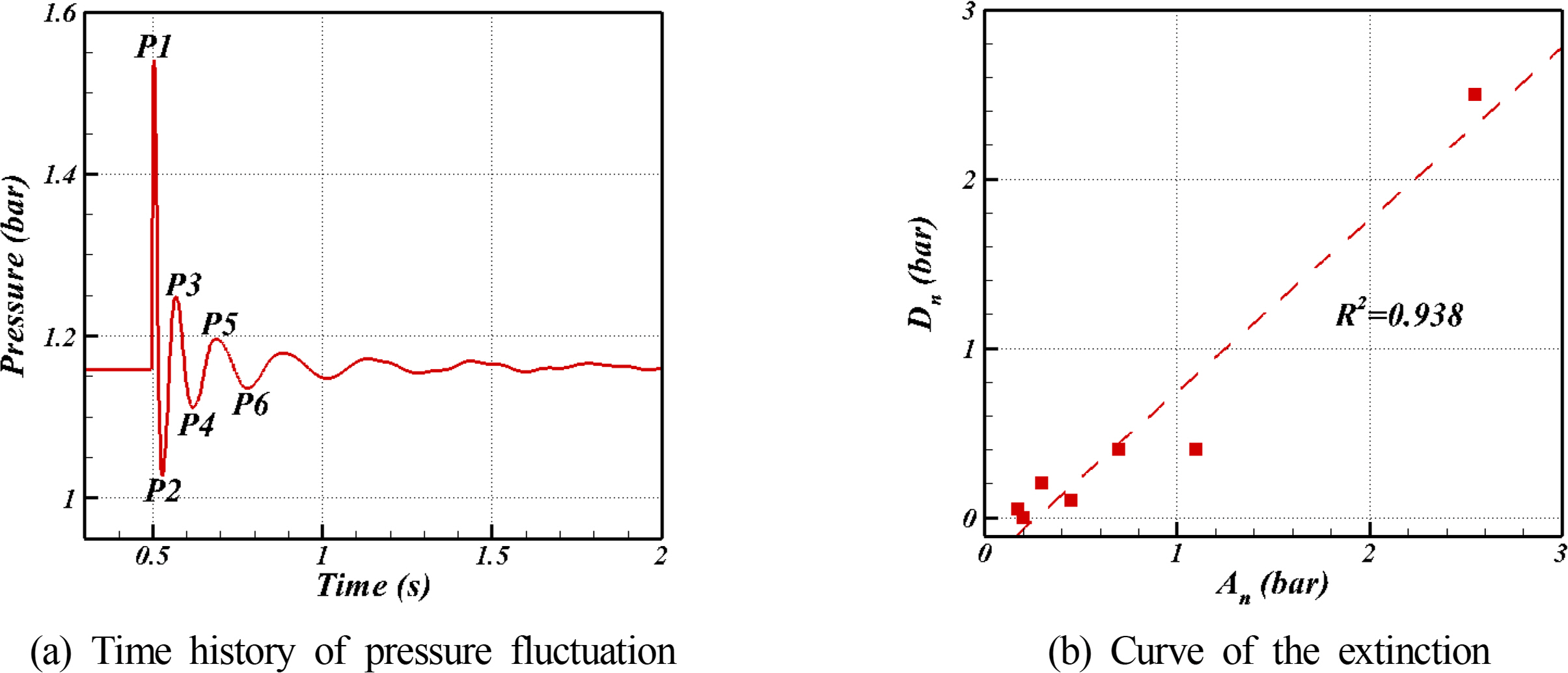
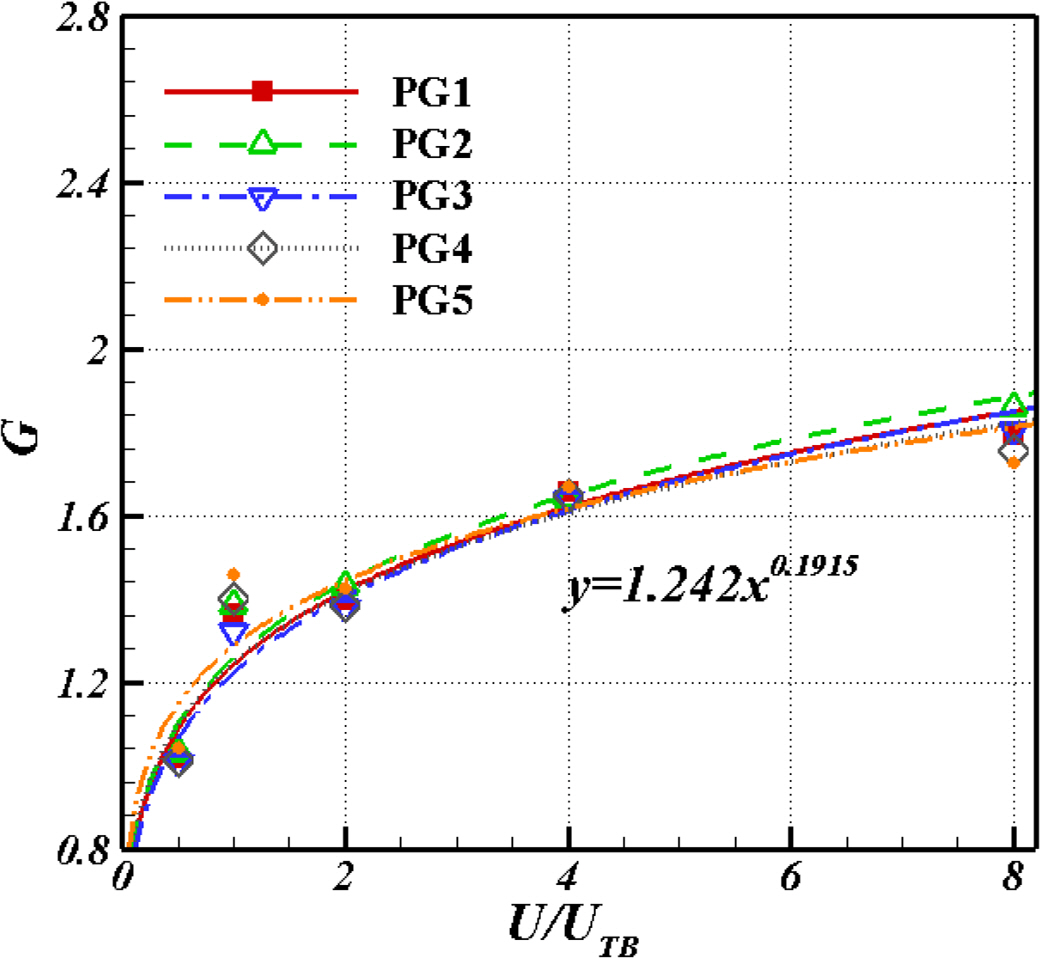
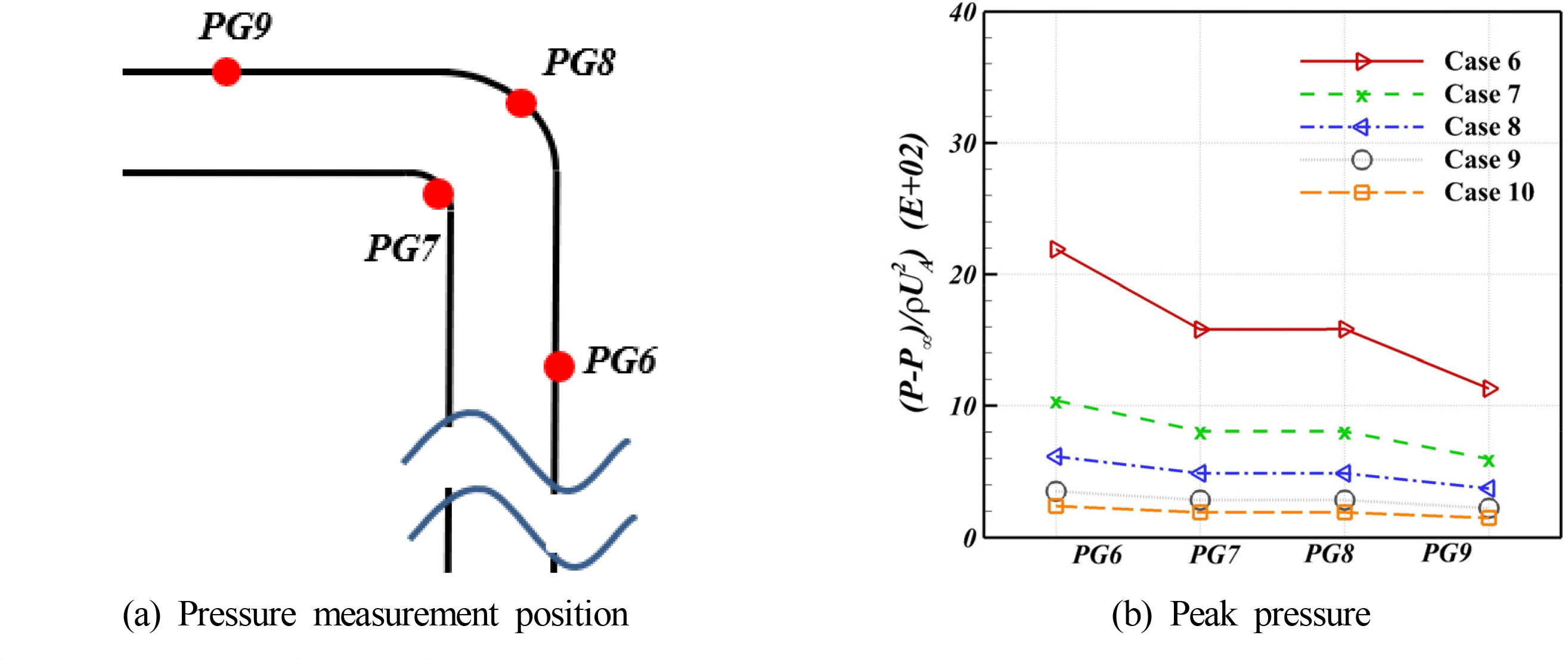
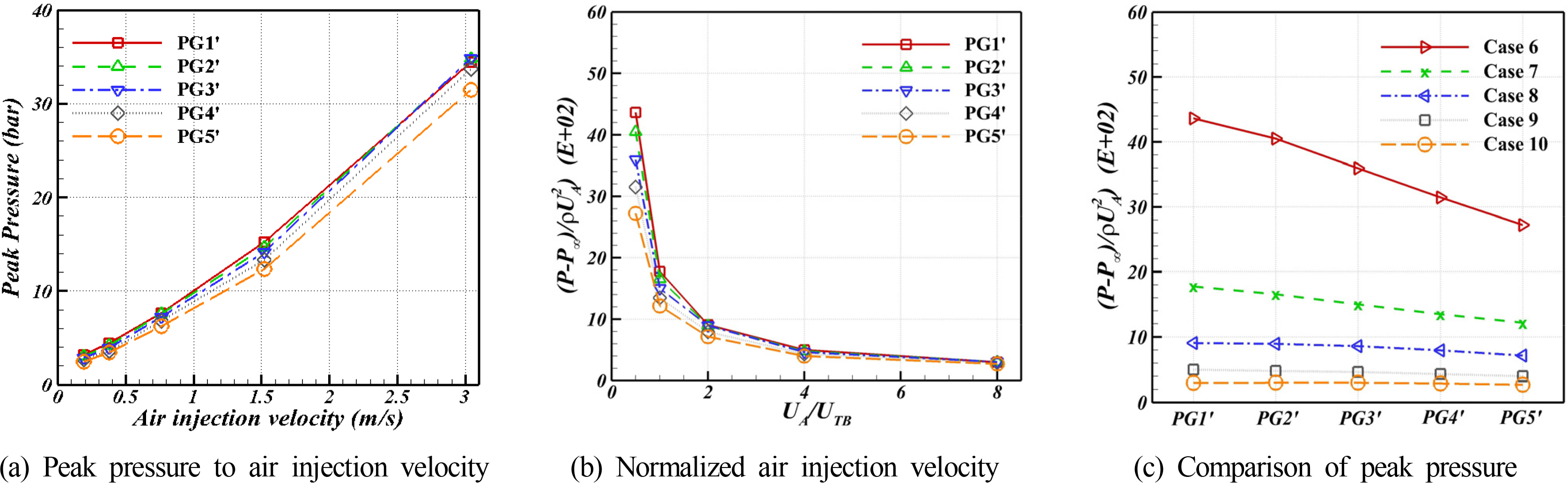
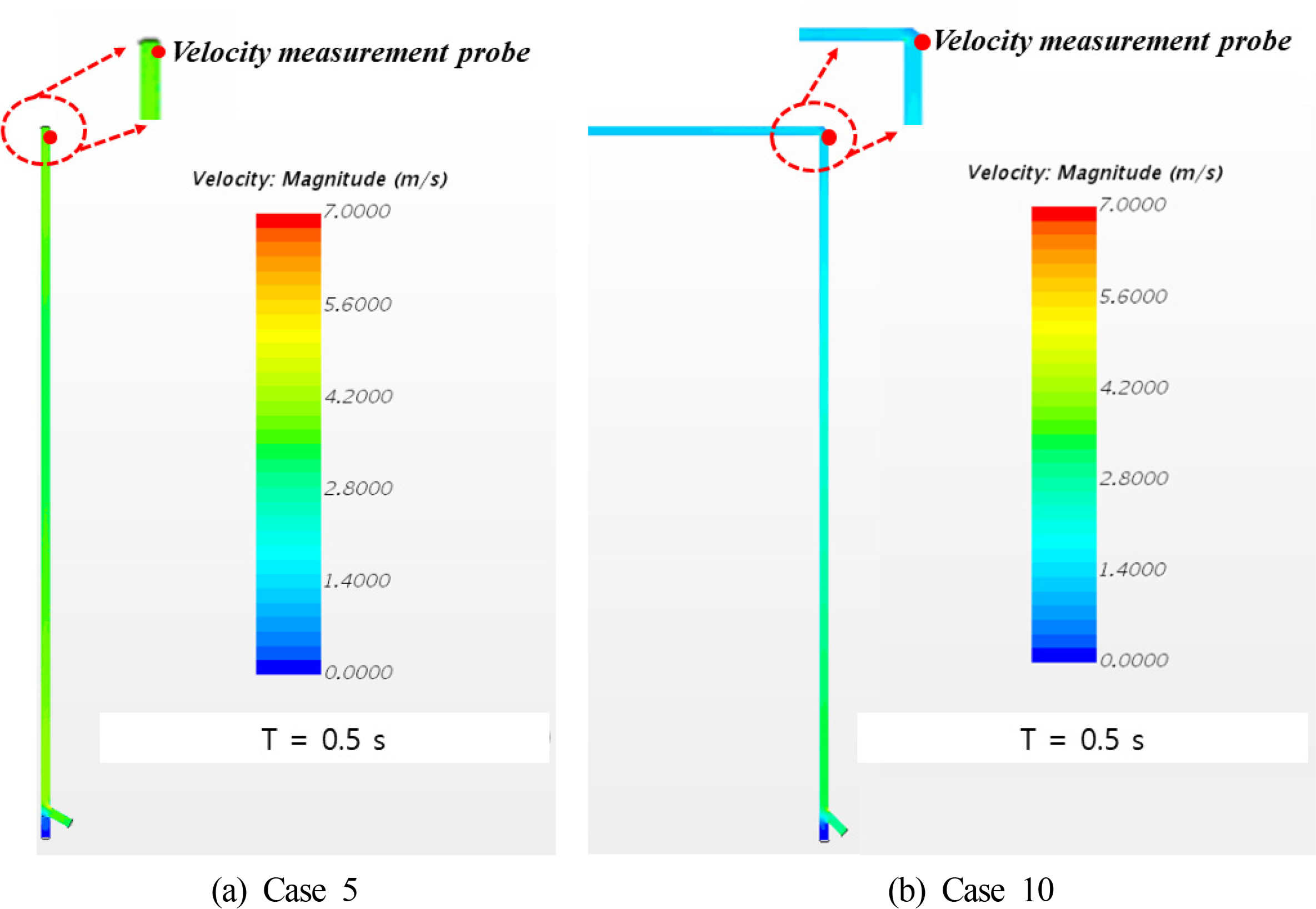
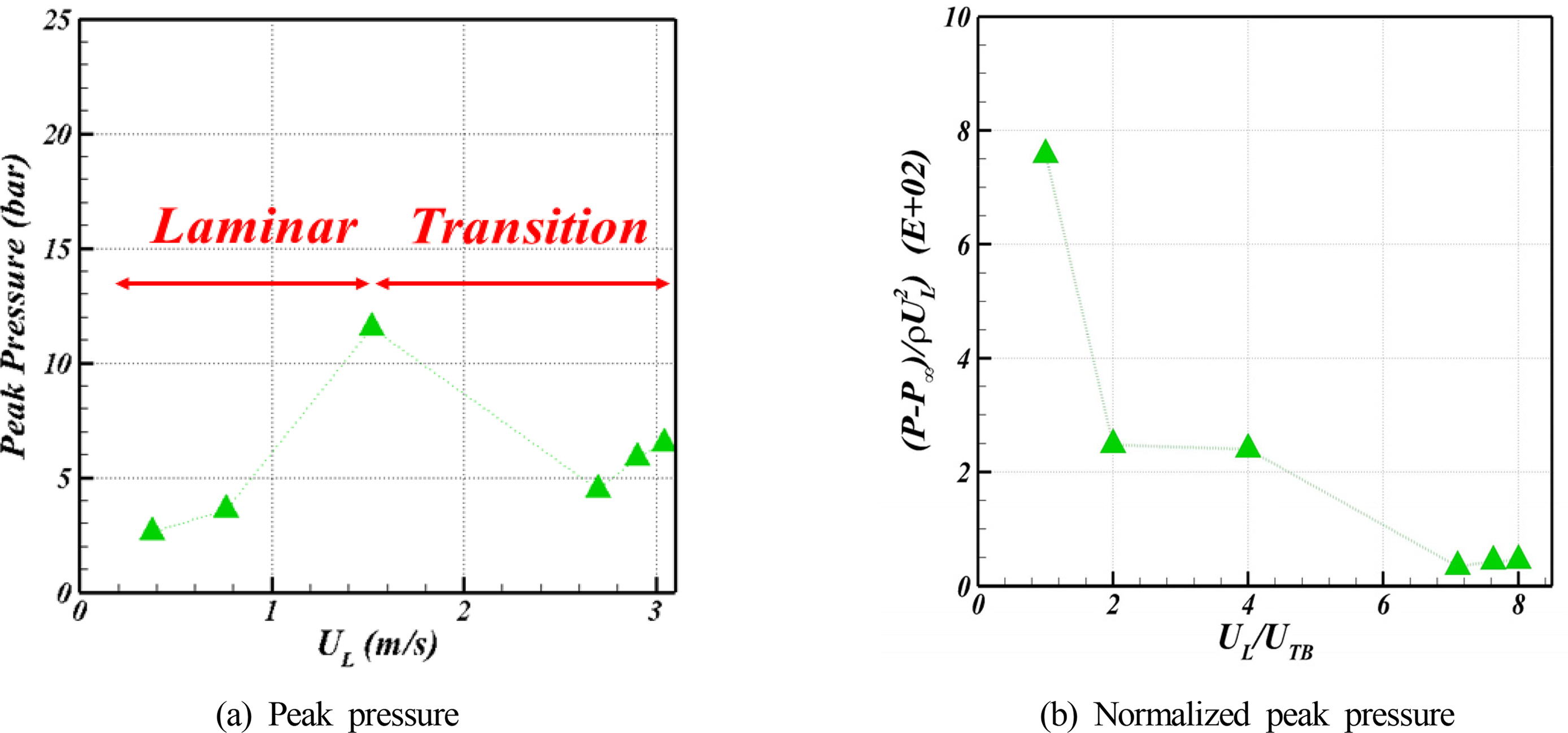
Araújo, JDP., Miranda, JM., Pinto, AMFR., & Campos, JBLM. (2012). Wide-ranging Survey on the Laminar Flow of individual Taylor Bubbles Rising Through Stagnant Newtonian Liquids.
International Journal of Multiphase Flow,
43, 131-148.
https://doi.org/10.1016/j.ijmultiphaseflow.2012.03.007

Bøckmann, A., Pâkozdi, C., Kristiansen, T., Jang, H., & Kim, J. (2014). An Experimental and Computational Development of a Benchmark Solution for the Validation of Numerical Wave Tanks. Proceedings of the ASME 2014 33rd International Conference Ocean, Offshore and Arctic Engineering (Volume 2: CFD and VIV) San Francisco, California, USA: V002T08A092.
https://doi.org/10.1115/OMAE2014-24710

Biberg, D. (2005). Mathematical Models for Two-phase Stratified Pipe Flow (Ph. D Thesis). University of Oslo.
Brennen, CE. (2005). Fundamentals of Multiphase Flow. Cambridge University Press.
Brown, RAS. (1965). The Mechanics of Large Gas Bubbles in Tubes: I. Bubble Velocities in Stagnant Liquids.
The Canadian Journal of Chemical Engineering,
43(5), 217-223.
https://doi.org/10.1002/cjce.5450430501

Bugg, JD., Mack, K., & Rezkallah, KS. (1998). A Numerical Model of Taylor Bubbles Rising Through Stagnant Liquids in Vertical Tubes.
International Journal of Multiphase Flow,
24(2), 271-281.
https://doi.org/10.1016/S0301-9322(97)00047-5

CD-Adapco. (2015). Star-CCM+ 1004 User’s Manual.
Davies, RM., & Taylor, GI. (1950). The Mechanics of Large Bubbles Rising Through Extended Liquids and Through Liquids in Tubes. Proceedings of the Royal Society of London. Series A.
Mathematical and Physical Sciences,
200(1062), 375-390.
https://doi.org/10.1098/rspa.1950.0023

Hirsch, C. (1988). Numerical Computation of Internal and External Flows (Volume 1: Fundamentals of Numerical Discretization). John Wiley and Sons.
Hirt, CW., & Nichols, BD. (1981). Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries.
Journal of Computational Physics,
391, 201-225.

Kang, CW., Quan, S., & Lou, J. (2010). Numerical Study of a Taylor Bubble Rising in Stagnant Liquids.
Physical Review E,
81(6), 066308.

Massoud, EZ., Xiao, Q., El-Gamal, HA., & Teamah, MA. (2018). Numerical Study of an Individual Taylor Bubble Rising Through Stagnant Liquids under Laminar Flow Regime.
Ocean Engineering,
162, 117-137.
https://doi.org/10.1016/j.oceaneng.2018.04.096

Ndinisa, NV., Wiley, DE., & Fletcher, DF. (2005). Computational Fluid Dynamics Simulations of Taylor Bubbles in Tubular Membranes: Model Validation and Application to Laminar Flow Systems.
Chemical Engineering Research and Design,
83(1), 40-49.
https://doi.org/10.1205/cherd.03394

Nicklin, DJ. (1962). Two-phase Flow in Vertical Tubes. Transactions of the Institution of Chemical Engineers, 40(1), 61-68.
Nogueira, S., Riethmuller, ML., Campos, JBLM., & Pinto, AMFR. (2006). Flow Patterns in the Wake of a Taylor Bubble Rising through Vertical Columns of Stagnant and Flowing Newtonian Liquids: An experimental Study.
Chemical Engineering Science,
61(22), 7199-7212.
https://doi.org/10.1016/j.ces.2006.08.002

Polonsky, S., Barnea, D., & Shemer, L. (1999). Averaged and Time-dependent Characteristics of the Motion of an Elongated Bubble in a Vertical Pipe.
International Journal of Multiphase Flow,
25(5), 795-812.
https://doi.org/10.1016/S0301-9322(98)00066-4

Roache, PJ. (1998). Verication and Validation in Computational Science and Engineering. Hermosa Publishers: Albuquerque, NM.
Seo, S., Song, S., & Park, S. (2016). A Study on CFD Uncertainty Analysis and Its Application to Ship Resistance Performance Using Open Source Libraries.
Journal of the Society of Naval Architects of Korea,
53(4), 329-335.
https://doi.org/10.3744/SNAK.2016.53.4.329

Stern, F., Wilson, R., & Shao, J. (2006). Quantitative V&V of CFD Simulations and Certification of CFD Codes.
International Journal for Numerical Methods in Fluids,
50(11), 1335-1355.
https://doi.org/10.1002/fld.1090

Van Hout, R., Gulitski, A., Barnea, D., & Shemer, L. (2002). Experimental Investigation of the Velocity Field Induced by a Taylor Bubble Rising in Stagnant Water.
International Journal of Multiphase Flow,
28(4), 579-596.
https://doi.org/10.1016/S0301-9322(01)00082-9

Zheng, D., & Che, D. (2007). An Investigation on Near Wall Transport Characteristics in an Adiabatic Upward Gas–liquid Two-phase Slug Flow.
Heat and Mass Transfer,
43(10), 1019-1036.
https://doi.org/10.1007/s00231-006-0193-8