A Study on the Dynamic Analysis of Mooring System During Hook-up Installation
Article information
Abstract
This study evaluated the Hook-up installation of an offshore site construction process, which is the final step in an offshore site installation process. During Hook-up installation, the offshore structure can have a detrimental effect on the work stability due to low-frequency motion. Moreover, economic costs can be incurred by the increase in available days of a tugboat. Therefore, this study developed a numerical analysis program to assess the dynamic behavior of mooring systems during hook-up installation to analyze the generally performed installation process and determine when the tugboat should be released. In this program, the behavior of an offshore structure was calculated using Cummin’s time-domain motion equation, and the mooring system was calculated by Lumped mass method (LMM). In addition, a tugboat algorithm for hook-up installation was developed to apply the Hook-up procedure. The model used in the calculations was the barge type assuming FPSO (Floating production storage and off-loading) and has a taut mooring system connected to 16 mooring lines. The results of the simulation were verified by comparing with both MOSES, which is a commercial program, and a calculation method for restoring coefficient matrix, which was introduced by Patel and Lynch (1982). Finally, the offset of the structure according to the number of tugboats was calculated using the hook-up simulation, and the significant value was used to represent the calculation result.
1. Introduction
According to the environment of the operating site, offshore structures that are used to develop submarine resources generally use a range of mooring systems, such as mooring lines, a dynamic positioning system. The offshore structure should be operated on a specific site for a long time, so mooring lines are generally used for safety. The conventional installation procedure of a mooring system is divided largely into four steps, as shown in Fig. 1. First, anchor piles should be installed at the seabed (Anchor installation). Second, mooring lines are connected to the installed anchor pile on the seabed (Pre-laying installation). Third, the constructed offshore structures are transported to the site (Transportation). Finally, the installation process of the mooring system is completed after attaching mooring lines, which are pre-layed on the seabed, with the offshore structure (Hook-up installation). In particular, the likelihood of low-frequency motion during the hook-up installation process is high. Therefore, a work safety assessment is needed to prevent negligent accidents due to the marine environment.
Regarding the general installation of a mooring system in the ocean, Lee (2011) examined the transportation of a truss spar using a barge. Song and Kim (2018) assessed the installation of a suction anchor pile in the deep sea to determine if it is possible to install, dividing three steps: lifting the anchor pile from the barge (Pick-up), passing the water level (Lowering through the splash zone) and putting down the anchor pile on the seabed (Landing). In addition, Yoon and Kim (2018) analyzed pre-laying installation in the deep sea to review work safety.
Before analyzing the motion response of the moored offshore structure, the motion calculation module of the structure is first required. Jo (1991) developed an analysis program that applied frequency domain analysis results using the Green function to the time domain motion equation and studied the dynamic response characteristics of a semi-submersible offshore structure. The reliability was verified by comparing the results of Pinkster’s theory and model experiments. The Lumped mass method (LMM) and Finite element method (FEM) are generally used to analyze the mooring system. The LMM has the advantage of a relatively simple calculation process and fast calculation time (Hwang, 1988).
This study developed the numerical analysis program to calculate the motion response of the offshore structure during the hook-up procedure based on Jo (1991)’s program. The structure has the taut mooring system composed of fiber ropes considering the excessive weight due to an increase in the mooring line length (Park et al., 2017) in the deep sea. The results derived from the developed program were then verified using the commercial program, MOSES (Multi operational structural engineering simulator), and a determination method for restoring coefficient matrix. Finally, the hook-up installation, which is generally known, was analyzed, and dynamic analysis of the mooring system related to the work stability was performed. This paper also suggests the withdrawal timing of a tugboat during the hook-up installation using the results of the simulation.
2. Theoretical Background
2.1 Motion Equation
In this study, the motion response of the floating body was calculated using the time domain motion equation reported by Cummins (1962) as Eq. (1). Time-domain analysis takes relatively more time to yield results than frequency domain analysis, but it can be calculated with high accuracy, including non-linear properties.
2.2 Analysis of Mooring System
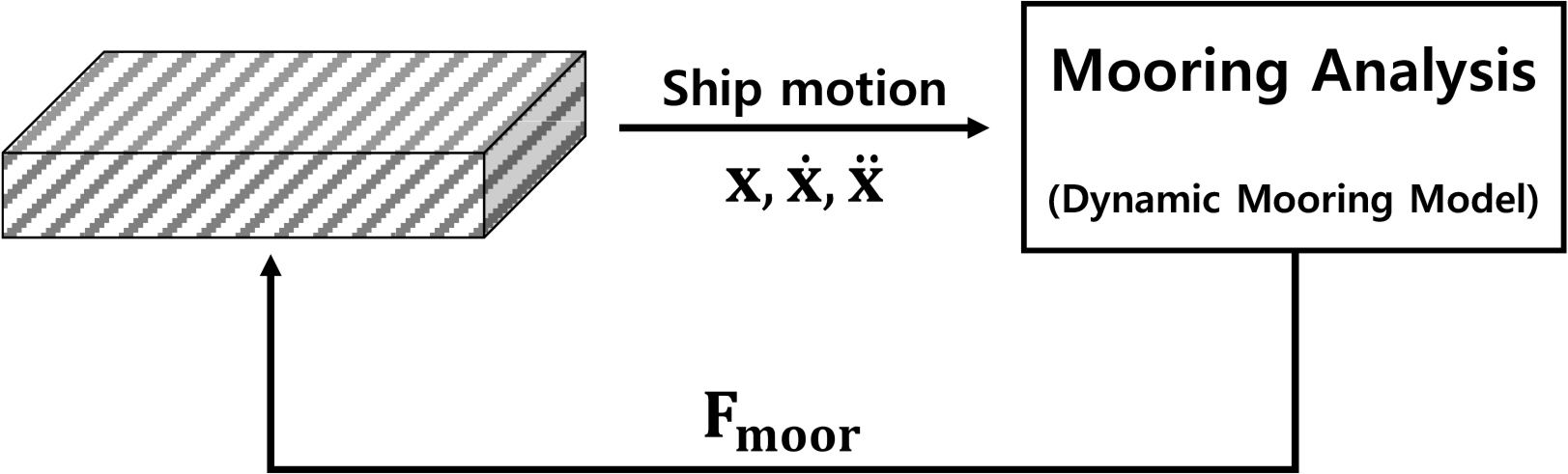
An analysis of the mooring system is classified largely into two steps: static analysis and dynamic analysis. According to Berteaux (1976), it can be possible to calculate the initial coordinate and the tension of mooring lines using the suggested equation, which is about static analysis. The fluctuating tension can be estimated by dynamic mooring analysis. Moreover, dynamic analysis of a mooring system can be performed by applying the displacement information of a floating body derived from the motion equation after conducting static analysis of a mooring system (as shown in Fig. 2). This study estimated the fluctuating tension for dynamic analysis of a mooring system using LMM. The results were verified by comparing it with the determination method of restoring coefficient matrix.
2.2.1 Lumped Mass Method (LMM)
LMM is based on the FEM, which means analyzing the mooring line by dividing the segment according to the number of nodes and imposing mass on each node. At this time, each segment of the mooring line comprised the mass-spring system. Van den Boom (1985) introduced the LMM, which is relatively fast and simplifies the problem of complex mooring systems (Hwang, 1998). In particular, because the calculation, including the mass, is performed, it can analyze the catenary mooring system in the shallow water afterward
2.2.2 Determination Method of Restoring Coefficient Matrix
Patel and Lynch (1982) proposed a 6 × 6 restoring coefficient matrix, which can estimate restoring forces due to the taut mooring system. The fluctuating tension can be calculated by multiplying the matrix suggested by Patel and the displacement matrix of the structure. While Patel’s theory yielded high-accuracy results for the taut mooring system, it did not consider the effects of inertia and damping of mooring lines.
2.3 Wind and Current Force
Wind and current forces that affect a floating body are determined by their respective velocities and the incident angle of the force (Kim et al., 2018). They are defined as Eqs. (2)–(3), respectively. Eq. (4) defines the variation of the projected area by the incident angle.
2.4 Tugboat
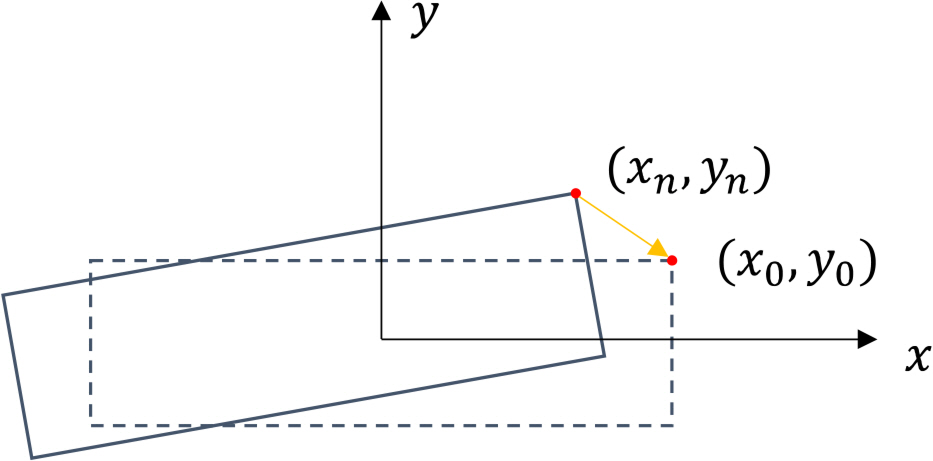
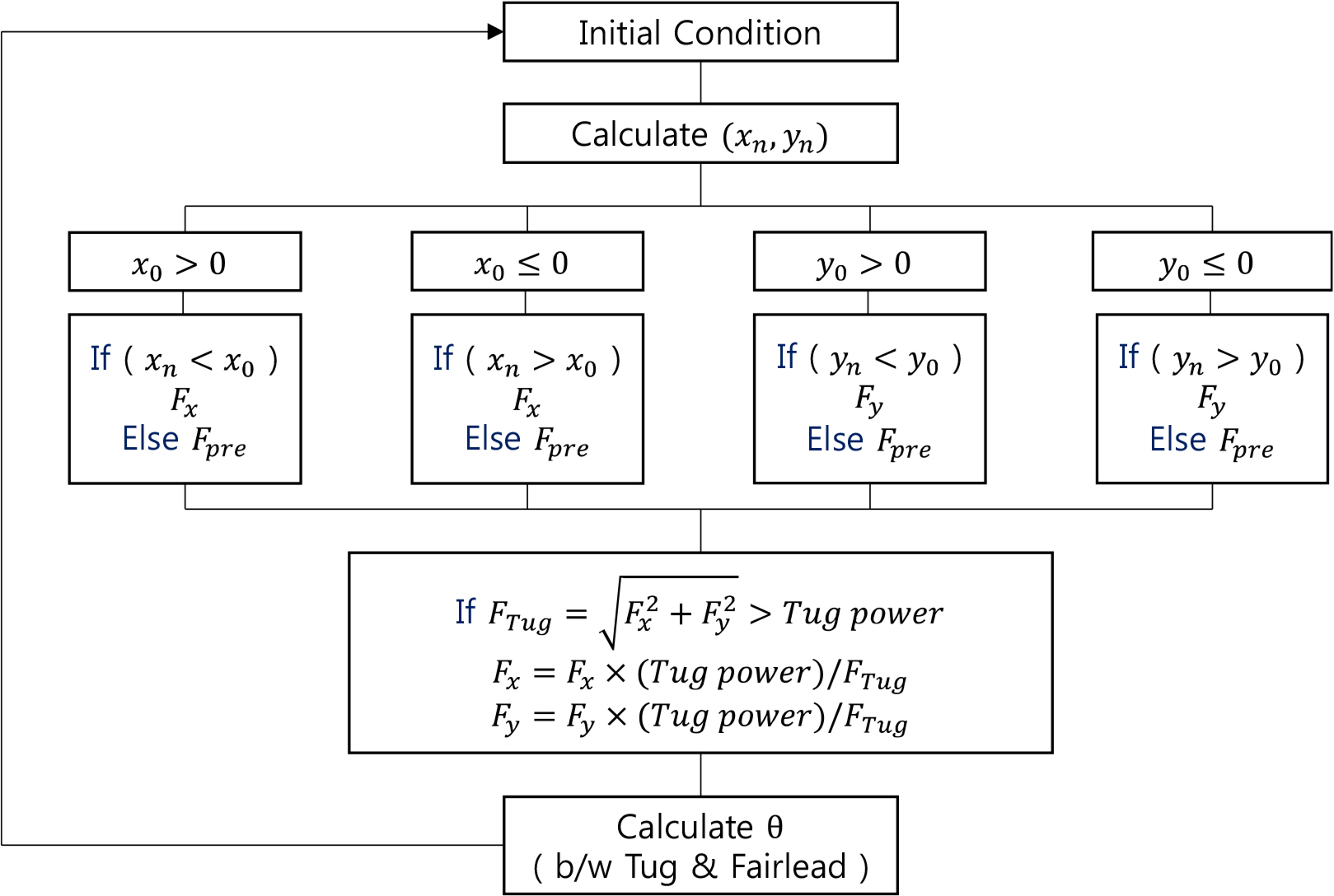
The hook-up algorithm of a tugboat, which is applied in this study, is a method for calculating the fairlead coordinate (xn,yn), which varies at every time step and returns to the initial coordinate (x0,y0), as shown in Figs. 3–4. Each thrust induced by the tugboat is calculated by the relationship between the calculated coordinate (xn,yn) and the initial coordinate (x0,y0), but the thrust does not exceed their maximum capacity. Finally, the position of the tugboat and the relative angle with the structure are calculated and used as the initial condition for the next time step. On the other hand, the motion of the structure by the thrust only considers surge, sway, and yaw (x,y,θz), and the behavior of the tugboat by the external force can be ignored.
2.5 Analysis Process
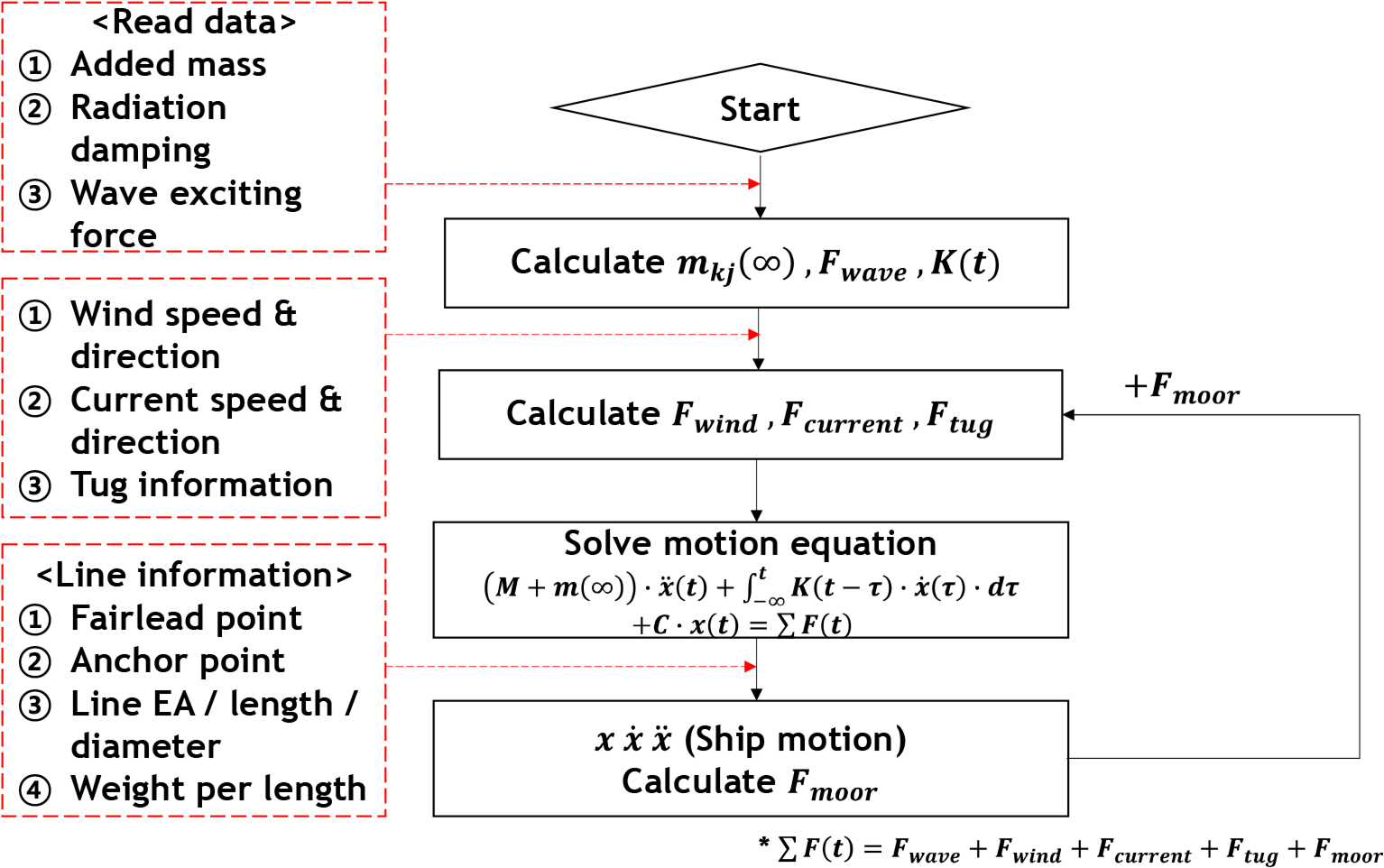
Fig. 5 shows the analysis process of the program developed in this study. First, the infinite frequency-added mass mkj(ω), memory effect function Kkj(t), and wave exciting force Fwave(t) are calculated using the input data: added mass coefficient mkj(ω), wave-making damping coefficient bkj(ω), and the transfer function of wave-exciting force Fwave(t) from the analysis result of the frequency domain. And then, each external force (Fwind(t), Fcurrent(t), Ftug(t)) is calculated by applying their information, and numerical simulation is performed, including the external force term of the motion equation. Finally, the fluctuating tension of the mooring line Fmoor is calculated using the displacement information of the structure and mooring information. The iterative calculation is then performed by including this force (Fmoor) in the external force term of the motion equation at the next step.
3. Validation of the Program
3.1 Definition of the Model and Mooring System
The structure used in this study is a barge model that assumes Floating production storage and off-loading (FPSO). Table 1 and Fig. 6 present the main dimension and shape of the model, respectively.
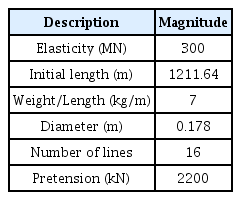
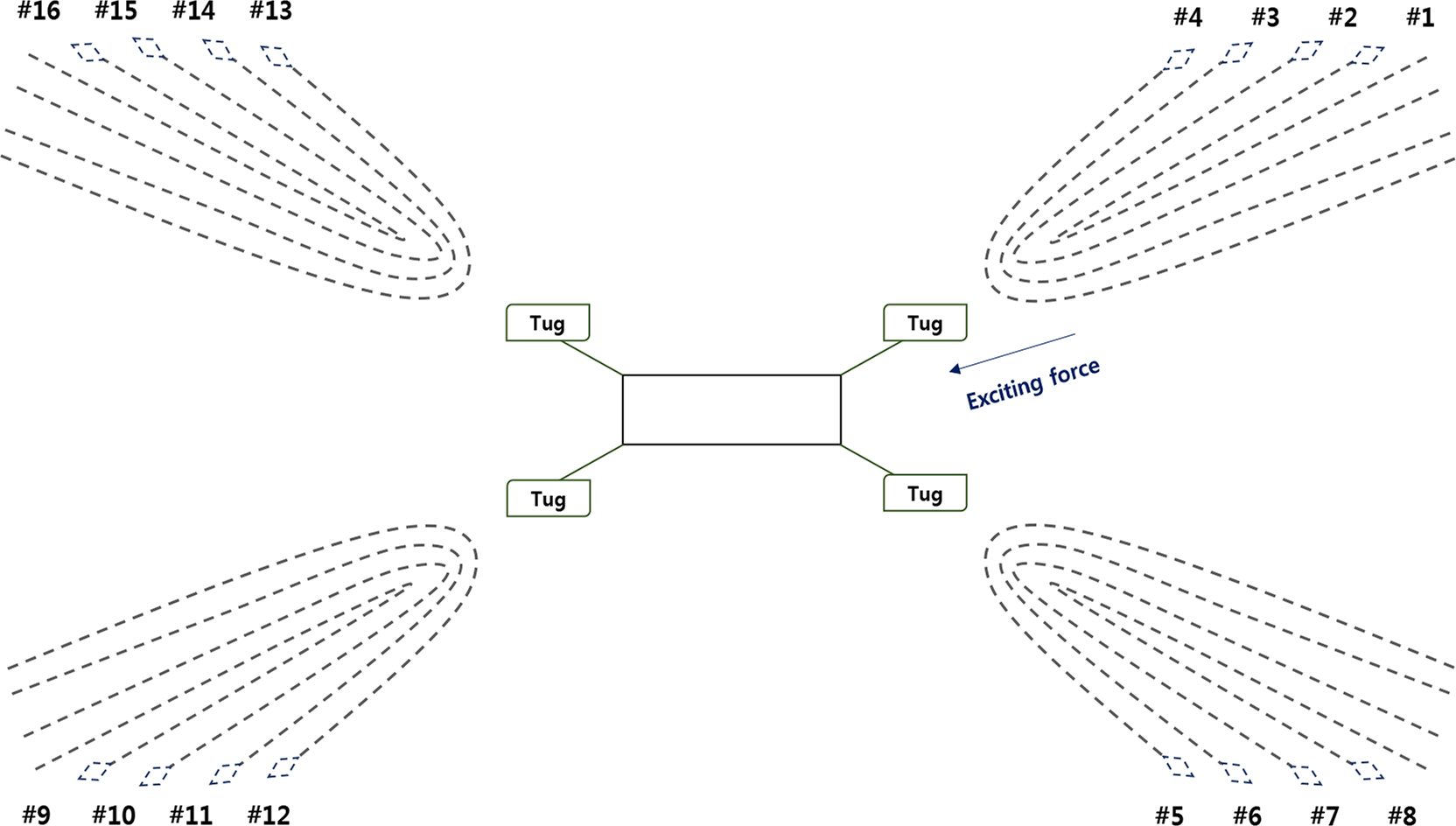
The mooring type is a taut mooring comprised of fiber ropes. In addition, 16 mooring lines consist of four bundles of four each and are spread structure (as shown in Fig. 7). Table 1 lists the main dimensions of the mooring line.
3.2 Motion Response
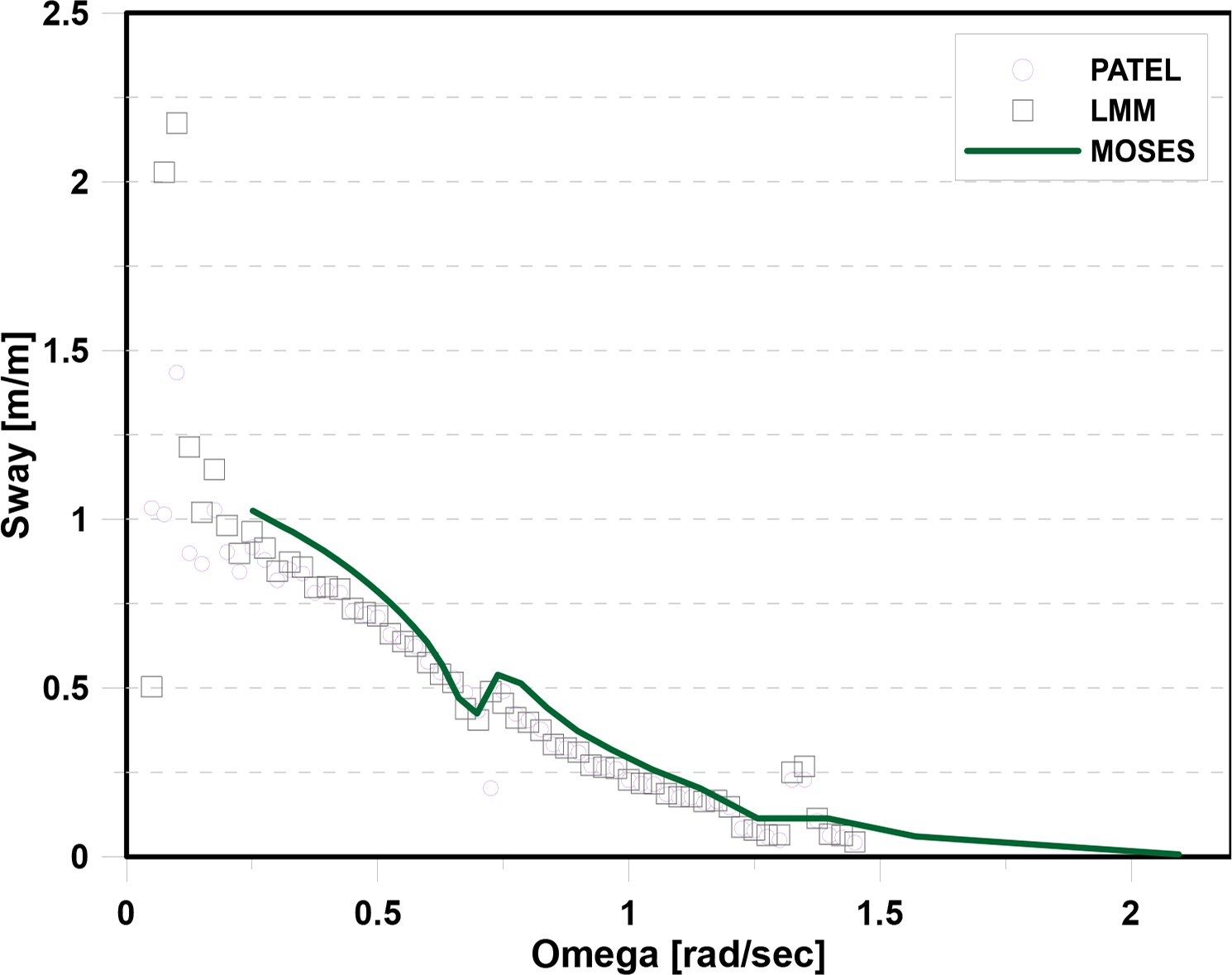
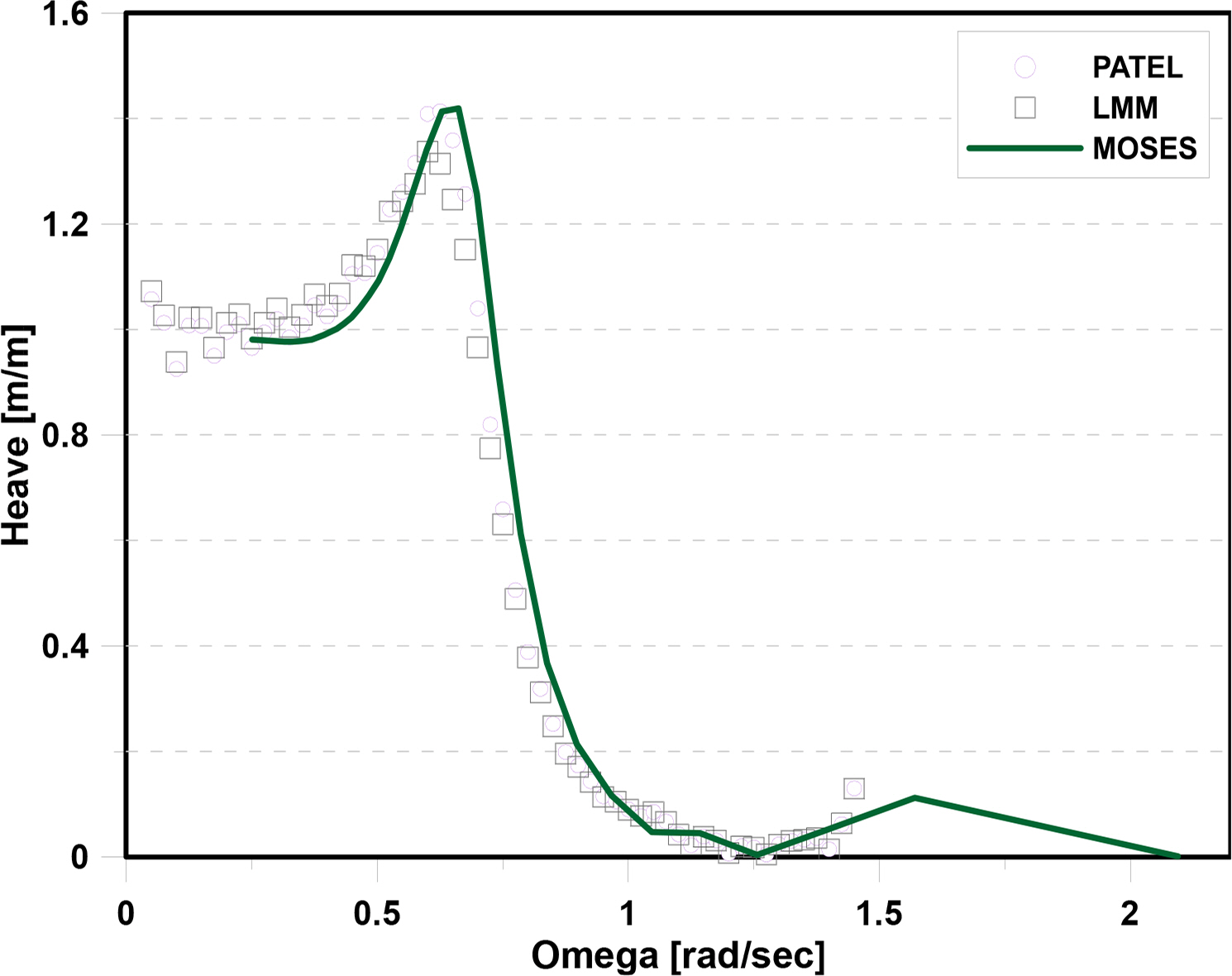
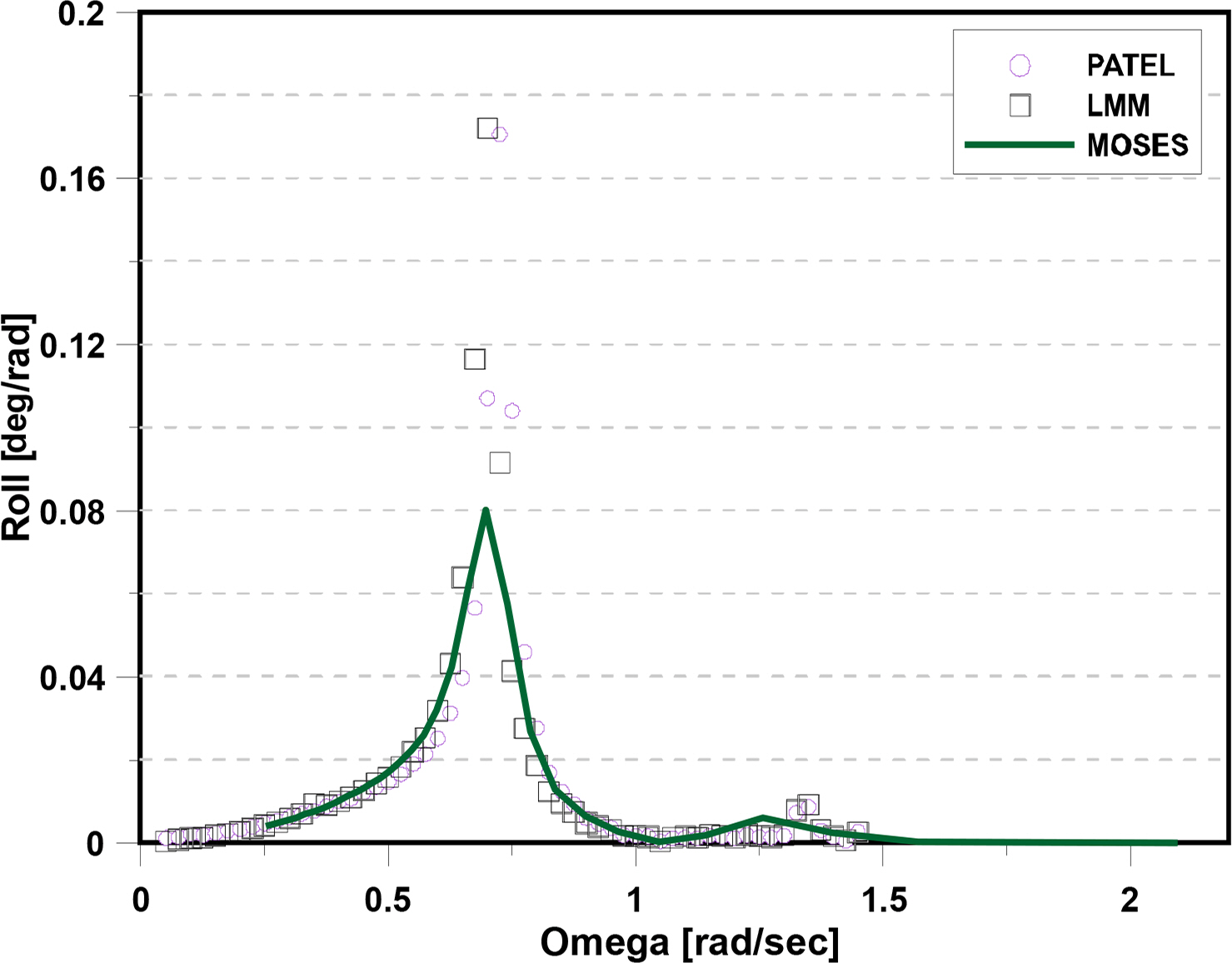
To verify the analysis results of the program (LMM) developed in this study, the motion response results of the moored structures are compared using MOSES and Patel’s theory (as shown in Figs. 8–10). Each graph represents the motion response to sway, heave, and roll, and they are in good agreement.
3.3 Hook-up Algorithm of a Tugboat
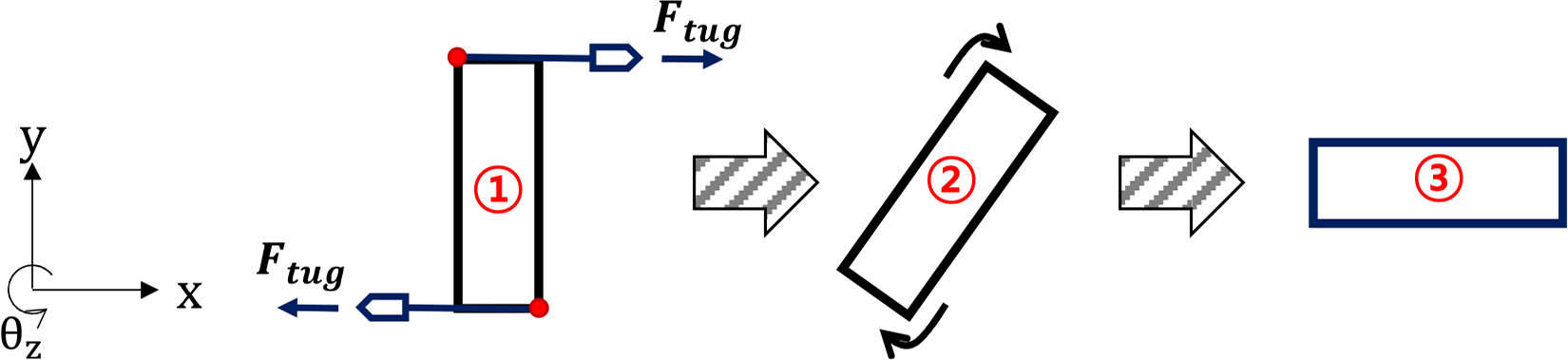
Tugboats are used for station keeping of the structure in the hook-up procedure. The analysis results of MOSES are compared to determine if the algorithm of the tugboat applied in this study is suitable for an analysis of the hook-up procedure. First, the structure and two tugboats are positioned, as shown in ① of Fig. 11, and when a thrust is generated by tugboats in both horizontal directions, an examination is performed to determine if the structure rotates to the target position, as shown in ③ of Fig. 11. Fig. 12 shows the analysis results of LMM and MOSES. In the case of LMM, the structure converges to the target position (0°), as shown in ③ of Fig. 9, but in the case of MOSES, it converges to −18.39°. According to Bentley systems (2016), the tugboat can be analyzed by receiving the initial towing direction and the maximum capacity of the tugboat. Once the towing direction is applied, it is towed at a certain angle without change until the end time of the calculation. Therefore, the calculated result in MOSES does not converge to 0°, as shown in ③ of Fig. 11, but converges to −18.39°, where the two tugboats and the structure are in equilibrium.
4. Hook-up Simulation
The hook-up installation refers to lifting the mooring line previously arranged on the sea bed and connecting it with the structure that has arrived at the installation site. The dynamic behavior of the structure can be controlled using several tugboats and, at the same time, proceeds with a hook-up installation using AHTS (Anchor handling tug supply vessels) and ROV (Remotely operated vehicle). The procedure can be planned in various ways depending on the environmental conditions, shape of the structure, number of mooring lines, and mooring method. In this study, an analysis was conducted on the hook-up procedure, which is generally performed during offshore installation work.
4.1 General Hook-up Procedure
The hook-up installation procedure is generally performed as shown in Table 3. ‘Step’ is the order of installation, ‘Line number’ is the number assigned to each mooring line, and ‘Pre-tension’ is the ratio of the designed initial tension. After the structure arrives at the site, Step 1 represents the waiting situation before the hook-up installation, and Steps 2–5 mean that each mooring line is connected to the structure and maintains 50% of the designed pre-tension. When the four lines and the structure are in equilibrium, the designed pre-tension is set in Step 6 (Pre-tension: 100%). The pre-tension can be adjusted using winches inside the structure, and Steps 7–21 are repeated in the same way as the work of Steps 2–6. The mooring line arrangement, at this time, is shown in Fig. 13.
4.2 Environmental Condition
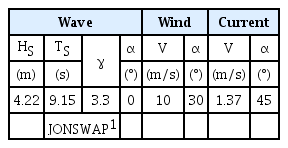
According to DNV (2011), an appropriate environmental condition should be selected considering the working period when conducting an offshore construction. In this case, the work period was expected to take approximately one month. The environmental conditions at this time were selected, as shown in Table 4, by referring to Yoon and Kim (2018) and DNVGL (2018).
4.3 Hook-up Simulation
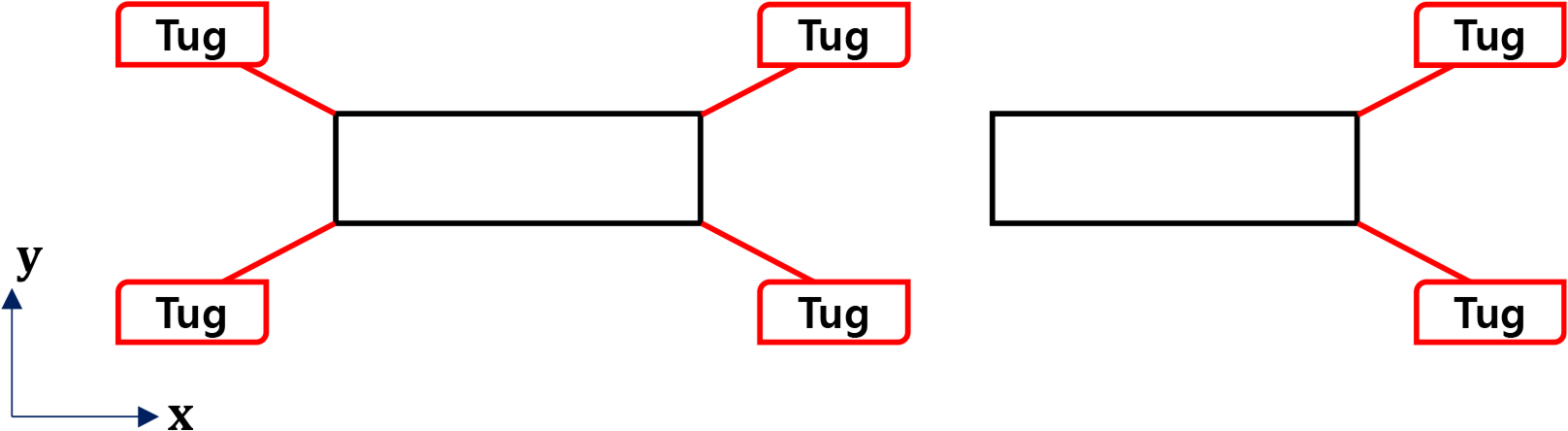
In this study, a simulation was performed to evaluate the stability of the structure during hook-up installation. Table 5 lists the main dimensions of the tugboat for station keeping of the structure, and Fig. 14 shows the arrangement of the tugboat. In the simulation, the analysis was performed for all hook-up procedures (Steps 1—21) for the case where four tugboats were arranged (Tug 4). For two tugboats (Tug 2) and no tugboat (Tug 0), the analysis was performed from Step 6, where four mooring lines were connected and adjusted to designed pre-tension, to Step 21.
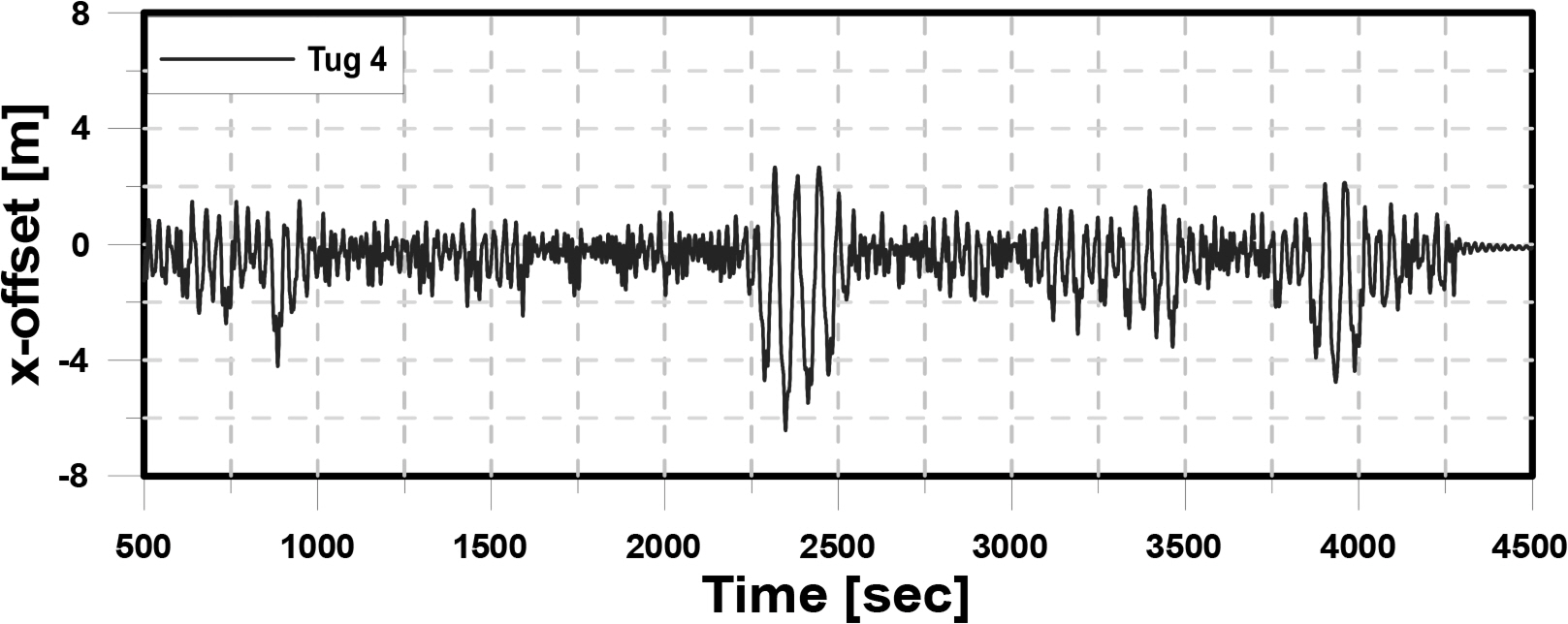
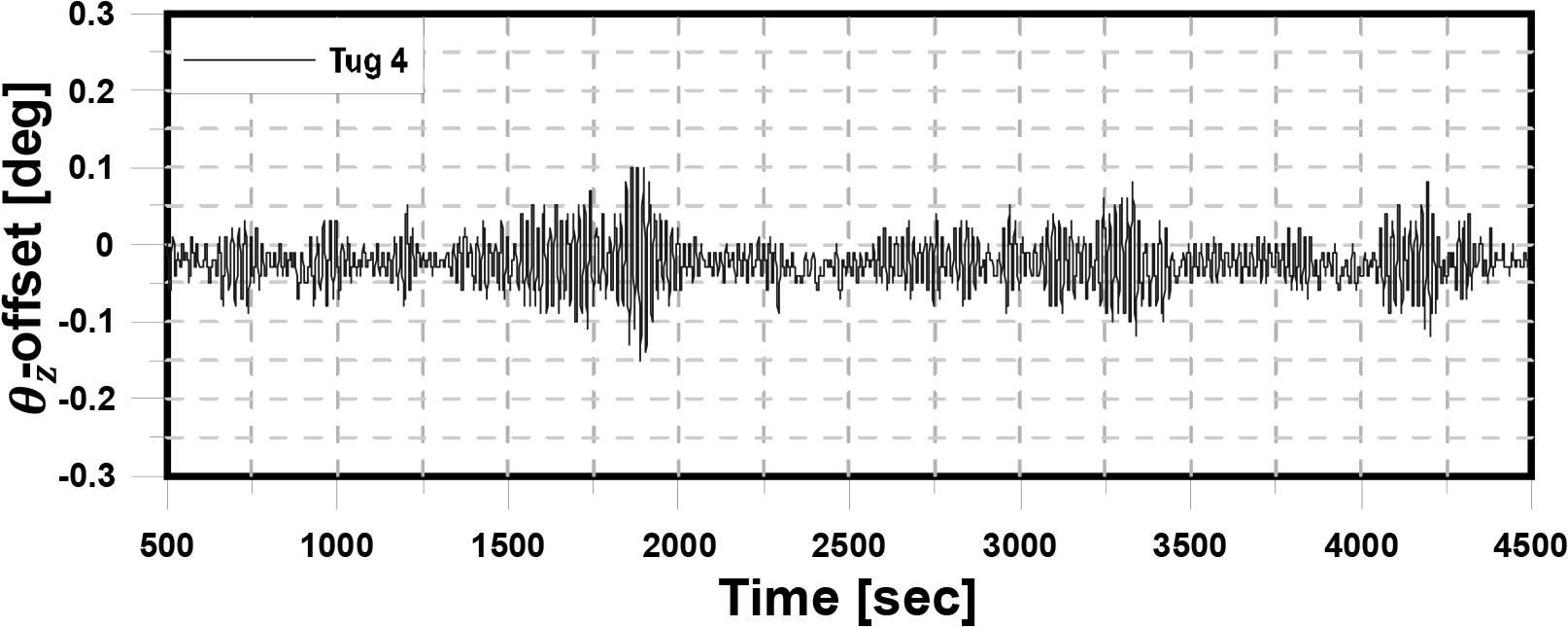
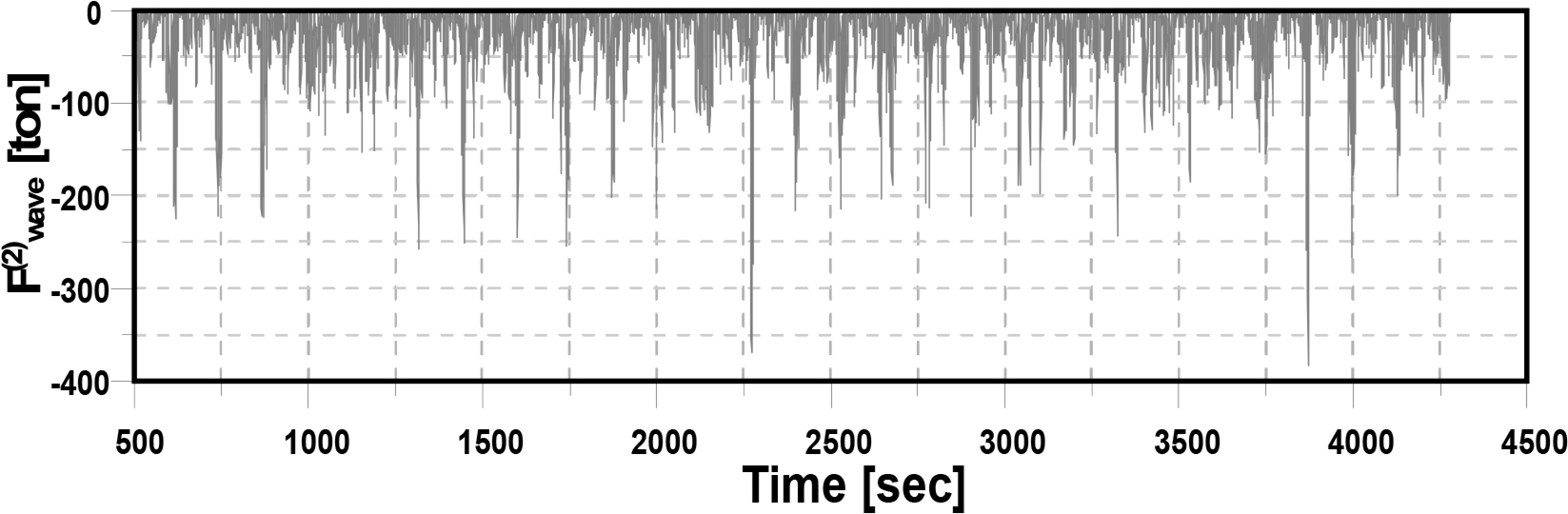
Figs. 15–17 show the x, y offset of the structure and the rotational direction θz on the x − y plane in Step 1, which is the step of maintaining the position only with the thrust of four tugboats without connecting mooring lines. First, the structure shows large movement in the x-direction after 2,250 s have passed (as shown in Fig. 15). To determine the cause, Fig. 18 shows the time history of the second-order wave force, which confirmed that more than 300 t of wave force was acting before the large behavior of the structure occurred. As shown in Table 5, the maximum thrust of one tugboat is 100 t, and the upper limit of the total thrust of a tugboat that can be produced in one direction is 200 t. In other words, due to the limit of the total thrust of the tugboat, the large motion of the structure occurred by the second-order wave force. The behavior in the y-direction and θz -direction is a result of the current and wind forces acting on the structure in different directions, suggesting that the offset of the structure is well maintained with only the thrust of the four tugboats.
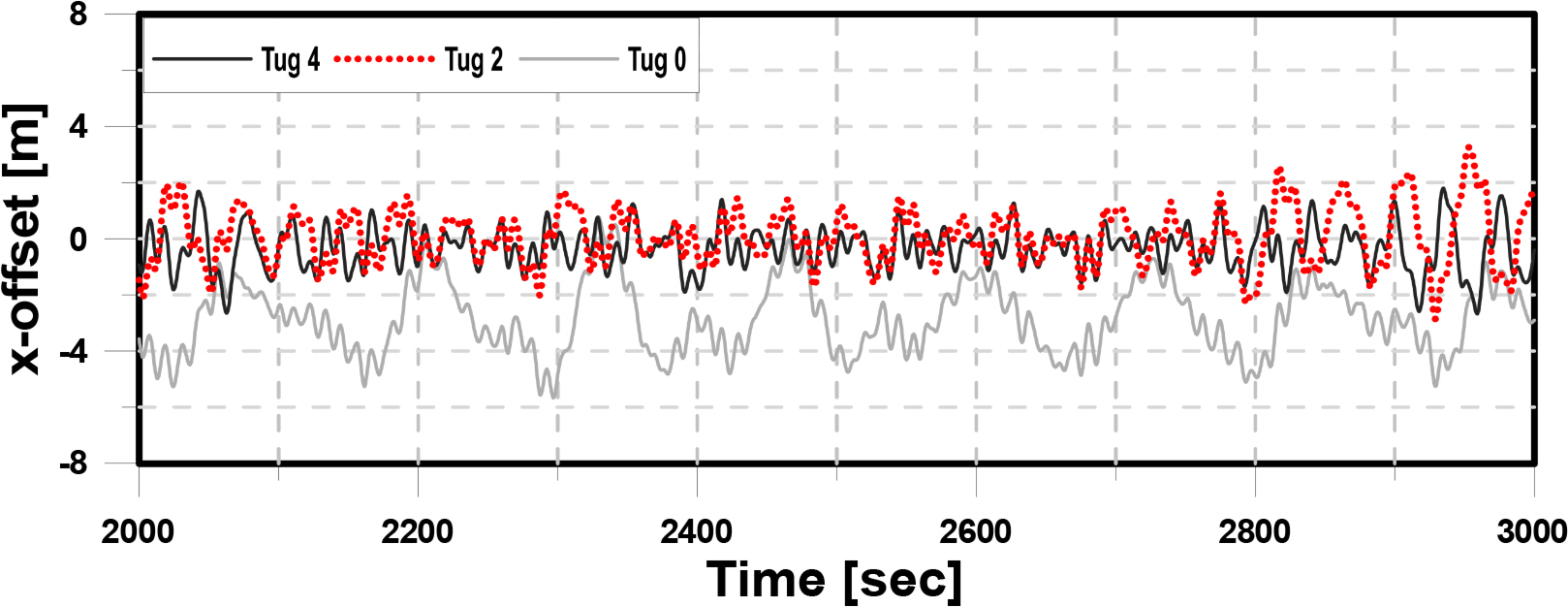
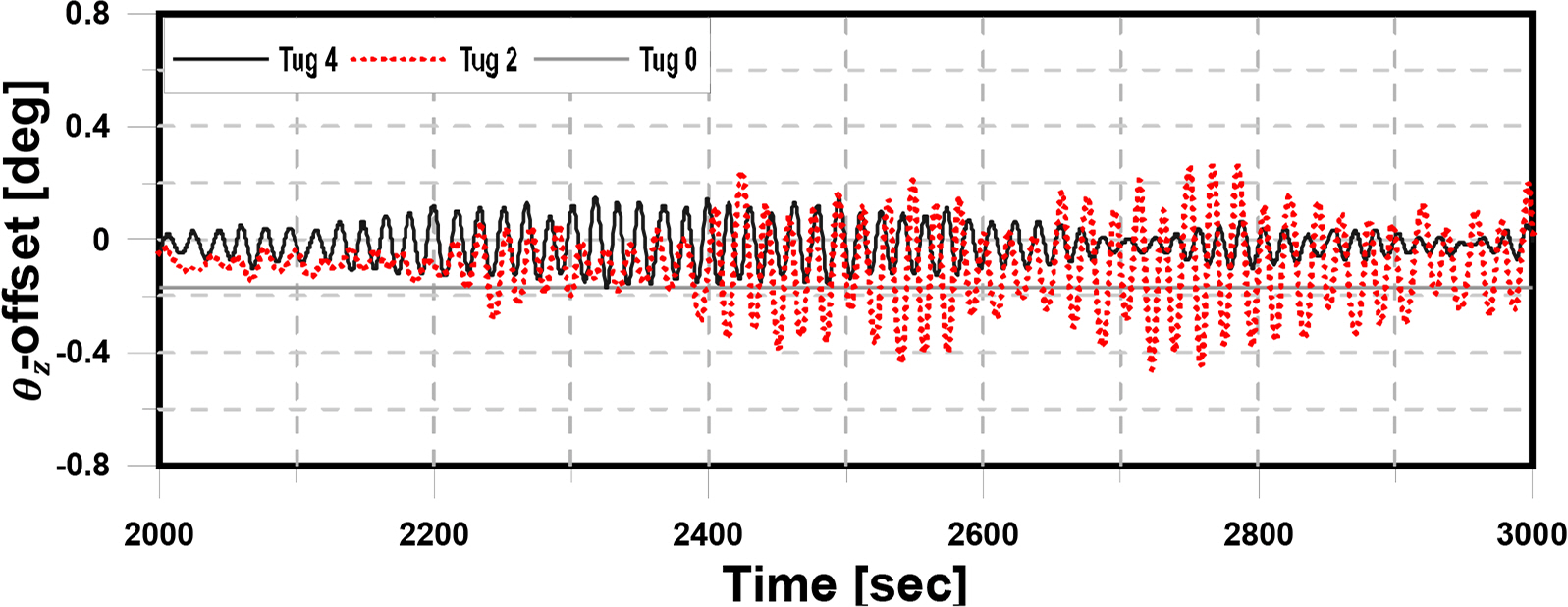
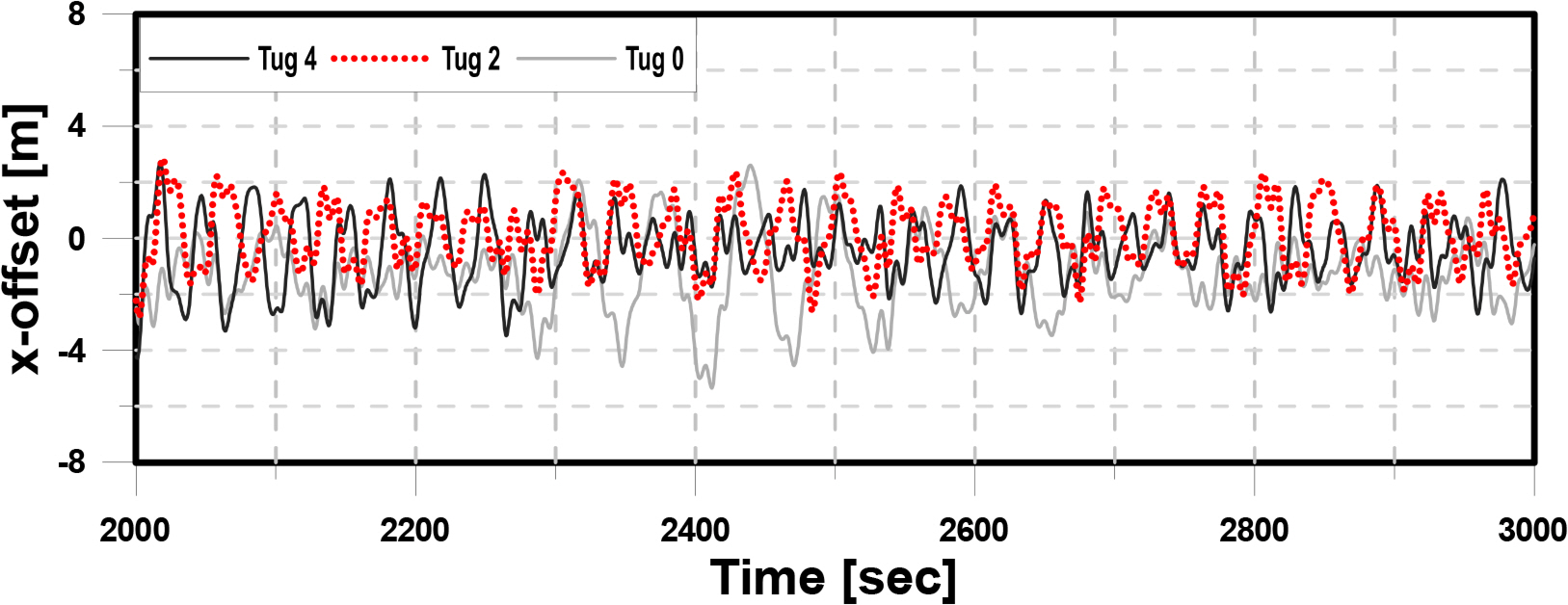
Figs. 19–21 present the x, y, and θz offset of the structure in Step 6, which is connected with four mooring lines by designed pre-tension. Each graph compares the behavior of the structure according to the number of tugboats. Tug 4 has four tugboats with mooring lines; Tug 2 has two tugboats with mooring lines; Tug 0 has no tugboat with connecting mooring lines only. First, the analysis of the time history of the x-direction offset resulted in stronger behavior when there were two tugs than when there were four tugs. When there was no tugboat, large motion of the structure occurred at a distance away from the origin due to the steady drift force.
Among the external forces acting on the structure, the wave force is dominant. To control it, the tugboat generates an excessive force in the x-direction. The thrust in the x-direction of the tugboat causes a rotational moment in the structure. To control the y-direction offset of the structure due to the rotational moment, the tugboat produces a moment in the opposite direction by generating thrust. Therefore, when maintaining the position of the structure using two tugboats, the offset of the structure is larger in the case of the y-direction and θz -direction than the other cases. Therefore, the offset of the structure without connecting the tugboat converges to the point away from the origin and returns to the origin when using four tugboats. In other words, if two tugboats are used in Step 6, the x offset of the structure can be controlled, but and θz offset appears unstable. In addition, when the tugboat is not connected, the offset of the structure deviates from the origin due to the steady drift force, causing instability. Therefore, it is important to maintain the position of the structure using four tugboats in this step.
And in the situation where two tug boats were arranged, the structure shows larger amplitudes in the y and θz directions than other cases, but was relatively stable compared to Step 6.
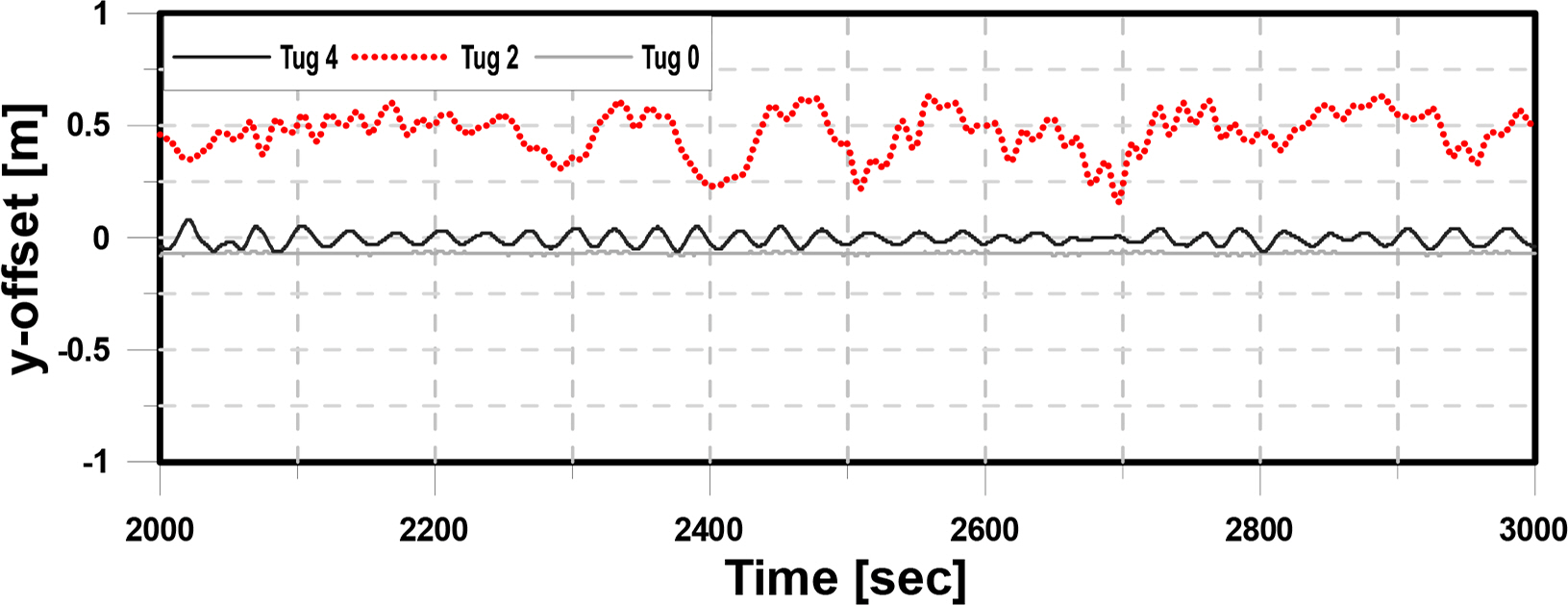
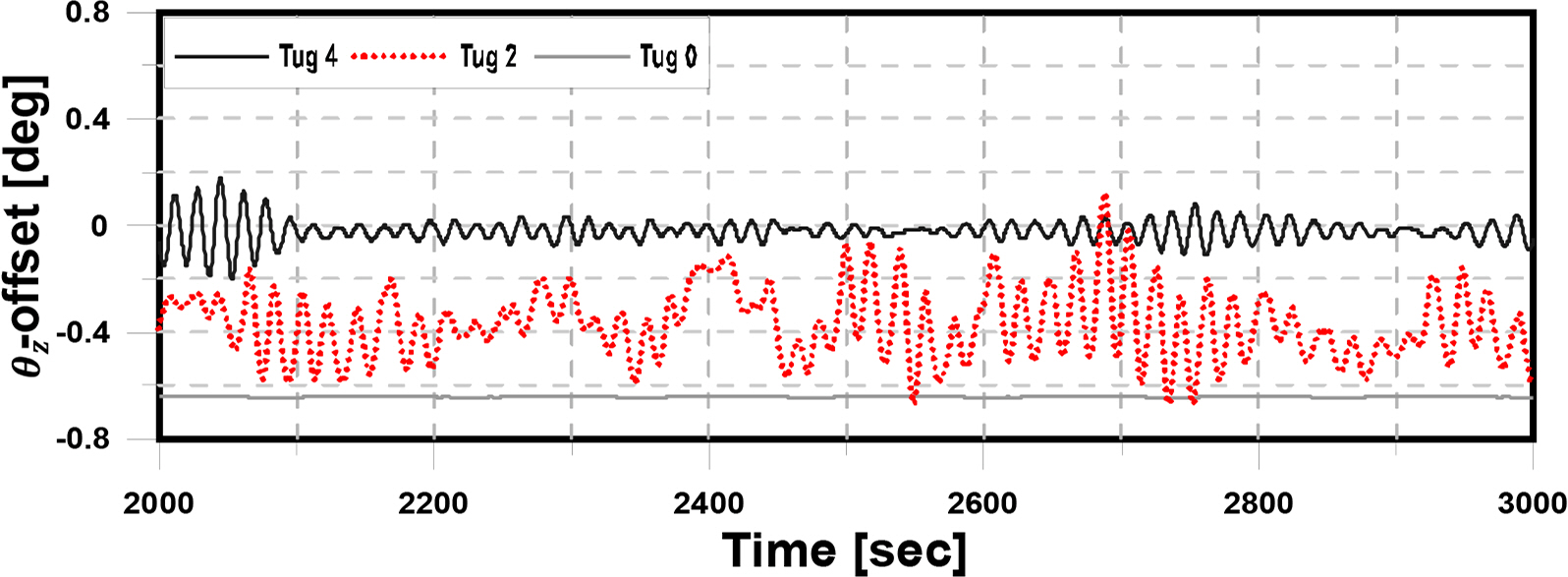
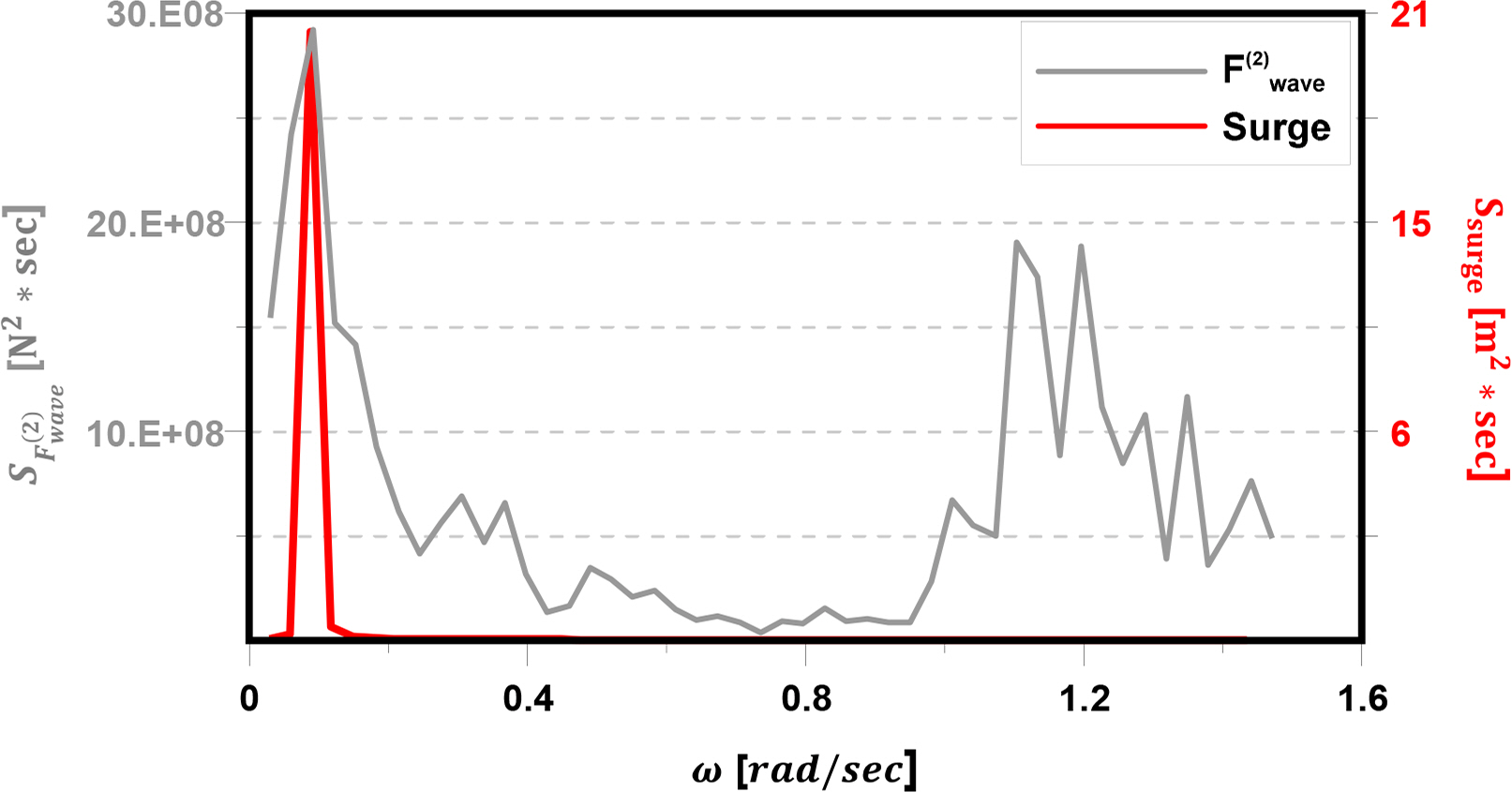
Figs. 22–24 show the x, y, and θz offset of the structure in Step 11, which is connected to eight mooring lines by designed pre-tension. In this step, the x-offset of the structure was largely reduced by four tugboats, and there was no difference in the behavior of the structure between Tugs 2 and 4. In the absence of a tugboat, the effect of the steady drift force was reduced significantly compared to Step 6, as shown in Fig. 19, but the amplitude of the offset was increased. Fig. 25 presents the results of frequency analysis, i.e., FFT (Fast Fourier transform), of the time history of surge motion and second-order wave force when the tension of eight mooring lines was set to the designed pre-tension. In this graph, the two peak frequencies almost coincided. As a result, a large amplitude of x-offset occurred.
In the situation where two tugboats were arranged, the structure showed larger amplitudes in the y and θz directions than the other cases, but it was relatively stable compared to Step 6.
Figs. 26–28 show the x, y, and θz offset of the structure in Step 16, which is connected to 12 mooring lines by designed pre-tension. No significant differences in the offset of the structure were observed between Tugs 4 and 2. When the position is maintained only by the tension of the mooring line without a tugboat, the y and θz offset is extremely small. In the case of the x-offset, the movement was reduced significantly compared to Step 11.
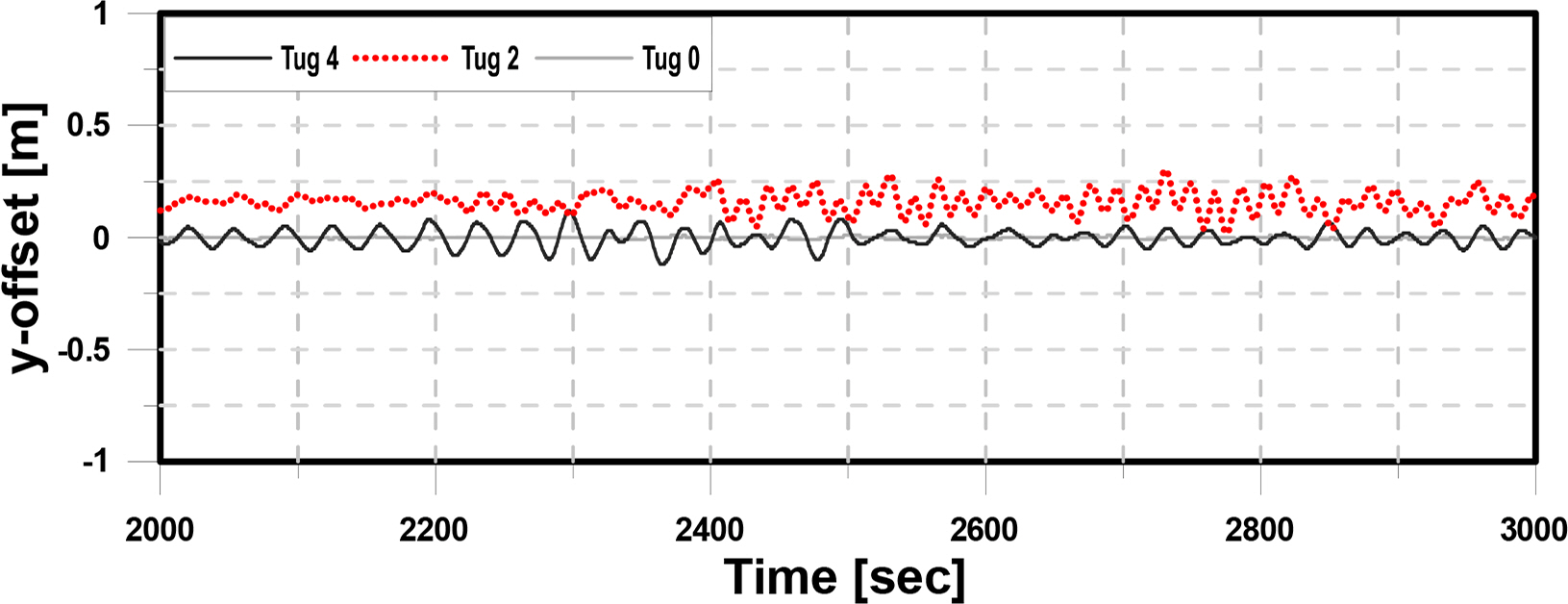
Figs. 29–31 show the x, y, and θz offset of the structure in Step 21, which is the final step in the hook-up procedure. When the entire mooring line was connected to the structure, the x-offset behaves stably without connecting a tugboat (as shown in Fig. 29). In addition, even in the y and θz offsets, the motion of the structure maintained a minute value without connecting a tugboat.
4.4 Results
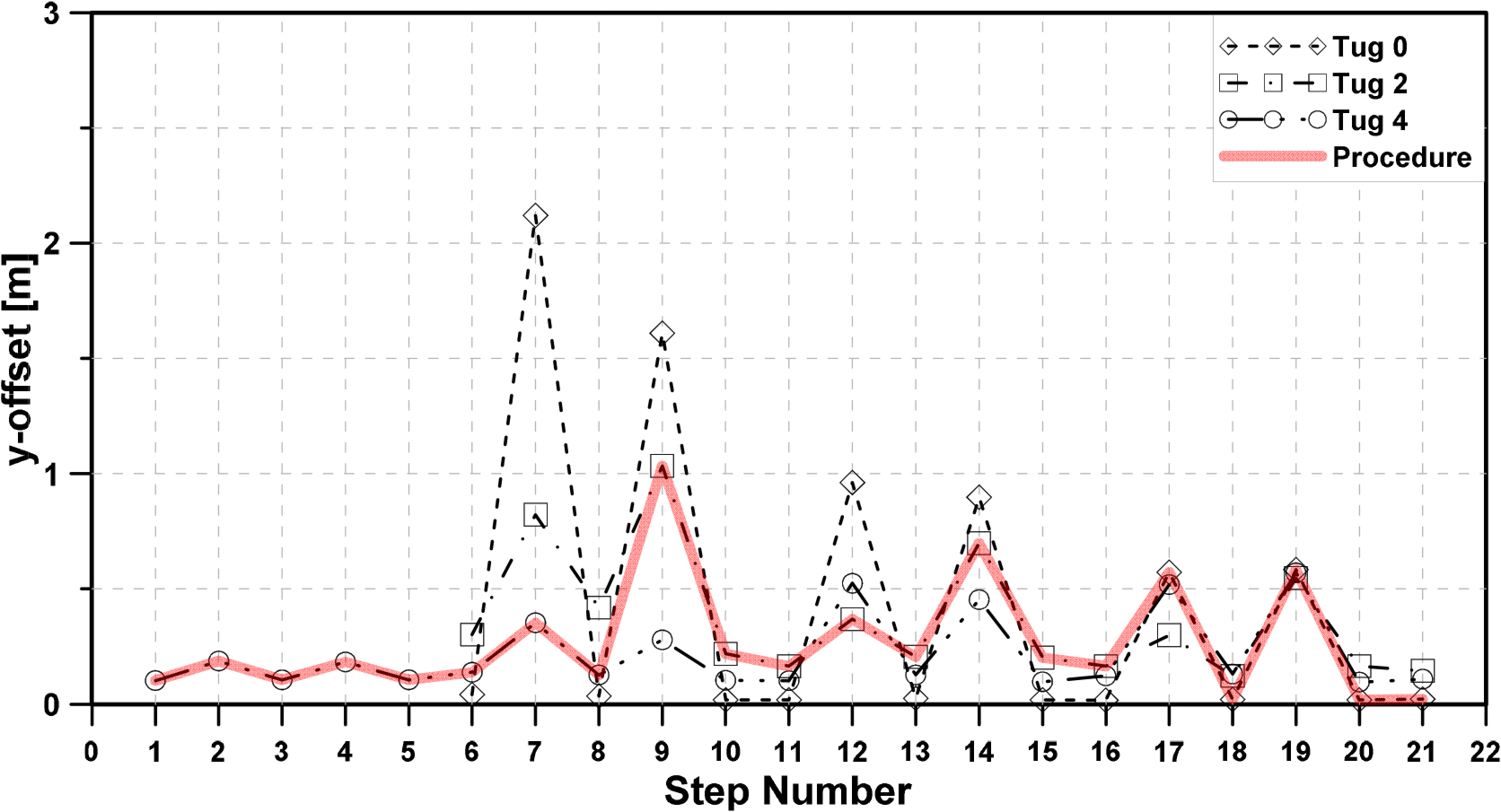
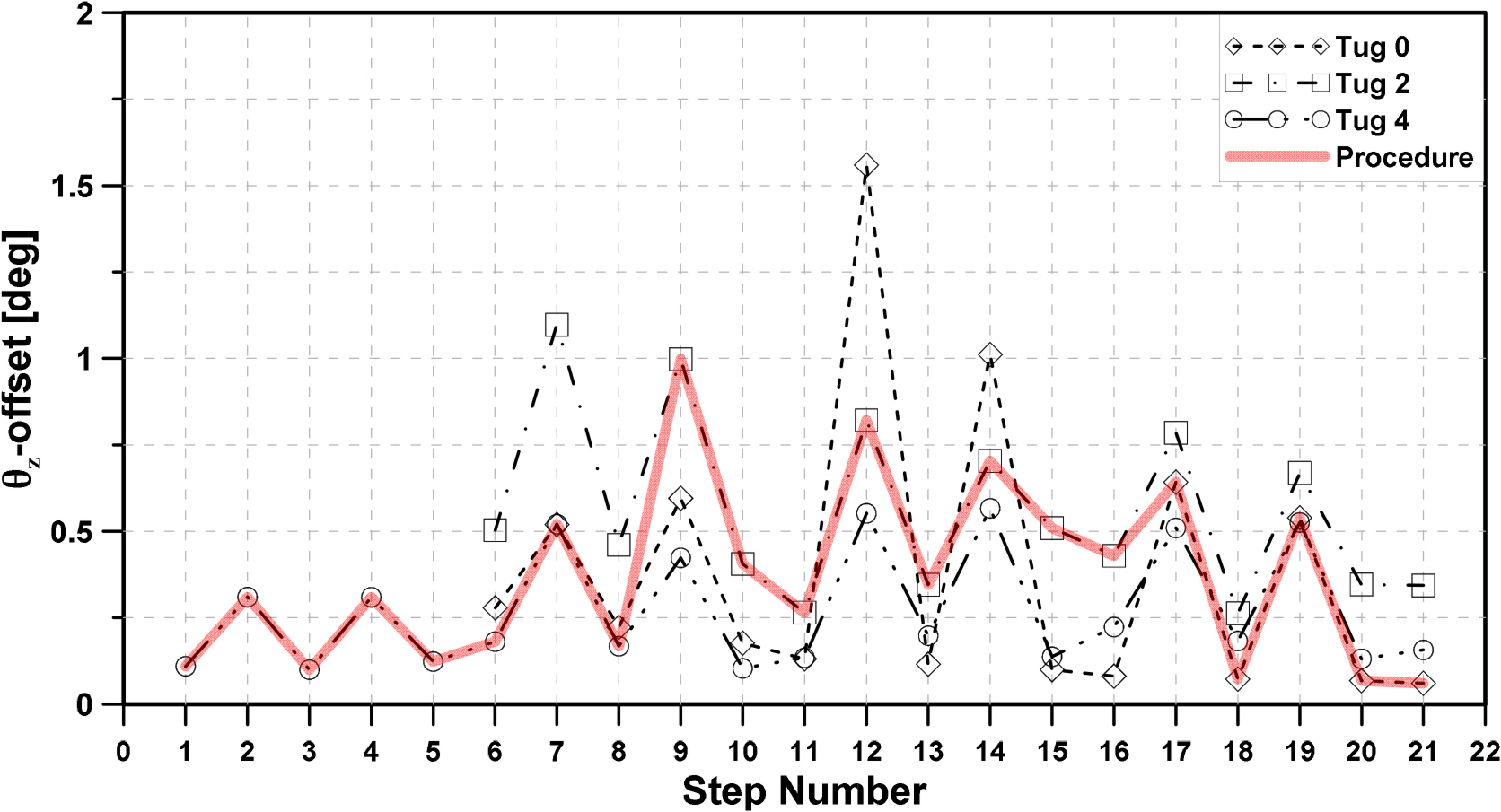
The simulation results for the behavior of the structure during the hook-up installation derived in this study are represented using significant values (as shown in Figs. 32–34). The thick solid line indicates the final hook-up procedure. The structure, which arrived at the installation site by transportation, starts the hook-up installation by connecting the first mooring line while maintaining its position using four tugboats. When the step of connecting the 6th mooring line (Step 8) was over, the two tugboats were withdrawn, and the position of the structure was maintained until 12 mooring lines were connected with the remaining two tugboats (Step 16). In this way, by arranging only two tugboats, the structure can control large movements in the x-direction, which occurred due to the second-order wave force in Step 11 (eight mooring lines are connected with designed pre-tension). All tugboats were withdrawn at Step 17, and installation was carried out until Step 21, which is a final step, while the structure maintains its position by only mooring lines.
Therefore, the significant value of the structure offset was set not to exceed 6 m when organizing the installation procedure by summarizing the simulation results according to the arrangement of the tugboat. Each classification society and certification body present only the external environmental conditions according to the installation period for mooring system installation. Moreover, there were no regulations during the installation process, such as stability and installation plans. Normally, during hook-up installation, all tugboats are withdrawn when half of the entire mooring line is connected. In the case of this study, however, at the stage of Step 11, when half of the mooring lines are connected, the structure exhibited large behavior due to the low-frequency motion. Therefore, the significant x-offset of the structure in Step 16, which is considered relatively stable, was adopted and used as a reference. In addition, after the four mooring lines were connected (Step 6), the structure did not exceed the reference value with only two tugs, but considering the steady drifting force and unstable motion of the structure in the y and θz direction, two tugboats were configured to withdraw after Step 8.
5. Conclusion
In this study, a dynamic analysis program of a mooring system during the hook-up installation was developed, and the simulation results were analyzed for the generally performed procedure. The reliability was verified by comparing the analysis results of the developed program with the simulation results of the commercial program MOSES, and the behavior of the structure during the hook-up installation was analyzed according to the number of tugboats under the complex environmental conditions. The installation procedure was configured so that the significant value of the structure offset did not exceed 6m by comparing the simulation results according to the arrangement of the tugboat.
The conclusions of this study are as follows:
The reliability was verified by comparing the developed program with the simulation result of MOSES. The appropriateness of the hook-up algorithm used in this study was confirmed during the hook-up installation procedure.
During the hook-up installation, the motion response of the structure at the stage where eight mooring lines were connected with designed pre-tension was the greatest due to the second-order wave force, but it could be controlled by arranging only two tugboats.
There are various methods and steps in the hook-up procedure considering the offshore structure, tugboat, mooring type, and installation site. Hence, it will be is necessary to review and analyze the installation procedures other than the simulation performed in this study.
Overall, the timing of the withdrawal of the tugboat with secure work stability can be determined, and the thrust of the tugboat required for hook-up installation can be predicted.
Acknowledgements
Following are the results of a study on the ‘Leaders in INdustry-university Cooperation +’ Project, supported by the Ministry of Education and National Research Foundation of Korea
References
Article information Continued
Notes
Nomenclature
Mkj Ship mass (kg, kg·m2)
mkj(∞) Infinite frequency added mass (kg, kg·m2)
Kkj(t) Memory effect function
Ckj Restoring coefficient (N/m, N·m)
Fk(t) Exciting force (N, N·m)
Fw, Fc Wind force, Current force (N, N·m)
ρair, ρwater Air density, Water density (kg/m3)
Vw, Vc Wind velocity, Current velocity (m/s)
CX(β), CY(β), Cθ(β) Drag coefficient
AX, AY, Aθ(β) Projected Area (m2)
mkj(ω) Added mass coefficient (kg, kg·m2)
bkj(ω) Wave-making damping coefficient
H(ω) Wave exciting force transfer function
Fwave Wave exciting force (N, N·m)
Fmoor Mooring tension (N, N·m)
HS Significant wave height (m)
TS Significant wave period (s)
γ Peak parameter
α Heading angle (deg)