Numerical Study on Characteristics and Control of Heading Angle of Floating LNG Bunkering Terminal for Improvement of Loading and Off-loading Performance

2.1 Off-loading Scenario

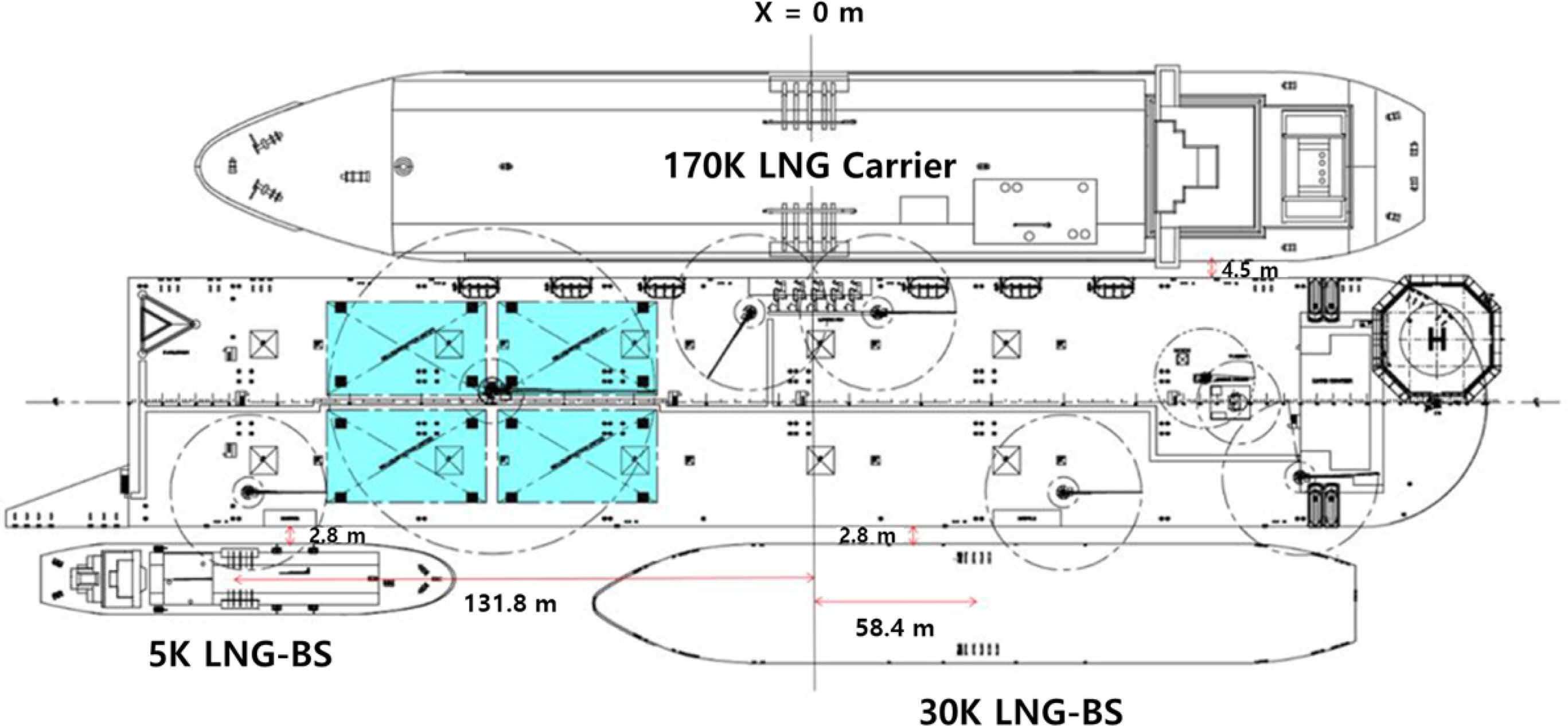
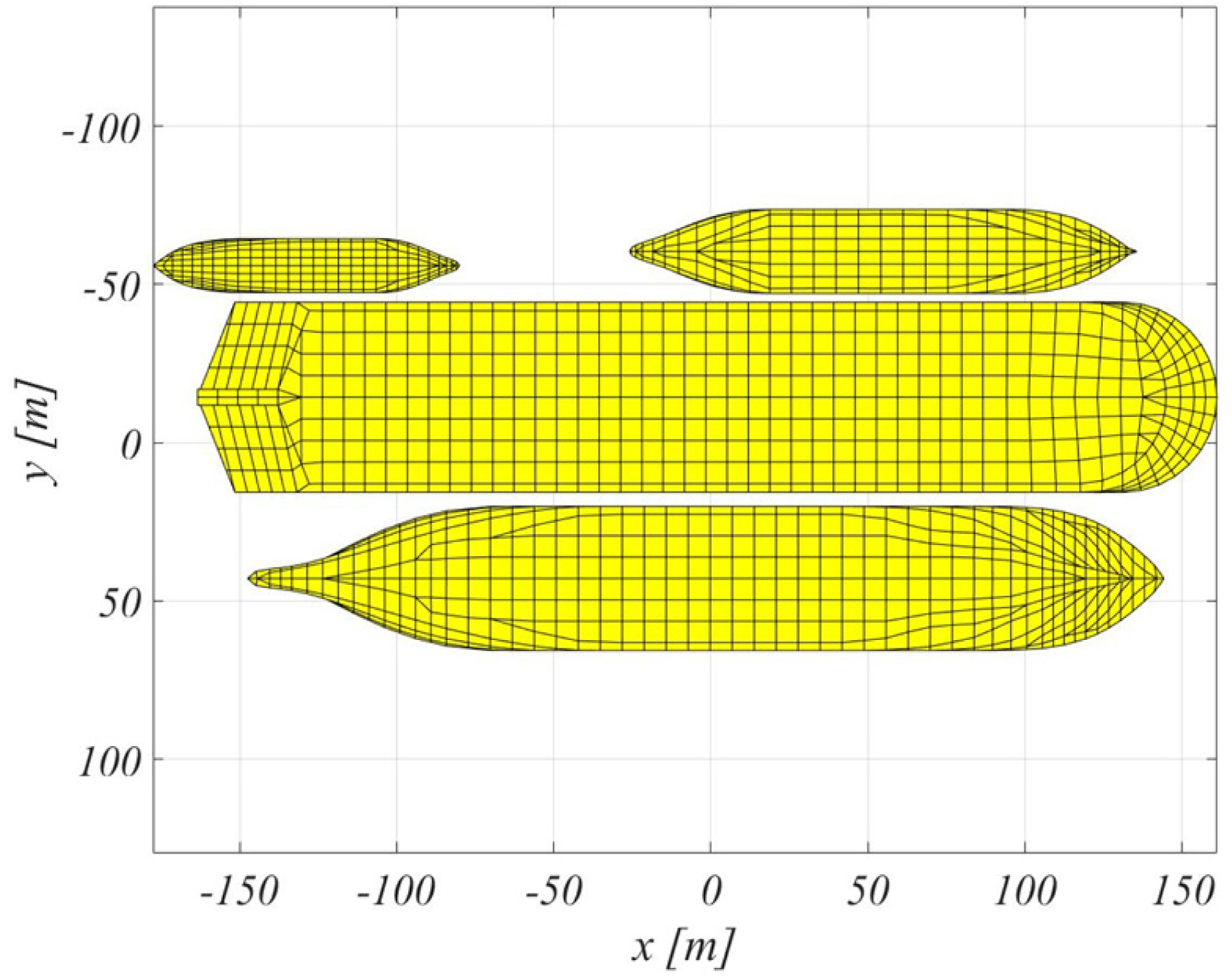
The FLBT receives LNG from LNG carriers and supplies the received LNG to the vessels with LNG propulsion systems through the LNG-BS. The FLBT developed in this study is shown in Fig. 1. It was designed to receive LNG from a 170K LNG carrier and unload the LNG to 30K and 5K LNG-BSs simultaneously. According to a study on the operating procedure of the developed FLBT, it can dock up to three vessels simultaneously, and the total operation time when three vessels are docked in the FLBT for off-loading was analyzed to be significantly short compared with the entire off-loading operation time. However, to determine the range of loading and off-loading, the operating conditions when the maximum number of vessels is docked should be considered.

Kim et al. (2017), Kim et al. (2018), Jung et al. (2018), and Jung (2019) conducted model tests and numerical analysis of the relative motion of docked vessels in an FLBT during operation to examine the loading and off-loading performances of the FLBT. They confirmed that it is necessary to have the shielding effect from the sea waves and maintain the heading angle to improve the loading and off-loading performances of the 5K LNG-BS. The results of the study conducted by Jung (2019) confirmed that all the vessels docked in the FLBT with the heading angles ranging from 202.5° to 225° were capable of stable loading and off-loading as shown in Fig. 2. In this study, based on studies on the operating procedure of the FLBT and the loading and off-loading performances (Kim et al., 2017; Kim et al., 2018; Jung et al., 2018; Jung, 2019), the heading angle characteristics and heading angle control performance will be evaluated to improve the loading and off-loading performances.

2.2 Environmental Conditions

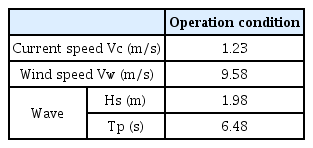
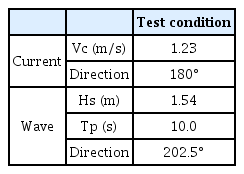
Based on the data survey on the environmental load, the wave deformation and seawater flow were numerically analyzed in the estimated installation area to evaluate the design conditions according to the frequency. As shown in Table 1, it was assumed the operating condition, under which docking, loading, and off-loading are performed, with a one-year return period.

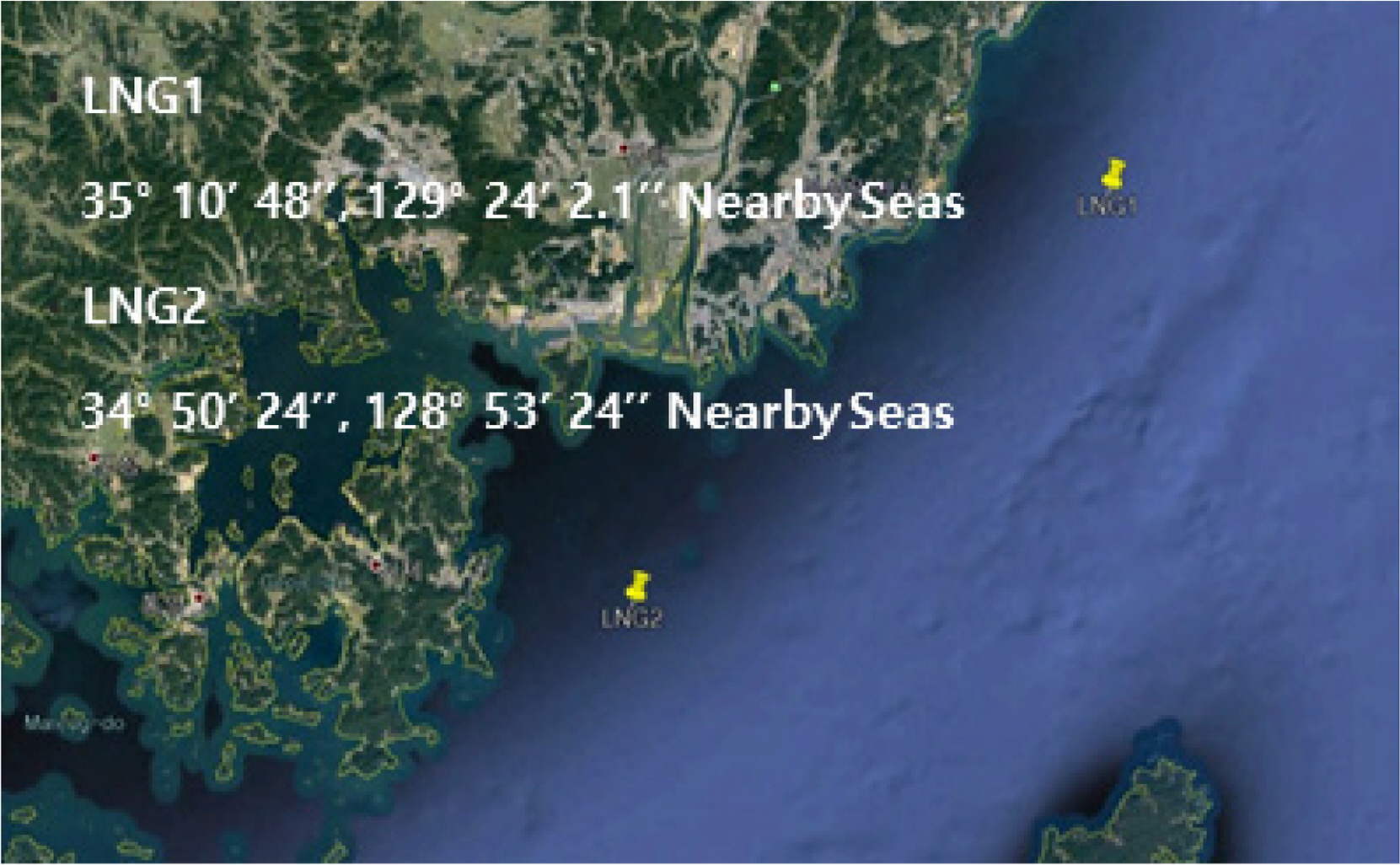
The environmental conditions were determined by selecting the expected installation area, as shown in Fig. 3, to evaluate the design conditions of the FLBT.

2.3 Simplified Model for Evaluation of Heading Angle Control Performance

The vessels under test in the LNG loading and off-loading scenarios are a 170K LNG carrier, 30K LNG-BS, and 5K LNG-BS including the FLBT. The principal dimensions of these vessels are shown in Table 2.

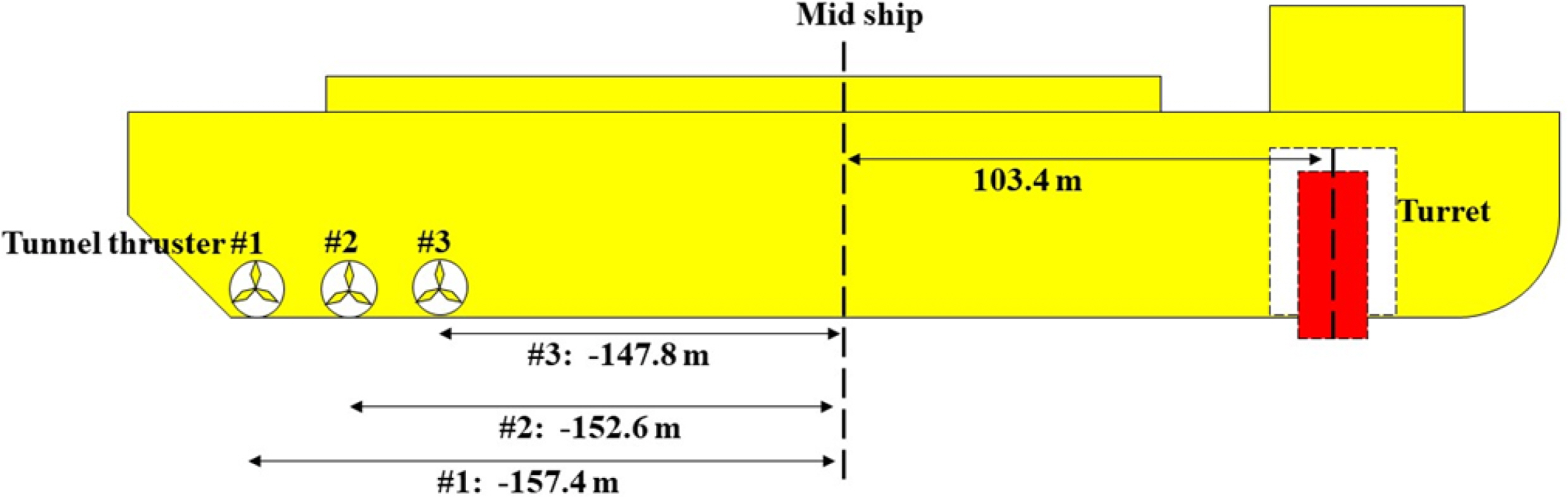
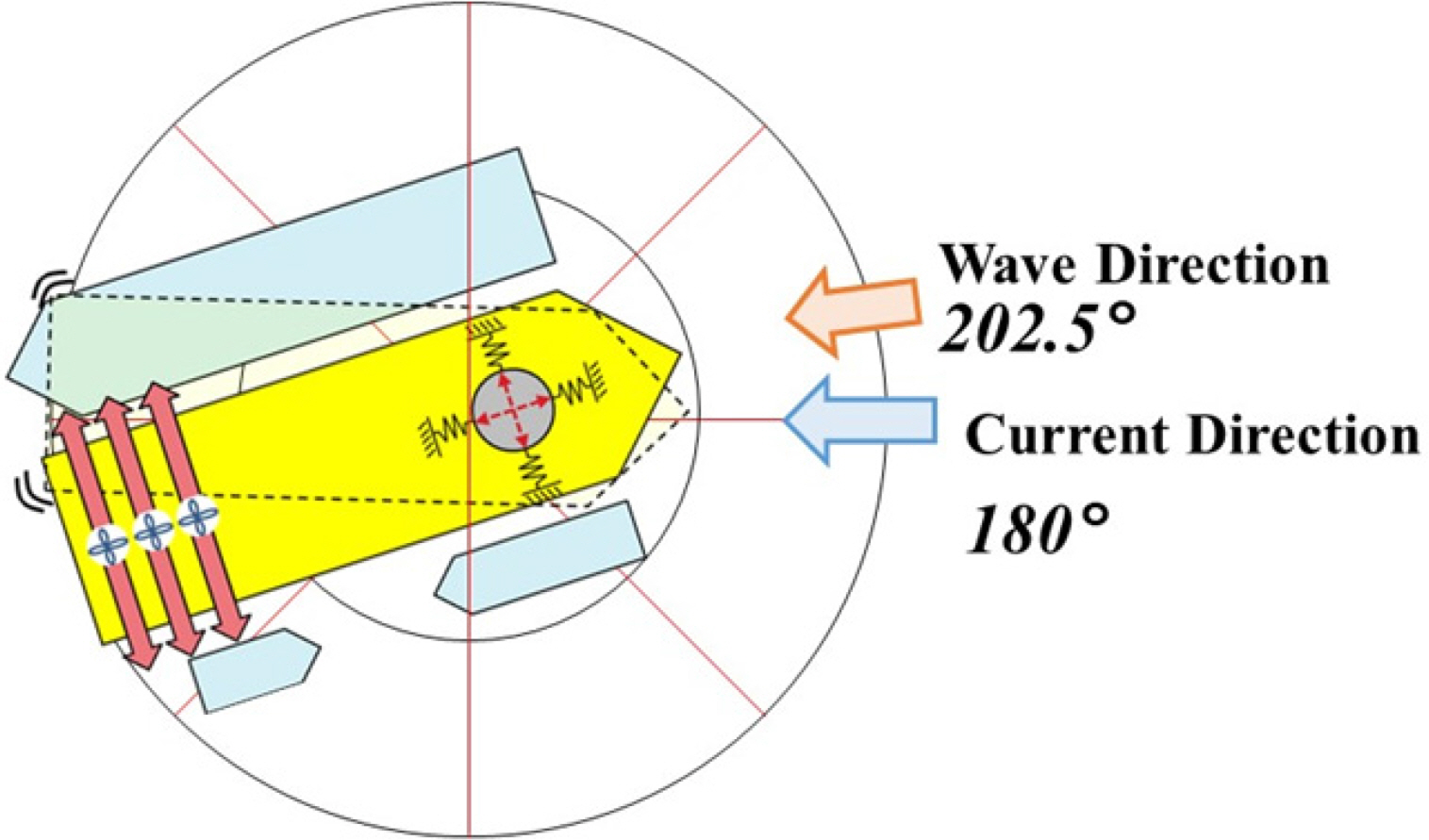
As shown in Fig. 4, the FLBT is moored through the heading turret to maintain its position, and three tunnel thrusters are installed at the stern for the heading angle control, which is advantageous for berthing, loading, and off-loading. Each thruster is designed through advanced static analysis and has a capacity of 561 kN (Oh et al., 2019).

The FLBT is designed to maintain its position by using 15 mooring lines connected to the turret. Five mooring lines form a cluster and the angle between clusters is 120°. In this study, the mooring system was simplified to a simple tensile model as shown in Fig. 5. As three simple elongation springs are attached to the center of the turret, the turret is modeled in the simulation to have free rotation without a resistance force against rotation. This simplification process is considered suitable for accomplishing the objective of this study i.e., to understand the characteristics of the heading angle of the FLBT. In the modeling, the modeled spring constant was similar to that of the recovery curve of the mooring system (Oh et al., 2019).

An LNG carrier, 30K LNG-BS, and 5K LNG-BS are deployed in relative positions, as shown in Table 3, via taut mooring on the FLBT, as shown in Fig. 1.

In this study, it was assumed that the vessel, which was moored on the FLBT, does not show any relative motion in the heading angle control. According to the previously conducted review studies on loading and off-loading performances (Kim et al., 2017; Kim et al., 2018; Jung et al., 2018; Jung, 2019), this assumption is reasonable because the maximum relative motion of the vessel was 3.27 m and most relative motions were 1.5 m or smaller. As it was assumed that there is no relative motion between floating bodies, four vessels can be simplified into one rigid body. For simplicity, the load and inertia acting on each floating body are replaced by the FLBT single-hull loading.

The mass and moment of inertia can be simply substituted with Eqs. (1)–(2).

where M_total, M_FLBT, M_170K, M_30K and M_5K indicate the substituted mass, and the masses of the FLBT, 170K LNG carrier, 30K LNG-BS, and 5K LNG-BS, respectively.I_zz,total, I_zz,FLBT, I_zz,170K, I_zz,30K and I_zz,5K indicate the substituted yawing moment of inertia, and the yawing moments of inertia of the FLBT, 170K LNG carrier, 30K LNG-BS, and 5K LNG-BS calculated at each center of gravity, respectively. r_FLBT, r_170K, r_30K, and r_5K indicate the distances from the single center of gravity of all the four floating bodies to the center of gravity of the corresponding floating body.

The added mass should also be replaced with a part of the hull of the FLBT. As the heading angle simulation simulates the long-period motion, the added mass at zero frequency was calculated and used. If the frequency is assumed to be zero, then the free surface boundary condition for horizontal motion becomes a rigid wall condition. Therefore, it is defined as a double body problem. The boundary element method was used to solve the boundary value for the double body problem. This method uses the basic solution, G(x⃗, ξ⃗),, which is represented by Eq. (3), and the boundary integral in Eq. (4).

where where x⃗ and ξ⃗ are the field and source points, respectively, and the density function, σ(ξ⃗), is an unknown value determined only by the boundary conditions. The density function, σ, can be determined through a system of equations derived from the boundary conditions of an object. The surface potential of the object, ϕ, can be calculated using the determined density function, σ, and Eq. (4). The calculated mass, a_ij, can be obtained by substituting the calculated potential, ϕ, into Eq. (5). where ρ is the seawater density and n_j(j = 1,2,6) represents the normal vectors of the body surface. The panel mesh applied to the calculation is shown in Fig. 6 and the displacement error was within 0.065% in the modeling. The calculated added mass is summarized in Table 4.

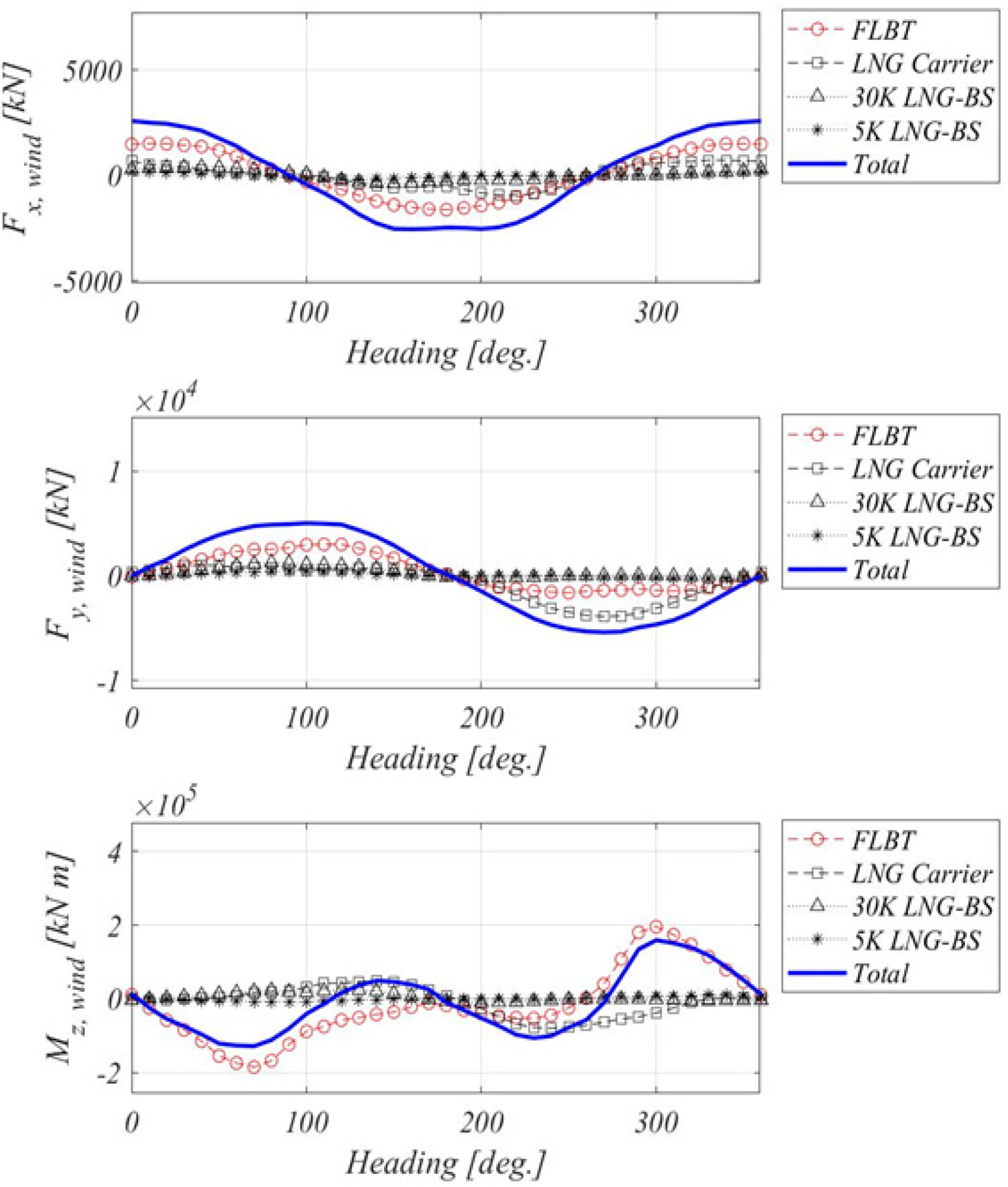
The load acting on each floating body was composed of wind load, current load, and wave drift load. For the wind load, the result of the wind tunnel test conducted in the study by Park et al. (2017) was used. The wind tunnel test was conducted in Force Technology in Denmark, as shown in Fig. 7. The model ship was made of high-density polyurethane foam and was used for the test by separating the top part of the ship under test from the repair surface and below.

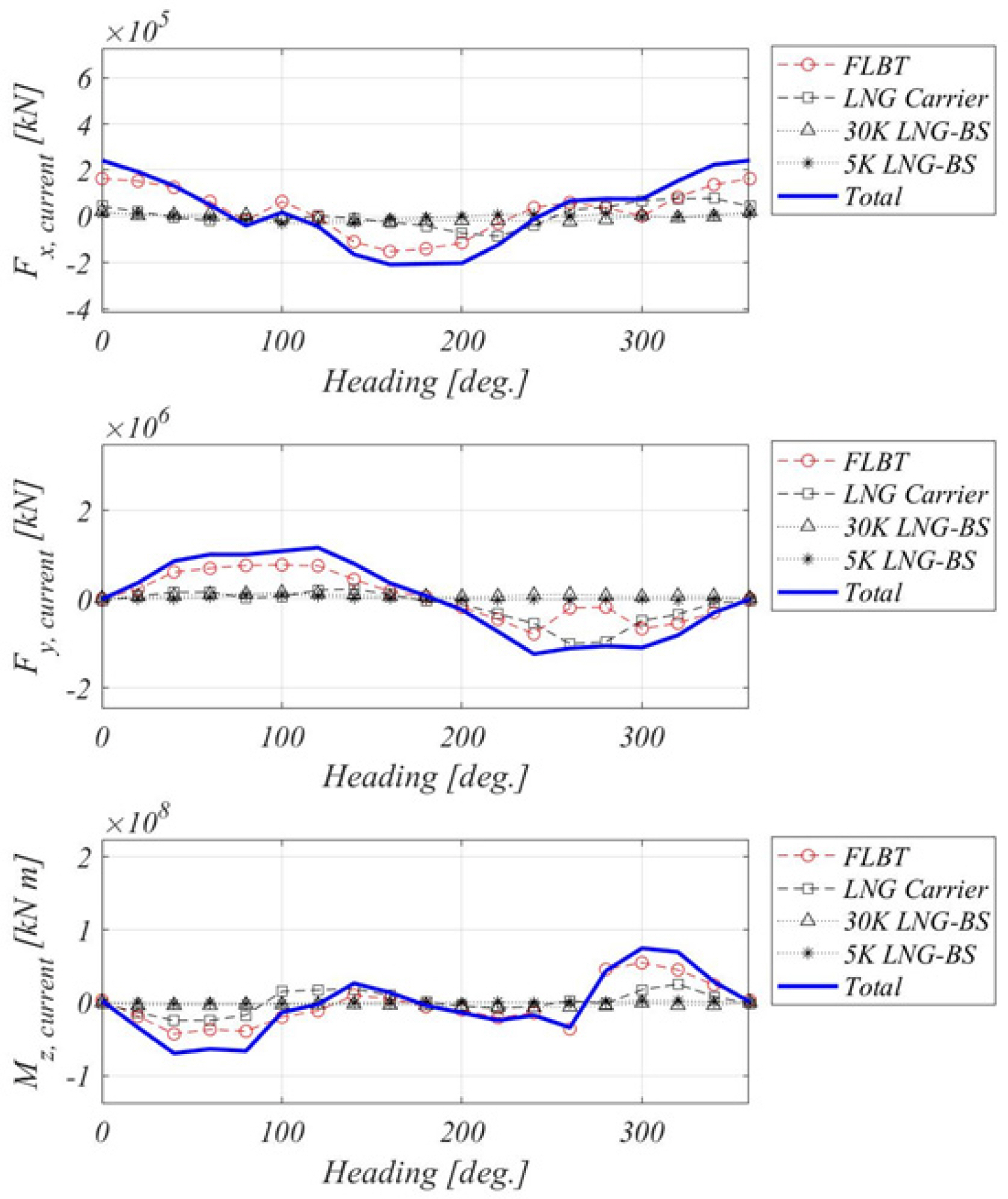
The current load was calculated based on the study conducted by Jung et al. (2017), in which computational fluid dynamics calculations were performed and the current load coefficient was calculated. Based on the computational analysis, which was systematically performed by Jung et al. (2017), the current load coefficient was measured in the wind tunnel test, and it was confirmed that the coefficient was affected by the experimental environment of the wind tunnel. Furthermore, the analysis indicated that Boundary conditions for unbounded flow were not satisfied. Based on the study by Jung et al. (2017), the docked current loads of four floating bodies were calculated in this study as shown in Fig. 8.

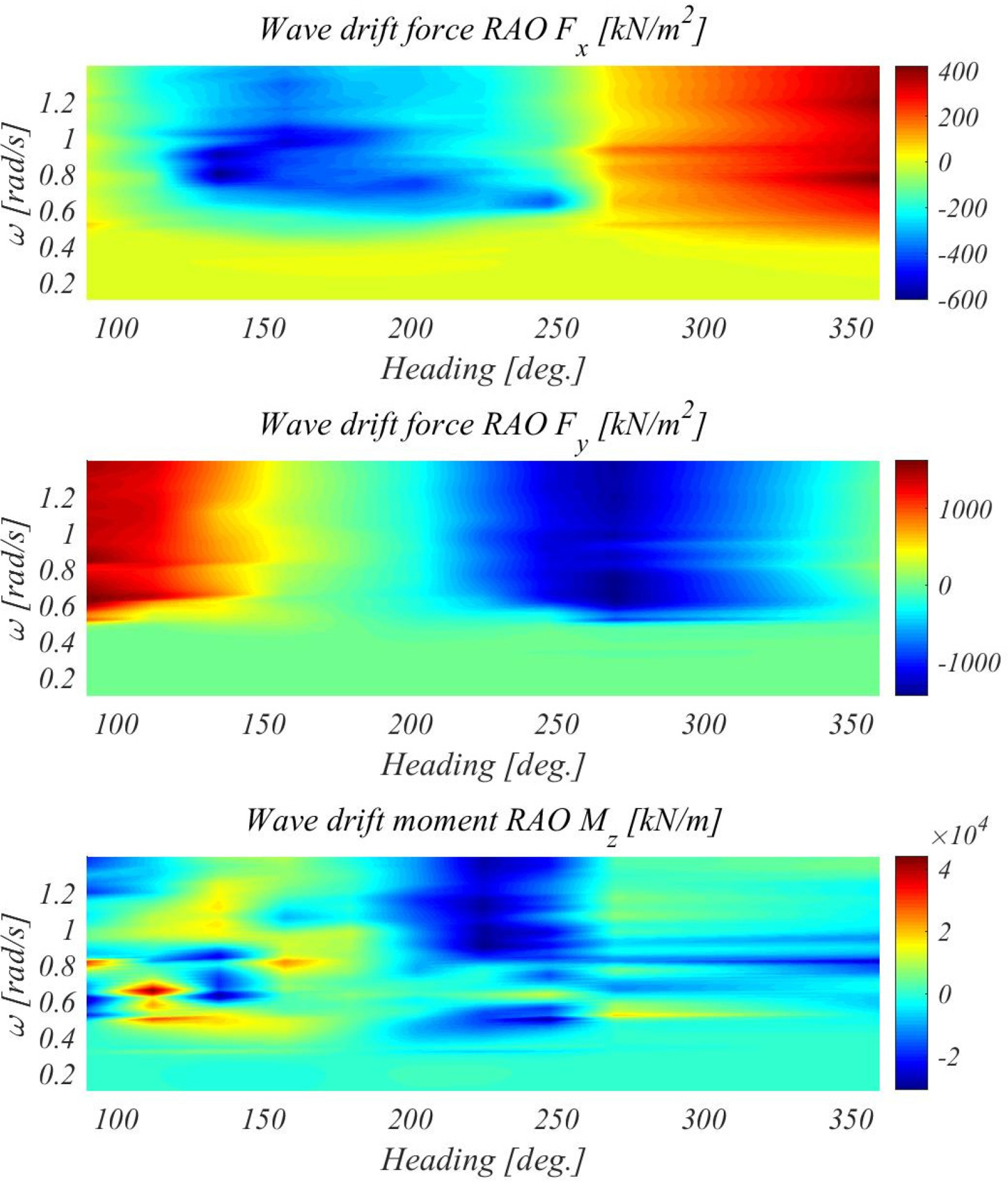
The wave drift load was calculated based on a study by Kim et al. (2018). To calculate the wave drift load, a high-order boundary element method based on the free-surface green function (Choi and Hong 2002) was used, and a gap flow damping term was applied to reduce the non-physical resonance of the gap of the floating body. Detailed calculations can be found in the study by Kim et al. (2018).

For the calculated environmental load, the load acting on each floating body was also simplified to a single FLBT hull load. The individual loads of the floating bodies were replaced with a single load using Eqs. (6)–(8).

where F⃗_total, F⃗_FLBT, F⃗_170K, F⃗_30K are F⃗_5K the substituted horizontal load, and the horizontal loads of the FLBT, 170K LNG carrier, 30K LNG-BS, and 5K LNG-BS, respectively. M_z,_total, M_z,_FLBT, M_z,170K, M_z,30K and M_z,5K are the substituted yawing load moment, and the yawing load moments of the FLBT, 170K LNG carrier, 30K LNG-BS, and 5K LNG-BS, respectively. r⃗_FLBT, r⃗_170K, r⃗_30K, and r⃗_5K are the distance vectors from the center of gravity of all the four floating bodies to the center of gravity of the corresponding floating body. The substituted wind and current loads are shown in Figs. 9 and 10. For the wave drift load, the load response amplitude operator (RAO) was regenerated by the wave height of the incident wave and shown in Fig. 11.

Based on the inertia, added mass, and environmental loads substituted by the load of a single floating body, two-dimensional planar low-frequency motion equations, i.e., Eqs. (9)–(11), which consist of turret mooring and tunnel thruster, can be derived, which allow to simulate the heading angle control.

In the derived motion equation, M and I_ii represent the mass and moment of mass inertia of the floating body, respectively.a_ij, ẍ_i and ẋ_i represent the added mass, acceleration, and velocity in each direction of motion, respectively, where the values of 1, 2, and 6 for i and j represent the surging, swaying, and yawing directions, respectively. Moreover, Fxm, Fym, and Mzm represent the forces in the surging, swaying, and yawing directions, respectively, where the superscript m indicates the type of load, including the loads due to wind, current, wave, mooring, and thrust.

The heading angle of the FLBT is controlled by using the stern thruster, and accordingly, it is necessary to produce and distribute the thruster outputs. In this study, a PD controller was used to control the output of the thruster, and a Lagrange multiplier was used as the thrust allocation algorithm.

3.1 Simplified Model Verification through Model Test

The model test was conducted at the ocean engineering basin in KRISO. The specifications of the floating body used in the model test are shown in Table 2, and the accumulation ratio was 1:65. The models of the 170K LNG carrier, 30K LNG-BS, and 5K LNG-BS in addition to the FLBT were constructed and arranged according to the loading and off-loading scenarios as described previously and shown in Fig. 12.

The FLBT was moored through the turret mooring system inside the structure and was designed to rotate freely in the hull heading. Pneumatic fenders and parallel mooring lines were modeled for the mooring between floating bodies in the same manner as in the study conducted by Jung et al. (2018). The environmental conditions of the model test are shown in Table 5 and Fig. 13, with a total of five cases including the cases where the heading angle was not controlled and where the heading angle was maintained and controlled at 10°, −10°, −20°, and −30°. The model test results were used for verification.

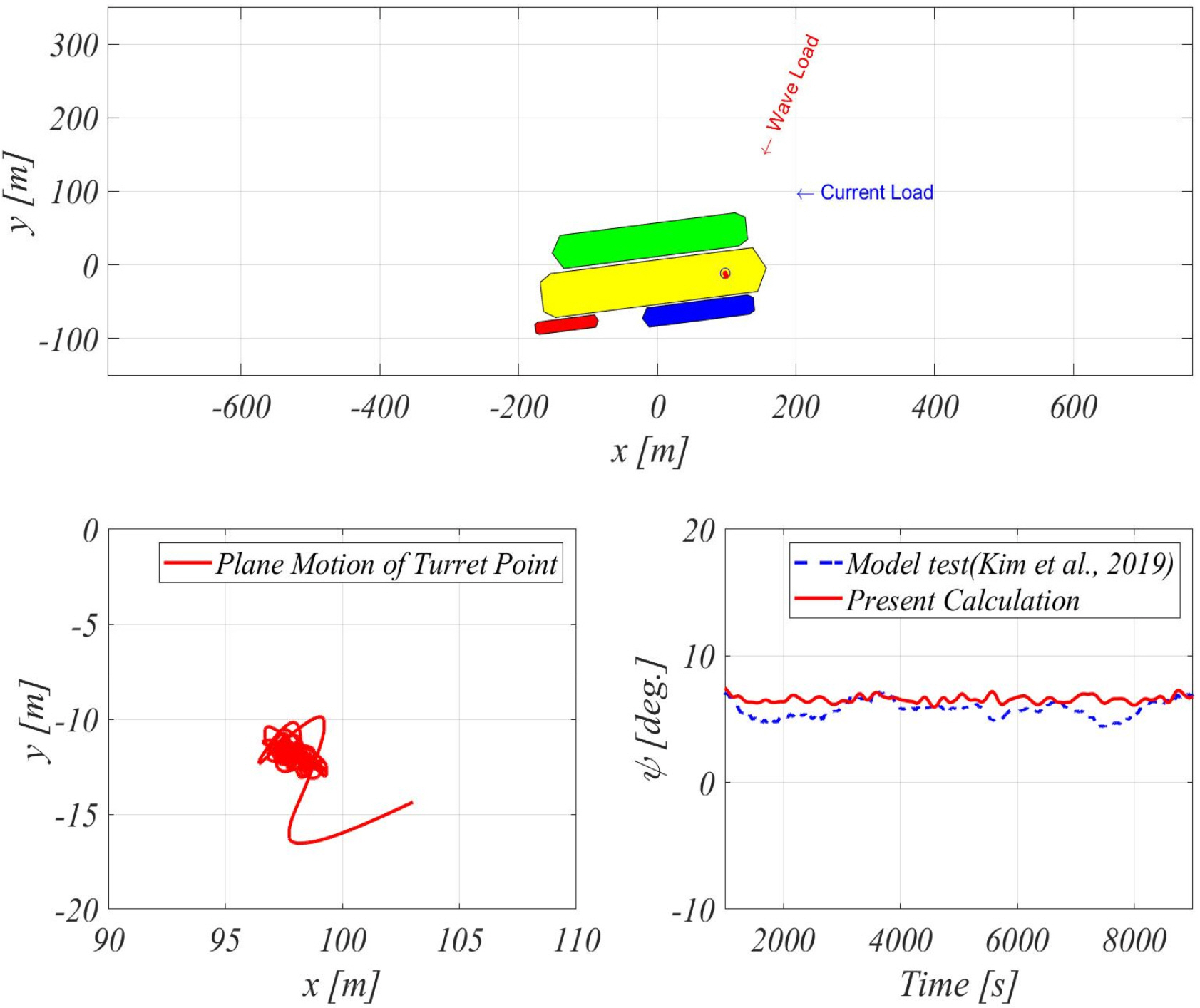
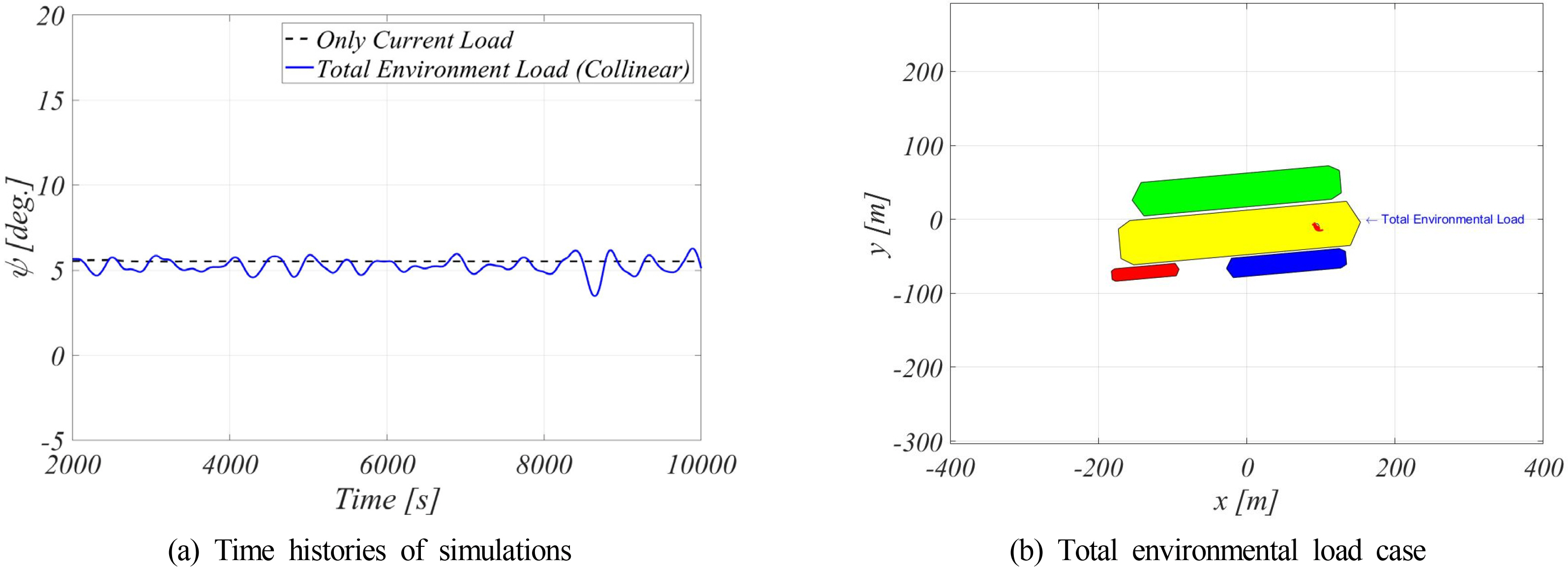
The simulation was performed for the case where there was no heading angle control and the result was compared with the model test result, as shown in Fig. 14. As a result of the numerical analysis, the heading angle reached a static equilibrium point at an average of 6.6°, which shows a similar result to the average heading angle of 5.8° in the model test. Through the model tests and numerical analysis, it was confirmed that there is no slewing motion phenomenon.

The simulation was performed for the case where the heading angle was controlled and the result was compared with the model test result, as shown in Fig. 15.

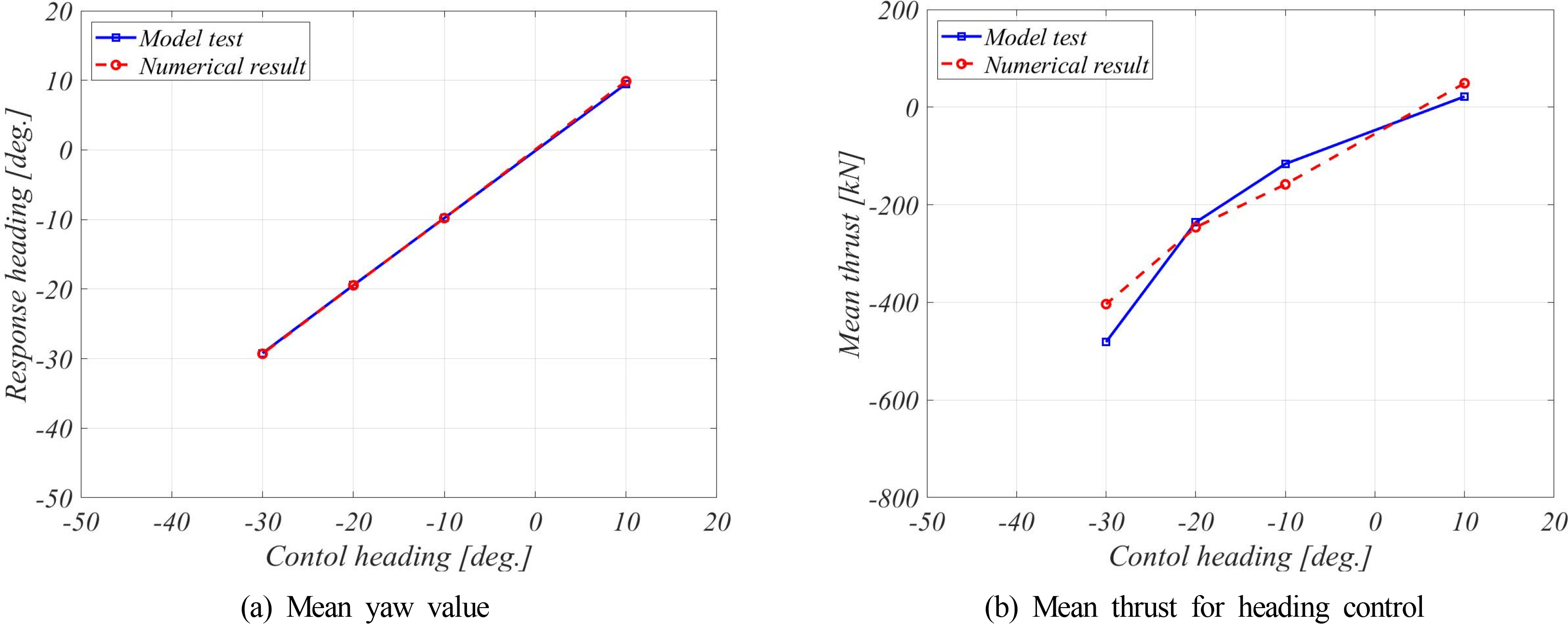
It can be confirmed from the time series results that the heading angle of the numerical analysis was controlled by the reference heading angle, as in the model test. The required thrust time series, which was calculated from the numerical analysis, also has a sectional difference from the result in the model test, but the similarity was observed in the time series results. The average heading angle and the average required thrust calculated using the numerical analysis were compared with the results of the model test and the comparisons are shown in Fig. 16. As shown in Fig. 15, it can be confirmed that the heading angle matches the reference heading angle and the angle is well controlled. It can be verified that the average required thrust also shows a similar trend to the model test result. Through comparative studies, it was determined that the heading angle characteristics and the required thrust calculated through the numerical analysis using a simplified model were similar to the results of the model test. Therefore, the effectiveness of the simplified model was verified.

3.2 Heading Angle Characteristics of FLBT with Moored Loading and Off-loading Vessels

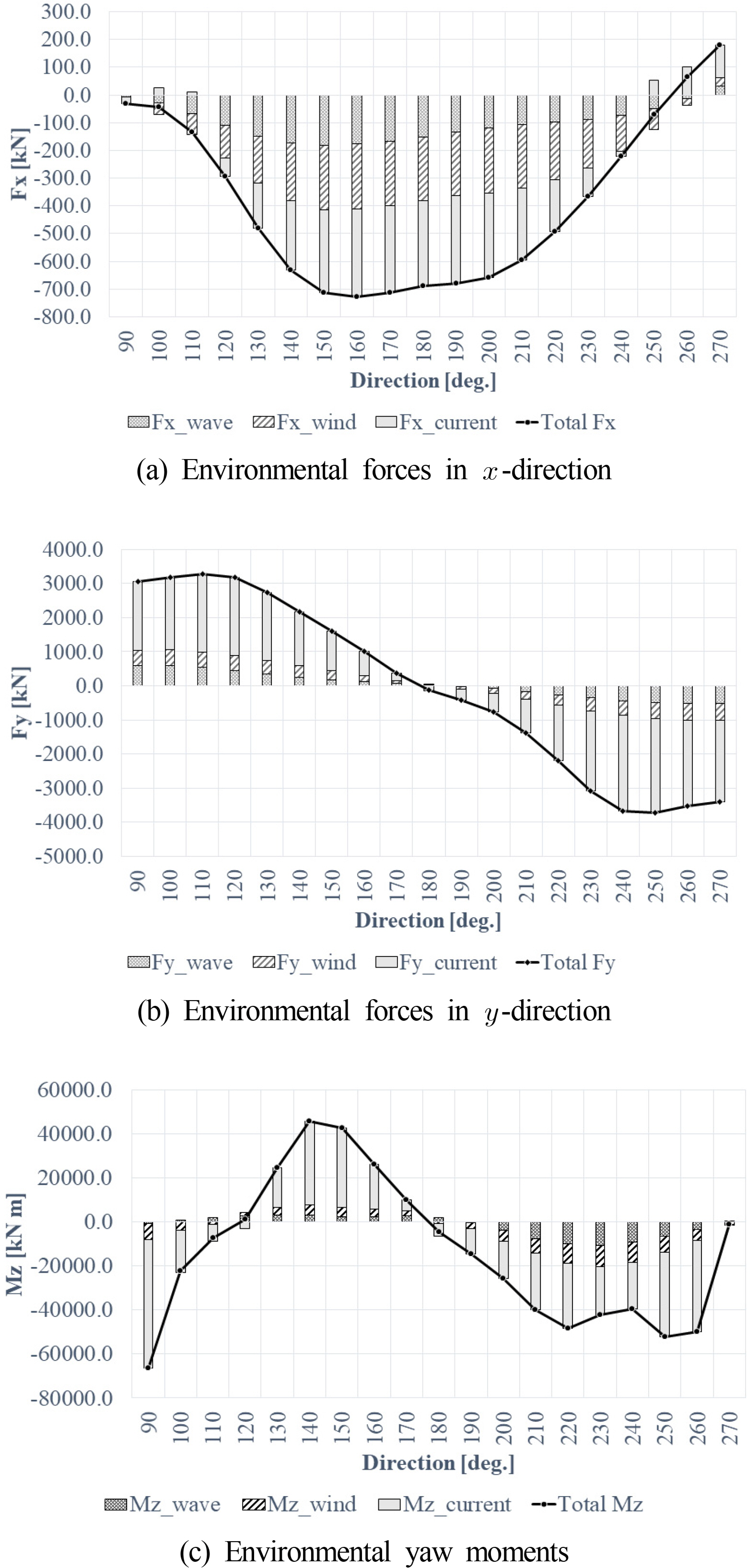
A simulation was performed for the case with no heading angle control to understand the heading angle characteristics of the FLBT with moored loading and off-loading vessels. As the heading angle characteristics are governed by the environmental load acting on the marine structure, the static environmental load for the environmental conditions shown in Table 1 was calculated for the incident direction and the result is shown in Fig. 17. As shown in Fig. 17, the main components of the environmental load in the y-direction and the moment of the horizontal plane are attributed to the current, and it can be easily predicted that the direction of the current will have the most significant effect on the change in the heading angle.

Fig. 18 shows the heading angle simulation for each environmental load and all the linear disturbance loads (collinear environmental load; hereafter denoted as the unidirectional composite environmental load). In Fig. 18(a), when only the wind and wave drift loads are included in the simulation, a long period slewing motion is observed. This is mainly due to the yawing instability that occurs in the vessel, and it is known that the yawing stability is improved when the surging resistance increases (Nam et al., 2013). Such characteristics can be confirmed by simply conducting a simulation with increased wind speed as shown in Fig. 18(b). When only the current load is included in the analysis, the heading angle is maintained to a static value. In Fig. 19 (a), it can be confirmed that the heading angle for the unidirectional composite environmental load in the simulation is almost similar to the heading angle when only the current load acts. As shown in Fig. 17, the current load has the greatest effect on the composite environmental load. In the case of the unidirectional composite environmental load, the slewing motion, which occurred in the wind and wave drift loads, did not occur, and this indicates that the current suppresses the slewing motion. Through the results of the heading angle simulation for various loads, when there is no DP control, the slewing motion occurs with an average heading angle of approximately 5° as shown in Fig. 19(b). This is because the 5K LNG-BS and 30K LNG-BS, which are vulnerable to relative motion due to the wave load, are exposed to the wave load, and thus, it is not possible to have the shielding effect against the ocean waves of the FLBT and LNG carriers. Such a heading angle characteristic indicates that the heading angle control of the FLBT is essential to improve the loading and off-loading performances.

3.3 Control Performance of Heading Angle of FLBT with Moored Loading and Off-loading Vessels

The heading angle control was simulated to understand the heading angle control performance of the FLBT on which the loading and off-loading vessels are moored, as shown in Table 6, for the fixed collinear environmental load condition, fixed wave direction, and changing wind and current loads (hereafter denoted as pseudo-operating conditions). For the heading angle control, the PD control using three stern thrusters was performed. The P gain was calculated based on the yawing and it was set to approximately 300 s, which is the natural period. The D gain was set to 35% of the critical damping.

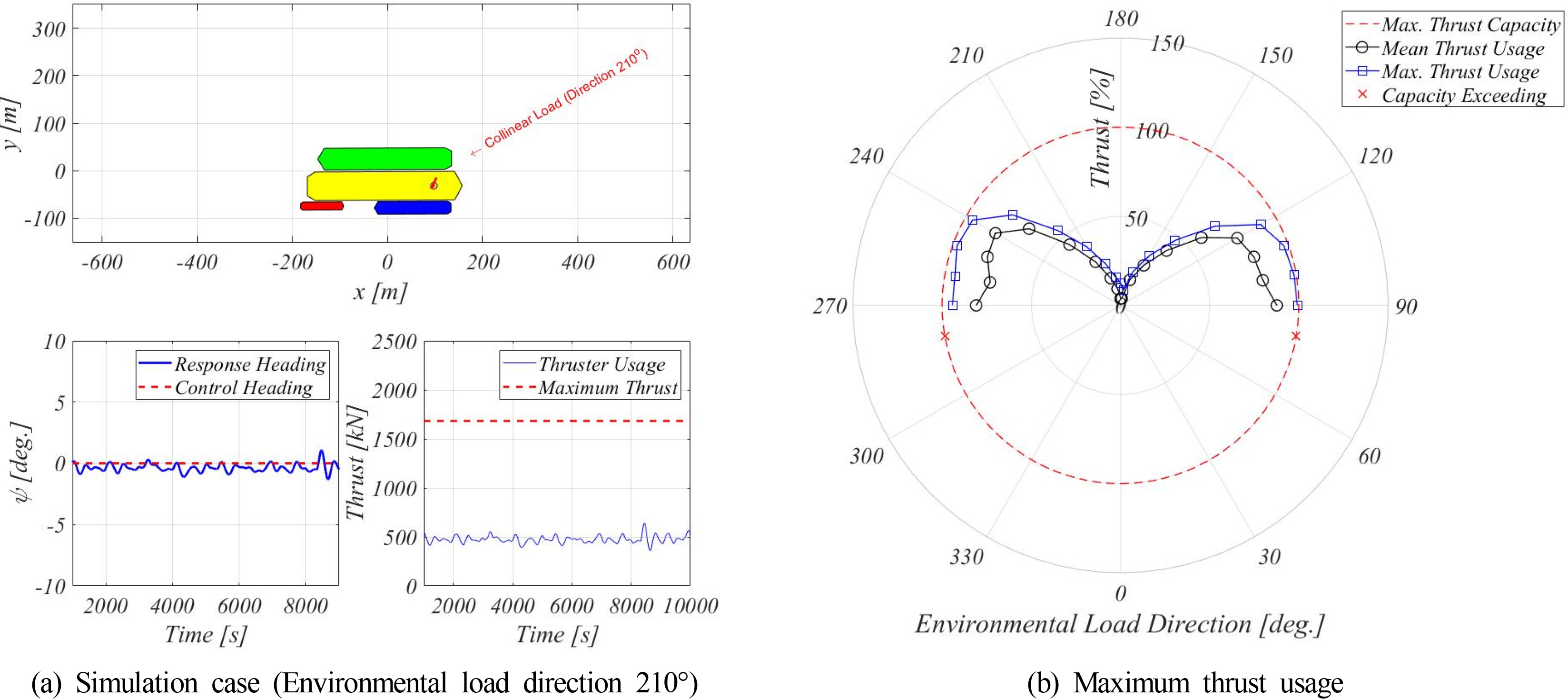
As shown in Fig. 20(a), the heading angle control was simulated for the collinear environmental load condition. Fig. 20(b) shows the amount of thrust used for environmental disturbances based on the dynamic simulation of the heading angle. It was confirmed that heading angle control is possible for the directions of the environmental load ranging from 90° to 270°.

According to a previous study (Jung, 2019), if the heading angle is maintained at 202.5° or higher based on the incident direction of the 180° wave, the loading and off-loading performances can be improved by the shielding effect of the ocean wave. The simulation for the collinear environmental load condition shows that it is possible to maintain a heading angle at 202.5° or higher against environmental disturbances.

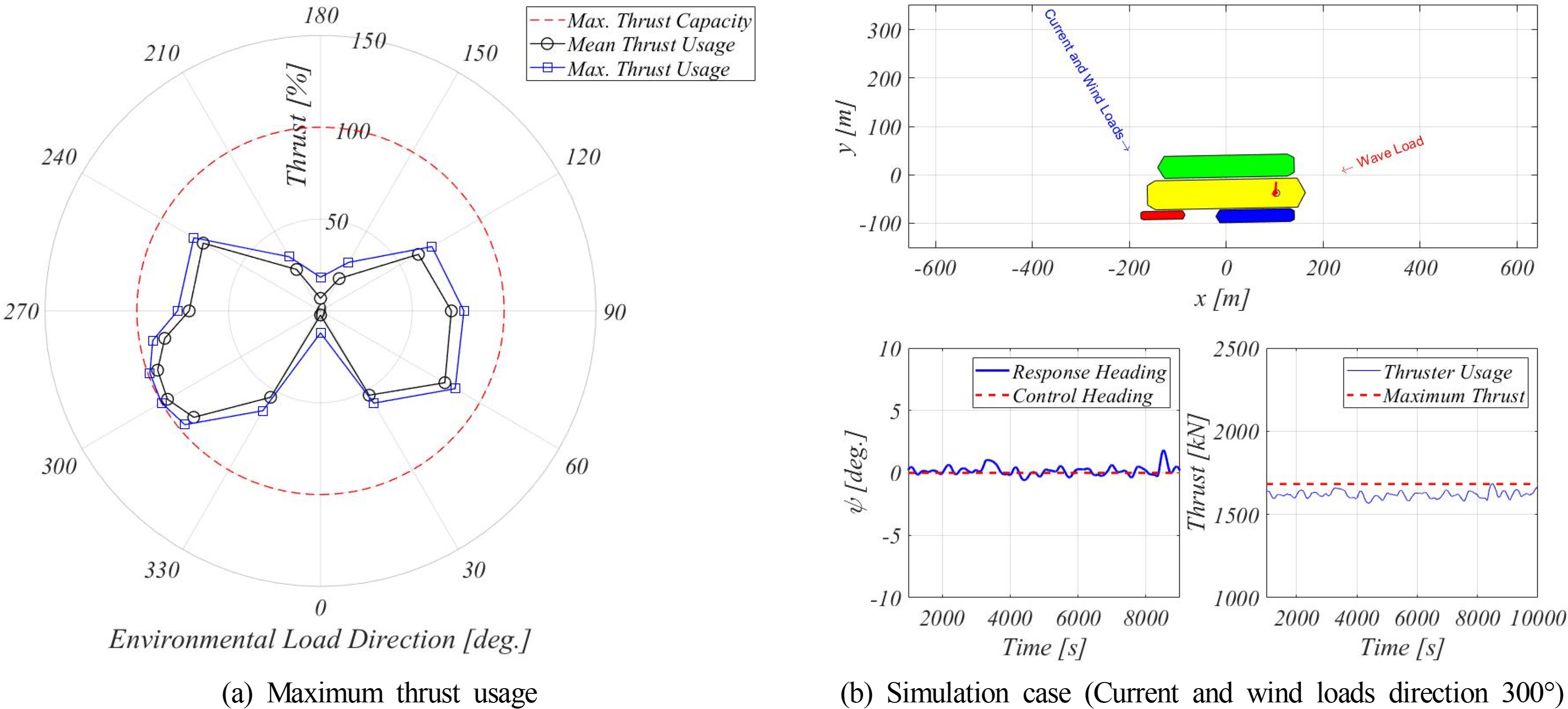
Furthermore, simulations for the pseudo-operating condition were performed. As shown in the heading angle characteristics, the static heading angle is mainly affected by the direction of the current. However, the loading and off-loading performances are considerably affected by the wave-induced relative motion of the vessel. Through these characteristics, by fixing the wave direction to have the shielding effect against the ocean wave and understanding the heading angle control performance against environmental disturbances except for the wave, the range of environmental conditions that ensure the improvement of the loading and off-loading work performances can be estimated. A simulation was performed at 30° intervals under the pseudo-operating condition as shown in Table 6, and an additional simulation was performed at 10° intervals in the range of 280° to 310° to confirm the maximum thrust around 300°, where the maximum required thrust is expected. The simulation result of the heading angle control is shown in Fig. 21(a), where the results are specified in terms of the thrust usage. The section where the maximum thrust occurred is a scenario in which the current and wind loads act at 300° as shown in Fig. 21(b). Therefore, as shown in Fig. 21(a), the heading angle for having the shielding effect against the ocean waves is maintained for all the current and wind load directions. This indicates that the heading angle control secures an additional work operation period and improves work performance in operating condition with a one-year return period. The capacity of the designed stern thruster was also confirmed through numerical analysis results.