|
 |
- Search
| J. Ocean Eng. Technol. > Volume 33(2); 2019 > Article |
|
Abstract
Among the various wave power systems, Salter’s duck (rotor) is one of the most effective wave absorbers for extracting wave energy. The rotor shape is designed such that the front part faces the direction of the incident wave, which forces it to bob up and down due to wave-induced water particle motion, whereas the rear part, which is mostly circular in shape, reflects no waves. The asymmetric geometric shape of the duck makes it absorb energy efficiently. In the present study, the rotor was investigated using WAMIT (a program based on the linear potential flow theory in three-dimensional diffraction/radiation analyses) in the frequency domain and verified using OrcaFlex (design and analysis program of marine system) in the time domain. Then, an experimental investigation was conducted to assess the performance of the rotor motion based on the model scale in a two-dimensional (2D) wave tank. Initially, a free decay test (FDT) was carried out to obtain the viscous damping coefficient. The pitch response was extracted from the experimental time series in a periodic regular wave for two different wave heights (1 cm and 3 cm). In addition, the viscous damping coefficient was calculated from the FDT result and fluid forces, obtained from WAMIT, are incorporated into the final response of the rotor. Finally, a comparative study based on experimental and numerical results (WAMIT & OrcaFlex) was performed to confirm the performance reliability of the designed rotor.
파랑에너지로부터 전기에너지를 추출하기 위한 Salter가 제안한 1차 변환장치는 잠긴 부분의 모양이 수면에 떠 있는 오리와 같다고 하여 Salter's duck 또는 Edinburgh duck이라 불린다. Salter's duck은 입사파 방향으로의 전면형상과 반대편의 후면형상을 서로 다르게 비대칭적으로 설계하여 파의 에너지를 흡수하고, 이를 통해서 약 90%에 가까운 에너지 흡수 효율을 가질 수 있다고 알려져 있다(Swift-Hook et al., 1975). 이는 1970년대 후반부터 1980년대 초반까지 모형실험(Salter et al., 1975; Jeffrey et al., 1976)과 이론해석(Evans, 1976; Count, 1978; Mynett et al., 1979)등을 통하여 폭 넓게 연구되었다. 또, 조석을 고려한 Salter's duck의 성능 연구(Wu et al., 2017), 제주 서부 해역에 최적화 되도록 여러 가지 설계변수에 대한 로터의 성능 변화 연구(Poguluri and Bae, 2018) 그리고 전산유체역학(Computational fluid dynamics, CFD)을 통해서 로터의 점성계수를 산정(Poguluri et al., 2019) 등 최근에도 Salter's duck에 대한 연구는 많은 관심을 받고 있다. 하지만 최근 연구들은 수치해석을 기반으로 하였다. 본 논문에서는 실험적 연구를 진행하여 수치해석의 결과를 검증하였다.
선행연구에서는 Salter's duck의 로터의 다양한 설계 변수를 검토하여 제주 서부 해역 해양환경에 적용 가능하도록 로터를 설계하였다(Poguluri and Bae, 2018). 본 연구에서는 이 결과를 바탕으로 축소모형(Model)을 이용한 2차원 조파수조 실험을 수행하고 이를 수치해석의 결과와 비교 분석 하였다. 설계된 Salter's duck의 거동 특성은 먼저, 선형 포텐셜 이론을 근거로 한 3차원 회절/방사 프로그램인 WAMIT을 이용하여 주파수 영역에서 해석하였고, 다음, 부유체의 시간 영역 거동 해석 프로그램인 OrcaFlex로 부터 주기별 규칙파에 따른 운동을 확인하고 RAO (Response amplitude operator)를 도출하여 WAMIT의 거동 특성 결과와 비교 검증하였다. 마지막으로, 수치해석으로 확인한 거동 특성을 검증하기 위하여 제주대학교 2차원 조파수조에서 파고에 따른 주기별 규칙파 실험을 행하였다. 이를 통해 종운동(Pitch) 변위를 측정하였고 실험 결과를 토대로 RAO를 도출하여 최종적으로 수치해석 결과와 비교하였다.
본 연구에서는 WAMIT과 OrcaFlex로 부터 산출한 수치적 거동 특성과 모형실험(Model test)을 통해서 얻은 거동 특성을 비교하여 수치해석의 신뢰성을 확인하였다. 모형실험은 실물(Prototype)의 특성을 확인하기 위한 가장 편리하고 경제적인 방법이다. 모형실험을 위해서는 실험이 가능한 범위 내에서의 축척비 선정을 시작으로, 상사법칙을 이용한 축소 제원 산출 및 축소모형의 재질 선정 등 여러 가지 조건의 고려가 필요하다.
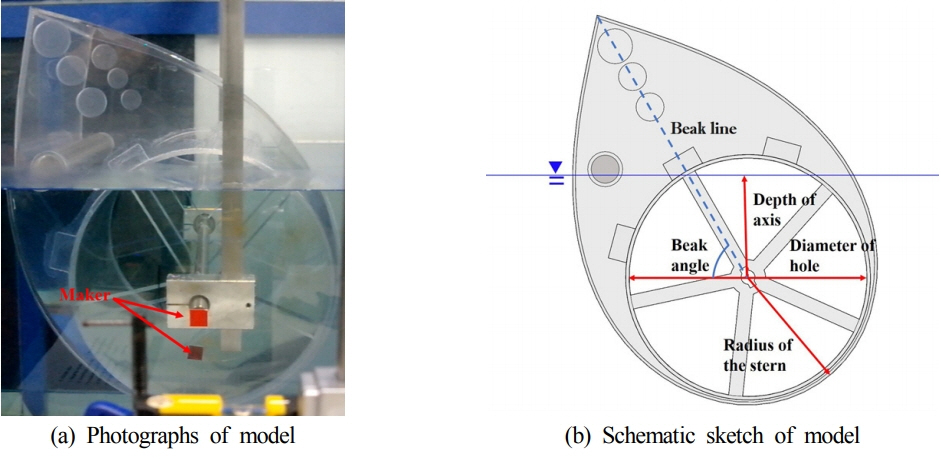
프루드(Froud)수 상사비 λ를 1/11로 하여 실물을 축소하였으며, 재질은 주로 사용되는 아크릴로 선정하였다. 모형실험에서 사용된 축소모형은 Fig. 1과 같다.
실물은 해수(Sea water)에서 적용되지만 축소모형은 담수(Fresh water)에서 적용되므로 로터가 정수 중 정적 평형을 이룰 수 있도록 축소모형 설계과정에서 보완하였다. 보완과정에서 최대한 실물의 특성을 가질 수 있도록 질량비를 유지하였으며, 적절한 로터의 종운동 비감쇠 고유주기(Undamped natural period, T0)를 갖도록 하였다. 로터의 종운동에 대한 비감쇠 고유주기는 질량분포에 따른 질량 관성모멘트(Moment of inertia)와 종운동의 복원력(Restoring force)에 의해 결정되며, 식 (1)과 같이 계산할 수 있다.
여기서 비감쇠 고유주기는 감쇠가 전혀 고려되지 않은 고유주기를 의미하며, I55는 로터의 질량 관성모멘트, a55는 부가질량 관성모멘트(Added mass moment of inertia) 그리고 k55는 정적 복원계수(Restoring coefficient)를 나타낸다. 밑첨자 55는 종운동을 의미한다. 모든 값들은 회전중심에서의 계산 결과를 사용하였다. 부가질량 관성모멘트와 정적 복원계수는 WAMIT을 이용하여 산출된 결과를 적용하였고, 최종적으로 모형실험에 사용된 로터의 제원 및 특성은 Table 1과 같으며 Fig. 1(b)에서 확인 가능하다.
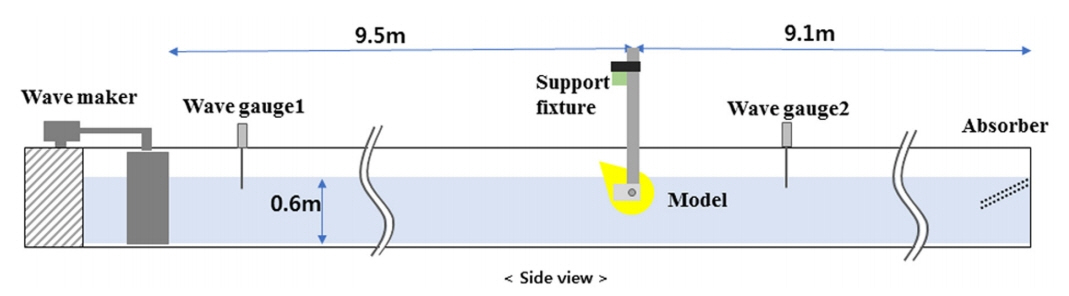
모형실험은 제주대학교 2차원 조파수조에서 실시하였다. 수조는 길이 20m, 폭 0.8m의 제원을 가지며 수심은 0.6m이다. Fig. 2는 모형실험의 구성도를 보여준다.
조파수조 한쪽 끝에는 피스톤 타입의 조파기(Wave maker)가 있으며, 반대쪽에는 경사형 소파장치(Absorber)가 설치되어 있다. 조파기로부터 약 2m 떨어진 위치에 저항식 파고계(Wave gauge)를 설치하여 입사파를 계측하였고, 조파기로부터 약 9.5m 떨어진 위치에 축소모형을 설치하여 영상 추적 기법(Image tracking)으로 운동변위를 측정하였다.
로터의 운동은 종운동만을 할 수 있도록 나머지 운동에 대해서는 최대한 구속시키지만 종운동 변위가 크게 일어나면 지지축의 처짐 현상으로 전후운동(Surge)과 상하운동(Heave)이 발생한다. 하지만 본 실험에서는 선형 거동 특성을 확인하고자 비교적 낮은 파고를 선정하였으며, 이는 주요 특성인 종운동 변위 외에는 무시할 수 있는 정도였다.
자유감쇠실험(Free decay test)은 초기각도(Initial angle, α0)를 다르게 하여 총 6차례 실시하였고, 파고에 따른 주기별 규칙파 실험은 파고를 0.01m와 0.03m로 구분하여 실시하였다. 낮은 파고를 선정한 이유는 앞서 설명하였듯이 비선형 효과를 최대한 줄여 선형 거동 특성을 확인하기 위함이다. 규칙파의 주기범위는 고유주기를 포함하고 있는 0.8~2.0s 내에서 수행하였다.
모형실험은 제주대학교 2차원 조파수조에서 자유감쇠실험, 파고에 따른 주기별 규칙파 실험 순으로 진행하였다. 자유감쇠실험은 초기각도를 다르게 하여 총 6차례 실시하였다. 이와 같이 실험을 계획한 이유는 크게 두 가지가 있다. 첫째는, 제작된 축소모형이 설계모델에 맞게 제작이 되었는지 확인해보기 위함이다. 종운동의 고유주기가 위 모델의 주요 특성이기에 자유감쇠실험을 통해 결과를 산출한 후 감쇠 고유주기(Damped natural period, TN)를 확인하였으며, 또한 이 결과를 바탕으로 파고에 따른 주기별 규칙파 실험의 주기범위를 선정하는데 참고하였다. 둘째는, WAMIT과 OrcaFlex 수치해석에 적용할 적절한 점성감쇠계수를 산정하기 위함이다. WAMIT은 선형 포텐셜 이론을 근거로 하기에 점성이 고려되지 않은 결과가 산출되지만 외부감쇠계수를 선형적으로 부가할 수 있다. 즉, 외부감쇠계수에 점성감쇠계수 값을 적용하면 선형 범위에서의 점성효과를 고려할 수 있다. OrcaFlex 또한 외부감쇠계수를 선형적으로 부가할 수 있다. 본 연구에서는 자유감쇠실험을 통해 감쇠비를 산출하고, 이를 이용하여 근사적인 점성감쇠계수를 계산하였다. 결과적으로 WAMIT 수치해석 결과와 OrcaFlex를 이용하여 도출한 RAO를 실험결과와 비교하기 위해서는 감쇠비(Damping ratio, κ)의 산출은 꼭 필요한 부분이다. 또한, 다양한 초기각도에 따른 결과를 가지고 있는 것은 실험결과와 비교 가능한 수치해석 결과를 도출하는데 유리하다.
로터의 정수상태에서의 자유 종운동 방정식을 선형 미분방정식 형태로 표현하면 식 (2)와 같이 간단히 나타낼 수 있다(Journee and Massie, 2001).
여기에서 ξ ¨ ξ ˙
식 (5)의 ω0는 비감쇠 고유주파수(Undamped natural frequency)를 의미한다. 또, 식 (4)와 식 (5)를 이용하여 식 (7)과 같이 무차원 값인 감쇠비(κ)로 표현할 수 있다(Journee and Massie, 2001).
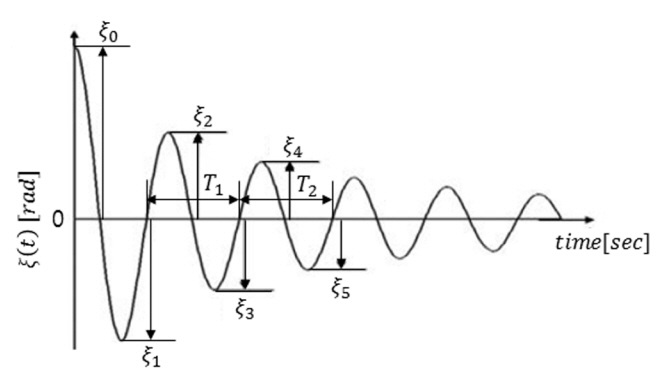
또한, 감쇠비(κ)는 Fig. 3과 같이 자유감쇠실험을 통해 얻은 시계열 자료로부터 대수감쇠법(Logarithmic decrement method)을 이용하여 산출할 수 있다.
시계열 자료는 영상 추적 기법을 이용하여 얻었다. Fig. 3은 시간에 따른 종운동 변위를 나타내는데, ξi, (i=1, 2, ..., 5)는 양 혹은 음의 극값(Positive or negative peaks)을 의미한다. 본 연구에서는 감쇠비를 산출하기 위해 ξ2, ξ3, ξ4 그리고 ξ5 값만을 적용하였다. ξ0 과 ξ1 을 적용하지 않은 이유는 초기각도만큼 기울이는 과정에서 인위적인 힘이 가해진다. 즉, 실험 수행에 있어 부정확성을 유발할 수 있는 요인들을 최대한 배제한 것이다. 시계열 자료로부터 Zero-crossing 방법을 사용하여 감쇠 고유주기(TN)를, 식 (8)과 같이 대수감쇠법으로 감쇠비(κ)를 산출하였다(Journee and Massie, 2001).
규칙파 실험에서의 파 주기범위는 0.8~2.0s로 하였고, 1.50~1.60s 범위에서는 주기를 좀 더 세분화하여 파고가 0.01m와 0.03m 일 때의 실험을 실시하였다. 주기별 규칙파 실험 또한 영상 추적 기법을 이용하여 시계열 자료를 얻었으며, 주기별로 반사파가 로터에 도달하기 전까지의 유효한 데이터를 추출하여 분석하였다. 시계열 자료로부터 종운동 RAO를 도출하기 위하여 식 (9)와 같이 주기별 규칙파에 따라 종운동 진폭(ξ*)을 입사파 진폭(A)으로 나누었다.
종운동 진폭은 Zero-crossing 방법을 사용하여 구한 평균값이다. 파고(H)가 각각 0.01m와 0.03m일 때의 주기별 규칙파 실험을 통해 도출한 RAO 그래프는 Fig. 4와 같다.
그래프에서 파란색 별 기호와 빨간색 마름모 기호는 각각 파고가 0.01m와 0.03m일 때의 RAO 결과를 나타낸다. 각각 감쇠 고유주기(TN)는 1.54s와 1.60s의 근삿값이다. 파고가 0.03m일 때 확인된 감쇠 고유주기가 파고가 0.01m일 때보다 0.06s 정도 길어지고 피크 값이 낮아진 것을 확인했다. 이는 입사파의 파고가 높아짐으로써 로터 운동에 작용하는 점성효과가 더 커졌으며, 정적 복원계수, 동유체력 계수(부가질량 관성모멘트, 방사감쇠계수) 및 파 기진력의 비선형성 때문이라고 사료된다. 수치해석에서 회전축을 기준으로 계산한 RAO와 감쇠 고유주기는 식 (10)과 식 (11)과 같다.
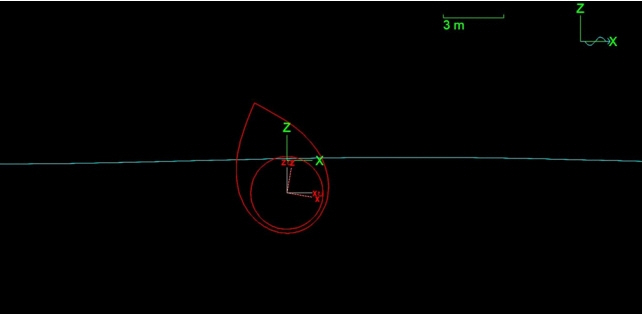
각 파고별로 피크 값을 갖는 입사파 주기에서의 종운동 변위 시계열 자료를 Fig. 5에 나타내었다.
Fig. 5의 시계열 자료는 반사파의 영향이 없는 유효한 데이터를 추출한 구간이다. 두 결과 모두 로터의 종운동은 수면 아래로의 회전운동보다 수면 위로의 회전운동이 더 큰 것을 볼 수 있으며, 파고가 커질수록 더 두드러지는 것을 확인 할 수 있다.
비대칭 형상 파력발전 로터의 거동특성을 확인하고자 WAMIT과 OrcaFlex 프로그램을 사용하여 각각 주파수 영역과 시간 영역에서 수치해석을 하였다. 두 경우 모두 종운동 외의 자유도는 구속하였고, 방사감쇠와 점성감쇠 이외의 감쇠력에 대해서는 무시하였다. 주파수 영역과 시간 영역의 운동 방정식은 각각 식 (12)와 식 (13)과 같다.
fexc, 5와 Fexc, 5는 각각 주파수 영역과 시간 영역에서의 파 기진력을 나타낸다. B55는 리타데이션 함수(Retardation function)이며 주파수 영역에서의 방사감쇠 계수 b 55 r a d ( ω )
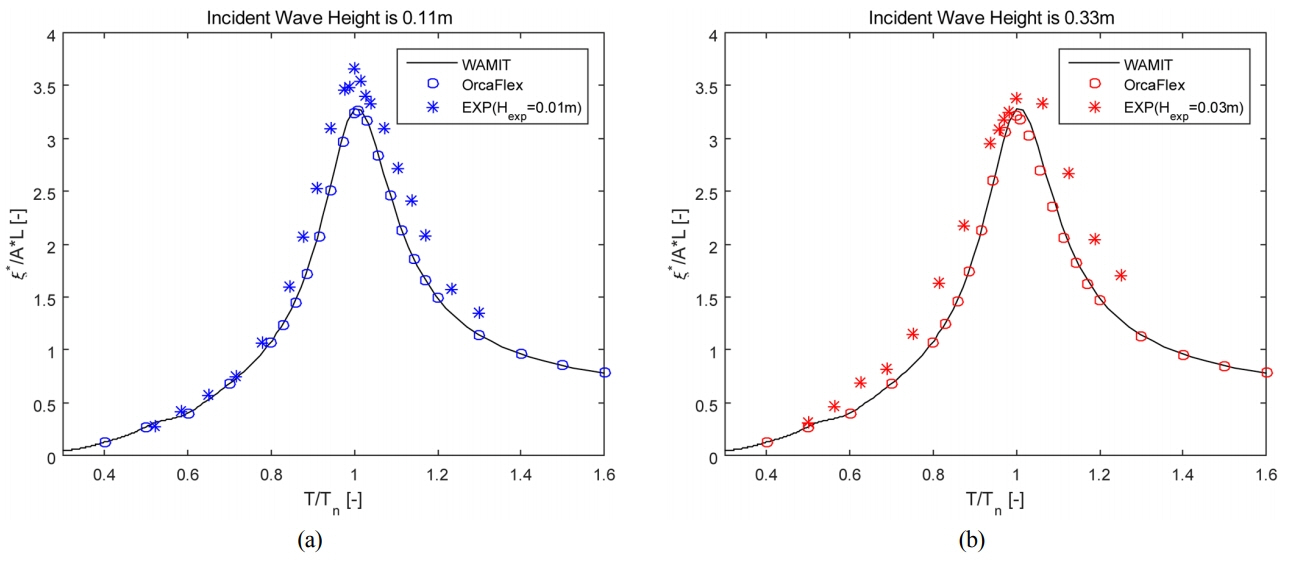
식 (13)에서 k55는 WAMIT으로 산출한 정적 복원계수를 기반으로 하지만 파고에 따른 비선형 효과를 확인하고자 무게중심과 부력중심 간의 모멘트 암(Moment arm) 변화를 매 시간단계마다 계산하여 로터의 순간적인 변위에 따라 정적 복원계수가 가변적으로 변하도록 비선형 조건을 주었다. 실험결과와의 비교를 위해 파고를 0.11m와 0.33m로 하여 주기별 규칙파에 대한 종운동 변위를 산출하였으며, 각 주기별 종운동 변위에서 규칙적인 구간을 최대한 추출하여 RAO 결과를 도출하였다. 최종적으로 수치해석 결과를 주기별 규칙파 실험결과와 비교하였다(Fig. 7).
Fig. 7에서 (a)와 (b)는 각각 입사파의 파고가 0.11m와 0.33m인 결과이다. (a)와 (b)에서 검정색 실선은 실물을 WAMIT으로 수치해석한 RAO 결과이고, 파란색과 빨간색 원 기호는 실물을 OrcaFlex를 이용하여 시간 영역에서 수치해석한 후 도출한 결과이다. 파란색과 빨간색 별 기호는 축소모형의 주기별 규칙파 실험을 통해 도출한 RAO 결과이다. 실험시, 파고는 0.01m와 0.03m이다. 실물과 축소모형의 RAO 결과를 상대적으로 비교하고자 두 그래프 모두 세로축과 가로축을 무차원화 하였다. 세로축은 RAO 값인 식 (9)에 대표길이(L)을 곱하여 무차원화 하였다. 대표길이 L은 실물일 경우 Lp, 축소모형의 경우 Lm이 각각 적용되며, 값은 각각 1m와 1/11m이다. 이는 축소모형과 실물의 직접적인 비교를 위해 척도인자(Scale factor)를 길이차원화한 값이다. 가로축은 주기(T)를 감쇠 고유주기(TN)로 나누었고, 각 결과의 감쇠 고유주기는 Table 3과 같다.
위 결과에서 실험결과와 WAMIT 및 OrcaFlex 수치해석 결과가 정성적으로 잘 일치함을 확인할 수 있다. OrcaFlex 결과의 경우, 정적 복원계수의 비선형 조건으로 인해 파고가 0.11m일 때보다 0.33m일 때의 피크 값이 낮은 것을 확인할 수 있다. 이로써 실험결과에서 파고가 커짐으로써 비선형 특성을 갖게 된다는 것을 검증하였다. 실험과 수치해석의 결과가 정량적으로 차이를 보이는 것은 축소모형 제작 과정 및 실험환경조건의 한계로 사료된다. 위 한계로 인한 오차를 무시하고 실물의 전체 감쇠계수를 산출하기 위해 축소모형으로부터 얻은 감쇠비를 적용하였다. 감쇠비로 얻은 전체 감쇠계수가 방사감쇠계수와 점성감쇠계수만을 포함한다고 가정하면, 동일한 감쇠비를 적용할 경우 위 오차로 인해 점성감쇠계수의 오차가 발생한다. 이렇듯 실질적으로 정확한 점성감쇠계수의 산출 과정에는 한계가 있다. 본 연구에서는 정성적으로 일치한 것을 바탕으로 WAMIT과 OrcaFlex를 이용하여 산출한 수치적 거동 특성은 선형범위에서 신뢰 가능하다고 판단하였다.
본 연구에서는 선형 포텐셜 이론을 근거로 한 3차원 회절/방사 프로그램 WAMIT을 이용하여 제주 서부 해역에 최적화된 비대칭 형상 로터의 선형 거동을 확인하였다. 다음, 이에 대한 검증을 위하여 시간 영역 거동 해석 프로그램인 OrcaFlex로 시간 영역 운동 해석을 수행하고, 제주대학교 2차원 조파수조에서 모형실험을 실시하여 거동 특성을 비교하였다. 모형실험은 감쇠비()를 얻기 위한 자유감쇠실험과 선형 거동 확인을 위한 파고에 따른 주기별 규칙파 실험으로 진행되었다. 주기별 규칙파 실험시 선형 거동 확인을 위해 비교적 낮은 파고를 선정하였다. WAMIT을 이용한 수치해석 결과는 선형 포텐셜 이론을 근거로 하므로 점성이 고려되지 않는다. 하지만 모형실험에서 방사감쇠와 점성감쇠만 작용한다고 가정하면, 자유감쇠실험을 통해 얻은 감쇠비를 이용하여 근사적인 점성감쇠계수를 산출한 후 적용할 수 있다. 또한, 본 연구에서는 로터의 종운동 고유주기에서의 시계열 자료로부터 확인된 수면 위 방향으로 회전하는 운동의 진폭만큼을 초기각도로 한 자유감쇠실험 결과가 외부감쇠계수로 적용하기에 가장 적절하다고 판단하였다. 이를 WAMIT과 OrcaFlex에서 외부감쇠계수로 선형적으로 부가하여 점성감쇠에 대해 선형적으로 고려하였다. 축소모형의 설계 비감쇠 고유주기는 1.53s였으며, 자유감쇠실험을 통해 확인한 감쇠 고유주기는 초기각도에 따라 달랐지만 1.55s에 근접하였다. 이로써 설계 의도대로 잘 제작되었음을 확인하였다. 모형실험을 통해 도출한 RAO결과를 WAMIT 및 OrcaFlex를 통한 수치해석 RAO결과와 비교하면 정성적으로 잘 일치하였다. 실험과 수치해석의 결과가 정량적으로 차이를 보이는 이유는 축소모형 제작 과정 및 실험환경조건의 한계로 사료되며, 이러한 이유 등으로 정확한 점성감쇠계수의 산출 과정에는 한계가 있다. 본 연구에서는 정성적으로 일치한 것을 바탕으로 WAMIT과 OrcaFlex 수치해석 결과의 신뢰성을 확인할 수 있었다.
본 연구에서는 파고를 0.01m, 0.03m로 낮은 파고에 대한 실험을 통해서 선형거동만을 확인하였다. 향후에는 높은 파고에서의 비선형적인 거동 특성에 대한 추가적인 연구가 필요하다.
후기
본 연구는 2018년도 산업통상자원부(MOTIE)의 재원으로 한국에너지기술평가원(KETEP)의 에너지인력양성사업 ‘육해상 풍력터빈 신뢰성 및 발전량 향상을 위한 O&M 기술 고급트랙’으로 지원받아 수행한 인력양성 성과입니다(No. 20184030202200). 또한 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(No. 20163010071690).
Fig. 5
Time series data when wave period equals to natural period(wave height (a) : 0.01 m, (b) : 0.03 m)
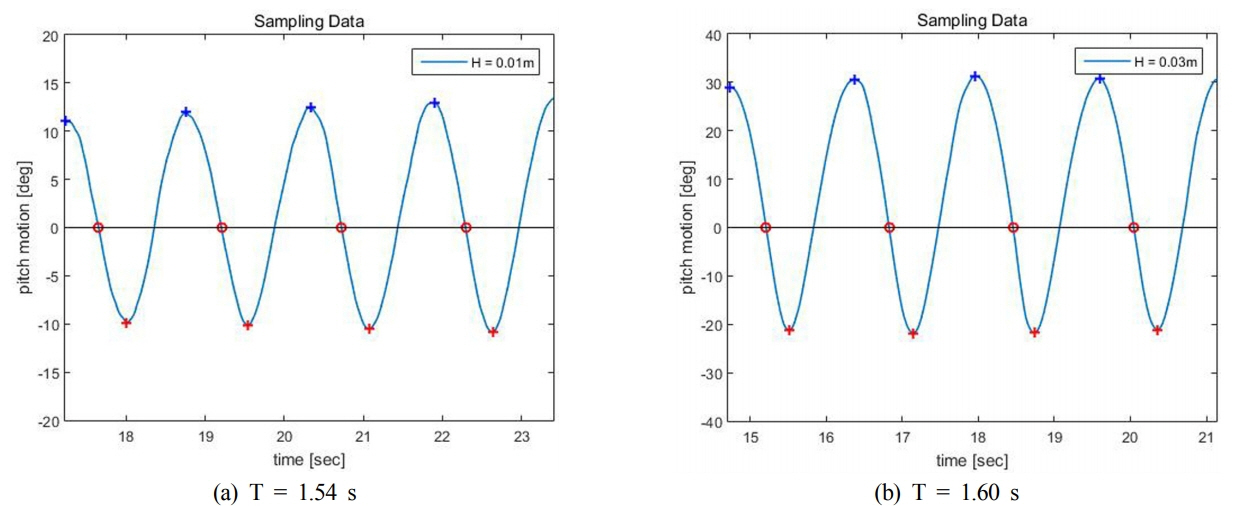
Table 1
Specification of experimental model
Table 2
Specification of experimental model
References
Count, BM. (1978). On the Dynamics of Wave-power Devices. Proceedings of the Royal Society. A Mathematical and Physical Sciences, 363(1715), 559-579. https://doi.org/10.1098/rspa.1978.0183

Evans, DV. (1976). A Theory for Wave-power Absorption by Oscillating Bodies. Journal of Fluid Mechanics, 77(1), 1-25. https://doi.org/10.1017/S0022112076001109

Jeffrey, DC., Richmond, DJE., Salter, SH., Taylor, JRM., & Young, IA. (1976). Second Year Interim Report on Edinburgh Wave Power Project: Study of Mechanism to Extract Power from Sea Waves. University of Edinburgh.
Journee, JMJ., & Massie, WW. (2001). Offshore Hydromechanics. Firs Edition Delft University of Technology.
Mynett, AE., Serman, DD., & Mei, CC. (1979). Characteristics of Salter’s Cam for Extracting Energy from Ocean Waves. Applied Ocean Research, 1(1), 13-20. https://doi.org/10.1016/0141-1187(79)90004-X

Poguluri, SK., & Bae, YH. (2018). A Study on Performance Assessment of WEC Rotor in the Jeju Western Waters. Ocean System Engineering, 8(4), 361-380. https://doi.org/10.12989/ose.2018.8.4.361

Poguluri, SK., Cho, IH., & Bae, YH. (2019). A Study of the Hydrodynamic Performance of a Pitch-type Wave Energy Converter-Rotor. Energies, 12(5), 842. https://doi.org/10.3390/en12050842

Salter, SH., Jeffrey, DC., & Taylor, J. (1975). First Year Interim Report on Edinburgh Wave Power Project: Study of Mechanism to Extract Power from Sea Waves. University of Edinburgh.
Swift-Hook, DT., Count, BM., Glendenning, I., & Salter, S. (1975). Characteristics of a Rocking Wave Power Device. Nature, 254(5500), 504-506. https://doi.org/10.1038/254504a0

Wu, J., Yao, Y., Li, W., Zhou, L., & Göteman, M. (2017). Optimizing the Performance of Solo Duck Wave Energy Converter in Tide. Energies, 10(3), 289. https://doi.org/10.3390/en10030289

- TOOLS
-
METRICS

-
- 13 Crossref
- Scopus
- 8,561 View
- 147 Download
- Related articles in JOET
-
Numerical Investigation of Multi-body Wave Energy Converters’ Configuration2022 April;36(2)
Experimental Study on Reducing Motion of Circular Cylinder in Currents2019 August;33(4)
An Experimental Study on the Appendage Development of the Incinerating Vessel1999 February;13(1)