|
 |
- Search
| J. Ocean Eng. Technol. > Volume 33(1); 2019 > Article |
|
Abstract
This paper considers a numerical assessment of the self-propulsion performance of a damaged ferry carrying cars in irregular waves. Computational fluid dynamics(CFD) simulations were performed to see whether the ferry complied with the Safe Return to Port (SRtP) regulations of LloydŌĆÖs register, which require that damaged passenger ships should be able to return to port with a speed of 6 knots (3.09 m/s) in Beaufort 8 sea conditions. Two situations were considered for the damaged conditions, i.e., 1) the portside propeller was blocked but the engine room was not flooded and 2) the portside propeller was blocked and one engine room was flooded. The self-propulsion results for the car ferry in intact condition and in the damaged conditions were assessed as follows. First, we validated that the portside propeller was blocked in calm water based on the available experimental results provided by KRISO. The active thrust of starboard propeller with the portside propeller blocked was calculated in Beaufort 8 sea conditions, and the results were compared with the experimental results provided by MARIN, and there was reasonable agreement. The thrust provided by the propeller and the brake horsepower (BHP) with one engine room flooded were compared with the values when the engine room was not flooded. The numerical results were compared with the maximum thrust of the propeller and the maximum brake horse power of the engine to determine whether the damaged car ferry could attain a speed of 6 knots(3.09 m/s).
ņäĀļ░Ģ ņÜ┤ĒĢŁ ņŗ£ ņĀüņÜ®ļÉśļŖö ņĢłņĀäņŚÉ Ļ┤ĆĒĢ£ ĻĘ£ņĀĢļōżņØś ļ¦īņĪ▒ ņŚ¼ļČĆņÖĆ ņé¼Ļ│ĀļĪ£ ņØĖĒĢ£ ņåÉņāü ņØ┤Ēøä ņĢłņĀĢņä▒ ĒÖĢļ│┤ņŚÉ ļīĆĒĢ£ ĒÅēĻ░ĆĻĖ░ņłĀ Ļ░£ļ░£ņØ┤ Ļ┤ĆļĀ© ņŚ░ĻĄ¼ ļČäņĢ╝ņŚÉņä£ ļŗżņ¢æĒĢ£ ņĀæĻĘ╝ļ▓Ģņ£╝ļĪ£ ņ¦äĒ¢ēļÉśĻ│Ā ņ׳ļŗż. ņØ┤ņÖĆ Ļ┤ĆļĀ©ļÉ£ ņ£Āņ▓┤ņŚŁĒĢÖņĀü ņŚ░ĻĄ¼ļōż Ļ░ĆņÜ┤ļŹ░, Papanikolau at al.(2000)ņØ┤ ņåÉņāüņ£╝ļĪ£ ļČĆļČä ņ╣©ņłśļÉ£ Ro-RoņäĀņØś Ēīīļ×æ ņżæ ņĀäļ│Ą(Capsizing) ņāüĒÖ®ņŚÉ ļīĆĒĢ£ ļ¼╝ļ”¼ņĀü ņØ┤ĒĢ┤ļź╝ ņ¢╗ĻĖ░ ņ£äĒĢ┤ ņłśĒ¢ēĒĢ£ ļ¬©ĒśĢņŗ£ĒŚś Ļ▓░Ļ│╝ņÖĆ Ļ▓ĮĒŚśņŗØĻ│╝ ĒżĒģÉņģ£ņ£ĀļÅÖ ĻĖ░ļ░śņØś ņłśņ╣śĒĢ┤ņäØ Ļ▓░Ļ│╝ļź╝ ņåīĻ░£ĒĢ£ ļ░ö ņ׳ļŗż. ņØ┤Ēøä, Korkut et al.(2004)ņØ┤ ņåÉņāüĻ│╝ ļ╣äņåÉņāü ņāüĒā£ Ro-RoņäĀņØś Ēīīļ×æ ņżæ ņÜ┤ļÅÖņØæļŗĄņŚÉ ļīĆĒĢ£ ļ¬©ĒśĢņŗ£ĒŚśņ£╝ļĪ£ ņŚ░ĻĄ¼ĒĢśņśĆņ£╝ļ®░, Lee et al.(2007) ņŚŁņŗ£, ņåÉņāüļÉ£ Ro-RoņäĀņØś Ēīīļ×æ ņżæ ņÜ┤ļÅÖĒŖ╣ņä▒ņØä ņØ┤ļĪĀņĀü ņŗ£ļ«¼ļĀłņØ┤ņģś ļ░®ļ▓ĢĻ│╝ ļ¬©ĒśĢņŗ£ĒŚśņ£╝ļĪ£ ņŚ░ĻĄ¼ĒĢ£ Ļ▓░Ļ│╝ļź╝ ļ░£Ēæ£ĒĢśņśĆļŗż. Cho et al.(2006)ņØĆ ņåÉņāüļÉ£ ņśüņŚŁņØś ņ╣©ņłśņ£ĀļÅÖņØś ļÅÖņŚŁĒĢÖņĀü ĒŖ╣ņä▒ņØä ņĪ░ņé¼ĒĢśĻĖ░ ņ£äĒĢ£ ļ¬©ĒśĢņŗ£ĒŚśĻ│╝ CFD(Computational fluid dynamics) ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆņ£╝ļ®░, ļ╣äņŖĘĒĢ£ ņŚ░ĻĄ¼ļĪ£ņä£ Ruponen(2007)ņØ┤ ņåÉņāüļÉ£ ņäĀņ▓┤ļĪ£ ĒĢ┤ņłśĻ░Ć ņ£Āņ×ģļÉśļŖö Ļ│╝ņĀĢņŚÉ ļīĆĒĢ£ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśĻ│Ā ļ¬©ĒśĢņŗ£ĒŚśĻ│╝ ļ╣äĻĄÉĒĢ£ ņŚ░ĻĄ¼Ļ▓░Ļ│╝ļź╝ ļ░£Ēæ£ĒĢśņśĆļŗż.
ĒĢ£ĒÄĖņ£╝ļĪ£, ņĄ£ĻĘ╝ ņĀüņÜ®ļÉśļŖö ņĢłņĀäĻĘ£ņĀĢļōż Ļ░ĆņÜ┤ļŹ░, ņŖ╣ņäĀ ņØĖņøÉņØ┤ ļ¦ÄņØĆ ņŚ¼Ļ░ØņäĀĻ│╝ Ļ░ÖņØĆ ņäĀļ░ĢņØś Ļ▓ĮņÜ░ ĒĢ┤ņāü ņé¼Ļ│ĀļĪ£ ņäĀņ▓┤ ņåÉņāüņØ┤ ļ░£ņāØĒĢ£ ņĪ░Ļ▒┤ņŚÉņä£ļÅä ĒĢŁĻĄ¼ļĪ£ ļ¼┤ņé¼Ē׳ ĻĘĆĒÖśĒĢĀ ņłś ņ׳ņ¢┤ņĢ╝ ĒĢ£ļŗżļŖö ĻĘ£ņĀĢļōżņØ┤ Ļ░ĢĒÖöļÉśĻ│Ā ņ׳ļŗż. ņØ┤ļ¤¼ĒĢ£ ņĢłņĀäĻĘĆĒĢŁ(Safe return to port, SRtP)ĻĘ£ņĀĢņŚÉ Ļ┤ĆĒĢśņŚ¼ļŖö IMO(International Maritime Organization, 2009)ņŚÉņä£ ļ│╝ ņłś ņ׳ļō»ņØ┤ 1914ļģä IMOņŚÉņä£ ņ▓┤Ļ▓░ļÉ£ SOLAS(Safety of life at sea)ņØś Ļ░ĢĒÖöļÉ£ ĻĘ£ņĀĢņ£╝ļĪ£ 2010ļģä 7ņøö ņØ┤Ēøä ĻĖĖņØ┤ 120m ņØ┤ņāüņØĖ ņäĀļ░ĢņŚÉ ņĀüņÜ®ļÉśĻ│Ā ņ׳ļŗż. SRtP ĻĘ£ņĀĢņØĆ ņé¼Ļ│ĀņÖĆ ņĢłņĀäĻĘĆĒĢŁņØä ļŗ¼ņä▒ĒĢĀ ņłś ņ׳ļŖö ņäĀļ░ĢņØś ņŗ£ņŖżĒģ£ļōżņØä Ļ▓Ćņ”ØĒĢśļŖö ļŗżņ¢æĒĢ£ ĒĢŁļ¬®ļōżņØä ņäżļ¬ģĒĢśĻ│Ā ņ׳ļŗż. ĻĘĖļ¤¼ļéś ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö SRtP ĻĘ£ņĀĢņŚÉņä£ ņČöņ¦ä ņŗ£ņŖżĒģ£ņŚÉ Ļ┤ĆļĀ©ļÉ£ ņåÉņāü ņäĀļ░ĢņØś Ēīīļ×æ ņżæ ņĢłņĀäĻĘĆĒĢŁ ņäĀņåŹņØä ņ£Āņ¦ĆĒĢĀ ņłś ņ׳ļŖö ņåīņÜöļ¦łļĀź ņČöņĀĢņŚÉ Ļ┤ĆĒĢ£ ļé┤ņÜ®ņ£╝ļĪ£ ņĀ£ĒĢ£ĒĢśņŚ¼ ļŗżļŻ©Ļ│Āņ×É ĒĢ£ļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ┤ĆņĀÉņŚÉņä£ SRtP ĻĘ£ņĀĢņØĆ ņäĀĻĖēļ│äļĪ£ ņĢĮĻ░ä ļŗżļź┤Ļ▓ī ņĀüņÜ®ļÉśĻ│Ā ņ׳ļŗż. ņśüĻĄŁņäĀĻĖēĒśæĒÜī(LloydŌĆÖs resister)ņŚÉņä£ļŖö ŌĆ£ņåÉņāüņäĀļ░ĢņØ┤ Beaufort 8ņØś ĒĢ┤ņāüņĪ░Ļ▒┤ņŚÉņä£ 6ļģĖĒŖĖ(knot), ņĢĮ 3.09m/sņØś ņåŹļÅäļĪ£ ļ¼┤ņé¼Ē׳ ĻĘĆĒÖśĒĢĀ ņłś ņ׳ņ¢┤ņĢ╝ ĒĢ£ļŗż(LloydŌĆÖs register, 2010).ŌĆØĻ│Ā ĻČīĻ│ĀĒĢśĻ│Ā ņ׳ņ£╝ļ®░ ļÅģņØ╝ņäĀĻĖēĒśæĒÜī(Germanischer Lioyd)ņØĆ ŌĆ£ņØ╝ļ░śņĀüņØĖ ĻĖ░ņāüņĪ░Ļ▒┤(Normal weather)ņŚÉņä£ 7ļģĖĒŖĖ(3.6m/s) ņäĀņåŹ ļśÉļŖö ņäżĻ│äņåŹļÅäņØś ņĀłļ░śņŚÉ ņżĆĒĢśļŖö ņåŹļÅäļĪ£ ļ¼┤ņé¼Ē׳ ĒÜīĒĢŁĒĢĀ ņłś ņ׳ņ¢┤ņĢ╝ĒĢ£ļŗż(Germanischer Lloyd, 2009).ŌĆØļØ╝Ļ│Ā ņĀ£ņŗ£ĒĢśĻ│Ā ņ׳ļŗż. ņĄ£ĻĘ╝, ņØ┤ļ¤¼ĒĢ£ SRtP ĻĘ£ņĀĢņØä ņ¦üņĀæņĀüņ£╝ļĪ£ ĒĢ┤ņäØĒĢ£ ņé¼ļĪĆļĪ£ļŖö Lim(2014)Ļ│╝ Espinoza Haro(2016)ņŚÉ ņØśĒĢ£ ļ¬©ĒśĢņŗ£ĒŚśĻ│╝ CFD ĒĢ┤ņäØ Ļ▓░Ļ│╝Ļ░Ć Ļ░üĻ░ü ļ░£Ēæ£ļÉ£ ļ░ö ņ׳ļŗż. ļīĆņāü ņŚ¼Ļ░ØņäĀņØĆ ņĖĪļ®┤ ņåÉņāüņ£╝ļĪ£ ņäĀņŗżņØ┤ ļČĆļČä ņ╣©ņłśļÉ£ ņāüĒÖ®ņØ┤ļ®░, ļÅģņØ╝ņäĀĻĖēņØś SRtP ĻĘ£ņĀĢņŚÉ ļö░ļØ╝ ļ¬©ĒśĢņŗ£ĒŚśĻ│╝ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņŚ¼ ņåÉņāü ņāüĒā£ņŚÉņä£ ņ╣©ņłśĻĄ¼ņŚŁņØś ļé┤ļČĆņ£ĀļÅÖ, ņČöļĀź ļ│ĆĒÖö, ņäĀņ▓┤ņÜ┤ļÅÖ ļ│ĆĒÖö ĻĘĖļ”¼Ļ│Ā ņäĀņåŹņØś Ļ░ÉņåŹ ņĀĢļÅäļź╝ ņČöņĀĢĒĢśņśĆļŗż. ļŗżļ¦ī, ņĀĆņ×ÉļōżņØś ņŚ░ĻĄ¼ņŚÉņä£ ĒĢ┤ņāüņĪ░Ļ▒┤ņØĆ ĻĘ£ņ╣ÖĒīī(Regular wave) ņĪ░Ļ▒┤ņØä ņé¼ņÜ®ĒĢśņśĆļŗż.
ļ│Ė ļģ╝ļ¼ĖņØĆ ĻĖ░Ļ┤Ć Ļ│Āņןņ£╝ļĪ£ ņóīĒśäņØś ĒöäļĪ£ĒÄĀļ¤¼Ļ░Ć ņ×æļÅÖĒĢśņ¦Ć ņĢŖļŖö ņīŹņČĢ ņ╣┤ĒÄśļ”¼ņäĀ(Car ferry)ņØä ļīĆņāüņ£╝ļĪ£ ņśüĻĄŁņäĀĻĖēņØś SRtP ĻĘ£ņĀĢņŚÉ ļīĆĒĢ┤ CFDĒĢ┤ņäØņØä ņłśĒ¢ēĒĢ£ ņŚ░ĻĄ¼Ļ▓░Ļ│╝ļź╝ ņåīĻ░£ĒĢśĻ│Ā ņ׳ļŗż. ļ©╝ņĀĆ, ļģ╝ļ¼ĖņØĆ SRtP ņłśņ╣śĒĢ┤ņäØņŚÉ ņĢ×ņä£ ņĀĢņłśņżæ ņ×ÉĒĢŁņāüĒā£ļź╝ ĒĢ┤ņäØĒĢśĻ│Ā ņäĀļ░ĢĒĢ┤ņ¢æĒöīļ×£ĒŖĖņŚ░ĻĄ¼ņåī, KRISO(Korea Research Institute of Ships and Ocean Engineering)ņØś ļ¬©ĒśĢņŗ£ĒŚś Ļ▓░Ļ│╝ņÖĆ ļ╣äĻĄÉĒĢśņŚ¼ Ļ▓Ćņ”ØĒĢ£ ļé┤ņÜ®ņØä ļŗżļŻ©ņŚłļŗż. SRtP ņĪ░Ļ▒┤ ņłśņ╣śĒĢ┤ņäØņØĆ Beaufort 8ņØś ļČłĻĘ£ņ╣ÖĒīī ņĪ░Ļ▒┤ņŚÉņä£ ļŗ©ņČĢ ņČöņ¦äņ£╝ļĪ£ ņ×ÉĒĢŁņżæņØĖ ņ╣┤ĒÄśļ”¼ ņäĀļ░ĢņØ┤ 6ļģĖĒŖĖ(3.09m/s)ņØś ņåŹļĀźņØä ļé┤ļŖöļŹ░ ĒĢäņÜöĒĢ£ ņŗżņäĀ ļ¦łļĀźņØä ņČöņĀĢĒĢśņśĆļŗż. ņŚ¼ĻĖ░ņä£, ņłśņ╣śĒĢ┤ņäØ Ļ▓░Ļ│╝ļŖö ļäżļŹĖļ×Ćļō£ MARIN(Maritime Research Institute Netherlands)ņŚÉņä£ ņłśĒ¢ēĒĢ£ ļ¬©ĒśĢņŗ£ĒŚś Ļ▓░Ļ│╝ņÖĆ ļ╣äĻĄÉĒĢśĻ│Ā, ņČöņĀĢļÉ£ ņåīņÜöļ¦łļĀźņØĆ Ēāæņ×¼ļÉ£ ņŚöņ¦äņØ┤ ļé╝ ņłś ņ׳ļŖö ņĄ£ļīĆ ļ¦łļĀźĻ│╝ ļ╣äĻĄÉĒĢśņŚ¼ SRtP ņäĀņåŹ ļŗ¼ņä▒ ņŚ¼ļČĆļź╝ Ļ▓ĆĒåĀĒĢśņśĆļŗż. ļŗżņØīņ£╝ļĪ£ ĻĖ░Ļ┤Ćņŗż ņ╣©ņłś ņāüĒÖ®ņØä Ļ│ĀļĀżĒĢ£ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśĻ│Ā ņ╣©ņłśĻ░Ć ļ░£ņāØĒĢśņ¦Ć ņĢŖļŖö ņĪ░Ļ▒┤Ļ│╝ ļ╣äĻĄÉĒĢśņŚ¼ Beaufort 8ņØś Ēīīļ×æ ņżæ 6ļģĖĒŖĖ(3.09m/s)ņØś ņäĀņåŹņØä ņ£Āņ¦ĆĒĢśļŖöļŹ░ ņåīņÜöļÉśļŖö ļ¦łļĀź ņ”ØĻ░Ćļ¤ēņŚÉ ļīĆĒĢ┤ ļģ╝ņØśĒĢśņśĆļŗż.
Ēīīļ×æ ņżæ ņ╣┤ĒÄśļ”¼ ņäĀļ░Ģ ņŻ╝ņ£ä ņ£ĀļÅÖ ĒĢ┤ņäØņØĆ ļ▓öņÜ®ĒöäļĪ£ĻĘĖļש STAR-CCM+(Siemens, 2018)ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņłśĒ¢ēĒĢśņśĆļŗż. ņäĀņ▓┤ ņŻ╝ņ£ä ņ£ĀļÅÖņØĆ ņÖäņĀäĒ׳ ļ░£ļŗ¼ļÉ£ ļ╣äņĢĢņČĢņä▒ ļé£ļźśņ£ĀļÅÖ(Incompressible turbulent flow)ņ£╝ļĪ£ Ļ░ĆņĀĢĒĢśĻ│Ā ņ¦Ćļ░░ļ░®ņĀĢņŗØņ£╝ļĪ£ ņŚ░ņåŹ ļ░®ņĀĢņŗØĻ│╝ ņÜ┤ļÅÖļ¤ē ļ│┤ņĪ┤ļ░®ņĀĢņŗØņØĖ RANS(Reynolds averaged navier-stokes) ļ░®ņĀĢņŗØņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ņ¦Ćļ░░ļ░®ņĀĢņŗØņØĆ ņ£ĀĒĢ£ņ▓┤ņĀüļ▓Ģ(Finite volume method)ņ£╝ļĪ£ ņØ┤ņé░ĒÖöĒĢśņŚ¼ ĻĘĖ ĒĢ┤ļź╝ ĻĄ¼ĒĢ£ļŗż. ņŚ¼ĻĖ░ņä£, ņ¦Ćļ░░ļ░®ņĀĢņŗØņØś ņŗ£Ļ░ä ņĀüļČä ļ░Å Ļ│ĄĻ░äņŚÉ ļīĆĒĢ£ ņØ┤ņé░ĒÖöņŚÉļŖö 2ņ░© ņĀĢĒÖĢļÅäņØś ĻĖ░ļ▓ĢņØ┤ ņé¼ņÜ®ļÉśņŚłļŗż. ļ╣äņĢĢņČĢņä▒ ņ£ĀļÅÖ ĒĢ┤ņäØņŚÉņä£ ņ£Āņ▓┤ņØś ņåŹļÅäņÖĆ ņĢĢļĀźņØä ņŚ░ņä▒ĒĢśļŖö ļ░®ļ▓Ģņ£╝ļĪ£ SIMPLE(Semi-Implicit method for pressure-linked equation) ļ░®ļ▓ĢņØä ņäĀĒāØĒĢśņśĆļŗż.
ļé£ļźśļ¬©ĒśĢņØĆ ņäĀļ░ĢņØś ņĀĆĒĢŁĻ│╝ ņ×ÉĒĢŁņä▒ļŖź ĒĢ┤ņäØņŚÉņä£ ļ¬©ĒśĢņŗ£ĒŚś Ļ▓░Ļ│╝ņÖĆ ļ╣äĻĄÉĒĢśņŚ¼ ļ╣äĻĄÉņĀü ļ¦īņĪ▒ņŖżļ¤¼ņÜ┤ ņóŗņØĆ ņØ╝ņ╣śļź╝ ļ│┤ņŚ¼ņŻ╝ļŖö Realizable k-ŌłŖ ļ¬©ĒśĢņØä ļ▓Įļ®┤ĒĢ©ņłś(Wall function) ĻĖ░ļ▓ĢĻ│╝ ĒĢ©Ļ╗ś ņé¼ņÜ®ĒĢśņśĆļŗż.
ņ╣┤ĒÄśļ”¼ ņäĀļ░ĢņØś ĒöäļĪ£ĒÄĀļ¤¼ļŖö ĒśĢņāüņØä ņ¦üņĀæ ļ¬©ļŹĖļ¦üĒĢśņ¦Ć ņĢŖĻ│Ā ĒöäļĪ£ĒÄĀļ¤¼ņØś ņ¦üĻ▓ĮņØä Ļ░Ćņ¦ĆļŖö ļæÉĻ╗śĻ░Ć ņØ╝ņĀĢĒĢ£ ņøÉĒīÉņØ┤ ņŻ╝ņ¢┤ņ¦ä ņĀäņ¦äļ╣ä(Advance ratio)ņŚÉņä£ ņČöļĀźĻ│╝ ĒåĀņśżĒü¼ļź╝ ļé┤ļŖö ļ░®ļ▓Ģņ£╝ļĪ£ Ļ│ĀļĀżĒĢśņśĆļŗż. ņØ┤ļŖö Virtual diskļ▓Ģņ£╝ļĪ£ ļČłļ”¼ļŖö ņłśņ╣śĻĖ░ļ▓Ģņ£╝ļĪ£ STAR-CCM+ņŚÉņä£ ņĀ£Ļ│ĄĒĢśĻ│Ā ņ׳ņ£╝ļ®░, ņØ┤ļĢī ņ×ģļĀźņ£╝ļĪ£ ĒĢäņÜöĒĢ£ ņĀäņ¦äļ╣ä(Advance ratio)ņŚÉ ļö░ļźĖ ņČöļĀźĻ│╝ ĒåĀņśżĒü¼ņØś ĒöäļĪ£ĒÄĀļ¤¼ ļŗ©ļÅģņä▒ļŖź Ļ│ĪņäĀ(Propeller open water curve)ņØĆ KRISOņŚÉņä£ ņłśĒ¢ēĒĢ£ ļ¬©ĒśĢņŗ£ĒŚś Ļ▓░Ļ│╝ļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż. ĒöäļĪ£ĒÄĀļ¤¼ņØś ņČöļĀźĻ│╝ ĒåĀņśżĒü¼ļŖö Virtual diskļé┤ņŚÉņä£ ļŗżņØīĻ│╝ Ļ░ÖņØĆ ļ░®ņŗØņ£╝ļĪ£ Ēæ£ĒśäļÉśļŖö ņ▓┤ņĀüļĀź(Body-force) ļČäĒżļź╝ ĒåĄĒĢ┤ ņ¦Ćļ░░ļ░®ņĀĢņŗØņŚÉņä£ Ļ│ĀļĀżļÉ£ļŗż.
ņŚ¼ĻĖ░ņä£, fbx ņÖĆ fb╬ĖļŖö ņČĢļ░®Ē¢źĻ│╝ ņøÉņŻ╝ļ░®Ē¢ź ņ▓┤ņĀüļĀź ņä▒ļČäņØä ļéśĒāĆļé┤Ļ│Ā, rņØĆ ļ░śĻ▓Įļ░®Ē¢ź ņóīĒæ£, ĻĘĖļ”¼Ļ│Ā RHļŖö ĒöäļĪ£ĒÄĀļ¤¼ ĒŚłļĖīļ░śĻ▓Į, ĻĘĖļ”¼Ļ│Ā RPļŖö ĒöäļĪ£ĒÄĀļ¤¼ņØś ļ░śĻ▓ĮņØä ļéśĒāĆļéĖļŗż. ņŗØ (1)Ļ│╝ ņŗØ (2)ņŚÉņä£ ņāüņłś Ax ņÖĆ A╬ĖļŖö ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ņĀĢņØśļÉ£ļŗż.
ņŚ¼ĻĖ░ņä£, TņÖĆ QļŖö Ļ░üĻ░ü ĒöäļĪ£ĒÄĀļ¤¼ņØś ņČöļĀźĻ│╝ ĒåĀņśżĒü¼ļź╝ ļéśĒāĆļé┤Ļ│Ā ŌłåļŖö Virtual diskņØś ļæÉĻ╗śļź╝ ļéśĒāĆļéĖļŗż.
ņ╣┤ĒÄśļ”¼ ņäĀļ░Ģņ£╝ļĪ£ ņ×ģņé¼ļÉśļŖö ĒīīņÖĆ ņäĀņ▓┤ņØś ņÜ┤ļÅÖņ£╝ļĪ£ ļ░£ņāØĒĢśļŖö ņ×Éņ£Āņłśļ®┤ņāüņØś ĒīīļŖö 2ņ░© ņĀĢļÅäņØś VOF(Volume of fluid)ļ▓ĢņØä ņäĀĒāØĒĢśņŚ¼ ĒĢ┤ņäØĒĢśņśĆļŗż(Muzaferija et al., 1998). ļČłĻĘ£ņ╣ÖĒīīļŖö ņ£ĀņØśĒīīĻ│Ā(Significant wave height)ņÖĆ ĒīīņØś ņ▓©ļæÉņŻ╝ĻĖ░(Peak wave period) ĻĘĖļ”¼Ļ│Ā ļ░öļ×īņØś ņåŹļÅäļź╝ ņ×ģļĀźņ£╝ļĪ£ ĒĢśļŖö STAR-CCM+ņŚÉņä£ ņĀ£Ļ│ĄĒĢśļŖö JONSWAP(Joint North Sea wave project) ņŖżĒÄÖĒŖĖļ¤╝ņ£╝ļĪ£ ņāØņä▒ĒĢśņśĆļŗż(Siemens, 2018). ņØ┤ļĢī, ļČłĻĘ£ņ╣ÖĒīīļŖö ņäĀĒśĢĒīī(Linear wave)ļōżņØś ņżæņ▓®ņ£╝ļĪ£ Ļ░ĆņĀĢĒĢśĻ│Ā Ļ│äņé░ņśüņŚŁ(Computational domain)ņØś ņ£Āņ×ģ Ļ▓ĮĻ│äļ®┤ņŚÉņä£ VOF Ļ░Æņ£╝ļĪ£ Ēæ£ĒśäļÉśļŖö ĒīīĻ│ĀņÖĆ ĒīīņŚÉ ņØśĒĢ£ ņ£ĀņåŹ ņä▒ļČäļōżņØä ņ×ģļĀźĒĢśņŚ¼ ņāØņä▒ĒĢ£ļŗż.
ņÜ┤ļÅÖļ░®ņĀĢņŗØņŚÉņä£ ņ¢╗ņØĆ Ēīīļ×æ ņżæ ņäĀņ▓┤ņØś ņÜ┤ļÅÖ ļ│Ćņ£äļŖö ņäĀņ▓┤ ņŻ╝ņ£ä ņäĀņ▓┤ņÖĆ Ļ░ÖņØ┤ ņÜ┤ļÅÖĒĢśļŖö Ļ▓®ņ×ÉĻ│äņÖĆ ĻĘĖ ņŻ╝ņ£äņØś Ļ│ĀņĀĢļÉ£ ļ░░Ļ▓Į Ļ▓®ņ×ÉĻ│äļĪ£ ĻĄ¼ļČäĒĢśļŖö ņżæņ▓®Ļ▓®ņ×Éļ▓Ģņ£╝ļĪ£ ņ¦Ćļ░░ļ░®ņĀĢņŗØņØś ĒĢ┤ļź╝ ĻĄ¼ĒĢĀ ļĢī Ļ│ĀļĀżļÉ£ļŗż. ņÜ┤ļÅÖĒĢśļŖö Ļ▓®ņ×ÉĻ│äņÖĆ Ļ│ĀņĀĢļÉ£ Ļ▓®ņ×ÉĻ│ä Ļ░ä ņ£ĀļÅÖ ņĀĢļ│┤ ĻĄÉĒÖśņØĆ Ļ▓®ņ×ÉļōżņØś ņżæņ▓®ņśüņŚŁņŚÉņä£ ĒÖ£ņä▒ņĀÉ(Active point), ļ╣äĒÖ£ņä▒ņĀÉ(Hole point) ĻĘĖļ”¼Ļ│Ā ļé┤ņéĮņĀÉ(Interpolated point) ļō▒ņØś Ļ░£ļģÉņØä ĒåĄĒĢ┤ 2ņ░© ņĀĢĒÖĢļÅäņØś ņäĀĒśĢļé┤ņéĮļ▓Ģņ£╝ļĪ£ ņ▓śļ”¼ļÉ£ļŗż.
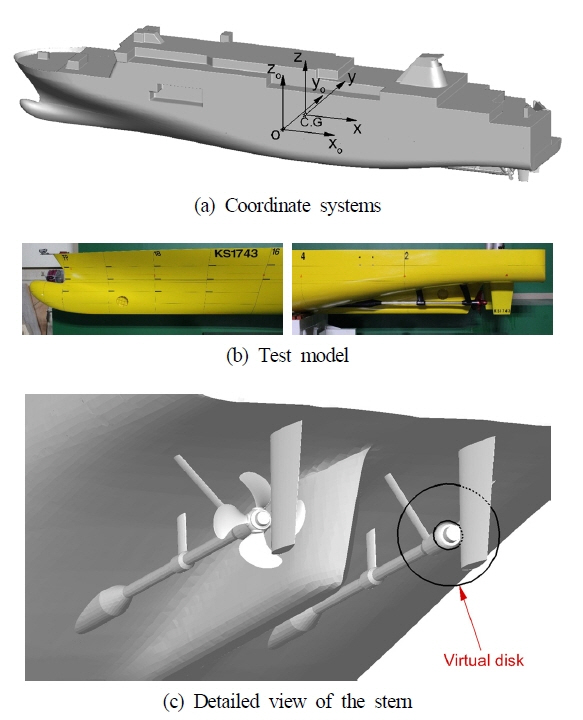
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ļīĆņāü ņäĀļ░ĢņØĆ ĻĖĖņØ┤ 148m, ĒÅŁ 24.8mņØĖ ņīŹņČĢ ņäĀĒśĢņØś ņ╣┤ĒÄśļ”¼ņäĀņØ┤ļŗż. ņŗżņäĀĻ│╝ ļ¬©ĒśĢņäĀņØś ņŻ╝ņÜö ņĀ£ņøÉņØĆ Table 1ņŚÉņä£ ļ│╝ ņłś ņ׳ņ£╝ļ®░, Fig. 1ņŚÉņä£ļŖö ņłśņ╣śĒĢ┤ņäØņŚÉņä£ ņé¼ņÜ®ĒĢ£ ņĀĢņłśņżæ ņäĀņ▓┤ ņżæņĢÖņŚÉ ļåōņØĖ ĻĖ░ļ│Ė ņóīĒæ£Ļ│ä(xo, yo, zo)ņÖĆ ņäĀņ▓┤ ņÜ┤ļÅÖ ĒĢ┤ņäØņØä ņ£äĒĢ£ ļ¼┤Ļ▓īņżæņŗ¼(Center of gravity) ņóīĒæ£Ļ│ä(x, y, z) ĻĘĖļ”¼Ļ│Ā ņäĀņ▓┤ņØś ĒśĢņāüņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. Fig. 1(b)ļŖö KRISO ļ¬©ĒśĢņŗ£ĒŚśņŚÉņä£ ņé¼ņÜ®ļÉ£ ņāüļČĆ ĻĄ¼ņĪ░ļ¼╝ņØ┤ ņŚåņØ┤ ņĀ£ņ×æļÉ£ ļ¬©ĒśĢņäĀņØś ļ¬©ņŖĄņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ņ£╝ļ®░, Fig. 1(c)ļŖö ĒÜīņĀäņČĢ, IĒśĢ ļ░Å VĒśĢ ņŖżĒŖĖļ¤┐(Strut) ĻĘĖļ”¼Ļ│Ā ĒāĆļź╝ ĒżĒĢ©ĒĢ£ ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀņØś ņäĀļ»Ėļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ņóīĒśä ĻĖ░Ļ┤ĆņØś ņåÉņāüņ£╝ļĪ£ ņóīĒśä ĒöäļĪ£ĒÄĀļ¤¼ļŖö ĒÜīņĀäĒĢśņ¦Ć ņĢŖļŖö Ļ│ĀņĀĢļÉ£ ņĪ░Ļ▒┤ņ£╝ļĪ£ Ļ▓®ņ×ÉĻ│äļź╝ ņāØņä▒ĒĢśĻ│Ā ņłśņ╣śĒĢ┤ņäØņŚÉ ņ¦üņĀæ ļ░śņśüĒĢśĻ│Ā, ņÜ░ĒśäņØś ĒöäļĪ£ĒÄĀļ¤¼ļŖö ņĢ×ņä£ 2ņןņŚÉņä£ ņäżļ¬ģĒĢ£ Virtual disk ļ¬©ļŹĖļĪ£ ĒĢ┤ņäØĒĢśņśĆļŗż.
Fig. 2ļŖö ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀņØś ņĀĢņłśņżæ ļ░Å Ēīīļ×æ ņżæ ņ×ÉĒĢŁņä▒ļŖź ļ¬©ĒśĢ ņŗ£ĒŚśņŚÉ ņé¼ņÜ®ļÉ£ KRISO KP1378 ĒöäļĪ£ĒÄĀļ¤¼ņØś ĒśĢņāüĻ│╝ Virtual diskļ¬©ļŹĖņØś ņ×ģļĀźņĀĢļ│┤Ļ░Ć ļÉśļŖö ļ¬©ĒśĢņŗ£ĒŚśņŚÉņä£ ņ¢╗ņØĆ ļīĆņāü ĒöäļĪ£ĒÄĀļ¤¼ņØś ņČöļĀźĻ│äņłś KT, ĒåĀņśżĒü¼Ļ│äņłś KQ ĻĘĖļ”¼Ļ│Ā ĒöäļĪ£ĒÄĀļ¤¼ ļŗ©ļÅģĒÜ©ņ£© ╬ĘoļĪ£ ļéśĒāĆļéĖ ļŗ©ļÅģņä▒ļŖź Ļ│ĪņäĀņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż.
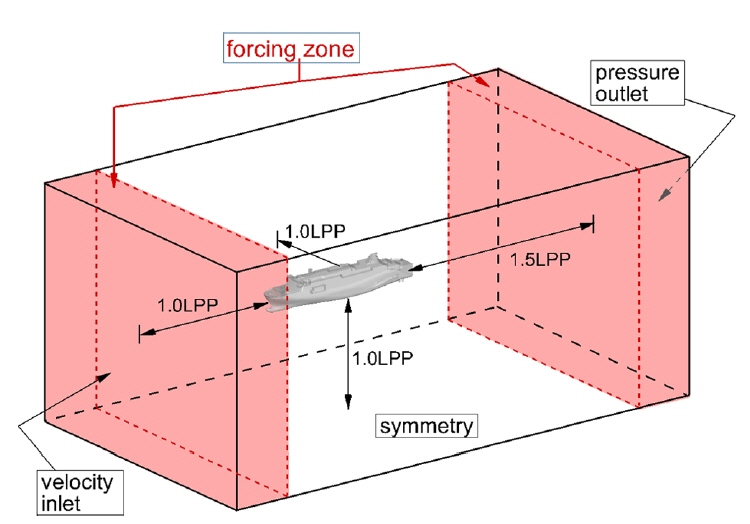
Fig. 3ņØĆ ņ╣┤ĒÄśļ”¼ ņäĀļ░ĢņØś Ēīīļ×æ ņżæ ņ×ÉĒĢŁņä▒ļŖź ĒĢ┤ņäØņŚÉ ņé¼ņÜ®ļÉ£ Ļ│äņé░ņśüņŚŁĻ│╝ Ļ▓ĮĻ│äņĪ░Ļ▒┤ņØä ņäżļ¬ģĒĢśĻ│Ā ņ׳ļŗż. Ļ│äņé░ņśüņŚŁņØĆ ņäĀņ▓┤ ņāüļźś ļ░®Ē¢źņ£╝ļĪ£ 1.0Lpp, ņäĀņ▓┤ ĒĢśļźśļĪ£ 2.0Lpp, ņäĀņ▓┤ņŚÉņä£ ņóīņÜ░ ņśüņŚŁ Ļ░üĻ░ü 1.0Lpp ĻĘĖļ”¼Ļ│Ā Ļ│äņé░ņśüņŚŁņØś ļ░öļŗźĻ╣īņ¦Ć 1.0LppņØś Ļ▒░ļ”¼ļź╝ Ļ░Ćņ¦äļŗż. Ļ│äņé░ņśüņŚŁņØś ņāüļźś Ļ▓ĮĻ│äļ®┤ņŚÉņä£ļŖö ņåŹļÅäņ£Āņ×ģ(Velocity inlet) ņĪ░Ļ▒┤, ĒĢśļźś Ļ▓ĮĻ│äļ®┤ņŚÉņä£ļŖö ņĢĢļĀźņ£ĀņČ£(Pressure outlet)ņĪ░Ļ▒┤ ĻĘĖļ”¼Ļ│Ā ļ▓Įļ®┤(Solid wall)ņĪ░Ļ▒┤ņØä Ļ░Ćņ¦ĆļŖö ņäĀņ▓┤ļź╝ ņĀ£ņÖĖĒĢ£ ļéśļ©Ėņ¦Ć Ļ▓ĮĻ│äļ®┤ļōżņŚÉņä£ļŖö ļīĆņ╣Łļ®┤(Symmetry plan) ņĪ░Ļ▒┤ņØä ņé¼ņÜ®ĒĢśņśĆļŗż.
ĒĢ£ĒÄĖ, ņ×ģņé¼ĒīīņØś ņäĀņ▓┤ņŚÉ ņØśĒĢ£ ņé░ļ×ĆĻ│╝ ņäĀņ▓┤ņØś ņÜ┤ļÅÖņŚÉ ņØśĒĢ£ ļ░®ņé¼ĒīīļōżņØś ņāüĒśĖņ×æņÜ® ņśüĒ¢źņ£╝ļĪ£ Ļ│äņé░ņśüņŚŁņØś Ļ▓ĮĻ│äņŚÉ ĒŖ╣ļ│äĒĢ£ ņłśņ╣śĒĢ┤ņäØ ņ▓śļ”¼ļź╝ ĒĢśņ¦Ć ņĢŖļŖö Ļ▓ĮņÜ░ ļ░śņé¼ĒīīĻ░Ć ļ░£ņāØĒĢĀ ņłś ņ׳ļŗż. ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ņé¼ņÜ®ļÉ£ ĒöäļĪ£ĻĘĖļשņŚÉņä£ ņĀ£Ļ│ĄĒĢśļŖö Forcingļ▓ĢņØ┤ļØ╝ ļČłļ”¼ļŖö ļ░®ļ▓Ģņ£╝ļĪ£ Fig. 3ņŚÉ ļ│┤ņØ┤ļŖö Forcing ņśüņŚŁņŚÉņä£ CFDļĪ£ ĻĄ¼ĒĢ£ ĒīīĻ│ĀņÖĆ ņ£ĀļÅÖņØś ņÜ┤ļÅÖļ¤ēņØä cos2 ļČäĒżĒĢ©ņłśļĪ£ ņŻ╝ņ¢┤ņ¦ä ĒĢ┤ņäØĒĢ┤ņÖĆ ņĪ░ĒÖöņŗ£ņ╝£ ļ░śņé¼Ēīīļź╝ ĒÜ©ņ£©ņĀüņ£╝ļĪ£ ņĀ£Ļ▒░ĒĢśļŖö ņĀæĻĘ╝ļ▓ĢņØä ņé¼ņÜ®ĒĢśņśĆļŗż.
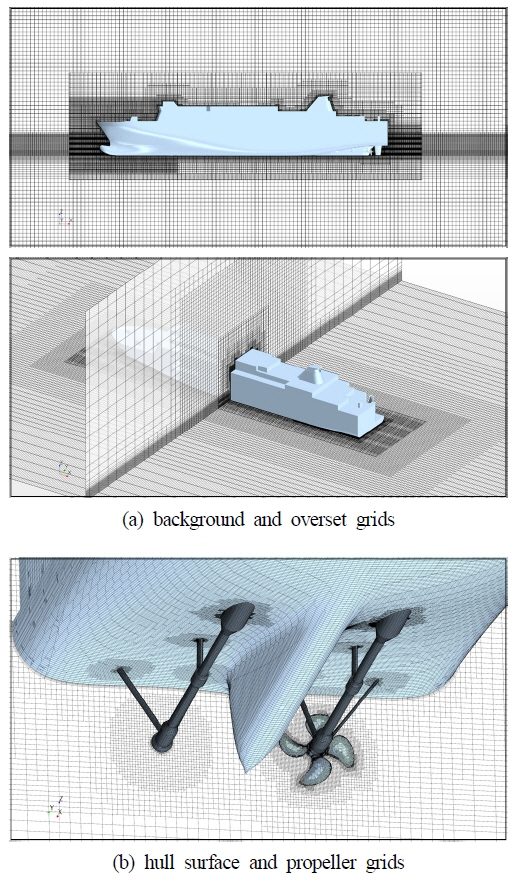
Fig. 4(a)ļŖö ņ╣┤ĒÄśļ”¼ņäĀ ņŻ╝ņ£äņŚÉ ņāØņä▒ļÉ£ Ļ▓®ņ×É ļČäĒżņØś ļ¬©ņŖĄņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ņłśņ╣ś Ļ▓®ņ×ÉĻ│äļŖö Kim et al.(2018)ņØś 2ņ░©ņøÉ Stokes 5ņ░©ĒīīņÖĆ Ēīīļ×æ ņżæ FPSO(Floating production storage offloading) ņÜ┤ļÅÖĒĢ┤ņäØņŚÉņä£ ņé¼ņÜ®ļÉ£ ļŗżņ¢æĒĢ£ ĻĘ£ļ¬©ņØś Ļ▓®ņ×ÉĻ│äņŚÉ ļīĆĒĢ£ ĒĢ┤ņØś ļ»╝Ļ░ÉļÅä ņŚ░ĻĄ¼Ļ▓░Ļ│╝ļź╝ ņ░ĖņĪ░ĒĢśņŚ¼ ņāØņä▒ĒĢśņśĆļŗż. Kim et al.(2018)ņØĆ ļŗżņ¢æĒĢ£ ĒīīņŻ╝Ēīīņłś ņĪ░Ļ▒┤ņŚÉņä£ Ēīīņןļŗ╣ ĻĘĖļ”¼Ļ│Ā ĒīīĻ│Āļŗ╣ Ļ▓®ņ×Éņłś ļ│ĆĒÖöņŚÉ ļö░ļźĖ ņłśņ╣śĒĢ┤ņäØ Ļ▓░Ļ│╝ļź╝ ĒåĄĒĢ┤ ĒīīĻ│Āļŗ╣ 15~20Ļ░£, Ēīīņןļŗ╣ 95Ļ░£ ņØ┤ņāüņØś Ļ▓®ņ×Éļź╝ ņé¼ņÜ®ĒĢĀ ļĢī ņłśņ╣śĻ░ÉņćĀĻ░Ć ņĀüņØĆ ļ¦īņĪ▒ĒĢĀļ¦īĒĢ£ ĒĢ┤ņäØĻ▓░Ļ│╝ļź╝ ņ¢╗ņØä ņłś ņ׳ļŗżĻ│Ā ļ│┤Ļ│ĀĒĢśņśĆļŗż. ļ│Ė ļģ╝ļ¼ĖņØĆ ņŻ╝ņ¢┤ņ¦ä ĒĢ┤ņāüņĪ░Ļ▒┤ņØĖ Beaufort 8ņØś ņ£ĀņØśĒīīĻ│ĀņÖĆ ĒÅēĻĘĀņśüņĀÉĻĄÉņ░©ņŻ╝ĻĖ░(Zero-up crossing period)ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ĒīīņןņŚÉ ļīĆĒĢ┤ Ļ░üĻ░ü ņĢĮ 20Ļ░£ņÖĆ 98Ļ░£ņØś Ļ▓®ņ×É ņÜöņåīĻ░Ć ļōżņ¢┤Ļ░ĆļÅäļĪØ ĒĢśņśĆļŗż. ņØ┤ļĢī ņäĀņ▓┤ņÖĆ ĒĢ©Ļ╗ś ņÜ┤ļÅÖĒĢśļŖö Ļ▓®ņ×ÉĻ│äļŖö ņĢĮ 300ļ¦īĻ░£ ĻĘĖļ”¼Ļ│Ā Ļ│ĀņĀĢļÉ£ ļ░░Ļ▓Į Ļ▓®ņ×ÉĻ│äļŖö 250ļ¦īĻ░£ņØś Ļ▓®ņ×ÉņÜöņåīĻ░Ć ņé¼ņÜ®ļÉśņ¢┤ ņ┤ØĻ▓®ņ×ÉņłśļŖö ņĢĮ 550ļ¦īĻ░£ņØ┤ļŗż. Ļ▓®ņ×ÉĻ│ä ņāØņä▒ņØĆ TrimmerļØ╝ ļČłļ”¼ļŖö ņ¦üņ£Īļ®┤ņ▓┤ Ļ▓®ņ×ÉņÜöņåīļź╝ ĻĖ░ļ░śņ£╝ļĪ£ ĒĢśļŖö ļ╣äņĀĢļĀ¼ Ļ▓®ņ×É(Unstructured grid) ņāØņä▒ļ▓ĢņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ļ▓Įļ®┤ ĻĘ╝ļ░® Ļ▓ĮĻ│äņĖĄ ņśüņŚŁņØĆ Prism layerļØ╝ ļČłļ”¼ļŖö Ļ▓®ņ×ÉņÜöņåīļź╝ 5Ļ░£ ņĀüņĖĄĒĢśņŚ¼ ņé¼ņÜ®ĒĢśĻ│Ā, ļ▓Įļ®┤ņŚÉņä£ ņ▓½ Ļ▓®ņ×ÉņÜöņåīņØś Ļ│äņé░ņĀÉĻ╣īņ¦ĆņØś ļ¼┤ņ░©ņøÉ Ļ▒░ļ”¼ņØĖ y+Ļ░ÆņØĆ 50ņĀĢļÅäĻ░Ć ļÉśļÅäļĪØ ĒĢśņśĆļŗż. Fig. 4(b)ļŖö ņäĀļ»Ė ņäĀņ▓┤ Ēæ£ļ®┤Ļ▓®ņ×É ļČäĒżņÖĆ ņ¦üņĀæ Ļ▓®ņ×ÉļĪ£ Ēæ£ĒśäļÉ£ ĒÜīņĀäĒĢśņ¦Ć ņĢŖĻ│Ā Ļ│ĀņĀĢļÉ£ ņóīĒśä ĒöäļĪ£ĒÄĀļ¤¼ļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ĻĘĖļ”╝ņŚÉņä£ ņÜ░Ēśä ĒöäļĪ£ĒÄĀļ¤¼ņØś ņ¦üĻ▓ĮĻ│╝ ļæÉĻ╗ś ĻĘĖļ”¼Ļ│Ā ĒŚłļĖīņ¦üĻ▓ĮņØä Ļ░Ćņ¦ĆļŖö Virtual diskĻ░Ć ņ£äņ╣śĒĢ£ ņśüņŚŁņØś Ļ▓®ņ×ÉļČäĒż ļ¬©ņŖĄņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ņĀĢņłśņżæ ņłśņ╣śĒĢ┤ņäØ ņŗżĒŚśņØä ĒåĄĒĢ┤ ļæÉĻ╗ś ļ░®Ē¢źņ£╝ļĪ£ ņĢĮ 4Ļ░£ ņØ┤ņāüņØś Ļ▓®ņ×Éļź╝ ļČäĒżņŗ£Ēé¼ ļĢī ĒĢ┤ņäØņØś Ļ▓░Ļ│╝ļŖö Ēü░ ņ░©ņØ┤Ļ░Ć ņŚåņŚłļŗż.
ļ│Ė ņĀłņŚÉņä£ļŖö ĒöäļĪ£ĒÄĀļ¤¼ļź╝ ļ¬©ļŹĖļ¦üĒĢ£ Virtual diskļ▓ĢņØä ņĀüņÜ®ĒĢ£ ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀņØś ņ×ÉĒĢŁņä▒ļŖź ĒĢ┤ņäØ ņĀĢĒÖĢļÅäļź╝ Ļ▓Ćņ”ØĒĢśĻĖ░ ņ£äĒĢ┤ ņĀĢņłśņżæ ļ╣äņåÉņāü ņāüĒā£ņÖĆ ņĢ×ņä£ ņäżļ¬ģĒĢ£ ņåÉņāü ņāüĒā£ņØś KRISO ļ¬©ĒśĢņŗ£ĒŚś Ļ▓░Ļ│╝ņÖĆ ļ╣äĻĄÉ, Ļ▓ĆĒåĀĒĢ£ ņé¼ĒĢŁņØä ņåīĻ░£ĒĢ£ļŗż. Ļ│äĒÜŹĒØśņłś(Design draft) 5.5m ņĪ░Ļ▒┤ņØś ļ╣äņåÉņāü ņāüĒā£ņØś ņłśņ╣śĒĢ┤ņäØņØĆ ņäĀņ▓┤ ņżæņĢÖņØä ļīĆņ╣ŁņĪ░Ļ▒┤ņ£╝ļĪ£ ļæÉĻ│Ā ņäĀņ▓┤ņØś ņÜ░Ēśä ņśüņŚŁļ¦īņØä ĒĢ┤ņäØĒĢśņśĆļŗż. ņØ┤ļĢī ņŗżņäĀ ņäĀņåŹ VSļŖö 15ļģĖĒŖĖ(7.72m/s), 19ļģĖĒŖĖ(9.77m/s) ĻĘĖļ”¼Ļ│Ā 23ļģĖĒŖĖ(11.83)ļź╝ ĒĢ┤ņäØĒĢśņśĆļŗż. ņåÉņāü ņāüĒā£ļŖö ļ¦īņ×¼ĒØśņłś(Scantling draft) 5.8mņÖĆ SRtP ņĪ░Ļ▒┤ņØś ņäĀņåŹņØĖ 6ļģĖĒŖĖ(3.09m/s)ņŚÉņä£ ņóīĒśä ĒöäļĪ£ĒÄĀļ¤¼ļŖö Ļ│ĀņĀĢĒĢśĻ│Ā ņÜ░Ēśä ĒöäļĪ£ĒÄĀļ¤¼ļŖö Virtual diskļ▓Ģņ£╝ļĪ£ ĒĢ┤ņäØĒĢśņŚ¼ ņ×ÉĒĢŁņāüĒā£ļź╝ ĒĢ┤ņäØĒĢśņśĆļŗż. ņØ┤ļĢī, ņśłņØĖļĀź FDļź╝ Ļ│ĀļĀżĒĢśņśĆņ£╝ļ®░ ļŗżņØīĻ│╝ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£, CFMĻ│╝ CFSļŖö Ļ░üĻ░ü ļ¬©ĒśĢņäĀĻ│╝ ņŗżņäĀņØś ļ¦łņ░░ņĀĆĒĢŁĻ│äņłśļź╝ ļéśĒāĆļé┤Ļ│Ā, CAļŖö Ļ░ü ņäĀĒśĢņŗ£ĒŚśņłśņĪ░(Towing tank)ļōżņØ┤ Ļ░Ćņ¦ĆļŖö Ļ│Āņ£ĀĻ░ÆņØĖ ņāüĻ┤ĆĻ┤ĆĻ│ä(Correlation allowance) Ļ│äņłśņØ┤ļŗż. ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ņé¼ņÜ®ļÉ£ CAļŖö 0.00015ņØ┤ļ®░ KRISO ņäĀĒśĢņŗ£ĒŚśņłśņĪ░ņØś Ļ░ÆņØä ņé¼ņÜ®ĒĢśņśĆļŗż.
Table 2ļŖö ļ╣äņåÉņāü ņāüĒā£ ņ×ÉĒĢŁņä▒ļŖź ĒĢ┤ņäØĻ▓░Ļ│╝ņŚÉņä£ ņŻ╝ņ¢┤ņ¦ä ņäĀņåŹņØä ļé┤ļŖöļŹ░ ĒĢäņÜöĒĢ£ ĒöäļĪ£ĒÄĀļ¤¼ņØś ņČöļĀź TM, ĒåĀņśżĒü¼ QM ĻĘĖļ”¼Ļ│Ā ĒÜīņĀäņłś NMņØä KRISOņØś ļ¬©ĒśĢņŗ£ĒŚś Ļ▓░Ļ│╝ņÖĆ ļ╣äĻĄÉĒĢśĻ│Ā ņ׳ļŗż. Ļ│äņé░ĒĢ£ ņäĀņåŹļōżņŚÉņä£ ĒöäļĪ£ĒÄĀļ¤¼ņØś ĒÜīņĀäņłśļŖö ņĢĮ 5%ņĀĢļÅä ļåÆĻ▓ī ņłśņ╣śĒĢ┤ņäØņŚÉņä£ ņČöņĀĢļÉśņŚłņ¦Ćļ¦ī, ņČöļĀźĻ│╝ ĒåĀņśżĒü¼ļŖö ņĢĮ 2%ļé┤ņŚÉņä£ ļ¬©ĒśĢņŗ£ĒŚśĻ│╝ ļ¦īņĪ▒ņŖżļ¤¼ņÜ┤ ņØ╝ņ╣śļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ņĀüņÜ®ĒĢ£ Virtual diskļ▓ĢņØ┤ ļ╣äĻĄÉņĀü ļ¦īņĪ▒ņŖżļ¤¼ņÜ┤ ņØ╝ņ╣śļź╝ ļ│┤ņØ┤ļŖö ņØ┤ņ£ĀļŖö Fig. 1(b)ņŚÉņä£ ļ│╝ ņłś ņ׳ļō»ņØ┤ ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀņØś Ļ░£ļ░®ļÉ£ ĒÜīņĀäņČĢ ļ░®ņŗØņØś ņČöņ¦ä ņŗ£ņŖżĒģ£ņØś ņ▒äĒāØņ£╝ļĪ£ ņØĖĒĢśņŚ¼ ņäĀļ»Ė ņ£ĀļÅÖņØ┤ ņØ╝ļ░śņĀüņØĖ ļŗ©ņČĢ(Single skeg) ņäĀļ»ĖņØś ņāüņäĀļōżņØ┤ ļ│┤ņØ┤ļŖö ļåÆņØĆ ļ░śļźś(Wake)ņŚÉņä£ ņ×æņÜ®ĒĢśļŖö ĒöäļĪ£ĒÄĀļ¤¼ ņ£ĀļÅÖĻ│╝ļŖö ļŗżļźĖ ĒŖ╣ņ¦Ģ ļĢīļ¼Ėņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż. ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀņØś ļ░śļźśņØś Ļ▓ĮņÜ░ ņäĀņ▓┤ņŚÉ ņØśĒĢ£ ĻĄÉļ×ĆņØ┤ ņāüļīĆņĀüņ£╝ļĪ£ ņĀüĻĖ░ ļĢīļ¼ĖņŚÉ Virtual diskļ▓ĢņØś ņĀüņÜ®ņ£╝ļĪ£ ļ¬©ĒśĢņŗ£ĒŚśĻ│╝ ņ£Āņé¼ĒĢ£ Ļ▓░Ļ│╝ļź╝ ņ¢╗ņØä ņłś ņ׳ļŖö ņĪ░Ļ▒┤ņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.
Table 3ņØĆ ņĀĢņłśņżæ ņóīĒśäņØś ĒöäļĪ£ĒÄĀļ¤¼Ļ░Ć Ļ│ĀņĀĢļÉ£ ņåÉņāü ņāüĒā£ņŚÉņä£ ņäĀņåŹ 6ļģĖĒŖĖ(3.09m/s)ļź╝ ļé┤ļŖöļŹ░ ņåīņÜöļÉśļŖö ļ¬©ĒśĢņäĀ ņÜ░Ēśä ĒöäļĪ£ĒÄĀļ¤¼ņØś ņČöļĀźĻ│╝ ĒåĀņśżĒü¼ļź╝ ļ╣äĻĄÉĒĢśĻ│Ā ņ׳ļŗż. ņØ┤ Ļ▓ĮņÜ░ ĒÜīņĀäņłśļŖö ļ¬©ĒśĢņŗ£ĒŚśĻ│╝ ņĢĮ 7.3%ļĪ£ ļ╣äņåÉņāü ņāüĒā£ļ│┤ļŗżļŖö ņĢĮĻ░ä ļŹö ņ░©ņØ┤Ļ░Ć ļéśĻ│Ā, ņČöļĀźņØĆ ņĢĮ 4.5% ĻĘĖļ”¼Ļ│Ā ĒåĀņśżĒü¼ļŖö 1.7%ņØś ņ░©ņØ┤ļź╝ ļ│┤ņśĆļŗż. Ļ▓░ļĪĀņĀüņ£╝ļĪ£, Virtual diskļ▓ĢņØä ļ│Ė ņłśņ╣śĒĢ┤ņäØ ļ¼ĖņĀ£ņŚÉ ņĀüņÜ®ĒĢ£ Ļ▓░Ļ│╝ ĒÜīņĀäņłśņØś ņ░©ņØ┤Ļ░Ć ņĢĮĻ░ä ņ׳ņ£╝ļéś, ĒלņØś ņČöņĀĢņŚÉ ņ׳ņ¢┤ ļ╣äĻĄÉņĀü ĒāĆļŗ╣ĒĢ£ ņĀĢļÅäņØś Ļ▓░Ļ│╝ļź╝ ņĀ£Ļ│ĄĒĢśĻ│Ā ņ׳ņ¢┤, Ēīīļ×æ ņżæ ņ×ÉĒĢŁņĪ░Ļ▒┤ ĒĢ┤ņäØņŚÉņä£ļÅä ĒāĆļŗ╣ĒĢ£ Ļ▓░Ļ│╝ļź╝ ņ¢╗ņØä ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż.
Fig. 5ļŖö Table 3ņØś ĒĢ┤ņäØĻ▓░Ļ│╝ņŚÉņä£ ĒöäļĪ£ĒÄĀļ¤¼ņÖĆ ĒāĆ ņé¼ņØ┤ ĒÜĪļŗ©ļ®┤ņŚÉņä£ ņČĢļ░®Ē¢ź ņ£ĀņåŹļČäĒżļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ĻĘĖļ”╝ņØĆ ņóīĒśäņØś ĒÜīņĀäĒĢśņ¦Ć ņĢŖĻ│Ā Ļ│ĀņĀĢļÉ£ ĒöäļĪ£ĒÄĀļ¤¼ļĪ£ ņØĖĒĢ£ ļéĀĻ░£ ļÆżņ¬ĮņØś ļé«ņØĆ ņ£ĀņåŹļČäĒżļź╝ ļ│╝ ņłś ņ׳Ļ│Ā, Virtual diskļĪ£ ļ¬©ļŹĖļ¦üĒĢ£ ĒÜīņĀäĒĢśļŖö ņÜ░Ēśä ĒöäļĪ£ĒÄĀļ¤¼ņØś ņČöļĀźņ£╝ļĪ£ ļ░£ņāØĒĢśļŖö ļåÆņØĆ ņ£ĀņåŹļČäĒżļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż.
ļ│Ė ņĀłņŚÉņä£ļŖö Table 4ņŚÉ ļéśĒāĆļéĖ ņ£ĀņØśĒīīĻ│Ā H1/3, ņ▓©ļæÉņŻ╝ĻĖ░ TP ĻĘĖļ”¼Ļ│Ā ļ░öļ×īņØś ņåŹļĀź VwindņŚÉ ļīĆĒĢ£ Beaufort 8ņØś ļČłĻĘ£ņ╣ÖĒīī ņĪ░Ļ▒┤ņŚÉņä£ SRtP ņäĀņåŹ 6ļģĖĒŖĖ(3.09m/s)ļź╝ ņ£Āņ¦ĆĒĢśļŖöļŹ░ ĒĢäņÜöĒĢ£ ĒöäļĪ£ĒÄĀļ¤¼ņØś ņČöļĀźņØä ĒĢ┤ņäØĒĢ£ Ļ▓░Ļ│╝ļź╝ ņåīĻ░£ĒĢ£ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĪ░ņÜ░Ļ░üļÅä(Encounter angle) 180ļÅäņØś ņäĀņłśĒīī(Head sea) ņĪ░Ļ▒┤ļ¦īņØä Ļ│ĀļĀżĒĢśņśĆņ£╝ļ®░, ņäĀņåŹņ£╝ļĪ£ ĒīīņØś ņāüļÅäņåŹļÅäĻ░Ć Ļ│ĀļĀżļÉśņ¢┤ Ļ│äņé░ņśüņŚŁņØś ņ£Āņ×ģņĪ░Ļ▒┤ņ£╝ļĪ£ Ļ│ĀļĀżļÉśĻ│Ā ņØ┤ļĢī ņŻ╝ņ¢┤ņ¦ä ņ▓©ļæÉņŻ╝ĻĖ░ņŚÉ ļö░ļźĖ ņĪ░ņÜ░ņŻ╝ĻĖ░ļŖö ņĢĮ 1.71sņØ┤ļŗż. Ēīīļ×æ ņżæ ņ×ÉĒĢŁĒĢ┤ņäØņŚÉņä£ ĒלļōżņØĆ ņØ┤ļÅÖĒÅēĻĘĀ(Running mean) Ļ░ÆļōżņØä ņé¼ņÜ®ĒĢśĻ│Ā ņĀĢņłśņżæ ĒĢ┤ņäØĻ│╝ Ļ░ÖņØ┤ ņśłņØĖļĀźņØä Ļ│ĀļĀżĒĢśņśĆļŗż. ņäĀņ▓┤ņØś ņÜ┤ļÅÖņØĆ ņāüĒĢśļÅÖņÜö(Heave), ĒÜĪļÅÖņÜö(Roll) ĻĘĖļ”¼Ļ│Ā ņóģļÅÖņÜö(Pitch)ņØś 3ņ×Éņ£ĀļÅä ņÜ┤ļÅÖņØä Ļ│ĀļĀżĒĢśņśĆņ£╝ļ®░, Ļ│äņé░ ņŗ£Ļ░ä Ļ░äĻ▓®(Computational time step)ņØĆ ņŻ╝ņ¢┤ņ¦ä ļČłĻĘ£ņ╣ÖĒīī ņ▓©ļæÉņŻ╝ĻĖ░ļź╝ 418ļō▒ļČäĒĢśļŖö 0.005sļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż. ņØ┤ļŖö ņŻ╝ņ¢┤ņ¦ä ņ▓©ļæÉņŻ╝ĻĖ░ ņĪ░Ļ▒┤ņØä ĻĘ£ņ╣ÖĒīīļĪ£ Ēæ£ĒśäĒĢśĻ│Ā ņ╣┤ĒÄśļ”¼ņäĀņåŹņØä Ļ│ĀļĀżĒĢśņŚ¼ Ļ│äņé░ļÉ£ CFL(Courant-Friedrichs_Lewy condition)ņłś ņĢĮ 0.29ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö Ļ░ÆņØ┤ļŗż.
CFDĒĢ┤ņäØņŚÉņä£ ļČłĻĘ£ņ╣ÖĒīī ņŗ£ļ«¼ļĀłņØ┤ņģśņØś ņĀäņ▓┤ ņŗ£Ļ░äņŚÉ Ļ┤ĆļĀ©ĒĢ┤ņä£, ņØ╝ļ░śņĀüņ£╝ļĪ£ ņäĀņ▓┤ņØś ņÜ┤ļÅÖĻ│╝ ĒīīņÖĆņØś ņāüļīĆņÜ┤ļÅÖņŚÉ ļö░ļźĖ ļÅÖņĀü ņśüĒ¢ź(Dynamic effect)ļōżņØä ļ®┤ļ░ĆĒ׳ ņé┤ĒÄ┤ļ│┤ļŖö ņŚ░ĻĄ¼ņŚÉņä£ ĒåĄĻ│ä ĒĢ┤ņäØņĀüņ£╝ļĪ£ ņ£ĀĒÜ©ĒĢśĻĖ░ ņ£äĒĢ┤ ņāüļīĆņĀüņ£╝ļĪ£ ĻĖ┤ ņŗ£Ļ░äņØś ĒĢ┤ņäØņŗ£Ļ░äņØ┤ ĒĢäņÜöĒĢśļŗż. ĻĘĖļ¤¼ļéś, ļ│Ė ļģ╝ļ¼ĖņØĆ ņĢ×ņä£ ņäżļ¬ģĒĢ£ ļ░öņÖĆ Ļ░ÖņØ┤ SRtP ņäĀņåŹ 6ļģĖĒŖĖ(3.09m/s)ņŚÉ ļīĆĒĢ£ ļČłĻĘ£ņ╣Ö Ēīīļ×æ ņżæ ļČĆĻ░ĆņĀĆĒĢŁļōżņŚÉ ņØśĒĢ£ ļīĆļץņĀüņØĖ ņåīņÜöļ¦łļĀź ņČöņĀĢ ĒĢ┤ņäØņŚÉ ņŻ╝ņĢłņĀÉņØä ļæÉĻ│Ā ņ׳ņ¢┤ ĒלņØś ĒÅēĻĘĀ ļ│ĆļÅÖņØ┤ Ēü¼ņ¦Ć ņĢŖļŖö ņŗ£ņĀÉĻ╣īņ¦Ć ņāüļīĆņĀüņ£╝ļĪ£ ņ¦¦ņØĆ ņŗ£ļ«¼ļĀłņØ┤ņģś ņŗ£Ļ░äņØä ņäżņĀĢĒĢśņśĆļŗż. ņ×ÉĒĢŁņĀÉņØä ņ░ŠĻĖ░ ņ£äĒĢ┤ ņłśņ╣śĒĢ┤ņäØņØĆ ļæÉ ņĪ░Ļ▒┤ņØś ĒöäļĪ£ĒÄĀļ¤¼ ĒÜīņĀäņłśņŚÉ ļīĆĒĢ┤ 80s ļÅÖņĢłņØś ņŗ£ļ«¼ļĀłņØ┤ņģśņØä Ļ░üĻ░ü ņłśĒ¢ēĒĢśĻ│Ā, ņØ┤ļōżņØś Ļ▓░Ļ│╝ļź╝ ļ░öĒāĢņ£╝ļĪ£ ļé┤ņéĮņØä ĒåĄĒĢ┤ ņ×ÉĒĢŁņĀÉņØä ņ░ŠņØĆ Ēøä ņĄ£ņóģ ņ×ÉĒĢŁņĀÉņŚÉ ļīĆĒĢ┤ 120sļź╝ ļŹö ņØ┤ņ¢┤ņä£ ņłśĒ¢ēĒĢśņśĆļŗż.
MARINņØś ļ¬©ĒśĢņŗ£ĒŚśņØĆ KRISOņØś ņĀĢņłśņżæ ņ×ÉĒĢŁņŗ£ĒŚśĻ│╝ ļ│Ė ņłśņ╣śĒĢ┤ņäØ ņłśĒ¢ē ņØ┤Ēøä ņłśĒ¢ēļÉśņŚłņ£╝ļ®░, ņĪ░ĒīīĻĖ░Ļ░Ć ņäżņ╣śļÉ£ 250m├Ś10.5m├Ś5.5m ĻĘ£ļ¬©ņØś Ļ░ÉņĢĢņłśņĪ░(Depressurized wave basin)ņŚÉņä£ ņłśĒ¢ēļÉśņŚłļŗż. ņŗżĒĢ┤ņŚŁ 1ņŗ£Ļ░ä ļČłĻĘ£ņ╣ÖĒīīļź╝ ņ×¼ĒśäĒĢśĻĖ░ ņ£äĒĢ┤ ņŻ╝ņ¢┤ņ¦ä ņäĀņåŹ 6ļģĖĒŖĖ(3.09m/s)ņŚÉ ļīĆĒĢ┤ ĒĢ£ ļ▓ł ņłśĒ¢ēĒĢĀ ļĢī ņĢĮ 259sņØĖ ļ¬©ĒśĢņŗ£ĒŚśņØä 3ļ▓ł ņłśĒ¢ēĒĢśĻ│Ā ņĄ£ņóģņĀüņ£╝ļĪ£ ņØ┤ļōż ņĀäņ▓┤ ļŹ░ņØ┤Ēä░ļź╝ ĒĢ®ņ│Éņä£ Ēøäņ▓śļ”¼ĒĢśņśĆļŗż. ņŚ¼ĻĖ░ņä£, MARINņØś ļ¬©ĒśĢņŗ£ĒŚśņØĆ ņäĀņ▓┤ņØś ņāüĒĢśļÅÖņÜöņÖĆ ņóģļÅÖņÜöļź╝ Ļ│ĀļĀżĒĢśņśĆņ£╝ļ®░, Ļ│ĄĻĖ░ņĀĆĒĢŁņØĆ Ļ│ĄĻĖ░ņŚÉ ļģĖņČ£ļÉ£ ņ╣┤ĒÄśļ”¼ņäĀņØś ņāüļČĆ ĻĄ¼ņĪ░ļ¼╝ņØś ņĀäļ®┤ļČĆ ļ®┤ņĀü(Frontal area)Ļ│╝ ĒĢŁļĀźĻ│äņłś 0.7ņØś Ļ░ÆņØä ņé¼ņÜ®ĒĢ£ Ļ▓ĮĒŚśņŗØņ£╝ļĪ£ Ļ│äņé░ĒĢśņŚ¼ ļ░śņśüĒĢśņśĆļŗż. ņĄ£ņóģļ¬©ĒśĢņŗ£ĒŚśņØś ņŻ╝ņÜöĒĢ£ Ļ▓░Ļ│╝ļŖö SRtP ņäĀņåŹ 6ļģĖĒŖĖ(3.09m/s)ļź╝ ļé┤ļŖöļŹ░ ĒĢäņÜöĒĢ£ ĒöäļĪ£ĒÄĀļ¤¼ņØś ņŗżņäĀ ĒÅēĻĘĀ ņČöļĀź ņČöņĀĢĻ░ÆņØ┤ļŗż.
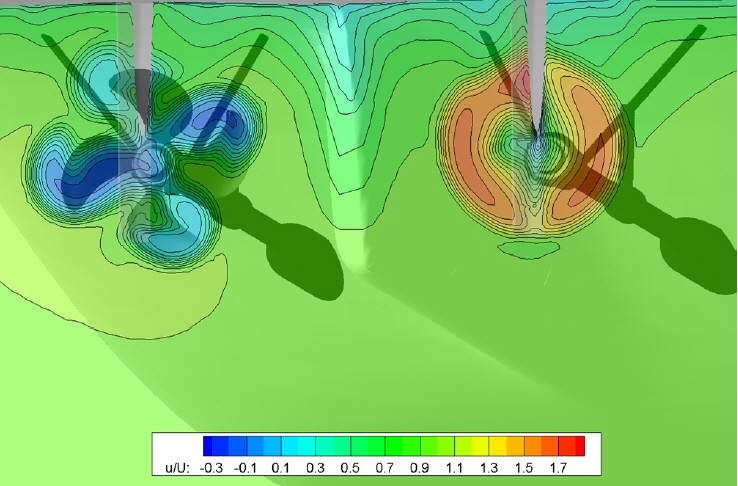
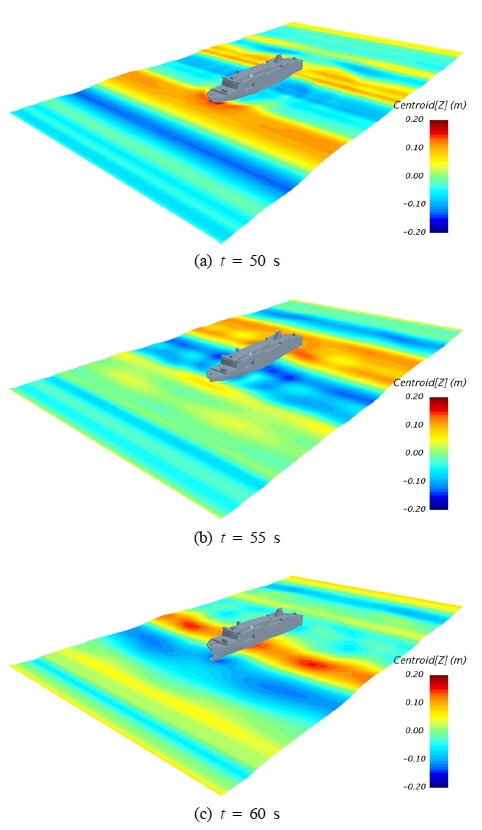
Fig. 6ņØĆ ņŗ£ļ«¼ļĀłņØ┤ņģś ņŗ£Ļ░ä 50s, 55s ĻĘĖļ”¼Ļ│Ā 60sņŚÉņä£ ĒīīņØś ņāüĒā£ņÖĆ ņäĀņ▓┤ņØś ņ×ÉņäĖ ļ│ĆĒÖöņØś ņāüĒÖ®ņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ĻĘĖļ”╝ņŚÉņä£ Fig. 6ņØś (a), (b)ņÖĆ (c)ļŖö Ļ░üĻ░ü ņāüļīĆņĀüņ£╝ļĪ£ ļåÆņØĆ ĒīīĻ│ĀņØś ĒīīĻ░Ć ņäĀņłśņÖĆ ņäĀļ»Ė ĻĘĖļ”¼Ļ│Ā ņäĀņ▓┤ ņżæņĢÖņØä ĒåĄĻ│╝ĒĢĀ ļĢī ņäĀņ▓┤ņÖĆ ĒīīņØś ņāüĒśĖņ×æņÜ®ņ£╝ļĪ£ ņØĖĒĢ£ ņäĀņ▓┤ ņŻ╝ņ£ä ĒīīĒśĢņØś ļ│ĆĒÖöņÖĆ ņäĀņ▓┤ņØś ņÜ┤ļÅÖ ļ│ĆĒÖöļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż.
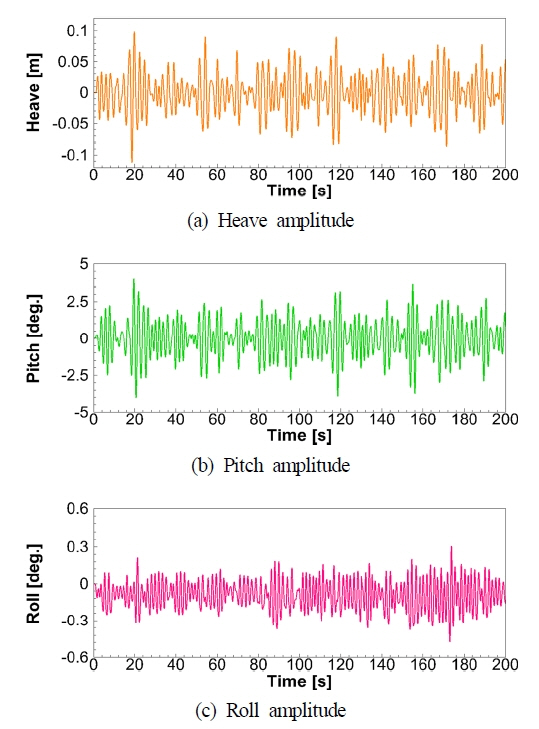
Fig. 7Ļ│╝ Fig. 8ļŖö ņ×ÉĒĢŁņĀÉ ņØ┤ņĀä ĒöäļĪ£ĒÄĀļ¤¼ ĒÜīņĀäņłśņŚÉņä£ 80sņÖĆ ņØ┤Ēøä 200sĻ╣īņ¦Ć ņ×ÉĒĢŁņĀÉņŚÉņä£ 120s ļÅÖņĢłņØś ņäĀņ▓┤ņØś ņĀĆĒĢŁ, ĒöäļĪ£ĒÄĀļ¤¼ ņČöļĀź, ĒåĀņśżĒü¼ ĻĘĖļ”¼Ļ│Ā ņäĀņ▓┤ņØś ņÜ┤ļÅÖ ļ│ĆĒÖöļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ĒלĻ│╝ ņÜ┤ļÅÖļōżņØĆ ĒīīņØś ņŻ╝ĻĖ░ļĪ£ ņØæļŗĄĒĢśĻ│Ā ņ׳ņ£╝ļ®░, ļīĆņ▓┤ļĪ£ ņĀĆĒĢŁĻ│╝ ĒöäļĪ£ĒÄĀļ¤¼ņØś Ēל ĻĘĖļ”¼Ļ│Ā ņāüĒĢśļÅÖņÜöņÖĆ ņóģļÅÖņÜöņØś ņ¦äĒÅŁņØś ļ│ĆĒÖöļŖö ņŗ£Ļ░äņŚÉ ļīĆĒĢ┤ ņä£ļĪ£ ņ£Āņé¼ĒĢ£ Ļ▒░ļÅÖņØä ļ│┤ņØ┤Ļ│Ā ņ׳ļŗż. ĒöäļĪ£ĒÄĀļ¤¼ ņČöļĀźņØś ņØ┤ļÅÖĒÅēĻĘĀ Ļ░ÆņØ┤ ņĢĮ 50s ņØ┤Ēøä ļ╣äņŖĘĒĢśņŚ¼ ņØ┤ ņŗ£ņĀÉ ņØ┤ĒøäņØś Ļ░ÆņØä ĒÅēĻĘĀņ£╝ļĪ£ ņé¼ņÜ®ĒĢśņśĆļŗż. ņłśņ╣śĒĢ┤ņäØņŚÉņä£ Ļ│ĀļĀżĒĢ£ ņ╣┤ĒÄśļ”¼ņäĀņØś ĒÜĪļÅÖņÜö ņÜ┤ļÅÖņØś ņ¦äĒÅŁņØĆ 0.4ļÅä ņØ┤ļé┤ļĪ£ Ēü¼ņ¦Ć ņĢŖņ£╝ļ®░, ĻĖ░Ļ┤Ć ņåÉņāüņ£╝ļĪ£ Ļ│ĀņĀĢļÉ£ ņóīĒśä ĒöäļĪ£ĒÄĀļ¤¼ļĪ£ ņØĖĒĢ£ ļ╣äļīĆņ╣Ł ņ£ĀļÅÖņØś Ļ▓░Ļ│╝ļĪ£ ņäĀņ▓┤Ļ░Ć ņÜ░Ēśäņ£╝ļĪ£ ņĢĮĻ░ä Ļ▓Įņé¼Ļ░Ć ļ░£ņāØĒĢ£ Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņØ┤ļŖö Ļ│ĀņĀĢļÉ£ ņóīĒśä ĒöäļĪ£ĒÄĀļ¤¼ ņŻ╝ņ£äĻ░Ć ņ£ĀņåŹņØś ļŖÉļĀżņ¦ÉĻ│╝ ĒĢ©Ļ╗ś ņĢĢļĀźņØ┤ ļåÆĻ│Ā, ņÜ░ĒśäņØś Ļ▓ĮņÜ░ ĒöäļĪ£ĒÄĀļ¤¼ņØś ņ×æļÅÖņ£╝ļĪ£ ņ£ĀņåŹņØ┤ ļ╣©ļØ╝ņĀĖ ņĢĢļĀźņØ┤ ņāüļīĆņĀüņ£╝ļĪ£ ļé«ņĢäņ¦ä ņøÉņØĖņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż.
Table 5ļŖö MARINņØś ļ¬©ĒśĢņŗ£ĒŚśņŚÉņä£ ņĀ£Ļ│ĄĒĢśļŖö ņŗżņäĀņŚÉ ļīĆĒĢ£ ņāüĒĢśļÅÖņÜöņÖĆ ņóģļÅÖņÜö ņÜ┤ļÅÖņØś 1/3 ņ£ĀņØśņÜ┤ļÅÖņ¦äĒÅŁ(Significant amplitude, SA)Ļ│╝ SRtP ņäĀņåŹ 6ļģĖĒŖĖ(3.09m/s)ļź╝ ļé┤ļŖöļŹ░ ĒĢäņÜöĒĢ£ ĒöäļĪ£ĒÄĀļ¤¼ņØś ņŗżņäĀ ĒÅēĻĘĀ ņČöļĀź ņČöņĀĢĻ░ÆņØä ļ╣äĻĄÉĒĢśĻ│Ā ņ׳ļŗż. ņŚ¼ĻĖ░ņä£, TsļŖö ņäżĻ│äļŗ©Ļ│äņŚÉņä£ Ļ▓░ņĀĢĒĢ£ ņŚöņ¦äņŚÉņä£ ņ¢╗ņØä ņłś ņ׳ļŖö ĒöäļĪ£ĒÄĀļ¤¼ņØś ņĄ£ļīĆ ņČöļĀźņØä ļéśĒāĆļéĖļŗż. Ļ▓░Ļ│╝ņŚÉņä£ ņāüĒĢśļÅÖņÜöņØś Ļ▓ĮņÜ░ ņĢĮ 0.24mņØś ņĢĮĻ░äņØś ņ░©ņØ┤ļź╝ ļ│┤ņØ┤Ļ│Ā ņóģļÅÖņÜöņØś Ļ▓ĮņÜ░ļŖö 0.08ļÅä ņĀĢļÅäņØś ņ×æņØĆ ņ░©ņØ┤ļź╝ ļéśĒāĆļé┤Ļ│Ā ņ׳ļŗż. Ļ│äņé░ļÉ£ ņŗżņäĀ ĒÅēĻĘĀ ņČöļĀźņØś Ļ▓ĮņÜ░ ņĀĢņłśņżæ ņ×ÉĒĢŁņāüĒā£ļ│┤ļŗżļŖö ņ░©ņØ┤Ļ░Ć Ēü░, ņĢĮ 9.7% ņĀĢļÅäņØś ņ░©ņØ┤ļĪ£ ņĢĮĻ░ä ļé«Ļ▓ī ņśłņĖĪĒĢśĻ│Ā ņ׳ļŗż. ņłśņ╣śĒĢ┤ņäØņØĆ ņÖäņĀäĒ׳ ļ░£ļŗ¼ļÉ£ ļé£ļźśņ£ĀļÅÖņØä Ļ░ĆņĀĢĒĢśĻ│Ā ņ׳ņ¦Ćļ¦ī, MARINņØś ņ¢ĖĻĖēņ▓śļ¤╝ 10ļģĖĒŖĖ(5.14m/s) ņØ┤ĒĢś ļé«ņØĆ ņäĀņåŹņØś Ļ▓ĮņÜ░ ļ¬©ĒśĢņŗ£ĒŚśņØś ņ£ĀļÅÖņØĆ ņĖĄļźśņØś ņśüĒ¢źņØ┤ ļ¼┤ņŗ£ļÉĀ ņłś ņŚåļŖö ņāüĒÖ®ņØ┤ ļÉśļŖö ņ░©ņØ┤Ļ░Ć Ļ▓░Ļ│╝ņŚÉ ņ¢┤ļŖÉ ņĀĢļÅä ļ░śņśüļÉ£ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż. ĻĘĖļ¤¼ļéś ļ│┤ļŗż ņŻ╝ņÜöĒĢ£ ņ░©ņØ┤ļŖö ņłśņ╣śĒĢ┤ņäØņŚÉņä£ ņé¼ņÜ®ĒĢ£ ĒöäļĪ£ĒÄĀļ¤¼ ļ¬©ļŹĖļ¦üņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż. Ēīīļ×æ ņżæ ņäĀņ▓┤ņØś ņ×ÉņäĖ ļ│ĆĒÖöņŚÉ ļö░ļźĖ ĒöäļĪ£ĒÄĀļ¤¼ļĪ£ ņ£Āņ×ģļÉśļŖö ņ£ĀļÅÖņ£╝ļĪ£ ņØĖĒĢ£ ņŗżņĀ£ ņČöļĀźņØĆ Virtual diskļ▓Ģņ£╝ļĪ£ ņØ┤ņāüņĀüņØĖ ĒĢśņżæļČäĒżļĪ£ ņ▓śļ”¼ĒĢ£ Ļ▓░Ļ│╝ņÖĆ ļŗżņåī ļŗżļź╝ Ļ▓āņ£╝ļĪ£ ņČöņĖĪļÉ£ļŗż.
ĻĘĖļ¤¼ļéś, ļ│Ė ņłśņ╣śĒĢ┤ņäØ Ļ▓░Ļ│╝ļź╝ ņé┤ĒÄ┤ļ│╝ ļĢī ļČłĻĘ£ņ╣Ö Ēīīļ×æ ņżæ SRtP ņäĀņåŹ 6ļģĖĒŖĖ(3.09m/s)ļź╝ ņ£Āņ¦ĆĒĢśļŖö ĒĢäņÜöĒĢ£ ļīĆļץņĀüņØĖ ņåīņÜöļ¦łļĀź ņČöņĀĢņŚÉ Virtual diskļ▓ĢņØä ņØ┤ņÜ®ĒĢ£ CFD ĻĖ░ļ▓ĢņØś ņĀüņÜ®ņ£╝ļĪ£ ļ╣äĻĄÉņĀü ĒāĆļŗ╣ĒĢ£ Ļ▓░Ļ│╝ļź╝ ņ¢╗ņØä ņłś ņ׳ņØīņØä ņĢī ņłś ņ׳ļŗż. ĒĢ£ĒÄĖ, Ēæ£ņŚÉņä£ ņ¢ĖĻĖēĒĢ£ ĒĢ£ ĻĖ░ņØś ņŚöņ¦äņŚÉņä£ Ļ░ĆņÜ®ĒĢĀ ņłś ņ׳ļŖö ĒöäļĪ£ĒÄĀļ¤¼ ņĄ£ļīĆ ņČöļĀź TmaxĻ░Ć 746kNņ£╝ļĪ£ ļ¬©ĒśĢņŗ£ĒŚśĻ│╝ ņłśņ╣śĒĢ┤ņäØņŚÉņä£ ņČöņĀĢļÉ£ ņČöļĀźļ│┤ļŗż ņŚ¼ņ£ĀĻ░Ć ņ׳ļŖö Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. ņØ┤ļŖö Ļ▓░ļĪĀņĀüņ£╝ļĪ£ Beaufort 8ņØś ļČłĻĘ£ņ╣ÖĒīī ņĪ░Ļ▒┤ņŚÉņä£ ļŗ©ņČĢ ņČöņ¦äņ£╝ļĪ£ ņ×ÉĒĢŁņżæņØĖ ļīĆņāü ņ╣┤ĒÄśļ”¼ ņäĀļ░ĢņØ┤ 6ļģĖĒŖĖ(3.09m/s)ņØś ņåŹļĀźņØä ļé┤ļŖö ļŹ░ļŖö ļ¼ĖņĀ£Ļ░Ć ņŚåļŖö Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.
ļ│Ė ņĀłņŚÉņä£ļŖö ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀņØś ĻĖ░Ļ┤Ć ņåÉņāüņØ┤ ņ׳ļŖö ņóīĒśä ņŚöņ¦äņØ┤ Ēāæņ×¼ļÉ£ ĻĖ░Ļ┤Ćņŗż ņ╣©ņłś ņāüĒÖ®ņØä Ļ░ĆņĀĢĒĢśĻ│Ā ņ╣©ņłśĻ░Ć ļ░£ņāØĒĢśņ¦Ć ņĢŖļŖö ņĪ░Ļ▒┤Ļ│╝ ļ╣äĻĄÉĒĢśņŚ¼ Beaufort 8ņØś Ēīīļ×æ ņżæ 6ļģĖĒŖĖ(3.09m/s)ņØś ņäĀņåŹņØä ņ£Āņ¦ĆĒĢśļŖöļŹ░ ņåīņÜöļÉśļŖö ļ¦łļĀź ņ”ØĻ░Ćļ¤ēņŚÉ ļīĆĒĢ┤ ļģ╝ņØśĒĢśņśĆļŗż. ņŚ¼ĻĖ░ņä£, ņ╣©ņłśļĪ£ ņØĖĒĢ£ ņäĀņ▓┤ ļé┤ļČĆ ņ¦łļ¤ēņØś ņŗ£Ļ░äļ│ĆĒÖöļŖö ņÜ┤ļÅÖļ░®ņĀĢņŗØ Ļ┤Ćņä▒ļĀź ĒĢŁņØś ņ¦łļ¤ēņŚÉ ņ¦üņĀæ ļŹöĒĢśņŚ¼ Ļ│ĀļĀżĒĢśņ¦Ć ņĢŖĻ│Ā, ņ╣©ņłś ņ£ĀļÅÖņØś ņÜ┤ļÅÖņ£╝ļĪ£ ļ░£ņāØĒĢśļŖö ņŗ£Ļ░äņŚÉ ļö░ļźĖ ņĀĢņĀü ļ░Å ļÅÖņĀü ĒלĻ│╝ ļ¬©ļ®śĒŖĖņØś ļ│ĆĒÖöļź╝ ņÜ┤ļÅÖļ░®ņĀĢņŗØņØś ņÜ░ļ│Ć ĒĢŁņŚÉ Ļ│ĀļĀżĒĢśņŚ¼ ĻĘĖ ņśüĒ¢źņØä ĒĢ┤ņäØĒĢśņśĆļŗż.
Fig. 9ņØĆ ņĢäļלņÖĆ ņ£ä Ļ│ĄĻ░äņØ┤ Ļ░£ļ░®ļÉśņ¢┤ņ׳ļŖö ļ│ĄņĖĄ ĻĄ¼ņĪ░ņØś ĻĖ░Ļ┤ĆņŗżņØś ĒśĢņāüĻ│╝ ņ╣©ņłśĻ░Ć ļ░£ņāØĒĢśļŖö ņłśļ®┤ ņĢäļל ĻĖ░Ļ┤ĆņŗżņØś ņóīĒśä ņ¬Į ļ▓ĮņŚÉ ņŗżņäĀ ĻĖ░ņżĆņØś 3.8m├Ś1.0mņØś ņåÉņāü ņśüņŚŁņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ņóīĒśä ņŚöņ¦äņØ┤ Ēāæņ×¼ļÉśļŖö ĻĘĖļ”╝ņØś ĻĖ░Ļ┤ĆņŗżņØĆ ņóīņÜ░ ļ╣äļīĆņ╣Łņ£╝ļĪ£ ņÜ░ĒśäņØś ņŚöņ¦äņŚÉņä£ ļéśņś© ĒÜīņĀäņČĢņØ┤ ņ¦ĆļéśļŖö ņśüņŚŁņØ┤ļ®░, ņłśņ╣śĒĢ┤ņäØņŚÉņä£ ĻĖ░Ļ┤Ćņŗż ļé┤ļČĆņØś ļŗżļźĖ ĻĄ¼ņĪ░ļ¼╝ņØĆ ņŚåļŖö ļ╣ł ņāüĒā£ļĪ£ Ļ░ĆņĀĢĒĢśņśĆļŗż. ņ╣©ņłśļŖö ņŗ£ļ«¼ļĀłņØ┤ņģś ņŗ£ņ×æĻ│╝ ļÅÖņŗ£ņŚÉ ļ░£ņāØĒĢśļŖö Ļ▓āņ£╝ļĪ£ ņäżņĀĢĒĢśņśĆļŗż. ņłśņ╣śĒĢ┤ņäØņØĆ Ļ│äņé░ņŗ£Ļ░ä ņ┤łĻĖ░ ņĢĮ 30sĻ╣īņ¦Ć ĻĖ░Ļ┤Ćņŗż ņ╣©ņłśĻ░Ć ļ░£ņāØĒĢśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢśņśĆņ£╝ļ®░, ņØ┤ļĢī ņ╣©ņłśļÉ£ ĻĄ¼Ļ░äņØś ļ░░ņłśļ¤ēņØĆ ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀņØś ņĀäņ▓┤ ļ░░ņłśļ¤ēņØś ņĢĮ 5.9%ņŚÉ ĒĢ┤ļŗ╣ĒĢśņśĆļŗż.
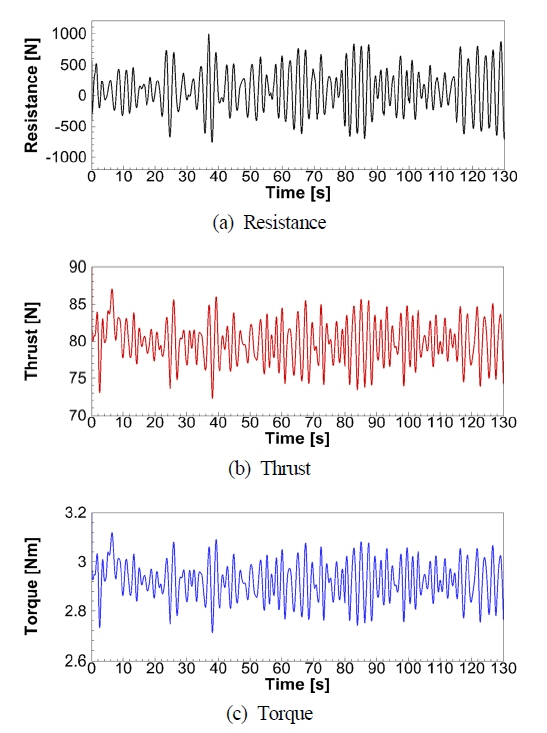
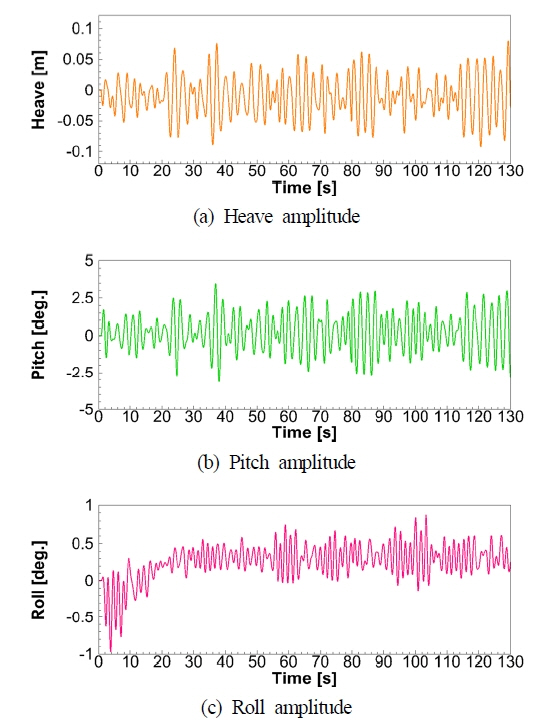
Fig. 10Ļ│╝ Fig. 11ļŖö ņ╣©ņłś ņāüĒÖ®ņŚÉņä£ ņ░ŠņØĆ ņ×ÉĒĢŁņĀÉņŚÉņä£ Ļ│äņé░ĒĢ£ 130s ļÅÖņĢłņØś ĒīīņØś ņ¦äļÅÖņłśļĪ£ ņØæļŗĄĒĢśļŖö ņäĀņ▓┤ņØś ņĀĆĒĢŁ, ĒöäļĪ£ĒÄĀļ¤¼ ņČöļĀź, ĒåĀņśżĒü¼ ĻĘĖļ”¼Ļ│Ā ņäĀņ▓┤ņØś ņÜ┤ļÅÖ ļ│ĆĒÖöļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ĻĖ░Ļ┤Ćņŗż ņ╣©ņłśļŖö ņ┤łĻĖ░ ņĢĮ 30s ļÅÖņĢł ļ░£ņāØĒĢśĻ│Ā, ņØ┤ ņŗ£Ļ░ä ļÅÖņĢł ņ╣©ņłś ņ£ĀļÅÖņØś ņśüĒ¢źņ£╝ļĪ£ ņäĀņ▓┤ļŖö ņÜ░Ēśäņ£╝ļĪ£ Ļ▓Įņé¼ņ¦ä ņāüĒā£ņŚÉņä£ ĒÜĪļÅÖņÜöĻ░Ć ļ░£ņāØĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņØ┤ ņŗ£Ļ░ä ņØ┤Ēøä, ņ╣©ņłśļÉ£ ĻĖ░Ļ┤ĆņŗżņØś ņóīņÜ░ ļ╣äļīĆņ╣ŁņØś ņśüĒ¢źņ£╝ļĪ£ ņäĀņ▓┤Ļ░Ć ņóīĒśäņ£╝ļĪ£ ņĢĮĻ░ä Ļ▓Įņé¼ņ¦ä ņāüĒā£ļĪ£ ĒÜĪļÅÖņÜö ņÜ┤ļÅÖņØ┤ ļ│ĆĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņÜ┤ļÅÖ ļ│Ćņ£äņØś ņŗ£Ļ░ä ļ│ĆĒÖöļź╝ ņĢ×ņäĀ ļ╣äņ╣©ņłś ņāüĒā£ņÖĆ ļ╣äĻĄÉĒĢĀ ļĢī ņ╣©ņłśļÉ£ ĻĖ░Ļ┤Ćņŗż ļé┤ ņŖ¼ļĪ£ņŗ▒(Sloshing) ļ¼ĖņĀ£ļŖö Ēü¼ņ¦Ć ņĢŖņØĆ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż. ņāüĒĢśļÅÖņÜöņØś Ļ▓ĮņÜ░ ņäĀļ»Ė ĻĖ░Ļ┤ĆņŗżņØś ņ╣©ņłśļĪ£ ņØĖĒĢ£ ņäĀļ»Ė ņ╣©ĒĢś ņāüĒā£ņŚÉņä£ ņÜ┤ļÅÖņØ┤ ļ░£ņāØĒĢśļŖö Ļ▓āņØä ņśłņāüĒĢĀ ņłś ņ׳ļŗż. ņĀäņ▓┤ņĀüņ£╝ļĪ£ ņĀĆĒĢŁĻ│╝ ņČöļĀź ĻĘĖļ”¼Ļ│Ā ĒåĀņśżĒü¼ļŖö ļ╣äņ╣©ņłś ņĪ░Ļ▒┤ļ│┤ļŗż Ļ░ÆņØ┤ ņ╗żņ¦ä Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż.
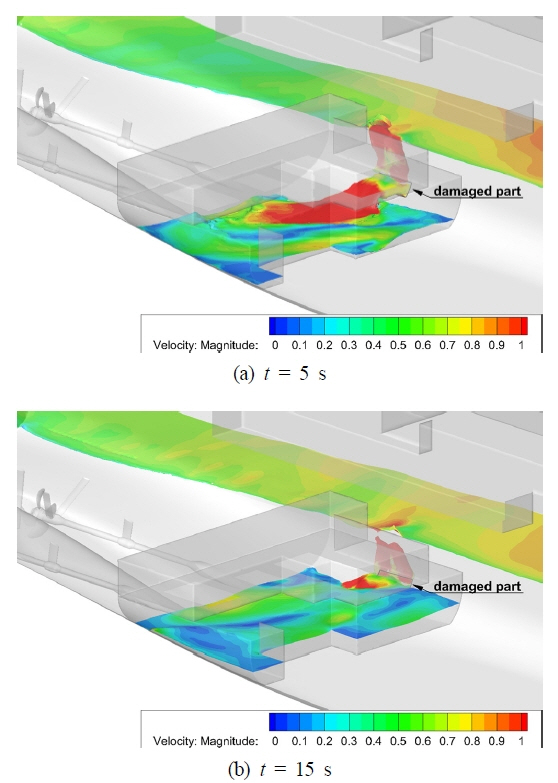
Fig. 12ņØĆ ņŗ£Ļ░ä 5sņÖĆ 15sņŚÉņä£ ņ╣©ņłśĻ░Ć ļ░£ņāØĒĢśĻ│Ā ņ׳ļŖö ĻĖ░Ļ┤Ćņŗż ļé┤ļČĆ ņ£ĀļÅÖņØś ļ│ĆĒÖöļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż. ĻĘĖļ”╝ņØś ņāēņØś ļČäĒżļŖö ņ£ĀņåŹņØś Ēü¼ĻĖ░ļź╝ ļéśĒāĆļé┤Ļ│Ā ņ׳ņ£╝ļ®░, ņÜ░ĒśäņŚÉņä£ ņäĀļ»Ėļź╝ ļ░öļØ╝ļ│┤ļŖö ņŗ£ņĀÉņŚÉņä£ ĻĖ░Ļ┤Ćņŗż ļ▓Į ņåÉņāüļČĆņ£äļĪ£ ļé┤ļČĆņØś Ļ│ĄĻĖ░Ļ░Ć ņ£ĀņČ£ļÉśļŖö Ļ▓āĻ│╝ ļÅÖņŗ£ņŚÉ ņÖĖļČĆņØś ļ¼╝ņØ┤ ņ£Āņ×ģļÉśĻ│Ā ņ׳Ļ│Ā ņäĀņ▓┤ņØś ņÜ┤ļÅÖĻ│╝ ĒĢ©Ļ╗ś ļé┤ļČĆņŚÉņä£ ņĢĮĒĢ£ ņŖ¼ļĪ£ņŗ▒ņØ┤ ļ░£ņāØĒĢśļŖö Ļ▓āņØä ļ│┤ņŚ¼ņżĆļŗż. ņ£ĀņåŹņØś Ēü¼ĻĖ░ļŖö ņ╣©ņłśĻ░Ć ļ░£ņāØĒĢśļŖö ĻĖ░Ļ┤Ćņŗż ļ▓Įļ®┤ ņåÉņāüļČĆņ£äļź╝ ĒåĄĻ│╝ĒĢśļŖö ņ£ĀļÅÖņŚÉņä£ ņāüļīĆņĀüņ£╝ļĪ£ Ēü░ Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż.
Table 6ņØĆ ĻĖ░Ļ┤Ćņŗż ņ╣©ņłś ņ£Āļ¼┤ņŚÉ ļö░ļźĖ Beaufort 8ņØś ļČłĻĘ£ņ╣ÖĒīī ņĪ░Ļ▒┤ņŚÉņä£ ĒĢ┤ņäØļÉ£ ļ¬©ĒśĢ ĒöäļĪ£ĒÄĀļ¤¼ ĒÜīņĀäņłś, ņĀĆĒĢŁ, ņČöļĀź, ĒåĀņśżĒü¼, ņŗżņäĀ ņČöļĀź ĻĘĖļ”¼Ļ│Ā ļŗżņØīņØś ņŗØ (9)ņÖĆ Ļ░ÖņØ┤ ļ¬©ĒśĢ ĒöäļĪ£ĒÄĀļ¤¼ņØś ĒåĀņśżĒü¼ļĪ£ ņČöņĀĢĒĢ£ ņŗżņäĀ ņĀ£ļÅÖļ¦łļĀź(Brake horse power, BHPS)ļź╝ ļ╣äĻĄÉĒĢśĻ│Ā ņ׳ļŗż.
ņŚ¼ĻĖ░ņä£, ŽüSļŖö ņŗżņäĀņØś ļ░ĆļÅä, ŽüMņØĆ ļ¬©ĒśĢņäĀņØś ļ░ĆļÅä ĻĘĖļ”¼Ļ│Ā ╬╗ļŖö ļ¬©ĒśĢņäĀĻ│╝ ņŗżņäĀņØś ņČĢņ▓Öļ╣äļź╝ ļéśĒāĆļéĖļŗż.
ĻĖ░Ļ┤Ćņŗż ņ╣©ņłśņØś ņśüĒ¢źņ£╝ļĪ£ ļ¬©ļōĀ Ļ░ÆņØ┤ ņ”ØĻ░ĆĒĢśņśĆņ£╝ļ®░, ņČöņĀĢļÉ£ ņŗżņäĀ ņČöļĀźņØś Ļ▓ĮņÜ░ ņĢĮ 9.5% ņ”ØĻ░ĆĒĢśņśĆĻ│Ā, ņĀ£ļÅÖļ¦łļĀźņØĆ ņĢĮ 15% ņ”ØĻ░ĆĒĢśņśĆļŗż. ĻĖ░Ļ┤Ćņŗż ņ╣©ņłśļĪ£ ņØĖĒĢ┤ ņ”ØĻ░ĆļÉ£ ņåīņÜöļ¦łļĀźņØä Ēæ£ ņĢäļלņ¬ĮņŚÉ Ēæ£ĻĖ░ĒĢ£ ĒĢ£ ĻĖ░ņØś ņČöņ¦äĻĖ░ņØś Ļ░ĆņÜ® ņĄ£ļīĆ ņČöļĀź ļ░Å ņĀ£ļÅÖļ¦łļĀźĻ│╝ ļ╣äĻĄÉĒ¢łņØä ļĢī, ņØ┤ Ļ░ÆļōżņØĆ ņĢĮ 70%ņŚÉ ĒĢ┤ļŗ╣ĒĢśļ®░ ņĢĮ 30%ņØś ņŚ¼ņ£Ā ļ¦łļĀźņØ┤ ņ׳ļŖö Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. ĻĘĖļ¤¼ļ»ĆļĪ£ ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ņäżņĀĢĒĢ£ ĻĖ░Ļ┤Ćņŗż ņ╣©ņłś ņāüĒÖ®ņØ┤ ļ░£ņāØĒĢśņŚ¼ļÅä ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀņØĆ Beaufort 8ņØś ļČłĻĘ£ņ╣ÖĒīī ņĪ░Ļ▒┤ņŚÉņä£ ļŗ©ņČĢ ņČöņ¦äņ£╝ļĪ£ 6ļģĖĒŖĖ(3.09m/s)ņØś ņåŹļĀźņØä ļé┤ļŖö ļŹ░ļŖö ļ¼ĖņĀ£Ļ░Ć ņŚåļŖö Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż.
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀņØś ņóīĒśä ĻĖ░Ļ┤ĆņØś Ļ│Āņןņ£╝ļĪ£ ĒöäļĪ£ĒÄĀļ¤¼Ļ░Ć Ļ│ĀņĀĢļÉ£ ņāüĒÖ®ņŚÉņä£ ņÜ░ĒśäņØś ļŗ©ņČĢ ņČöņ¦äļ¦īņ£╝ļĪ£ Beaufort 8ņØś ļČłĻĘ£ņ╣ÖĒīī ĒĢ┤ņāüņĪ░Ļ▒┤ņŚÉņä£ 6ļģĖĒŖĖ(3.09m/s)ņØś ņäĀņåŹņØä ņ£Āņ¦ĆĒĢśļŖöļŹ░ ņåīņÜöļÉśļŖö ļ¦łļĀźņØä CFDļĪ£ ĒĢ┤ņäØĒĢ£ ņŚ░ĻĄ¼Ļ▓░Ļ│╝ļź╝ ņåīĻ░£ĒĢśņśĆļŗż.
Ēīīļ×æ ņżæ ņäĀņ▓┤ņÜ┤ļÅÖĻ│╝ ĒĢ©Ļ╗ś ĒĢ┤ņäØĒĢ┤ņĢ╝ĒĢĀ ĒöäļĪ£ĒÄĀļ¤¼ ļ¼ĖņĀ£ļŖö Virtual diskļ▓Ģņ£╝ļĪ£ ļŗ©ņł£ĒÖöĒĢśņśĆņ£╝ļ®░, ņĀĢņłśņżæ ņ×ÉĒĢŁņāüĒā£ņŚÉ ļīĆĒĢ£ KRISO ļ¬©ĒśĢņŗ£ĒŚś Ļ▓░Ļ│╝ļź╝ ĒåĄĒĢ┤ ļ╣äņåÉņāü ļ░Å ņåÉņāü ņĪ░Ļ▒┤ņŚÉ ļīĆĒĢ┤ Ļ▓Ćņ”ØĒĢśņśĆļŗż. ņŚ¼ĻĖ░ņä£, ĒöäļĪ£ĒÄĀļ¤¼ ņČöļĀź ņČöņĀĢ Ļ┤ĆņĀÉņŚÉņä£ ņłśņ╣śĒĢ┤ņäØ Ļ▓░Ļ│╝ļŖö ļ¬©ĒśĢņŗ£ĒŚśĻ│╝ ļ¦īņĪ▒ĒĢĀļ¦īĒĢ£ ņóŗņØĆ ņØ╝ņ╣śļź╝ ļ│┤ņŚ¼ņŻ╝ņŚłļŗż.
ĻĖ░Ļ┤Ćņŗż ļ╣äņ╣©ņłś ņĪ░Ļ▒┤ņŚÉņä£ SRtPņŚÉ ļīĆĒĢ£ ņłśņ╣śĒĢ┤ņäØ Ļ▓░Ļ│╝ņŚÉņä£ ļČłĻĘ£ņ╣ÖĒīīņØś ņ¦äļÅÖņłśļĪ£ ņØæļŗĄĒĢśļŖö ņĀĆĒĢŁĻ│╝ ĒöäļĪ£ĒÄĀļ¤¼ņØś Ēל ĻĘĖļ”¼Ļ│Ā ņāüĒĢśļÅÖņÜöņÖĆ ņóģļÅÖņÜöņØś ņ¦äĒÅŁņØś ļ│ĆĒÖöļŖö ļīĆņ▓┤ļĪ£ ņ£Āņé¼ĒĢ£ Ļ▒░ļÅÖņØä ļ│┤ņśĆļŗż. MARINņØś ļ¬©ĒśĢņŗ£ĒŚś Ļ▓░Ļ│╝ņÖĆņØś ļ╣äĻĄÉņŚÉņä£ ņÜ┤ļÅÖņØæļŗĄņØś Ļ▓ĮņÜ░ ļ╣äĻĄÉņĀü ĒāĆļŗ╣ĒĢ£ ņØ╝ņ╣śļź╝ ļ│┤ņŚ¼ņŻ╝ņŚłļŗż. ņŗżņäĀ ĒÅēĻĘĀ ņČöļĀźņØś Ļ▓ĮņÜ░ ļ¬©ĒśĢņŗ£ĒŚśļ│┤ļŗż ņłśņ╣śĒĢ┤ņäØņØ┤ ņĢĮĻ░ä ļé«Ļ▓ī ņČöņĀĢĒĢśņśĆņ£╝ļéś, ņŻ╝ņ¢┤ņ¦ä ņŚöņ¦äņØś Ļ░ĆņÜ® ņĄ£ļīĆ ņČöļĀź ļīĆļ╣ä Beaufort 8ņØś ĒĢ┤ņāüņĪ░Ļ▒┤ņŚÉņä£ 6ļģĖĒŖĖ(3.09m/s) ņäĀņåŹņØä ļé┤ļŖöļŹ░ ĒĢäņÜöĒĢ£ ņČöļĀź ņČöņĀĢņŚÉ CFDĻĖ░ļ▓ĢņØ┤ ļ╣äĻĄÉņĀü ļ¦īņĪ▒ņŖżļ¤¼ņÜ┤ Ļ▓░Ļ│╝ļź╝ ņĀ£Ļ│ĄĒĢśĻ│Ā ņ£ĀņÜ®ĒĢ£ Ļ▓āņØä ĒÖĢņØĖĒĢśņśĆļŗż.
ļ¦łņ¦Ćļ¦ēņ£╝ļĪ£ ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀ ļ░░ņłśļ¤ēņØś ņĢĮ 5.9%ņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ņóīĒśä ņŚöņ¦äņØ┤ Ēāæņ×¼ļÉ£ ĻĖ░Ļ┤ĆņŗżņØś ņ╣©ņłśĻ░Ć ļ░£ņāØĒ¢łņØä ļĢī ļ╣äņ╣©ņłś ņĪ░Ļ▒┤ ļīĆļ╣ä 6ļģĖĒŖĖ(3.09m/s) ņäĀņåŹņØä ņ£Āņ¦ĆĒĢśļŖö ļŹ░ ĒĢäņÜöĒĢ£ ņŗżņäĀ ņČöļĀźņØś Ļ▓ĮņÜ░ ņĢĮ 9.5% ņ”ØĻ░ĆĒĢśņśĆĻ│Ā, ĒåĀņśżĒü¼ļĪ£ Ļ│äņé░ļÉ£ ņĀ£ļÅÖļ¦łļĀźņØĆ ņĢĮ 15% ņ”ØĻ░ĆĒĢśļŖö Ļ▓āņ£╝ļĪ£ Ļ│äņé░ļÉśņŚłļŗż. ņØ┤ļĢī, ĻĖ░Ļ┤Ćņŗż ņ╣©ņłśļĪ£ ņØĖĒĢ┤ ņ”ØĻ░ĆļÉ£ ņåīņÜöļ¦łļĀźņØĆ ņŻ╝ņ¢┤ņ¦ä ņČöņ¦äĻĖ░ņØś Ļ░ĆņÜ® ņĄ£ļīĆ ņČöļĀź ļ░Å ņĀ£ļÅÖļ¦łļĀźĻ│╝ ļ╣äĻĄÉĒ¢łņØä ļĢī ņØ┤ Ļ░ÆļōżņØĆ ņĢĮ 70%ņŚÉ ĒĢ┤ļŗ╣ĒĢśļ®░ ņĢĮ 30%ņØś ņŚ¼ņ£Ā ļ¦łļĀźņØ┤ ņ׳ļŖö Ļ▓āņ£╝ļĪ£ ĒĢ┤ņäØļÉśņŚłļŗż. Ļ▓░ļĪĀņĀüņ£╝ļĪ£, ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ņäżņĀĢĒĢ£ ĻĖ░Ļ┤Ćņŗż ņ╣©ņłś ņāüĒÖ®ņØ┤ ļ░£ņāØĒĢśņŚ¼ļÅä ļīĆņāü ņ╣┤ĒÄśļ”¼ņäĀņØĆ Beaufort 8ņØś ļČłĻĘ£ņ╣ÖĒīī ņĪ░Ļ▒┤ņŚÉņä£ ļŗ©ņČĢ ņČöņ¦äņ£╝ļĪ£ 6ļģĖĒŖĖ(3.09m/s)ņØś ņåŹļĀźņØä ļé┤ļŖö ļŹ░ļŖö ļ¼ĖņĀ£Ļ░Ć ņŚåļŖö Ļ▓āņ£╝ļĪ£ ĒÖĢņØĖļÉśņŚłļŗż.
Ē¢źĒøä, ļŗżņ¢æĒĢ£ ņäĀņ▓┤ ņåÉņāü ņāüĒÖ®ņŚÉņä£ ļīĆņāü ņäĀļ░ĢņØ┤ SRtPņĪ░Ļ▒┤ņØä ļ¦īņĪ▒ĒĢśļŖö ņŚ¼ļČĆņÖĆ ĒīīļØ╝ņżæ ņ¦üņ¦ä ĒĢŁņŻ╝ņŚÉ ļīĆĒĢ£ ņĪ░ņóģņä▒ļŖź ņŚ░ĻĄ¼Ļ░Ć ņ¦äĒ¢ēļÉśņ¢┤ņĢ╝ ĒĢĀ Ļ▓āņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż.
ĒøäĻĖ░
ļ│Ė ļģ╝ļ¼ĖņØĆ 2017ĒĢÖļģäļÅä ļÅÖņØśļīĆĒĢÖĻĄÉ ņŚ░ĻĄ¼ļģä ņ¦ĆņøÉĻ│╝ ņäĀļ░ĢĒĢ┤ņ¢æĒöīļ×£ĒŖĖņŚ░ĻĄ¼ņåīņØś KRISOļ¬©ĒśĢņŗ£ĒŚś ļ░Å ņäĀĒśĢņĀĢļ│┤ DBĻĄ¼ņČĢĻ│╝ DBļČäņäØņŗ£ņŖżĒģ£ ĻĖ░ļ░śĻĖ░ņłĀ Ļ░£ļ░£(PES3210) Ļ│╝ņĀ£ņØś ņ¦ĆņøÉņ£╝ļĪ£ ņ×æņä▒ļÉśņŚłņŖĄļŗłļŗż.
Table┬Ā1
Main dimensions of the car ferry ship
Table┬Ā2
Propeller rps and forces at self-propulsion points in calm water
Table┬Ā3
Propeller rps and forces at the self-propulsion point for ship speed of 6 knot (3.09m/s) at damaged condition in calm water
| VS [kt(m/s)] | VM [m/s] | TM [N] | QM [Nm] | NM [rps] | |||
|---|---|---|---|---|---|---|---|
|
|
|||||||
| CFD | EXP | CFD | EXP | CFD | EXP | ||
| 6 (3.09) | 0.72 | 14.27 | 14.95 | 0.57 | 0.58 | 4.73 | 4.41 |
Table┬Ā4
Wave and wind conditions
| H1/3 [m] | TP [s] | Vwind [m/s] | |
|---|---|---|---|
| Ship | 5.0 | 9.0 | 20.7 |
| Model | 0.27 | 2.09 | 4.81 |
Table┬Ā5
Comparisons of motions and propeller thrust in irregular waves
| Heave (1/3 SA, m) | Pitch (1/3 SA, deg.) | TS [kN] | |
|---|---|---|---|
| CFD | 1.63 | 3.62 | 474.8 |
| EXP | 1.39 | 3.70 | 526.0 |
References
Cho, SK., Hong, SY., & Kim, YH. (2006). Investigation of Dynamic Characteristics of the Flooding Water of the Damaged Compartment of an ITTC RoRo-Passenger. Journal of the Society of Naval Architects of Korea, 43(4), 451-459. https://doi.org/10.3744/SNAK.2006.43.4.451

Espinoza Haro, MP. (2016). Numerical Simulation of a Self-Propelling Damaged Cruise Ship in Head/Following Seas Using Computational Fluid Dynamics. M.D. Thesis, Seoul National University.
Germanischer Lloyd. (2009). Rules for Classification and Construction - Additional Rules and Guidelines: Preliminary Guidelines for Safe Return to Port Capability of Passenger Ships, Germanischer Lloyd.
International Maritime Organization. (2009). SOLAS, Consolidated Edition, 2009: Consolidated Text of the International Convention for the Safety of Life at Sea, 1974 and Its Protocol of 1988: Articles, Annexes and Certificates, London. International Maritime Organization.
Kim, JI., Park, IR., Suh, SB., Kang, YD., Hong, SY., & Nam, BW. (2018). Motion Simulation of FPSO in Waves through Numerical Sensitivity Analysis. Journal of Ocean Engineering and Technology, 32(3), 166-176. https://doi.org/10.26748/KSOE.2018.6.32.3.166

Korkut, E., Atlar, M., & Incecik, A. (2004). An Experimental Study of Motion Behaviour with an Intact and Damaged Ro-Ro Ship Model. Ocean Engineering, 31(3ŌĆō4), 483-512. https://doi.org/10.1016/j.oceaneng.2003.05.001

Lee, D., Hong, SY., & Lee, GJ. (2007). Theoretical and Experimental Study on Dynamic Behavior of a Damaged Ship in Waves. Ocean Engineering, 34(1), 21-31. https://doi.org/10.1016/j.oceaneng.2006.02.002

Lim, TG. (2014). Development of 6DOF Motion Measurement System for SRTP Test of a Damaged Ship in Head Seas. M.D. Thesis, Seoul National University.
LloydŌĆÖs Register. (2010). Safe Return to Port - Requirements and Compliance, LloydŌĆÖs Register.
Muzaferija, S., Peric, M., Sames, P., & Schellin, T. 1998 A Two-Fluid NavierŌĆōStokes Solver to Simulate Water Entry. Proceedings of the 22nd Symposium on Naval Hydrodynamics Washington, DC, U.S.Aa.: 277-289.
Papanikolau, D., Zaraphonitis, G., Spanos, D., Boulougouris, E., & Eliopoulou, E. 2000 Investigation into the Capsizing of Damaged Ro-Ro Passenger Ships in Waves. Proceedings of 7th International Conference on Stability of Ship and Ocean Vehicles.
Ruponen, P. (2007). Progressive Flooding of a Damaged Passenger Ship. PhD Thesis, Helsinki University of Technology.
Siemense. (2018). STAR-CCM+ 11.04 User Guide. [Online] Available at: https://support.industrysoftware.automation.siemens.com/general/documentation.shtml> [Accessed 01 Jan. 2018
- TOOLS
-
METRICS

-
- 2 Crossref
- Scopus
- 10,047 View
- 140 Download
- Related articles in JOET
-
Numerical Simulation of Flow around Free-rolling Rectangular Barge in Regular Waves2011 April;25(2)
Stochastic Prediction of Rolling of Ships in Irregular Waves1991 December;5(2)