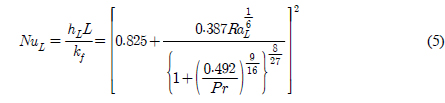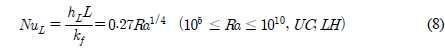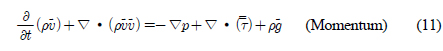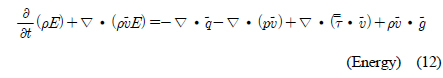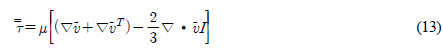ANSYS, F. 12.0 Theory Guide ANSYS Inc, 2009). 5.
Cable, M.. (An Evaluation of Turbulence Models for the Numerical Study of Forced and Natural Convective Flow in Atria Queen's University Kingston, Ontario, Canada: 2009.
Churchill, S.W., Chu, H.H.. (Correlating Equations for Laminar and Turbulent Free Convection from a Vertical Plate, International Journal of Heat and Mass Transfer, 1975). 18(11):1323-1329 10.1016/0017-9310(75)90243-4.

Eckert, E.R.G., Drake, R.M. Jr.. (Analysis of Heat and Mass Transfer 1987.
Gavory, T., De Seze, P.E.. (Sloshing in Membrane LNG Carriers and its Consequences from a Designer’s Perspective The Nineteenth International Offshore and Polar Engineering Conference 2009.
Han, K.C., Hwang, S.W., Cho, J.R., Kim, J.S., Yoon, J.W., Lim, O., Lee, S.B.. (A Study on the Boil-Off Rate Prediction of LNG Cargo Containment Filled with Insulation Powders, Journal of the Computational Structural Engineering Institute of Korea, 2011). 24(2):193-200.
Han, Y.Y., Kwon, J.C., Kim, W.S., Kim, M.S., Choe, I.H.. (The Development on the 3-Dimensional Calculation Program of Temperature Distribution for Gas Carriers Proceedings of the 2006 Joint Conference on Korean Association of Ocean Science and Technology Societies(KAOSTS) 2006). 504-510.
Heo, J.U., Lee, Y.J., Cho, J.R., Ha, M.K., Lee, J.N.. (Heat Transfer Analysis and BOG Estimation of Membrane-Type LNG Cargo during Laden Voyage, Transactions of the Korean Society of Mechanical Engineers A, 2003). 27(3):393-400 10.3795/KSME-A.2003.27.3.393.

Heo, J.H.. (Heat Flux Calculation for Thermal Equilibrium of Cofferdam in a LNG Carrier, Journal of the Society of Naval Architects of Korea, 1998). 35(1):98-106.
Heo, J.H., Jeon, Y.H.. (Temperature Distribution for a Membrane type LNGC Cargo Tank, Journal of the Society of Naval Architects of Korea, 1997). 34(4):108-118.
Holman, J.P.. (Heat Transfer McGraw-Hill, 2010.
IMO International Code for the Construction and Equipment of Ships Carrying Liquefied Gases in Bulk (I.G.C code) International Maritime Organization; 2003.
International Gas Union (IGU) World LNG Report International Gas Union; 2016.
Jin, K.K., Yoon, I.S., Yang, Y.C.. (An Effect of Surface Dashpot for KC-1 Basic Insulation System Under Sloshing Loads, Transactions of the KSME C: Industrial Technology and Innovation, 2015). 3(3):193-199 10.3795/KSME-C.2015.3.3.193.

Lee, B.J., Kim, S.B.. (Current State of the Polymer Material Technology for Cryogenic, Prospectives of Industrial Chemistry, 2014). 17(5):1-11.
Lee, J.H.. (Thermal Analysis Comparison of IMO with USCG Design Condition for the LNGC During the Cool-down Period, Transactions of the Korean Society of Mechanical Engineers B, 2004). 28(11):1390-1397 10.3795/KSME-B.2004.28.11.1390.

Lee, J.H., Choi, H.K., Choi, S., Oh, C., Kim, M.H., Kim, K.K.. (Thermal Analysis for the GT-96 Membrane Type LNGC during the Cool-down Period Proceedings of the Korean Society of Mechanical Engineers 2004). 1346-1351.
Lee, J.H., Kim, K.K., Ro, S.T., Chung, H.S., Kim, S.G.. (A Study on the Thermal Analysis of Spray Cooling for the Membrane Type LNGC During the Cool-Down Period, Transactions of the Korean Society of Mechanical Engineers B, 2003). 27(1):125-134 10.3795/KSME-B.2003.27.1.125.

Lee, Y.B., Choe, K.H.. (Development of Polyurethane Foam Insulator with High Thermal Insulation Performance for KC-1 LNG Carrier The Twenty-fifth International Offshore and Polar Engineering Conference 2015.
Miana, M., Legorburo, R., Díez, D., Hwang, Y.H.. (Calculation of Boil-Off Rate of Liquefied Natural Gas in Mark III Tanks of Ship Carriers by Numerical Analysis, Applied Thermal Engineering, 2016). 93, 279-296 10.1016/j.applthermaleng.2015.09.112.

Rhee, S.H.. (Unstructured Grid Based Reynolds-Averaged Navier-Stokes Method for Liquid Tank Sloshing, Journal of Fluids Engineering, 2005). 127(3):572-582 10.1115/1.1906267.

Song, S.O., Lee, J.H., Jun, H.P., Sung, B.Y., Kim, K.K., Kim, S.G.. (A Study on the Three-Dimensional Steady State Temperature Distributions and BOR Calculation Program Deveolpment for the Membrane Type LNG Carrier, Journal of Korean Society of Marine Engineering, 1999). 23(2):140-149.
Vargaftik, N.B., Vinogradov, Y.K., Yargin, V.S.. (Handbook of Physical Properties of Liquids and Gases 1996). p 663-717 Pure Substances and Mixtures.
Zakaria, M.S., Osman, K., Saadun, M.N.A., Manaf, M.Z.A., Hanafi, M., Hafidzal, M.. (Computational Simulation of Boil-Off Gas Formation inside Liquefied Natural Gas Tank Using Evaporation Model in ANSYS Fluent, Applied Mechanics and Materials, 2013). 839-844.

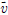 는 속도벡터를 나타낸다. 식 (11)에서 p는 정압,
는 속도벡터를 나타낸다. 식 (11)에서 p는 정압,  항은 중력에 의한 체적력을 의미하며,
항은 중력에 의한 체적력을 의미하며, 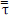 는 응력 텐서를 나타내며, 다음의 기본적인 식으로 표현된다.
는 응력 텐서를 나타내며, 다음의 기본적인 식으로 표현된다.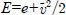 , e는 내부에너지이며,
, e는 내부에너지이며, 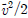 는 운동에너지이다. 그리고
는 운동에너지이다. 그리고 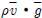 는 점성력에 작용한 일을 나타낸다. 운동량 방정식에서 난류효과를 모사하기 위해 본 연구에서는 구획 내 공기의 유동을 Reynolds-averaged Navier-stokes(RANS) 기법 중 Standard k−ε turbulence model을 증진시킨 Realizable model 설정하였고, 이 때 계산되는 레이놀즈 응력(Reynolds stresses)를 사용하여 다음과 같이 계산하였다.
는 점성력에 작용한 일을 나타낸다. 운동량 방정식에서 난류효과를 모사하기 위해 본 연구에서는 구획 내 공기의 유동을 Reynolds-averaged Navier-stokes(RANS) 기법 중 Standard k−ε turbulence model을 증진시킨 Realizable model 설정하였고, 이 때 계산되는 레이놀즈 응력(Reynolds stresses)를 사용하여 다음과 같이 계산하였다. 는 각속도를 고려한 회전 텐서의 평균 속도를 의미하며 Sij는 변형률 텐서, As는 각각 4.04,
는 각속도를 고려한 회전 텐서의 평균 속도를 의미하며 Sij는 변형률 텐서, As는 각각 4.04,  로 계산된다. Realizable model은 Standard model보다 박리 유동(Separation flow)과 복잡한 이차적 흐름에서 정밀한 해를 제공한다(Cable, 2009).
로 계산된다. Realizable model은 Standard model보다 박리 유동(Separation flow)과 복잡한 이차적 흐름에서 정밀한 해를 제공한다(Cable, 2009).