1. м„ң лЎ
м„қм…ҳ м•өм»ӨлҠ” мғҒл¶Җк°Җ л°ҖнҸҗлҗң мӣҗнҶө л§җлҡқнҳ• м•өм»ӨлЎң мһҗмӨ‘м—җ мқҳн•ң кҙҖмһ… мқҙнӣ„м—җ, м•өм»Ө лӮҙВ·мҷёл¶Җмқҳ м••л Ҙм°ЁлҘј мқҙмҡ©н•ҳм—¬ м§ҖмӨ‘м—җ кҙҖмһ…н•ҳлҠ” мӣҗлҰ¬лҘј мқҙмҡ©н•ҳм—¬ м„Өм№ҳлҗҳлҠ” м•өм»ӨмқҙлӢӨ. мқҙлЎң мқён•ҙ нҒ¬кё° л°Ҹ м„Өм№ҳ мҲҳмӢ¬м—җ м ңм•Ҫмқ„ л°ӣм§Җ м•ҠмңјлҜҖлЎң лҢҖк·ңлӘЁмқҳ н•ҙмғҒ кө¬мЎ°л¬ј л°Ҹ мӢ¬н•ҙ м„қмң мӢңм¶”м„ л“ұм—җ л„җлҰ¬ мқҙмҡ©лҗҳкі мһҲлӢӨ. нҳ„мҲҳм„ (Catenary)нҳ•мӢқмқҳ кі„лҘҳм„ мқ„ мң„н•ҙ м„қм…ҳ м•өм»Өк°Җ мӮ¬мҡ©лҗҳлҠ” кІҪмҡ°, мҲҳнҸү н•ҳмӨ‘мқҙ м§Җл°°м ҒмңјлЎң мһ‘мҡ©н•ҳкІҢ лҗҳлҜҖлЎң м„қм…ҳ м•өм»Өмқҳ мҲҳнҸү м§Җм§Җл Ҙмқ„ мӮ°м •н•ҳлҠ” мқјмқҖ л§Өмҡ° мӨ‘мҡ”н•ҳлӢӨ. м җм„ұнҶ м§Җл°ҳмқҳ кІҪмҡ°, мҲҳнҸү н•ҳмӨ‘мқ„ мӮ°м •н•ҳкё° мң„н•ң л°©лІ•мқҙ лӘҮлӘҮ м„ н–ү м—°кө¬лҘј нҶөн•ҙ м ңмӢңлҗҳм—ҲлӢӨ(Anderson and Jostad, 1999; Randolph and House, 2002; Aubeny and Murff, 2003; Anderson and Jostad, 2004; Kim et al., 2011). мӮ¬м§ҲнҶ м§Җл°ҳм—җ кҙҖмһ…лҗң м„қм…ҳ м•өм»Өмқҳ мҲҳнҸү м§Җм§Җл Ҙ мӮ°м •мқҖ мқҙлЎ м Ғ л°©лІ• л°Ҹ мӢӨн—ҳм Ғ л°©лІ•мңјлЎң Cho and Bang (2002) л°Ҹ Bang et al.(2011)м—җ мқҳн•ҙ м—°кө¬лҗң л°” мһҲм§Җл§Ң, лӢӨмҶҢ ліөмһЎн•ң м•Ңкі лҰ¬мҰҳмқ„ м ңмӢңн•ҳкі мһҲм–ҙ м„Өкі„лҘј мң„н•ң к°„нҺён•ң м Ҳм°Ёк°Җ н•„мҡ”н•ң мӢӨм •мқҙлӢӨ. лҳҗн•ң, мІңн•ҙм—ӯм—җ м„ёлҰҪ мӮ¬м§ҲнҶ к°Җ л§Һмқҙ 분нҸ¬н•ҳкі мһҲм–ҙ мқҙ м§Җм—ӯм—җ м„Өм№ҳлҗң м„қм…ҳ м•өм»Өмқҳ кұ°лҸҷм—җ кҙҖн•ң м—°кө¬ мӮ¬лЎҖк°Җ л¶ҖмЎұн•ҳлӢӨ. нҢҗ м•өм»Ө(Plate anchor)мқҳ кІҪмҡ° көӯлӮҙм—җм„ңлҸ„ мӮ¬м§ҲнҶ лҘј лҢҖмғҒмңјлЎң н•ҳм—¬ мқёл°ң м Җн•ӯл Ҙм—җ кҙҖн•ң м—°кө¬к°Җ мҲҳн–үлҗң л°” мһҲлӢӨ(Seo et al., 2008).
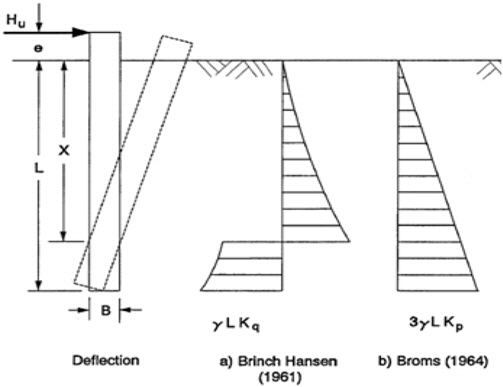
м „нҶөм ҒмңјлЎң мңЎмғҒ нҶ лӘ© кө¬мЎ°л¬јм—җ мӮ¬мҡ©лҗң лӢЁл§җлҡқмқҳ мҲҳнҸү м§Җм§Җл Ҙмқ„ мӮ°м •н•ҳкё° мң„н•ҳм—¬ л§җлҡқ мЈјліҖм—җ нҳ•м„ұлҗң нҶ м•• 분нҸ¬ мҳҲмёЎмқ„ нҶөн•ҙ м§Җм§Җл Ҙмқҙ кі„мӮ°лҗңлӢӨ(Brinch Hansen, 1961; Broms, 1964; Meyerhof et al., 1981; Prasad and Chari, 1999). м„қм…ҳ м•өм»Өмқҳ нҳ•мғҒмқҙ лӢЁл§җлҡқкіј мң мӮ¬н•ҳкё° л•Ңл¬ём—җ, лҸҷмқјн•ң л°©лІ•мңјлЎң м„қм…ҳ м•өм»Өмқҳ мҲҳнҸү нҢҢм§Җл Ҙмқ„ кі„мӮ°н• мҲҳ мһҲм§Җл§Ң, мқҙлҠ” м•өм»Өмқҳ нҳ•мғҒкіј м§ҖмӨ‘ н•ҳмӨ‘ мһ¬н•ҳмң„м№ҳ(Pad-eye)к°Җ лӢ¬лқјм§ҖлҠ” м•өм»Өмқҳ нҠ№м„ұмқ„ л°ҳмҳҒн• мҲҳ м—ҶлӢӨ. мөңм Ғмқҳ м„қм…ҳм•өм»Ө нҢҢм§Җл Ҙмқ„ нҷ•ліҙн•ҳкё° мң„н•ҳм—¬ м•өм»Ө лІҪл©ҙм—җ Pad-eyeк°Җ мң„м№ҳн•ҳлҠ” нҳ•нғңмқҳ м•өм»ӨлҠ” м—¬лҹ¬ нҳ„мһҘм—җм„ң мӢңкіөлҗң л°” мһҲмңјл©°(Aas et. al., 2009; Langford et. al., 2012), л…ёлҘҙмӣЁмқҙмқҳ Skarv fieldм—җ мӢңкіөлҗң м•өм»Өмқҳ нҳ•мғҒкіј Pad-eyeмқҳ мң„м№ҳлҠ” Fig. 1кіј к°ҷлӢӨ.
л”°лқјм„ң ліё м—°кө¬м—җм„ңлҠ” мөңлҢҖмқҳ м§Җм§Җл Ҙмқҙ л°ңнҳ„лҗ мҲҳ мһҲлҸ„лЎқ н•ҳмӨ‘ мһ¬н•ҳмң„м№ҳ(Pad-eye)лҘј кі л Өн•ҳм—¬ м—°кө¬ н•ҳмҳҖмңјл©°, мӮ¬м§ҲнҶ м§Җл°ҳм—җ кҙҖмһ…лҗң м„қм…ҳ м•өм»Өк°Җ мҲҳнҸү н•ҳмӨ‘мқ„ л°ӣлҠ” кІҪмҡ°мқҳ к·№н•ң м§Җм§Җл Ҙ мӮ°м •мқ„ лӘ©н‘ңлЎң н•ҳмҳҖлӢӨ. м•өм»Өмқҳ кІҪмҡ°, н•ҳмӨ‘мқҳ мһ¬н•ҳ мң„м№ҳлҠ” нҡЁмңЁм Ғмқё м§Җм§Җл Ҙ нҷ•ліҙлҘј мң„н•ҳм—¬ л‘җл¶Җк°Җ м•„лӢҢ м•өм»Ө лІҪмІҙм—җ мЎҙмһ¬ н•ҳл©°, н•ҳмӨ‘мқҳ мһ¬н•ҳ мң„м№ҳм—җ л”°лқј м•өм»Өмқҳ кұ°лҸҷ л°Ҹ м§Җм§Җл Ҙмқҙ лӢ¬лқјм§ҖлҜҖлЎң к°Ғ н•ҳмӨ‘ мһ¬н•ҳ мң„м№ҳм—җ л”°лҘё мҲҳнҸү м§Җм§Җл Ҙмқ„ мӮ°м •В·л¶„м„қн•ҳмҳҖлӢӨ. мқҙлҘј мң„н•ҳм—¬ 3D мң н•ңмҡ”мҶҢлІ• н•ҙм„қмқ„ мҲҳн–үн•ҳмҳҖмңјл©°, мғҒмҡ© н”„лЎңк·ёлһЁмқё ABAQUS 6.11(ABAQUS, 2011)мқ„ мқҙмҡ©н•ҳмҳҖлӢӨ.
2. мҲҳм№ҳн•ҙм„қ лӘЁлҚёл§Ғ
2.1 м•өм»Ө л°Ҹ м§Җл°ҳ лӘЁлҚёл§Ғ
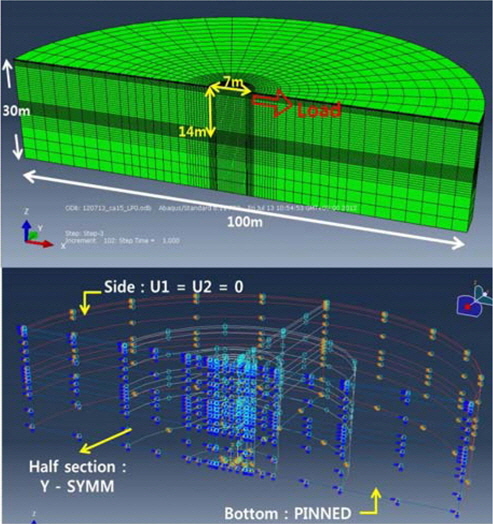
ліё м—°кө¬м—җм„ңлҠ” м§ҒкІҪ 7m, кёёмқҙ 14mлЎң кёёмқҙмҷҖ м§ҒкІҪмқҳ 비(L/D ratio)к°Җ 2мқё м•өм»ӨлҘј лӘЁлҚёл§Ғ н•ҳмҳҖлӢӨ. л‘җк»ҳлҠ” м§ҒкІҪмқҳ 3пј…м—җ н•ҙлӢ№н•ҳлҠ” к°’мңјлЎң 0.21mмқҙл©°, мһ¬м§ҲмқҖ к°•мһ¬лЎң к°Җм •н•ҳмҳҖлӢӨ. м§Җл°ҳмқҖ 100mмқҳ м§ҒкІҪкіј 30mмқҳ к№ҠмқҙлЎң лӘЁмӮ¬н•ҳм—¬ м•өм»ӨмҷҖ м§Җл°ҳмқҳ м§ҒкІҪ 비к°Җ м•Ҫ 14л°°к°Җ лҗҳлҸ„лЎқ н•ҳмҳҖлӢӨ(Fig. 2). мқҙлҠ” лӢӨм–‘н•ң нҒ¬кё°мқҳ м§Җл°ҳ лӘЁлҚёмқ„ 비көҗн•ҳм—¬ кІ°м •н•ң кІғмңјлЎң, кІҪкі„нҡЁкіјк°Җ лӮҳнғҖлӮҳм§Җ м•ҠмқҢмқ„ нҷ•мқён•ҳмҳҖлӢӨ. лҳҗн•ң м•өм»Өмқҳ нҳ•мғҒ л°Ҹ н•ҳмӨ‘мқҳ л°©н–Ҙмқҙ лҢҖм№ӯм Ғ кө¬мЎ°мқҙлҜҖлЎң л°ҳ лӢЁл©ҙмңјлЎң кө¬м„ұн•ҳмҳҖлӢӨ. лҢҖм№ӯл©ҙмқҖ Y-SYMM кІҪкі„мЎ°кұҙмқ„ м Ғмҡ©н•ҳм—¬ x-zнҸүл©ҙм—җ лҢҖн•ҳм—¬ лҢҖм№ӯлҗҳлҸ„лЎқ н•ҳмҳҖмңјл©°, м§Җл°ҳ мҡ”мҶҢмқҳ к°ҖмһҘ мҷёкіҪмқҳ мёЎл©ҙмқҖ xл°©н–Ҙкіј yл°©н–Ҙмқҳ ліҖмң„к°Җ л°ңмғқн•ҳм§Җ м•ҠлҸ„лЎқ н•ҳмҳҖлӢӨ(U1=U2=0). лҳҗн•ң м§Җл°ҳ мҡ”мҶҢмқҳ л°”лӢҘл©ҙмқҖ PinnedлЎң кө¬м„ұн•ҳм—¬ лӘЁл“ л°©н–Ҙмқҳ ліҖмң„к°Җ л°ңмғқн•ҳм§Җ м•ҠлҸ„лЎқ н•ҳмҳҖлӢӨ.
м•өм»ӨмҷҖ м§Җл°ҳлӘЁлҚёмқҖ кіөнҶөм ҒмңјлЎң 8м Ҳм җмқ„ к°–лҠ” 3м°Ёмӣҗ м—°мҶҚмІҙ мҡ”мҶҢлЎңм„ң, мқ‘л Ҙ ліҖнҳ•лҘ мқҳ кі„мӮ°мқ„ мң„н•ҙ м Җк°җм Ғ분(Reduced integration)мқ„ мұ„нғқн•ҳмҳҖлӢӨ. н•ҙм„қм—җ мӮ¬мҡ©лҗң м•өм»ӨмҷҖ м§Җл°ҳ лӘЁлҚёмқҖ мҙқ 5л§Ңм—¬к°ңмқҳ мҡ”мҶҢлЎң кө¬м„ұлҗҳм—Ҳмңјл©°, 2л§Ңм—¬к°ңмқҳ мҡ”мҶҢлЎң кө¬м„ұлҗң лӘЁлҚёл¶Җн„° мҡ”мҶҢмқҳ к°ңмҲҳлҘј м җм°Ё мҰқк°ҖмӢңмјң 10л§Ңк°ң мқҙмғҒмқҳ мҡ”мҶҢлҘј к°–лҠ” лӘЁлҚём—җ лҢҖн•ҳм—¬ н•ҙм„қмқ„ мҲҳн–үн•ң кІ°кіј, кұ°лҸҷм—җ нҒ° м°ЁмқҙлҘј ліҙмқҙм§Җ м•Ҡм•ҳмңјлҜҖлЎң н•ҙм„қ мӢңк°„мқ„ кі л Өн•ҳм—¬ м•Ҫ 5л§Ңм—¬к°ңлЎң кІ°м •н•ҳмҳҖлӢӨ. лӢӨл§Ң м•өм»ӨмҷҖ м§Җл°ҳмқҙ мқём ‘н•ң л¶Җ분м—җм„ңлҠ” мҲҳл ҙм„ұмқ„ кі л Өн•ҳм—¬ мЎ°л°Җн•ҳкІҢ мҡ”мҶҢл§қмқ„ 분нҸ¬мӢңмј°лӢӨ(Fig. 2).
2.2 м§Җл°ҳ л¬јм„ұ
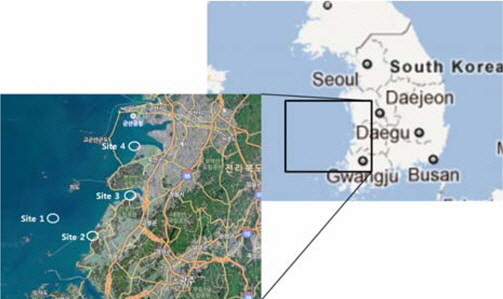
ліё м—°кө¬м—җм„ңлҠ” м„ңн•ҙм•Ҳ н•ҙм Җл©ҙ(Seabed)м—җ 분нҸ¬н•ң м„ёлҰҪ мӮ¬м§ҲнҶ лҘј лҢҖмғҒмңјлЎң н•ҳм—¬ м„қм…ҳ м•өм»Өмқҳ м§Җм§Җл Ҙмқ„ мӮ°м •н•ҳмҳҖлӢӨ. Fig. 3кіј к°ҷмқҙ м „л¶Ғ кі м°Ҫкө° л°Ҹ м „лӮЁ мҳҒкҙ‘кө° мЈјліҖ мӢңлЈҢлҘј 4 кө°лҚ°м—җм„ң м§Ғм ‘ мұ„м·Ё н•ҳмҳҖлӢӨ(Choo, et al., 2012).
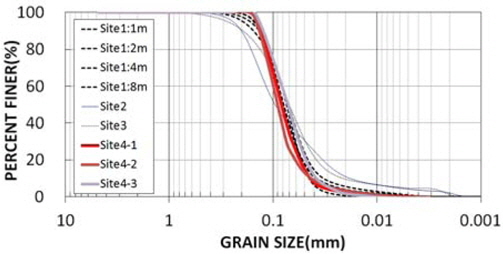
к°Ғ мӢңлЈҢм—җ лҢҖн•ҳм—¬ мІҙ분м„қ, 비мӨ‘кі„ 분м„қ л°Ҹ л Ҳмқҙм Җ 분м„қмқ„ мҲҳн–үн•ҳм—¬ Fig. 4мқҳ мһ…лҸ„ 분нҸ¬кіЎм„ мқ„ м–»м—ҲлӢӨ. лӘЁл“ мӢңлЈҢк°Җ нҶөмқјл¶„лҘҳлІ•(USCS, unified soil classification system) 분лҘҳ мІҙкі„м—җ мқҳн•ҙ SM(silty sand, м„ёлҰҪм§Ҳ лӘЁлһҳ)мңјлЎң 분лҘҳлҗҳм—Ҳмңјл©° нҡҚл“қн•ң мӢңлЈҢм—җ лҢҖн•ң кё°ліё л¬јм„ұ мһҗлЈҢлҠ” Table 1м—җ лӮҳнғҖлӮҙм—ҲлӢӨ.
ліё мҲҳм№ҳн•ҙм„қм—җм„ң мӮ¬м§ҲнҶ м§Җл°ҳмқҳ кө¬м„ұ лӘЁлҚёлЎң Mohr-Coulomb лӘЁлҚёмқ„ мӮ¬мҡ©н•ҳмҳҖмңјл©° мң н•ңмҡ”мҶҢ н•ҙм„қ н”„лЎңк·ёлһЁм—җ м Ғмҡ©н•ҳм—¬ мҲҳм№ҳм Ғмқё мҳҲмёЎмқ„ н•ҳлҠ” кІҪмҡ° лӘЁлһҳмқҳ мқ‘л Ҙ-ліҖнҳ•лҘ кұ°лҸҷмқ„ лӮҳнғҖлӮҙкё° мң„н•ҙ мқҙмҡ©лҗң лҢҖл¶Җ분мқҳ лӘЁлҚёл“Өмқҙ н•ӯліөл©ҙкіј мҶҢм„ұнҸ¬н…җм…ңмқҳ нҳ•нғңлҘј л”°лЎң м •мқҳн•ҳлҜҖлЎң(Desai and Siriwardane, 1984), н•ӯліөл©ҙкіј кҙҖл Ён•ң лӮҙл¶Җл§Ҳм°°к°Ғ(ПҶ) л°Ҹ мҶҢм„ұнҸ¬н…җм…ңкіј кҙҖл Ён•ң нҢҪм°Ҫк°Ғ(ПҲ)лҘј м§Ғм ‘ м „лӢЁмӢңн—ҳмңјлЎңл¶Җн„° нҡҚл“қн•ҳм—¬ м Ғмҡ©н•ҳмҳҖлӢӨ(Table 2). мқҙл•Ң, нҢҪм°Ҫк°ҒмқҖ мҲҳнҸү ліҖнҳ• мҰқ분м—җ лҢҖн•ң мІҙм Ғ ліҖнҳ• мҰқ분мқҳ мөңлҢҖк°’мңјлЎңл¶Җн„° кІ°м •н•ҳмҳҖлӢӨ(Simoni and Houlsby, 2006).
мӮ¬м§ҲнҶ лҠ” кө¬мҶҚм••мқҳ мҳҒн–Ҙмқ„ нҒ¬кІҢ л°ӣмңјлҜҖлЎң к№Ҡмқҙм—җ л”°лҘё нғ„м„ұкі„мҲҳ(E)мқҳ мӮ°м •мқҙ н•„мҡ”н•ҳлӢӨ. нғ„м„ұнҢҢ мӢӨн—ҳмқ„ нҶөн•ҳм—¬ кө¬н•ҙ진 нғ„м„ұкі„мҲҳлҘј нҶ лҢҖлЎң м§Җл°ҳ лӘЁлҚёмқ„ 6мёөмңјлЎң лӮҳлҲ„м–ҙ к°Ғ к№Ҡмқҙм—җм„ңмқҳ нҸүк· нғ„м„ұкі„мҲҳ к°’мқ„ мһ…л Ҙн•ҳмҳҖмңјл©° мһ…л Ҙк°’мқҖ Table 2мҷҖ к°ҷлӢӨ.
2.3 н•ҙм„қ кё°лІ•
мҲҳм№ҳ н•ҙм„қмқҖ лӢӨмқҢмқҳ лӢЁкі„м—җ л”°лқј мҲҳн–үн•ҳмҳҖлӢӨ.
1) м§Җл°ҳ лӘЁлҚём—җ лҢҖн•ҳм—¬, к№Ҡмқҙм—җ л”°лҘё мҙҲкё° мқ‘л Ҙмқ„ мһ¬нҳ„н•ҳкё° мң„н•ҳм—¬, Geostatic мЎ°кұҙмқ„ м Ғмҡ©н•ҳм—¬ нҸүнҳ•мғҒнғңк°Җ лҗҳлҸ„лЎқ н•ҳмҳҖлӢӨ.
2) м„қм…ҳ м•өм»Өмқҳ м„Өм№ҳлҘј мң„н•ҳм—¬, м•өм»Өк°Җ лҶ“мқј мң„м№ҳмқҳ м§Җл°ҳ лӘЁлҚёмқ„ м ңкұ°н•ҳмҳҖлӢӨ. мқҙл•Ң, м§Җл°ҳкіј м•өм»Өмқҳ кІҪкі„л©ҙм—җлҠ” лЎӨлҹ¬лҘј мқҙмҡ©н•ҳм—¬ ліҖмң„лҘј м–өм ңн•ҳмҳҖлӢӨ. м•өм»Өмқҳ лІҪл©ҙкіј л§һлӢҝкІҢ лҗҳлҠ” м§Җл°ҳ мҡ”мҶҢлҠ” xл°©н–Ҙ л°Ҹ yл°©н–Ҙмқҳ мӣҖм§Ғмһ„мқ„ кө¬мҶҚн•ҳм—¬ zл°©н–ҘмңјлЎңмқҳ ліҖмң„л§Ңмқ„ н—Ҳмҡ©н•ҳмҳҖмңјл©°, к°ҷмқҖ л°©лІ•мңјлЎң м•өм»Өмқҳ м„ лӢЁл¶ҖмҷҖ м ‘н•ҳкі мһҲлҠ” м§Җл°ҳмҡ”мҶҢлҠ” zл°©н–Ҙмқҳ мӣҖм§Ғмһ„мқ„ кө¬мҶҚн•ҳм—¬ xл°©н–Ҙ л°Ҹ yл°©н–Ҙмқҳ ліҖмң„ л°ңмғқл§Ңмқ„ н—Ҳмҡ©н•ҳмҳҖлӢӨ. мқҙлҠ” м•өм»Өк°Җ м„Өм№ҳлҗ мЈјліҖ м§Җл°ҳ мҡ”мҶҢмқҳ ліҖнҳ•мңјлЎң мқён•ҙ м•өм»Өк°Җ м„Өм№ҳлҗ кіөк°„мқҙ нҳ•м„ұлҗҳм§Җ м•ҠлҠ” мғҒнҷ©мқ„ л°©м§Җн•ҳкё° мң„н•ң кІғмқҙлӢӨ.
3) м„қм…ҳ м•өм»Ө лӘЁлҚёмқ„ нҷңм„ұнҷ” мӢңмјң, м•өм»ӨлҘј м§Җл°ҳм—җ м„Өм№ҳн•ҳмҳҖлӢӨ. мқҙл•Ң, м•өм»Ө лӮҙвҖӨмҷёмёЎкіј м§Җл°ҳ мӮ¬мқҙмқҳ кІҪкі„л©ҙм—җм„ңлҠ” Surface-tosurface contactлҘј м Ғмҡ©н•ҳм—¬ Gappingкіј Slippageк°Җ л°ңмғқн•ҳлҸ„лЎқ лӘЁмӮ¬н•ҳмҳҖлӢӨ. м ‘мҙүл©ҙмқҖ Coulombмқҳ нҢҢкҙҙ мқҙлЎ м—җ л”°лҘҙл©°, л§Ҳм°°кі„мҲҳ(Ој)лҠ” м§Җл°ҳмқҳ лӮҙл¶Җ л§Ҳм°°к°Ғмқҳ м•Ҫ 2/3м—җ н•ҙлӢ№н•ҳлҠ” 0.41мқ„ м Ғмҡ©н•ҳмҳҖлӢӨ.
4) мҲҳнҸүл°©н–Ҙмқҳ н•ҳмӨ‘мқ„ мһ¬н•ҳ н•ҳмҳҖлӢӨ. мқҙл•Ң, н•ҳмӨ‘м—җ мқҳн•ң м ңм–ҙк°Җ м•„лӢҢ мқјм •лҹүмқҳ ліҖмң„лҘј л°ңмғқн•ҳлҸ„лЎқ м ңм–ҙн•ҳм—¬ м•өм»Өмқҳ мҲҳнҸү м§Җм§Җл Ҙмқ„ мӮ°м •н•ҳмҳҖлӢӨ.
2.4 к·№н•ң м§Җм§Җл Ҙмқҳ м •мқҳ
м„қм…ҳ м•өм»Өмқҳ к·№н•ң м§Җм§Җл ҘмқҖ кё°мЎҙ л§җлҡқмқҳ к·№н•ң мҲҳнҸүм Җн•ӯл Ҙ мӮ°м •л°©лІ•мңјлЎңл¶Җн„° 비көҗлҘј нҶөн•ҳм—¬ кІ°м •н•ҳмҳҖлӢӨ. л„җлҰ¬ мқҙмҡ©лҗҳлҠ” кІғмңјлЎңмҚЁ Brinch Hansen(1961)мқҳ л°©лІ•кіј Broms(1964)мқҳ л°©лІ•мқҙ мһҲлӢӨ. л‘җл¶Җ мһҗмң л§җлҡқм—җ мҲҳнҸүл Ҙмқҙ мһ‘мҡ©н• л•Ң м§Җл°ҳмқҳ к№Ҡмқҙлі„ л°ҳл Ҙ 분нҸ¬лҠ” Fig. 5мҷҖ к°ҷмқҙ лӮҳнғҖлӮј мҲҳ мһҲлӢӨ. кёёмқҙк°Җ L, нҸӯмқҙ Bмқё л§җлҡқм—җ лҢҖн•ҳм—¬ мҲҳнҸү н•ҳмӨ‘ HUк°Җ мһ‘мҡ©н•ҳмҳҖмқ„ л•Ң, нҡҢм „ мӨ‘мӢ¬мқҖ м§Җн‘ңл©ҙмңјлЎңл¶Җн„° xл§ҢнҒј л–Ём–ҙ진 кіім—җм„ң л°ңмғқн•ңлӢӨ. л§җлҡқ мЈјліҖм—җ нҳ•м„ұлҗҳлҠ” нҶ м••мқҙ м§Җл°ҳл°ҳл ҘмңјлЎң мһ‘мҡ©н•ҳм—¬ к·№н•ң мҲҳнҸүм Җн•ӯл Ҙмқ„ мӮ°м •н•ҳлҠ” к°ңл…җмңјлЎң Brinch Hansenкіј BromsлҘј 비лЎҜн•ҳм—¬ Meyerhof et al.(1981) л°Ҹ Prasad(1999) л“ұмқҙ мӮ¬мҡ©н•ҳмҳҖлӢӨ.
Brinch HansenмқҖ нҡҢм „ мӨ‘мӢ¬м җмқ„ кё°мӨҖмңјлЎң н•ҳм—¬ л°ҳлҢҖ л°©н–Ҙмқҳ л°ҳл Ҙмқҙ л°ңмғқн•ҳлҜҖлЎң, мқҙлҘј мҲҳнҸү л°©н–Ҙм—җ лҢҖн•ң нһҳмқҳ нҸүнҳ•кіј л§җлҡқ л‘җл¶ҖлҘј кё°мӨҖмңјлЎң н•ң лӘЁл©ҳнҠё нҸүнҳ•мӢқмқ„ м·Ён•ЁмңјлЎңмҚЁ нҡҢм „ мӨ‘мӢ¬ мң„м№ҳлҘј кө¬н•ңлӢӨ. л§җлҡқмқҳ к№Ҡмқҙ Lм—җ лҢҖн•ҳм—¬ мғҒмҲҳк°’мқё KqлҘј кіұн•ҳм—¬ мЈјліҖ л°ҳл Ҙмқ„ мӮ°м •н•ҳмҳҖлӢӨ. л§җлҡқмқҳ нҡҢм „ мӨ‘мӢ¬м җмқ„ м°ҫмңјл©ҙ, нһҳмқҳ нҸүнҳ• л°©м •мӢқмңјлЎңл¶Җн„° мҲҳнҸүл°©н–ҘмңјлЎңмқҳ к·№н•ң м Җн•ӯл Ҙмқ„ мӮ°м •н• мҲҳ мһҲлӢӨ.
BromsлҠ” л¬ём ңлҘј лӢЁмҲңнҷ”н•ҳкё° мң„н•ҳм—¬ м§Җл°ҳ мЎ°кұҙмқ„ мҲңмҲҳн•ң лӘЁлһҳм§Җл°ҳмқҙкұ°лӮҳ мҲңмҲҳн•ң м җм„ұнҶ м§Җл°ҳмңјлЎң к°Җм •н•ҳкі , 짧мқҖ к°•л§җлҡқкіј кёҙліҖнҳ•л§җлҡқмқ„ к°Ғк°Ғ лі„лҸ„лЎң кі л Өн•ҳмҳҖлӢӨ. 짧мқҖ л§җлҡқмқҳ кІҪмҡ° л§җлҡқ л’ӨмӘҪмқҳ мЈјлҸҷнҶ м••мқ„ л¬ҙмӢңн•ҳкі м•һмӘҪмқҳ мҲҳлҸҷнҶ м••м—җ лҢҖн•ҳм—¬ к·№н•ң м§Җм§Җл Ҙмқ„ мӮ°м •н•ҳмҳҖмңјл©° мҲҳлҸҷнҶ м••кі„мҲҳ Kpмқҳ 3л°°м—җ н•ҙлӢ№н•ҳлҠ” к°’мңјлЎң л°ҳл Ҙмқ„ кі„мӮ°н•ҳмҳҖлӢӨ.
ліё м—°кө¬м—җм„ңлҠ” н•ҙм„қн•ҳкі мһҗ н•ҳлҠ” м•өм»Өмқҳ L/D비к°Җ 2мқҙкё° л•Ңл¬ём—җ, л‘җл¶Җ мһҗмң мЎ°кұҙмқҳ 짧мқҖ к°•л§җлҡқ(Short rigid pile)мңјлЎң к°Җм •н•ҳм—¬ кі„мӮ°н•ҳмҳҖлӢӨ.
м•өм»Ө м§ҒкІҪмқҳ 5пј… мҷҖ 10пј… (35cm, 70cm)м—җ н•ҙлӢ№н•ҳлҠ” ліҖмң„к°Җ н•ҳмӨ‘ мһ¬н•ҳмң„м№ҳм җм—җ л°ңмғқн• л•Ңмқҳ мҲҳнҸү м Җн•ӯл Ҙмқ„ Brinch Hansen л°©лІ• л°Ҹ Broms л°©лІ•м—җ мқҳн•ҙ кі„мӮ°н•ң кІ°кіјлҘј Fig. 6м—җ лӮҳнғҖлӮҙм—ҲлӢӨ.
нҡЎл°©н–Ҙ н•ҳмӨ‘мқ„ л°ӣлҠ” л§җлҡқмқҳ кІҪмҡ° н•ӯліөм җмқҙ 분лӘ…н•ҳкІҢ лӮҳнғҖлӮҳм§Җ м•ҠлҠ” нҠ№м„ұмқҙ мһҲм–ҙ ліҖмң„лҘј кё°мӨҖмңјлЎң н•ҳлҠ” кІҪмҡ°к°Җ л§ҺмңјлҜҖлЎң ліё м—°кө¬м—җм„ңлҸ„ ліҖмң„лҘј кё°мӨҖмңјлЎң н•ҳм—¬ к·№н•ң м§Җм§Җл Ҙмқ„ м •мқҳн•ҳмҳҖлӢӨ. Brinch Hansen л°©лІ•мқҳ кІҪмҡ°, м§Җм§Җл Ҙ кі„мӮ°мқ„ мң„н•ң Kqк°’мқҙ м ңмӢңлҗҳм–ҙмһҲмңјлӮҳ ліё м—°кө¬м—җм„ң мӮ¬мҡ©лҗң м•өм»Өк°Җ мғҒлӢ№нһҲ 짧мқҖ кІҪмҡ°м—җ н•ҙлӢ№н•ҳлҜҖлЎң лӢӨмҶҢ мһ‘кІҢ нҸүк°Җлҗң кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ. л°ҳл©ҙ Broms л°©лІ•мқҖ лӢӨмҶҢ нҒ° к°’мқ„ ліҙмқҙм§Җл§Ң 10пј…лҘј кё°мӨҖмңјлЎң н•ҳм—¬ мҲҳн–үлҗң мҲҳм№ҳн•ҙм„қ кІ°кіјмҷҖ мң мӮ¬н•ң кІғмңјлЎң нҢҗлӢЁн•ҳм—¬ мқҙлҘј кё°мӨҖмңјлЎң н•ҳм—¬ л§Өк°ңліҖмҲҳ м—°кө¬лҘј мҲҳн–үн•ҳмҳҖлӢӨ.
3. н•ҙм„қ кІ°кіј
3.1 н•ҳмӨ‘ мһ¬н•ҳ к№Ҡмқҙм—җ л”°лҘё к·№н•ң м§Җм§Җл Ҙ
н•ҳмӨ‘мқҳ мһ‘мҡ©м җм—җ л”°лҘё мҲҳнҸү м§Җм§Җл Ҙ ліҖнҷ”лҘј нҸүк°Җн•ҳкё° мң„н•ҳм—¬ к°Ғ н•ҳмӨ‘ мң„м№ҳлі„лЎң н•ҙм„қмқ„ мҲҳн–үн•ҳмҳҖлӢӨ.
Fig. 7мқҖ м•өм»Ө лІҪмІҙлҘј л”°лқј н•ҳмӨ‘ мһ‘мҡ©м җмқҙ ліҖнҷ”н• л•Ңмқҳ к·№н•ң мҲҳнҸү м§Җм§Җл Ҙмқ„ лӮҳнғҖлӮёлӢӨ. н•ҳмӨ‘мқҙ м•өм»Өмқҳ л‘җл¶Җм—җ мһ‘мҡ©н•ҳлҠ” кІҪмҡ° 17451kNмқҳ м§Җм§Җл Ҙмқҙ л°ңмғқн•ҳмҳҖмңјл©° мқҙлҠ” Fig. 6м—җм„ң лӮҳнғҖлӮё л°”мҷҖ к°ҷмқҙ кё°мЎҙмқҳ мқҙлЎ мӢқкіј 비көҗн•ҳм—¬ нҒ° м°ЁмқҙлҘј ліҙмқҙм§Җ м•ҠлҠ”лӢӨ.
н•ҳмӨ‘ мһ¬н•ҳ мң„м№ҳк°Җ м•„лһҳлЎң лӮҙл Өк°җм—җ л”°лқј м§Җм§Җл Ҙмқҙ м җм җ мҰқк°Җн•ҳмҳҖлӢӨ. м•өм»Ө кёёмқҙмқҳ м•Ҫ 2/3мң„м№ҳм—җ н•ҙлӢ№н•ҳлҠ” 9m к№Ҡмқҙм—җм„ң н•ҳмӨ‘мқҙ мһ‘мҡ©н–Ҳмқ„ л•Ң, 4л§Ң kN мқҙмғҒмқҳ м§Җм§Җл Ҙмқҙ л°ңмғқн•ҳм—¬ мөңлҢҖк°’мқ„ лӮҳнғҖлғҲмңјл©°, мқҙлҠ” н•ҳмӨ‘мқҙ л‘җл¶Җм—җ мһ‘мҡ©н•ң кІҪмҡ°мҷҖ 비көҗн•ҳм—¬ м•Ҫ2.5л°° м°ЁмқҙлҘј ліҙмҳҖлӢӨ.
н•ҳмӨ‘мқҙ 9m мқҙмғҒмқҳ к№Ҡмқҙм—җм„ң мһ¬н•ҳ лҗ л•Ң, к·№н•ң м§Җм§Җл ҘмқҖ н•ҳмӨ‘ мң„м№ҳк°Җ к№Ҡм–ҙм§җм—җ л”°лқј к°җмҶҢн•ҳмҳҖлӢӨ. м•өм»Ө м„ лӢЁм—җ н•ҳмӨ‘мқҙ мһ‘мҡ©н•ң кІҪмҡ°мқҳ мҲҳнҸү м§Җм§Җл ҘмқҖ 25925kNмңјлЎң мөңлҢҖк°’мқё 44133kNмқҳ м•Ҫ60пј…м—җ н•ҙлӢ№н•ңлӢӨ.
3.2 нҡҢм „к°Ғ л°Ҹ нҡҢм „ мӨ‘мӢ¬
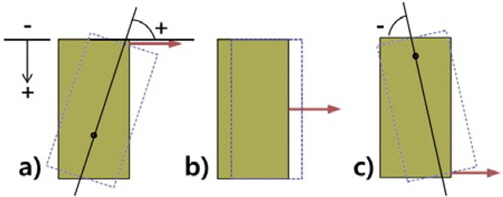
ліё м—°кө¬м—җм„ңлҠ” Fig. 7м—җ лӮҳнғҖлӮё л°”мҷҖ к°ҷмқҙ лӢӨм–‘н•ң мһ¬н•ҳмң„м№ҳм—җ л”°лқј м•өм»Өмқҳ м§Җм§Җл Ҙ л°Ҹ кұ°лҸҷмқ„ нҸүк°Җн•ҳмҳҖкі , к°Ғ н•ҳмӨ‘мң„м№ҳм—җм„ңмқҳ м•өм»Өмқҳ нҡҢм „к°Ғ л°Ҹ нҡҢм „ мӨ‘мӢ¬мқ„ 분м„қн•ң кІ°кіјлҠ” Fig. 8кіј к°ҷлӢӨ. Fig. 8мқҳ 분м„қмқ„ нҶ лҢҖлЎң м•өм»Өмқҳ кұ°лҸҷмқ„ к°ңл…җлҸ„лЎң лӮҳнғҖлӮҙл©ҙ Fig. 9мҷҖ к°ҷлӢӨ. мӢңкі„л°©н–Ҙмқҳ нҡҢм „к°Ғмқ„ (+)лЎң н•ҳмҳҖмңјл©°, (вҲ’)к°’мқҖ л°ҳмӢңкі„л°©н–Ҙмқҳ нҡҢм „к°Ғмқ„ лӮҳнғҖлӮёлӢӨ. к·№н•ң м§Җм§Җл Ҙмқҙ м•өм»Өм—җ мһ‘мҡ©н• л•Ң, м•өм»Өмқҳ мҙҲкё° мң„м№ҳмҷҖ ліҖнҳ• нӣ„мқҳ мң„м№ҳлҘј 비көҗн•ҳм—¬ м•өм»Өмқҳ нҡҢм „к°Ғкіј нҡҢм „ мӨ‘мӢ¬мқҳ мң„м№ҳлҘј мӮ°м •н•ҳмҳҖмңјл©° мқҙл•Ң м•өм»ӨлҠ” Rigidн•ң кұ°лҸҷмқ„ ліҙмқҙлҠ” кІғмңјлЎң к°Җм •н•ҳмҳҖлӢӨ.
н•ҳмӨ‘мқҙ м•өм»Өмқҳ л‘җл¶ҖлЎңл¶Җн„° 1/2мқҙн•ҳмқҳ м–•мқҖ к№Ҡмқҙм—җ мһ‘мҡ©н• л•Ң м•өм»ӨлҠ” м•Ҫ 3В°лӮҙмҷёмқҳ к°ҒмңјлЎң нҡҢм „н•ңлӢӨ. (+)мқҳ к°’мқ„ к°Җм§ҖлҜҖлЎң, Fig. 9мқҳ a)м—җ лӮҳнғҖлӮё л°”мҷҖ к°ҷмқҙ мӢңкі„л°©н–ҘмңјлЎң нҡҢм „н•Ёмқ„ лӮҳнғҖлӮёлӢӨ. мқҙл•Ң, нҡҢм „ мӨ‘мӢ¬ лҳҗн•ң м•өм»Ө мғҒлӢЁмңјлЎңл¶Җн„° м•Ҫ 12mм—җ мң„м№ҳн•ҳкі мһҲм–ҙ м•өм»Ө лӮҙл¶Җм—җ мЎҙмһ¬н•ҳл©° н•ҳмӨ‘ мң„м№ҳк°Җ ліҖн•Ём—җ л”°лқј нҡҢм „ мӨ‘мӢ¬мқҳ мң„м№ҳлҠ” нҒ¬кІҢ ліҖнҷ”н•ҳм§Җ м•ҠлҠ”лӢӨ.
к·ёлҹ¬лӮҳ н•ҳмӨ‘мқҳ мһ¬н•ҳ мң„м№ҳк°Җ 9mм—җ к·јм ‘н•Ём—җ л”°лқј нҡҢм „к°ҒмқҖ кёүкІ©нһҲ к°җмҶҢн•ҳмҳҖмңјл©°, нҡҢм „ мӨ‘мӢ¬мқҳ мң„м№ҳлҠ” нҒ¬кІҢ мҰқк°Җн•ҳмҳҖлӢӨ. нҡҢм „к°Ғмқҙ 0В°м—җ к°Җк№қкі , нҡҢм „мӨ‘мӢ¬мқҳ мң„м№ҳк°Җ м•өм»ӨлЎңл¶Җн„° л¬ҙн•ңнһҲ л–Ём–ҙм ё мһҲлҠ” кІғмқҖ м•өм»Өк°Җ нҡҢм „ мҡҙлҸҷ м—Ҷмқҙ мҲңмҲҳн•ҳкІҢ нҸүн–үмқҙлҸҷ(Translation)н•ҳлҠ” кІғмқ„ мқҳлҜён•ңлӢӨ. мқҙлҠ” Fig. 9мқҳ b)мҷҖ к°ҷмқҖ кұ°лҸҷмқҙлӢӨ. м•һм„ң Fig. 7мқҳ кІ°кіјм—җм„ң н•ҳмӨ‘мқҙ 9mм—җ мһ¬н•ҳ лҗ л•Ң мөңлҢҖ м§Җм§Җл Ҙмқҙ л°ңнҳ„лҗҳм—ҲлӢӨ. мҰү, м•өм»Өк°Җ нҡҢм „н•ҳм§Җ м•Ҡкі мҲҳнҸүмңјлЎң мқҙлҸҷн•ҳлҠ” кІҪмҡ° мөңлҢҖ м§Җм§Җл Ҙмқҙ л°ңнҳ„лҗЁмқ„ м•Ң мҲҳ мһҲлӢӨ.
3.3 м•өм»ӨмҷҖ м§Җл°ҳмқҳ м ‘мҙү мқ‘л Ҙ
мҲҳнҸү л°©н–Ҙмқҳ н•ҳмӨ‘мқ„ л°ӣлҠ” м•өм»Өмқҳ м§Җм§Җл Ҙмқ„ н•ҙм„қн•ҳкё° мң„н•ҙм„ңлҠ” м§Җл°ҳ л°ҳл Ҙмқ„ м Ғм ҲнһҲ мӮ°м •н•ҙм•ј н•ңлӢӨ. мһ„мқҳмқҳ к№Ҡмқҙм—җм„ңмқҳ м§Җл°ҳ л°ҳл ҘмқҖ м•өм»ӨлЎңл¶Җн„° мҲҳнҸүл°©н–ҘмңјлЎң л¬ҙн•ңмҳҒм—ӯк№Ңм§Җ нҳ•м„ұлҗҳлҠ” мқ‘л Ҙ 분нҸ¬мқҳ мҙқ н•©мңјлЎң лӮҳнғҖлӮҳлҠ” лӢЁмң„ кёёмқҙ лӢ№ нһҳмқҙлӢӨ.
мҰү м§Җл°ҳ л°ҳл Ҙмқ„ мӮ°м •н•ҳкё° мң„н•ҙм„ңлҠ” м•өм»Ө мЈјліҖм—җ мһ‘мҡ©н•ҳлҠ” мқ‘л Ҙмқ„ лӘЁл‘җ н•©мӮ°н•ҳм—¬ м•өм»ӨмҷҖ м§Җл°ҳмқҳ м ‘мҙүл©ҙм—җ мһ‘мҡ©н•ҳлҠ” м ‘мҙү мқ‘л Ҙмқ„ нҢҢм•…н•ҙм•ј н•ңлӢӨ.
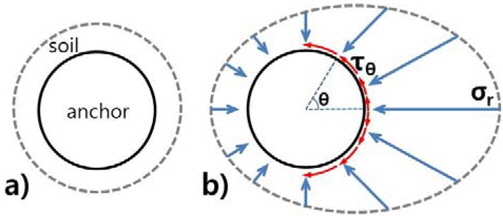
мһ„мқҳмқҳ к№Ҡмқҙм—җм„ң м•өм»ӨмҷҖ м§Җл°ҳ мӮ¬мқҙм—җ мһ‘мҡ©н•ҳлҠ” мқ‘л ҘмқҖ Fig. 10кіј к°ҷмқҙ лӮҳнғҖлӮј мҲҳ мһҲлӢӨ. н•ҳмӨ‘мқ„ л°ӣм§Җ м•ҠлҠ” м•өм»ӨлҠ” Fig. 10 мқҳ a)мҷҖ к°ҷмқҙ к· л“ұн•ң нҒ¬кё°мқҳ мҲҳнҸү мқ‘л Ҙмқ„ л°ӣлҠ”лӢӨ. мҲҳнҸү л°©н–Ҙмқҳ н•ҳмӨ‘мқ„ л°ӣм•„ м•өм»Өк°Җ мӣҖм§Ғмқҙл©ҙ мқҙлҸҷн•ҳлҠ” л°©н–Ҙ(Front side)м—җ мң„м№ҳн•ң м§Җл°ҳмҡ”мҶҢлҠ” мҲҳлҸҷ мғҒнғңк°Җ лҗҳм–ҙ м—°м§Ғ мқ‘л Ҙ(Пғr)мқҙ нҒ¬кІҢ мҰқк°Җн•ңлӢӨ.(Fig. 10мқҳ b)) лҳҗн•ң м•өм»Өмқҳ мӣҗмЈј л°©н–ҘмңјлЎң м „лӢЁ мқ‘л Ҙ(TОё)мқҙ нҳ•м„ұлҗҳлҠ”лҚ°, н•ҳмӨ‘мқҙ мһ‘мҡ©н•ҳлҠ” мң„м№ҳ(Оё=0В°) м—җм„ңлҠ” нҒ¬м§Җ м•ҠмқҖ к°’мқ„ к°–м§Җл§Ң м „лӢЁл©ҙмқҙ л„“м–ҙм§җм—җ л”°лқј мҰқк°Җн•ҳм—¬ Оё=90В° л°Ҹ Оё=270В°м—җм„ң мөңлҢҖк°’мқ„ к°–лҠ”лӢӨ.
к№Ҡмқҙм—җ л”°лқј м•өм»Өм—җ мһ‘мҡ©н•ҳлҠ” м—°м§Ғ мқ‘л Ҙ л°Ҹ м „лӢЁ мқ‘л Ҙмқҳ к°’мқҙ лӢ¬лқјм§ҖлҜҖлЎң, к°Ғ к№Ҡмқҙм—җм„ң мһ‘мҡ©н•ҳлҠ” мқ‘л Ҙмқ„ мӮ°м •н•ҳм—¬ м Ғ분함мңјлЎңмҚЁ мҲҳнҸү н•ҳмӨ‘м—җ лҢҖн•ң к№Ҡмқҙ лі„ м§Җл°ҳ л°ҳл Ҙмқ„ кө¬н• мҲҳ мһҲлӢӨ.
3.4 м§Җл°ҳ л°ҳл Ҙ 분нҸ¬
м§Җл°ҳ л°ҳл ҘмқҖ м—°м§Ғ мқ‘л Ҙм—җ мқҳн•ң м—°м§Ғл Ҙ(CNF, contact normal force)кіј м „лӢЁ мқ‘л Ҙм—җ мқҳн•ң м „лӢЁл Ҙ(CSF, contact shear force)мқҳ н•©мңјлЎң кі„мӮ°н• мҲҳ мһҲлӢӨ.
м„қм…ҳ м•өм»Өмқҳ кІҪмҡ° м§Җл°ҳкіјмқҳ м ‘мҙүл©ҙмқҙ мҷёмёЎ(Outside) лҝҗ м•„лӢҲлқј лӮҙмёЎ(Inside)м—җлҸ„ мЎҙмһ¬н•ҳкі , н•ҳмӨ‘мқ„ л°ӣлҠ” м „л©ҙ(Front side)кіј л°ҳлҢҖнҺё нӣ„л©ҙ(Rear side)м—җм„ңмқҳ кұ°лҸҷмқҙ м°ЁмқҙлҘј ліҙмқҙлҜҖлЎң л„Ө л¶Җ분мңјлЎң лӮҳлҲ„м–ҙ м§Җл°ҳ л°ҳл Ҙмқ„ лҸ„мӢңн•ҳмҳҖлӢӨ(Fig. 11).
м„ңлЎң лӢӨлҘё н•ҳмӨ‘ мһ¬н•ҳ мң„м№ҳм—җ лҢҖн•ҳм—¬ к·№н•ң мҲҳнҸү м§Җм§Җл Ҙмқҙ к°Җн•ҙмЎҢмқ„ л•Ң, м•өм»Өмқҳ к°Ғ м Ҳм җм—җм„ңмқҳ м—°м§Ғ мқ‘л Ҙ л°Ҹ м „лӢЁ мқ‘л Ҙ к°’мқ„ м–»м—ҲлӢӨ. мқҙл•Ң н•ҳмӨ‘мқҳ мһ¬н•ҳ л°©н–Ҙмқҙ x축(1 л°©н–Ҙ)мңјлЎң мһ‘мҡ©н•ҳмҳҖмңјлҜҖлЎң к°Ғ мқ‘л ҘлҸ„ x축м—җ лҢҖн•ң 분л Ҙ к°’мқ„ м·Ён•ҳмҳҖлӢӨ. лҸҷмқјн•ң к№Ҡмқҙм—җ мң„м№ҳн•ҳлҠ” лӘЁл“ м Ҳм җм—җм„ңмқҳ мқ‘л Ҙ к°’мқ„ н•©мӮ°н•ҳм—¬ x축мңјлЎң мһ‘мҡ©н•ҳлҠ” к№Ҡмқҙлі„ м—°м§Ғл Ҙ(CNF1) л°Ҹ м „лӢЁл Ҙ(CSF1)мқ„ мӮ°м •н•ҳмҳҖлӢӨ.
м „мІҙ к№Ҡмқҙм—җ лҢҖн•ң м§Җл°ҳ л°ҳл Ҙмқ„ н•©мӮ°н•ҳл©ҙ м•өм»Өмқҳ мҲҳнҸү м Җн•ӯл Ҙмқ„ мӮ°м •н• мҲҳ мһҲмңјл©° н•ҙм„қ кІ°кіј м–»м–ҙ진 м§Җл°ҳ л°ҳл Ҙмқҳ н•©мқҖ н•ҳмӨ‘ мһ‘мҡ©м җм—җм„ңмқҳ л°ҳл°ңл Ҙкіј мқјм№ҳн•ҳмҳҖлӢӨ.
кұ°лҸҷм—җ мһҲм–ҙ м°ЁмқҙлҘј ліҙмқҙлҠ” лҢҖн‘ңм Ғ мӮ¬лЎҖлЎң н•ҳмӨ‘мқҙ м§Җн‘ң к°Җк№Ңмқҙм—җ к°Җн•ҙм§ҖлҠ” кІҪмҡ°(0m), мөңлҢҖ мҲҳнҸү м§Җм§Җл Ҙмқҙ лӮҳнғҖлӮҳлҠ” кІҪмҡ°(9m) л°Ҹ н•ҳмӨ‘мқҙ м•өм»Ө м„ лӢЁм—җ мһ‘мҡ©н•ҳлҠ” кІҪмҡ°(14m)м—җ лҢҖн•ҳм—¬ к°Ғк°Ғ м§Җл°ҳ л°ҳл Ҙмқ„ мӮ°м •н•ҳм—¬ 비көҗн•ҳмҳҖлӢӨ. кі„лҘҳм„ м—җ мқҳн•ң мҷёл Ҙмқҙ м•өм»Өм—җ мһ‘мҡ©н•ЁмңјлЎңмҚЁ нҳ•м„ұлҗң м§Җл°ҳмқҳ м Җн•ӯл ҘмқҖ м•өм»ӨлҘј н–Ҙн•ҳм—¬ лӮҳнғҖлӮңлӢӨ. ліё л…јл¬ём—җм„ңлҠ” м§Җл°ҳмқҳ м Җн•ӯл Ҙмқҳ л°©н–Ҙмқ„ мҷёл Ҙн•ҳмӨ‘мқҳ мһ¬н•ҳ л°©н–Ҙм—җ л”°лқј лӮҳнғҖлӮҙм—Ҳмңјл©°, (вҲ’)л°©н–Ҙмқҳ л°ҳл ҘмқҖ н•ҳмӨ‘мқҳ мһ¬н•ҳ л°©н–Ҙкіј л°ҳлҢҖлҗҳлҠ” кІғмқҙл©°, (+)л°©н–Ҙмқҳ л°ҳл ҘмқҖ н•ҳмӨ‘мқҳ мһ‘мҡ© л°©н–Ҙкіј мқјм№ҳн•ҳлҠ” кІғмңјлЎң н•ҳмӨ‘кіј лҸҷмқјн•ң л°©н–Ҙмқҳ м Җн•ӯл Ҙмқҙ лҗңлӢӨ. кІ°кіјм ҒмңјлЎң (+)л°©н–ҘмқҖ м „мІҙ мҲҳнҸү м Җн•ӯл Ҙмқҳ н•©л Ҙмқ„ к°җмҶҢмӢңнӮӨлҠ” м—ӯн• мқ„ н•ҳкІҢ лҗңлӢӨ.
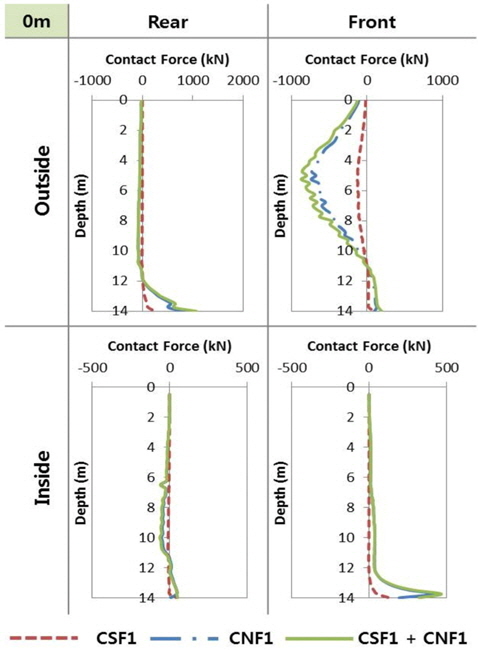
3.4.1 н•ҳмӨ‘ мһ¬н•ҳ мң„м№ҳ 0m (Fig. 12)
н•ҳмӨ‘мқҙ м•өм»Өмқҳ л‘җл¶Җм—җ мһ¬н•ҳ лҗҳлҠ” кІҪмҡ°, м•Ҫ 5m л¶Җк·јк№Ңм§ҖлҠ” (вҲ’)л°©н–Ҙмқҳ м§Җл°ҳ л°ҳл Ҙмқҙ мҰқк°Җн•ҳм§Җл§Ң мқҙнӣ„ к°җмҶҢн•ҳлҠ” кІҪн–Ҙмқҙ лӮҳнғҖлӮҳл©° 12m к·јмІҳм—җм„ң (+)л°©н–Ҙмқҳ л°ҳл Ҙмқҙ нҳ•м„ұлҗҳлҠ”лҚ° мқҙлҠ” м•өм»Өмқҳ нҡҢм „кіј кҙҖкі„лҗңлӢӨ. Fig. 8м—җ лӮҳнғҖлӮң кІғкіј к°ҷмқҙ м•өм»Ө л‘җл¶Җм—җ н•ҳмӨ‘мқҙ мһ‘мҡ©н• л•Ң м•өм»Өмқҳ нҡҢм „ мӨ‘мӢ¬мқҖ м•Ҫ 12m к·јмІҳм—җ мң„м№ҳн•ңлӢӨ. мҰү, м•өм»Өмқҳ нҡҢм „ мӨ‘мӢ¬мқ„ кё°мӨҖмңјлЎң н•ҳм—¬ м–•мқҖ к№Ҡмқҙм—җм„ңлҠ” м•өм»ӨмҷҖ м ‘н•ң м§Җл°ҳмқҙ мҲҳлҸҷ нҶ м••мқ„ л°ӣм§Җл§Ң к№ҠмқҖ к№Ҡмқҙм—җм„ңлҠ” м•өм»Өмқҳ нҡҢм „мңјлЎң мқён•ҙ мЈјлҸҷ мғҒнғңм—җ лҶ“мқҙкІҢ лҗңлӢӨ. мқҙмҷҖ к°ҷмқҖ нҳ„мғҒмқҖ нӣ„л©ҙ мҷёлІҪ(Rear outside)м—җм„ңлҸ„ л°ңмғқн•ҳл©° нҡҢм „мӨ‘мӢ¬ліҙлӢӨ к№ҠмқҖ к№Ҡмқҙм—җм„ң мҲҳлҸҷ нҶ м••мқҙ нҳ•м„ұлҗҳм–ҙ (+)л°©н–Ҙмқҳ м§Җл°ҳл°ҳл Ҙмқҙ лӮҳнғҖлӮңлӢӨ. мқҙлҠ” Binch-Hansen л°©лІ•м—җм„ң м ңмӢңн•ң н•ҳмӨ‘мқҙ л‘җл¶Җм—җ мһ¬н•ҳ лҗң л§җлҡқ мЈјліҖмқҳ мқ‘л Ҙ 분нҸ¬мҷҖ мң мӮ¬н•ҳлӢӨ. м•өм»Ө лӮҙмёЎм—җм„ңмқҳ л°ҳл ҘмқҖ мҷёмёЎм—җ 비н•ҳм—¬ нҒ¬м§Җ м•ҠмқҖ к°’мқ„ ліҙмқҙлӮҳ, нҡҢм „ мӨ‘мӢ¬ м•„лһҳмқҳ м „л©ҙ лӮҙлІҪ(Front inside)м—җм„ңлҠ” нӣ„л©ҙ мҷёлІҪкіј лҸҷмқјн•ҳкІҢ мҲҳлҸҷнҶ м••м—җ мқҳн•ң (+)л°©н–Ҙмқҳ м§Җл°ҳл°ҳл Ҙмқҙ лӮҳнғҖлӮңлӢӨ.
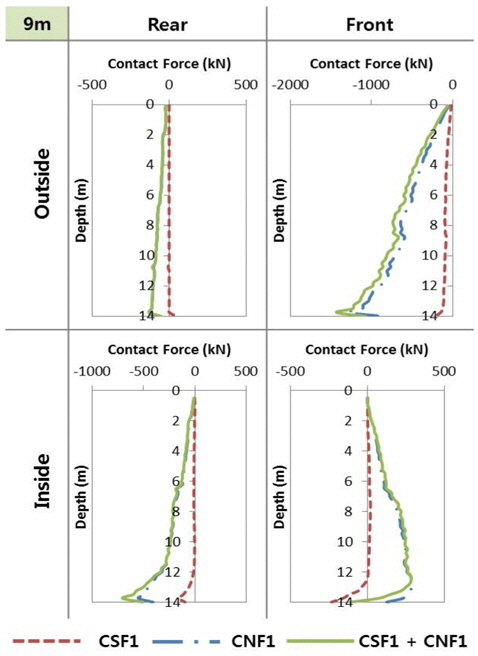
3.4.2 н•ҳмӨ‘ мһ¬н•ҳ мң„м№ҳ 9m (Fig. 13)
мөңлҢҖ мҲҳнҸү м§Җм§Җл Ҙмқҙ л°ңмғқн•ҳлҠ” кІҪмҡ° м „л©ҙ мҷёлІҪ(Front outside) м—җм„ңмқҳ нҶ м••мқҖ м•өм»Ө м „мІҙ кёёмқҙм—җ лҢҖн•ҳм—¬ к№Ҡмқҙм—җ л”°лқј мҰқк°Җн•ҳлҠ” кІҪн–Ҙмқ„ ліҙмқёлӢӨ. мқҙлҠ” н•ҳмӨ‘мқҙ л‘җл¶Җм—җ мһ¬н•ҳ лҗң кІҪмҡ°(3.4.1)м—җ нҡҢм „ мӨ‘мӢ¬мқ„ кё°мӨҖмңјлЎң н•ҳм—¬ м–•мқҖ к№ҠмқҙмҷҖ к№ҠмқҖ к№Ҡмқҙм—җм„ңмқҳ л°ҳл Ҙмқҙ м„ңлЎң лӢӨлҘё л°©н–ҘмңјлЎң нҳ•м„ұлҗң кІғкіјлҠ” лӢӨлҘё 분нҸ¬мқҙлӢӨ. нҡҢм „ мӨ‘мӢ¬мқҳ мң„м№ҳк°Җ м•өм»ӨлЎңл¶Җн„° л©ҖлҰ¬ л–Ём–ҙм ё мһҲм–ҙ нҡҢм „мқҙ кұ°мқҳ л°ңмғқн•ҳм§Җ м•Ҡкі н•ҳмӨ‘ л°©н–ҘмңјлЎң мҲҳнҸү мқҙлҸҷн•ҳлҜҖлЎң м•өм»Өмқҳ м „л©ҙл¶Җмқҳ лӘЁл“ л©ҙм—җ мҲҳлҸҷ нҶ м••мқҙ нҳ•м„ұлҗңлӢӨ. лҳҗн•ң нӣ„л©ҙ мҷёлІҪм—җм„ңлҠ” мЈјлҸҷ нҶ м••мқҙ нҳ•м„ұлҗҳм–ҙ кІ°кіј м ҒмңјлЎң м–‘мёЎ лӘЁл‘җм—җм„ң (вҲ’)л°©н–Ҙмқҳ л°ҳл Ҙмқ„ к°Җм§ҖлҜҖлЎң мөңлҢҖмқҳ м§Җм§Җл Ҙмқҙ лӮҳнғҖлӮңлӢӨ. н•ңнҺё м „л©ҙ лӮҙлІҪм—җм„ңлҠ” м•өм»Ө лӮҙл¶Җмқҳ м§Җл°ҳмқҙ м•өм»ӨмҷҖ н•Ё к»ҳ мқҙлҸҷн•ҳм—¬ (+)л°©н–Ҙмқҳ л°ҳл Ҙмқ„ лӮҳнғҖлӮҙл©° нӣ„л©ҙ лӮҙлІҪ(Rear inside) м—җм„ңлҠ” н•ҳмӨ‘ л°©н–ҘмңјлЎң мӣҖм§ҒмқҙлҠ” м•өм»Өм—җ мқҳн•ҙ лӮҙл¶Җмқҳ м§Җл°ҳкіј лІҪ мІҙ мӮ¬мқҙм—җ м „лӢЁ нҢҢкҙҙл©ҙмқҙ нҳ•м„ұлҗҳм–ҙ (вҲ’)л°©н–Ҙмқҳ м Җн•ӯл Ҙмқ„ к°–лҠ”лӢӨ.
3.4.3 н•ҳмӨ‘ мһ¬н•ҳ мң„м№ҳ 14m (Fig. 14)
м•өм»Ө м„ лӢЁм—җ мҲҳнҸү н•ҳмӨ‘мқҙ мһ‘мҡ©н•ҳлҠ” кІҪмҡ° м•өм»ӨлҠ” л°ҳмӢңкі„ л°©н–Ҙмқҳ нҡҢм „мқ„ ліҙмқёлӢӨ(Fig. 9). мқҙл•Ң, н•ҳмӨ‘мқҙ мһ‘мҡ©н•ҳлҠ” м „л©ҙ мҷёлІҪмқҳ м§Җн‘ң к°Җк№Ңмҡҙ кіім—җм„ңлҠ” м•өм»ӨмҷҖ м§Җл°ҳмӮ¬мқҙм—җ Gapмқҙ нҳ•м„ұлҗҳм–ҙ 분лҰ¬лҗңлӢӨ. к·ё кІ°кіј м „л©ҙ мҷёлІҪм—җм„ңмқҳ Contact forceлҠ” 0м—җ к°Җк№Ңмҡҙ к°’мқҙ лӮҳнғҖлӮҳл©° ліё м—°кө¬м—җм„ңлҠ” м•Ҫ 5m л¶Җк·јк№Ңм§Җ Gapмқҙ нҳ•м„ұлҗң кІғмңјлЎң 분м„қлҗҳм—ҲлӢӨ. мқҙнӣ„ мҲҳлҸҷнҶ м••м—җ мқҳн•ҙ нҳ•м„ұлҗҳлҠ” (вҲ’)л°©н–Ҙмқҳ м Җн•ӯл Ҙмқҙ к№Ҡмқҙм—җ л”°лқј мҰқк°Җн•ҳлҠ” кІҪн–Ҙмқ„ ліҙмқёлӢӨ.
л°ҳл©ҙ л°ҳмӢңкі„ л°©н–ҘмңјлЎң нҡҢм „н•ҳлҠ” м•өм»Өм—җ мқҳн•ҙ нӣ„л©ҙ мҷёлІҪм—җм„ңлҠ” м§Җн‘ңм—җ к°Җк№Ңмҡҙ м–•мқҖ к№Ҡмқҙм—җм„ң мҲҳлҸҷнҶ м••м—җ мқҳн•ң м Җн•ӯл Ҙмқҙ нҳ•м„ұлҗҳм§Җл§Ң м•өм»ӨлҘј л°Җм–ҙлӮҙлҠ” л°©н–Ҙ(+)мңјлЎң мһ‘мҡ©н•ҳлҜҖлЎң м „мІҙ м Җн•ӯл Ҙмқ„ к°җмҶҢмӢңнӮӨлҠ” м—ӯн• мқ„ н•ңлӢӨ. м•өм»Өмқҳ лӮҙмёЎ кұ°лҸҷмқҖ н•ҳмӨ‘мқҙ 9mк№Ҡмқҙм—җ мһ‘мҡ©н•ң кІҪмҡ°мҷҖ мң мӮ¬н•ҳкІҢ лӮҳнғҖлӮҳм§Җл§Ң, л°ҳмӢңкі„ л°©н–Ҙмқҳ нҡҢм „мңјлЎң мқён•ҙ м§Җн‘ң к°Җк№Ңмҡҙ кіім—җм„ңлҠ” м•өм»Өк°Җ н•ҳмӨ‘мқҳ л°©н–Ҙкіј л°ҳлҢҖлЎң мӣҖм§ҒмқҙлҜҖлЎң м§Җл°ҳ л°ҳл Ҙмқҙ нҒ¬кІҢ лӮҳнғҖлӮҳм§Җ м•ҠлҠ”лӢӨ.
3.4.4 м§Җл°ҳ л°ҳл Ҙмқҳ 비көҗ
Fig. 15лҠ” н•ҳмӨ‘ мһ¬н•ҳ мң„м№ҳлі„лЎң м•өм»ӨмҷҖ м§Җл°ҳмқҳ м ‘мҙүл©ҙм—җ мһ‘мҡ©н•ҳлҠ” м—°м§Ғл Ҙ(CNF1)кіј м „лӢЁл Ҙ(CSF1)мқ„ лӘЁл‘җ н•©мӮ°н•ҳм—¬ к№Ҡмқҙм—җ л”°лқј лҸ„мӢңн•ң кІғмқҙлӢӨ. 9m к№Ҡмқҙм—җ н•ҳмӨ‘мқҙ мһ¬н•ҳлҗҳм–ҙ мөңлҢҖ м§Җм§Җл Ҙмқҙ л°ңнҳ„лҗҳлҠ” кІҪмҡ°м—җлҠ” м•һм„ң м„ӨлӘ…н•ң л°”мҷҖ к°ҷмқҙ м „мІҙ к№Ҡмқҙм—җ лҢҖн•ҳм—¬ мҰқк°Җн•ҳлҠ” кІҪн–Ҙмқҳ м§Җл°ҳ л°ҳл Ҙмқҙ нҳ•м„ұлҗңлӢӨ. мқҙл•Ңмқҳ н•ҳмӨ‘ мһ¬н•ҳм җмқ„ мөңм Ғ мң„м№ҳ(Optimal loading depth)лқјкі м •мқҳн•ҳл©ҙ, мөңм Ғмң„м№ҳліҙлӢӨ м–•мқҖ к№Ҡмқҙм—җ н•ҳмӨ‘мқҙ мһ‘мҡ©н•ҳл©ҙ м•өм»Өк°Җ нҡҢм „мқ„ лҸҷл°ҳн•ҳм—¬ мҲҳнҸүмқҙ лҸҷ н•ҳлҜҖлЎң нҡҢм „ мӨ‘ мӢ¬ м•„лһҳм—җм„ңлҠ” л°ҳлҢҖ л°©н–Ҙмқҳ м§Җл°ҳ л°ҳл Ҙмқҙ нҳ•м„ұлҗңлӢӨ. лҳҗн•ң мөңм Ғ мң„м№ҳліҙлӢӨ к№ҠмқҖ к№Ҡмқҙм—җ н•ҳмӨ‘мқҙ мһ‘мҡ©н•ҳл©ҙ м§Җн‘ңл©ҙ л¶Җк·јм—җм„ң м•өм»ӨмҷҖ м§Җл°ҳ мӮ¬мқҙмқҳ GapмңјлЎң мқён•ҙ л°ҳл Ҙк°’мқҙ 0м—җк°Җк№қкІҢ лҗңлӢӨ. мқҙл•Ң м•өм»Өмқҳ м„ лӢЁм—җм„ңмқҳ м ҲлҢҖ к°’мқҖ мөңм Ғ мң„м№ҳмқё 9mм—җ н•ҳмӨ‘мқҙ мһ‘мҡ©н•ң кІҪмҡ°ліҙлӢӨ нҒ° к°’мқ„ к°–м§Җл§Ң м–•мқҖ к№Ҡмқҙм—җм„ңмқҳ лӮ®мқҖ м§Җл°ҳ л°ҳл ҘмңјлЎң мқён•ҙ м „мІҙ м Җн•ӯл Ҙмқҙ к°җмҶҢн•ҳлҠ” мӣҗмқёмқҙ лҗңлӢӨ.
4. кІ° лЎ
ліё л…јл¬ём—җм„ңлҠ” м„ёлҰҪ мӮ¬м§ҲнҶ м§Җл°ҳм—җ м„Өм№ҳлҗң м„қм…ҳ м•өм»Өк°Җ мҲҳнҸүл°©н–Ҙмқҳ н•ҳмӨ‘мқ„ л°ӣлҠ” кІҪмҡ°мқҳ м§Җм§Җл Ҙмқ„ мӮ°м •н•ҳкі мһҗ н•ҳмҳҖлӢӨ. к·№н•ң мҲҳнҸү м§Җм§Җл Ҙм—җ лҢҖн•ң кё°мӨҖмқ„ л§Ҳл Ён•ҳкё° мң„н•ҳм—¬ мқҙлЎ м Ғ л°©лІ•мңјлЎңмҚЁ л„җлҰ¬ нҶөмҡ©лҗҳлҠ” Brinch-hansenл°©лІ•кіј Bromsл°©лІ•мңјлЎң кі„мӮ°н•ҳм—¬ 비көҗн•ҳмҳҖмңјл©°, м•өм»Ө м§ҒкІҪмқҳ 10пј…мқҳ ліҖмң„к°Җ л°ңмғқн•ҳлҠ” кІҪмҡ°мқҳ м Җн•ӯл Ҙмқ„ к·№н•ң мҲҳнҸү м§Җм§Җл ҘмңјлЎң м •мқҳн•ҳмҳҖлӢӨ.
кё°мЎҙмқҳ мқҙлЎ кі„мӮ°мӢқм—җм„ңлҠ” н•ҳмӨ‘мқҙ м•өм»Ө лІҪмІҙлҘј л”°лқј м§ҖмӨ‘м—җ мһ‘мҡ©н•ҳлҠ” кІҪмҡ°лҘј кі л Өн•ҳм§Җ м•ҠмңјлҜҖлЎң, ліё м—°кө¬лҘј нҶөн•ҙ к°Ғ к№Ҡмқҙлі„лЎң н•ҳмӨ‘мқҙ мһ‘мҡ©н• л•Ңмқҳ м§Җм§Җл Ҙмқ„ 3D мң н•ңмҡ”мҶҢлІ• н•ҙм„қ л°©лІ•м—җ мқҳн•ҙ 분м„қн•ҳмҳҖлӢӨ. н•ҳмӨ‘мқҳ мһ¬н•ҳ мң„м№ҳк°Җ к№Ҡм–ҙм§җм—җ л”°лқј мҲҳнҸү м§Җм§Җл Ҙмқҙ мҰқк°Җн•ҳмҳҖмңјл©° м•Ҫ 2/3мқҳ мң„м№ҳм—җм„ң мөңлҢҖк°’мқ„ лӮҳнғҖлғҲлӢӨ. мөңлҢҖмқҳ мҲҳнҸү м Җн•ӯл Ҙмқҙ л°ңнҳ„лҗҳкё° мң„н•ҙм„ңлҠ” нҡҢм „мқҙ кұ°мқҳ л°ңмғқн•ҳм§Җ м•Ҡкі мҲңмҲҳн•ҳкІҢ нҸүн–ү мқҙлҸҷн•ҙм•ј н•ңлӢӨ. мқҙл•Ңмқҳ мҲҳнҸү м Җн•ӯл ҘмқҖ н•ҳмӨ‘мқҙ л‘җл¶Җм—җ мһ‘мҡ©н•ҳлҠ” кІҪмҡ°мҷҖ 비көҗн•ҳм—¬ м•Ҫ 2.5л°° нҒ° к°’мқ„ к°–лҠ”лӢӨ.
м•өм»ӨмҷҖ м§Җл°ҳмқҳ м ‘мҙүл©ҙм—җ нҳ•м„ұлҗҳлҠ” м§Җл°ҳ л°ҳл Ҙмқ„ к№Ҡмқҙм—җ л”°лқј н•©мӮ°н•ҳм—¬ мҲҳнҸү м Җн•ӯл Ҙмқ„ мӮ°м •н• мҲҳ мһҲмңјлҜҖлЎң ліё м—°кө¬м—җм„ңлҸ„ м„ё к°Җм§Җмқҳ м„ңлЎң лӢӨлҘё мЎ°кұҙм—җ лҢҖн•ң к№Ҡмқҙлі„ м§Җл°ҳ л°ҳл Ҙмқ„ 분м„қн•ҳмҳҖмңјл©° нҡҢм „ мЎ°кұҙм—җ мқҳн•ҙ м§Җл°ҳ л°ҳл Ҙмқҳ 분нҸ¬к°Җ лӢ¬лқјм§ҖлҠ” кІғмқ„ нҷ•мқён•ҳмҳҖлӢӨ. мөңлҢҖ м§Җм§Җл ҘмқҖ м•өм»Өк°Җ нҡҢм „ м—Ҷмқҙ нҸүн–ү мқҙлҸҷн• л•Ң, мҲҳлҸҷ л°Ҹ мЈјлҸҷ нҶ м••м—җ мқҳн•ҙ м „л©ҙ(Front side)кіј нӣ„л©ҙ(Rear side)м—җм„ң к№Ҡмқҙм—җ л”°лқј мҰқк°Җн•ҳлҠ” м§Җл°ҳ л°ҳл Ҙмқҙ нҳ•м„ұлҗҳлҠ” кІҪмҡ° лӮҳнғҖлӮ¬лӢӨ. мөңлҢҖ м§Җм§Җл Ҙмқҙ л°ңнҳ„лҗҳлҠ” н•ҳмӨ‘ мһ¬н•ҳ мң„м№ҳмқё мөңм Ғ мң„м№ҳ(Optimal depth)лҘј кё°мӨҖмңјлЎң н•ҳм—¬ м–•мқҖ к№ҠмқҙмҷҖ к№ҠмқҖ к№Ҡмқҙм—җм„ң к°Ғк°Ғ лӢӨлҘё кұ°лҸҷмқ„ ліҙмқҙл©° мөңлҢҖм§Җм§Җл ҘліҙлӢӨ мһ‘мқҖ к°’мқҳ мҲҳнҸү м Җн•ӯл Ҙмқ„ к°Җм§ҖлҜҖлЎң мөңм Ғ мң„м№ҳмқҳ мӮ°м •мқҙ мӨ‘мҡ”н•Ёмқ„ м•Ң мҲҳ мһҲлӢӨ.
мҲҳнҸүн•ҳмӨ‘мқ„ л°ӣлҠ” м•өм»Өмқҳ кұ°лҸҷ л°Ҹ мөңм Ғ н•ҳмӨ‘ мң„м№ҳлҠ” м•өм»Өмқҳ нҳ•мғҒ л°Ҹ м§Җл°ҳ мЎ°кұҙм—җ мқҳн•ң мҳҒн–Ҙмқ„ л°ӣмңјлҜҖлЎң мқҙм—җ лҢҖн•ң 추к°Җм Ғмқё м—°кө¬к°Җ 진н–үлҗҳм–ҙм•ј н• кІғмқҙлӢӨ.