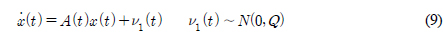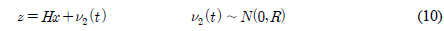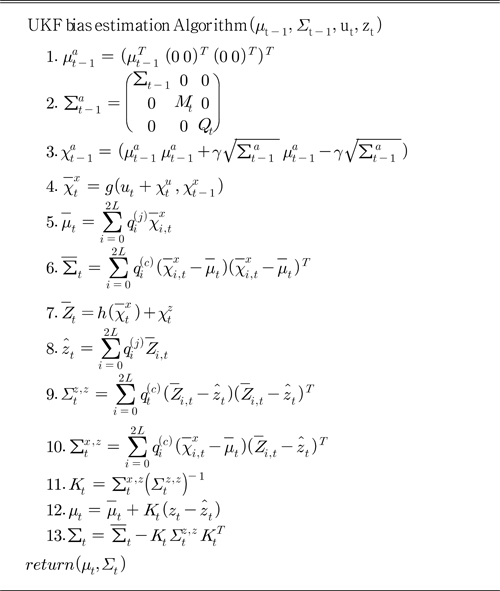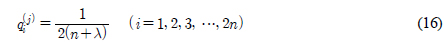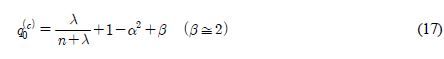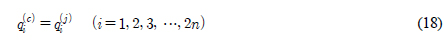Hashmall, J., Deutschmann, J.. (An Evaluation of Attitude-Independent Magnetometer-Bias Determination Methods Flight Mechanics/Estimation Theory Symposium 1996). 169-178.
Kim, E., Bang, H., Yong, K.L., Lee, S.H.. (Three-axis Magnetometer Bias Estimation The Korean Society For Aeronautical And Space Sciences 2006). 818-821.
Ko, N.Y., Choi, H.T., Lee, C.M.. (Navigation of Unmanned Surface Vehicle and Detection of GPS Abnormality by Fusing Multiple Sensor Measurements OCEANS 2016 MTS/IEEE Monterey California USA: 2016). 19-23.
Ko, N.Y., Choi, H.T., Lee, C.M., Moon, Y.S.. (Attitude Estimation Using Depth Measurement and AHRS for Underwater Vehicle Navigation OCEANS 2016 MTS/IEEE Shanghai, China: 2016). 10-13.
Ko, N.Y., Jeong, S.. (Fused Navigation of Unmanned Surface Vehicle and Detection of GPS Abnormality, Institute of Control, Robotics and Systems, 2016). 22(9):723-732 10.5302/J.ICROS.2016.16.0106.

Ko, N.Y., Jeong, S., Bae, Y.. (Sine Rotation Vector Method for Attitude Estimation of an Underwater Robot, Sensors, 2016). 16(8.

Ko, N.Y., Kim, T.G., Choi, H.T.. (Synchronous and Asynchronous Application of a Filtering Method for Underwater Robot Localization, International Journal of Humanoid Robotics, 2015). 13(2.

Thrun, S., Burgard, W., Fox, D.. (Probabilistic Robotics The MIT Press, Massachusetts: 2006). p 220-223.
Troni, G.C., Whitcomb, L.. (Adaptive Estimation of Measurement Bias in Three-Dimensional Field Sensors with Angular-Rate Sensors: Theory and Comparative Experimental Evaluation Robotics: Science and Systems, 2013.
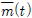 에 편차 b가 더해져 나타난다. 이는 센서좌표계에서 사용되는 식이며 식 (2)는 고정좌표계에서 나타내어진 자기장 벡터의 참값 m0을 구하는 과정이다. 여기서 R(t)은 센서좌표계에서 고정좌표계로의 회전행렬이다. 이를 통해 센서에 의해 측정된 자기장 벡터에서 편차를 빼준 결과에 회전행렬을 곱해줌으로써 고정좌표계에서 나타내어진 자기장 벡터의 참값을 구한다.
에 편차 b가 더해져 나타난다. 이는 센서좌표계에서 사용되는 식이며 식 (2)는 고정좌표계에서 나타내어진 자기장 벡터의 참값 m0을 구하는 과정이다. 여기서 R(t)은 센서좌표계에서 고정좌표계로의 회전행렬이다. 이를 통해 센서에 의해 측정된 자기장 벡터에서 편차를 빼준 결과에 회전행렬을 곱해줌으로써 고정좌표계에서 나타내어진 자기장 벡터의 참값을 구한다.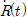 은 식 (4)처럼 표현된다.
은 식 (4)처럼 표현된다.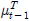 는 시각 t − 1의 추정 상태변수를 뜻한다. 2번 줄의
는 시각 t − 1의 추정 상태변수를 뜻한다. 2번 줄의  는 추정된 상태변수 μt − 1에 대한 오차 공분산 Σt − 1과 예측과정에 대한 오차 공분산 Mt, 그리고 측정값에 대한 오차 공분산 Qt로 이루어져있다. 회전각속도 w는 평균값이 0이고 공분산이 Mt인 가우시안 확률변수(w ~ N(0, Mt)) 이며, 측정값 z는 평균값이 0이고 공분산이 Qt인 가우시안 확률변수(z ~ N(0, Qt))이다.
는 추정된 상태변수 μt − 1에 대한 오차 공분산 Σt − 1과 예측과정에 대한 오차 공분산 Mt, 그리고 측정값에 대한 오차 공분산 Qt로 이루어져있다. 회전각속도 w는 평균값이 0이고 공분산이 Mt인 가우시안 확률변수(w ~ N(0, Mt)) 이며, 측정값 z는 평균값이 0이고 공분산이 Qt인 가우시안 확률변수(z ~ N(0, Qt))이다. 의 요소 개수를 n이라고 하면 2n − 1개 시그마 포인트가 생성된다. 1열의
의 요소 개수를 n이라고 하면 2n − 1개 시그마 포인트가 생성된다. 1열의  는 시그마 포인트 초기 정보이다.
는 시그마 포인트 초기 정보이다. 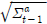 는 2번 줄에서 구한
는 2번 줄에서 구한  을 Cholesky 분해한 결과이다. γ는 다음 식을 통해 구해진다(Rhudy and Gu, 2013).
을 Cholesky 분해한 결과이다. γ는 다음 식을 통해 구해진다(Rhudy and Gu, 2013).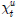 는 3번 줄에서 생성된 회전각속도에 대한 시그마 포인트를 뜻한다. 식 (9)인 상태천이 모델을 4번 줄에 적용한다.
는 3번 줄에서 생성된 회전각속도에 대한 시그마 포인트를 뜻한다. 식 (9)인 상태천이 모델을 4번 줄에 적용한다.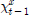 는 시그마 포인트에서 추정 상태변수만으로 구성된다. Δt는 t시각과 t − 1시각의 차이를 뜻한다. 식 (14)에서 A(t)는 식 (5)에서 사용한 반대칭 행렬 S(w)로 구성된 행렬이며 S(w)는 회전 각속도 벡터 ut로 구성된다.
는 시그마 포인트에서 추정 상태변수만으로 구성된다. Δt는 t시각과 t − 1시각의 차이를 뜻한다. 식 (14)에서 A(t)는 식 (5)에서 사용한 반대칭 행렬 S(w)로 구성된 행렬이며 S(w)는 회전 각속도 벡터 ut로 구성된다.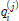 )을 통해 평균을 구한다.
)을 통해 평균을 구한다.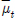 에 대한 오차공분산을 구한다. 오차 공분산을 구할 때 사용되는 가중치 (
에 대한 오차공분산을 구한다. 오차 공분산을 구할 때 사용되는 가중치 (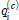 )는 다음과 같다.
)는 다음과 같다.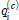 과
과 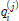 는 i = 1, 2, 3, ···, 2n에 대하여 동일하다. 본 논문에서 추정 상태변수
는 i = 1, 2, 3, ···, 2n에 대하여 동일하다. 본 논문에서 추정 상태변수 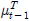 의 요소는 6개이며
의 요소는 6개이며  는 6×6 크기의 행렬이 된다.
는 6×6 크기의 행렬이 된다.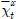 에서 자기장 벡터만을 사용하게 되어 측정값에 대한 시그마 포인트들이 생성된다. 8번 줄은 측정값에 대한 시그마 포인트들의 평균을 구한다. 9번 줄은 8번 줄의 측정값에 대한 시그마 포인트의 평균에 대한 오차공분산을 구한다. 8,9줄 모두 5,6줄과 동일한 방법으로 구해지며 측정값으로 사용되는 자기장 벡터는 3개이므로
에서 자기장 벡터만을 사용하게 되어 측정값에 대한 시그마 포인트들이 생성된다. 8번 줄은 측정값에 대한 시그마 포인트들의 평균을 구한다. 9번 줄은 8번 줄의 측정값에 대한 시그마 포인트의 평균에 대한 오차공분산을 구한다. 8,9줄 모두 5,6줄과 동일한 방법으로 구해지며 측정값으로 사용되는 자기장 벡터는 3개이므로 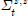 는 3×3 행렬이다.
는 3×3 행렬이다. 는 6×6 행렬이며
는 6×6 행렬이며 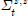 는 3×3 행렬이므로 연산의 결과는
는 3×3 행렬이므로 연산의 결과는 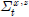 는 6×3 행렬이 된다. 11번 줄은 칼만 이득을 구하는 과정이다.
는 6×3 행렬이 된다. 11번 줄은 칼만 이득을 구하는 과정이다.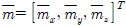 를 사용한다. 마지막으로 추정한 자세 정보와 DVL(Doppler velocity log)센서 정보를 사용하여 추측항법을 사용하여 위치를 추정한다.
를 사용한다. 마지막으로 추정한 자세 정보와 DVL(Doppler velocity log)센서 정보를 사용하여 추측항법을 사용하여 위치를 추정한다.