1. žĄú Ž°†
žąėž§Ď ž§ĎžěĎžóÖžö© ROV(Remotely operated vehicle)žĚė ž£ľžöĒ ÍĶ¨ŽŹôŽ∂ÄŽäĒ žú†žēēžčúžä§ŪÖúžúľŽ°ú žĚīŽ£®žĖīžßĄŽč§(
Lee et al., 2015). žú†žēēžčúžä§ŪÖúžĚī ÍįÄžßÄŽäĒ ŽÜížĚÄ ž∂úŽ†• Ūö®žú®žĚī žąėž§Ď žľÄžĚīŽłĒ Žß§žĄ§Í≥ľ ÍįôžĚÄ ŪĀį Ūēėž§ĎžĚĄ žöĒŪēėŽäĒ žěĎžóÖžóź ž†ĀŪē©ŪēėÍłį ŽēĆŽ¨łžĚīŽč§. ŪēėžßÄŽßĆ žú†žēēžčúžä§ŪÖúžĚÄ žě†žě¨ž†ĀžúľŽ°ú ŽąĄžú† Í≥†žě•žĚė ÍįÄŽä•žĄĪžĚĄ žßÄŽčąÍ≥† žěąžúľŽ©į žĚīŽäĒ žčúžä§ŪÖúžĚė žė§ŽŹôžěϞ̥ žĚľžúľŪā§ŽäĒ ž£ľžõźžĚłžĚī ŽźúŽč§. ŪäĻŪěą, žú°žēąžúľŽ°ú žčĚŽ≥ĄžĚī Ž∂ąÍįÄŽä•Ūēú ŽāīŽ∂Ä ŽąĄžú†ŽäĒ ŽįúžÉĚ žßĀŪõĄ Ž≥Ą Žč§Ž•ł žĚīžÉĀ žßēŪõĄŽ•ľ Ž≥īžĚīžßÄ žēäÍłį ŽēĆŽ¨łžóź Žį©žĻėŽź† ÍįÄŽä•žĄĪžĚī Žß§žöį ŽÜíŽč§. Žßƞ̾ žąėž§Ď žěĎžóÖ ž§Ď ŽąĄžú† Í≥†žě•žĚī Žį©žĻėŽźėžĖī žÉĀŪėł žóįÍ≤įŽźú ž£ľŽ≥Ä žú†žēē žě•ŽĻĄžĚė žĚīžÉĀŽŹôžěϞ̥ žú†ŽįúŪēúŽč§Ž©ī ž£ľžĖīžßĄ žěĄŽ¨īžóź žč§ŪĆ®Ūē† ŽŅź žēĄŽčąŽĚľ žĚłžĖĎ ŪõĄ žā¨ŪõĄž≤ėŽ¶¨Ž•ľ žúĄŪēú ŽÜížĚÄ ŽĻĄžö©žĚī ŽįúžÉĚŪē† žąė žěąŽč§.
ŽąĄžú†ŽäĒ žč§Ž¶įŽćĒ ŽāīŽ∂ÄžĚė ŪĒľžä§ŪܧÍ≥ľ ÍįôžĚī ŽŹôž†Ā žõÄžßĀžěĄžĚī ŽĻąŽ≤ąŪēú Í≥≥žóźžĄú ž£ľŽ°ú žĚľžĖīŽāúŽč§. žč§Ž¶įŽćĒ ŽāīŽ≤ĹÍ≥ľ ŪĒľžä§Ūܧ žā¨žĚīžĚė žú†ŽßȞ̥ ŪÜĶŪēī žěźžóį ŽįúžÉĚŪēėÍłįŽŹĄ ŪēėžßÄŽßĆ žěĎŽŹôžú† žė§žóľžóź žĚėŪēú ŪĒľžä§Ūܧ žč§(Seal) žÜźžÉĀžĚī žĚīžÉĀ ŽąĄžú†Ž•ľ žú†ŽįúŪē† ÍįÄŽä•žĄĪŽŹĄ žěąŽč§. ŽąĄžú†Ž•ľ žßĀž†Ď Í≥Ąžł°Ūē† žąėŽäĒ žóÜžúľŽāė Ž™®Žćł ÍłįŽįėžĚė ŪēīžĄĚž†Ā Žį©Ž≤ēžĚĄ žā¨žö©ŪēėŽ©ī žł°ž†ē ÍįÄŽä•Ūēú žēēŽ†•, Ž°úŽďú(Rod) žĚīŽŹôÍĪįŽ¶¨ŽďĪžĚė žĄľžĄú žč†ŪėłŽ•ľ ŪĒľŽďúŽįĪ ŽįõžēĄ žÉĀŪÉúž∂Ēž†ēžĚī ÍįÄŽä•ŪēėŽč§. Ž™®Žćł ÍłįŽįė Í≤Äž∂ú ÍłįŽ≤ēžĚÄ žÉĀŪÉúž∂Ēž†ēžė§žį®Ž°úŽ∂ÄŪĄį žó¨Ž∂Ą(Residual)žĚĄ žÉĚžĄĪŪēėÍ≥† ž†Āž†ąŪēú ŪĆźŽč® ŽÖľŽ¶¨žóź žĚėŪēī Í≥†žě•žĚĄ Í≤Äž∂úŪēėŽäĒ Žį©Ž≤ēžúľŽ°ú žĚīŽĮł ŽßéžĚÄ žóįÍĶ¨žóźžĄú Í∑ł žĄĪŽä•žĚī žěÖž¶ĚŽźėžóąŽč§(
Guo et al., 2009;
Jee et al., 2012;
Liu et al., 2005;
Wang et al., 2007).
žĶúÍ∑ľ žčúžä§ŪÖú žēąž†ēžĄĪ ŪôēŽ≥ī ŽįŹ žú†žßÄ Ž≥īžąėŽ•ľ žúĄŪēú ŽĻĄžö© ž†ąÍįźžĚė ŪēĄžöĒžĄĪžĚī ŽĆÄŽĎźŽź®žóź ŽĒįŽĚľ ŽąĄžú† Í≤Äž∂úžĚĄ žúĄŪēú Ž™®Žćł ÍłįŽįė žóįÍĶ¨ÍįÄ ŪĀ¨Í≤Ć ž£ľŽ™©žĚĄ ŽįõÍ≥† žěąŽč§(
Yao et al., 2014). žú†žēēžč§Ž¶įŽćĒžĚė ÍįēžĚł ž†úžĖīÍłį žĄ§Í≥Ą ÍłįŽ≤ēžóź ŽĆÄŪēú žóįÍĶ¨ŽäĒ Žč§žĖĎŪēú Ž∂ĄžēľžóźžĄú žąėŪĖČŽźėžóąžúľŽāė ÍīÄžł°Íłį ÍłįŽįė Í≥†žě• Í≤Äž∂úÍ≥ľ ÍįôžĚÄ Ž™®Žćł ÍłįŽįėžĚė žÉĀŪÉú ž∂Ēž†ē ÍłįŽ≤ē žóįÍĶ¨ŽäĒ Í∑ł ž§ĎžöĒžĄĪžóźŽŹĄ Ž∂ąÍĶ¨ŪēėÍ≥† žēĄžßĀ ÍįúŽįúžĚī ŽßéžĚī žĚīŽ£®žĖīžßÄžßÄ žēäžēėŽč§(
Alleyne and Liu, 2000;
Yao et al., 1998;
Yao et al., 2000).
žú†žēēžč§Ž¶įŽćĒŽäĒ T‚ÄĒS ŪćľžßÄžčúžä§ŪÖúžúľŽ°ú Ž™®ŽćłŽßĀ ÍįÄŽä•ŪēėŽč§. T‚ÄĒS ŪćľžßÄžčúžä§ŪÖúžĚÄ ŪćľžßÄ Í∑úžĻôžĚė ŪõĄŽįėŽ∂ÄÍįÄ ÍĶ≠Ž∂Äž†Ā žĄ†Ūėē Žį©ž†ēžčĚžúľŽ°ú Íłįžą†ŽźėŽäĒ IF‚ÄĒTHEN Í∑úžĻôŽď§žĚė žĽ®Ž≤°žä§ ž°įŪē©žúľŽ°ú žčúžä§ŪÖú ž†Ąžó≠ ŽŹôŪäĻžĄĪžĚĄ ŽāėŪÉÄŽāłŽč§. T‚ÄĒS ŪćľžßÄ Ž™®ŽćłžĚĄ žā¨žö©ŪēėŽ©ī žĄ†Ūėē ÍīÄžł°Íłį žĄ§Í≥Ą ÍłįŽ≤ēžĚĄ žú†žēēžč§Ž¶įŽćĒžôÄ ÍįôžĚÄ Ž≥Ķžě°Ūēú ŽĻĄžĄ†Ūėē žčúžä§ŪÖúžóź ž†Āžö©Ūē† žąė žěąŽč§. ŪäĻŪěą Ū鳎°úŽďú žč§Ž¶įŽćĒ Ž™®ŽćłžĚÄ žĖĎŽ°úŽďú žč§Ž¶įŽćĒ Ž™®Žćłžóź ŽĻĄŪēėžó¨ žčúžä§ŪÖú žį®žąėÍįÄ ŽÜížēĄ ŪėēŪÉúÍįÄ Ž≥Ķžě°ŪēėžßÄŽßĆ T‚ÄĒS ŪćľžßÄ Ž™®ŽćłžĚĄ žā¨žö©ŪēėŽ©ī IF‚ÄĒTHEN Í∑úžĻôžĚė ž†ĄŽįėŽ∂Ä Ž≥ÄžąėŽ•ľ ŪēėŽāė ž∂ĒÍįÄŪē®žúľŽ°úžć® žčúžä§ŪÖúžĚė ŪĎúŪėĄžĚī ÍįÄŽä•ŪēėŽč§.
žú†žēēžč§Ž¶įŽćĒžĚė ŽāīŽ∂Ä ŽąĄžú†ŽäĒ žē°žłĄžóźžĚīŪĄį Žį©ž†ēžčĚžĚė žÉĀŪÉúŽ≥Äžąėžóź žßĀž†Ďž†ĀžúľŽ°ú žėĀŪĖ•žĚĄ ŽĮłžĻėŽäĒ Í≥ĪŪėē(Multiplicative form) Í≥†žě•žúľŽ°ú Ž™®ŽćłŽßĀŽźúŽč§. Í≥†žě•žóź ŽĆÄŪēú žó¨Ž∂ĄžĚė ŽĮľÍįźŽŹĄŽ•ľ ŽāėŪÉÄŽāīŽäĒ
H- žĄĪŽä•žĚĄ ž†úžčúŪēėÍłįŽäĒ žĖīŽ†§žöįŽāė žôłŽěÄžóź ŽĆÄŪēú
H‚ąě žĄĪŽä•žĚĄ ÍįĖŽŹĄŽ°Ě ÍīÄžł°ÍłįŽ•ľ žĄ§Í≥ĄŪē®žúľŽ°úžć® Í≥†žě•žóź ŽĆÄŪēú žÉĀŽĆÄž†Ā ŽĮľÍįźŽŹĄŽ•ľ ŽÜížĚľ žąė žěąŽč§. ÍīÄžł°ÍłįžĚė
H‚ąě žĄĪŽä•žĚĄ ÍłįŽįėžúľŽ°ú ŪĆźŽč® ŽÖľŽ¶¨Ž•ľ ž†Āžö©ŪēėŽ©ī Í≥†žě• Í≤Äž∂úžĚī ÍįÄŽä•ŪēėŽč§(
Jee et al., 2016).
Ž≥ł ŽÖľŽ¨łžĚÄ žú†žēē žč§Ž¶įŽćĒžĚė ŽāīŽ∂Ä ŽąĄžú† Í≤Äž∂úžĚĄ žúĄŪēú ÍīÄžł°Íłį žĄ§Í≥Ą Ž¨łž†úŽ•ľ Žč§Ž£¨Žč§. ÍīÄžł°Íłį žĄ§Í≥ĄŽ•ľ žúĄŪēī Ž≥Ķžě°Ūēú ŽĻĄžĄ†Ūėē Žį©ž†ēžčĚžúľŽ°ú ŪĎúŪėĄŽźėŽäĒ Ū鳎°úŽďú(Single-rod) žč§Ž¶įŽćĒŽ•ľ 5žį®žĚė T‚ÄĒS ŪćľžßÄ Ž™®ŽćłŽ°ú ŪĎúŪėĄŪēėŽ©į ŪĒľžä§Ūܧ žč§ žÜźžÉĀžóź žĚėŪēī ŽįúžÉĚŪēėŽäĒ žĚīžÉĀ ŽąĄžú†Ž•ľ Í≥ĪŪėē Í≥†žě•žúľŽ°ú Ž™®ŽćłŽßĀŪēúŽč§. ÍīÄžł°Íłį žĄ§Í≥Ą ž°įÍĪīžĚÄ žĄ†ŪėēŪĖČŽ†¨Ž∂ÄŽďĪžčĚ ŪėēŪÉúŽ°ú ŽāėŪÉÄŽāīŽ©į ž†úžēąŪēú ÍīÄžł°ÍłįžĚė Í≤Äž∂ú žĄĪŽä•Í≥ľ ÍįēžĚł ž∂ĒžĘÖ žĄĪŽä•žĚĄ Í≤Äž¶ĚŪēėÍłį žúĄŪēī Ž™®žĚėžč§ŪóėžĚĄ Ž≥īžĚłŽč§.
Ž≥ł ŽÖľŽ¨łžĚÄ ŪĎúž§Ä ŪĎúÍłįŽ≤ēžĚĄ ŽĒįŽ•łŽč§.
X =
XT< 0ŽäĒ žĚĆŪēúž†ē ŪĖČŽ†¨žĚĄ žĚėŽĮłŪēúŽč§. žěĄžĚėžĚė Ž≤°ŪĄį
xk‚ąą‚ĄĚ
n,
k‚ąą{1, ...,
K}žóź ŽĆÄŪēėžó¨

ŽäĒ žú†ŪĀīŽ¶¨ŽĒĒžēą ŽÜąžĚĄ žĚėŽĮłŪēėŽ©į

ŽäĒ
l2 ŽÜąžĚĄ žĚėŽĮłŪēúŽč§. *ŽäĒ ŽĆÄžĻ≠ŪĖČŽ†¨žĚė ŽĆÄÍįĀ ž†ĄžĻėžöĒžÜĆžĚīŽč§.
2. Ū鳎°úŽďú žú†žēēžč§Ž¶įŽćĒ
Fig. 1žĚÄ Ū鳎°úŽďú žč§Ž¶įŽćĒžôÄ žõÄžßĀžĚīŽäĒ žąėŽ†ąŽ°ú ŪĎúŪėĄŽźėŽäĒ Ž∂ÄŪēėžßąŽüȞ̥ ŽŹĄžčĚŪôĒŪēėžó¨ ŽāėŪÉÄŽāł Í≤ÉžĚīŽč§. Í∑łŽ¶ľžóźžĄú žēĆ žąė žěąŽďĮžĚī Ž∂ÄŪēėžßąŽüČžĚÄ Ž°úŽďúžĚė žöįžł° ŽĀĚŽč®žóź žěąÍ≥† žč§Ž¶įŽćĒ žĘĆžöį žĪĒŽ≤ĄžóźžĄú ŪĒľžä§ŪܧžĚĄ ŽįÄžĖīŽāīŽäĒ ŪěėžĚė žį®žĚīžóź žĚėŪēī žõÄžßĀžĚłŽč§. Ž∂ÄŪēėžßąŽüČžĚÄ ÍįĀ žĪĒŽ≤Ąžóź ÍĪłŽ¶¨ŽäĒ žēēŽ†•, ž†ĎžīČ ŽßąžįįŽ†•, ŽąĄžú† ŽďĪžĚė žėĀŪĖ•žĚĄ ŽįõŽäĒŽč§. žú†žēēžč§Ž¶įŽćĒ ŽŹôž†Ā Ž™®ŽćłžĚė ÍįĄŽč®Ūēú ŪĎúŪėĄÍ≥ľ žąėžčĚ ž†ĄÍįúžĚė ŪéłžĚėŽ•ľ žúĄŪēī Žč§žĚƞ̥ ÍįÄž†ēŪēúŽč§.
Fig. 1
Single-rod cylinder

ÍįÄž†ē 1 (
Jee et al., 2015): Ū鳎°úŽďú žú†žēēžč§Ž¶įŽćĒ Ž™®ŽćłŽßĀžĚĄ žúĄŪēī Žč§žĚƞ̥ ÍįÄž†ēŪēúŽč§.
(1) Fig. 1žĚė Ž∂ÄŪēėžßąŽüČ mžĚÄ Ž≥ÄŪēėžßÄ žēäŽäĒ žÉĀžąėžĚīŽč§.
(2) žč§Ž¶įŽćĒžĚė ÍįĀ žĪĒŽ≤Ąžóź žěĎžö©ŪēėŽäĒ žú†ŽüČžĚė žú†žěÖ, Ū܆ž∂ú ž†úžĖī žěÖŽ†•žĚÄ 0žĚīŽč§.
(3) Ž°úŽďú žč§ žÜźžÉĀžóź ÍłįžĚłŪēú žôłŽ∂Ä ŽąĄžú†ŽäĒ ŽįúžÉĚŪēėžßÄ žēäŽäĒŽč§.
(4) žú†ŽßȞ̥ Í≤ĹÍ≥ĄŽ°ú ž†ĎžīČŪēú ŪĒľžä§ŪܧÍ≥ľ žč§Ž¶įŽćĒžĚė ŪĎúŽ©ī ÍĪįžĻ†ÍłįŽäĒ žĚľž†ēŪēėŽč§.
(5) žěĎŽŹôžú†žĚė ž≤īž†ĀŪÉĄžĄĪŽ•†žĚÄ Ž≥ÄŪēėžßÄ žēäŽäĒ žÉĀžąėžĚīŽč§.
žó¨ÍłįžĄú, ž≤®žěź 1Í≥ľ 2ŽäĒ ÍįĀÍįĀ žč§Ž¶įŽćĒ ŽāīŽ∂ÄžĚė žĘĆ, žöį žĪĒŽ≤ĄŽ•ľ žĚėŽĮłŪēúŽč§.
m[kg]‚ąą‚ĄĚ
>0žĚÄ Ž∂ÄŪēėžßąŽüČ
xL[m]‚ąą‚ĄĚžĚÄ ŪĒľžä§Ūܧ žĚīŽŹô ÍĪįŽ¶¨,
a[m
2]‚ąą‚ĄĚ
>0 žěĎŽŹôžú†žôÄ ž†ĎžīČŪēú Žě® Žč®Ž©īž†Ā ŪĀ¨Íłį,
p[N/m
2]‚ąą‚ĄĚ
>0ŽäĒ ÍįĀ žĪĒŽ≤ĄžĚė ŽāīŽ∂Ä žēēŽ†•,
b[kg/s]‚ąą‚ĄĚ
>0ŽäĒ ž†źžĄĪ Žßąžįį Í≥Ąžąė,
ŌČ[N]‚ąą‚ĄĚŽ™®ŽćłŽßĀ ŽźėžßÄ žēäŽäĒ žú†Í≥ĄŽźú ŽĻĄžĄ†ŪėēžĄĪÍ≥ľ žôłŽěÄ,
v[m
3]‚ąą‚ĄĚ
>0ÍįĀ žĪĒŽ≤ĄžĚė Ž∂ÄŪĒľ,
ő≤[N/m
2]‚ąą‚ĄĚ
>0ŽäĒ ž≤īž†ĀŪÉĄžĄĪŽ•†,
ln,
lf [m
5/Ns]‚ąą‚ĄĚ
>0ŽäĒ ÍįĀ žĪĒŽ≤ĄžĚė žēēŽ†•žį®žóź žĚėŪēī ŽįúžÉĚŪēėŽäĒ Í≥ĶžĻ≠ ŽąĄžú† Í≥ĄžąėžôÄ žĚīžÉĀ ŽąĄžú† Í≥ĄžąėžĚīŽč§.
őī[N]‚ąą‚ĄĚŽäĒ Žč§žĚĆÍ≥ľ ÍįôžĚī ŽĻĄžĄ†Ūėē Žį©ž†ēžčĚžúľŽ°ú ŪĎúŪėĄŽźėŽäĒ LuGre ŽßąžįįŽ†•žĚīŽč§(
Yao et al., 2014).
žó¨ÍłįžĄú,
FC[N]‚ąą‚ĄĚ
>0,
FS[N]‚ąą‚ĄĚ
>0ŽäĒ ÍįĀÍįĀ žŅ®Ž°Ī ŽßąžįįŽ†•, ž†ēžßÄ ŽßąžįįŽ†•žĚīŽ©į sgn(‚ąô)žĚÄ Ž∂ÄŪėł Ūē®žąė,
vs[m/s]‚ąą‚ĄĚ
>0ŽäĒ Stribeck žÜ掏ĄžĚīŽč§. žčĚ (2)žĚė žÜ掏Ą‚ÄĒŽßąžįįŽ†•žĚė ÍīÄÍ≥ĄŽ•ľ
Fig. 2žôÄ ÍįôžĚī ŽāėŪÉÄŽāľ žąė žěąŽč§.
Fig. 2
Velocity‚ÄĒFriction Plot of LuGre Model (FS = 78, FC = 52, vs = 0.5)
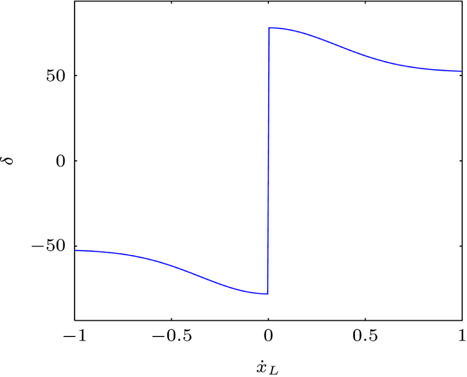
žč§Ž¶įŽćĒžĚė žÉĀŪÉú ž∂Ēž†ēžĚĄ žúĄŪēú žąėžĻė ŪēīžĄĚž†Ā žóįžāį žÜ掏ĄŽäĒ Ž≥ÄžąėŽď§žĚė ŪĀ¨Íłį Ž≥ÄŪôĒžóź žĚėž°īž†ĀžĚīŽč§. žóįžāį žÜ掏ĄžĚė ÍįúžĄ†žĚĄ žúĄŪēī Žč§žĚĆÍ≥ľ ÍįôžĚÄ žä§žľÄžĚľ Ž≥ÄŪôėŽźú žÉąŽ°úžöī Ž≥ÄžąėŽ•ľ ž†ēžĚėŪēúŽč§.
žó¨ÍłįžĄú,
s‚ąą‚ĄĚ
>0ŽäĒ ž†Āž†ąŪēú ŪĀ¨ÍłįžĚė žä§žľÄžĚľŽßĀ ŪĆ©ŪĄį,
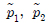
ŽäĒ
p1,
p2žĚė žä§žľÄžĚľ Ž≥ÄŪôėŽźú ÍįížĚīŽč§. žÉĀŪÉúŽ≥Äžąė
xŽ•ľ Žč§žĚĆÍ≥ľ ÍįôžĚī ž†ēžĚėŪēėžěź.
ÍįĀ žĪĒŽ≤ĄžĚė Ž∂ÄŪĒľŽäĒ ÍĪįŽ¶¨Ž≥ÄŪôĒžóź žĚėž°īž†ĀžĚł Ž≥ÄžąėžĚīŽč§. ŪĒľžä§ŪܧžĚė žīąÍłį žúĄžĻė x1 = 0 žóźžĄú žĘĆ, žöį žĪĒŽ≤ĄžĚė Ž∂ÄŪĒľŽ•ľ ÍįĀÍįĀ v1, v2 ŽĚľÍ≥† ŪēúŽč§Ž©ī žĚīŽŹô ÍĪįŽ¶¨žóź ŽĒįŽ•ł ÍįĀ žĪĒŽ≤ĄžĚė Ž∂ÄŪĒľŽäĒ v1 = v10 + a1x1, v2= v20 - a2x1žĚī ŽźúŽč§. žčĚ (1)žĚÄ Žč§žĚĆÍ≥ľ ÍįôžĚÄ 4žį®žĚė žÉĀŪÉúŽį©ž†ēžčĚžúľŽ°ú žďł žąė žěąŽč§.
ŽßąžįįŽ†• ž∂Ēž†ēžĚĄ žúĄŪēī őī(x2)Ž•ľ x5Ž°ú žĻėŪôėŪēėÍ≥† žÉĀŪÉúÍ≥ĶÍįĄŽį©ž†ēžčĚžóź ŽßąžįįŽ†• ŽŹôžó≠ŪēôžĚĄ ŪŹ¨Ūē®ŪēúŽč§. žčĚ (2)Ž•ľ ŽĮłŽ∂ĄŪēėŽ©ī Žč§žĚĆÍ≥ľ ÍįôžĚÄ x5ŽŹôžó≠ŪēôžĚĄ žĖĽžĚĄ žąė žěąŽč§.
žúĄ ŽĮłŽ∂ĄŽį©ž†ēžč̞󟞥ú ž†ēžßÄ žÉĀŪÉú(x2 = 0)žóźžĄúžĚė Žßąžįį ŽŹôžó≠ŪēôžĚÄ ž†ēžĚėŽźėžßÄ žēäŽäĒŽč§. žč§ž†úŽ°ú ž†ēžßÄŽßąžįįŽ†•žĚÄ ÍįÄŪēīžßÄŽäĒ žôłŽ†•žóź ŽĒįŽĚľ Ž≥ÄŪēėŽĮÄŽ°ú ŪēėŽāėžĚė ÍįížúľŽ°ú ž†ēžĚėŪē† žąė žóÜŽč§. žÉĀŪÉúž∂Ēž†ēžĚĄ žúĄŪēú žąėžĻė ŪēīžĄĚž†Ā žóįžāįŽüČžĚÄ x2ÍįÄ 0žĚĄ žßÄŽā† ŽēĆ Žß§žöį ŽÜížúľŽ©į žĚīŽäĒ žč§žčúÍįĄ ÍīÄžł°žĚĄ žĖīŽ†ĶÍ≤Ć ŽßƎč§. ŪēėžßÄŽßĆ x2 ‚Čą 0 ŽēĆžĚė žßßžĚÄ žĄ†ŪėēŽŹôžěĎ žėĀžó≠žĚĄ ÍįÄž†ēŪēėŽ©ī ŪēīžĄĚžĚī žö©žĚīŪē† ŽŅź žēĄŽčąŽĚľ žč§ž†ú žč§Ūóėžóź ž†Āžö©ŪēėŽćĒŽĚľŽŹĄ žė§žį®ÍįÄ ÍĪįžĚė ŽįúžÉĚŪēėžßÄ žēäŽäĒŽč§. Žß§žöį žěĎžĚÄ ŪēúÍ≥Ą žÜ掏Ą vth [m/s] ‚ąą ‚ĄĚ>0Ž•ľ žĄ§ž†ēŪēėÍ≥† |x2| ‚ȧ vth žĚł Í≤Ĺžöįžóź ŽĆÄŪēėžó¨ žĄ†Ūėē ŽŹôžěĎ žėĀžó≠žĚĄ ÍįÄž†ēŪēėŽ©ī žčĚ (4)ŽäĒ Žč§žĚĆÍ≥ľ ÍįôžĚÄ žĄ†ŪėēŽŹôžěĎ žėĀžó≠žĚĄ ŪŹ¨Ūē®ŪēėŽäĒ ŽŹôžó≠ŪēôžúľŽ°ú Žč§žčú žďł žąė žěąŽč§.
žó¨ÍłįžĄú,
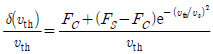
žĚīŽ©į
x2 -
x5 ŪŹČŽ©īžóźžĄúžĚė žĄ†Ūėē ÍłįžöłÍłį ÍįížĚīŽč§. žĚīž†ú žčĚ (3)Í≥ľ (5)Ž°úŽ∂ÄŪĄį Žč§žĚĆÍ≥ľ ÍįôžĚÄ 5žį® žÉĀŪÉúÍ≥ĶÍįĄŽį©ž†ēžč̞̥ žú†ŽŹĄŪē† žąė žěąŽč§.
žó¨ÍłįžĄú
žĚīŽč§.
Ž≥Ķžě°Ūēú ŪėēŪÉúžĚė ŽĻĄžĄ†Ūėē Žį©ž†ēžčĚ (6)žóźžĄú x3, x4, x5, ŽŹôžó≠ŪēôžĚÄ ÍįĀÍįĀ žĄ†ŪėēŽį©ž†ēžčĚžĚė ŽĻĄžĄ†Ūėē Í≤įŪē© ŪėēŪÉúŽ•ľ ÍįĞߥŽč§. T‚ÄĒS ŪćľžßÄ Ž™®ŽćłžĚĄ žā¨žö©ŪēėŽ©ī žĚīŽü¨Ūēú ŪėēŪÉúžĚė ŽĻĄžĄ†Ūėē Ūē®žąėŽ•ľ ž†ĄŽįėŽ∂Ä Í∑úžĻôžóź ŽĒįŽ•ł ÍĶ≠Ž∂Äž†Ā žĄ†Ūėē žėĀžó≠žúľŽ°ú ŽāėŽąĄžĖī Íłįžą†Ūē† žąė žěąžúľŽ©į ÍįĀÍįĀžĚė žĄ†Ūėē ŽŹôžěĎ žėĀžó≠žóźžĄú ŽŹôžěĎ ÍįÄŽä•Ūēú ÍīÄžł°ÍłįŽ•ľ žĄ§Í≥ĄŪēėŽ©ī žĚīŽď§žĚė žĽ®Ž≤°žä§ ž°įŪē©žúľŽ°ú ŪĎúŪėĄŽźėŽäĒ ŽĻĄžĄ†Ūėē ž†Ąžó≠žčúžä§ŪÖúžĚė žÉĀŪÉúž∂Ēž†ēžĚī ÍįÄŽä•ŪēėŽč§. žčĚ (6)žĚÄ ž†ĄŽįėŽ∂Ä Ž≥ÄžąėŽď§ z1‚ąą[z11, z12], z2‚ąą[z21, z22], z3‚ąą[z31, z32], z4‚ąą[z41, z42]žóź ŽĆÄŪēėžó¨ žīĚ 16(24)ÍįúžĚė Í∑úžĻôžĚĄ ÍįÄžßÄŽäĒ ŪćľžßÄ Ž™®ŽćłŽ°ú ŪĎúŪėĄ ÍįÄŽä•ŪēėŽč§. Žč§žĚĆ ŪćľžßÄ Ž™®ŽćłžĚė p‚ąą{1.2...,16}Ž≤ąžßł Í∑úžĻôžĚĄ Ž≥īžěź.
žó¨ÍłįžĄú, ž≤®žěź Í∑úžĻô Ž≤ąŪėł
pžóź ŽĆÄžĚĎŪēėŽäĒ ž≤®žěźŽď§
i,
j,
k,
l žĚÄ
Table 1Í≥ľ ÍįôžúľŽ©į
Table 1
Indices of fuzzy rules
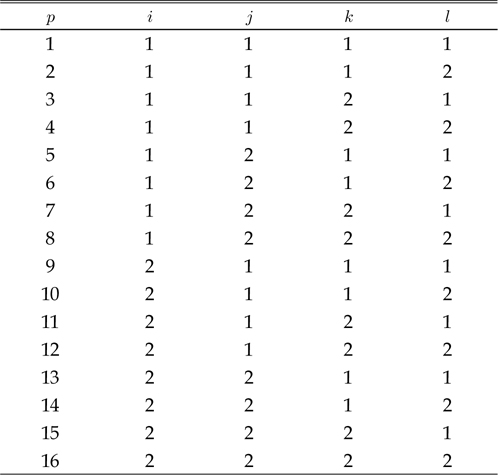
žĚīŽč§. žčĚ (6)Í≥ľ ŽďĪÍįĞ̳ ŽĻĄŪćľžßÄŪôĒŽźú ž†Ąžó≠ ŽŹôŪäĻžĄĪžĚÄ Žč§žĚĆÍ≥ľ ÍįôžĚī Íłįžą†Ūē† žąė žěąŽč§.
žó¨ÍłįžĄú
žĚīŽč§.
žąėŽ†ąžĚė žĚīŽŹô ÍĪįŽ¶¨ xLÍ≥ľ žĪĒŽ≤Ą žĖώ讞Ěė žēēŽ†• p1, p2 ÍįÄ ŽĒĒžßÄŪĄł žĄľžĄúžóź žĚėŪēī žł°ž†ēŽźúŽč§Í≥† ÍįÄž†ēŪēėžěź. žÉėŪĒĆŽßĀ ž£ľÍłį T‚ąą‚ĄĚ>0 Ž•ľ ÍįÄžßÄŽäĒ k‚ąą‚Ą§‚Č• 0Ž≤ąžßł žĚīžāįžčúÍįĄ ž∂úŽ†•Žį©ž†ēžč̞̥ Žč§žĚĆÍ≥ľ ÍįôžĚÄ ŪėēŪÉúŽ°ú ŪĎúŪėĄŪēúŽč§.
žó¨ÍłįžĄú, žēĄŽěėž≤®žěź
kŽäĒ
KT žčúž†ź,
ykŽäĒ ž∂úŽ†• žč†ŪėłŽ•ľ žĚėŽĮłŪēėŽ©į

žĚīŽč§.
ÍįÄž†ē 2 (
Jee et al., 2013): ŽÖľžĚėžĚė ŪéłžĚėŽ•ľ žúĄŪēī ž∂©Ž∂ĄŪěą žßßžĚÄ žčúÍįĄÍĶ¨ÍįĄ
t‚ąą[
kT,
kT +
T)žóź ŽĆÄŪēėžó¨
x(
t) ‚Č°
xk,
z(
t) ‚Č°
zk,
lf(
t) ‚Č°
lfk,
ŌČ(
t) ‚Č°
ŌČk Ž•ľ ÍįÄž†ēŪēúŽč§.
ÍįÄž†ē 2Ž•ľ ž†Āžö©Ūēėžó¨ žčĚ (7)žĚĄ kTžóźžĄú kT + TÍĻĆžßÄ ž†ĀŽ∂ĄŪēėŽ©ī Žč§žĚĆÍ≥ľ ÍįôžĚÄ žĚīžāįžčúÍįĄ Ž™®ŽćłžĚĄ žú†ŽŹĄŪē† žąė žěąŽč§.
ŪĒľžä§Ūܧ žč§žóź žĚīžÉĀžĚī žÉĚÍłīŽč§Ž©ī žĪĒŽ≤Ą žĖώ讞Ěė žēēŽ†•žį®žóź žĚėŪēú žĚīžÉĀ ŽąĄžú† ŪėĄžÉĀžĚī ŽįúžÉĚŪē† žąė žěąŽč§. ŽąĄžú† Í≤Äž∂úžĚĄ žúĄŪēú žÉĀŪÉúž∂Ēž†ēžĚÄ Žč§žĚĆÍ≥ľ ÍįôžĚÄ žĚīžāįžčúÍįĄ ÍīÄžł°Íłįžóź žĚėŪēī žĚīŽ£®žĖīžßĄŽč§.
žó¨ÍłįžĄú,

ŽäĒ
xžĚė ž∂Ēž†ēžĻė,

ŽäĒ
yžĚė ž∂Ēž†ēžĻė,
r‚ąą‚ĄĚ
3žĚÄ žó¨Ž∂Ą,

žĚÄ ÍīÄžł°Íłį žĚīŽďĚ ŪĖČŽ†¨,
H‚ąą‚ĄĚ
3√ó3žĚÄ žó¨Ž∂Ą žĚīŽďĚ ŪĖČŽ†¨žĚīŽč§. žÉĀŪÉúž∂Ēž†ēžė§žį®
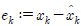
Ž•ľ ž†ēžĚėŪēėŽ©ī žčĚ (8)Í≥ľ žčĚ (9)Ž°úŽ∂ÄŪĄį Žč§žĚĆÍ≥ľ ÍįôžĚÄ žė§žį®Žį©ž†ēžč̞̥ žĖĽžĚĄ žąė žěąŽč§.
žó¨Ž∂Ą rŽ°úŽ∂ÄŪĄį Í≥†žě•žĚĄ ŪĆźŽč®ŪēėÍłį žúĄŪēī Žč§žĚĆÍ≥ľ ÍįôžĚÄ žó¨Ž∂ĄŪŹČÍįÄŪē®žąė JkžôÄ Ž¨łŪĄĪÍįí JthkžĚĄ ž†ēžĚėŪēúŽč§.
žó¨ÍłįžĄú, KW‚ąą‚ĄĚ>0ŽäĒ žÉĀžąė žčúÍįĄ žįĹ(Constant time window)žĚīŽč§.
ž†ēžĚė 1 (Í≥†žě• ŪĆźŽč® ŽÖľŽ¶¨): Í≥†žě• ŽįúžÉĚ žó¨Ž∂ÄŽäĒ Žč§žĚĆžĚė Í≥†žě•ŪĆźŽč® ŽÖľŽ¶¨žóź žĚėŪēī Í≤įž†ēŽźúŽč§.
ž†ēžĚė 2: žė§žį® žčúžä§ŪÖú(žčĚ (10))žóźžĄú ŌČkŽ°úŽ∂ÄŪĄį rkÍĻĆžßÄ H‚ąě žĄĪŽä•žĚĄ Žč§žĚĆÍ≥ľ ÍįôžĚī ž†ēžĚėŪēúŽč§.
Ž¨łž†ú 1: ž£ľžĖīžßĄ
ő≥‚ąą‚ĄĚ
>0 žóź ŽĆÄŪēėžó¨ ÍīÄžł°Íłį(žčĚ (9))ÍįÄ Žč§žĚĆ ž°įÍĪīžĚĄ ŽßĆž°ĪŪēėŽŹĄŽ°Ě ÍīÄžł°Íłį žĚīŽďĚ ŪĖČŽ†¨Žď§

Í≥ľ žó¨Ž∂Ą žĚīŽďĚ ŪĖČŽ†¨
HŽ•ľ žĄ§Í≥ĄŪēėŽĚľ:
C1) žė§žį® žčúžä§ŪÖú(žčĚ (10))žĚÄ ŌČk = 0, lf = 0žóź ŽĆÄŪēėžó¨ ž†źÍ∑ľž†ĀžúľŽ°ú žēąž†ēŪēėŽč§;
C2) ||O||‚ąě < ő≥.
4. Ž™®žĚėžč§Ūóė
Ž≥ł ž†ąžóźžĄúŽäĒ žč§Ž¶įŽćĒÍįÄ ž†ēžÉĀ ŽŹôžěĎŪēėŽäĒ Í≤ĹžöįžôÄ ŽąĄžú† Í≥†žě•žĚī ŽįúžÉĚŪēú Í≤ĹžöįžĚė ŽŹôŪäĻžĄĪÍ≥ľ ÍīÄžł°ÍłįžĚė ž∂ĒžĘÖ žĄĪŽä•žĚĄ ŽĻĄÍĶźŪēėÍ≥† ž†úžēąŪēú ÍīÄžł°Íłį(žčĚ (9))žĚė Í≤Äž∂ú žĄĪŽä•žĚĄ ŪôēžĚłŪēėÍłį žúĄŪēī ÍįÄžÉĀžĚė žĚīžÉĀ ŽąĄžú†Ž•ľ ŽįúžÉĚžčúžľú žó¨Ž∂Ą ŪŹČÍįÄŽ•ľ žč§žčúŪēúŽč§. Žč§žĚĆÍ≥ľ ÍįôžĚÄ ŪĆĆŽĚľŽĮłŪĄįžôÄ žīąÍłįÍįížĚĄ ÍįÄžßÄŽäĒ žčĚ (3) ŪėēŪÉúžĚė žú†žēēžč§Ž¶įŽćĒŽ•ľ Í≥†Ž†§Ūēėžěź(
Yao et al., 2014).
ž£ľžĖīžßĄ
ő≥=0.05,
T=10
-3[s]žóź ŽĆÄŪēėžó¨ ž†ēŽ¶¨ 1žĚė žĄ§Í≥Ą ž°įÍĪīžĚĄ ŽßĆž°ĪŪēėŽäĒ ÍīÄžł°Íłį(žčĚ (9))žĚė žĚīŽďĚŪĖČŽ†¨Žď§

Ž•ľ ÍĶ¨Ūē† žąė žěąŽč§(Ž∂ÄŽ°Ě žįłž°į).
žôłŽěÄ
ŌČ‚ąą‚ĄĚŽäĒ
Fig. 3Í≥ľ ÍįôžĚī ŪĀ¨Íłį ÍĶ¨ÍįĄ (-0.5, 0.5)žóźžĄú Ž∂ąÍ∑úžĻôŪēėÍ≤Ć ŽįúžÉĚŪē®žĚĄ ÍįÄž†ēŪēúŽč§. žąėŽ†ąžĚė žÜ掏Ą
x2 ŽäĒ žł°ž†ē ÍįÄŽä•Ūēú ÍįížĚī žēĄŽčąžßÄŽßĆ žł°ž†ē ÍįÄŽä•Ūēú žĚīŽŹô ÍĪįŽ¶¨
x1žúľŽ°úŽ∂ÄŪĄį Í≥ĄžāįžĚī ÍįÄŽä•ŪēėŽč§. žčúÍįĄ ÍĶ¨ÍįĄ
t‚ąą[0, 1]žóźžĄú žĚīžÉĀ ŽąĄžú† Í≥Ąžąė
lf ‚Č°0žóź ŽĆÄŪēú ŽŹôžó≠Ūēô(žčĚ (3))Í≥ľ ÍīÄžł°Íłį(žčĚ (9))žĚė žčúŽģ¨Ž†ąžĚīžÖė Í≤įÍ≥ľŽ•ľ
Fig. 4-
5žóź ŽāėŪÉÄŽāłŽč§.
Fig. 4žôÄ
5žĚė žč§žĄ†žĚÄ ÍįĀÍįĀ žąėŽ†ąžĚė ÍĪįŽ¶¨ žł°ž†ēžĻė, žÜ掏Ą Í≥ĄžāįÍįížĚĄ žĚėŽĮłŪēėŽ©į ÍīėžĄ†žĚÄ ÍīÄžł°Íłįžóź žĚėŪēī ž∂Ēž†ēŽźú Í∂§ž†ĀžĚīŽč§. Í∑łŽ¶ľžóźžĄú žēĆ žąė žěąŽďĮžĚī Í≥†žě•žĚī ŽįúžÉĚŪēėžßÄ žēäžĚÄ Í≤Ĺžöį ÍīÄžł°ÍłįžĚė žÉĀŪÉúž∂Ēž†ēžĻėÍįÄ žÉĀŪÉúŽ≥ÄžąėžôÄ ÍĪįžĚė žĚľžĻėŪēėŽäĒ Í≤ɞ̥ žēĆ žąė žěąŽč§.
Fig. 3
Disturbance

Fig. 4
Cart displacement and estimate (solid: x1, dashed:  ) when lf ‚Č° 0
) when lf ‚Č° 0
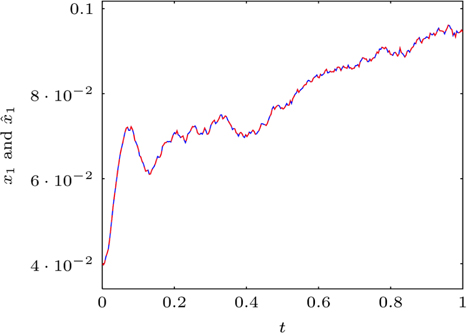
Fig. 5
Cart velocity and estimate (solid: x2 , dashed:  ) when lf ‚Č° 0
) when lf ‚Č° 0

žĚīžÉĀ ŽąĄžú†ÍįÄ ŽįúžÉĚŪēú Í≤ĹžöįžĚė ÍīÄžł°ÍłįžĚė Í≤Äž∂ú žĄĪŽä•žĚĄ ŪôēžĚłŪēėÍłį žúĄŪēī 0.1žīąŽ•ľ Íłįž†źžúľŽ°ú Žč§žĚĆÍ≥ľ ÍįôžĚÄ žĚīžÉĀ ŽąĄžú† Í≥ĄžąėÍįÄ ŽįúžÉĚŪē®žĚĄ ÍįÄž†ēŪēúŽč§.
Fig. 6Í≥ľ
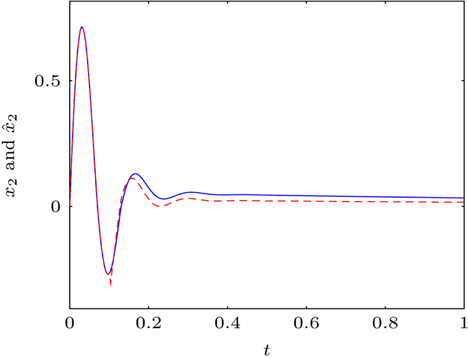
7žĚė žč§žĄ†žĚÄ ÍįĀÍįĀ žąėŽ†ąžĚė ÍĪįŽ¶¨ žł°ž†ēžĻė, žÜ掏ĄžĚė Í≥ĄžāįÍįížĚīŽ©į ÍīėžĄ†žĚÄ ÍīÄžł°Íłįžóź žĚėŪēī ž∂Ēž†ēŽźú žÉĀŪÉúŽ≥ÄžąėžĚīŽč§.
Fig. 6žĚÄ ŽąĄžú†žôÄ žÉĀÍīÄžóÜžĚī ž†ēžÉĀž†ĀžúľŽ°ú žÉĀŪÉúŽ≥ÄžąėŽ•ľ ž∂Ēž†ēŪēėÍ≥† žěąžúľŽāė
Fig. 7žóźžĄúŽäĒ 0.1žīą žĚīŪõĄ žÉĀŪÉúž∂Ēž†ēžė§žį®ÍįÄ ŽįúžÉĚŪēėŽäĒ Í≤ɞ̥ žēĆ žąė žěąŽč§.
Fig. 6
Cart displacement and estimate (solid: x1 , dashed:  ) when lf ‚Ȇ 0
) when lf ‚Ȇ 0
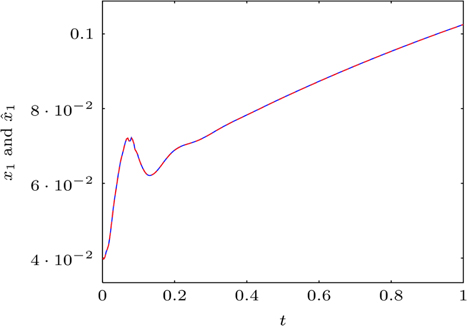
Fig. 7
Cart velocity and estimate (solid: x2 , dashed:  ) when lf ‚Ȇ 0
) when lf ‚Ȇ 0
žÉĀŪÉúž∂Ēž†ēžė§žį®Ž°úŽ∂ÄŪĄį ŽąĄžú†Ž•ľ ŪĆźŽč®ŪēėÍłįŽäĒ žĖīŽ†§žöįŽāė ž†ēžĚė 1žĚė ŪĆźŽč® ŽÖľŽ¶¨Ž•ľ ž†Āžö©ŪēėŽ©ī ŽąĄžú† ŽįúžÉĚ žó¨Ž∂ÄŽ•ľ ŪôēžĚłŪē† žąė žěąŽč§. ÍīÄžł°Íłį (žčĚ (9))ŽäĒ lf ‚Č° 0žóź ŽĆÄŪēėžó¨ Žč§žĚĆ ÍīÄÍ≥ĄŽ•ľ ŽßĆž°ĪŪēúŽč§.
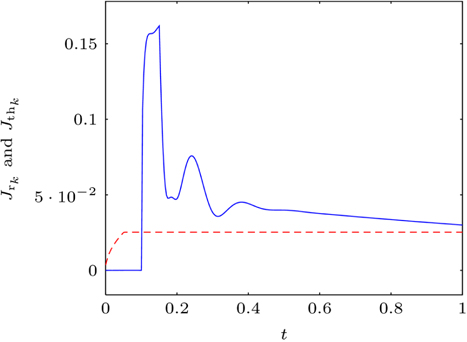
ž£ľžĖīžßĄ ő≥ = 0.05, Kw = 50, , ŌČ‚ąą(‚ąí0.5, 0.5)žóź ŽĆÄŪēėžó¨ Ž¨łŪĄĪÍįí JthkŽ•ľ Žč§žĚĆÍ≥ľ ÍįôžĚī Í≥ĄžāįŪē† žąė žěąŽč§.
Fig. 8žĚÄ žúĄžóźžĄú Í≥ĄžāįŽźú Ž¨łŪĄĪÍįíÍ≥ľ Í≥ĄžāįžčĚ (11)žóź žĚėŪēī žĖĽžĖīžßĄ žó¨Ž∂ĄŪŹČÍįÄŪē®žąėŽ•ľ Í∑łŽěėŪĒĄŽ°ú ŽāėŪÉÄŽāł Í≤ÉžĚīŽč§. žó¨Ž∂ĄŪŹČÍįÄŪē®žąėŽäĒ 0.1021žīąžóź Ž¨łŪĄĪÍįížĚĄ žīąÍ≥ľŪēėžėÄžúľŽ©į ž†ēžĚė 1žĚė ŪĆźŽč® ŽÖľŽ¶¨žóź ŽĒįŽĚľ žĚī žčúž†źžóź ŽąĄžú†ÍįÄ ŽįúžÉĚŪēėžėÄžĚƞ̥ ŪĆźŽč®Ūē† žąė žěąŽč§.
Fig. 8
Residual Evaluation 1 (solid: Jrk, dashed: Jthk)

Žč§žĖĎŪēú žÉĀŪô©žóźžĄúžĚė žč§ŪóėžĚĄ žúĄŪēī Žč§žĚĆÍ≥ľ ÍįôžĚÄ žīąÍłįÍįížĚĄ ÍįÄžßÄŽäĒ žč§Ž¶įŽćĒ Ž™®ŽćłžĚĄ Í≥†Ž†§Ūēėžěź.
žīąÍłįÍįížĚĄ ž†úžôłŪēú Ž™®Žćł ŪĆĆŽĚľŽĮłŪĄį ŽįŹ žč§Ūóė Žį©Ž≤ēžĚÄ žēěžĚė žč§ŪóėÍ≥ľ ŽŹôžĚľŪēėŽč§. žó¨Ž∂ĄŪŹČÍįÄ Í≤įÍ≥ľŽ•ľ
Fig. 9žóź ŽāėŪÉÄŽāīžóąžúľŽ©į
Fig. 8Í≥ľ žú†žā¨ŪēėÍ≤Ć ŽąĄžú† ŽįúžÉĚ žßĀŪõĄžĚł 0.1013žīąžóź žó¨Ž∂ĄŪŹČÍįÄŪē®žąėÍįÄ Ž¨łŪĄĪÍįížĚĄ žīąÍ≥ľŪēėžó¨ ŽąĄžú†ÍįÄ ŽįúžÉĚŪēėžėÄžĚƞ̥ ŪôēžĚłŪē† žąė žěąŽč§.
Fig. 9
Residual Evaluation 2 (solid: Jrk, dashed: Jthk)
 ŽäĒ žú†ŪĀīŽ¶¨ŽĒĒžēą ŽÜąžĚĄ žĚėŽĮłŪēėŽ©į
ŽäĒ žú†ŪĀīŽ¶¨ŽĒĒžēą ŽÜąžĚĄ žĚėŽĮłŪēėŽ©į  ŽäĒ l2 ŽÜąžĚĄ žĚėŽĮłŪēúŽč§. *ŽäĒ ŽĆÄžĻ≠ŪĖČŽ†¨žĚė ŽĆÄÍįĀ ž†ĄžĻėžöĒžÜĆžĚīŽč§.
ŽäĒ l2 ŽÜąžĚĄ žĚėŽĮłŪēúŽč§. *ŽäĒ ŽĆÄžĻ≠ŪĖČŽ†¨žĚė ŽĆÄÍįĀ ž†ĄžĻėžöĒžÜĆžĚīŽč§.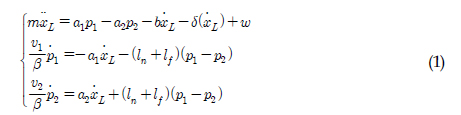
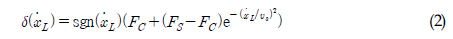

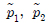 ŽäĒ p1, p2žĚė žä§žľÄžĚľ Ž≥ÄŪôėŽźú ÍįížĚīŽč§. žÉĀŪÉúŽ≥Äžąė xŽ•ľ Žč§žĚĆÍ≥ľ ÍįôžĚī ž†ēžĚėŪēėžěź.
ŽäĒ p1, p2žĚė žä§žľÄžĚľ Ž≥ÄŪôėŽźú ÍįížĚīŽč§. žÉĀŪÉúŽ≥Äžąė xŽ•ľ Žč§žĚĆÍ≥ľ ÍįôžĚī ž†ēžĚėŪēėžěź.
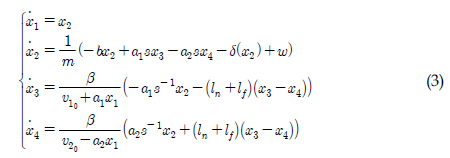

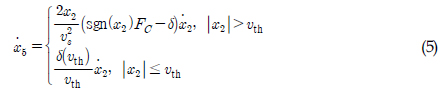
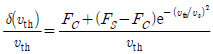 žĚīŽ©į x2 - x5 ŪŹČŽ©īžóźžĄúžĚė žĄ†Ūėē ÍłįžöłÍłį ÍįížĚīŽč§. žĚīž†ú žčĚ (3)Í≥ľ (5)Ž°úŽ∂ÄŪĄį Žč§žĚĆÍ≥ľ ÍįôžĚÄ 5žį® žÉĀŪÉúÍ≥ĶÍįĄŽį©ž†ēžč̞̥ žú†ŽŹĄŪē† žąė žěąŽč§.
žĚīŽ©į x2 - x5 ŪŹČŽ©īžóźžĄúžĚė žĄ†Ūėē ÍłįžöłÍłį ÍįížĚīŽč§. žĚīž†ú žčĚ (3)Í≥ľ (5)Ž°úŽ∂ÄŪĄį Žč§žĚĆÍ≥ľ ÍįôžĚÄ 5žį® žÉĀŪÉúÍ≥ĶÍįĄŽį©ž†ēžč̞̥ žú†ŽŹĄŪē† žąė žěąŽč§.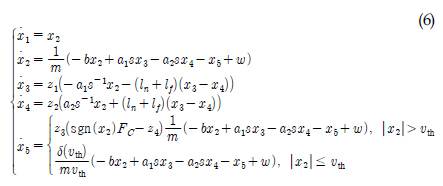


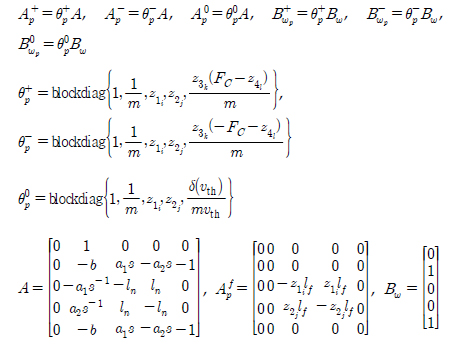



 žĚīŽč§.
žĚīŽč§.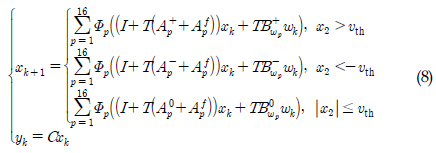
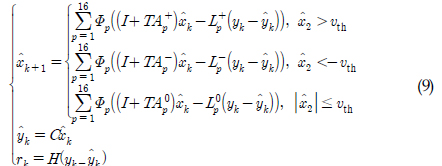
 ŽäĒ xžĚė ž∂Ēž†ēžĻė,
ŽäĒ xžĚė ž∂Ēž†ēžĻė,  ŽäĒ yžĚė ž∂Ēž†ēžĻė, r‚ąą‚ĄĚ3žĚÄ žó¨Ž∂Ą,
ŽäĒ yžĚė ž∂Ēž†ēžĻė, r‚ąą‚ĄĚ3žĚÄ žó¨Ž∂Ą,  žĚÄ ÍīÄžł°Íłį žĚīŽďĚ ŪĖČŽ†¨, H‚ąą‚ĄĚ3√ó3žĚÄ žó¨Ž∂Ą žĚīŽďĚ ŪĖČŽ†¨žĚīŽč§. žÉĀŪÉúž∂Ēž†ēžė§žį®
žĚÄ ÍīÄžł°Íłį žĚīŽďĚ ŪĖČŽ†¨, H‚ąą‚ĄĚ3√ó3žĚÄ žó¨Ž∂Ą žĚīŽďĚ ŪĖČŽ†¨žĚīŽč§. žÉĀŪÉúž∂Ēž†ēžė§žį®  Ž•ľ ž†ēžĚėŪēėŽ©ī žčĚ (8)Í≥ľ žčĚ (9)Ž°úŽ∂ÄŪĄį Žč§žĚĆÍ≥ľ ÍįôžĚÄ žė§žį®Žį©ž†ēžč̞̥ žĖĽžĚĄ žąė žěąŽč§.
Ž•ľ ž†ēžĚėŪēėŽ©ī žčĚ (8)Í≥ľ žčĚ (9)Ž°úŽ∂ÄŪĄį Žč§žĚĆÍ≥ľ ÍįôžĚÄ žė§žį®Žį©ž†ēžč̞̥ žĖĽžĚĄ žąė žěąŽč§.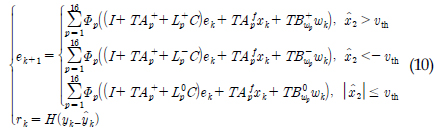

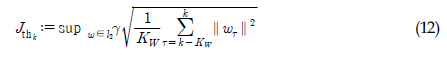


 Í≥ľ žó¨Ž∂Ą žĚīŽďĚ ŪĖČŽ†¨ HŽ•ľ žĄ§Í≥ĄŪēėŽĚľ:
Í≥ľ žó¨Ž∂Ą žĚīŽďĚ ŪĖČŽ†¨ HŽ•ľ žĄ§Í≥ĄŪēėŽĚľ: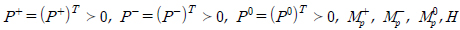 žĚī ž°īžě¨ŪēúŽč§Ž©ī žė§žį® žčúžä§ŪÖú(žčĚ (10))žĚÄ ž†źÍ∑ľž†ĀžúľŽ°ú žēąž†ēŪēėŽ©į ŌČk‚ąąl2žóź ŽĆÄŪēėžó¨ ő≥- H‚ąě žĄĪŽä•žĚĄ ÍįĞߥŽč§.
žĚī ž°īžě¨ŪēúŽč§Ž©ī žė§žį® žčúžä§ŪÖú(žčĚ (10))žĚÄ ž†źÍ∑ľž†ĀžúľŽ°ú žēąž†ēŪēėŽ©į ŌČk‚ąąl2žóź ŽĆÄŪēėžó¨ ő≥- H‚ąě žĄĪŽä•žĚĄ ÍįĞߥŽč§.

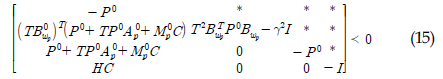
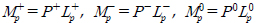 žĚīŽč§.
žĚīŽč§.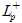 Í≥ľ HŽ•ľ ÍĶ¨ŪēėÍłį žúĄŪēú žĄ§Í≥Ąž°įÍĪī(žčĚ (13))žĚĄ ž¶ĚŽ™ÖŪēúŽč§. žĖĎŪēúž†ē ŪĖČŽ†¨ P+ = (P+)T > 0žóź ŽĆÄŪēėžó¨ žĖĎŪēúž†ē Ūē®žąė
Í≥ľ HŽ•ľ ÍĶ¨ŪēėÍłį žúĄŪēú žĄ§Í≥Ąž°įÍĪī(žčĚ (13))žĚĄ ž¶ĚŽ™ÖŪēúŽč§. žĖĎŪēúž†ē ŪĖČŽ†¨ P+ = (P+)T > 0žóź ŽĆÄŪēėžó¨ žĖĎŪēúž†ē Ūē®žąė  žôÄ žį®Ž∂ĄŽį©ž†ēžčĚ
žôÄ žį®Ž∂ĄŽį©ž†ēžčĚ  žĚĄ ž†ēžĚėŪēúŽč§. Žč§žĚĆ ŪēīŽįÄŪĄī‚ÄĒžěźžĹĒŽĻĄ‚ÄĒŽ≤®ŽßĆ (Hamilton‚ÄĒJacobi‚ÄĒBellman) Ž∂ÄŽďĪžč̞̥ Í≥†Ž†§Ūēėžěź.
žĚĄ ž†ēžĚėŪēúŽč§. Žč§žĚĆ ŪēīŽįÄŪĄī‚ÄĒžěźžĹĒŽĻĄ‚ÄĒŽ≤®ŽßĆ (Hamilton‚ÄĒJacobi‚ÄĒBellman) Ž∂ÄŽďĪžč̞̥ Í≥†Ž†§Ūēėžěź.

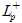 Í≥ľ HŽ•ľ ÍĶ¨ŪēúŽč§Ž©ī x2 > vthžóź ŽĆÄŪēėžó¨ Ž¨łž†ú 1žĚė C2)Ž•ľ ŽßĆž°ĪŪēėŽäĒ ÍīÄÍ≥ĄŪē† žąė žěąŽč§. žčĚ (16)žĚĄ ž†ĄÍįúŪēėŽ©ī Žč§žĚĆÍ≥ľ ÍįôžĚÄ Ž∂ÄŽďĪžčĚÍ≥ľ ŽŹôžĻėÍīÄÍ≥ĄŽ•ľ žú†ŽŹĄŪē† žąė žěąŽč§.
Í≥ľ HŽ•ľ ÍĶ¨ŪēúŽč§Ž©ī x2 > vthžóź ŽĆÄŪēėžó¨ Ž¨łž†ú 1žĚė C2)Ž•ľ ŽßĆž°ĪŪēėŽäĒ ÍīÄÍ≥ĄŪē† žąė žěąŽč§. žčĚ (16)žĚĄ ž†ĄÍįúŪēėŽ©ī Žč§žĚĆÍ≥ľ ÍįôžĚÄ Ž∂ÄŽďĪžčĚÍ≥ľ ŽŹôžĻėÍīÄÍ≥ĄŽ•ľ žú†ŽŹĄŪē† žąė žěąŽč§.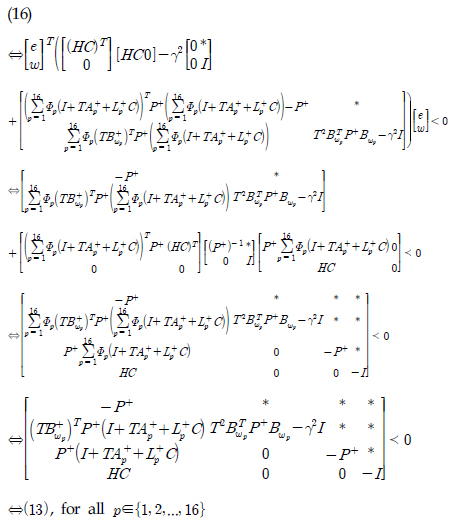
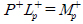 žĚė Ž≥ÄžąėžĻėŪôėžĚĄ žā¨žö©ŪēėŽ©ī ŽßąžßÄŽßČ ŽŹôžĻėÍīÄÍ≥ĄÍįÄ žĄĪŽ¶ĹŪēúŽč§. ŪĖČŽ†¨Ž∂ÄŽďĪžčĚ (14)žôÄ žčĚ (15)žĚė ž¶ĚŽ™ÖžĚÄ žúĄ ž¶ĚŽ™ÖÍ≥ľ žú†žā¨ŪēėŽĮÄŽ°ú žÉĚŽěĶŪēúŽč§.
žĚė Ž≥ÄžąėžĻėŪôėžĚĄ žā¨žö©ŪēėŽ©ī ŽßąžßÄŽßČ ŽŹôžĻėÍīÄÍ≥ĄÍįÄ žĄĪŽ¶ĹŪēúŽč§. ŪĖČŽ†¨Ž∂ÄŽďĪžčĚ (14)žôÄ žčĚ (15)žĚė ž¶ĚŽ™ÖžĚÄ žúĄ ž¶ĚŽ™ÖÍ≥ľ žú†žā¨ŪēėŽĮÄŽ°ú žÉĚŽěĶŪēúŽč§.
 Ž•ľ ÍĶ¨Ūē† žąė žěąŽč§(Ž∂ÄŽ°Ě žįłž°į).
Ž•ľ ÍĶ¨Ūē† žąė žěąŽč§(Ž∂ÄŽ°Ě žįłž°į).









 ) when lf ‚Č° 0
) when lf ‚Č° 0
 ) when lf ‚Č° 0
) when lf ‚Č° 0













