Brincker, R., Zhang, L., Andersen, P.. (Modal Identification of Output-only Systems using Frequency Domain Decomposition, Smart Materials and Structures, 2001). 10, 441-445 10.1088/0964-1726/10/3/303.

Dong, Y., Sun, Z., Jia, H.. (A Cosine Similarity-based Negative Selection Algorithm for Time Series Novelty Detection, Mechanical Systems and Signal Processing, 2006). 20, 1461-1472 10.1016/j.ymssp.2004.12.006.

Kim, J.T., Ryu, Y.S., Jung, S.O., Choo, S.H.. (Pattern Recognition of Modal Sensitivity for Structural Damage Identification of Truss Structure, Journal of Ocean Engineering and Techn, 2000). 14(1):80-87.
Kim, J.T., Sim, S.H., Cho, S., Yun, C.B., Min, J.. (Recent R&D Activities on Structural Health Monitoring in Korea, Structural Monitoring and Maintenance, 2016). 3(1):91-114 10.12989/smm.2016.3.1.091.

Kim, J.T., Stubbs, N.. (Damage Detection in Jacket-type Offshore Structures from Few Mode Shapes, Journal of Ocean Engineering and Technology, 1994). 8(1):144-153.
Kim, S.R., Lee, J.W., Kim, B.K., Lee, J.S.. (Damage Estimation Method for Monopile Support Structure of Offshore Wind Turbin, Transactions of the Korean Society for Noise and Vibration Engineering, 2012). 22(7):667-675 10.5050/KSNVE.2012.22.7.667.

Li, H., Li, P., Hu, S.L.J.. (Modal Parameter Estimation for Jacket-type Platforms using Noisy Free-vibration Data: Sea Test Study, Applied Ocean Research, 2012). 37, 45-53 10.1016/j.apor.2012.03.002.

Li, H., Wang, J., Hu, S.L.J.. (Using Incomplete Modal Data for Damage Detection in Offshore Jacket Structures, Ocean Engineering, 2008). 35, 1793-1799 10.1016/j.oceaneng.2008.08.020.

Liu, F., Li, H., Li, W., Wang, B.. (Experimental Study of Improved Modal Strain Energy Method for Damage Localisation in Jacket-type Offshore Wind Turbines, Renewable Energy, 2014). 72, 174-181 10.1016/j.renene.2014.07.007.

Malekzehtab, H., Golafshani, A.A.. (Damage Detection in an Offshore Jacket Platform using Genetic Algorithm based Finite Element Model Updating with Noisy Modal Data, Procedia Engineering, 2013). 54, 480-490 10.1016/j.proeng.2013.03.044.

Min, C.H., Cho, S.G., Oh, J.W., Kim, H.W., Hong, S., Nam, B.W.. (Study on Damage Detection Method using Meta Model, Journal of Ocean Engineering and Technology, 2015). 29(5):351-358 10.5574/KSOE.2015.29.5.351.

Min, J., Shim, H., Yun, C.B., Yi, J.H.. (Impedance-based Long-term Structural Health Monitoring for Tidal Current Power Plant Structure in Noisy Environments, Journal of Ocean Engineering and Technology, 2011). 25(4):59-65 10.5574/KSOE.2011.25.4.059.

Mojtahedi, A., Lotfollahi Yaghin, M.A., Hassanzadeh, Y., Ettefagh, M.M., Aminfar, M.H., Aghdam, A.B.. (Developing a Robust SHM Method for Offshore Jacket Platform using Modal Updating and Fuzzy Logic System, Applied Ocean Research, 2011). 33, 398-411 10.1016/j.apor.2011.05.001.

Park, S.Y., Park, D.C., Kim, E.H., Kim, H.S.. (Damage Evaluation on a Jacket Platform Structure Using Modal Prope Proceeding of the Twenty-first International Offshore and Polar Engineering Conference Maui, Hawaii, USA: 2011). 1: 245-250.
Rivero-Angeles, F.J., Vazquez-Hernandez, A.O., Martinez, U.. (Vibration Analysis for the Determination of Modal Parameters of Steel Catenary Risers Based on Response-only Data, Engineering Structures, 2014). 59, 68-79 10.1016/j.engstruct.2013.10.003.

Shen, J., Liu, F., Li, H., Xu, L., Liang, B.. (Assessment of the Damages Occurring Between Two Adjacent Measurements for an Aging Offshore Platform, Ocean Engineering, 2015). 109, 372-380 10.1016/j.oceaneng.2015.09.024.

Yang, H.Z., Park, H.L., Choi, K.S., Li, H.J.. (Comparison Between Field Test and Numerical Analysis for a Jacket Platform in Bohai Bay, China, Journal of Ocean Engineering and Technology, 2006). 20(2):1-7.

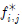 은 i번째 요소의 강성이 변경되었을 때 계산되는 j차 모드 고유진동수를 의미하며, fj은 강성이 변경되기전(손상이 없는 상태) 계산된 j차 모드 고유진동수를 나타낸다. 요소강성 변형에 따른 고유진동수 변형율 행렬은 아래와 같다.
은 i번째 요소의 강성이 변경되었을 때 계산되는 j차 모드 고유진동수를 의미하며, fj은 강성이 변경되기전(손상이 없는 상태) 계산된 j차 모드 고유진동수를 나타낸다. 요소강성 변형에 따른 고유진동수 변형율 행렬은 아래와 같다.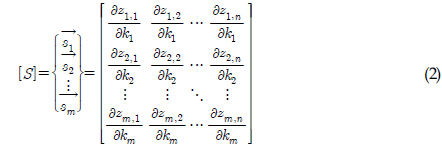
 로 나타낸다.
로 나타낸다.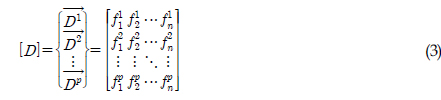
 는 p번째 주기에서 측정된 고유진동수들의 벡터를 의미하며,
는 p번째 주기에서 측정된 고유진동수들의 벡터를 의미하며, 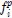 는 p번째 주기에서 획득된 i차 고유진동수를 나타낸다.
는 p번째 주기에서 획득된 i차 고유진동수를 나타낸다.

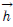 로 표현한다.
로 표현한다.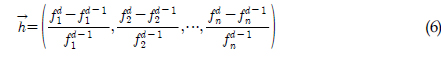
 와
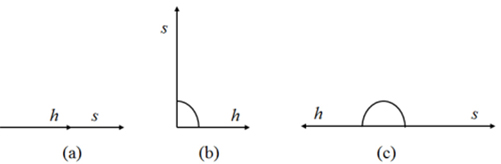
와 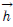 의 유사도를 검색한다. 코사인 유사도는 두 벡터간의 내적 값으로 교각을 구하고, 교각의 코사인 값을 이용하여 두 벡터의 유사도를 계산하는 방법으로 최근 데이터 마이닝 분야에 많이 활용되고 있다. Fig. 1(a)는 두 벡터의 방향이 완전히 일치하는 경우로 유사도 값은 1이며, Fig. 1(b)와 같이 두 벡터가 직교하는 경우 코사인 유사도는 0이며, Fig. 1(c)와 같이 180°인 경우 코사인 유사도는 −1를 갖는다(Dong et al., 2006). 코사인 유사도는 Fig. 1(a)에서 보여지듯이 두 벡터 방향의 유사성을 판단하는 것으로 벡터 크기의 유사도는 평가하지 못한다.
의 유사도를 검색한다. 코사인 유사도는 두 벡터간의 내적 값으로 교각을 구하고, 교각의 코사인 값을 이용하여 두 벡터의 유사도를 계산하는 방법으로 최근 데이터 마이닝 분야에 많이 활용되고 있다. Fig. 1(a)는 두 벡터의 방향이 완전히 일치하는 경우로 유사도 값은 1이며, Fig. 1(b)와 같이 두 벡터가 직교하는 경우 코사인 유사도는 0이며, Fig. 1(c)와 같이 180°인 경우 코사인 유사도는 −1를 갖는다(Dong et al., 2006). 코사인 유사도는 Fig. 1(a)에서 보여지듯이 두 벡터 방향의 유사성을 판단하는 것으로 벡터 크기의 유사도는 평가하지 못한다.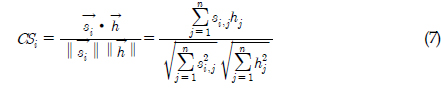
 를
를 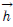 로 나누면 다음과 같다. 만약
로 나누면 다음과 같다. 만약  가
가 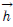 와 크기는 다르지만 방향성이 일치하는 벡터라면
와 크기는 다르지만 방향성이 일치하는 벡터라면  의 각 성분은 모두 같은 값을 가질 것이다.
의 각 성분은 모두 같은 값을 가질 것이다.

 의 성분의 표준편차를 나타내며 모든 성분이 완전히 같을수록 표준편차는 0에 가깝게 된다. σq,i가 작을수록 크기 지수는 커지며, 크기 지수가 클수록 해당 요소에 손상이 발생된 가능성이 큰 것으로 판단할 수 있다.
의 성분의 표준편차를 나타내며 모든 성분이 완전히 같을수록 표준편차는 0에 가깝게 된다. σq,i가 작을수록 크기 지수는 커지며, 크기 지수가 클수록 해당 요소에 손상이 발생된 가능성이 큰 것으로 판단할 수 있다.
 의 평균을 손상의 크기로 고려한다.
의 평균을 손상의 크기로 고려한다. 부터
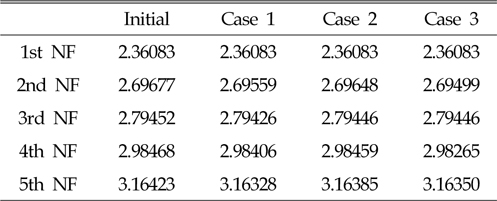
부터  까지는 손상이 없는 상태에서 측정된 고유진동수로 구성되며,
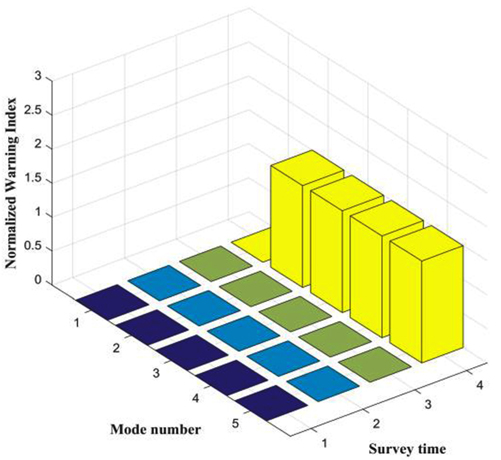
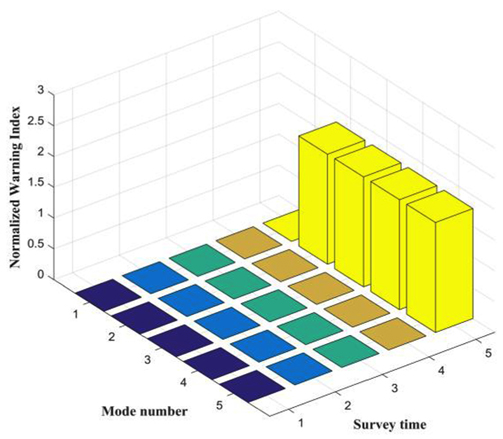
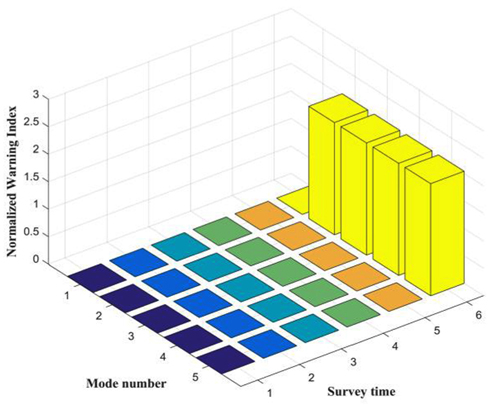
까지는 손상이 없는 상태에서 측정된 고유진동수로 구성되며, 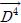 는 구조물에 Case 1의 손상이 발생된 경우 계산된 고유진동수가 적용되었다. Case 2와 Case 3의 경우 각각 5번째 측정 시점과 6번째 측정 시점으로 각각의 손상시나리오에서 모두 다른 시점에서 손상이 발생된 것으로 가정하였다. Fig. 3에서 Fig. 5는 Case 1 ~ Case 3의 경우에 계측된 정규화된 손상지수이다. 각 경우 모두에서 x축은 측정시점, y축은 고유진동수 차수, z축은 정규화된 손상지수를 나타낸다. 손상판단 기준값을 1(84% 신뢰도)로 정할 경우 Case 1은 4번째, Case 2와 Case 3은 5번째와 6번째 측정시점에 구조 어딘가에 손상이 발생했다는 것을 감지할 수 있었으며, 이 결과는 손상시나리오를 정확히 판단한 것이다.
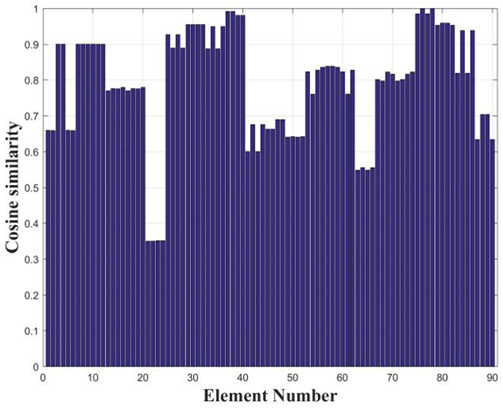
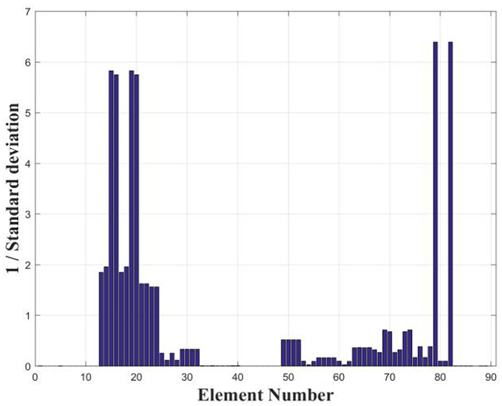
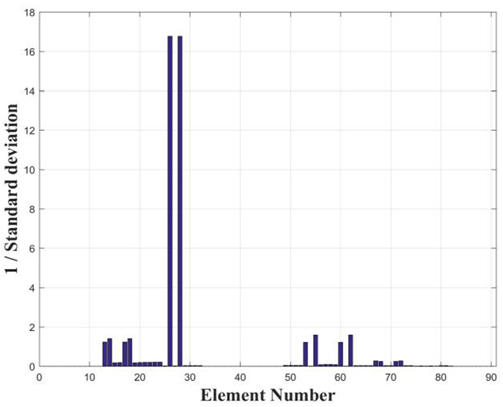
는 구조물에 Case 1의 손상이 발생된 경우 계산된 고유진동수가 적용되었다. Case 2와 Case 3의 경우 각각 5번째 측정 시점과 6번째 측정 시점으로 각각의 손상시나리오에서 모두 다른 시점에서 손상이 발생된 것으로 가정하였다. Fig. 3에서 Fig. 5는 Case 1 ~ Case 3의 경우에 계측된 정규화된 손상지수이다. 각 경우 모두에서 x축은 측정시점, y축은 고유진동수 차수, z축은 정규화된 손상지수를 나타낸다. 손상판단 기준값을 1(84% 신뢰도)로 정할 경우 Case 1은 4번째, Case 2와 Case 3은 5번째와 6번째 측정시점에 구조 어딘가에 손상이 발생했다는 것을 감지할 수 있었으며, 이 결과는 손상시나리오를 정확히 판단한 것이다.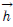 를 획득하였다. 식 (8) ~ 식 (10)을 통해 계산된 코사인 유사도, 크기지수, 손상지수를 Case 1의 경우 Fig. 6 ~ 8에, Case 2의 경우 Fig. 9 ~ Fig. 11에, Case 3의 경우 Fig. 12 ~ Fig. 14에 각각 나타내었다. 손상추정 결과 Case 1은 76 혹은 78번 라인에서 23.55%의 손상이 발생된 것으로 예측되었으며, Case 2에서는 79번 혹은 82번에서 9.77%의 손상이 Case 3에서는 26번 혹은 28번 라인에서 19.12%의 손상이 발생된 것으로 추정되었다. 3가지 경우 모두에서 2개의 요소에서 손상 가능성과 정도가 동일하게 예측되었는데 이러한 원인은 모델의 대칭성에 의한 것으로 판단된다. 이상의 추정 결과를 Fig. 15와 Table 4에 정리하였다.
를 획득하였다. 식 (8) ~ 식 (10)을 통해 계산된 코사인 유사도, 크기지수, 손상지수를 Case 1의 경우 Fig. 6 ~ 8에, Case 2의 경우 Fig. 9 ~ Fig. 11에, Case 3의 경우 Fig. 12 ~ Fig. 14에 각각 나타내었다. 손상추정 결과 Case 1은 76 혹은 78번 라인에서 23.55%의 손상이 발생된 것으로 예측되었으며, Case 2에서는 79번 혹은 82번에서 9.77%의 손상이 Case 3에서는 26번 혹은 28번 라인에서 19.12%의 손상이 발생된 것으로 추정되었다. 3가지 경우 모두에서 2개의 요소에서 손상 가능성과 정도가 동일하게 예측되었는데 이러한 원인은 모델의 대칭성에 의한 것으로 판단된다. 이상의 추정 결과를 Fig. 15와 Table 4에 정리하였다.