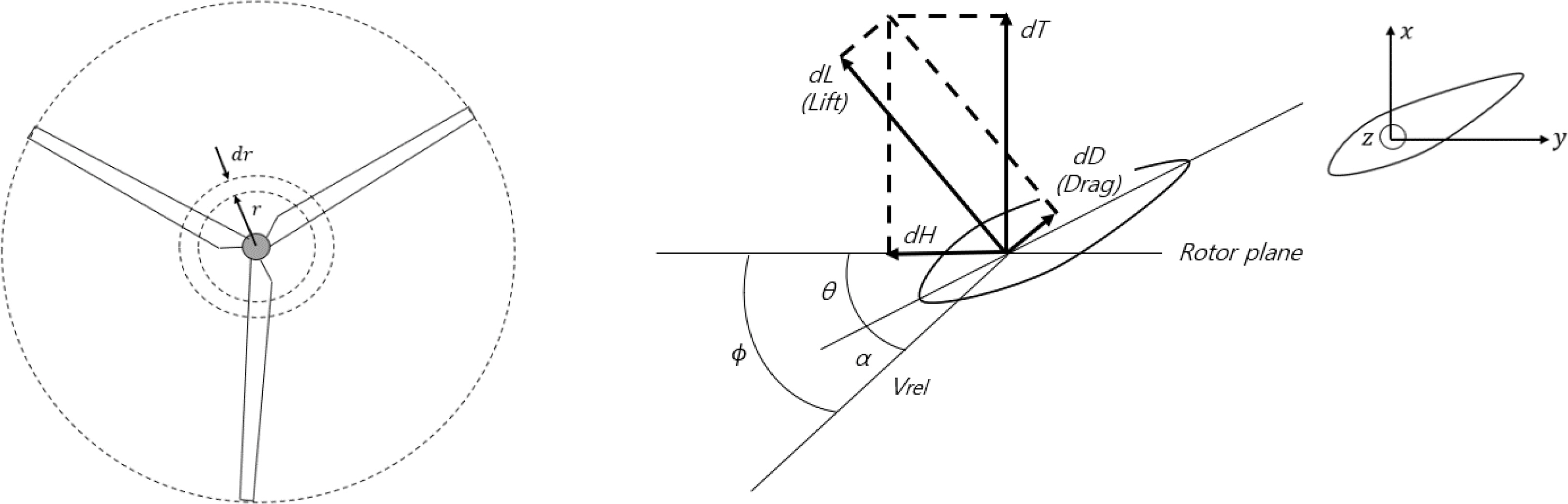
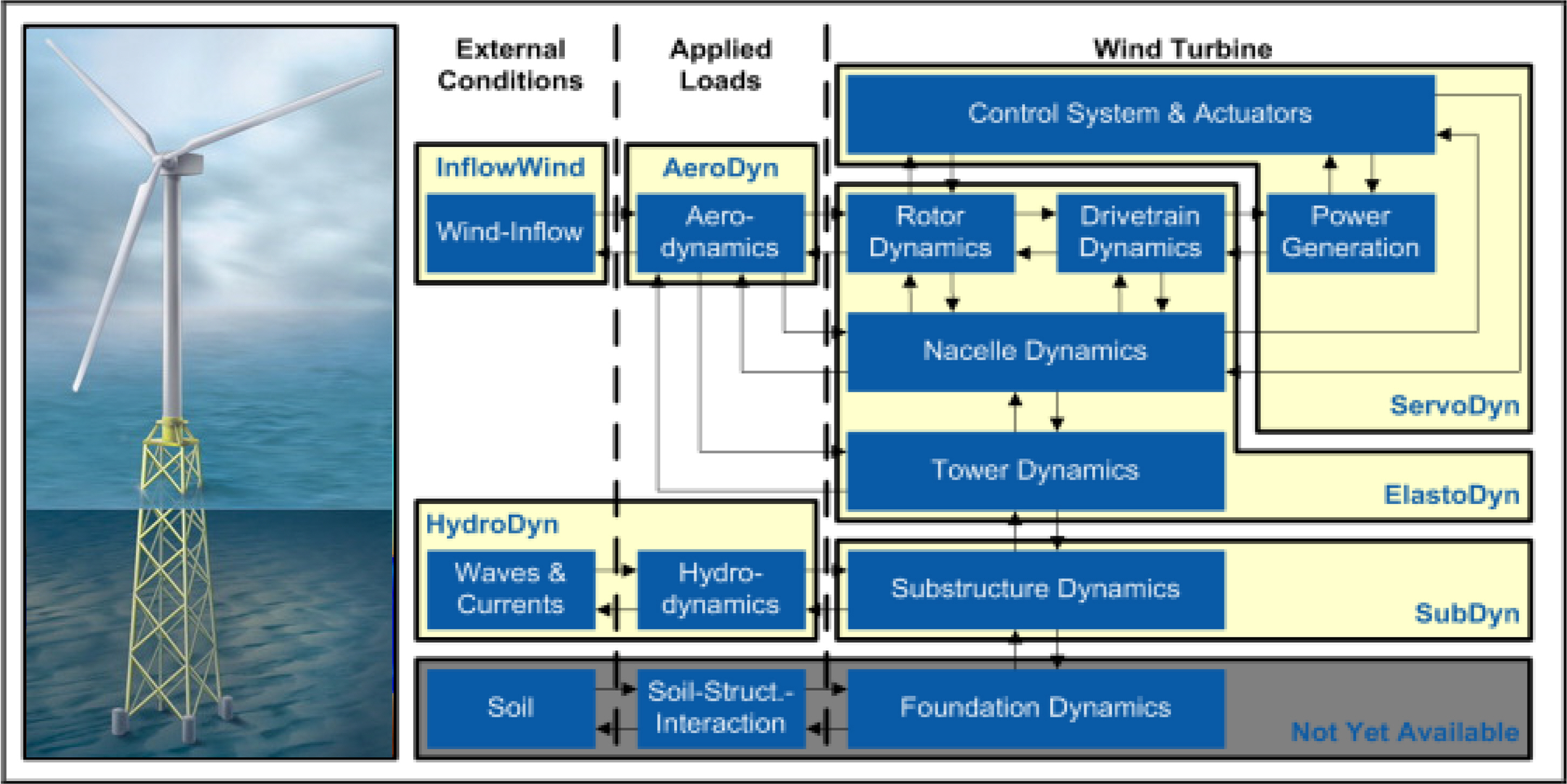
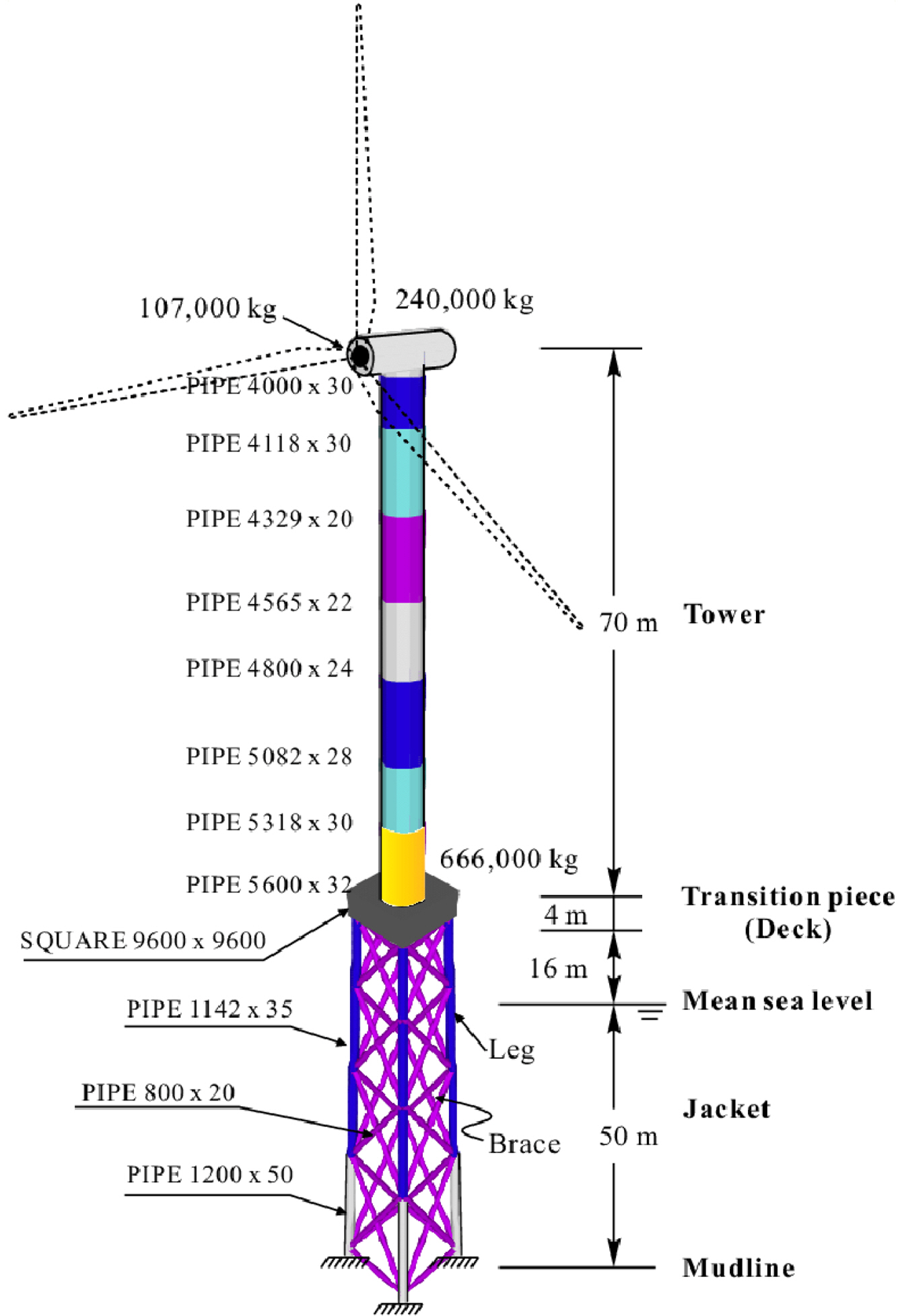
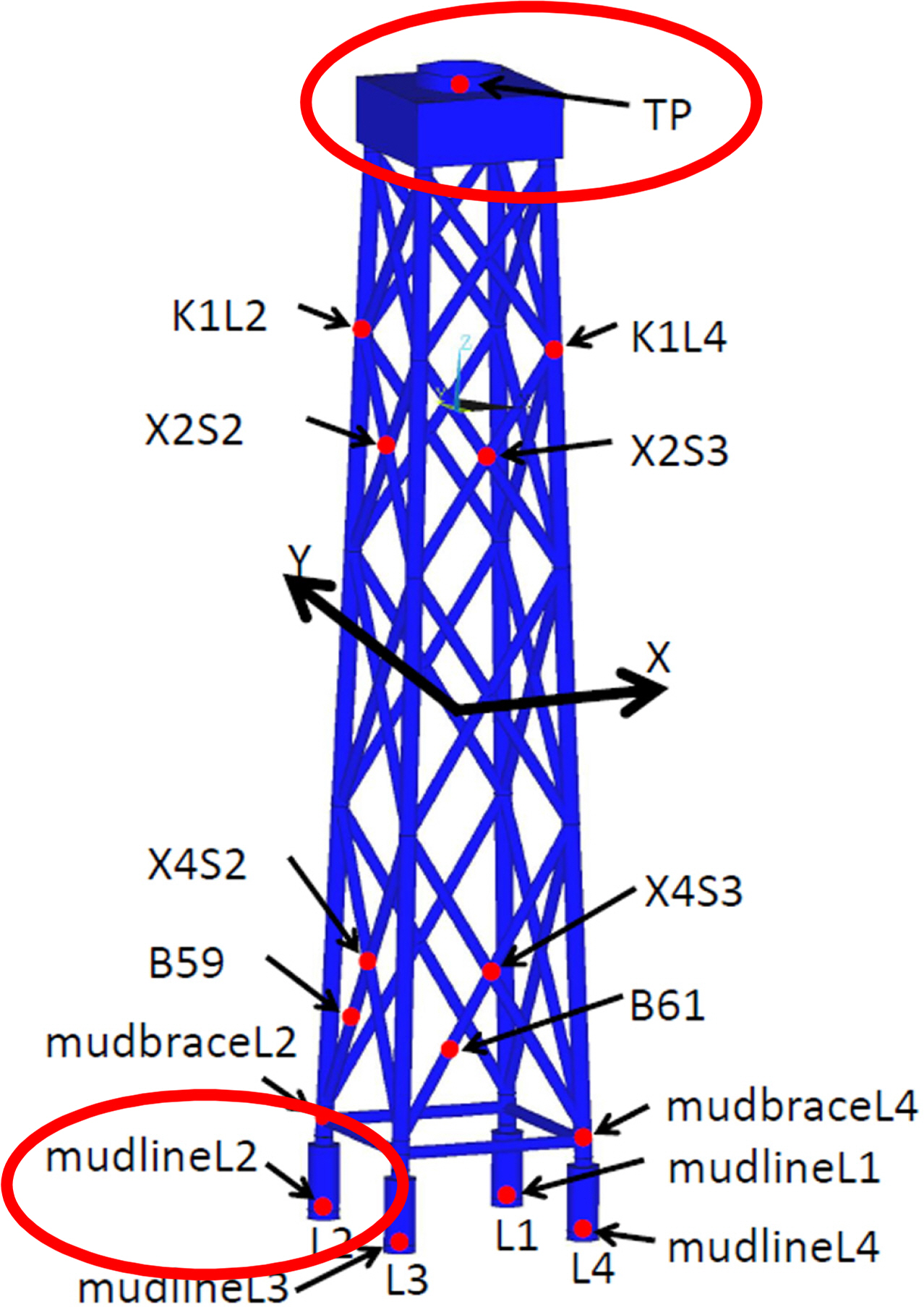
Agarwal, P., & Manuel, L. (2008). Extreme Loads for an Offshore Wind Turbine Using Statistical Extrapolation from Limited Field Data.
Wind Energy,
11(6), 673-684.
https://doi.org/10.1002/we.301

Burton, T., Sharpe, D., Jenkins, N., & Bossanyi, E. (2001). Wind Energy Handbook. New York. Wiley.
Damiani, R., Jonkman, J., & Hayman, G. (2015).
SubDyn UserŌĆÖs Guide and Theory Manual (Technicla Report NREL/TP-500063062). USA. National Renewable Energy Laboratory:
https://doi.org/10.2172/1225918

de Vries, W., Vemula, NK., Passon, P., Fischer, T., Kaufer, D., Matha, D., & Vorpahl, F. (2011). Final Report WP4.2: Support Structure Concepts for Deep Water (UpWind_WP4_D4.2.8).
Faltinsen, O. (1993). Sea Loads on Slips and Offshore Structures USA:. Cambridge University Press.
Fenu, B., Attanasio, V., Casalone, P., Novo, R., Cervelli, G., Bonfanti, M., & Mattiazzo, G. (2020). Analysis of a Gyroscopic-Stabilized Floating Offshore Hybrid Wind-Wave Platform.
Journal of Marine Science and Engineering,
8(6), 439.
https://doi.org/10.3390/jmse8060439

International Electrotechnical Commission (IEC). (2019). Wind Energy Generation Systems ŌĆō Part 3-1: Design Requirements for Fixed Offshore Wind Turbines (IEC 61400-3-1), IEC.
Jang, JS., & Sohn, JH. (2011). Analysis of Dynamic Behavior of Floating Offshore Wind Turbine System.
Transactions of the Korean Society of Mechanical Engineers A,
35(1), 77-83.
https://doi.org/10.3795/KSME-A.2011.35.1.077

Jeong, SM., Oh, UG., Lee, YC., Lim, JT., Lee, KB., & Choi, JS. (2020). A Study on the Evaluation of the Economics and Environmental Contribution to the Jeju Power System from Tamla Offshore Wind Farm.
The Transactions of The Korean Institute of Electrical Engineers,
69(7), 955-963.
https://doi.org/10.5370/KIEE.2020.69.7.955

Jonkman, JM. (2007). Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine (Technicla Report NREL/TP-500-41958). USA. National Renewable Energy Laboratory.
Jonkman, JM., & Buhl, ML Jr. (2005). FAST UserŌĆÖs Guide (Technical Report, NREL/EL-500-38230). USA. National Renewable Energy Laboratory.
Jonkman, JM., Butterfield, S., Musial, W., & Scott, G. (2009). Definition of a 5-MW Reference Wind Turbine for Offshore System Development (NREL/TP-500-38060). USA. National Renewable Energy Laboratory.
Jonkman, JM., Hayman, GJ., Jonkman, BJ., Damiani, RR., & Murray, RE. (2015). AeroDyn v15 UserŌĆÖs Guide and Theory Manual. USA. National Renewable Energy Laboratory.
Jonkman, JM., Robertson, AN., & Hayman, GJ. (2014). HydroDyn UserŌĆÖs Guide and Theory Manual. USA. National Renewable Energy Laboratory.
Kim, KH., Kim, DH., Kwak, YS., & Kim, SH. (2015). Design Load Case Analysis and Comparison for a 5MW Offshore Wind Turbine Using FAST, GH Bladed and CFD Method.
The KSFM Journal of Fluid Machinery,
18(2), 14-21.
https://doi.org/10.5293/kfma.2015.18.2.014

Li, L., Gao, Y., Hu, Z., Yuan, Z., Day, S., & Li, H. (2018). Model Test Research of a Semisubmersible Floating Wind Turbine with and Improved Deficient Thrust Force Correaction Approach.
Renewable Energy,
119, 95-105.
https://doi.org/10.1016/j.renene.2017.12.019

Morison, J., Johnson, J., & Schaaf, S. (1950). The Force Exerted by Surface Waves on Piles.
Journal of Petroleum Technology,
2, 149-154.
https://doi.org/10.2118/950149-G

Oh, HT., Yeo, MY., Jung, HE., & Shim, JM. (2020). Status and Improvement of Environmental Impacts Assessment on the Marine Endangered Species Around the Coastal Area of Offshore Wind Energy ŌĆō Case Study of the Marine Mammals and Sea Birds.
Journal of fishries and Marine Sciences Education,
32(6), 1428-1444.
https://doi.org/10.13000/JFMSE.2020.12.32.6.1428

Park, MK., Park, SG., Seong, BC., Choi, YJ., & Jung, SH. (2021). Current Status and Prospective of Offshore Wind Power to Achieve Korean Renewable Energy 3020 Plan.
Journal of Korean Society of Environmental Engineers,
43(3), 196-205.
https://doi.org/10.4491/KSEE.2021.43.3.196

Peters, DA., Boyd, DD., & He, CJ. (1989). Finite-State Induced- Flow Model for Rotors in Hover and Forward Flight.
Journal of the American Helicopter Society,
34(4), 5-17.
https://doi.org/10.4050/JAHS.34.5

Popko, W., Vorpahl, F., Zuga, A., Kohlmeier, M., Jonkman, J., Robertson, A., & von Waaden, H. (2012). Offshore Code Comparison Collaboration Continuation (OC4), Phase 1-Results of Coupled Simulations of an Offshore Wind Turbine with Jacket Support Structure. In The Twenty-second International Offshore and Polar Engineering Conference Rhodes, Greece, ISOPEI-12-117.

Shi, W., Park, HC., Chung, CW., & Kim, YC. (2011). Comparison of Dynamic Response of Monopile, Tripod and Jacket Foundation System for a 5-MW Wind Turbine. In the Twenty-first International Offshore and Polar Engineering Conference Maui, Hawaii, USA, ISOPE-I-11-266.
Song, CY., & Yoo, J. (2017). Dynamic Response Analyses of Fixed Type Substructures for 2.5 MW Class Offshore Wind Turbine.
Journal of Advanced Research in Ocean Engineering,
3(1), 15-24.
https://doi.org/10.5574/JAROE.2017.3.1.015

Suzuki, A. (2000). Application of Dynamic Inflow Theory to Wind Turbine Rotors (Ph. D. thesis). University of Utah.
Tran, TT., Kang, S., Lee, JH., & Lee, D. (2021). Directional Bending Performance of 4-Leg Jacket Substructure Supporting a 3MW Offshore Wind Turbine.
Energies,
14(9), 2725.
https://doi.org/10.3390/en14092725

Wei, K., Sanjay, RA., & Myers, AT. (2014). Incremental Wind-Wave Analysis of the Structural Capacity of Offshore Wind Turbine Support Structures under Extreme Loading.
Engineering Structures,
79, 58-69.
https://doi.org/10.1016/j.engstruct.2014.08.010

Zwick, D., & Muskulus, M. (2015). The Simulation Error Caused by Input Loading Variability in Offshore Wind Turbine Structural Analysis.
Wind Energy,
18(8), 1421-1432.
https://doi.org/10.1002/we.1767