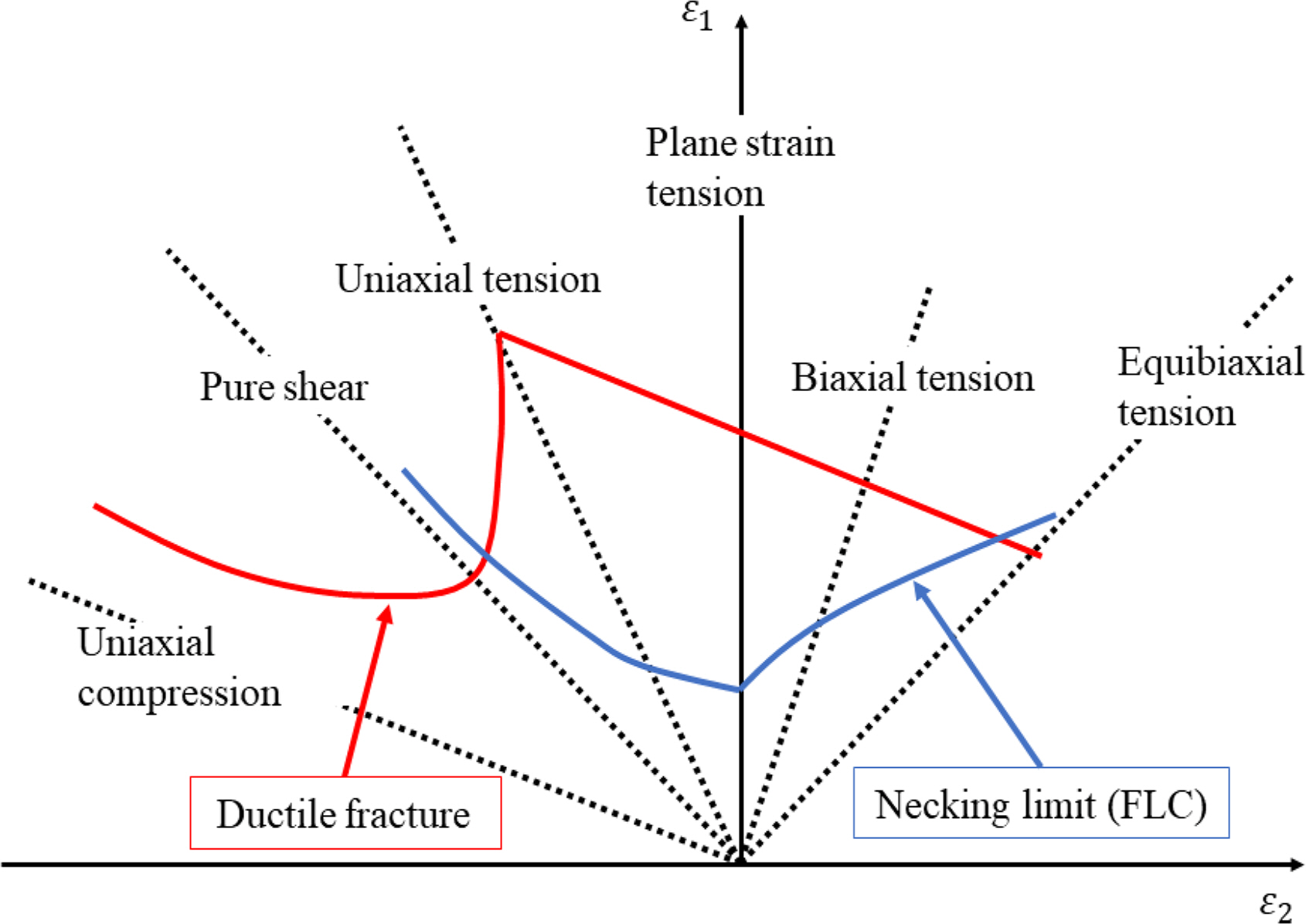
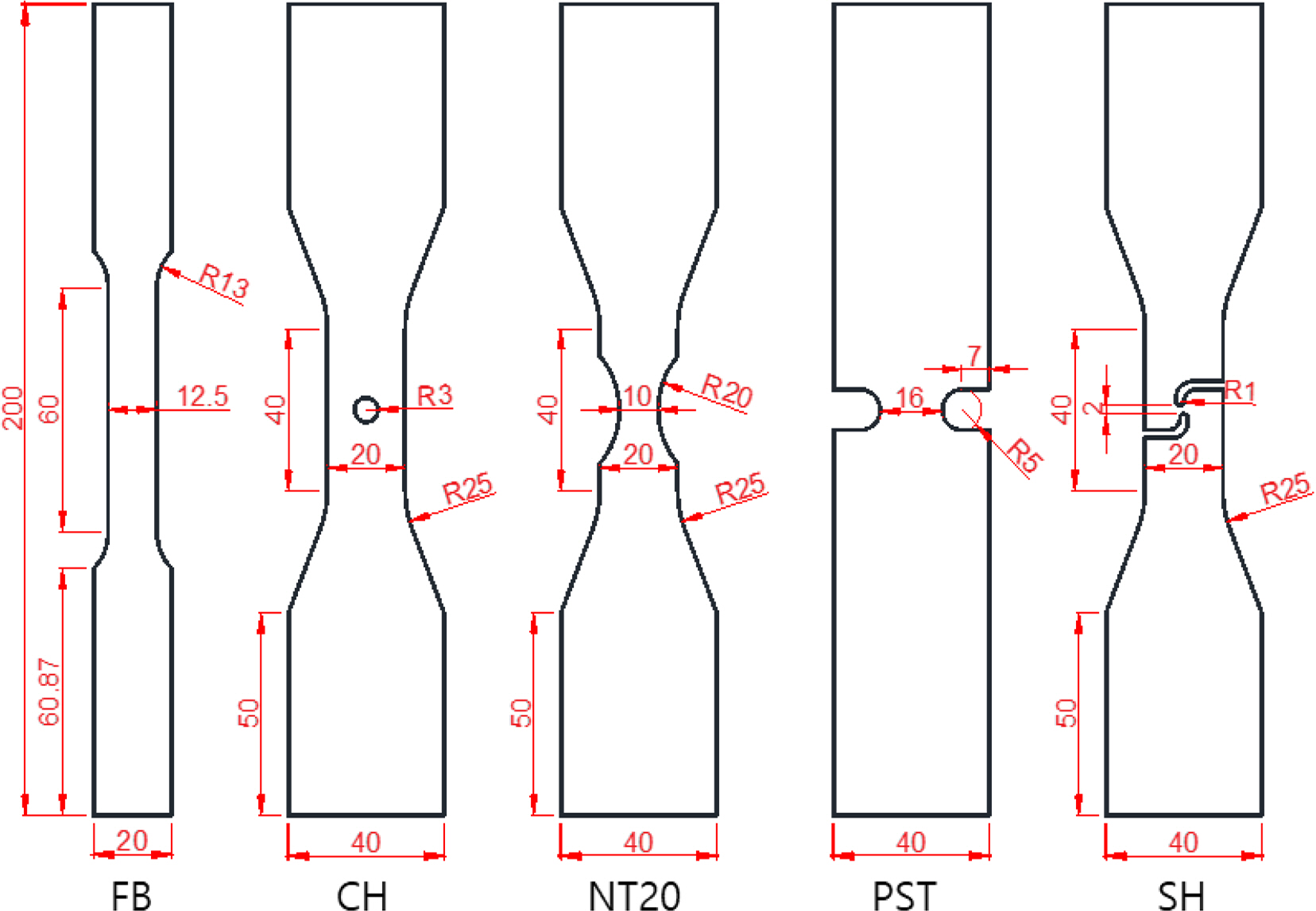
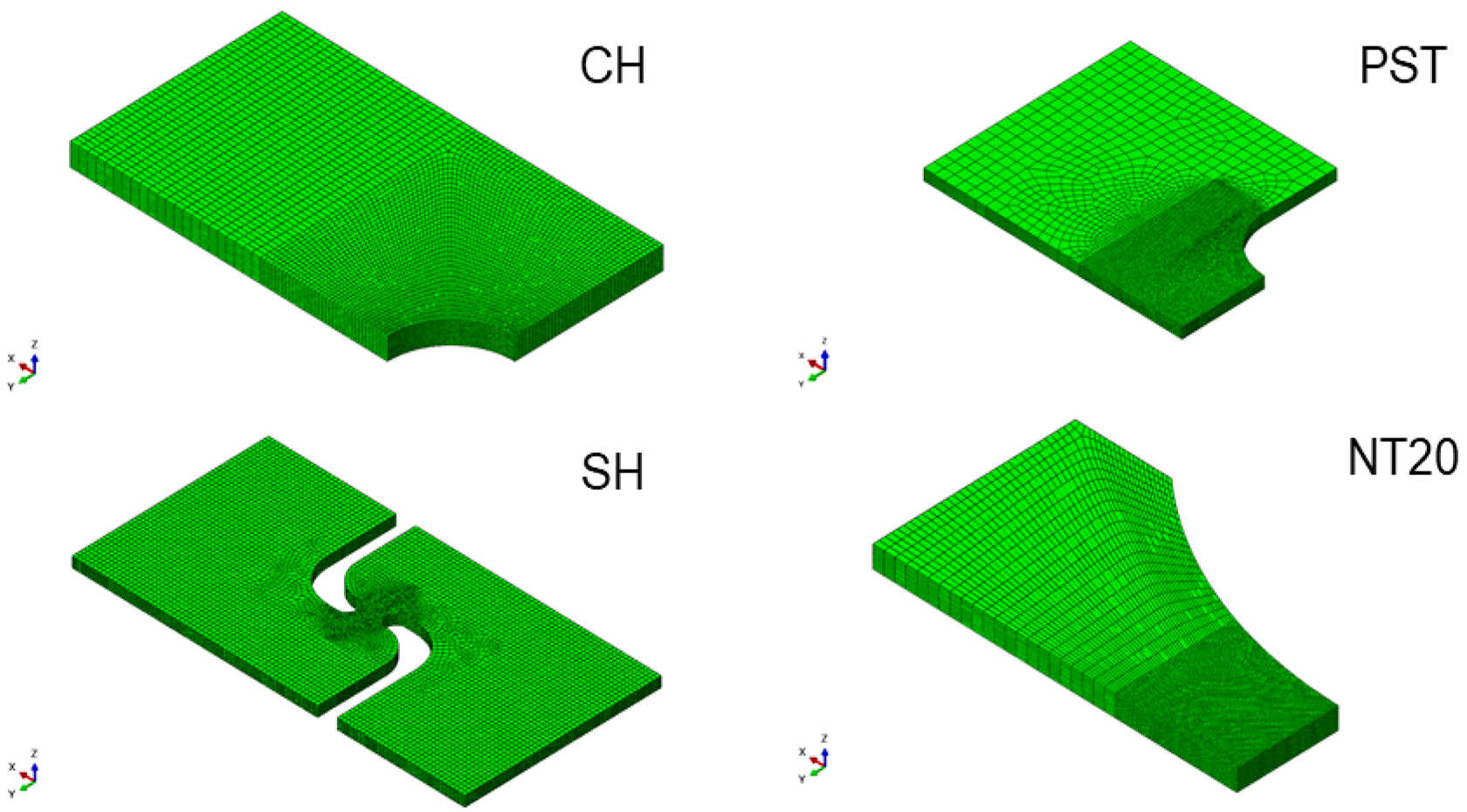
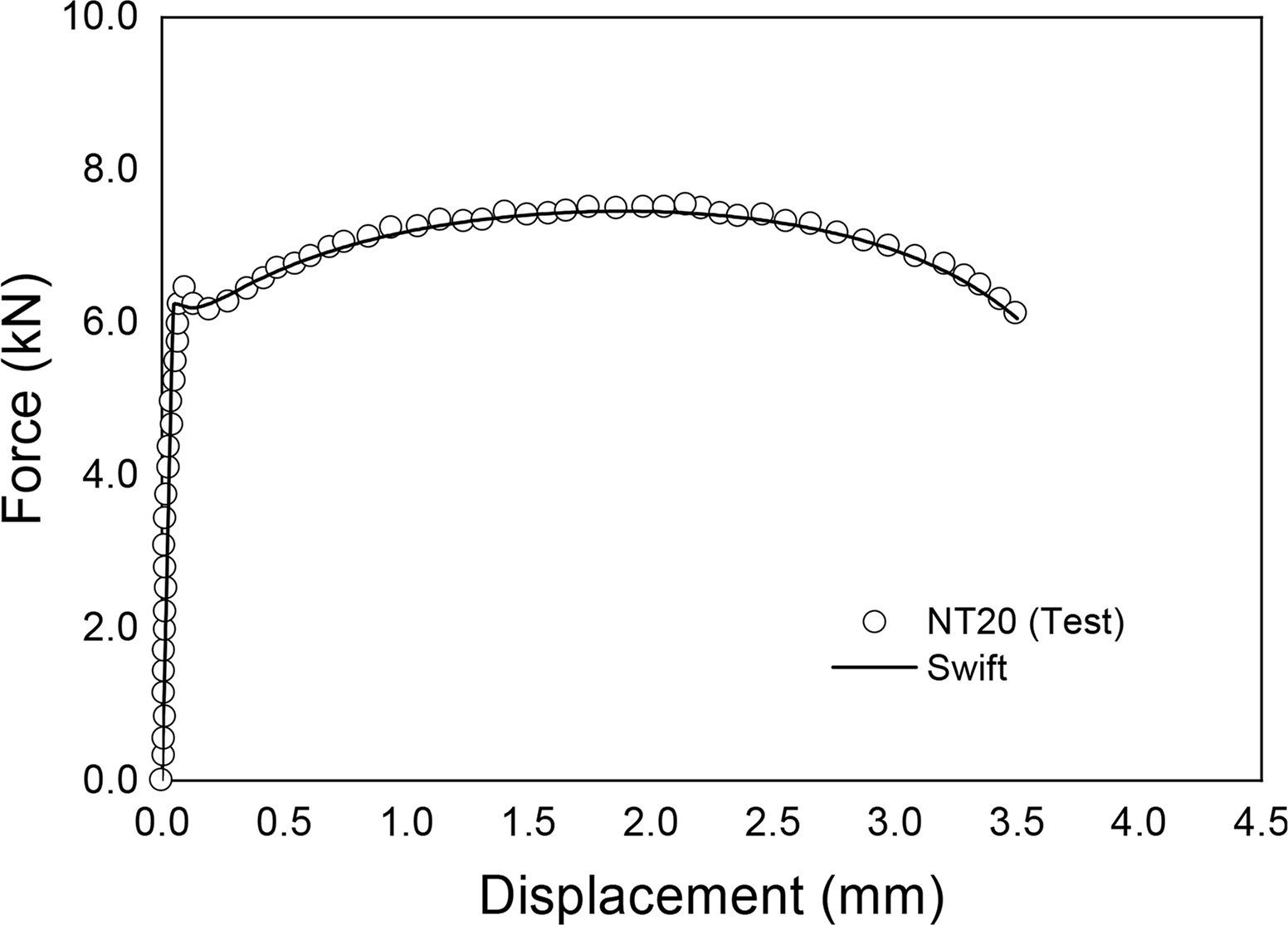
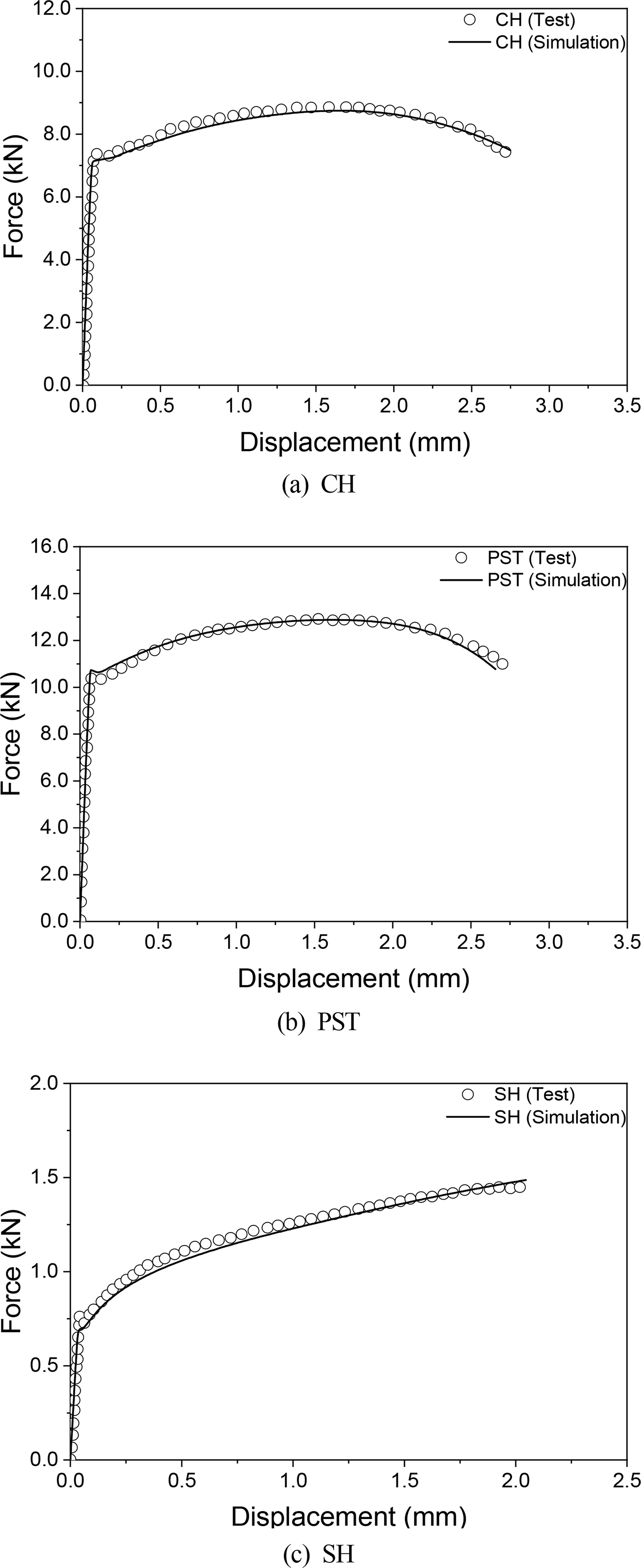
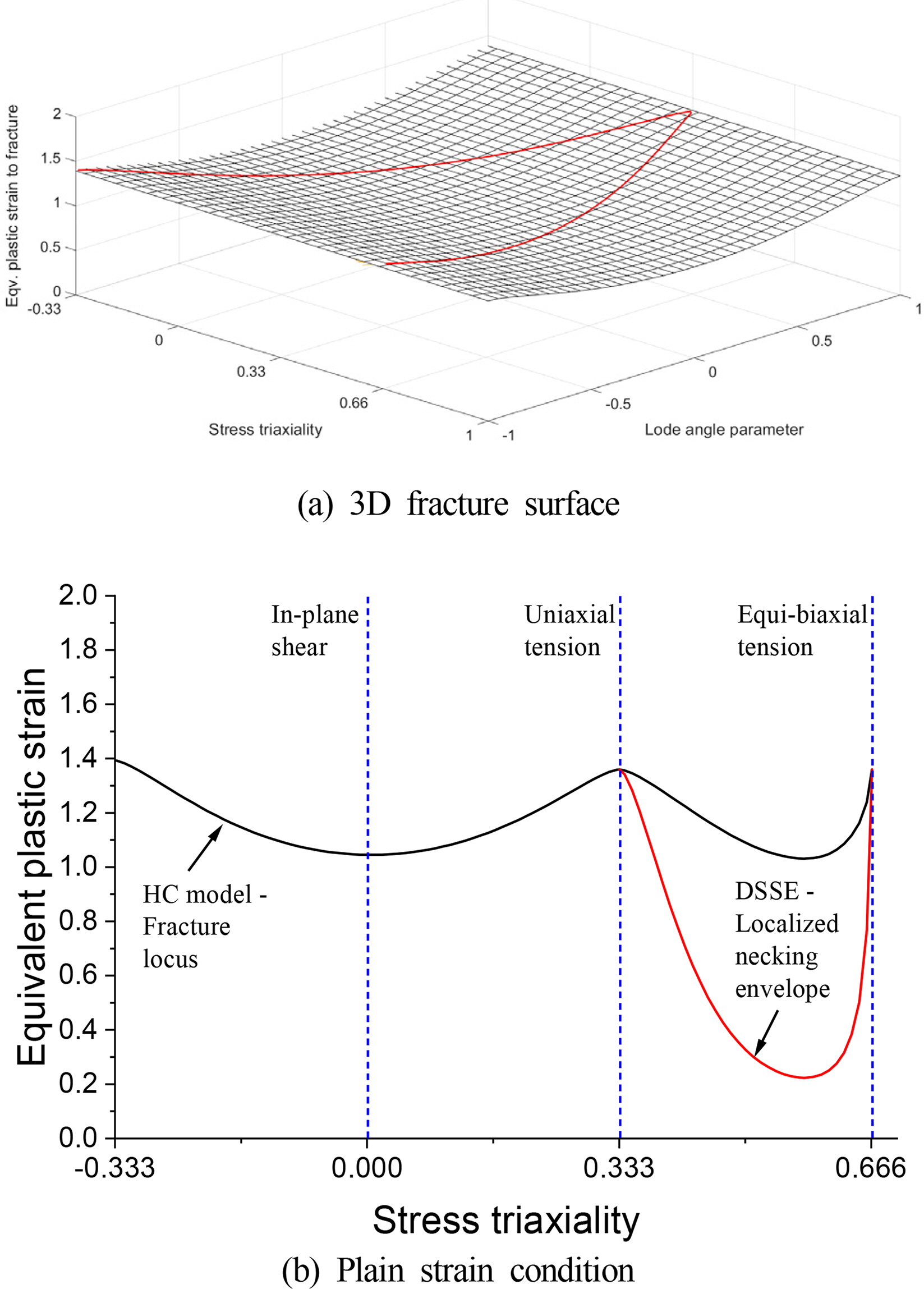
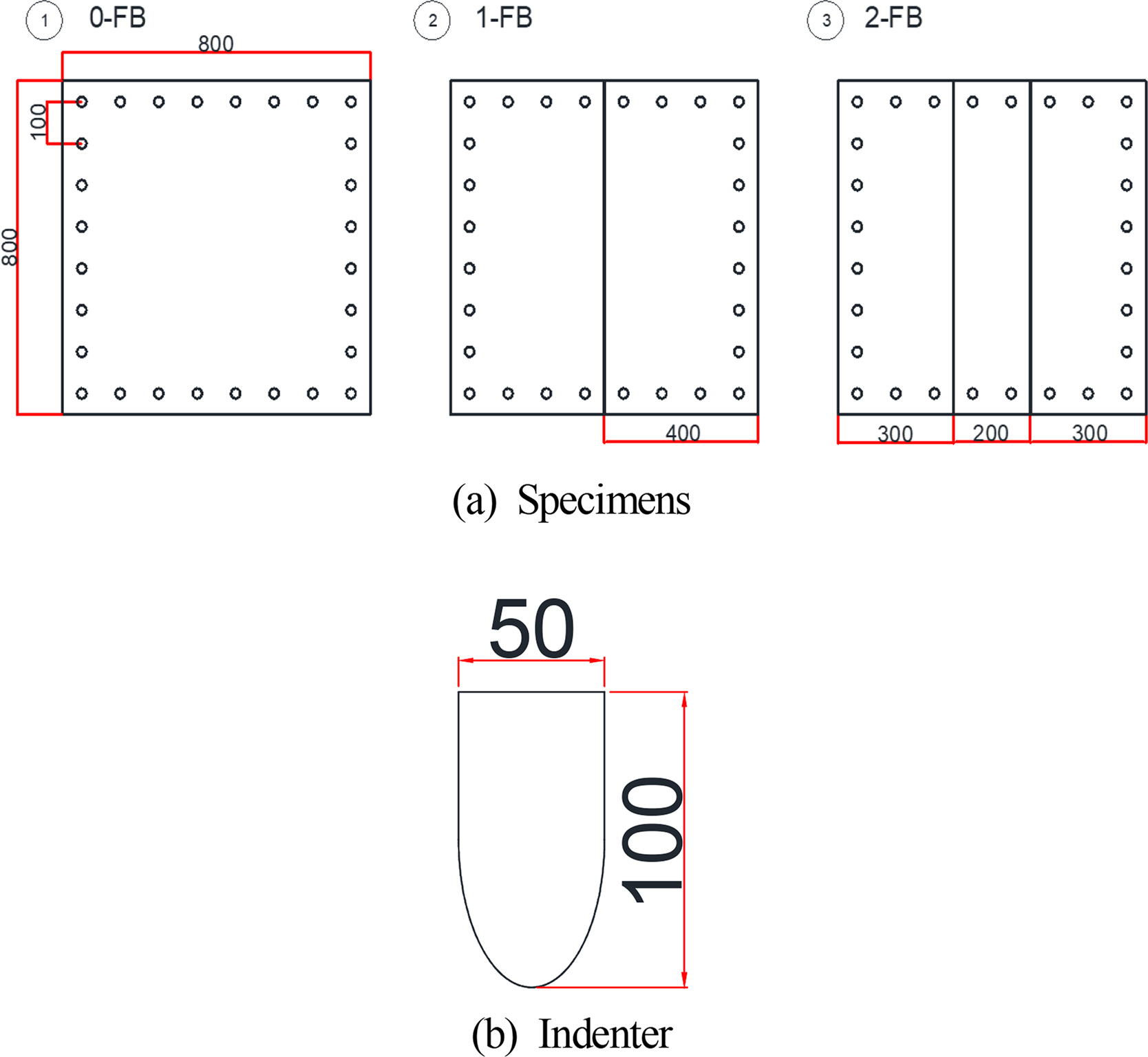
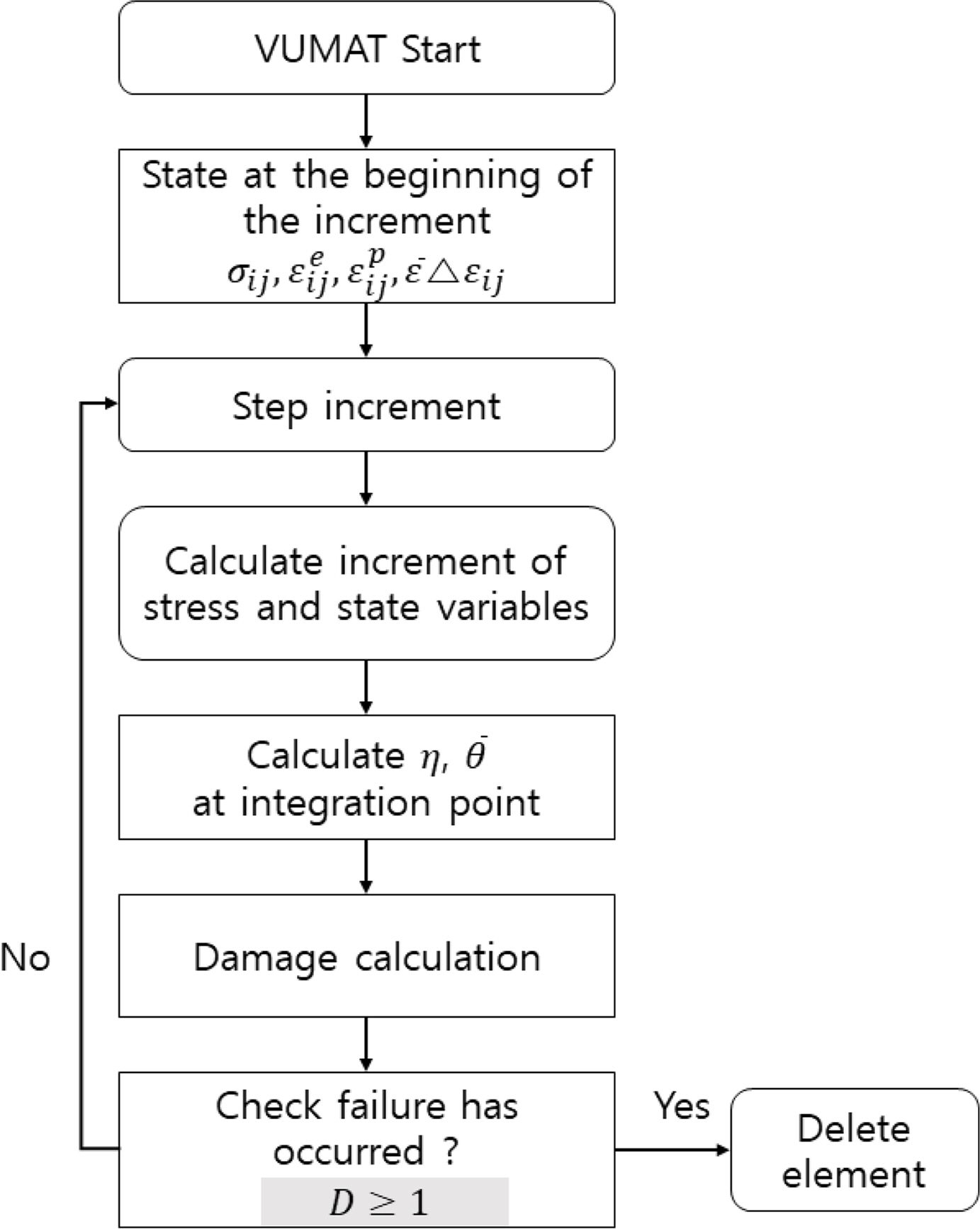
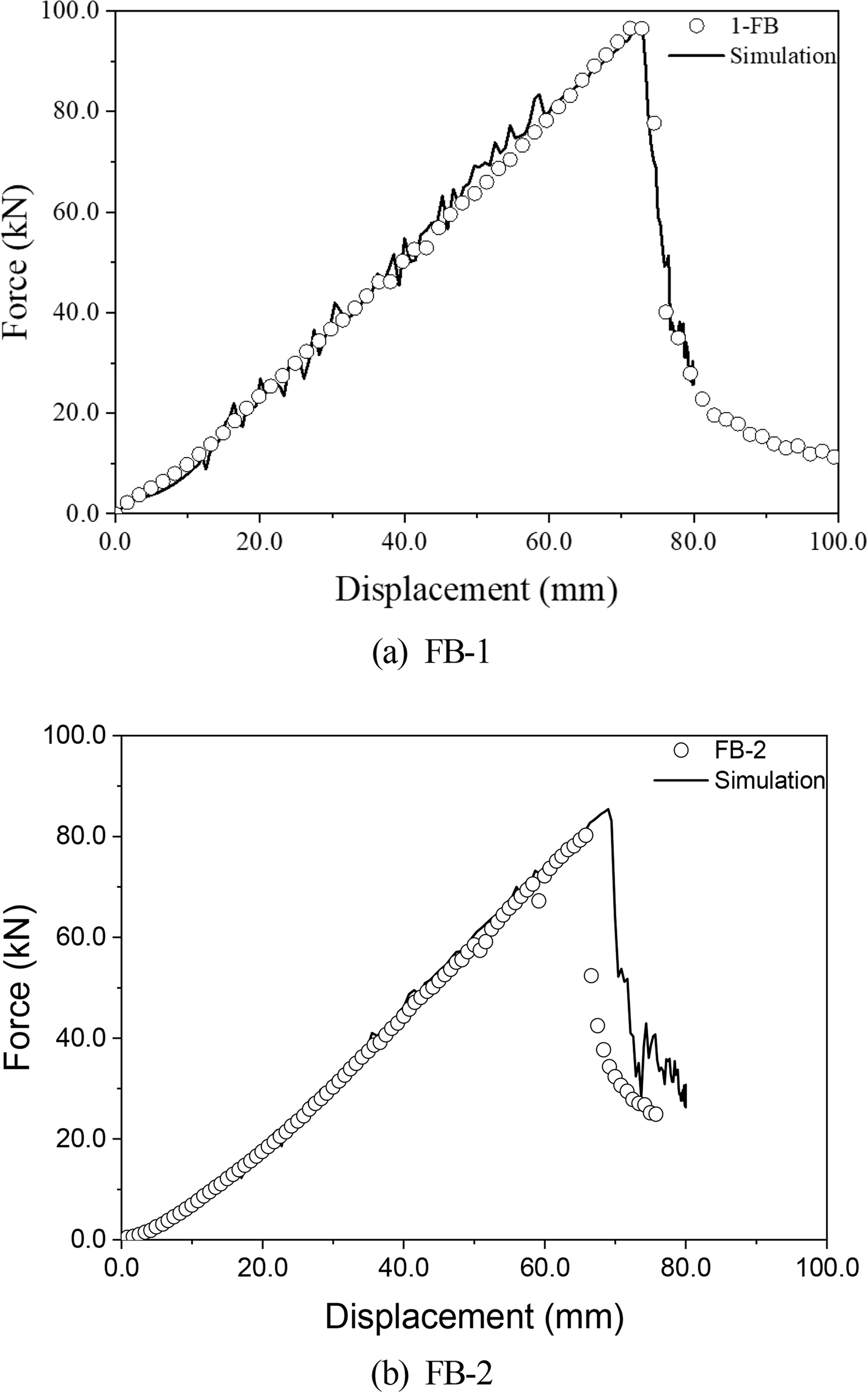
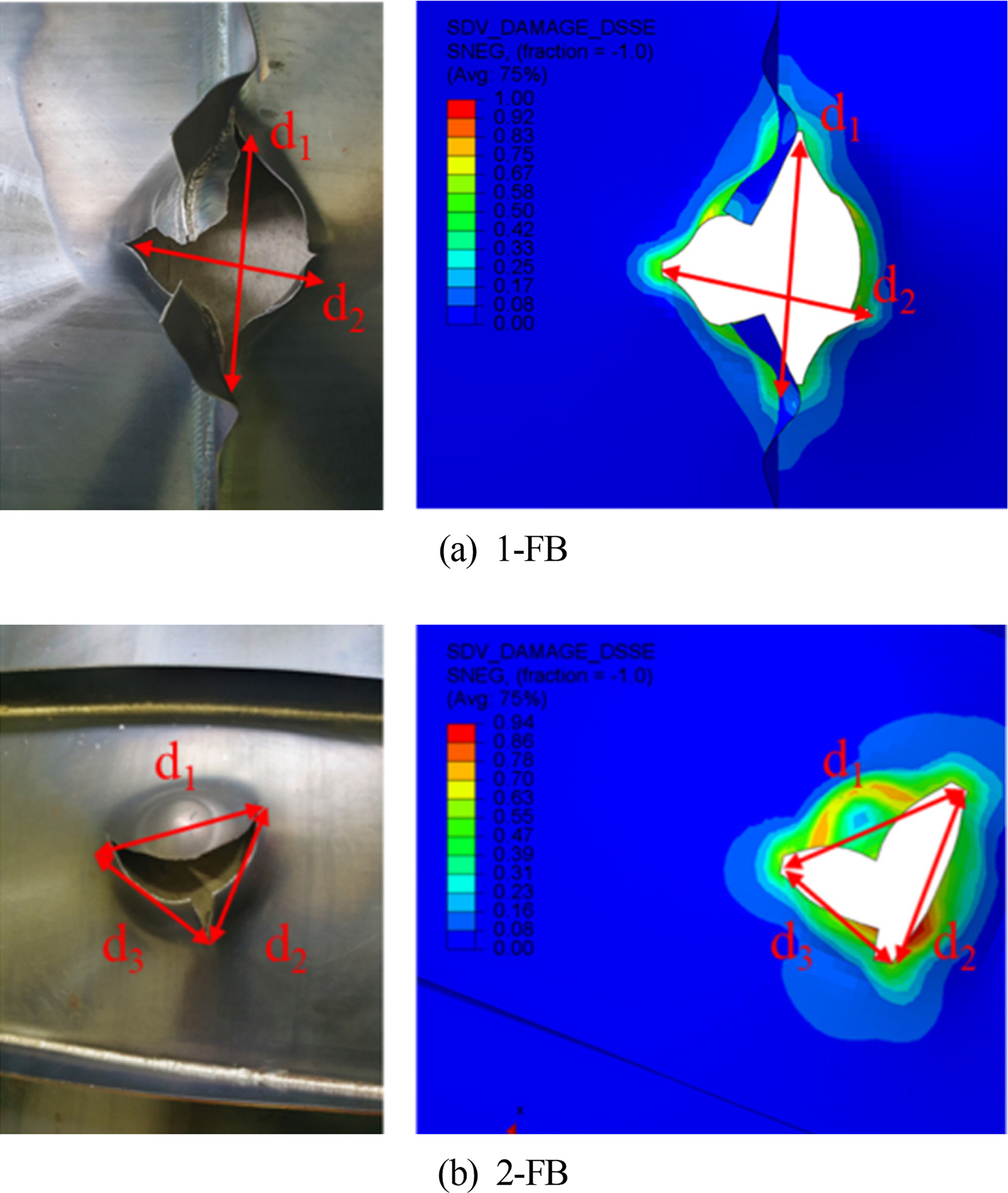
Algarni, M., Choi, Y., & Bai, Y. (2017). A Unified Material Model for Multiaxial Ductile Fracture and Extremely Low Cycle Fatigue of Inconel 718.
International Journal of Fatigue,
96, 162-177.
https://doi.org/10.1016/j.ijfatigue.2016.11.033

American Society for Testing and Materials (ASME). (2004). Standard Test Methods of Tension Testing of Metallic Materials (ASTM E8), American Society for Testing and Materials.
Cerik, BC., & Choung, J. (2020). On the prediction of ductile fracture in ship structures with shell elements at low temperatures.
Thin-Walled Structures,
151, 106721.
https://doi.org/10.1016/j.tws.2020.106721

Cerik, BC., Lee, K., Park, SJ., & Choung, J. (2019a). Simulation of Ship Collision and Grounding Damage Using Hosford-Coulomb Fracture Model for Shell Elements.
Ocean Engineering,
173, 415-432.
https://doi.org/10.1016/j.oceaneng.2019.01.004

Cerik, BC., Ringsberg, JW., & Choung, J. (2019b). Revisiting MARSTRUCT Benchmark Study on Side-shell Collision with a Combined Localized Necking and Stress-state Dependent Ductile Fracture Model.
Ocean Engineering,
187, 106173.
https://doi.org/10.1016/j.oceaneng.2019.106173

Cerik, BC., Park, B., Park, SJ., & Choung, J. (2019c). Modeling, Testing and Calibration of Ductile Crack Formation in Grade DH36 Ship Plates.
Marine Structures,
66, 27-43.
https://doi.org/10.1016/j.marstruc.2019.03.003

Choung, J., Park, SJ., & Kim, Y. (2015a). Development of Three Dimensional Fracture Strain Surface in Average Stress Triaxiaility and Average Normalized Lode Parameter Domain for Arctic High Tensile Steel: Part I Theoretical Background and Experimental Studies.
Journal of Ocean Engineering and Technology,
29(6), 445-453.
https://doi.org/10.5574/KSOE.2015.29.6.445


Choung, J., Park, SJ., & Kim, Y. (2015b). Development of Three-Dimensional Fracture Strain Surface in Average Stress Triaxiaility and Average Normalized Lode Parameter Domain for Arctic High Tensile Steel: Part II Formulation of Fracture Strain Surface.
Journal of Ocean Engineering and Technology,
29(6), 454-462.
https://doi.org/10.5574/KSOE.2015.29.6.454


Cho, SR., Park, JY., Song, SU., & Park, SH. (2018). Scale Effects on the Structural Behavior of Steel Unstiffened Plates Subjected to Lateral Collisions.
Journal of the Society of Naval Architects of Korea,
55(2), 178-186.
https://doi.org/10.3744/SNAK.2018.55.2.178

Ehlers, S., Broekhuijsen, J., Alsos, HS., Biehl, F., & Tabri, K. (2008). Simulating the collision response of ship side structures: A failure criteria benchmark study.
International Shipbuilding Progress,
55(1), 127-144.
https://doi.org/10.3233/ISP-2008-0042

Johnson, GR., & Cook, WH. (1985). Fracture Characteristics of Three Metals Subjected to Various Strain, Strain Rates Temperatures and Pressures.
Engineering Fracture Mechanics,
21(1), 31-48.
https://doi.org/10.1016/0013-7944(85)90052-9

Mohr, D., & Marcadet, S. (2015). Micromechanically-motivated Phenomenological Hosford-coulomb Model for Predicting Ductile Fracture Initiation at Low Stress Triaxialites.
International Journal of Solids and Structures, 67-68 40-55.
https://doi.org/10.1016/j.ijsolstr.2015.02.024

Min, DK., & Cho, SR. (2012). On the Fracture of Polar Class Vessel Structures Subjected to Lateral Impact Loads.
Journal of the Society Naval Architects of Korea,
49(4), 281-286.
https://doi.org/10.3744/SNAK.2012.49.4.281


Nho, IS., Park, MJ., & Cho, YS. (2018). Preliminary Structural Design of Blast Hardened Bulkhead (The 2nd Report : Scantling Formula for Curtain Plate Type Blast Hardened Bulkhead).
Journal of the Society Naval Architects of Korea,
55(5), 379-384.
https://doi.org/10.3744/SNAK.2018.55.5.379

Park, SJ., Lee, K., & Choung, J. (2016). Punching Fracture Simulations of Circular Unstiffened Steel Plates Using Three-dimensional Fracture Surface.
Journal of Ocean Engineering and Technology,
30(6), 474-483.
https://doi.org/10.5574/KSOE.2016.30.6.474


Park, SJ., Park, B., & Choung, J. (2017). Ductile fracture predictions of High Strength Steel (EH36) Using Linear and Non-Linear Damage Evolution Models.
Journal of Ocean Engineering and Technology,
31(4), 288-298.
https://doi.org/10.26748/KSOE.2017.08.31.4.288


Park, SJ., Lee, K., Cerik, BC., Kim, Y., & Choung, J. (2019a). Ductile Fracture of a Marine Structural Steel Based on HC-DSSE Combined Fracture Strain Formulation.
Journal of the Society of Naval Architects of Korea,
56(1), 82-93.
https://doi.org/10.3744/SNAK.2019.56.1.082

Ringsberg, JW., Amdahl, J., Chen, BQ., Cho, SR., Ehlers, S., Hu, Z., & Zhang, S. (2018). MARSTRUCT Benchmark Study on Nonlinear FE Simulation of an Experiment of an Indenter Impact with a Ship Side-shell Structure.
Marine Structures,
59, 142-157.
https://doi.org/10.1016/j.marstruc.2018.01.010

Xue, L. (2007). Damage Accumulation and Fracture Iinitiation in Uncracked Ductile Solids Subject to Triaxial Loading.
International Journal of Solids and Structures,
44(16), 5163-5181.
https://doi.org/10.1016/j.ijsolstr.2006.12.026