Impact of the Thruster Jet Flow of Ultra-large Container Ships on the Stability of Quay Walls
Article information
Abstract
As the size of ships increases, the size and output power of their thrusters also increase. When a large ship berths or unberths, the jet flow produced from its thruster has an adverse effect on the stability of quay walls. In this study, we conducted a numerical analysis to examine the impact of the thruster jet flow of a 30,000 TEU container ship, which is expected to be built in the near future, on the stability of a quay wall. In the numerical simulation, we used the fluid–structure interaction analysis technique of LS-DYNA, which is calculated by the overlapping capability using an arbitrary Lagrangian Eulerian formulation and Euler–Lagrange coupling algorithm with an explicit finite element method. As the ship approached the quay wall and the vertical position of the thruster approached the mound of the quay wall, the jet flow directly affected the foot-protection blocks and armor stones. The movement and separation of the foot-protection blocks and armor stones were confirmed in the area affected directly by the thruster jet flow of the container ship. Therefore, the thruster jet flows of ultra-large ships must be considered when planning and designing ports. In addition, the stability of existing port structures must be evaluated.
1. Introduction
Increasingly large container ships are being constructed to accommodate increasing shipping volumes. Based on the definition of container capacity by Prokopowicz and Berg-Andreassen (2016), the construction of ultra-large container ships (ULCSs) of 20,000 twenty-foot equivalent units (TEU) or larger is being realized at a higher rate than that of very large container ships (VLCSs) of 10,000–20,000 TEU. Currently (as of August 2021), the largest container ships among the ULCS are of 24,000 TEU, with 36 in operation. The size of the ship is up to 399.9 m in length and 61.5 m in width. The Korea Maritime Institute (KMI) predicted that ULCSs of 30,000 TEU with a length of 493.2 m, width of 64.1 m, and load draft of 17.5 m would be designed in the near future (Jeon, 2015).
As the size of the ship increases, the size of its bow and stern thrusters, which are dynamic positioning systems (DPSs), also increases. The thruster of a ship is generally used as an auxiliary propulsion device to maintain a route in coastal waters with low water depth, waterways with narrow channels such as canals, and seas with strong currents or winds. If no mandatory regulations exist on the use of tugs, ship thrusters can considerably save time and money by enabling lateral movement during berthing and deberthing. The jet flow produced from the thruster, however, directly affects the quay wall while the ship is berthing and deberthing, which should be analyzed.
Studies on ship thrusters focus on their hydrodynamic properties and performance (Bulten and Suijkerbuijk, 2013; Yu and Yang, 2016; Abramowicz-Gerigk and Gerigk, 2020; Feng et al., 2020) and their operation, as well as berthing and deberthing simulation results (Bui et al., 2010; Tran and Im, 2012; Jeong et al., 2012; Benedict et al., 2017; Artyszuk and Zalewski, 2021). To understand the effects of thruster jet flow, flow characteristics around the quay wall (van Blaaderen, 2006; Irene, 2020), pressure (Abramowicz-Gerigk et al., 2018), and bottom scour (van den Brink, 2014; Roelse, 2014; Galal et al., 2016; Galal et al., 2019) have been analyzed. However, the behavior of the quay wall corresponding to the direct action of the thruster jet flow has hardly been discussed. As the size of the ship increases, the size of its thrust and draft considerably increase, thereby exhibiting a more considerable impact on the surrounding waters. Therefore, to build a safe port, the thruster jet flow of large container ships in existing port facilities should be analyzed before designing a new port.
This study aims to analyze the effect of thruster jet flow on a quay wall for a ULCS of 30,000 TEU, which is expected to be built in the near future. LS-DYNA, which allows for the analysis of fluid–structure interaction (FSI) and the simulation of complex nonlinear problems such as collisions and material shaping, is used to realize numerical simulations. The hydraulic characteristics of the jet flow of the ship thruster as well as the stability of the quay wall caissons, foot-protection blocks, and armor stones are discussed by applying the arbitrary Lagrangian Eulerian (ALE) method, which is selected among the several other FSI analysis methods of LS-DYNA.
2. Numerical Method
In this study, the ALE method of LS-DYNA R12 (LSTC, 2020), which can simultaneously consider the behaviors of the fluid and structure, was applied to simulate the nonlinear mutual interference of the thruster jet flow and the quay wall. LS-DYNA not only specializes in nonlinear analyses such as collision and destruction based on the explicit method, but also facilitates collision analyses between multiple objects as it does not require the contact elements to be created separately.
2.1 LS-DYNA
The ALE method (Santini et al., 1998; Souli et al., 2000; Sedden et al., 2004; Poehlmann-Martins et al., 2005) facilitates a bidirectional nonlinear interaction analysis between fluids and structures without deformation or movement of the computational grid. This method requires a reference coordinate system in addition to the Lagrangian and Eulerian coordinate systems, and it can handle boundary conditions, large deformations, and contact surface problems according to arbitrary motion. The following equation represents the relationship between the material time derivative and the reference configuration time derivative:
In LS-DYNA, the ALE technique method tracks the transfer of energy, mass, and momentum between elements by applying the continuity equation in the finite element method (FEM). The equations for the conservation of mass, momentum, and energy in the ALE methods are given below:
The ALE method was employed to supplement the shortcomings of the Lagrangian and Eulerian methods and to employ only the advantages. The fluid–structure coupling algorithm (FSCA) was applied to the contact surfaces of Lagrangian and Eulerian elements through operator splitting. If a significant element deformation occurred in the Lagrangian stage, the element was corrected by resetting the node position through the smoothing algorithm. In the Eulerian stage, the material properties of the element were transformed after the nodes were reset. During this process, the displacement and velocity of the Lagrangian structure model were substituted into the boundary conditions of the Eulerian fluid model, and the reaction force estimated by the FSCA acted on the elements of the Lagrangian structure model.
2.2 Numerical Condition
2.2.1 Numerical water tank
The container ship and quay wall were placed in a numerical water tank with a length of 85 m, width of 30 m, and height of 50 m, configured as shown in Fig. 1. Radiation boundary conditions were applied to the outer sea and both sides of the water tank, and no flux boundary conditions were applied to the floor and ceiling. For the ship and caisson, the fixed constraint conditions were considered, and for the armor stones on the slope of the mound and the foot-protection blocks on the floor, the free movement conditions were considered. The calculation grid and the calculation time interval of the numerical tank were set considering the Courant–Friedrichs–Lewy (CFL) and diffusive limit (DL) conditions, with the horizontal grid at 1 m and the vertical grid at 0.5 m; further, the initial calculation time interval (∆t) was 1/100 s. During calculation, ∆t was automatically varied to satisfy the CFL and DL conditions according to the fluid flow situation.
The berthing distance (Ls) of the ship is based on the horizontal distance of 33 m between the wall of the caisson and the center of the thruster during berthing. The water depth (h) in the port is set considering a load draft of 17.5 m for the ULCS of 30,000 TEU. Table 1 summarizes the nine limited calculation conditions, where the distances to the ship were set as Ls = 33 m, Ls = 38 m, and Ls = 43 m, and the water depth conditions in the port as h = 18 m (low tide level), h = 20 m (mean tide level), and h = 22 m (high tide level).
2.2.2 Ship and thruster
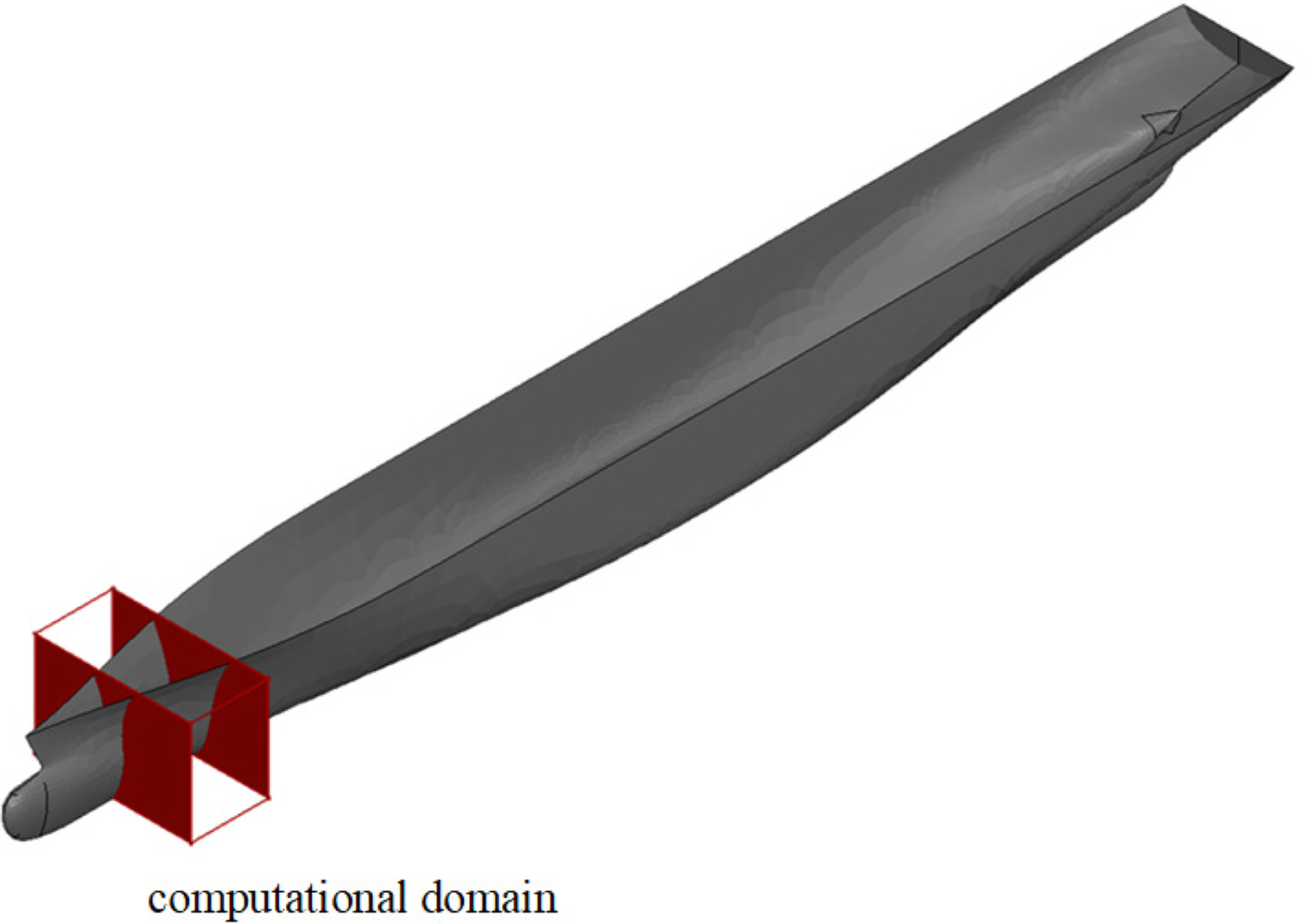
The hull applied to the numerical analysis of this study is shown in Fig. 2. The hull model of the Korea Research Institute of Ships & Ocean Engineering Container Ship (KCS) with a size of 7.2786 m × 1.019 m × 0.6013 m was used. With reference to the KMI data (Jeon, 2015), the basic KCS was enlarged according to the specifications (493.2 m × 64.1 m × 17.5 m) of a ULCS of 30,000 TEU.
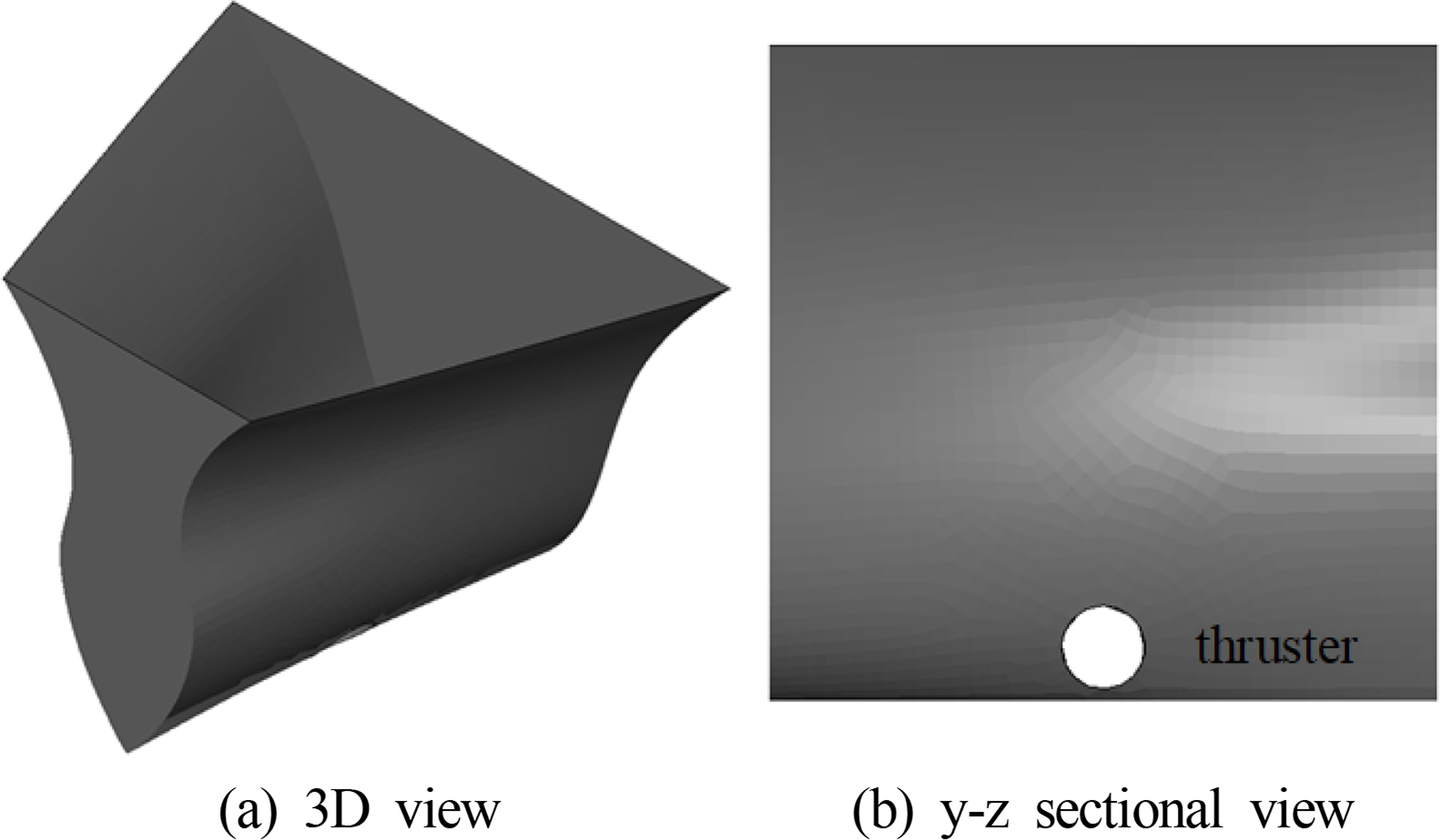
The domain shown in Fig. 2 is the section including the bow thruster, which was cut by 30 m and fixed to fit the width of the numerical water tank in Fig. 1. The computational domain, including this bow thruster, is shown in Fig. 3(a). No flux boundary conditions were applied to the hull. In this study, a single thruster with a diameter of 3.75 m was considered, as shown in Fig. 3(b), and the position of the center was 57 m from the bow and 2.58 m from the bottom of the ship, where the diameter and position of the thruster were set by referring to PIANC (2015).
2.2.3 Quay wall
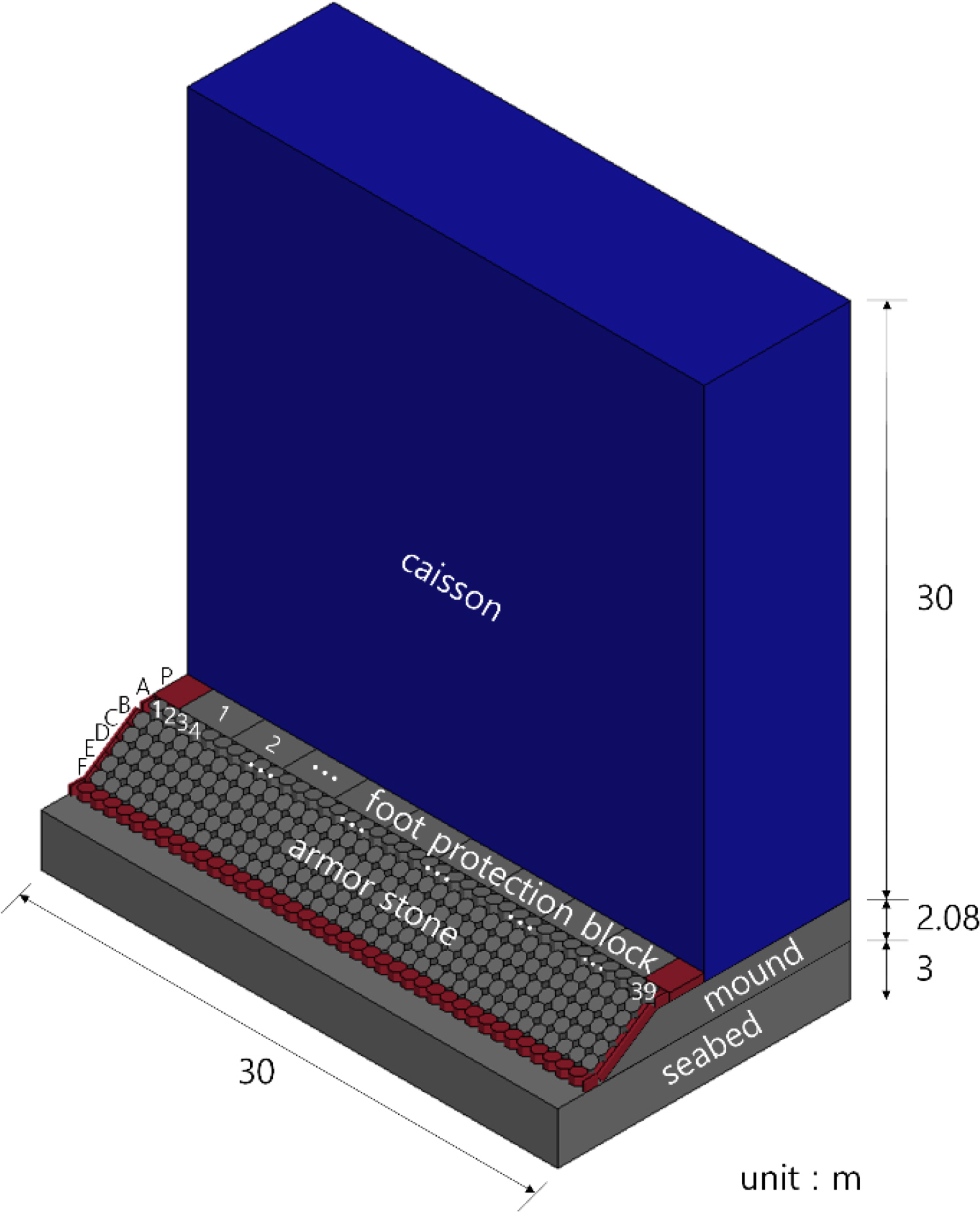
Since this study aimed to examine the stability of the quay wall against the thruster jet flow, a simple quay wall that can minimize the flow change according to the caisson and the shape of the armor stones and foot-protection blocks was considered. The quay wall was in the form of a 30 m high non-perforated caisson mounted on a mound with a height of 2.1 m and a slope of 1:1.5. One row of 2 m × 3 m × 0.5 m concrete heavy-duty blocks was placed on the mound floor at the bottom of the caisson, and seven rows of armor stones, each row with a side length of 3.11 m, were arranged in a regular octagonal shape on the slope of the mound (Fig. 4). The thickness of a foot-protection block and an armor stone was the same at 0.5 m. To reduce the computational load, the thickness of the caisson was limited to 8.5 m, and fixed boundary conditions were considered for the ground, mound, and caisson. Fixed constraint conditions were applied to the foot-protection blocks and armor stones at the water tank boundary and at the toe of the mound indicated in red in Fig. 4. For convenience, the foot-protection blocks installed in one row were numbered from P1 to P9, and the armor stones installed in the six rows (A to F) were numbered from A1 to A39, B1 to B39, C1 to C39, D1 to 39, E1 to 39, and F1 to F39, excluding those under the fixed constraint conditions.
Table 2 summarizes the physical properties of the caisson, foot-protection block, and armor stone. The physical properties provided by Ansys were applied. As for the foot-protection block, which was considered to comprise concrete, a unit weight of 2,300 kg/m3, Young’s modulus of 30,000 MPa, and Poisson’s ratio of 0.18 were applied. As for the armor stone, a unit weight of 2,600 kg/m3, Young’s modulus of 30,010 MPa, and Poisson’s ratio of 0.234 were applied, based on the Rock Physics Handbook (Mavko et al., 2009). The weight of each foot-protection block was 6,900 kg, and the weight of each armor stone was 731 kg.
2.2.4 Thruster flow
The maximum flow velocity of the jet flow generated by the thruster is calculated using Eq. (5), which was proposed by Fuehrer and Romisch (1977):
Regarding the specifications and performance of the single thruster of the 30,000 TEU ULCS, D is set as 3.75 m, n as 188 RPM, and K as the median value of 3.5, with reference to PIANC (2015) and Rolls-Royce (2013).
2.3 Validation
To validate the numerical model created using LS-DYNA, the propeller wake velocity equation in the Rock Manual (CIRIA et al., 2007) was used, based on the concept illustrated in Fig. 5.
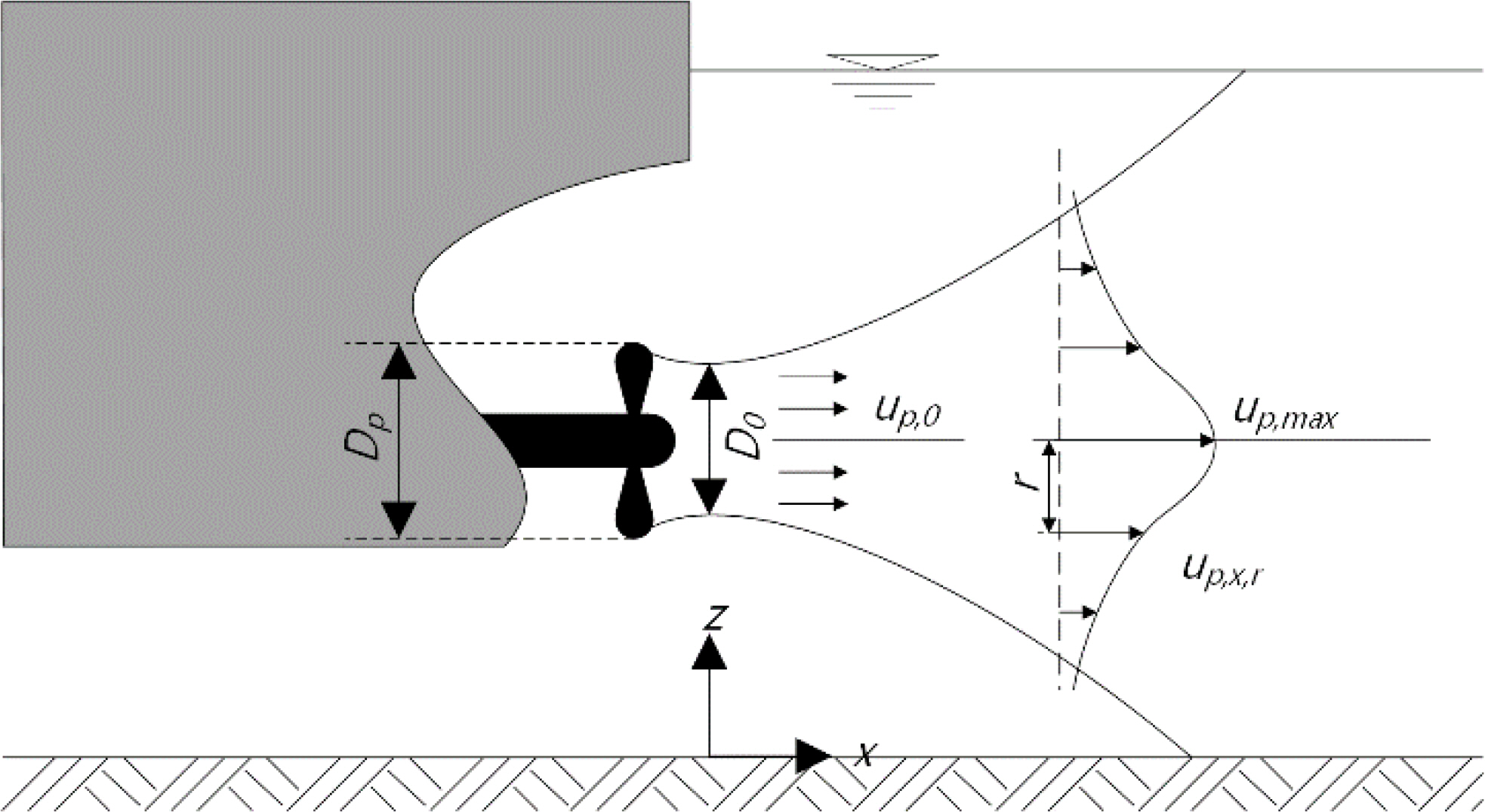
Conceptual diagram of propeller wake (Reproduced from CIRIA et al., 2007)
Here, P denotes the propulsion force of the marine engine (W),D0 denotes the effective diameter of the propeller (0.7 times the diameter of the propeller with no nozzle), ρw denotes the unit weight of the fluid (kN/m3), and r denotes the vertical distance from the center of the propeller (m). a, b, and m are empirical constants with values of 2.8, 5.2, and 1, respectively.
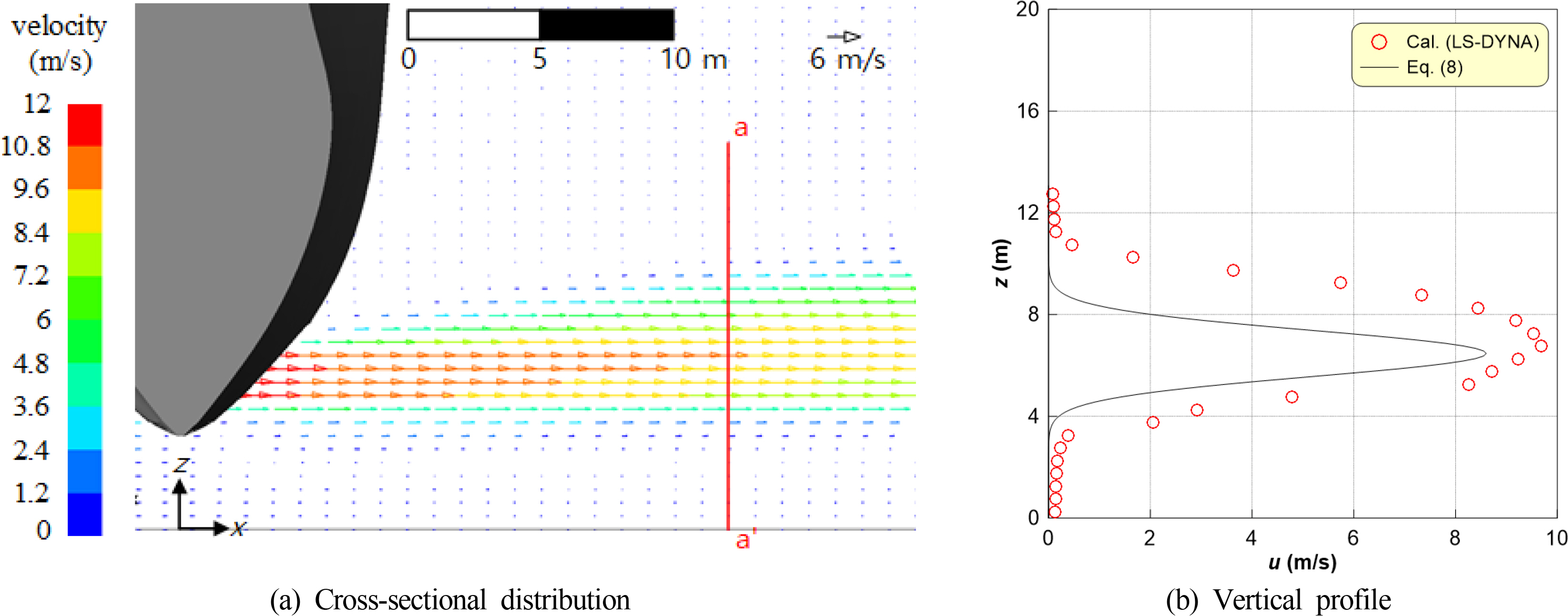
Fig. 6(a) shows the steady-state thruster flow field obtained using LS-DYNA. The vertical profiles for the a-a’ cross-section are compared in Fig. 6(b) for verification (the a-a’ section is 15 m away from the center of the thruster).
In Fig. 6(a), the jet flow generated by the thruster shows an upward flow pattern under the influence of floor friction. This accurately represents the typical characteristics of a jet flow, i.e., the distribution range of the propagated flow widens with a decrease in the flow velocity due to fluid viscosity. As seen in Fig. 6(b), the theoretical flow rate reaches its maximum at the thruster center (z = 7 m); however, the maximum flow velocity occurs slightly upward from the center, based on the LS-DYNA simulation results. This can be understood as a phenomenon that occurs as the flow spreads to the upper layer, since the upper part of the outlet opens first in the thruster structure. As a result, the theoretical flow rate generated by the open propeller is symmetric with respect to z = 7 m; however, the flow rate obtained based on the LS-DYNA simulation has an asymmetric structure with the developed upward flow velocity.
Although the maximum flow velocity and flow velocity distribution predicted using LS-DYNA are slightly overestimated compared with the theoretical values, the overall characteristics of the thruster jet flow generated by the ship appear to be accurately reproduced. In addition, Yeom et al. (2009) and Yeom et al. (2017) validated simulation results on the behavioral collision of structures obtained using LS-DYNA. Accordingly, the validity and effectiveness of LS-DYNA were partially confirmed in this study.
3. Numerical Results
3.1 Flow Field
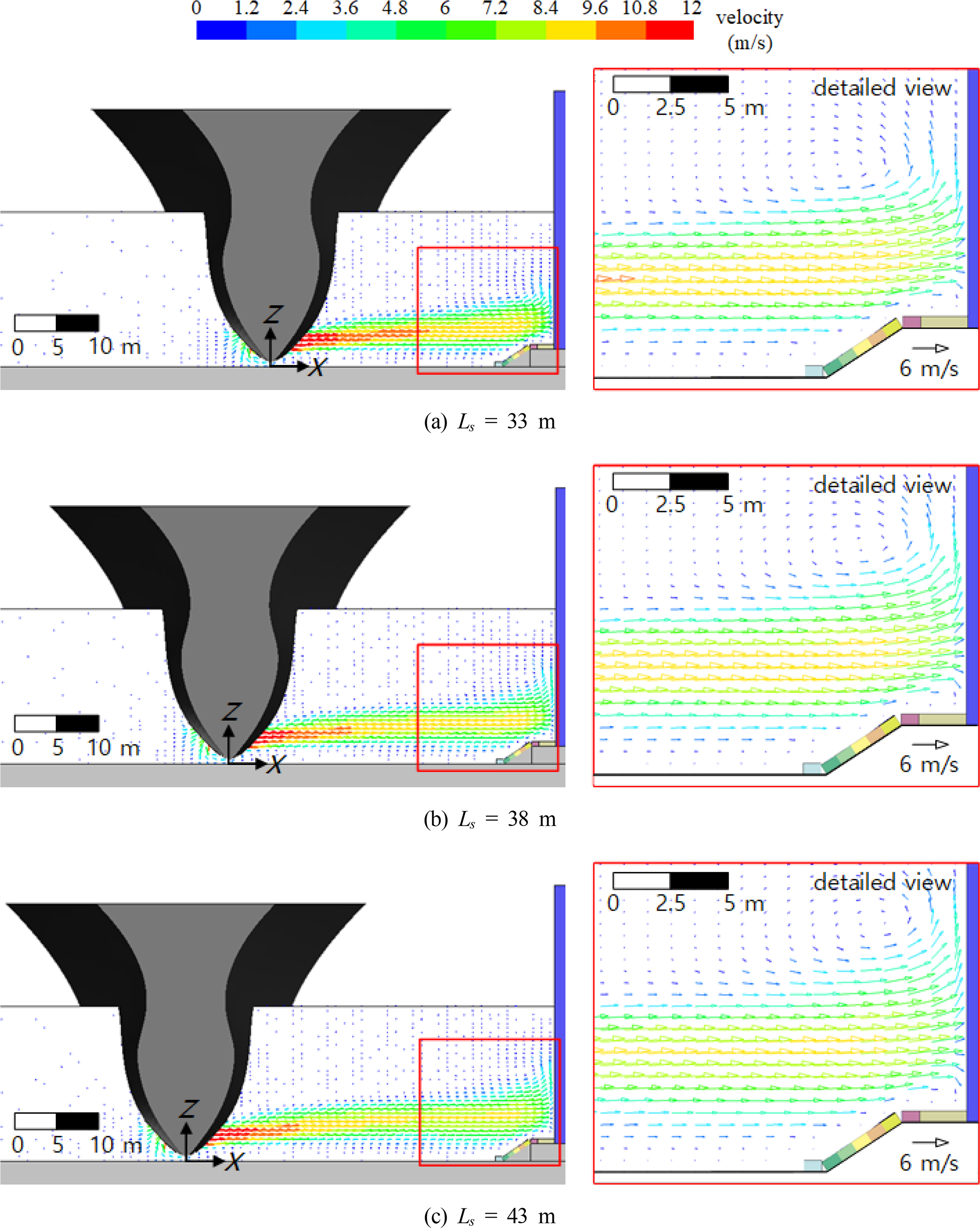
Figs. 7 and 8 show the steady-state flow velocity distribution around the quay wall, which is attributed to the thruster jet flow of the 30,000 TEU ULCS. Fig. 7 shows the flow fields according to the water depth for Ls = 33 m. Fig. 8 shows the flow fields according to the distance to the ship under the low-tide condition (h = 18 m).
In Fig. 7(a), at h = 18 m, the direction of the flow toward the water surface is shown on the slope as the thruster jet flow moves directly to the quay wall caisson and mound. In other words, the caisson of the quay wall and the armor stones of the mound slope are directly affected by the thruster jet flow, and the foot-protection blocks placed on the mound floor are affected indirectly. Under the mean- and high-tide conditions, shown in Figs. 7(b)–7(c), the quay wall caisson is directly affected by the thruster jet flow (h = 20 m and h = 22 m), whereas the mound (foot-protection blocks and armor stones) is not significantly affected. In addition, for h = 22 m, a secondary flow that collides with the quay wall caisson and descends may develop.
Based on the thruster jet flow characteristics (Fig. 8) according to the separation distance of the ship, a wider distribution with a decrease in the flow velocity is observed as the propagation distance increases, as suggested in the theoretical flow characteristics of CIRIA et al. (2007). Thus, the larger Ls is, the lower is the impact of the thruster jet flow on the quay wall caisson, foot-protection blocks, and armor stones.
3.2 Stability
3.2.1 Response of structure
Figs. 9 and 10 show the behavior of the foot-protection blocks and the armor stones covering the mound, which constitute the substructure of the quay wall, according to the action of the thruster jet flow of the 30,000 TEU ULCS. Fig. 9 shows the behavioral characteristics according to h for Ls = 33 m. Fig. 10 shows the behavioral characteristics according to Ls for h = 18 m.
At h = 18 m, as mentioned earlier, as the strong fluid force from the thruster jet flow of the ship acts on the mound shoulder, movement and departure of the armor stones are observed, which even induces movement of the adjacent foot-protection blocks. As the tide rises, the influence of the thruster jet flow is reduced; this reduces the movement of not only the armor stones but also the adjacent foot-protection blocks.
With regard to the behavioral characteristics of the foot-protection blocks and armor stones according to Ls, the larger Ls is, the wider the distribution of the flow acting on the quay wall becomes with decreasing flow velocity; thereby, the movement of the foot-protection blocks and armor stones is reduced, as evident from Fig. 8.
3.2.2 Maximum moving distance
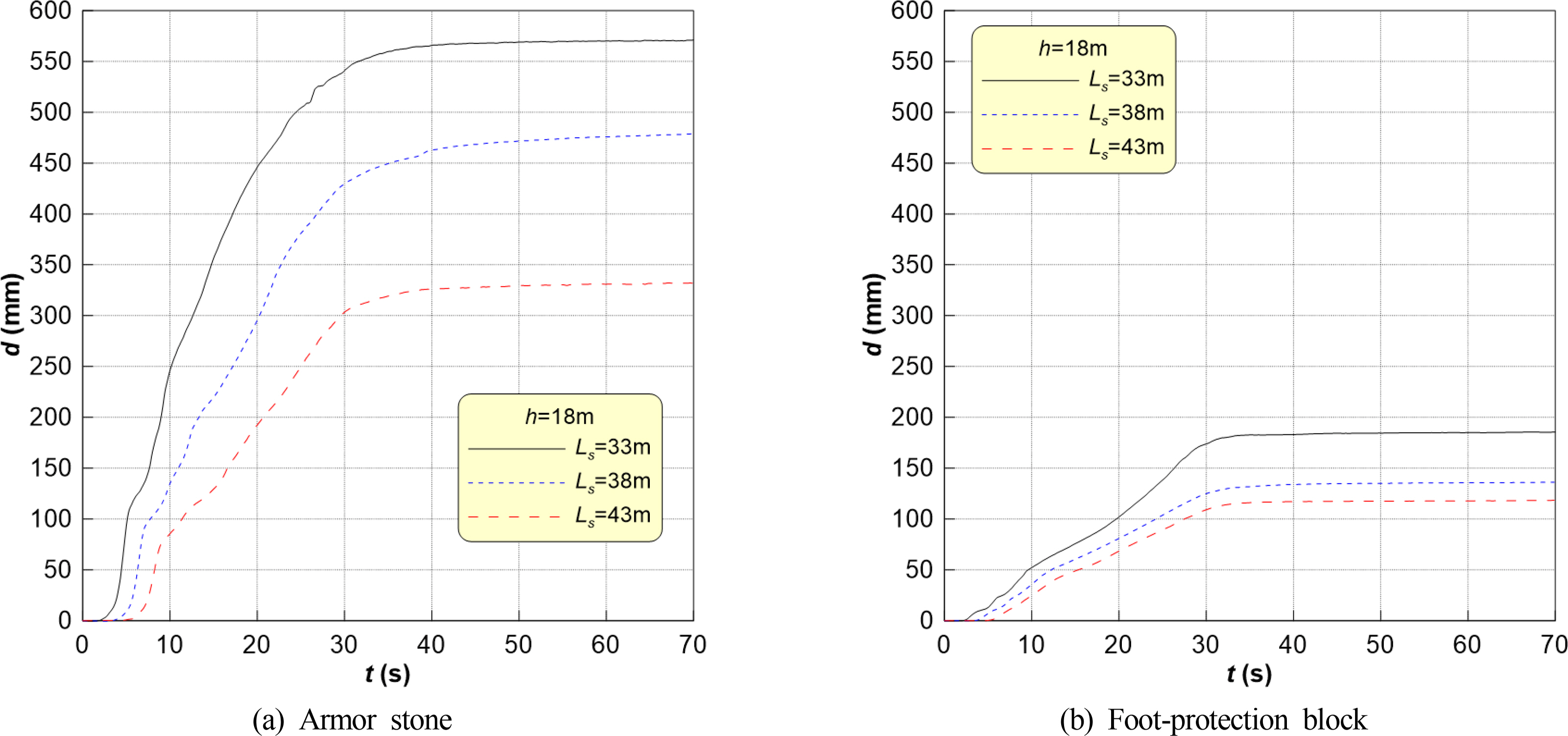
Fig. 11 depicts the change in the moving distances of foot-protection block P5 and armor stone B20, which moved the most among all the foot-protection blocks and armor stones covering the mound, under the action of the thruster jet flow generated by the 30,000 TEU ULCS. Figs. 11(a) and 11(b) present the moving distances of the armor stone and foot-protection block, respectively.
As seen in Fig. 11, as the thruster jet flow is induced by the ship, the armor stone and foot-protection block begin to move, and they move considerably for up to 30 s. However, the movement of the relatively heavy foot-protection block decreases significantly thereafter. The movement of the lighter armor stone slows slightly after 30 s and then decreases significantly after 40 s. Overall, the foot-protection block and armor stone do not move significantly after 50 s. Therefore, in this study, the maximum moving distance (dmax) is defined as the moving distance of the foot-protection block and armor stone at 70 s after the generation of the thruster jet flow by the 30,000 TEU ULCS.
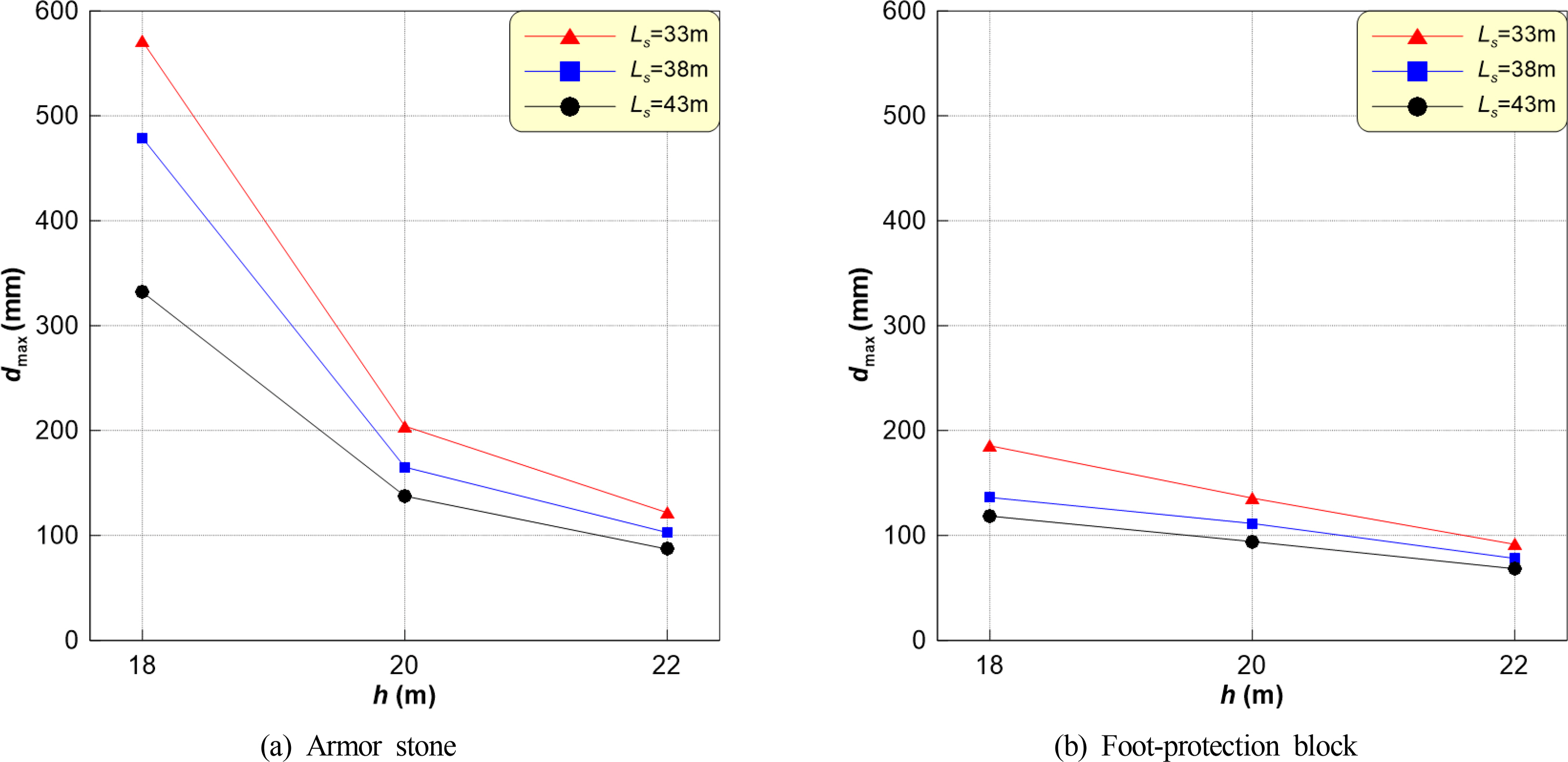
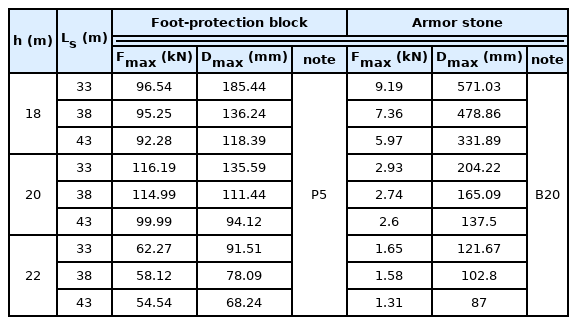
Fig. 12 and Table 3 show the dmax of P5 and B20, calculated as described above.
While Fig. 12 and Table 3 show the numerical analysis results under limited-port conditions, the moving distances of P5 and B20 under the thruster jet flow are the greatest under the low-tide (h = 18 m) and vessel-berthing conditions (Ls = 33 m); in fact, dmax was 571.03 mm, which may cause B20 to fall off. The maximum moving distances of the foot-protection block and armor stone show a clear tendency to increase as the tide becomes lower and the separation distance becomes decreases; this is confirmed by the thruster jet flow characteristics and quay wall behavior discussed earlier.
4. Conclusions
In this study, numerical analysis was performed to examine the effect of the thruster jet flow generated by a 30,000 TEU ULCS on the stability of a quay wall. For numerical analysis, LS-DYNA was used, which enables FSI analysis and simulation of complex nonlinear problems such as collisions between multiple objects and material molding. The main numerical analysis results considering the limited computation conditions are as follows:
For h = 18 m and Ls= 33 m, the thruster jet flow generated by a ULCS of 30,000 TEU directly affects the caisson of the quay wall and the armor slopes of the mound slope, and indirectly affects the foot-protection blocks on the mound floor. For h = 18 m and h = 22 m, the entire mound is not directly affected by the thruster jet flow. As the propagation distance increases, the distribution of the thruster jet flow increases, and the flow velocity decreases. Consequently, the effect of the thruster jet flow on the quay wall caisson, foot-protection blocks, and armor stones is reduced as Ls increases.
At h = 18 m, the thruster jet flow generated by the ship directly affects the shoulder of the mound, causing movement and separation of the armor stones and even inducing movement of the adjacent foot-protection blocks. As h increases, the influence of the thruster jet flow is reduced, which considerably reduces the movement of the armor stones and adjacent foot-protection blocks. As Ls increases, the distribution of the flow acting on the quay wall is widened, and the flow velocity decreases; this reduces the movement of the armor stones and adjacent foot-protection blocks.
Foot-protection block P5 and armor stone B20 moved the most under the ship thruster flow. Under Ls = 33 m and h = 18 m, dmax was 571.03 mm for B20; such a large dmax may even cause separation of the armor stone. For P5, the movement was not as significant, with dmax = 185.44 mm.
Based on these results, when the tide is lower and the ship is closer to the quay wall, the berthing or deberthing of the ship using a thruster has more adverse effects the foot-protection blocks and armor stones of the mound, which constitute the substructure of the quay wall. Therefore, when designing a new port, the stability of the port structures, such as those analyzed in this study, should be sufficiently considered. Furthermore, even at existing ports, it is necessary to dredge the waterways and expand and reinforce the berthing piers in line with the increasing sizes of ships, considering the stability of port facilities for accommodating ULCSs. This should be supported by a hydraulic model experiment considering actual port conditions or a numerical analysis, such as that conducted in this study.
Notes
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2021R1A2C4002665).