피스톤 타입 조파기의 형상 매개변수에 대한 조파성능 연구
A Parametric Study of the Wave-Generation Performance of a Piston-Type Wave Maker
Article information
Trans Abstract
The wave-generation performance of a piston-type wave maker was analyzed using the numerical wave tank technique, and the numerical results were compared with theoretical solutions. A two-dimensional frequency domain analysis was conducted based on the Rankine panel method. Various parameters were used to examine the wave-generation performance, such as the width and gap of the wave board. The effects of the thickness of the wave board and of the gap from the bottom of the tank were evaluated. The difference in the amplitude of the generated wave between the analytical solution and the numerical result was examined, and its causes were addressed due to the gap flow between the bottom of the tank and the wave board. This parametric analysis can be utilized to design an optimum wave make parametric analysis to design an optimum wave maker that can generate waves with amplitudes that can be predicted accurately.
1. 서 론
해양구조물 설계에서 파랑중 구조물의 거동 해석은 설계의 핵심적인 요인이다. 특히, 구조물의 동적 거동에 절대적인 영향을 미치는 파의 전파와 구조물간의 상호작용의 이해는 매우 중요한 문제이다. 또한, 수치해석뿐만 아니라, 모형실험을 통해 정확하고 정밀한 해석이 중요하다. 파랑 현상을 정확히 이해하기 위해 모형실험을 수행할 때, 시험수조에서 정확하고 안정적인 입사파를 생성하기 위해서는 조파기의 성능을 이해하고 이를 제어할 수 있는 알고리듬이 중요하다. 고전적인 조파기 설계는 조파판을 파도의 입자 운동이 생기도록 동력장치와 연동하는 왕복운동 개념의 기구설계에 초점이 맞춰졌다. 왕복운동에 따른 조파판의 운동으로 이론해를 구하고 이를 바탕으로 조파기를 설계하였다(Liao and Roddier, 1998).
조파판 운동에 대한 이론적 해석의 발전과 함께 조파기에서 정밀한 정현파를 발생시키기 위한 연구도 진행되었다. 먼저, Dean and Dalrymple(1991) 은 피스톤(Piston) 타입 조파기와 플랩(Flap)타입 조파기의 조파 성능에 대한 포텐셜 유동 이론을 기반으로 한 이론해를 나타낸바 있다. 또한, 이를 바탕으로 Kwon et al.(2017)은 수중 피스톤 타입 및 플랩 타입 조파판의 조파 성능을 조파판 진폭과 생성 파고와의 관계에 대한 이론식으로 정리하고 일반해를 도출하였다. 여기서 수중 조파판은 기존의 조파판 밑부분이 수조 바닥까지 닿아있는 것과 달리, 수중에 잠겨 있어 수중에서 자유로이 움직이는 조파판을 의미한다.
본 연구는 다양한 제원의 피스톤 타입 조파장치에 대한 조파성능을 유체동역학적 관점에서 수치 해석을 수행하였다. 이를 위해, 경계요소법과 랜킨 패널법(Rankine panel method)을 기반으로 한 이차원 주파수 영역 해석을 수행하였다. 이를 Kwon et al.(2017)의 이론해와 비교하여 해의 정확성을 검증하였다. 또한, 조파판의 두께와 잠긴 깊이(흘수)에 대해 매개변수 해석을 수행하였다.
2. 문제의 정식화
2.1 랜킨 패널법
유체 유동을 비압축성, 비회전성, 비점성의 포텐셜 유동으로 가정하면, 식 (1)과 같은 라플라스 방정식(Laplace equation) 형태의 지배 방정식을 얻을 수 있다.
본 지배 방정식은 그린의 이차 정리(Green's 2nd identity)에 의해 경계 적분 방정식(Boundary integral equation)으로 변환할 수 있다.
여기서, α는 입체각, G는 영향 함수로서 식 (3)과 같은 단순 랜킨 항으로 나타낼 수 있다.
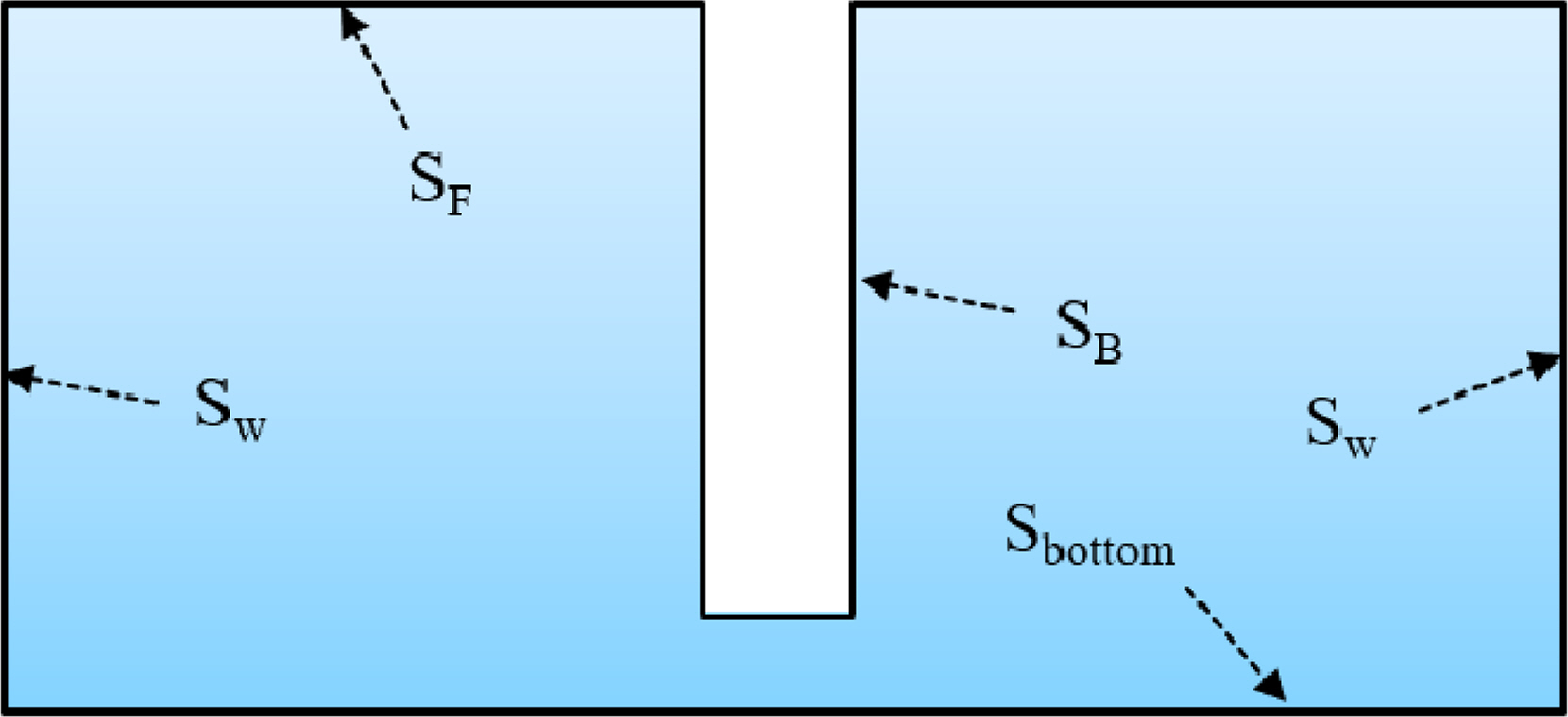
여기서, R은 소스 점(Source point)과 필드 점(Filed point) 간의 거리를 의미한다(Brebbia and Dominguez, 1992). 본 연구에서는 수치조파수조 기법을 사용하여 조파판의 경계면 뿐만 아니라 자유표면 경계면, 수조 바닥면 경계면, 벽면 경계면에 특이점을 분포하였다. Fig. 1은 본 해석 유체 영역의 개략도이다.
2.2 경계 조건
수평 운동하는 조파판의 유체동역학적 조파 성능을 추정하기 위해, 조파판의 움직임과 유사한 조파판의 수평 운동(Surge motion)에 관한 유체내 방사문제의 형태로 경계 조건을 적용하였다. 식 (4)는 조파판의 경계 조건을 나타낸다.
여기서, Vx 는 조파판의 강제 수평 운동 속도를 의미하는데, 계산의 편의를 위해 ‘1’을 적용하였다. nx는 조파판 경계면에 위치한 요소의 법선 벱터의 x방향 성분을 의미한다. 또한, 자유 표면 경계조건은 선형화된 동역학적 경계조건과 운동학적 경계조건을 결합하여 식 (5)로 나타냈다.
여기서, w는 조파판 운동 주파수를 의미하며, g는 중력 가속도를 의미한다. 조파수조 끝단면 및 수조 바닥면의 경계 조건은 식 (6)과 같은 불투과성 경계면으로 나타내었다.
2.3 인공 감쇠 영역
계산 유체 영역의 크기적 한계로 인해 발생되는 불필요한 반사파를 억제하기 위해 인공 감쇠 영역(Artificial damping zone)을 적용하였다. Fig. 2와 같이 인공 감쇠 영역은 자유표면의 양 끝단에 존재하여 (감쇠계수 크기는 램프함수 적용으로 곡선으로 증가함), 전파된 파가 계산 영역 벽면에서 반사되지 않게 된다.
본 연구의 주파수 영역 해석에서 감쇠영역의 길이는 발생된 파장의 두 배(2λ)로 정하였고, 감쇠는 속도포텐셜 ϕ에 비례하도록 실수부와 허수부에 대해 적용하였다(Kim, 2003; Min and Koo, 2017; Kim et al., 2019).
위 식에서, μ1, μ2는 각각 허수부와 실수부에 대한 인공 감쇠 계수를 의미한다. 두 계수의 관계는 다음과 같다.
μ1, μ2에 적용된 감쇠 계수는 시행 착오법을 통해 각각 6과 9로 결정하였다. 인공 감쇠 영역을 자유수면 조건에 적용하였을 때, 계산영역에서 생성파의 변위를 Fig. 3에 표시하였다. 계산영역 양 끝단에서 방사파가 제거됨을 확인할 수 있다.
2.4 자유수면 진폭 계산
계산 영역의 모든 경계면에 소오스를 분포 시키고, 경계 적분방정식을 해결함으로 조파기 수평 운동에 의한 유체내 속도 포텐셜을 모든 계산점에서 손쉽게 계산할 수 있다. 이를 선형화된 동역학적 자유표면 경계조건에 적용하여 식 (9)와 같이 해당 위치에서의 방사파의 진폭(Wave elevation, η)을 계산할 수 있다.
여기서, S는 조파판의 스트로크(Stoke)를 의미하고, ϕ1은 조파판 수평 운동에 의한 자유표면에서의 방사 속도 포텐셜을 의미한다.
3. 수치 결과 및 분석
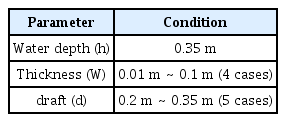
본 연구에서는 조파판의 두께와 흘수에 대해 각각 4가지, 5가지 조건에 대한 매개 변수 해석을 수행하였다(Table 1). 또한, 조파판의 강제 수평 운동 주기를 0.6초~1.2초로 하여 균일 파고 3cm의 규칙파를 발생시키기 위한 연구를 수행하였다. 조파판에 의해 발생될 방사파의 파장(Wave length)과 수심과 파장의 비(h/λ) 는 Table 2와 같이 나타냈다.
Fig. 4는 조파판 경계면에 분포한 요소 개수 조건에 따른 생성파의 진폭을 비교함으로써 수치 해석의 정확도를 확인하기 위한 수렴도 평가를 나타낸다. 수평축은 수심을 각 주기에서의 파장으로 무차원화 하였고, 수직축은 각 노드 조건에서의 파고를 이론해로부터 계산된 진폭 A로 무차원화 하였다. 파고 3cm를 발생시키기 위한 조파판의 스트로크는 Kwon et al.(2017)의 식을 사용하였고, 수심과 흘수의 차(h-d)가 0.025m인 경우를 고려하였다. 다시 말해 조파판 하단과 수조바닥은 약 2.5cm 정도 간격이 있음을 의미한다. 수렴도 평가에 따라 조파판 측면 경계의 요소 개수가 50개 이상일 때, 계산된 파고가 수렴하였다. 따라서 본 연구에서는 조파판 단일 측면의 요소 개수를 50개로 고정하였고 조파판 바닥면 2개, 자유수면 400개, 양 벽면 100개, 바닥면 405개 등 전체 노드 개수를 1,007개로 하여 수치해석을 수행하였다.
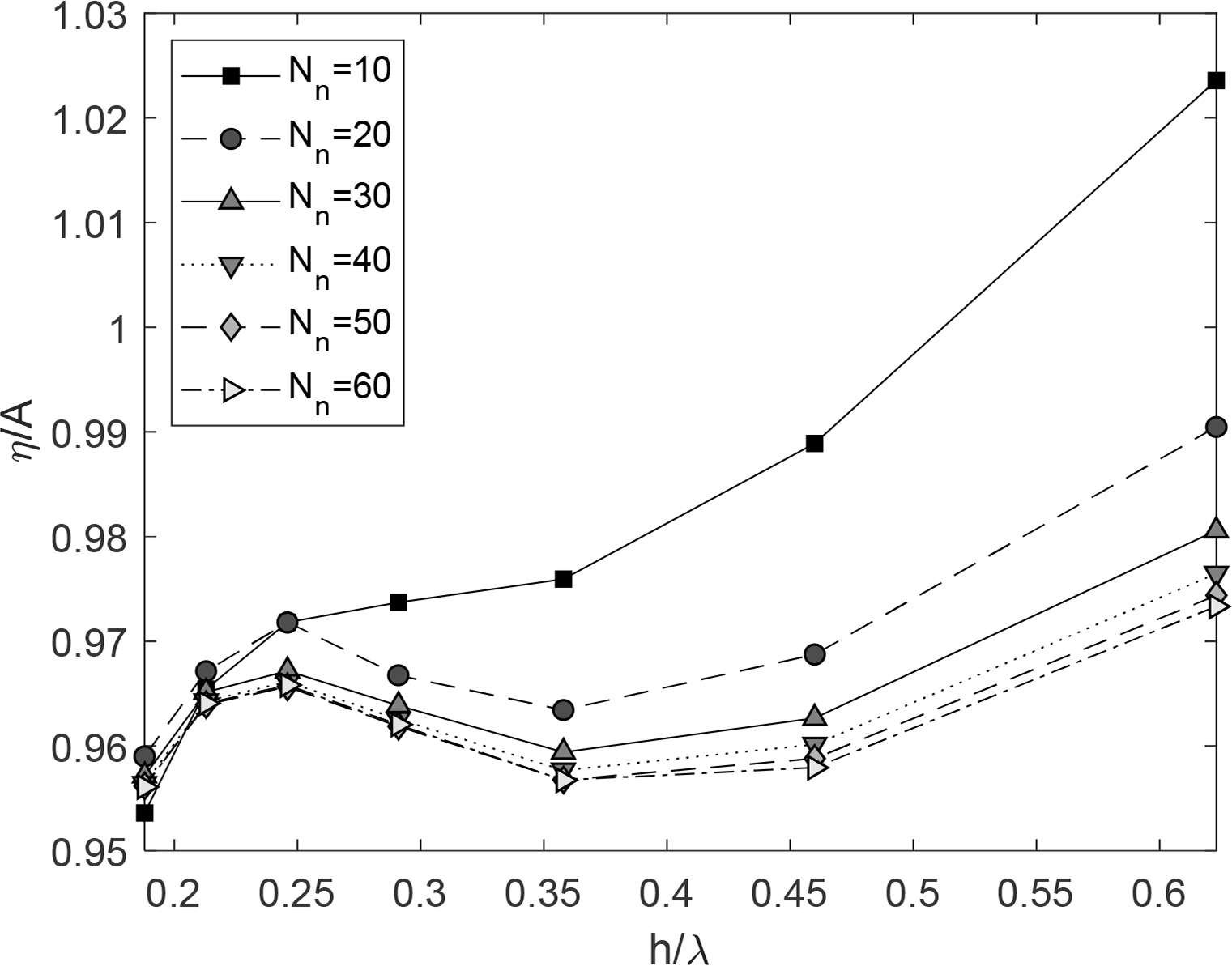
Comparison of wave elevations for various number of nodes on wave maker (H = 0.03 m, h = 0.35 m, h – d = 0.025 m, W = 0.015 m)
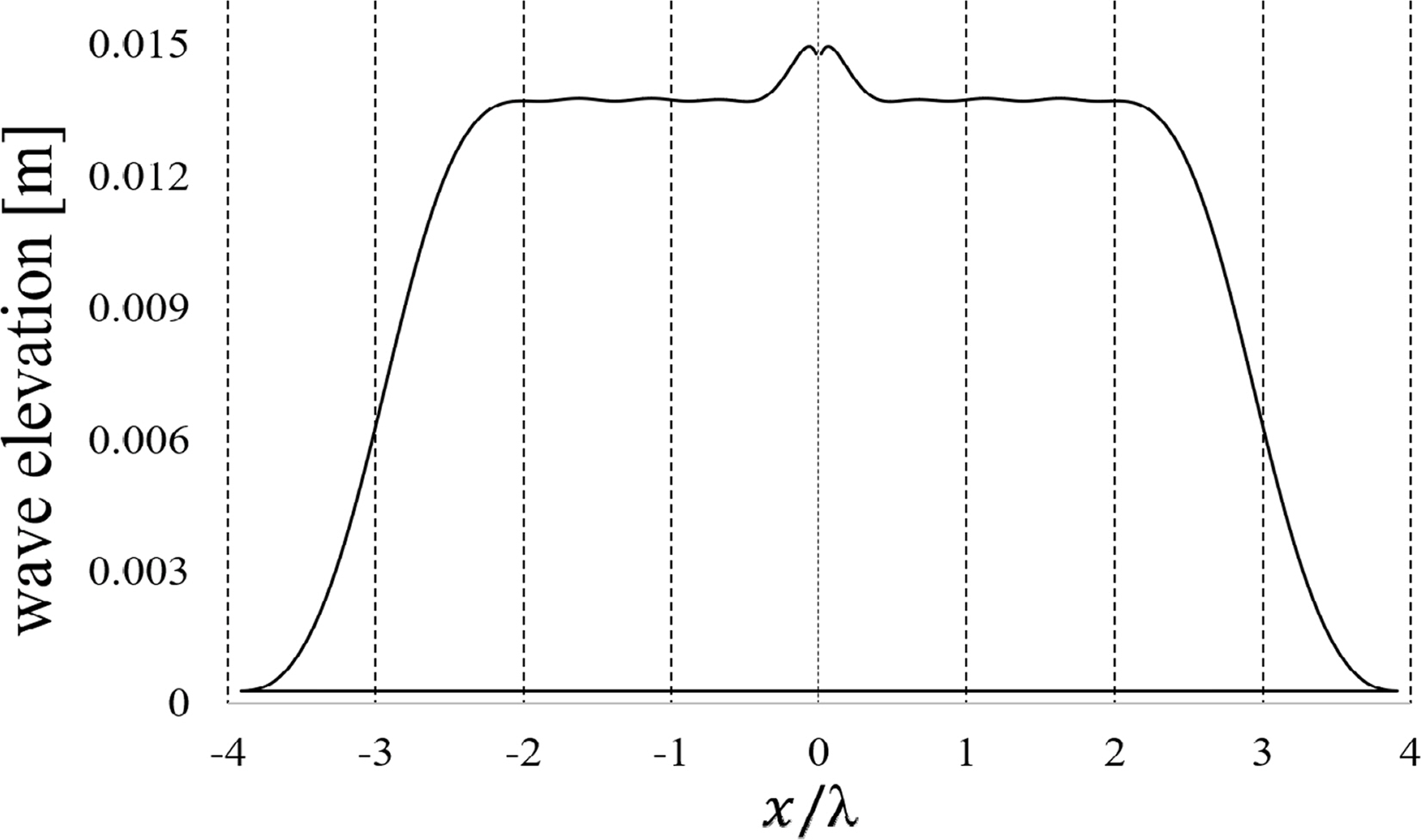
Fig. 5는 발생된 파 주기 0.6 초 조건에서 인공 감쇠 영역을 제외한 모든 자유표면 요소에서의 자유표면 진폭을 보여준다. 이때, 파고는 3cm가 발생되기 위한 조파판의 스트로크(1.51 cm)를 적용하였고, 조파판의 흘수는 수심과 동일하게 하였다. 즉 조파판과 수조 바닥면이 붙어있는 경우이다. 조파판 근처의 |x/λ|=0.2 부근에서는 예측된 방사파고 대비 약 25% 이상 큰 파가 발생되는 것을 볼 수 있다. 이는 방사파의 소멸파 모드(Evanescent mode)로, 조파기의 운동에 의해 생성된 방사파의 정재파(Standing wave)에 의한 영향이다. 이런 정재파의 영향은 파전파 방향을 따라서 기하급수적으로 감소하는 것을 Fig. 5를 통해 확인할 수 있다. 이후, 모든 계산에서 소멸파 모드가 영향을 주지 않도록 x/λ=0에 위치한 조파판으로부터 약 1λ~2λ 거리의 방사파 진폭값의 평균값을 수치해석 결과 분석에 이용하였다.
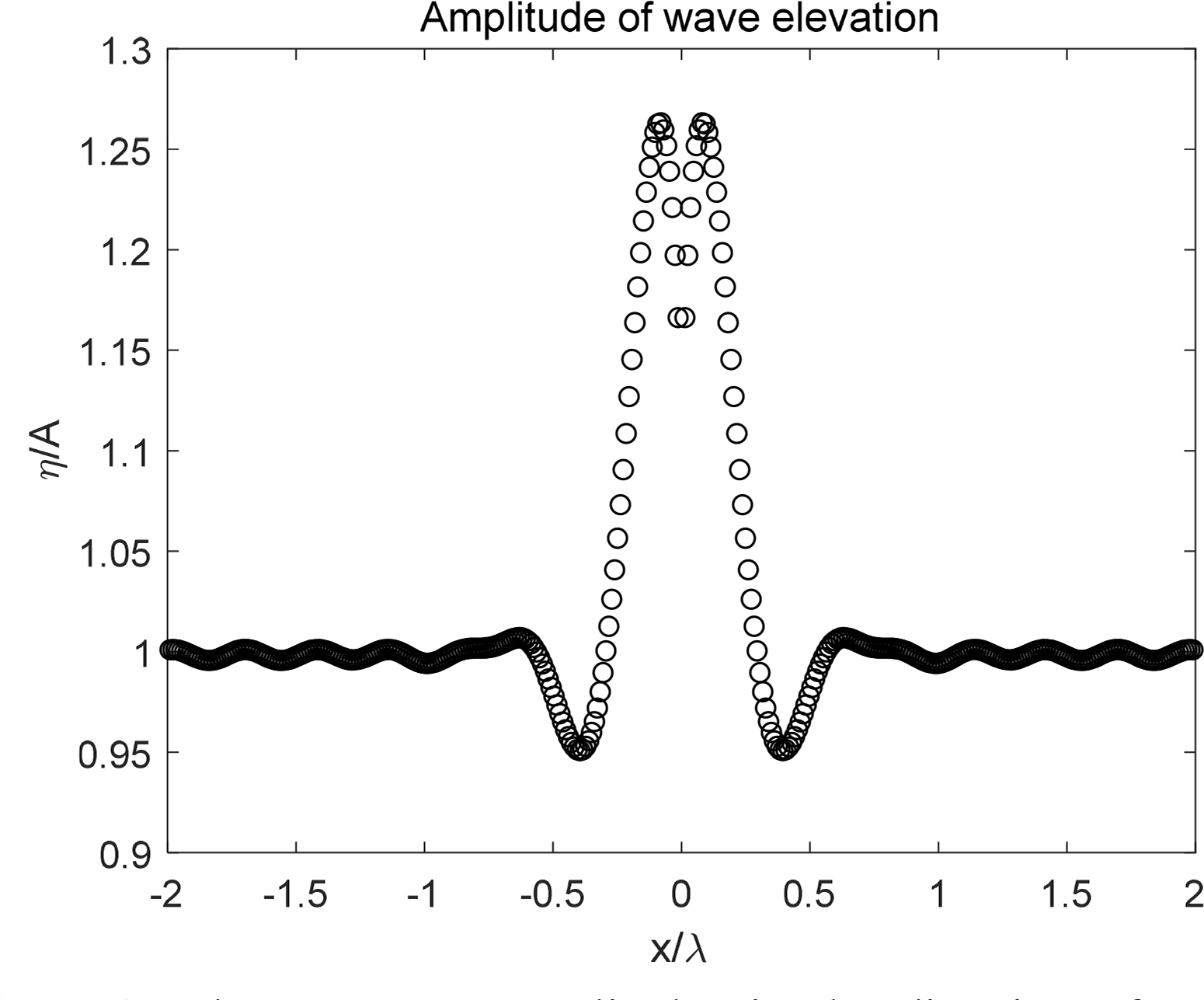
Steady-state wave amplitudes in the direction of wave propagation (T = 0.6 s, H = 0.03 m, S = 0.0151 m, h = 0.35 m, h – d = 0, W = 0.015 m)
조파판의 조파 성능에 관한 본 해석 방법에 대한 타당성을 검증하기 위해, Kwon et al.(2017)의 이론해와 비교하였다. 이론해는 고전적인 섭동 이론에 근거한 일차 선형 근사해법(Khalilabadi and Bidokhti, 2012)을 적용하여 해를 구하였다. 수중에서 조파기가 수평방향 왕복 조화운동을 할 때, 조파판의 스트로크를 S, 파수를 k, 수심을 h라 하면 조파판의 동요운동으로 발생되는 파고는 식 (10)과 같이 정리할 수 있다(Kwon et al., 2017).
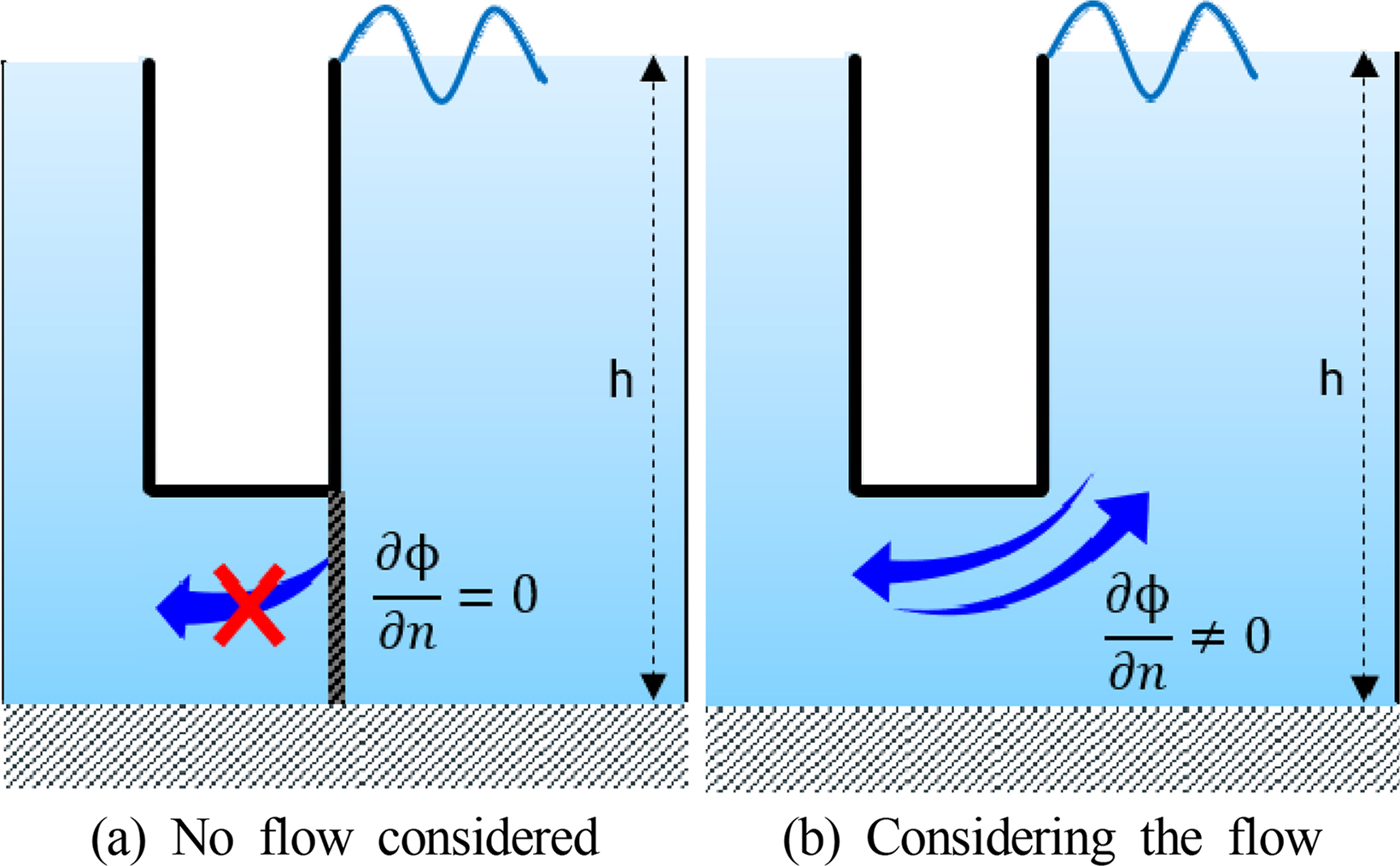
여기서, zd는 수조 바닥에서 조파판 하단까지의 거리(간격)이다. 본 이론식(식 (10))에서는 조파판 하단 간격의 유체영역은 ∂ϕ/∂n=0으로 가정하였다(Fig. 6).
본 연구의 수치해석 결과와 이론해의 비교 검증을 위해, 조파판과 바닥면 사이가 막혀 있는 경우와 그 간격이 각각 0.025m, 0.05m인 경우에 대해 생성된 방사파의 진폭을 비교하였다. 이론해(식 (10))의 경우 조파판의 두께가 고려되지 않았고 조파판과 바닥면 사이 간격에서 유체 속도를 ‘0’으로 가정하였으며, 조파판의 운동 영향만을 고려한 결과이다. 이론해의 가정과 동일한 조건을 적용하기 위해, 수치해석에서 조파판의 두께를 충분히 넓게 하여 수조 바닥면과 조파판 하단면 사이의 유속이 ‘0’에 가깝도록 모델링하여 해석을 수행하였다(Fig. 6(a) 모델).
이와 같은 계산 조건으로, Fig. 7에서 다양한 흘수 조건의 조파판에서 생성되는 방사파고에 대해 이론해와 수치해석 결과를 비교하였다. 명확한 비교를 위해, 모든 해석 조건에서 조파판 스트로크를 0.01m로 고정하였다. 조파판의 다양한 흘수 조건에서 이론해와 수치해석 결과가 잘 일치하는 것을 확인할 수 있다. 그리고 조파판 흘수가 증가할수록, 즉 조파판과 수조 바닥면 사이의 공간이 작을수록, 동일 크기의 스트로크에서 생성되는 방사파고가 증가하는 것을 확인할 수 있다. 이는 동일한 조파판 스트로크를 유지하기 위해 더 많은 에너지가 투입되기 때문으로 판단된다. 또, 심해 조건에 가까울수록(h/λ가 클수록) 파고가 증가함을 알 수 있다.
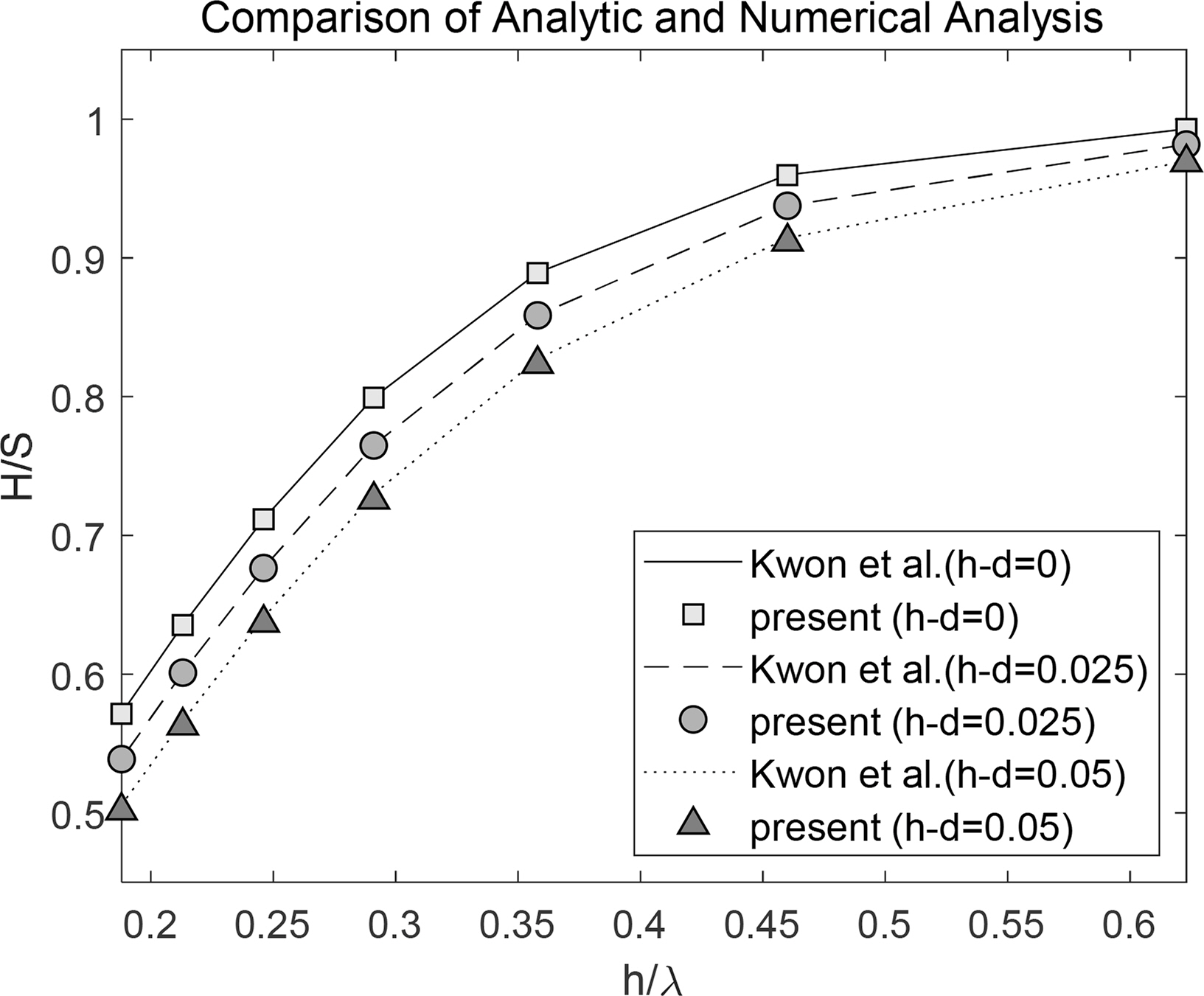
Comparison of the radiated wave heights of analytic solution with numerical results for various gap conditions (S = 0.01 m, h = 0.35 m, W = 0.1 m)
한편, 실제 수조 실험 환경에서는, 이론해의 가정과 달리 조파판과 바닥면 사이 간격에서 유동이 발생할 수 있다(Fig. 6(b) 모델). 따라서 본 수치해석에서는 이를 고려하여 계산을 수행하고 조파판 두께(W)와 흘수(d)에 따른 매개변수 해석을 수행하였다. 매개변수 수행을 위한 조파판의 스트로크는 Kwon et al.(2017)의 이론해 값을 적용하였다. 계산 유체 영역은 랜킨 패널법을 기반으로 한 주파수 영역 해석을 수행하여 방사파의 파고를 계산하고 이를 비교하였다.
Fig. 8은 조파판의 다양한 흘수와 두께 조건에서 생성된 방사파의 진폭을 비교하였다. 이때, 수평축은 방사파의 파장을 수심으로 무차원화 하였고, 수직축은 방사파 진폭을 이론해(식 (10))로 구한 방사파 진폭으로 무차원화 하였다. Fig. 8에서 조파판 두께/흘수 조건과 다양한 파장 조건에서 방사파고는 이론해로 계산된 파고보다 대체로 작게 나타남을 알 수 있다. 이는 Fig. 6(b) 모델과 같이 조파판 하단 간격의 유체 유동을 고려하여 계산했기 때문으로 추정된다. 특히, 조파판 하단 간극의 유동이 가장 활발할 것으로 예상되는, 조파판 두께 0.01m와 작은 흘수(h-d=10cm) 조건에서, 이론해에 비해 최대 7% 이상 작은 진폭의 방사파가 발생하였다. 또한, 동일한 조파판 흘수 조건(h-d)에서는 조파판의 두께(W)가 클수록 수치해석 결과와 이론해의 차이가 작아짐을 확인할 수 있다(Fig. 9). 이는 조파판 두께가 증가함에 따라 조파판 하단 간격에서의 유동 변화가 감소하기 때문으로 판단할 수 있다.
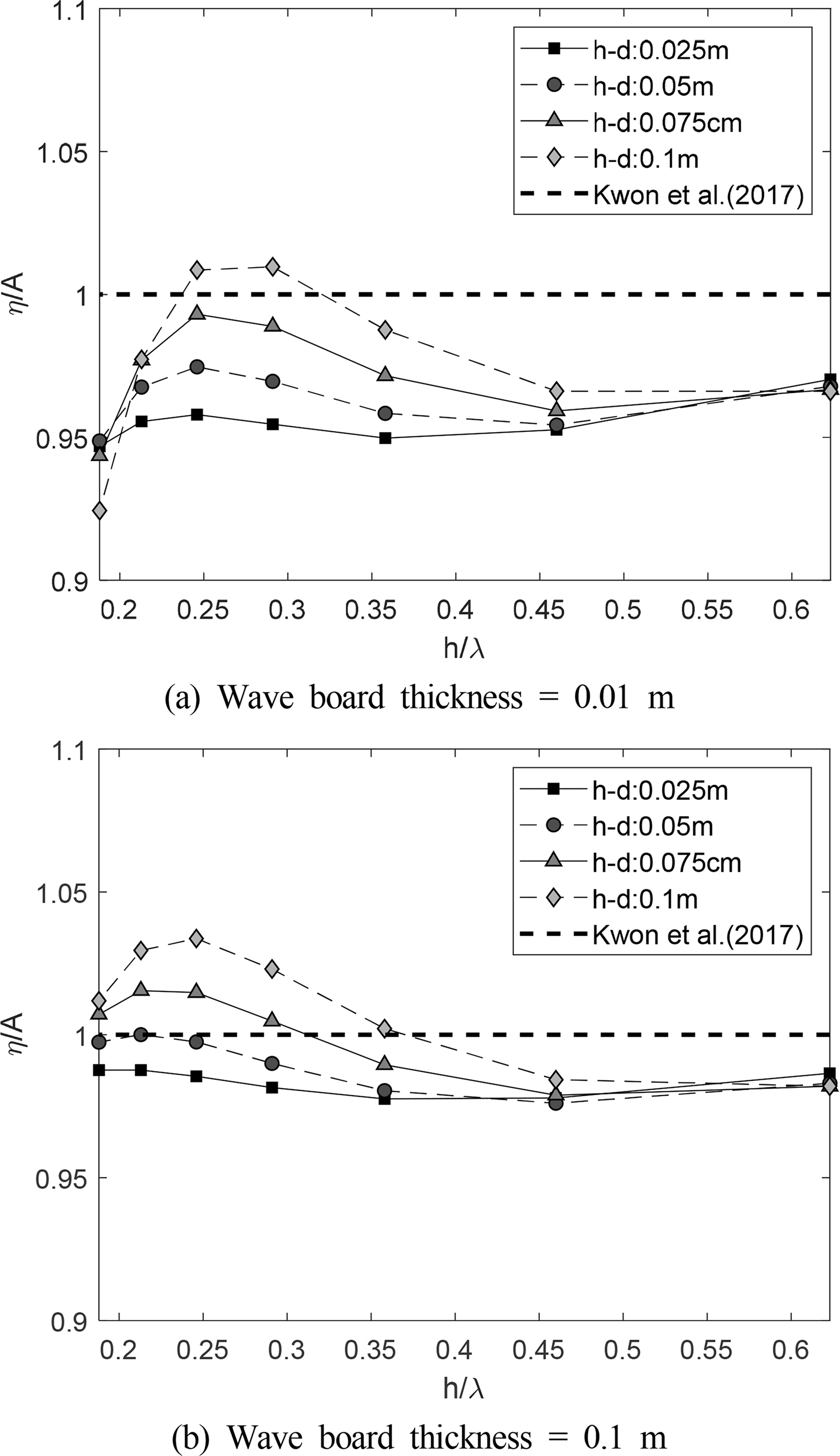
Comparison of generated radiated wave amplitudes on various draft-thickness conditions (H = 0.03 m, h = 0.35 m)
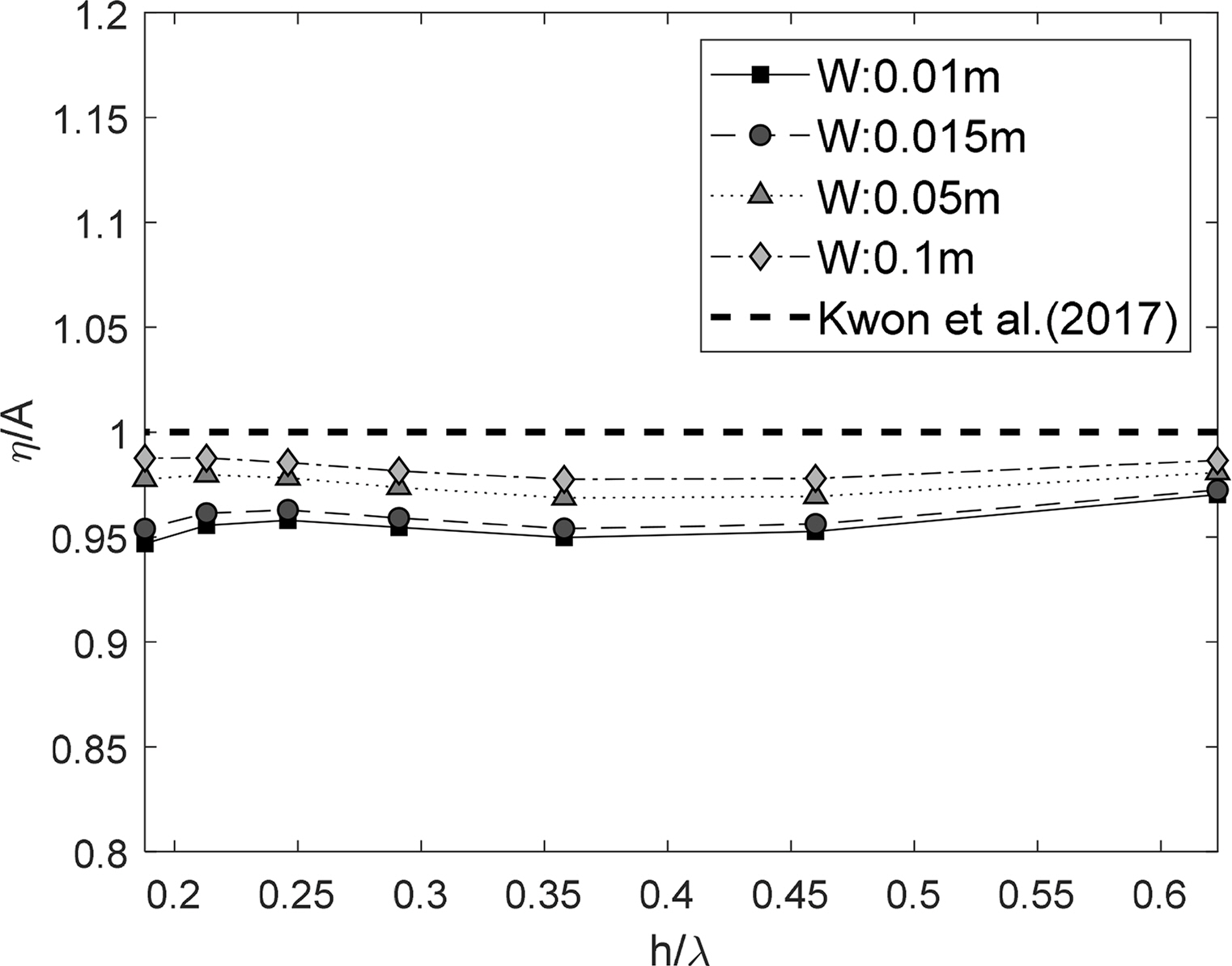
Comparison of generated wave amplitudes on various board thickness (H = 0.03 m, h = 0.35 m, d = 0.325 m)
이와 같은 결과 분석을 통해, 이론해에서 고려하지 못한 조파판 하단 간극에서의 유동 여부는 조파성능에 상당한 영향을 줌을 알 수 있다. 수치조파수조는 계산 영역 전체의 유동을 모사할 수 있기 때문에 이론해와의 차이를 정확하게 나타냄을 확인하였다.
한편, 조파판 스트로크로 발생시킨 단파 생성 영역에서는 이론해와 수치해석 결과간의 차이가 크지 않은데, 이는 방사파의 파장이 짧아 조파판 하단의 유동에 미치는 영향이 작기 때문으로 판단된다.
Fig. 10은 다양한 조파판 스트로크와 주기 조건에서 생성된 방사파의 파고를 등고선 형태로 나타내었다. 조파판 하단과 바닥면 사이 간극(h-d)은 0.025m이고 조파판 두께는 0.015m이다. 조파판의 강제 운동 주기 조건 및 조파판 스트로크 조건에 따른 방사파의 파고를 이차원 주파수영역 랜킨 패널법을 적용하여 계산하였으며, 이를 이론해(Kwon et al., 2017)와 비교하였다. 생성되는 방사파 주기가 증가할수록 동일한 방사파 진폭을 발생하기 위해 필요한 스트로크가 증가하였다. 이는 동일한 파고에서 장파를 발생시키기 위해서는 더 많은 에너지가 필요함을 나타낸다.

Contour line for generated wave amplitude (m) with given stroke and period (h – d = 0.025 m, W = 0.015 m)
Table 3은 진폭 0.01m인 방사파를 생성하기 위한 조파판 스트로크를 비교한 표이다. 이때, 조파판의 조건은 인하대학교 이차원 미니 조파 수조의 조파판의 제원과 동일한 두께 1.5cm, 흘수 32.5cm로 하였다. 해당 조건의 경우, 이론해와 수치해석 결과간의 차이가 최소 2.76%에서 최대 4.60%로 나타났다. 이를 토대로 다양한 크기의 시험 수조 실험을 위해서는 조파판의 흘수와 두께에 따른 조파 성능 해석에 대해 보다 심도 있는 연구의 필요성을 확인할 수 있다.
4. 결 론
본 논문에서는 피스톤 타입 조파기의 조파판 형상 조건에 따른 조파성능을 계산하고 이를 이론해와 비교하였다. 조파판의 조파 성능 추정을 위해 경계요소법과 랜킨 패널법을 기반으로 한 이차원 주파수 영역 유체동역학적 수치해석을 수행하였다. 단순 직사각형 판 모양의 조파판에 대해 유체동역학적 이차원 방사문제로 해석함으로 다양한 조파판 제원 조건에 대한 조파판의 조파 성능을 추정하였다. 이론해는 조파판의 수평 운동만 고려하고, 조파판의 두께와 조파판 하단 간극에서의 유체 유동을 고려하지 않았다.
조파판 노드 개수에 대한 수렴도 평가를 수행하였고, 이론해와 동일한 가정하에 비교 검증을 통해, 본 수치해석 모델링의 타탕성을 검증하였고, 이론해의 한계를 분석하였다. 이를 기반으로, 조파판의 다양한 두께와 흘수 조건을 매개변수로 하여 조파 성능을 조사하였다. 조파판 하단 간극의 유동 영향으로 인해 대부분의 조파판 두께와 흘수 조건에서 방사파 진폭이 이론해보다 작았고, 조파판 하단과 바닥면 사이의 간극이 작아지거나 조파판 두께가 증가할수록 이론해와 수치해석 결과의 차이가 감소하였다. 파장이 짧은 단파 생성 영역에서는 조파판 하단 간극의 유동 현상의 영향이 상대적으로 작아서, 수치결과와 이론해의 차이가 크지 않았다.
따라서, 조파기 하단 간극의 유동현상을 포함한 계산 유체 영역 전체를 고려할 수 있는 수치조파수조를 이용한 조파기 성능 분석의 유용성을 증명하였다. 이를 토대로 다양한 크기의 시험 수조 실험을 위해서는 조파판의 흘수와 두께에 따른 조파 성능 해석에 대해 보다 심도 있는 연구의 필요성을 확인할 수 있다.
향후 본 연구에서 계산된 수치해석 결과를 실제 조파수조 실험 결과와 비교 검증할 예정이다. 이와 함께, 다양한 형상의 조파판에 대한 수치적 실험적 연구를 수행할 예정이다.
Acknowledgements
이 논문은 산업통상자원부 ‘산업전문인력역량강화사업’의 재원으로 한국산업기술진흥원(KIAT)의 지원을 받아 수행된 연구(2018년 한-영 해양플랜트 글로벌 전문인력 양성사업, 과제번호: N0001287)이며, 연구 지원에 감사드립니다.