제3세대 파랑모델의 비선형 에너지 이송항 계산 효율 증대를 위한 SRIAM 계산모듈 개발
Development of SRIAM Computation Module for Enhanced Calculation of Nonlinear Energy Transfer in 3rd Generation Wave Models
Article information
Abstract
Because of the rapid development of computer technology in recent years, wave models can utilize parallel calculations for the high-resolution prediction of open sea and coastal areas with high accuracy. Parallel calculations also allow national agencies in the relevant sectors to produce marine forecasting data through massive parallel calculations. Meanwhile, the eastern coast of the Korean Peninsula has been increasingly damaged by swell-like high waves, and many researchers and scientists are continuing their efforts to anticipate and reduce the damage. In general, the short-term transformation of swell-like high waves can be reproduced relatively well in the third generation wave models, but the transformation of relatively long period waves needs to be simulated with higher accuracy in terms of the nonlinear wave interactions to gain a better understanding of the low-frequency wave generation and development mechanisms. In this study, we developed a calculation module to improve the calculation of the nonlinear energy transfer in the 3rd generation wave model and integrated it into the wave model to effectively consider the nonlinear wave interaction. First, the nonlinear energy transfer calculation module and third generation model were combined. Then, the combined model was used to reproduce the wave transformation due to the nonlinear interaction, and the performance of the developed operation module was verified.
1. 서 론
최근 컴퓨터 기술이 급격하게 발달함에 따라 파랑모델의 연산을 수행하는데 병렬계산을 활용할 수 있게 되어 넓은 해역에 걸친 고해상도 파랑예측이 가능해졌다. 기상청과 해양조사원 등의 관련 기관에서는 대규모 병렬계산을 통한 파랑모델링을 통해 해양예보자료를 생산하여 대국민서비스 및 유사시 인명구조 등 관련 현업에 활용하고 있다. 이처럼 파랑모델의 활용도가 커짐에 따라 정확도 향상이 요구되고 있고 관련 연구자들이 다방면으로 모델의 성능 향상을 위해 노력하고 있다. 이 중 파랑모델의 비선형 에너지 이송항은 파랑의 비선형 상호작용에 의한 변형을 예측할 수 있어 초창기부터 관심을 받아왔으나 이를 재현하는 Boltzmann 적분은 4차 적분을 포함한 복잡한 수식으로 구성되어 있기 때문에 정확한 해석을 위해서는 막대한 계산시간이 소요되어 실용적이지 못하다(Hasselmann, 1962; Hasselmann and Hasselmann, 1981; Hasselmann and Hasselmann, 1985a; Masuda, 1980). 이에 따라 제3세대 파랑모델에서는 하나의 공명상호작용쌍만을 고려하는 방법을 사용하여 왔다(Hasselmann and Hasselmann, 1985b). 그러나 획기적인 접근으로 정확성을 상당히 유지시켰음에도 불구하고 단순화로 인해 주기가 상대적으로 긴 파랑을 모델링할 경우 제대로 재현해내지 못하는 한계가 있다(Hashimoto et al., 1998; Van Vledder, 2006; Tolman, 2013).
최근 동해안에서 이상고파라 알려져 있는 너울성 고파랑에 의한 피해가 증가하여 이를 예측하고 피해를 저감하기 위한 노력이 계속되고 있다. 그러나 앞서 살펴본 바와 같이 파랑모델에서 너울성 고파랑을 재현하기 위해서는 주기가 상대적으로 긴 파랑에 대한 재현 정확도를 높일 필요가 있으며, 이에 대한 대안으로 파랑의 비선형 상호작용을 고려하는 비선형 에너지 이송항의 계산효율을 증대시키는 계산기법의 도입이 요구되고 있다. 이러한 요구에 발맞추어 본 연구에서는 제3세대 파랑모델의 비선형 에너지 이송항 계산 효율 증대를 위한 계산모듈을 개발하고 파랑모델에 이를 접합하여 파랑의 비선형 상호작용을 효율적으로 고려할 수 있는 모델링 기법을 제안하였다. 먼저 비선형 에너지 이송항 계산모듈과 파랑모델의 접합을 수행하였으며, 접합된 파랑모델을 활용하여 비선형 상호작용에 의한 파랑 변형을 재현하고 개발된 계산모듈의 성능을 검증하였다.
2. 파랑모델
2.1 비선형 상호작용
파랑모델에서 에너지 방정식은 식 (1)과 같이 나타낼 수 있다.


여기서, E(ω, θ)는 파랑의 방향 스펙트럼, Cg는 파랑의 군속도, S는 Source항을 나타낸다. Source항은 식 (2)와 같이 각각 바람에 의한 입사에너지(S∈), 파랑의 전파과정에서 발생하는 감쇠에너지(Sdis), 비선형 에너지 이송항(Snl)으로 구성되어 있다. 이 중 Low frequency대에서는 비선형 파랑 상호작용에 의한 영향이 상대적으로 크기 때문에 파랑에너지 전달시 Frequency downshift가 발생하는 등 파랑의 발달과정에서 수치모델이 비선형 파랑 상호작용을 제대로 구현하지 못하게 되면 Low frequency대 에너지가 제대로 전파되지 못하고 소멸되어 파랑의 발달이 제대로 재현되지 못하는 문제가 발생하는 것으로 알려져 있다.
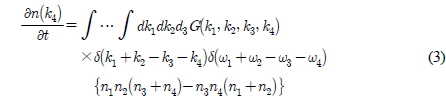
제3세대 파랑모델에서 비선형 상호작용은 Hasselmann(1962)에 의한 식 (3)의 Boltzmann 적분을 계산하여 구현하게 된다. 여기서, ni = n(ki) = Φ(ki)/ωi는 Wave action density, Φ(ki)는 파수 스펙트럼, G(k1, k2, k3, k4)는 Coupling 계수를 각각 나타낸다. 식 (3)에 나타난 것처럼 Boltzmann 적분은 4차 적분을 포함한 매우 복잡한 형태를 가지고 있기 때문에 정확해를 계산하여 파랑을 예측하는 일은 매우 어렵다. Boltzmann 적분을 정교하게 해석하는 연구는 미국, 네덜란드, 일본 등을 중심으로 수십 년 전부터 진행되어 왔다(Hashimoto et al., 1998; Hashimoto et al., 2002; Hasselmann and Hasselmann, 1981; Masuda, 1980; Resio and Perrie, 1991; Webb, 1978). 하지만 여러 연구에서 밝혀낸 계산 기법을 파랑모델에 적용하게 되면 계산이 매우 복잡하게 되며, 현대의 컴퓨터 기술로도 막대한 계산시간이 소요되어 실제 지형에서 파랑변형을 수치모델링 하는 일은 대규모 병렬연산 시스템을 활용하더라도 현실적으로 수행하기 어려운 수준이다(Komatsu and Masuda, 1996; Tolman, 2013; Van Vledder, 2006).
2.2 SRIAM(Simplified RIAM) 기법
SWAN, WAM, WAVEWATCHⅢ 등 현업에서 사용하는 많은 파랑모델은 이러한 어려움에 봉착하여 계산이 용이한 DIA(Discrete interaction approximation; Hasselmann and Hasselmann, 1985b) 기법을 사용하고 있으나 수많은 비선형 상호작용을 하나의 대표값으로 나타내기 때문에 많은 문제점을 보여주고 있다(Fig. 1). 이에 따라 파랑모델에 WRT(Webb-resio-tracy) 기법(Van Vledder, 2006)이나 EDIA(Extended DIA) 기법(Hashimoto and Kawaguchi, 2001), GMD(Generalized multi-DIA) 기법(Tolman, 2013) 등을 도입하여 그 한계를 극복하려 하고 있다. 본 연구에서는 이 중 계산의 효율성이 높고 상당한 정확도를 보이는 것으로 알려진 SRIAM(Simplified RIAM) 기법(Fig. 2; Komatsu, 1996)을 현업에서 사용되는 파랑모델에 접합하여 비선형 파랑상호작용을 구현하고 파랑 예측에 활용하고자 한다.
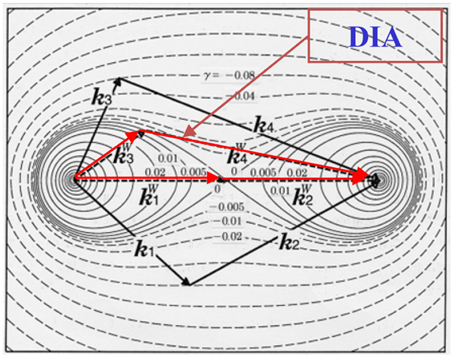
DIA scheme (Hasselmann and Hasselmann, 1985b)
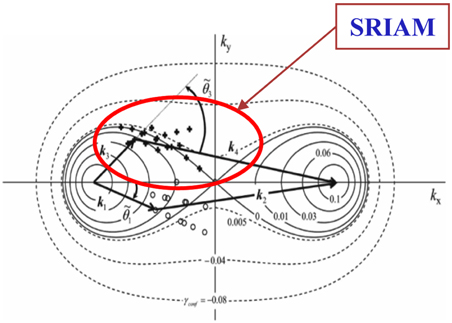
SRIAM scheme (Hashimoto et al., 2014)
Komatsu and Masuda(1996)는 대칭 조건을 도입하여 Masuda(1980)의 정확해에 상응하는 정확도를 가지면서 300배 이상 빠르게 계산할 수 있는 RIAM 기법을 제안하였다. 비록 300배 이상의 속도향상 효과를 얻는다하더라도 RIAM 기법은 현업 파랑모델에서 사용하는 단순화 기법인 DIA 기법에 비해 대략 2,000배 이상의 계산시간을 필요로 하기 때문에 여전히 막대한 계산시간이 소요되어 실용성이 떨어진다. 이를 개선하기 위해 Komatsu(1996)는 수 많은 파수의 조합 중 파랑 에너지를 효율적으로 재현해낼 수 있는 20개의 최적화된 계수를 유도하여 RIAM 기법을 단순화하였으며, 이를 통해 약간의 정확도 손해가 발생하지만 RIAM 기법에 비해 100배 이상의 계산 효율을 높인 SRIAM 기법을 제안하였으며 RIAM 기법에 상응하는 정확도를 가지고 있는 것으로 알려져 있다 (Hashimoto and Kawaguchi, 2001). RIAM 기법은 높은 정확도에 반해 DIA 기법에 비해 약 2,000배 높은 계산시간이 소요되기 때문에 현업에서 운용되는 파랑모델에 적용하는 것은 사실상 불가능하고 연구목적으로도 사용에 제한이 많다. 반면, 그보다 100배 이상 빠른 SRIAM 기법을 대규모 병렬 계산을 통해 활용할 수 있다면 DIA보다 20여배 정도 시간이 더 걸리지만 현업에서 운용되는 파랑모델에 적용하여 파랑 예측 정확도를 높이는데 기여할 수 있다고 사료된다.
2.3 SRIAM 기법의 파랑 모델 접합
2008년 일본의 JAMSTEC(Japan agency for marine-earth science and technology)에서는 비선형 상호작용 계산을 개선하기 위해 WAVEWATCHⅢ에 SRIAM과 RIAM을 접합하는 연구를 수행하여 모델의 성능을 검증하는 연구를 발표하였으나(Tamura et al., 2008), WAVEWATCHⅢ의 공식 버전에 포함하기 위한 NOAA(National oceanic and atmospheric administration)의 공식적인 공개 요청을 거절하여 현재 비공개로 연구를 수행하고 있다. 하지만 WAVEWATCHⅢ에 접합된 SRIAM 기법이 RIAM의 정확해에 상응하는 정확도를 보여주어 파랑의 비선형 상호작용을 상당히 정확하게 재현할 수 있는 것이 검증되었으며, SRIAM 기법이나 RIAM 기법의 계산 결과와 비교 할 때 기존의 DIA 기법은 매우 상이한 거동을 보이는 것을 확인할 수 있다(Tamura et al., 2008).
Hashimoto et al.(2014)은 기존의 Komatsu(1996)의 SRIAM 기법에서 일부 나타나는 계산오류를 수정하여 파랑의 전파를 고려하지 않고 Source항의 변화만을 계산할 수 있도록 단순화한 WAM모형에 도입하여 저주파대에서의 Frequency downshift를 계산하여 발표하였다. 본 연구에서는 JAMSTEC에서 수행한 연구를 토대로 미국 해양대기국(NOAA, National oceanic and atmospheric administration)에서 공식적으로 파랑 예측에 사용하고 있으며, 우리나라에서도 기상청과 해양수산부에서 이미 현업 모델로 사용하고 있는 WAVEWATCHⅢ에 Hashimoto et al.(2014)가 개발한 SRIAM 기법을 접합하였다.
SRIAM 기법의 WAVEWATCHⅢ 접합에 필요한 요소기술은 크게 2가지로 나눌 수 있다. 첫 번째로 음해법(Lavrenov, 2003)을 활용하여 에너지 방정식의 비선형 에너지 이송항을 계산하는 수치모델을 개발하였다. SRIAM 기법이나 RIAM 기법을 통해 Source항에서 비선형 에너지 이송항을 계산할 때 기존의 파랑모델이 사용하는 Semi-implicit 기법을 활용할 경우 수치모델의 오차가 기준을 초과하여 파랑모델의 정확도에 크게 영향을 주는 것으로 알려져 있다. 이에 Tamura et al.(2008)은 기존의 Source항 계산에서 사용하는 Semi-implicit 기법 대신 음해법을 도입하여 Semi-implicit 기법에 의한 결과보다 정확도를 크게 향상시켰다. 이에 본 연구에서는 WAVEWATCHIII에서 Hashimoto et al.(2014)의 SRIAM 기법을 사용할 경우 Source항에서 비선형 에너지 이송항을 Lavrenov(2003)의 음해법을 통해 계산하고 갱신할 수 있도록 수치 알고리즘을 개발하여 사용하였다. 두 번째로 파랑모델에 접합하여 병렬계산을 활용하기 위해 병렬계산을 지원하지 않는 기존의 모델을 병렬계산을 지원하는 모델로 변환하는 병렬 계산 소스코드를 개발하였다. SRIAM 기법의 도입을 위해 기존의 모델 구성을 분석하여 수치오류를 최소화하였으며, WAVEWATCHIII 접합을 위해 기존의 Source code에서 제공하고 있는 개발자 모듈(W3SNLX,ftn)을 활용하여 SRIAM 기법을 활용하는 비선형 에너지 이송항 계산기법을 개발하였다.
3. 파랑변형 수치모델링
3.1 비선형 에너지 이송항 계산기법 비교
2장에서 설명한 SRIAM 기법 접합을 위한 요소기술을 활용하여 WAVEWATCHIII에 SRIAM 기법으로 비선형 에너지 이송항을 계산하는 모듈을 접합하고, 접합한 모듈의 성능 검증을 위해 다양한 조건의 초기 파랑 스펙트럼을 생성하여 WAVEWATCHIII의 비선형 에너지 이송항 기법들을 비교하였다. WAVEWATCHIII에서 고려할 수 있는 파랑의 전파, 에너지 소산 등의 영향을 포함하여 실험을 수행할 경우 비선형 에너지 이송항 계산 결과가 타 조건에 의해 교란되어 계산기법의 차이에 따른 비선형 에너지 이송항의 역할을 분석하기 어렵기 때문에, WAVEWATCHIII의 계산 조건에서 비선형 에너지 이송항을 제외한 다른 계산을 모두 끈 상태로 시간의 흐름에 따른 비선형 에너지 이송항을 수치 계산하여 결과를 비교하였다. 바람 조건은 Duration-limited 조건으로 수치모델링을 수행하였으며, 총 모의 시간은 120시간으로 하였다.
초기 파랑 스펙트럼 생성을 위해 JONSWAP 스펙트럼(Hasselmann et al., 1980)을 초기 조건으로 활용하였으며, 파고와 파랑의 주기에 관해 Goda(2003)가 제안한 공식 T1/3 = 3.3(H1/3)0.63을 활용하여 스펙트럼을 생성하였다. 주기의 변화와 스펙트럼의 에너지 분포양상에 따른 비선형 에너지 이송항과 스펙트럼의 변화를 종합적으로 살펴보기 위해 JONSWASP 스펙트럼의 변수 중 첨두 주기와 γ값을 다양하게 조합하여 초기 스펙트럼을 생성하였으며, 각각의 조합에 따른 비선형 에너지 이송항과 스펙트럼 변화 양상을 각각 분석하였다.
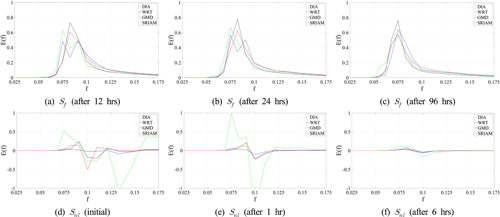
Fig. 3은 상대적으로 주기가 긴(f = 0.075s-1) 초기 파랑 스펙트럼에서 시간의 흐름에 따른 비선형 에너지 이송항과 파랑 스펙트럼의 변화를 도시한 것이다. 스펙트럼의 변화를 살펴보면 앞서 설명한대로 Frequency downshift가 발생하였으며, SRIAM 기법을 통해 비선형 에너지 이송항을 계산한 경우에 Semi-exact 계산기법인 WRT 기법의 결과와 가장 유사하게 나타난 것을 확인할 수 있다. 특히, WAVEWATCHIII에서 기본적으로 제공하고 있는 GMD 기법의 결과와 비교할 때 더 정확한 계산 결과를 보여줌을 확인할 수 있으며, 향후 비선형 에너지 이송항에 의한 파랑변형을 좀 더 효율적으로 계산할 수 있을 것으로 기대된다.

Numerical results of nonlinear energy transfer(Snl, Bottom) and wave energy spectrum(Sf, Top) using different numerical schemes (γ = 3.3, Tp = 13.3s)
Fig. 5는 상대적으로 주기가 긴 γ = 3.3, Tp = 13.3s 인 조건에서 비선형 에너지 이송항의 변화를 주파수와 파향으로 세분하여 2차원으로 도시한 결과이다. 앞서 설명한대로 SRIAM 기법을 통해 계산된 결과는 Semi-exact 계산기법인 WRT 기법의 결과와 정성적인 분포양상을 상당히 유사하게 나타내고 있으며, 정량적으로도 DIA 기법이나 GMD 기법에 비해 탁월한 결과를 나타내고 있다. DIA 기법은 정성적으로 WRT 기법이나 SRIAM 기법의 결과를 단순화한 형태로 재현하고 있으나 정량적으로는 두 기법과 현저한 차이를 보여주고 있다. 이와 반대로 GMD 기법은 정량적으로 WRT 기법이나 SRIAM 기법과 유사하나 정성적으로 주파수와 파향 모두에서 상당한 차이를 보이고 있다. 다만, 본 연구에서는 GMD 기법에서 매개 변수 조정 없이 WAVEWATCHIII ver. 4.18의 기본값을 사용했기 때문에 매개 변수를 조정을 통해 GMD 기법을 실험 케이스에 최적화한다면 결과가 좀 더 개선될 수 있을 것으로 사료된다.
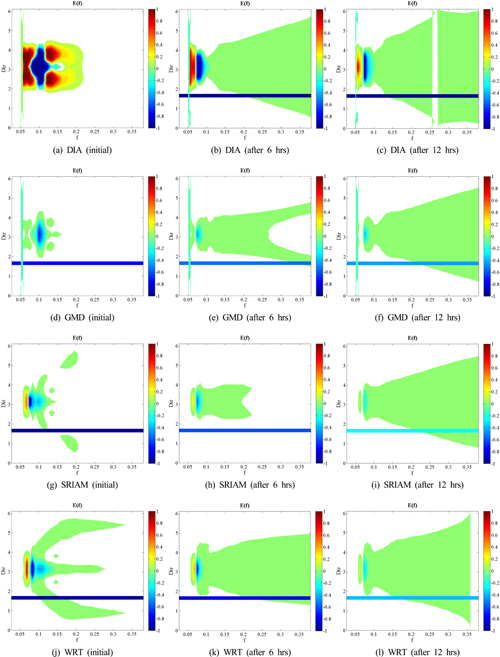
Comparison of frequency-direction distribution of nonlinear energy transfer(Snl) among different numerical schemes (γ = 3.3, Tp = 13.3s)
Fig. 6은 앞선 조건보다 일반적인 풍파의 특성을 나타내도록 주기를 조금 낮춘 γ = 7.0, Tp = 10.0s 인 조건에서 비선형 에너지 이송항의 변화를 주파수와 파향으로 세분하여 도시한 결과이다. Fig. 5와 유사하게 SRIAM 기법은 DIA 기법이나 GMD 기법에 비해 정량적 뿐 아니라 정성적으로도 WRT 기법에 거의 상응하는 정확도를 보여주고 있다. 특히, 주파수에서는 어느 정도 비슷한 경향을 보이고 있으나, 파향의 측면에서 보면 매우 상이한 결과를 나타내는 것을 확인할 수 있다. DIA 기법은 저주파수 부근에서 비선형 에너지 이송항이 과다하게 계산되어 Frequency downshift가 WRT 기법에 비해 과하게 재현되었으며, 반대로 GMD 기법은 저주파수 부근에서 비선형 에너지 이송항이 작게 계산되어 Frequency downshift가 충분히 발달하지 못하였다. 이로 인한 스펙트럼의 발달 오차를 Fig. 4에서 확인할 수 있다. 이러한 결과로부터 본 연구를 통해 개발한 SRIAM 기법을 활용하는 비선형 에너지 이송항 계산모듈이 WAVEWATCHIII의 기존 코드와 충돌 없이 잘 접합된 것을 확인할 수 있었다. Hashimoto et al.(2014)은 γ값이 작은 경우에 비선형 에너지 이송항의 영향이 상대적으로 원만하게 나타나 수치모델의 계산기법의 차이가 미미하게 나타나는 것을 실험을 통해 밝혀내었으며, 본 연구에서도 γ값이 작은 경우에는 4가지 비선형 에너지 이송항 계산기법에 따른 스펙트럼의 변화 양상에 거의 차이가 없는 것을 확인할 수 있었으나 지면상 본 논문에 결과를 포함하진 않았다.
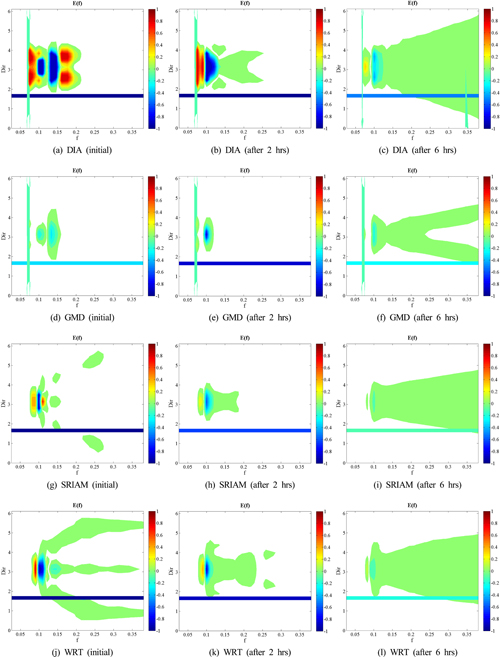
Comparison of frequency-direction distribution of nonlinear energy transfer(Snl) calculated by different numerical schemes (γ = 7.0, Tp = 10.0.s)
3.2 다양한 초기조건(JONSWAP 스펙트럼)에 대한 비선형 에너지 이송항 변화 비교
수치실험 결과에서 알 수 있듯이 비선형 에너지 이송항을 계산할 때 DIA 기법은 타 기법에 비해 초기부터 매우 큰 값을 가지는 것으로 나타났으며, 나머지 기법들은 양적으로 비슷한 값을 보였으나 발달과 소멸 양상이 기법에 따라 상이했다. 그에 따라 비선형 에너지 이송항의 초기 계산 결과부터 누적되어 스펙트럼의 변화가 나타났으며, Fig. 3과 Fig. 4의 스펙트럼 변화에서 모두 시간의 흐름에 따라 Semi-exact 계산기법인 WRT 기법에 SRIAM 기법이 가장 유사한 결과를 나타내었다. Hashimoto et al.(2014)은 풍파(Wind wave)의 조건에서는 Frequency downshift 현상이 매우 두드러지게 나타나고 풍파에서 너울(Swell)의 조건으로 변해감에 따라 Frequency downshift 현상이 작아지는 것을 실험을 통해 확인하였으며, 본 연구에서도 유의 주기 Tp가 상대적으로 길어 보다 너울에 가까운 Fig. 3보다 풍파 조건에 가까운 Fig. 4에서 Frequency downshift가 뚜렷하게 나타났다. 또한, γ값이 커짐에 따라 비선형 에너지 이송항의 영향이 커지는 것으로 나타났으며, 이로 인해 스펙트럼의 변화에서 Frequency downshift 현상이 심해지는 것을 확인할 수 있었다. 비선형 에너지 이송항에 대한 스펙트럼의 변화는 Semi-exact 계산기법인 WRT 기법을 기준으로 볼 때 SRIAM 기법이 DIA 기법이나 GMD 기법에 비해 상대적으로 정확하게 스펙트럼의 변화를 계산해 내는 것을 확인할 수 있다.
2.2절에서 설명한 바와 같이 SRIAM 기법은 DIA 기법에 비해 약 20여배 계산시간이 더 소요되는 것으로 알려져 있으며, 본 연구에서도 SRIAM 기법이 DIA 기법에 비해 계산시간이 약간 더 소요되었다. 이는 하나의 공명상호작용쌍만을 고려하는 DIA 기법과 달리 SRIAM 기법에서 20개의 대표 공명상호작용쌍을 고려하여 비선형 상호작용을 계산하기 때문으로, GMD 기법과 같이 다중으로 DIA 기법을 고려할 때에도 몇 개의 조합을 고려하는가에 따라 계산시간이 더 소요될 수 있다. 그러나 본 연구에서와 같이 이상적인 조건의 소규모 격자에서 실험을 수행할 경우 단일 PC를 사용하더라도 계산시간에는 거의 차이가 없었으며, Semi-exact 계산기법인 WRT 기법에 비해서는 월등히 빠른 계산 속도를 나타냈다. WRT 기법에 의한 계산시간은 본 연구와 같이 단순한 실험에서도 다른 기법에 비해 몇 십 배 이상인 수분이 소요되었다. 실제 지형에서 파랑모델링을 수행할 경우 WRT 기법은 현업에 적용이 불가능한 수준의 계산시간이 필요하며, SRIAM 기법은 병렬연산을 활용한다면 현업에서 충분히 사용 가능할 것으로 사료된다.
4. 결 론
본 연구에서는 제3세대 파랑모델의 저주파 파랑의 재현 정확도 향상을 위해 비선형 에너지 이송항을 효율적으로 계산할 수 있는 SRIAM 기법을 활용한 계산모듈을 개발하고, 이를 파랑모델에 접합하여 파랑의 비선형 상호작용을 효율적으로 고려할 수 있는 모델링 기법을 제안하였다. 이를 위해 비선형 에너지 이송항 계산에 음해법을 도입한 수치 알고리즘을 개발하였으며, 제3세대 파랑모델인 WAVEWATCHIII의 개발자 모듈을 활용하여 비선형 에너지 이송항 계산모듈을 접합하였다. 끝으로 접합된 파랑모델을 활용하여 비선형 상호작용에 의한 파랑 변형을 재현하고 개발된 계산모듈의 성능을 검증하였다. 검증결과 파랑모델에 접합된 SRIAM 기법을 활용할 경우 파랑모델이 비선형 에너지 이송항에 대한 스펙트럼 변화를 기존의 DIA 기법이나 GMD 기법에 비해 Semi-exact 계산기법인 WRT 기법에 준하는 정확도로 재현하였다. 또한, SRIAM 기법이 기존의 DIA 기법이나 GMD 기법에 비해 계산시간이 약간 더 소요되는 것으로 나타났으나 WRT 기법과 비교할 때 월등히 빠른 계산속도를 나타냈다. 본 연구를 통해 개발된 계산모듈은 동해 이상고파와 같은 장주기 파랑예측에 효율적으로 활용할 수 있을 것으로 기대되며, 조류와 해류 등의 바다의 흐름과 파랑의 상호작용 등의 해석에 적용이 가능할 것으로 사료된다. 그러나 아직까지 실해역에 대한 적용이 미흡하여 이에 대한 추가 연구가 필요하며, 바다의 흐름과의 상호작용을 재현하기 위해서는 관련된 후속 연구가 반드시 필요할 것으로 판단된다.
Acknowledgements
본 연구는 해양수산부 재원으로 한국해양과학기술진흥원(사업명: 해양과학국제연구사업, 과제번호: 20170265, 과제명: 극한 폭풍파 대응 연안 직립형 도시 구조물 취약성 함수 개발)의 지원과 기상청 연구개발 프로그램의 재원으로 한국기상산업진흥원(KMIPA 2015-1072)의 지원을 받아서 수행하였습니다. 또한, 2015년도 강원대학교 대학회계 학술연구조성비로 연구하였음을 밝히며, 연구비 지원에 감사드립니다.
References
Goda, Y., 2003. Revisiting Wilson’s Formulas for Simplified Wind-wave Prediction. Journal of Waterway, Port, Coastal, and Ocean Engineering, 129(2), 93-95.
Goda Y.. Revisiting Wilson’s Formulas for Simplified Wind-wave Prediction. Journal of Waterway, Port, Coastal, and Ocean Engineering 2003;129(2):93–95. 10.1061/(ASCE)0733-950X(2003)129:2(93).Hashimoto, N., Kawaguchi, K., 2001. Extension and Modification of the Discrete Interaction Approximation (DIA) for Computing Nonlinear Energy Transfer of Gravity Wave Spectra. Proceedings of the 4th ASCE International Symposium on Ocean Wave Measurement and Analysis, San Francisco USA, 530-539.
Hashimoto N., Kawaguchi K.. Extension and Modification of the Discrete Interaction Approximation (DIA) for Computing Nonlinear Energy Transfer of Gravity Wave Spectra In : Proceedings of the 4th ASCE International Symposium on Ocean Wave Measurement and Analysis. San Francisco USA; 2001. p. 530–539.Hashimoto, N., Haagsma, I.G., Holthuijsen, L.H., 2002. Four-wave Interactions in SWAN. Proceedings of the 28th International Conference on Coastal Engineering, ASCE, Cardiff UK, 392-404.
Hashimoto N., Haagsma I.G., Holthuijsen L.H.. Four-wave Interactions in SWAN In : Proceedings of the 28th International Conference on Coastal Engineering. Cardiff UK. ASCE; 2002. p. 392–404.Hashimoto, N., Tsuruya, H., Nakagawa, Y., 1998. Numerical Computations of the Nonlinear Energy Transfer of Gravity-wave Spectra in Finite Water Depth. Coastal Engineering Journal, 40(1), 23-40.
Hashimoto N., Tsuruya H., Nakagawa Y.. Numerical Computations of the Nonlinear Energy Transfer of Gravity-wave Spectra in Finite Water Depth. Coastal Engineering Journal 1998;40(1):23–40. 10.1142/S0578563498000030.Hashimoto, N., Suciaty, F., Yamashiro, M., Yokota, M., Kodama, M., 2014. Numerical Study on Frequency Downshift of Gravity Wave Spectra in Deep and Intermediate Water Depths Due to Nonlinear Energy Transfer. Proceedings of the 34th International Conference on Coastal Engineering, ASCE, Seoul Korea, 146-158.
Hashimoto N., Suciaty F., Yamashiro M., Yokota M., Kodama M.. Numerical Study on Frequency Downshift of Gravity Wave Spectra in Deep and Intermediate Water Depths Due to Nonlinear Energy Transfer In : Proceedings of the 34th International Conference on Coastal Engineering. Seoul Korea. ASCE; 2014. p. 146–158.Hasselmann, D.E., Dunckel, M., Ewing, J.A., 1980. Directional Wave Spectra observed during JONSWAP 1973. Journal of Physical Oceanography, 10, 1264-1280.
Hasselmann D.E., Dunckel M., Ewing J.A.. Directional Wave Spectra observed during JONSWAP 1973. Journal of Physical Oceanography 1980;10:1264–1280. 10.1175/1520-0485(1980)010<1264:DWSODJ>2.0.CO;2.Hasselmann, K., 1962. On the Non-linear Energy Transfer in a Gravity-wave Spectrum: Part 1. General Theory. Journal of Fluid Mechanics, 12, 481-500.
Hasselmann K.. On the Non-linear Energy Transfer in a Gravity-wave Spectrum: Part 1. General Theory. Journal of Fluid Mechanics 1962;12:481–500. 10.1017/S0022112062000373.Hasselmann, K., Hasselmann, S., 1981. A Symmetrical Method of Computing the Non-linear Transfer in a Gravity Wave Spectrum. Hamburger Geophysikalische Einzelschriften, Wittenborn.
Hasselmann K., Hasselmann S.. A Symmetrical Method of Computing the Non-linear Transfer in a Gravity Wave Spectrum Hamburger Geophysikalische Einzelschriften. Wittenborn: 1981.Hasselmann, S., Hasselmann, K., 1985a. The Wave Model EXACT-NL. Ocean Wave Modelling, The SWAMP group. Plenum Press, New York.
Hasselmann S., Hasselmann K.. The Wave Model EXACT-NL. Ocean Wave Modelling, The SWAMP group Plenum Press. New York: 1985a.Hasselmann, S., Hasselmann, K., 1985b. Computation and Parameterizations of the Nonlinear Energy Transfer in a Gravitywave Spectrum: Part 1. A New Method for Efficient Computations of the Exact Nonlinear Transfer Integral. Journal of Physical Oceanography, 15, 1369-1377.
Hasselmann S., Hasselmann K.. Computation and Parameterizations of the Nonlinear Energy Transfer in a Gravitywave Spectrum: Part 1. A New Method for Efficient Computations of the Exact Nonlinear Transfer Integral. Journal of Physical Oceanography 1985b;15:1369–1377. 10.1175/1520-0485(1985)015<1369:CAPOTN>2.0.CO;2.Komatsu, K., A. Masuda, 1996. A New Scheme of Nonlinear Energy Transfer among Wind Waves: RIAM Method - Algorithm and Performance, Journal of Oceanography, 52, 509-537.
Komatsu K., Masuda A.. A New Scheme of Nonlinear Energy Transfer among Wind Waves: RIAM Method - Algorithm and Performance. Journal of Oceanography 1996;52:509–537. 10.1007/BF02239052.Komatsu, K. 1996. Development of a New Generation Wave Forecasting Model based on a New Scheme of Nonlinear Energy Transfer among Wind Waves, Dr. Thesis, University of Kyushu, 155.
Komatsu K.. Development of a New Generation Wave Forecasting Model based on a New Scheme of Nonlinear Energy Transfer among Wind Waves, Dr. Thesis University of Kyushu; 1996. 155.Lavrenov, I., 2003. Wind-waves in Oceans: Dynamics and Numerical Simulations. Springer.
Lavrenov I.. Wind-waves in Oceans: Dynamics and Numerical Simulations Springer; 2003.Masuda, A., 1980. Nonlinear Energy Transfer between Wind Waves. Journal of Physical Oceanography, 10, 2082-2093.
Masuda A.. Nonlinear Energy Transfer between Wind Waves. Journal of Physical Oceanography 1980;10:2082–2093. 10.1175/1520-0485(1980)010<2082:NETBWW>2.0.CO;2.Resio, D.T., Perrie, W., 1991. A Numerical Study of Nonlinear Energy Fluxes Due to Wave-wave Interactions. Part 1: Methodology and Basic Results, Journal of Fluid Mechanics, 223, 609-629.
Resio D.T., Perrie W.. A Numerical Study of Nonlinear Energy Fluxes Due to Wave-wave Interactions. Part 1: Methodology and Basic Results. Journal of Fluid Mechanics 1991;223:609–629.Tamura, H., Waseda, T., Miyazawa, Y., Komatsu, K., 2008. Current Induced Modulation of the Ocean Wave Spectrum and the Role of Nonlinear Energy Transfer, Journal of Physical Oceanography, 38, 2662-2684.
Tamura H., Waseda T., Miyazawa Y., Komatsu K.. Current Induced Modulation of the Ocean Wave Spectrum and the Role of Nonlinear Energy Transfer. Journal of Physical Oceanography 2008;38:2662–2684. 10.1175/2008JPO4000.1.Tolman, H.L., 2013. A Generalized Multiple Discrete Interaction Approximation for Resonant Four-wave Nonlinear Interactions in Wind Wave Models with Arbitrary Depth. Ocean Modelling, 70, 11-24.
Tolman H.L.. A Generalized Multiple Discrete Interaction Approximation for Resonant Four-wave Nonlinear Interactions in Wind Wave Models with Arbitrary Depth. Ocean Modelling 2013;70:11–24. 10.1016/j.ocemod.2013.02.005.Van Vledder, G.P., 2006. The WRT Method for the Computation of Non-linear Four Wave Interactions in Discrete Spectral Wave Models. Coastal Engineering, 53, 223-242.
Van Vledder G.P.. The WRT Method for the Computation of Non-linear Four Wave Interactions in Discrete Spectral Wave Models. Coastal Engineering 2006;53:223–242. 10.1016/j.coastaleng.2005.10.011.Webb, D.J., 1978. Nonlinear Transfer between Sea Waves. Deep Sea Research, 25(3), 279-298.
Webb D.J.. Nonlinear Transfer between Sea Waves. Deep Sea Research 1978;25(3):279–298. 10.1016/0146-6291(78)90593-3.