안벽 앞에 부분 잠긴 진자판에 의한 파랑에너지 추출
Wave Energy Extraction using Partially Submerged Pendulum Plate with Quay Wall
Article information
Abstract
The performance of a wave energy converter (WEC) that uses the rolling motion of a partially submerged pendulum plate in front of a quay wall was analyzed. The wave exciting moment and hydrodynamic moment were obtained using a matched eigenfunction expansion method (MEEM) based on the linear potential theory, and then the roll motion response of a pendulum plate, time averaged extracted power, and efficiency were investigated. The optimal PTO damping coefficient was suggested to give the optimal extracted power. The peak value of the optimal extracted power occurs at the resonant frequency. The resonant peak and its width increase as the submergence depth of the pendulum plate decreases and thickness of the pendulum plate increases. An increase in the wave incidence angle reduces the efficiency of the wave energy converter. In addition, the WEC using a rolling pendulum plate contributes not only to the extraction of the wave energy, but also to a reduction in the waves reflected from the quay wall, which helps to stabilize ships going near the quay wall.
1. 서 론
파랑 중 회전 운동하는 진자판을 이용한 파력발전장치(Oscillating wave surge converter)는 회전 중심점(Hinge point)이 수면 위에 놓인 형태와 해저면 바닥에 놓인 형태로 분류할 수 있다. 이러한 유형의 파력발전장치로 현재 상용화 단계에 와 있는 대표적인 파력발전장치로 Oyster(Whittaker and Folley, 2012)와 Waveroller(Lucas et al., 2012)가 있다. 2000년대 초반부터 Aquamarine Power사에 의해 개발된 Oyster는 연안 가까이에 위치하여 파랑에너지를 흡수한다(Whittaker et al., 2007; Whittaker and Folley, 2012). 1차 변환과정을 통하여 얻은 진자판의 운동에너지는 높은 압력으로 물을 육상으로 보내 터빈을 구동시켜 전기를 생산한다. Oyster의 장점은 최소한의 장치만을 물속에 잠기게 하여 유지보수가 용이하다는 점이다. 또한 자동 제어장치, 변속 기어장치, 비상시 제동장치가 불필요하다. 실물 크기의 Oyster 2기가 2009년과 2011년에 스코틀랜드 Orkney에 위치한 EMEC(European marine energy centre)에서 실해역 실증실험을 마쳤다. Waveroller는 해안선으로부터 0.3-2km, 수심 8-20m에 적합한 천수용 파력발전장치이다. 1차 변환장치의 개념은 Oyster와 비슷하나 2차 변환장치는 Oyster와 달리 직접 전기를 생산하는 타입이다. 파랑중 회전 운동하는 진자판은 피스톤 타입의 유압펌프를 작동시켜 폐회로 파이프 관내에 있는 작동 유체를 순환시킨다. 그 결과 높은 압력의 작동유체는 유압모터를 구동시키며, 이는 전기에너지를 생산하는 원동력이 된다. 이때 유압시스템내의 모든 부품들은 정교하게 만든 하우징으로 수밀상태를 유지해야한다. 국내에서는 선박해양플랜트연구소(Korea research institute of ships & ocean engineering, KRISO)에서 Waveroller를 변형한 부유식 진자형 파력발전장치를 개발하여 현재 실증실험을 준비 중에 있다(Nam et al., 2011; Park et al., 2012; Nam et al., 2012).
파력발전장치의 연구 및 개발의 역사를 살펴보았을 때, 진자판을 이용한 파력발전장치에 대한 관심은 최근에 높아졌다. 이는 천수역에서 이용 가능한 파랑에너지의 밀도가 심해역보다 낮다고 알려졌기 때문이다. 그 이유는 파가 해안에 가까워짐에 따라 수심이 점점 얕아지면서 많은 양의 파랑에너지가 해저면에서의 마찰과 수면에서의 쇄파로 소멸된다. 그러나 마찰과 쇄파에 의한 천수역에서의 입사 파고의 제한은 입력 에너지의 크기를 일정하게 유지시켜 파력발전장치의 작동률을 높이는데 기여한다. 또한 천수역에서 수심 변화에 따른 굴절현상으로 파정선(Wave crest line)은 등 수심선과 거의 평행해진다. 따라서 천수역에서의 파의 진행방향은 심해역과 달리 다방향으로 분산되지 않고 일정한 방향을 유지시켜 에너지 집중 효과를 가져온다. 이러한 이유들로 Whittaker and Folley(2012)는 에너지 추출 측면에서 심해역과 천수역 사이에는 큰 차이가 없다고 주장하였다.
파랑중 운동하는 진자판의 동유체역학적 특성은 몇몇 저자에 의해 포텐셜 유동의 가정 아래에서 해석적으로 연구되었다. Evans(1970)는 운동변위가 작다는 가정 아래에서 몰수형 진자판에 작용하는 회절력을 구하였다. Cho(2003)는 안벽 앞에 놓인 일정 깊이 부분 잠긴 투과성 슬릿판에 의한 반사율을 슬릿판의 공극율과 잠긴 깊이 그리고 입사파의 경사각을 바꿔가면서 해석하였다. 해석방법으로 고유함수전개법을 사용하였다. 진자판에 의한 파의 방사문제는 2차원 조파수조 한쪽 끝단에 설치한 조파판에 대한 연구를 확장한 것이다(Dean and Dalrymple, 1984; Falnes, 2002). Evans and Porter(1996)는 몰수형 진자판의 동유체 역학적 문제를 풀어 수심과 진자판 높이의 비에 따른 부가 관성모멘트 및 방사감쇠계수에 대한 해석해를 얻었다. 3차원 수면 관통형 진자판에 대한 회절문제는 방파제 연구와 관련하여 여러 저자들에 의해 다루어졌다. Penney and Price(1952)는 두께를 무시한 직립판을 이용한 방파제에 의한 투과율과 반사율에 대한 근사해를 구하였다. Queen's 대학 연구진은 진자판을 이용한 파력발전장치에 대한 많은 연구들을 수행하였다(Whittaker et al., 2007; Folley et al., 2007; Whittaker and Folley, 2012). 이로부터 유체역학적 효율이 우수한 진자판의 중요성을 강조하였고, 이는 Oyster 개발로 이어졌다.
본 연구에서는 직립 안벽 앞에 놓인 일정 깊이 잠긴 진자판의 파랑중 회전운동 특성을 살펴보고 추출파워의 극대화를 위하여 여러 설계변수들을 바꿔가면서 최적의 변수 값들을 도출하는 과정을 다루었다. 선형 포텐셜이론에 근거한 고유함수전개법을 사용하여 회절과 방사 포텐셜을 구하는 과정을 2.1절과 2.2절에 소개하였다. 안벽 앞에 놓인 진자판의 파랑중 회전운동 특성과 추출파워 그리고 효율은 2.3절에서 살펴보았다. 3장에서는 진자판 파력발전장치의 여러 설계변수(진자판의 두께와 잠긴 깊이, 안벽과의 거리, 입사 각도)등이 추출 효율에 미치는 영향에 관한 여러 결과들을 제시하고 설계에 반영하였고, 끝으로 중요한 결론들을 4장에서 언급하였다.
2. 문제의 정식화
Fig. 1과 같이 수심(h)이 일정한 유체영역 내에 일정깊이(d) 잠긴 진자판이 직립 안벽(x = s) 앞에 놓여 있다고 생각하자. 진자판의 폭(W)은 진자판의 잠긴 깊이(d)와 두께(tf)에 비하여 무한히 길다고 가정하였다. 입사파는 x축과 β의 경사 각도를 갖고 들어온다. 선형포텐셜 이론에 따라 속도포텐셜(Φ)을 도입하고, 유동은 주파수 ω를 갖고 조화운동을 하고 진자판이 폭 방향(y축)으로 일정하다고 가정하면 속도포텐셜과 파형식 그리고 진자파의 수평속도와 진자판의 회전운동 변위는 아래와 같이 쓸 수 있다.
Definition sketch of a rolling pendulum plate.
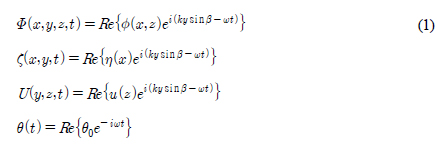
새로 도입된 속도포텐셜 ϕ(x, z)는 y축에 무관한 함수가 되어 2차원 문제로 바뀐다. 전체 속도포텐셜 ϕ(x, z)는 아래와 같이 회절포텐셜(ϕD)과 방사포텐셜(ϕR)의 합으로 표현할 수 있다.
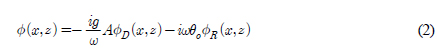
여기서 g는 중력가속도이며, A는 입사파의 진폭이다. 입사파와 산란파의 합으로 표현되는 회절포텐셜(ϕD = ϕI + ϕS)과 진자판의 회전운동으로 유기되는 방사포텐셜(ϕR)은 아래와 같은 경계치 문제를 만족한다.
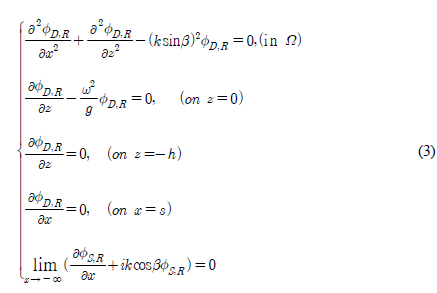
여기서 k는 입사파의 파수(Wave number)를 나타낸다.
2.1 회절문제
해석방법으로 유체영역을 진자판을 경계로 2개의 영역(영역 (1), 영역 (2))으로 나누고, 각 영역에서 속도포텐셜을 구하고 부족한 경계조건으로부터 생기는 미지수는 진자판이 놓여 있는 정합면(x = 0)에서 두 영역의 해를 정합시켜 완전한 해를 구하는 고유함수전개법을 사용하였다. 회절포텐셜은 경계조건식 (3)과 함께 진자판에서 경계조건식(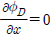
)을 만족한다. 영역 (1)과 영역 (2)의 회절포텐셜을 변수분리법을 사용하여 표현하면 다음과 같다.
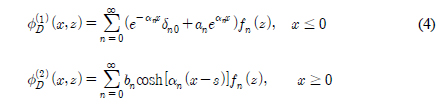
여기서 δn0는 n = 0일 때 1이고, n이 0보다 크면 0의 값을 갖는 Kronecker-Delta함수이다.
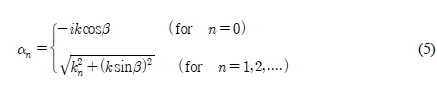
윗식에서 n = 0일 때를 진행 모드(Propagating mode)라 부르며, n이 0보다 클 때를 비진행 모드(Evanescent modes)로 진자판으로부터 멀어짐에 따라 지수함수 형태로 사라지는 항이다. 고유함수 fn(z)와 고유치 kn은 다음과 같다.
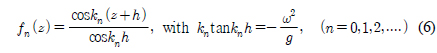
여기서 k0 =−ik이다.
식 (4)에 나타난 미지수인 an, bn을 구하기 위하여 두 영역이 만나는 정합면(x = 0, −h ≤ z ≤ 0)에서 수평방향 속도가 서로 같다는 정합조건식을 적용하여야 한다.
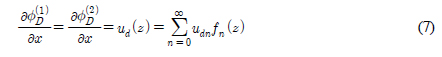
식 (4)를 윗식에 대입하여 정리하면 미지수 an, bn을 미지수 udn으로 표현할 수 있다.
식 (8)을 식 (4)에 대입하여 영역 (1)과 (2)에서의 속도포텐셜을 다시 쓰면 다음식과 같다.
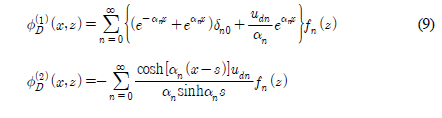
식 (9)에서 미지수로 남아있는 udn, (n = 0, 1, 2,...)을 구하기 위해서는 추가적인 정합조건식이 필요하다. 먼저 x = 0, −h ≤ z ≤ −d에서 영역 (1)과 영역 (2)의 속도포텐셜은 서로 같아야 한다(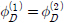
).
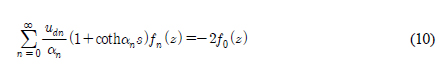
양변에 fm (z)을 곱한뒤 −h부터 −d까지 적분하여 정리하면 아래와 같은 적분방정식을 유도할 수 있다.
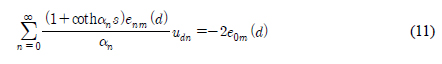
여기서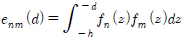 
이다.
끝으로 진자판이 놓인 정합면(x = 0, −d ≤ z ≤ 0)에서 다음과 같은 물체경계조건식을 만족하여야 한다.
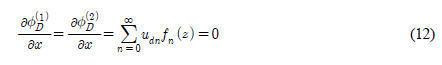
윗식의 양변에 fm (z)을 곱한뒤 −d부터 0까지 적분한 뒤 고유함수의 직교성 성질을 적용하면 다음과 같다.
여기서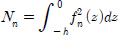 
이다.
대수방정식 (11)과 (13)을 더하면 회절문제에 대한 최종적으로 풀어야 할 대수방정식을 얻을 수 있다.
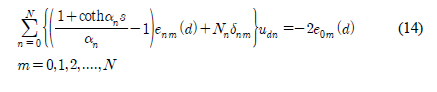
이때 고유함수개수를 유한개(N) 취한다. 대수방정식 (14)을 풀어 N+1개의 미지수 udn, (n = 0, 1, 2,..., N)을 구한다. 구한 결과를 식 (9)에 대입하면 각 영역에서 타당한 완전한 해를 구할 수 있다.
파기진 모멘트(ME(t) = ARe{mE(β,ω)e−iωt})는 베르누이방정식으로부터 얻은 동압력을 적분하여 구해진다.
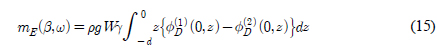
여기서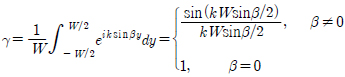 
고정된 진자판에 의한 반사율은 식 (9)로부터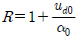 
이며, 안벽(x = s)에서의 파형식의 복소진폭은 
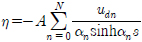이다.
2.2 방사문제
앞 절에서는 고정된 진자판에 의한 파의 회절문제를 살펴보았다. 이 절에서는 진자판의 회전운동에 의한 방사문제(Radiation problem)를 살펴보겠다. 진자판의 회전운동이 작다는 가정 (sinθ ≈ θ) 아래에서 식 (1)의 진자판 수평속도는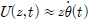 
이다. 진자판이 주파수 ω를 갖고 조화운동을 한다면 u(z) = −iωθ0z 이다. 진자판의 수평속도는 물입자의 속도와 서로 같다는 경계조건식을 이용하면 방사문제에 대한 진자판에서의 경계조건식 (
)을 유도할 수 있다. 해석방법으로 앞 절에서와 같이 유체영역을 2개의 영역(영역 (1), 영역 (2))으로 나누고, 인접한 영역의 해를 정합시켜 해를 구하는 고유함수전개법을 사용하였다. 각 영역에서의 속도포텐셜은 다음과 같다.
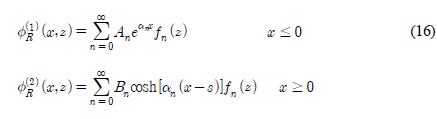
(2.1)절과 같은 방법으로 두 영역이 만나는 정합면 (x = 0, −h ≤ z ≤ 0)에서 속도(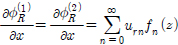
)가 서로 같다는 정합조건식을 적용하여 각 영역의 속도포텐셜을 다시 쓰면 다음과 같다.
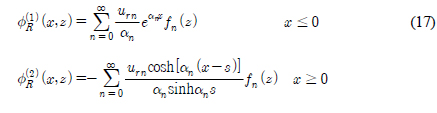
식 (17)을 정합면(x = 0, −h ≤ z ≤ −d)에서 속도포텐셜이 서로 같아야 한다는 정합조건식(
)에 대입하면 아래와 같은 대수방정식을 유도할 수 있다.
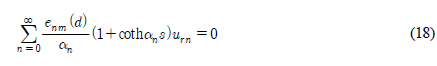
끝으로 x = 0, −d ≤ z ≤ 0에서 물체경계조건식(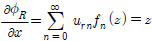
)으로부터 두 번째 대수방정식을 유도할 수 있다.
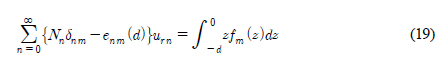
대수방정식 (18)과 (19)을 더하면 최종 대수방정식을 얻을 수 있다.
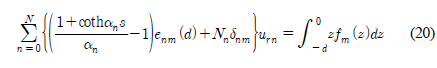
대수방정식 (20)을 풀어 urn, (n = 0, 1, 2,..., N)를 구한다. 구한 결과를 식 (17)에 대입하여 각 영역에서의 방사포텐셜을 구할 수 있다. 진자파의 회전운동에 의한 무한원방(x = −∞)에서의 방사파는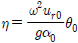 
이다.
진자판의 회전운동에 의한 동유체 모멘트(MR (t) = Re {mR(β, ω)e−iωt)는 다음과 같다.
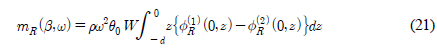
동유체 모멘트(mR)은 부가 관성모멘트(a55)와 방사감쇠계수(b55)의 합으로 표현된다.
2.3 운동방정식
파랑중 진자판의 회전운동 변위를 구하기 위해 아래와 같은 운동방정식을 풀어야 한다.
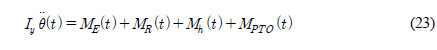
여기서 Iy는 진자판의 관성모멘트, Mh (=−C55 θ(t))는 정유체 복원모멘트를 뜻한다.
진자판의 두께가 진자판의 폭과 깊이에 비하여 작고, 질량이 균일하게 분포되어 있다고 가정하면 진자판의 관성모멘트와 정유체 복원모멘트 계수는 다음과 같다(Gomes et al., 2015). 진자판의 무게중심(zg)과 부력중심(zb)은 d/2이다.
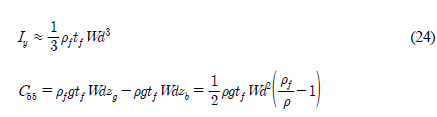
여기서 ρf는 진자판의 밀도이다.
MPTO는 에너지 추출을 위한 PTO(Power take-off) 장치 설치에 따른 감쇠 모멘트로 진자판의 회전운동 변위와 선형적으로 변한다고 가정하였다.
식 (23)을 주파수 영역의 운동방정식으로 바꾼 후 구한 진자판의 회전운동 복소진폭은 다음과 같다.
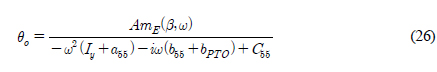
PTO 감쇠계수와 진자판의 운동속도의 제곱에 비례하는 시간평균 파워는 아래와 같다.
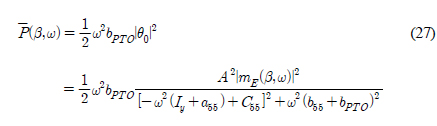
윗식에서 시간평균 파워가 최대값을 갖도록 식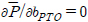 
을 만족하는 최적의 PTO 감쇠계수를 구하면 다음과 같다.
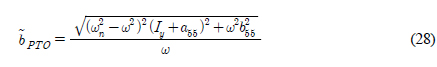
여기서 ωn는 회전운동의 비감쇠 고유주파수(Undamped natural frequency)로 아래와 같다.
식 (29)는 초기값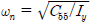 
을 가지고 주파수 별로 미리 구해 놓은 부가질량 a55(ω)을 가지고 축차법(Iteration method)을 사용하여 계산된다.
식 (28)을 식 (26)에 대입하면 PTO-on상태에서의 진자판의 회전운동 변위를 구할 수 있으며, 식 (27)에 대입하면 시간평균 파워를 구할 수 있다. 시간평균 파워를 단위 폭당 입사파의 파워로 나누면 식 (30)에 주어진 취득 폭(Capture width)을 구할 수 있다. 취득 폭을 진자판 파력발전장치의 폭(W)으로 나누면 파력발전장치의 효율이 된다.
여기서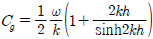 
는 군속도(Group velocity)이다.
최대 추출파워와 효율을 얻기 위해서는 각 입사파의 주파수에 대하여 
와 입사파의 주파수와 진자판의 회전운동 고유주파수가 일치하는 공진조건(ω = ωn)을 동시에 만족하여야 한다(Falnes, 2002). 이 조건은 식 (28)의 최적의 PTO 감쇠계수가 진자판의 운동 진폭만을 최적화했다면 진자판 운동 진폭과 함께 위상도 최적화하였을 때 얻어지는 조건이다. 따라서 식 (28)을 사용하여 얻은 추출파워와 효율의 상한계(Upper bound)를 형성한다.
진자판의 회전운동을 허용한 상태에서 반사율과 안벽에서의 파형의 복소진폭은 다음식과 같다.
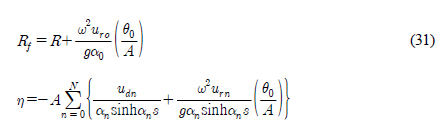
여기서 R는 고정된 진자판에 의한 반사율이다.
3. 계산결과 및 고찰
Fig. 2는 안벽이 없고 진자판의 무차원화된 잠긴 깊이가 d/h = 0.5로 고정되어 있을 때 부가 관성모멘트, 방사감쇠계수, 파기진 모멘트에 대한 2차원 해석해와 3차원 수치해를 비교하였다. 여기서 굵은 실선은 고유함수전개법을 사용한 2차원 해석해의 결과이며, 기호는 WAMIT를 사용한 수치계산 결과이다. x축은 무차원화된 주파수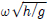 
로 잡았다. 상용코드 WAMIT은 Green 적분방정식을 풀어 구하는 수치해석코드이다. 따라서 진자판을 일정한 크기의 격자로 분할하는데 수치계산 과정에서 진자판의 두께 tf = 0일 때 Green 적분방정식은 특이 거동(Singular behavior)을 보인다. 이를 해결하기 위하여 진자판 위에 일정 강도를 갖는 다이폴(Dipole)을 분포시켰다. 격자수는 W/h = 0.5을 기준하여 깊이 방향으로 25개, 폭 방향으로 25개의 격자를 두었고 폭이 증가함에 따라 폭 방향의 격자수를 비례하여 증가시켰다. 진자판의 폭이 증가할수록 수치해는 점점 2차원 해석해에 가까워져 W/h = 10일 때 해석해에 가장 근접하였다. 해석해를 구할 때 사용한 고유함수의 개수(N)는 200개이며 이후 모든 계산에서 동일한 값을 사용하였다. 진자판의 폭이 상대적으로 작아 3차원 효과가 큰 경우에 부가 관성모멘트와 방사감쇠계수는 작은 값을 갖고 주파수에 따른 변화폭도 작게 나타났다. 무차원화된 파기진 모멘트도 진자판의 폭이 감소할수록 3차원 효과로 인해 전반적으로 작게 나타났다. 또한 W/h가 증가할수록 부가 관성모멘트, 방사감쇠계수, 파기진 모멘트의 최대값을 주는 특정 주파수가 저주파수영역으로 이동함을 볼 수 있다.
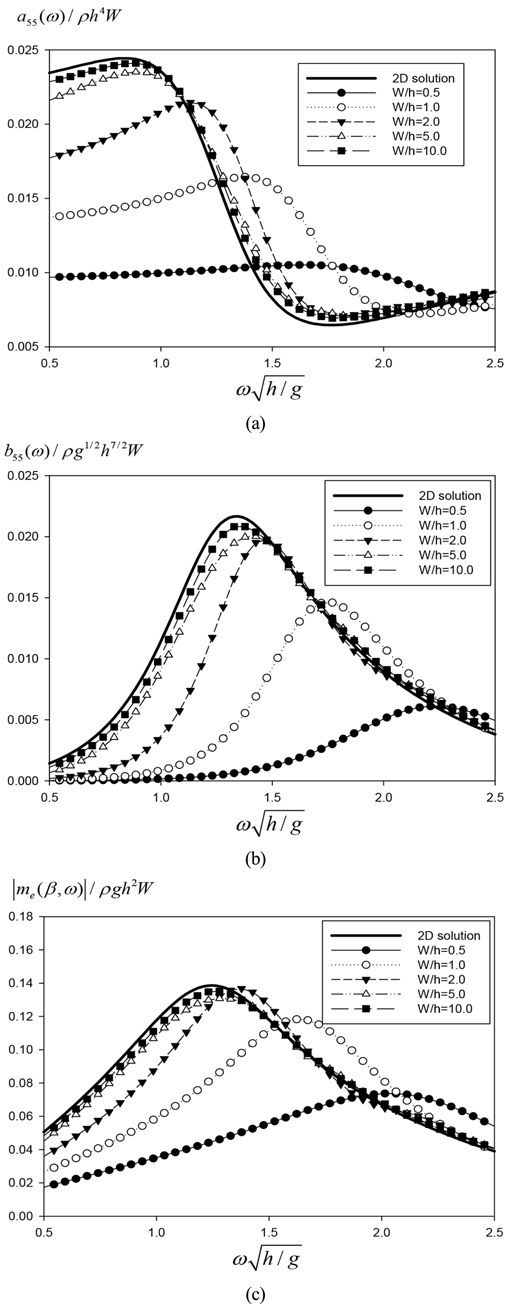
Non-dimensional added moment of inertia(a), radiation damping coefficients(b), wave exciting moment(c) as a function of width of a rolling pendulum plate for d/h = 0.5, tf/h = 0.0, h = 10m : Lines are for present MEEM solutions and symbols are for Wamit solutions.
Fig. 3은 안벽이 없는 상태에서 진자판의 3개의 무차원화된 잠긴 깊이 (d/h = 0.3, 0.5, 0.7) 변화에 따른 부가 관성모멘트, 방사감쇠계수, 파기진 모멘트를 보여주고 있다. 예상대로 진자판의 잠긴 깊이가 증가할수록 주파수에 관계없이 부가 관성모멘트, 방사감쇠계수, 파기진 모멘트 모두 증가하는 것을 알 수 있다. 특히, 방사감쇠계수와 파기진 모멘트는 유사한 곡선의 형태를 보여주고 있다. 진자판의 잠긴 깊이가 증가할수록 피크값은 증가하고 피크값을 주는 주파수가 저주파수 영역으로 이동하는 것을 볼 수 있다.
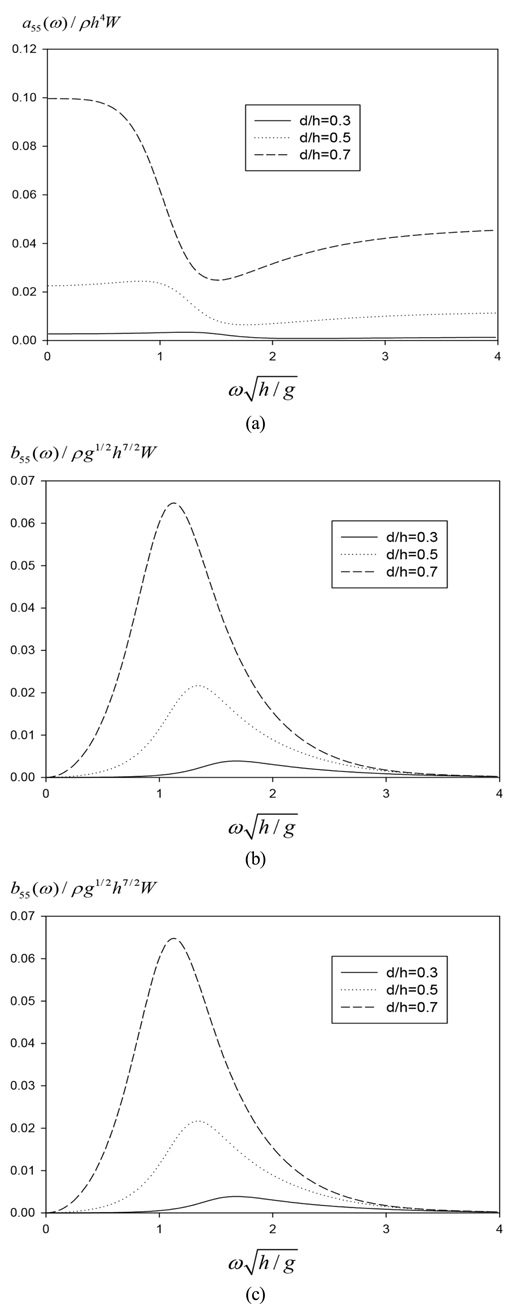
Non-dimensional added moment of inertia(a), radiation damping coefficients(b), wave exciting moment(c) of a rolling pendulum plate as a function of submergence depth of pendulum plate d/h for β = 0° without quay wall.
Fig. 4는 안벽 앞에 진자판이 놓인 경우이다. 진자판과 안벽사이의 거리는 수심과 같다(s/h = 1.0). 앞선 안벽이 없는 경우와 비교하면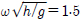 
보다 작은 저주파수영역에서는 부가 관성모멘트, 방사감쇠계수, 파기진 모멘트의 피크값이 다소 증가한 것을 제외하곤 유사한 곡선의 패턴을 보여주고 있다. 그러나 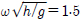보다 큰 고주파수영역에서는 일정 주파수 간격으로 스파이크(Spike)가 발생함을 볼 수 있다. 이는 진자판과 안벽사이에서 발생하는 공진현상과 밀접한 관련이 있다. 특히, 진자판이 잠긴 깊이가 깊을수록 진자판과 안벽사이의 유체가 밖으로 빠져나가지 못하여 공진현상은 뚜렷이 나타난다. 
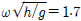에 서 일어나는 공진은 공진조건식(s/λ = m/2, m = 0.1,...)에서 공진모드 m = 1에 해당하는 s/λ = 0.5와 일치한다.
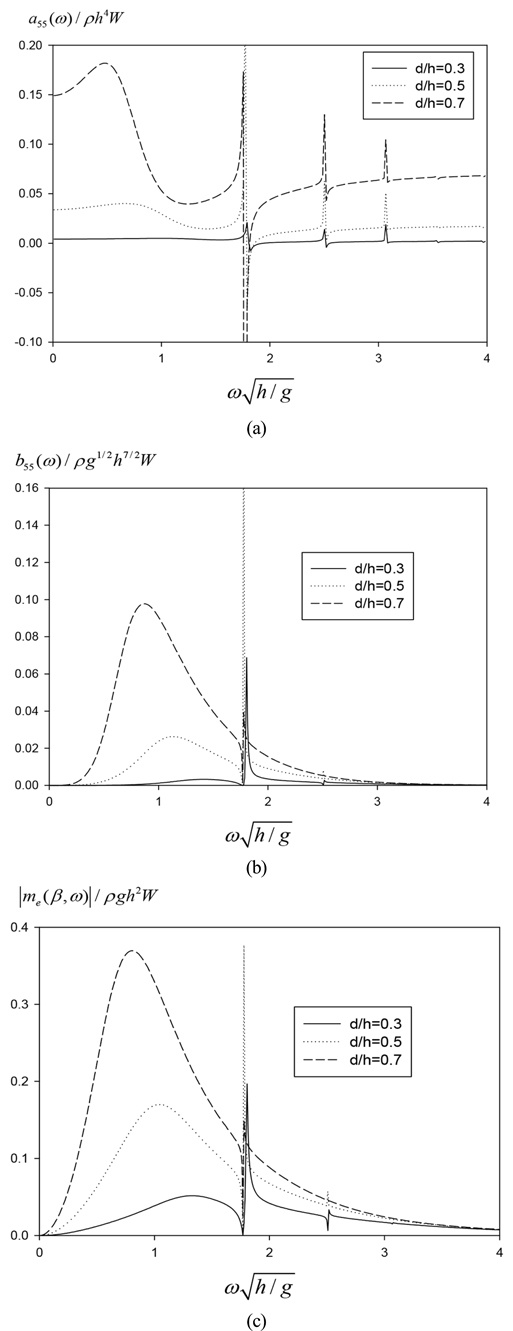
Non-dimensional added moment of inertia(a), radiation damping coefficients(b), wave exciting moment(c) of a rolling pendulum plate as a function of submergence depth of pendulum plate d/h for s/h = 1.0, β = 0° with quay wall.
Fig. 5는 추출파워의 최대값을 주는 최적의 PTO감쇠계수(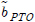
)를 안벽의 없는 경우와 안벽이 있는 경우로 나눠 무차원화된 주파수(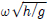)와 진자판의 잠긴 깊이(d/h)에 따라 살펴보았다. 이때 사용한 계산모델의 제원은 W/h = 10, ρf/ρ = 2.0, tf/h = 0.1이며, 수심은 10m로 잡았다. 최적 PTO감쇠계수는 어떤 특정 주파수에서 최소값을 갖는 특징을 보인다. 이때 최소값을 주는 특정 주파수는 식 (29)에 주어진 진자판의 회전운동 고유주파수와 일치한다. 잠긴 깊이 d/h = 0.3, 0.5, 0.7에 해당하는 회전운동 고유주파수는 
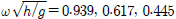이다. 최적의 PTO감쇠계수 중에서 최소값을 가짐은 진자판의 회전운동을 증가시켜 회전운동 변위의 제곱에 비례하는 추출파워의 증가함을 의미한다. 또한 안벽의 유무에 관계없이 최적 PTO감쇠계수의 최소값을 주는 주파수는 진자판의 회전운동 고유주파수와 일치한다.
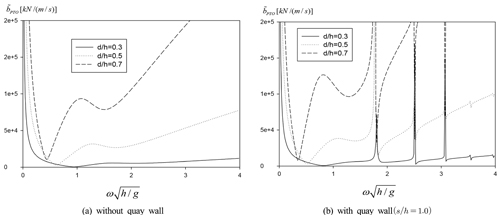
Optimal PTO damping coefficients as a function of submergence depth of pendulum plate d/h for W/h = 10, ρf/ρ = 2.0, tf/h = 0.1, β =0° and h = 10m.
Fig. 6은 PTO-on 상태에서 안벽의 없는 경우와 안벽이 있는 경우에 대하여 회전운동 RAO(Responses amplitude operator)를 무차원화된 주파수에 따라 그린 그림이다. PTO-on상태에서 사용한 PTO감쇠계수는 최대 파워가 추출되는 최적의 값(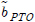)을 취했다. 계산에서 사용한 무차원화된 진자판의 두께는 tf/h = 0.1이고, 진자판에 복원력을 주기 위해 진자판의 밀도는 해수보다 무거운 ρf/ρ = 2.0이다. 회전운동 RAO곡선에서 저주파수영역에서 나타난 피크값은 예상대로 회전운동 고유주파수(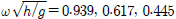)와 일치한다. 특히, 안벽이 있을 때 고주파수영역에서 나타나는 운동변위가 0이 나타나는 주파수는 진자판과 안벽사이의 닫쳐진 유체영역내에서 발생하는 공진모드에 해당하는 공진주파수와 일치한다. 안벽이 없는 경우, 진자판의 잠긴 깊이가 증가함에 따라 회전운동 공진주파수는 저주파수영역으로 이동하고, 피크값은 방사감쇠력의 증가로 줄어들며 공진폭도 줄어드는 경향을 보여주고 있다. 안벽이 놓여있는 경우, 앞선 그림과 비교하여 공진주파수에서 피크값이 약간 증가하며 공진폭이 줄어드는 경향이 나타난다.
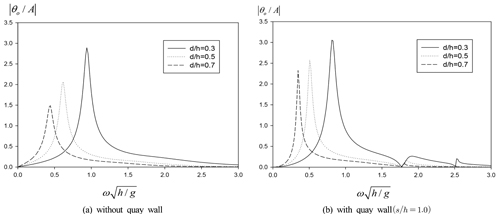
Roll motion amplitude as a function of submergence depth of pendulum plate d/h for W/h = 10, ρf/ρ = 2.0, tf/h = 0.1, β = 0°, and h = 10m.
Fig. 7은 Fig. 6과 동일한 계산조건하에서 취득 폭을 진자파의 폭으로 나눈 효율을 주파수에 따라 살펴보았다. 이때 PTO감쇠계수는 최적의 값(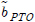)을 사용하였다. 저주파수 영역에서의 나타나는 효율의 피크값은 진자판의 회전운동 공진주파수에서 발생하였다. 진자판의 잠긴 깊이가 증가할수록 에너지 추출이 가능한 주파수 범위는 줄어드는 경향이 나타난다. 따라서 설치해역의 파랑에너지의 주파수 분포특성을 고려하여 진자판의 잠긴 깊이를 선정하는 것이 바람직하다. 안벽이 놓인 경우의 효율 곡선은 고주파수영역에서 나타나는 진자판과 안벽사이의 공진 효과로 좀 더 복잡한 양상을 띠고 있지만 진자판의 잠긴 깊이 변화에 따른 효율 곡선의 특징은 안벽의 없을 때의 경향과 유사하다.
Optimal efficiency as a function of submergence depth of pendulum plate d/h for ρf/ρ = 2.0, tf/h = 0.1, β = 0°, W/h = 10, and h = 10m.
안벽 앞에 놓인 진자판 파력발전장치는 진자판과 안벽사이의 정지파(Standing wave) 형성과 진자판을 통한 파랑에너지 흡수로 인하여 진자판이 없을 때 일어나는 안벽에서의 완전반사가 아닌 부분반사가 일어난다. 이를 살펴보기 위하여 최적의 PTO 감쇠계수를 적용하였을 때 진자판의 잠긴 깊이 변화에 따른 진자판의 운동을 고려한 반사율을 Fig. 8에 나타내었다. 완전반사가 아닌 부분반사를 보여주고 있으며 반사율이 낮게 나타나는 주파수 영역은 Fig. 7 (b)에서 효율이 최대가 되는 주파수 영역과 일치한다. 이 결과는 진자판 파력발전장치를 안벽 앞에 설치하였을 때 파랑에너지의 일부를 흡수하므로 안벽에 작용하는 하중을 줄임과 동시에 반사파를 줄일 수 있어 안벽 주변을 운항하는 선박의 안정성에 큰 도움을 줄 수 있음을 뜻한다.
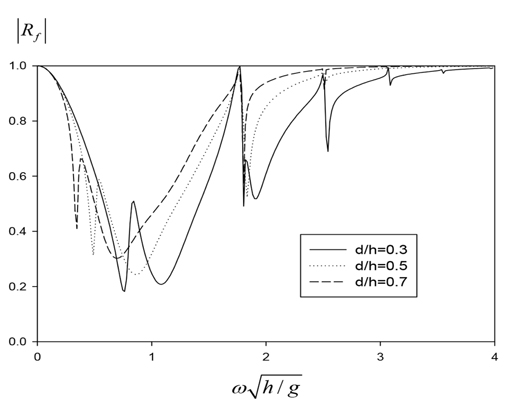
Reflection coefficients considering the rolling motion of a pendulum plate as a function of submergence depth of pendulum plate d/h for W/h = 10, s/h = 1.0, ρf/ρ = 2.0, tf/h = 0.1, β = 0°, and h = 10m.
Fig. 9는 d/h = 0.5에서 진자판의 두께 변화에 따른 효율을 살펴보았다. 본 해석모델에서 동유체력과 파기진 모멘트를 구할 때 진자판의 두께는 무시하였다. 따라서 진자판의 두께 변화는 진자판의 관성모멘트와 정유체 복원모멘트에만 영향을 주므로 단순히 진자판의 회전운동 고유주파수를 바꾸는데 기여한다. 만약 설치해역에서 주로 발생하는 파의 주기 범위를 안다면 공진이 일어날 수 있도록 진자판의 두께를 선정하여야 한다. 그러나 진자판의 두께 변화는 진자판과 안벽사이에서 발생하는 공진에는 전혀 영향을 미치지 않으므로 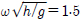이후 효율 곡선에는 큰 차이가 나타나지 않았다.
Optimal efficiency as a function of pendulum's thickness tf/h for W/h = 10, s/h = 1.0, d/h = 0.5, ρf/ρ = 2.0, tf/h = 0.1, and h = 10m.
Fig. 10은 진자판의 무차원화된 잠긴 깊이가 d/h = 0.5일 때 입사각도 변화에 따라 효율을 보여주고 있다. 진자판의 폭이 너무 길면 y축 방향의 주기적인 변동성으로 파기진 모멘트가 서로 상쇄되어 효율이 크게 줄어든다. 이를 방지하기 위하여 본 계산에서는 진자판 파력발전장치의 폭을 줄여 W/h = 1.0으로 정하였다. 예상했던 대로 파랑에너지 중에서 진자판에 수직으로 들어오는 성분만이 진자판의 운동에너지로 변환되므로 입사 각도의 증가는 추출파워의 감소로 이어지고 결과적으로 효율은 줄어든다. 에너지 추출 측면에서 가능한 한 입사파의 진행방향에 수직하게 진자판을 위치시키는 것이 바람직하다. 그러나 입사하는 파랑에너지 밀도가 너무 큰 경우에서는 진자판을 z축을 중심으로 회전시켜 입력 에너지를 낮출 수 있다. 최근 덴마크에서 개발한 Weptos 파력발전시스템(Pecher et al., 2012)은 Salter duck 파력발전장치(Salter, 1974)를 V자형 부유구조물에 장착한 것으로 V자형 부유구조물을 일점 계류시켜 Weather vane을 허용하여 파랑하중을 줄일 수 있도록 고안됨과 동시에 V자형 부유구조물의 회전각을 바꿔 입력 파랑에너지를 조절하여 균일한 에너지 추출이 가능하도록 하였다. 동시에 거친 해상상태에서 파력발전장치에 가하는 충격력을 낮출 수 있어 안정성을 도모할 수 있다.
Optimal efficiency as a function of incidence angle β for W/h = 1.0, d/h = 0.5, ρf/ρ = 2.0, tf/h = 0.1, and h = 10m.
4. 결 론
안벽 앞에서 회전 운동하는 진자판 파력발전장치의 경우 특성이 서로 다른 두 종류의 공진현상이 존재한다. 먼저 저주파수영역에 위치한 공진현상은 입사파의 주파수와 진자판의 회전운동 고유주파수가 일치할 때 발생하는 동적인 공진이며 고주파수영역에서 일정한 주파수 간격을 가지고 나타나는 좁은 주파수 범위내에서 발생하는 피크는 진자판과 안벽 사이의 닫쳐진 유체영역내에서 발생하는 공진현상이다. 각각의 공진주파수에서의 효율은 최대값 0.5로 나타났다. 최대 파워추출을 얻기 위해 사용한 최적의 PTO감쇠계수는 진자판의 공진주파수에서 최소값을 갖는다. 최적의 PTO감쇠계수를 적용하여 구한 회전운동 변위는 진자판의 잠긴 깊이가 감소할수록 공진주파수에서 피크값도 커지고 공진 폭도 더 넓게 나타났다. 이는 파랑에너지가 집중된 수면 아래 일정 깊이 범위내에 진자판을 설치해야 효과적으로 파랑에너지를 진자판의 운동에너지로 변환할 수 있음을 뜻한다. 효율도 진자판의 잠긴 깊이가 낮을수록 최대 효율을 주는 주파수 범위가 늘어나 파랑에너지 추출에 효과적이다.
진자판의 두께가 증가할수록 회전운동 공진주파수가 고주파수영역으로 이동하며 공진 폭도 넓어지는 것을 확인하였다. 구조적 안정성 확보뿐만 아니라 에너지 추출증가를 위하여 진자판의 두께는 어느 정도 유지하는 것이 바람직하다. 진자판 파력발전장치는 파랑에너지를 흡수하는 발전장치의 기능뿐만 아니라 안벽으로부터 생성되는 반사파를 줄이는 소파제의 기능을 동시에 수행할 수 있음을 계산결과를 통하여 확인하였다.
입사파가 일정 경사각도를 갖고 들어오는 경우 입사파의 파랑에너지 중에서 진자판에 수직으로 들어오는 성분만이 진자판의 운동에너지로 변환되어 파워 추출에 기여한다. 따라서 입사 각도의 증가는 추출 효율의 감소로 이어지므로 입사파의 진행 방향과 수직하게 진자판을 위치시키는 것이 바람직하다. 이러한 결과는 진자판의 회전각을 바꿔 입력 파랑에너지를 조절하여 균일한 에너지 추출이 가능토록 하거나, 거친 해상상태에서 파력발전장치에 가해지는 충격력을 낮추는 시스템 개발로 활용할 수 있다.
Acknowledgements
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(No. 20163010071690).
References
Cho, I.H., 2003. On an Analysis of Reflection Coefficients by a Partially Immersed Slotted Plate with a Back wall. Journal of Korea Society of Coastal and Ocean Engineers, 15(3), 143-150.
Cho I.H.. On an Analysis of Reflection Coefficients by a Partially Immersed Slotted Plate with a Back wall. Journal of Korea Society of Coastal and Ocean Engineers 2003;15(3):143–150.Dean, R.G., Dalrymple, R.A., 1984. Water Wave Mechanics for Engineers and Scientists, World Scientific, Singapore.
Dean R.G., Dalrymple R.A.. Water Wave Mechanics for Engineers and Scientists World Scientific. Singapore: 1984.Evans, D., 1970. Diffraction of Water Waves by a Submerged Vertical Plate. Journal of Fluid Mechanics, 40, 433-451.
Evans D.. Diffraction of Water Waves by a Submerged Vertical Plate. Journal of Fluid Mechanics 1970;40:433–451. 10.1017/S0022112070000253.Evans, D.V., Porter, R., 1996. Hydrodynamic Characteristics of a Thin Rolling Plate in Finite Depth of Water. Applied Ocean Research, 18(4), 215-228.
Evans D.V., Porter R.. Hydrodynamic Characteristics of a Thin Rolling Plate in Finite Depth of Water. Applied Ocean Research 1996;18(4):215–228. 10.1016/S0141-1187(96)00026-0.Falnes, J., 2002. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave Energy Extraction. Cambridge University Press, Cambridge UK.
Falnes J.. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave Energy Extraction Cambridge University Press. Cambridge UK: 2002.Folley, M., Whittaker, T.J.T., Henry, A., 2007. The Effect of Water Depth on the Performance of Small Surging Wave Energy Converter. Ocean Engineering, 34(8), 1265-1274.
Folley M., Whittaker T.J.T., Henry A.. The Effect of Water Depth on the Performance of Small Surging Wave Energy Converter. Ocean Engineering 2007;34(8):1265–1274. 10.1016/j.oceaneng.2006.05.015.Gomes, R.P.F,, Lopes, M.F.P., Henriques, J.C.C., Gato, L.M.C., Falcao, A.F.O., 2015. The Dynamics and Power Extraction of Bottom-Hinged Plate Wave Energy Converters in Regular and Irregular waves. Ocean Engineering, 96, 86-99.
Gomes R.P.F., Lopes M.F.P., Henriques J.C.C., Gato L.M.C., Falcao A.F.O.. The Dynamics and Power Extraction of Bottom-Hinged Plate Wave Energy Converters in Regular and Irregular waves. Ocean Engineering 2015;96:86–99. 10.1016/j.oceaneng.2014.12.024.Lucas, J., Livingstone, M., Vuorinen, M., Cruz, J., 2012. Development of a Wave Energy Converter(WEC) Design Tool-Application to the WaveRoller WEC Including Validation of Numerical Estimates. Proceedings of the Fourth International Conference on Ocean Energy, Dublin Ireland.
Lucas J., Livingstone M., Vuorinen M., Cruz J.. Development of a Wave Energy Converter(WEC) Design Tool-Application to the WaveRoller WEC Including Validation of Numerical Estimates In : Proceedings of the Fourth International Conference on Ocean Energy. Dublin Ireland; 2012.Nam, B.W., Hong, S.Y., Kim, K.B., Park, J., Shin, S.H., 2011. Numerical Analysis on Wave-Induced Motion of Floating Pendulor Wave Energy Converter. Journal of Ocean Engineering and Technology, 25(4), 28-35.
Nam B.W., Hong S.Y., Kim K.B., Park J., Shin S.H.. Numerical Analysis on Wave-Induced Motion of Floating Pendulor Wave Energy Converter. Journal of Ocean Engineering and Technology 2011;25(4):28–35.Nam, B.W., Hong, S.Y., Shin, S.H., Hong, S.W., Kim, K.B., 2012. Prediction of the Hydrodynamic Performance of the Floating Pendulum Wave Energy Converter in Regular and Irregular waves. Proceedings of The Twenty-second International Offshore and Polar Engineering Conference, Rhodes Greece, 607-612.
Nam B.W., Hong S.Y., Shin S.H., Hong S.W., Kim K.B.. Prediction of the Hydrodynamic Performance of the Floating Pendulum Wave Energy Converter in Regular and Irregular waves In : Proceedings of The Twenty-second International Offshore and Polar Engineering Conference. Rhodes Greece; 2012. p. 607–612.Park, J.Y., Shin, S.H., Hong, K.Y., Kim, S.H., 2012. Study on the Wave Response and Efficiency of a Pendulum Wave Energy Converter. Proceedings of The Twenty-second International Offshore and Polar Engineering Conference. Rhodes GreeceIn The Twenty-second International Offshore and Polar Engineering Conference, Rhodes Greece, 601-606.
Park J.Y., Shin S.H., Hong K.Y., Kim S.H.. Study on the Wave Response and Efficiency of a Pendulum Wave Energy Converter In : Proceedings of The Twenty-second International Offshore and Polar Engineering Conference. Rhodes GreeceIn The Twenty-second International Offshore and Polar Engineering Conference. Rhodes Greece; 2012. p. 601–606.Penney, W.G., Price, A.T., 1952. The Diffraction Theory of Sea Waves and the Shelter Afforded by Breakwaters. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 244(882), 236-253.
Penney W.G., Price A.T.. The Diffraction Theory of Sea Waves and the Shelter Afforded by Breakwaters. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 1952;244(882):236–253. 10.1098/rsta.1952.0003.Pecher, A., Kofoed, J.P., Larsen, T., Marchalot, T., 2012. Experimental Study of the WEPTOS Wave Energy Converter. Proceedings of the 31th International Conference on Ocean, 525-534.
Pecher A., Kofoed J.P., Larsen T., Marchalot T.. Experimental Study of the WEPTOS Wave Energy Converter In : Proceedings of the 31th International Conference on Ocean; 2012. p. 525–534.Salter, S.H., 1974. Wave Power. Nature, 249(5459), 720-724.
Salter S.H.. Wave Power. Nature 1974;249(5459):720–724. 10.1038/249720a0.Whittaker, T.J.T., Folley, M., 2012. Nearshore Oscillating Wave Surge Converters and the Development of Oyster. Philosophical Transactions of the Royal Society of London A, 370(1959) 345-364.
Whittaker T.J.T., Folley M.. Nearshore Oscillating Wave Surge Converters and the Development of Oyster. Philosophical Transactions of the Royal Society of London A 2012;370(1959):345–364. 10.1098/rsta.2011.0152.Whittaker, T.J.T., Collier, D., Folley, M., Osterried, M., Henry, A., Crowley, M., 2007. The Development of Oyster-a Shallow Water Surging Wave Energy Converter. Proceedings of the 7th European Wave and Tidal Energy Conference, Porto Portugal, 11-14.
Whittaker T.J.T., Collier D., Folley M., Osterried M., Henry A., Crowley M.. The Development of Oyster-a Shallow Water Surging Wave Energy Converter In : Proceedings of the 7th European Wave and Tidal Energy Conference. Porto Portugal; 2007. p. 11–14.