Designation of the Boundary Conditions for Estimating the Thrust Loss due to Thruster-Hull Interactions
Article information
Abstract
The azimuth thruster is mainly installed on a vessel that requires a dynamic positioning (DP) function for special purposes. When the azimuth thruster on a vessel operates for DP, the thrust loss is induced by the thruster-hull interaction. This study examined the influence of boundary conditions in numerical simulations for predicting thrust loss. Wind turbine installation vessels (WTIV) and floating production storage and offloading (FPSO) were chosen as a target vessels. In this study, two types of boundaries were defined. The first consideration is that the boundary condition was assigned with consideration of the azimuth angle of the thruster, whereas it is fixed regardless azimuth angle of the thruster. The predicted thrust loss according to these boundary conditions showed a difference. This observation originated from the current load of the vessel. Therefore, the boundary conditions for which the current load is not induced need to be designated to obtain a realistic thrust loss in a numerical simulation.
1. Introduction
In the design of various floating offshore facilities or special purpose vessels, such as floating production storage and offloading (FPSO), wind turbine installation vessels (WTIV), semi-submergible, and drillship, the dynamic positioning (DP) performance is one of the most important performance indicators that is related directly to the operating performance of the facility. Efficient use of the thrust generated by the propulsion system is essential to respond to various marine environments (wind, waves, and currents) and operate marine facilities or special vessels stably and economically simultaneously. Hence, multiple azimuth thrusters are generally installed in offshore facilities or special vessels. The installed azimuth thruster must consume minimum power and, at the same time, effectively produce thrust to achieve optimal DP performance. Hence, the operating direction, required thrust, and power consumption of the azimuth thruster are controlled according to the optimization algorithm. On the other hand, a loss of thrust occurs compared to the case where it exists alone when an azimuth thruster is attached to an offshore facility or special vessel. Dang and Laheij (2004) attributed this phenomenon is caused by four interference effects. These refer to the thruster-hull interference effect, thruster-thruster interference effect, thruster-tide interference effect, and thruster-wave interference effect, and accurate prediction of thrust reduction is an essential factor to consider while selecting an azimuth thruster with appropriate capacity at the design stage of offshore facilities and special vessels. The decrease in thrust due to these interference effects has been studied previously using model tests and numerical methods.
As a representative example, Lehn (1980) examined thrust reduction by the thruster-thruster interference effect. When two azimuth thrusters are placed in a row, they studied how the thrust performance of the azimuth thruster located at the rear deteriorates according to the distance (x) between the two thrusters or the operating direction (ϕ) of the azimuth thruster located at the front and proposed a simple estimation formula (Fig. 1). Nienhuis (1992) studied how the wake characteristics of an azimuth thruster located at the bottom of the hull change depending on the side curvature when the wake flows toward the side of the vessel. Cozijn et al. (2010) conducted a study similar to Nienhuis (1992) using the Particle image velocimetry test equipment and precisely measured and analyzed the wake. Since the 2000s, studies using numerical analysis methods have been conducted. Song et al. (2013) simulated the thruster-hull interference effect and the thruster-thruster interference effect using a numerical analysis method with the WTIV as a target vessel. They conducted a quantitative study to compare the thrust loss with the model test results. Ottens et al. (2011) numerically predicted the thrust loss due to the thruster-hull interference effect for semi-submergible. In addition, the duct or propeller axis of the azimuth thruster is rotated (tilt) downward by about 5°–7° to minimize the thrust loss due to the thruster-hull mutual interference effect and Palm et al. (2010) studied the resulting changes in thrust performance and mutual interference effect. Dang and Laheij (2004) reported that although there are numerous variables, such as vessel type, hull shape, stern appendage, and special thruster shape, the loss of thrust due to the thruster-hull interference effect can comprise up to approximately 40% of the thrust produced by an azimuth thruster in a single state. In addition, the actual DP is usually conducted under the bollard condition, in which only the thruster operates while offshore facilities or special vessels are stopped. Although there are points to note in implementing this condition in numerical analysis, research on the imposition of boundary conditions is lacking (Song et al., 2022).
In predicting the thrust loss that inevitably occurs due to the thruster-hull interference effect, this study compared the difference that occurs depending on the method of imposing boundary conditions in numerical analysis and proposed what boundary conditions can be practically applied when performing a similar analysis in the future. Chapter 2 describes the numerical analysis method in detail, and Chapter 3 compares the difference in thrust loss calculated according to the boundary condition imposition method. Chapter 4 considers the cause of the difference in thrust loss, and Chapter 5 presents the conclusions drawn from this study. The Samsung Ship Model Basin provided the shape of the target vessel used in this study, the shape of the azimuth thruster, and related model test results.
2. Numerical Analysis Method
2.1 Definition of Numerical Analysis Method
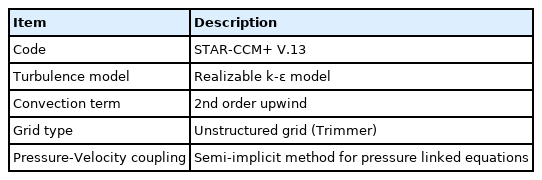
This study conducted a numerical analysis using STAR-CCM+ code, one of the commercial software for fluid analysis. Table 1 lists the basic numerical analysis techniques applied in this study.
2.2 Definition of Target Vessels
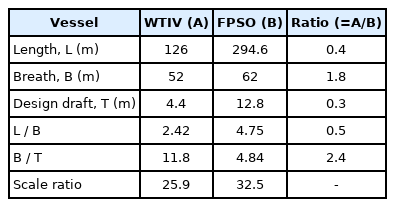
WTIV and FPSO were the target vessels, and their specifications are listed in Table 2. A large difference in specifications was observed because the inherent purpose of the two vessels is different. In particular, there is a large difference in the width/draft ratio (B/T) because WTIV has a relatively small draft compared to the width, resulting in a B/T value of 11.8. By contrast, FPSO has a relatively small value of 4.84, meaning that the draft is larger than WTIV. Fig. 2 shows target vessels, respectively.
2.3 Performance Comparison of the Azimuth Thruster in a Single State
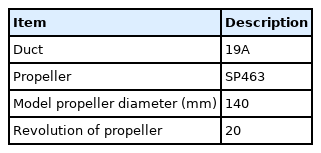
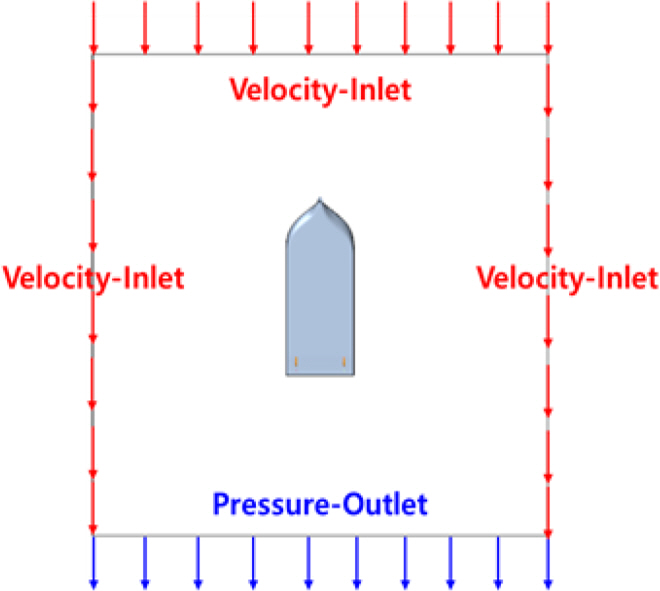
Azimuth thrusters were applied as the main propulsion system to all the above-mentioned vessels. The thrust calculated in a single state must be secured first before evaluating the thrust loss due to thruster-hull mutual interference in the actual target vessel. Therefore, this section discusses the single performance of the azimuth thruster predicted through numerical analysis. Table 3 lists the specifications of the model azimuth thruster manufactured for the model test. The thrust of an azimuth thruster is defined as the sum of three components because of its morphological characteristics. The total thrust (KTT) of the azimuth thruster is the sum of the thrust produced by the propeller (KTP), the thrust produced by the duct (KTD), and the resistance (R) of the remaining components (Housing, Leg, and Support). Numerical analysis was performed to construct a grid system so that the total thrust value calculated from the results of the single state of the azimuth thruster showed a <3% difference compared to the measured value of the model test. This analysis was performed using the direct rotation method (sliding mesh) that directly rotates the propeller, and Y1+, the dimensionless grid size, was set to 50 near the wall to use the wall function. The total grid was approximately 1.5 million; other numerical analysis conditions are listed in Table 1. To perform the single state analysis, the computational domain was defined as 7D × 4D × 4D based on the propeller diameter, and the velocity inlet condition, pressure outlet condition, and symmetry boundary condition were imposed, as shown in Fig. 3 (Song et al., 2013). In addition, the advance ratio (J) considered was from 0.1 to 0.5. Fig. 4 shows the model azimuth thruster installed on the towing carriage, the shape defined for numerical analysis, and the grid system around the azimuth thruster. The results of a single test and numerical analysis are shown in Fig. 5 and Table 4 (Song et al., 2013).
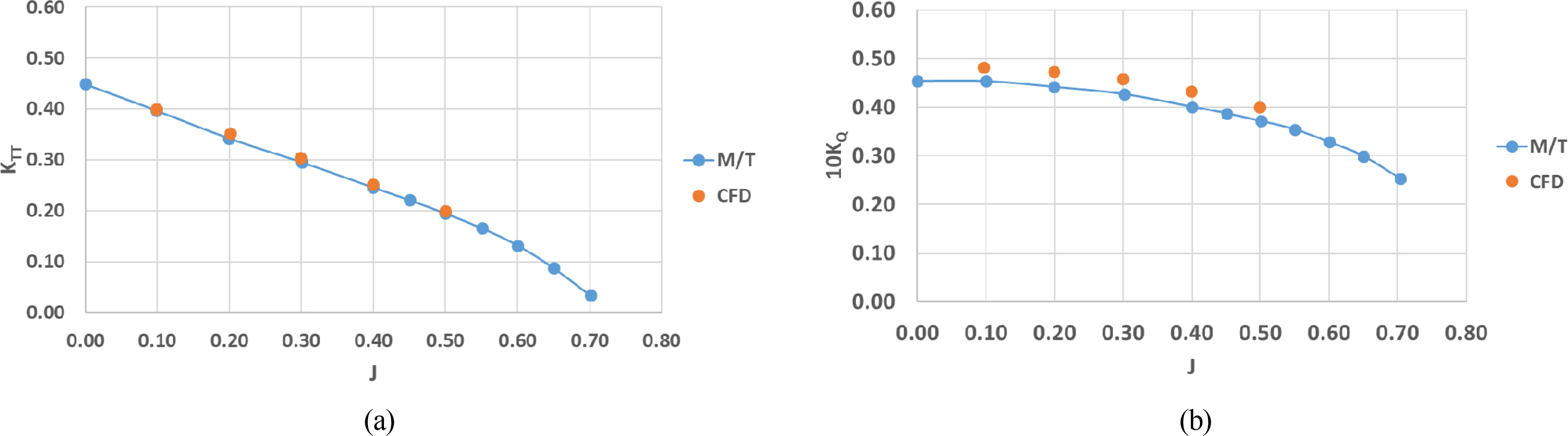
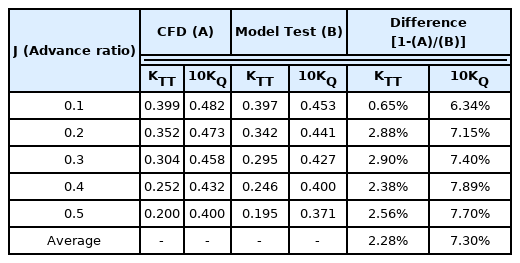
Comparison of the Propeller Open Water on azimuth thruster from the model test and CFD simulation: (a) Total thrust coefficient (KTT); (b) Torque coefficient (10KQ)
The total thrust of the azimuth thruster showed results within the target range of 3% in the area of an advance ratio where the analysis was performed, whereas the torque showed a consistent difference of approximately 7–8% overall. Because the purpose of this study was related to the thrust of the azimuth thruster, it was judged that the reliability of the numerical analysis for the single state of the azimuth thruster was secured based on the predicted thrust coefficient.
When the advance ratio, J = 0, the thrust coefficient under the bollard condition can be estimated and used as a reference thrust value when predicting the thrust reduction due to the actual thruster-hull interference effect.
2.4 Analysis Condition Definition
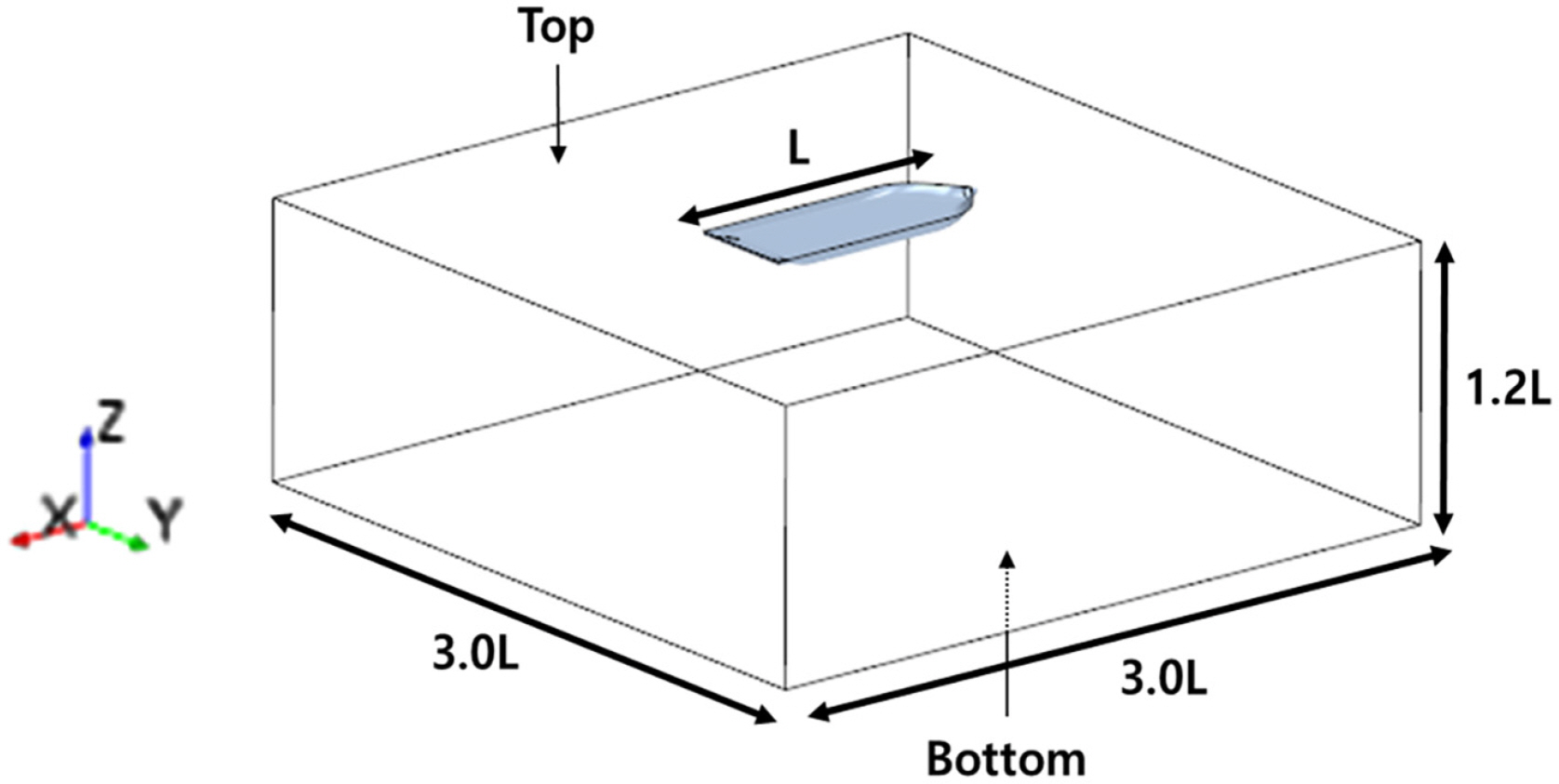
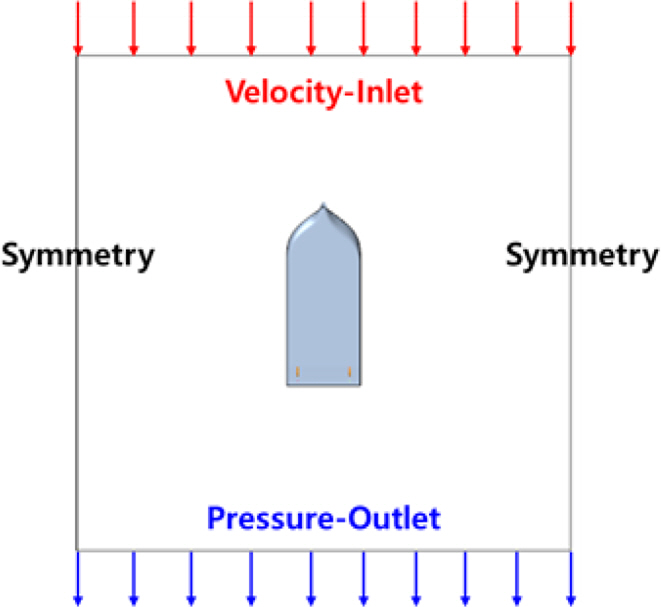
The computational domain was defined to numerically analyze the thrust reduction due to the thruster-hull interference effect, as shown in Fig. 6. The size of the computational area was defined based on the length (L) of the target vessel and had sizes of 3.0L, 3.0L, and 1.2L in the X, Y, and Z directions, respectively (Song et al., 2013; Song et al., 2022). In this study, the free water surface was not considered, and the area below the waterline of the vessel was defined as the analysis area. Symmetric boundary conditions were also applied to the top and bottom surfaces of the computational area.
2.4.1 Target vessel 1: WTIV
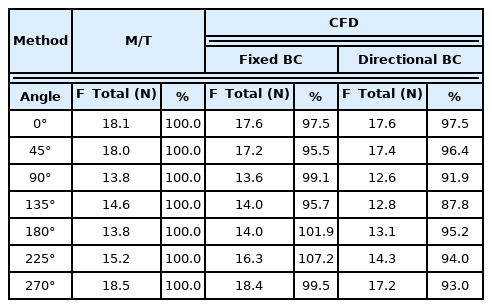
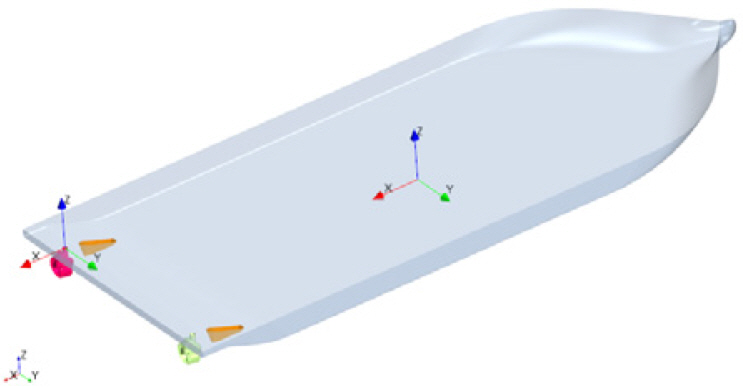
For WTIV, studies have been conducted on thrust reduction due to the thruster-hull interference effect through model tests, and Fig. 7 shows a model vessel manufactured for model testing (Song et al., 2013). In this vessel, two azimuth thrusters were installed: one on the port and one on the starboard sides of the stern. In the model test, a thrust reduction due to the thruster-hull interference effect was found by measuring all the applied forces in the longitudinal direction (X) and the transverse direction (Y) of the vessel when the azimuth thrusters calculate the thrust for each operating direction while the vessel is stationary. In the model test, the longitudinal/lateral forces applied to the hull were measured under 24 conditions while rotating the azimuth angle of the port azimuth thrusters once at 15° intervals. Numerical analysis was performed under seven azimuth conditions (0°, 45°, 90°, 135°, 180°, 225°, and 270°) where the thrust reduction result due to the thruster-hull interference effect can be known. Table 5 lists the reference coordinate system and the operating direction of the port azimuth thrusters. Moreover, to perform the analysis under the same conditions as the model test, the analysis was conducted by changing the azimuth angle of the port azimuth thrusters while azimuth thrusters were modeled on both sides.
Specifications of the coordinate system and simulation cases with respect to azimuthing angle on the port side
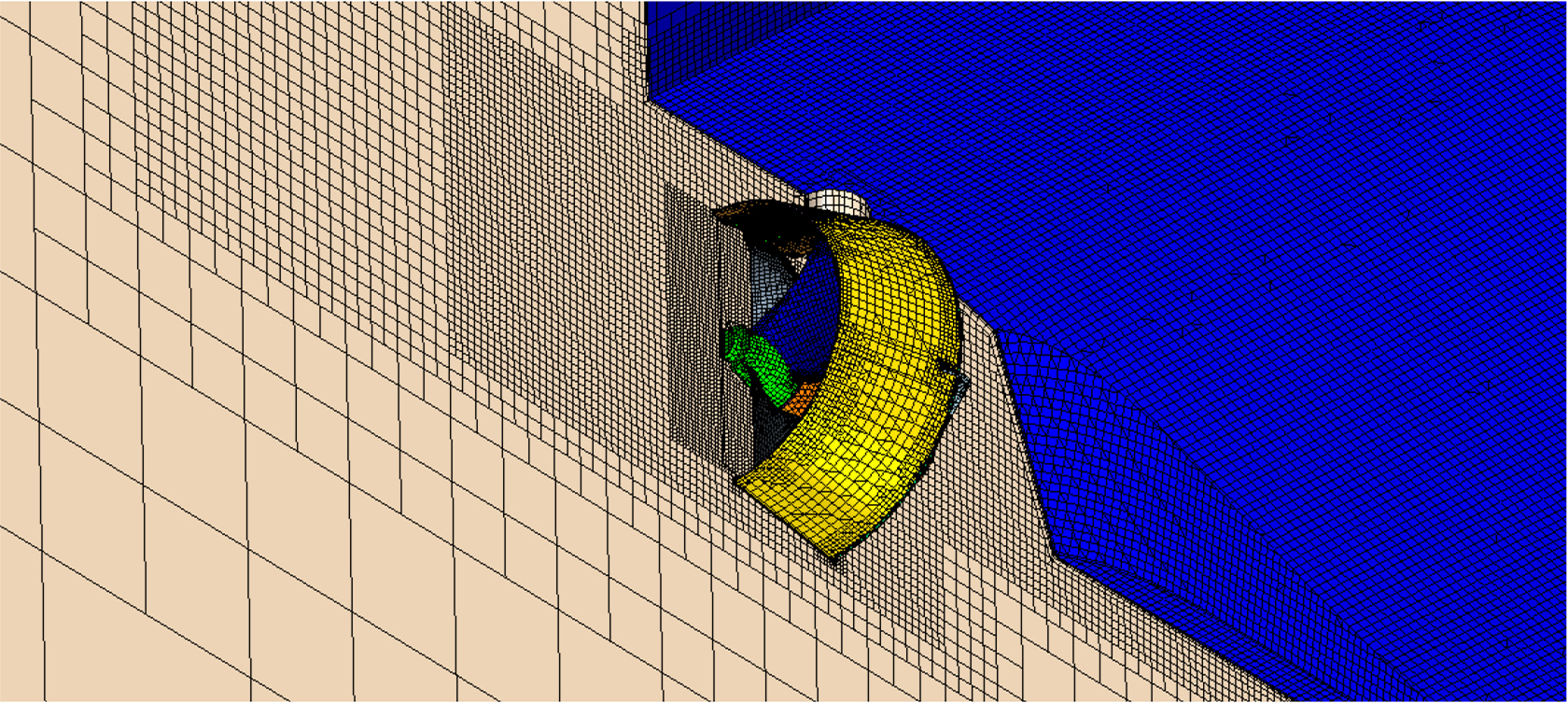
The grid system for numerical analysis was configured in the same way as the method applied to the single-state analysis of the azimuth thruster mentioned earlier. The thrust reduction due to the thruster-hull interference effect was ultimately caused by the wake of the azimuth thruster being attached to the hull surface by the Coanda effect, increasing the frictional resistance of the hull, or colliding with a part of the hull and increasing the pressure of the hull. Therefore, as the wake simulation of the azimuth thruster is important, the lattice system was densely constructed in this wake space, as shown in Fig. 8. Furthermore, if the direct rotation method of the propeller is applied, it is advantageous in terms of accuracy, but it takes a long time to calculate. Song et al. (2013) compared the thrust loss results by simulating propeller rotation. Based on their study, the moving reference frame (MRF) method was applied to this study. The total grid system defined for the two azimuth thrusters and the hull below the waterline was approximately 3.5 million (Song et al., 2022).
2.4.2 Target vessel 2: FPSO
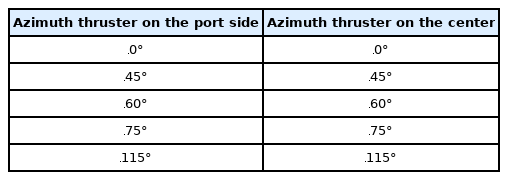
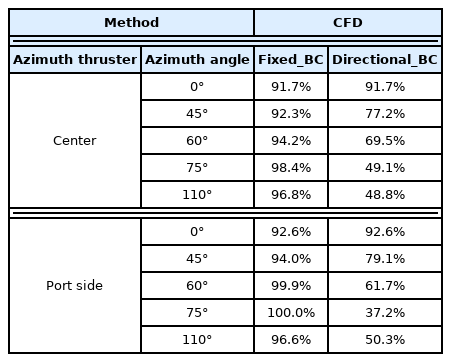
For FPSO, there are three mounting parts (hereafter, head box) at the stern, and one azimuth thruster is located on each side of the head box, as shown in Fig. 2. In the case of this target vessel, a separate model test was not conducted. The thrust loss due to the thruster-hull interference effect was calculated using a numerical analysis method. For this, five azimuth angles (0°, 45°, 60°, 75°, and 115°) were defined while each azimuth thruster was installed independently on the port side or center of the head box, as shown in Table 6.
The azimuth thrusters installed on the FPSO have the same shape as those installed on the previous target vessel, WTIV. On the other hand, they have different capacities and different scale ratios between the target vessels. The diameter of the model azimuth thrusters installed on the FPSO was defined as 120mm, the parts related to numerical analysis were the same as in the case of Section 2.4.1, and the total number of grids was approximately 4.7 million.
2.5 Definition of Boundary Condition
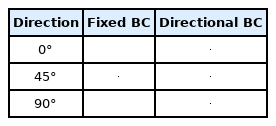
The boundary conditions that can appropriately simulate the hydrodynamic situation of the analysis target must be defined before performing a reliable numerical analysis. This study defined the appropriate boundary conditions when the thrust loss due to the thruster-hull was predicted under the bollard condition where the advance ratio (J) was zero, such as the DP operating situation, and the vessel was stationary. As mentioned by Funeno (2009), numerical analysis under the bollard condition is unstable with poor convergence, so an artificially small advance ratio must be defined for numerical stability. The value was defined as 0.05 in this study. With the symmetry boundary condition defined on the top and bottom of the computational domain, each of the four sides shown in Fig. 9 was intended to be imposed in the following two forms, as shown in Fig. 6. The first boundary condition imposition method always set the velocity-inlet condition on the bow-direction surface and the pressure-outlet condition on the stern-direction surface regardless of the direction of the azimuth thruster attached to the hull. A symmetry boundary condition was imposed on the remaining two surfaces, called Fixed BC. The second boundary condition imposition method was to impose inflow and outflow conditions to the side in the same operating direction as the azimuth thruster attached to the hull. This was called Directional BC. Table 7 lists the boundary conditions by selecting some of the azimuths mentioned in Tables 5 and 6 for one of the target vessels. In particular, when the inflow conditions were given for each azimuth angle, the velocity in the X direction and Y direction was decomposed into components and defined as much as the azimuth angle of the azimuth thruster.
3. Numerical Analysis Result
3.1 Target Vessel 1: WTIV
Fig. 10 presents the force in the X direction (Fx_Hull) and the force in the Y direction (Fy_Hull) measured across the entire hull, including the thruster, when the model azimuth thrusters attached to the port side operates in each azimuth direction under different boundary conditions, and the resulting force (F_Total) is shown according to the operating direction of the propeller. The resulting force (F_Total) is defined using Eq. (1).
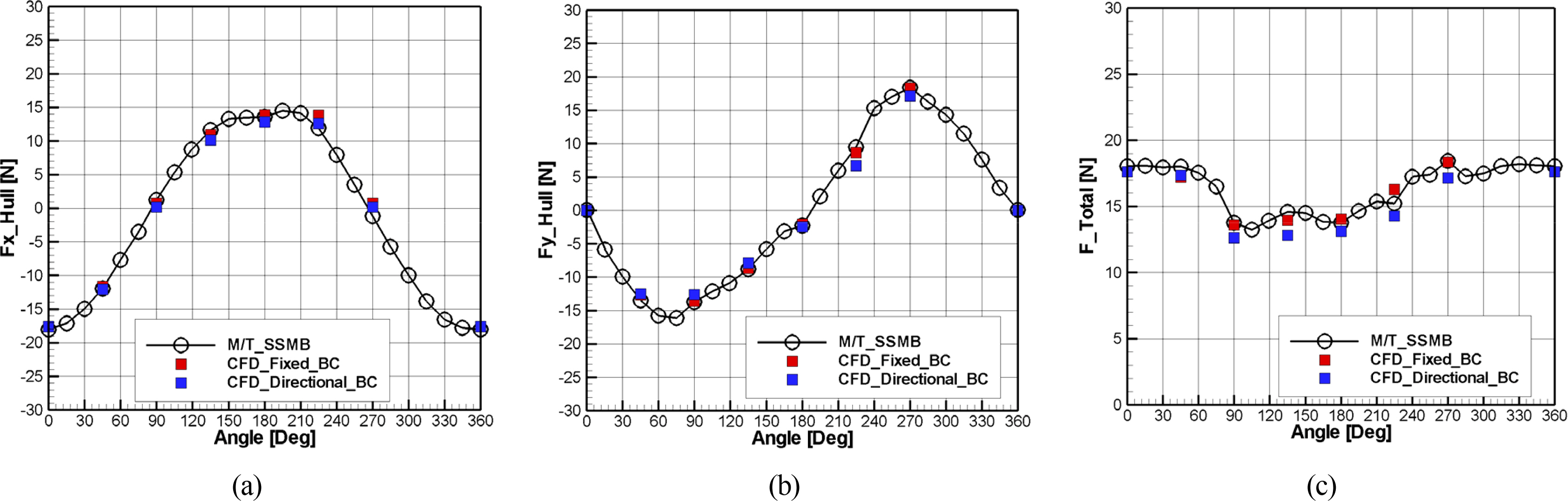
Comparison of FX_Hull (a), FY_Hull (b) and F_Total (c) with respect to azimuthing angle from CFD and model test
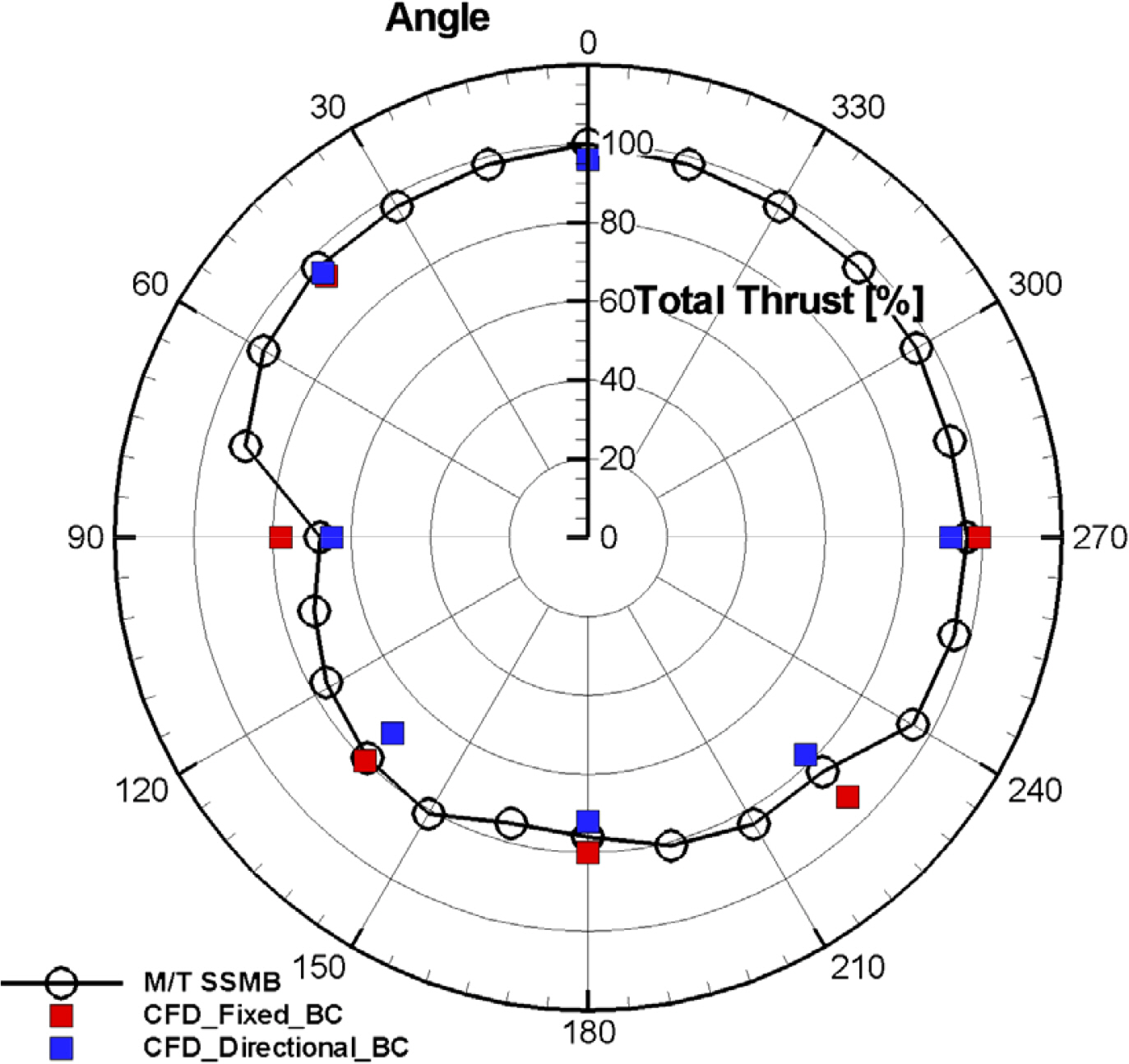
Table 8 lists the values of Fx_Hull and Fy_Hull among the numerical analysis results calculated from the model test and imposed boundary conditions. Table 9 presents the degree of conformity between the F_Total values and the model test. The numerical analysis results generally showed a similar trend to the test results. As shown in Fig. 10(c), for the force (F_Total), the thrust loss occurs due to the thruster-hull interference effect between approximately 75° and 240°. Comparing the differences according to the method of imposing boundary conditions, the resulting force (F_Total) calculated from Fixed BC showed a result closer to the model test result than the result calculated from Directional BC.
Fig. 11 shows the thrust loss due to the thruster-hull interference effect according to the operating azimuth of the port azimuth thrusters, and Table 10 lists the specific values. The model test showed that approximately 30% and 20% of the thrust loss occurs at 90° and 180°, respectively. Numerical analysis showed that the overall trend was similar to the test value, but the results of applying the Fixed BC at the remaining azimuth angles except for 90° and 225° were closer to the model test results than the results of applying the Directional BC. Moreover, the case of applying the Directional BC tends to predict a larger thrust loss than the case of applying the Fixed BC.
3.2 Target Vessel 2: FPSO
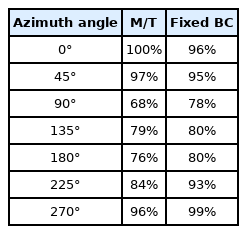
In the case of this target vessel, unlike the previous case, only numerical analysis was performed at the model scale without model tests. Three azimuth thrusters were attached to this target vessel (Table 6), and the analysis was performed on the thrust loss due to the thruster-hull interference effect targeting the azimuth thrusters located on the port side and in the center. At this stage, unlike the case of WTIV, where both azimuth thrusters were considered, the case of this target vessel was defined as a situation in which one azimuth thruster was installed independently on the port side and in the center, as shown in Table 6. In addition, five operating azimuth angles of the azimuth thrusters were considered in the numerical analysis: 0°, 45°, 60°, 75°, and 110°.
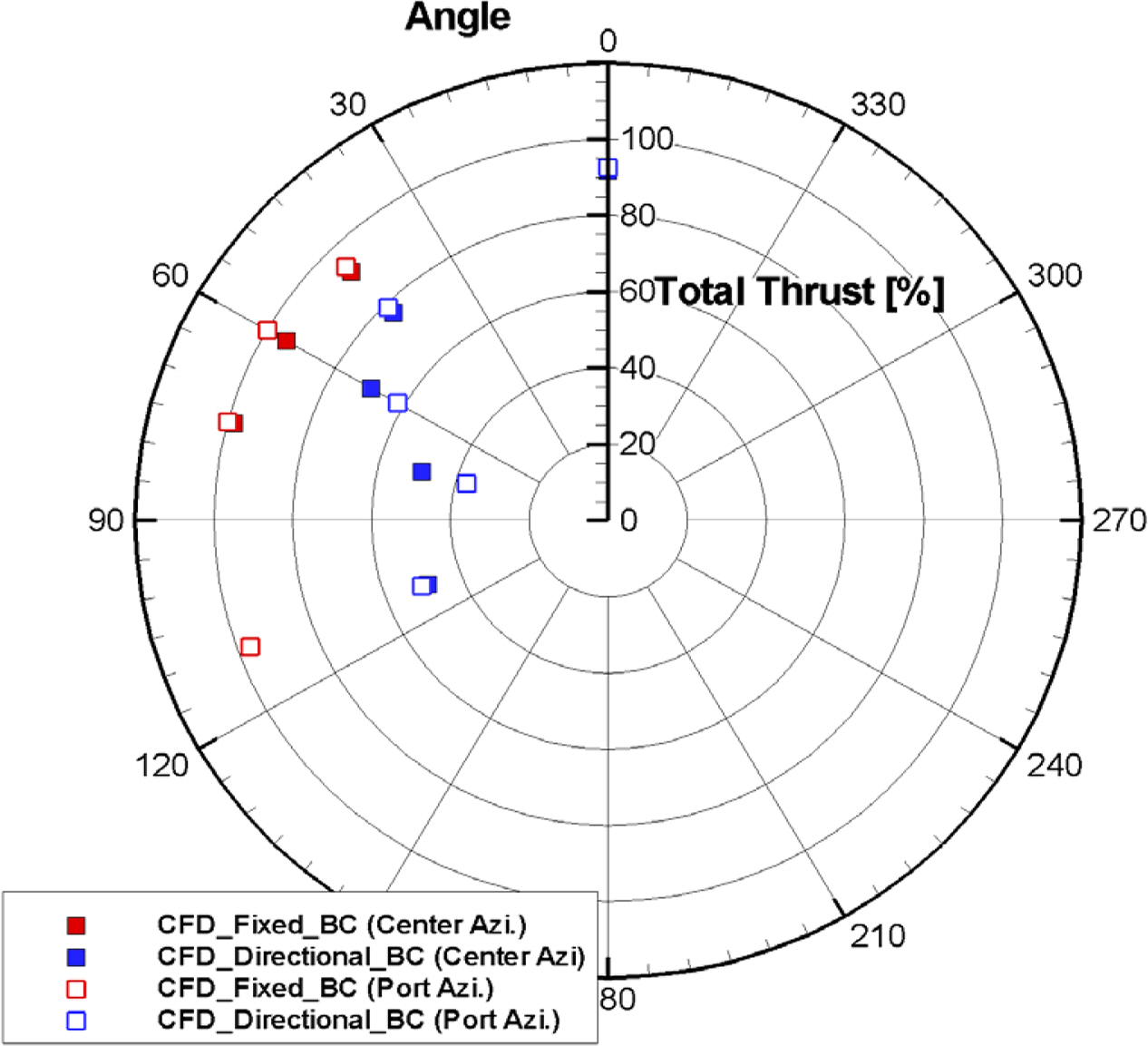
Similar to Fig. 10, Fig. 12 shows the force in the X direction (Fx_Hull) and the force in the Y direction (Fy_Hull) measured across the entire hull, including the thruster, when the model azimuth thrusters located independently at the port and center operates in each azimuth direction under different boundary conditions and the resulting force (F_Total) is shown according to the operating direction of the propeller. Table 11 lists the specific values. Numerical analysis showed that the force in the X direction (Fx_Hull) was similar overall, even though there was a difference in the attachment position of the azimuth thrusters or the method of imposing boundary conditions. On the other hand, for the force in the Y direction (Fy_Hull), there was no significant difference according to the attachment position of the azimuth thrusters under the same boundary conditions. On the other hand, even when the azimuth thrusters were installed in the same position, the results showed a large difference according to the imposed boundary conditions method. In particular, in a situation where the Directional_BC condition was imposed, the magnitude of the force in the Y direction (Fy_Hull) applied to the entire target vessel, including the hull and thruster, was reduced compared to the result of the Fixed_BC condition, and was approximately twice as large under an azimuth angle of 75°. Thus, the distribution of the resulting force (F_Total) of the entire target vessel according to the azimuth also showed a difference following the boundary condition imposition method. For the Fixed_BC condition, a constant resulting force was predicted regardless of the attachment position of the azimuth thruster. In contrast, the overall resulting force (F_Total) decreased as the azimuth increased for the Directional_BC condition.
Similar to Fig. 11, Fig. 13 shows the dimensionless thrust loss due to the thruster-hull interference effect according to the operating azimuth of the azimuth thruster located on the port side and the center; the specific values are listed in Table 12. Similar to Fig. 12(c), the dimensionless total thrust distribution also showed different tendencies according to the method of imposing boundary conditions. For the azimuth reviewed in this study, when Fixed_BC was imposed, a maximum of approximately 8% of thrust loss was expected to occur. In contrast, when the Directional_BC condition was imposed, a maximum of approximately 63% of thrust loss was expected. In particular, when the operating azimuth of the azimuth thruster was 45°, the difference in thrust loss according to the boundary condition imposition method was approximately 15%, but under the condition of 60° or more, the difference in thrust loss estimated according to the boundary condition imposition method was steep, where the difference was approximately two times.
4. Discussion
Chapter 3 compared the predicted thrust loss according to the boundary condition imposition method based on the two target vessels. As shown in Tables 9 and 11 as a comparison result, the thrust loss differed according to the vessel type. In the case of WTIV, the influence of the imposed boundary condition was relatively small. On the other hand, in the case of FPSO, the influence of the boundary condition was large, and the predicted thrust loss was estimated to be approximately 60%, exceeding the generally known level. This chapter discusses the reasons for the large difference in the estimated thrust loss tendency according to vessel types or boundary conditions.
The directional BC mentioned above was a method in which the velocity-inlet and pressure-outlet conditions were imposed on each side of the computational area according to the azimuth angle of the azimuth thruster. Therefore, from the point of view of the target vessel, it is the same situation as a current flowing at a certain azimuth. An azimuth of 0° corresponds to a situation in which the vessel is going straight, and an azimuth of 90° means a situation in which the current flows from the port side of the vessel to the starboard side. The actual vessels generate load according to the direction of the current, which is called the current load. This study conducted a separate numerical analysis to obtain the load. Tables 13 and 14 show the CX, CY, and the resulting force (CTotal) for the target vessels, WTIV and FPSO, by classifying the current loads according to each azimuth in the X and Y directions. At this stage, the applied flow rate was the flow rate when the advance ratio was defined as 0.05, and the own current load of the vessel was calculated without the azimuth thruster attached. Fig. 14 shows the total dimensionless loads calculated for each azimuth based on the value of the resultant force (CTotal) of the current load when the azimuth is 0° in each target vessel are shown together. As shown in Tables 13 and 14 and Fig. 14, the degree of increase in load varied greatly depending on the vessel type. In the case of WTIV, based on the resulting force (CTotal), when the azimuth was 0°, it increased to approximately four times when the azimuth was 90°. On the other hand, in the case of the FPSO, based on the resulting force (CTotal) when the azimuth was 0°, the load value was up to approximately 20 times greater when the azimuth was 75°. Moreover, the size of the load value itself according to the direction of the current also showed a large difference depending on the type of vessel. It was shown that FPSO is approximately 10 times larger than WTIV. These results showed that even if the azimuth thruster attached to the target vessel constantly calculates the thrust during numerical analysis. The total thrust (F_Total) effective for the vessel is greatly reduced as the current load of the vessel becomes excessively large. In particular, the magnitude of the current load may vary greatly according to the vessel characteristics, e.g., the vessel type, hull shape, appendage, and draft. Fig. 15 shows the distribution of the dimensionless pressure coefficient of the hull calculated under the condition of the current at the 45° azimuth from the port side of each target vessel. The distribution form has different characteristics depending on the target vessel. Therefore, when performing numerical analysis to predict thrust loss due to thruster-hull mutual interference, Fixed_BC can be imposed on the side of the computational area rather than Directional_BC, which unnecessarily causes a large current load of the target vessel to be induced and unrealistically large thrust loss to be estimated. When Fixed_BC is imposed, a corresponding flow rate with a small advance ratio artificially defined for numerical stability was additionally imposed, and the effect of the current load can be minimized because this flow rate was very low. As shown in Table 10, when the target vessel is WTIV, the loss of thrust estimated through numerical analysis matches well with the model test results. Even when the target vessel is FPSO, the thrust loss according to the azimuth was estimated to be within 10% regardless of the attachment position of the azimuth thruster, as shown in Table 12. Moreover, when Fixed_BC was imposed as a boundary condition, FPSO, one of the target vessels, was predicted to have relatively less thrust loss than the other target vessel, WTIV. The causes are as follows. The azimuth thruster was installed at the lower part of the head box protruding downward from the hull, so the distance from the hull was relatively far. Second, the duct of the azimuth thruster applied in this study rotated downward (tilt), which can reduce the Coanda effect. Third, the optimal arrangement of azimuth thruster that minimizes interference between the wake direction of the azimuth thruster and the hull, the selection of an azimuth thruster with appropriate capacity, and the advancement of DP control algorithms are fundamentally needed to prevent excessive thrust loss due to thruster-hull mutual interference in offshore facilities or special vessels.
5. Conclusion
The thrust loss due to thruster-hull mutual interference was estimated using the numerical analysis method. Different boundary conditions were imposed based on the two target vessels, and the predicted thrust loss was compared. Through this, the following conclusions could be drawn.
When estimating the thrust loss due to thruster-hull interference by the numerical analysis, it is practical to impose inflow conditions and pressure outflow conditions in the computational domains in the bow and stern directions, such as the boundary condition at 0° azimuth. On the other hand, if the velocity inflow condition and the pressure outflow condition are imposed according to the direction of the operating direction of the azimuth thruster, an unintended current load of the hull may occur, which results in excessive thrust loss may be excessively predicted.
Even if the aforementioned boundary conditions were imposed during the numerical analysis, the thrust loss due to the thruster-hull interference effect can show a difference depending on the vessel type, hull shape, various appendages, and arrangement of the azimuth thruster. In the case of the WTIV, a thrust loss of approximately 30% was expected. On the other hand, in the case of the FPSO, a thrust loss of less than 10% was expected at the azimuth angle of the azimuth thruster considered, and the differences in the azimuth thruster attachment position (port or center of the vessel) were up to approximately 5%.
The foreseeable areas that require additional research include securing additional verification data through model tests, considering the motion performance of the target vessel, and estimating the interference effect between the thruster and the free surface in the case of a vessel with a small draft.
Notes
The authors declare that they have no conflict of interests.
This thesis is research conducted with the support of the Korea Institute of Energy Technology Evaluation and Planning with financial resources from the government (Ministry of Trade, Industry, and Energy) in 2021 (No. 20213030020200, Development of an integrated load analysis program for floating offshore wind power systems).