A Study on Plate Bending Analysis Using Boundary Element Method

Article information

J. Ocean Eng. Technol. 2022;36(4):232-242

Publication date (electronic) : 2022 August 31

doi : https://doi.org/10.26748/KSOE.2022.015

Jae-hyeon Son ¹

, Yooil Kim ²^,

¹Ph.D. student, Department of Naval Architecture and Ocean Engineering, Inha University, Incheon, South Korea

²Professor, Department of Naval Architecture and Ocean Engineering, Inha University, Incheon, South Korea

Corresponding author Yooil Kim: +82-032-860-7347, yooilkim@inha.ac.kr

It is noted that this paper is revised edition based on proceedings of KAOST 2022 in Jeju (Son and Kim, 2022).

Received 2022 June 22; Revised 2022 July 18; Accepted 2022 July 18.

Abstract

This study presents a method for level ice-structure interaction analysis to estimate the fatigue damage of arctic structures by applying plate theory to the behavior of level ice. The boundary element method (BEM), which incurs a lower computational cost than the finite element method (FEM), was introduced to solve the plate bending problem. The BEM formulation was performed by applying the BEM to plate theory. Finally, to check the validity of the proposed method, the BEM results and FEM results obtained using the ABAQUS commercial software were compared. The response results of the BEM analysis agreed well with those of the FEM analysis. Based on the results of the analysis, the BEM approach is considered to be very powerful in level ice-structure interaction analysis for estimating level ice-induced fatigue damage. Further work is being conducted to perform level ice fracture analysis based on the stress field calculated using the boundary element method.

Keywords: Boundary element method; Plate theory; Level ice; Semi analytical method; Boundary integral equation

1. Introduction

The use of the Arctic route and the demand for ships operating in the polar region have greatly increased over time owing to global warming. Moreover, the structural stability of vessels operating in the polar regions has attracted increasing attention, and various studies to estimate the ice load have been conducted. Increases in computer performance have allowed studies to analyze the behaviors of ice using computer simulations. The methods used in these studies can be broadly classified as direct numerical methods or semi-analytical methods.

Among direct numerical methods, the finite element method (FEM) is mainly used for numerical analysis. The FEM has been used for many years to solve realistic engineering problems with linear and nonlinear behaviors involving arbitrary shapes and loads in 2D and 3D spaces. Such direct numerical methods have the advantage of obtaining sufficiently realistic results for fracture behaviors if material properties and elements are modeled according to physical phenomena, because they use the FEM to model ice. However, direct numerical methods have the disadvantage of high computational cost when the size of the elements becomes small enough to obtain a realistic result. Furthermore, this approach must be accompanied by non-linear analysis because of the non-linear properties of the material until failure; this also increases the analysis time. Therefore, direct numerical methods are basically used for detailed analysis of a short time domain. Jeon and Kim (2021) modeled the interaction between level ice and structures by performing a finite element collision simulation using a damage-based erosion model.

In contrast, semi-analytical methods aim to find a analytical solution by introducing specific situations and various assumptions. These methods have the advantage of very short analysis times because they obtain analytical solutions, unlike numerical analysis methods, which require long computational times. Therefore, this type of method is mainly used for long-term analysis. Consequently, in certain situation, the equation provides reliable results. However, there is a disadvantage in that it is difficult to obtain an accurate solution in this way, considering the complex shapes of ice and nonlinear characteristics of the material. One typical example of this type of method is the Simulator for Arctic Marine Structures (SAMS) developed by NTNU (Norwegian University of Science and Technology) in Norway (Lubbad and Løset, 2011; Lubbad et al., 2018; Raza et al., 2019).

This study proposes a numerical method for level ice-structure interaction analysis as a basic tool for long-term fatigue analysis of ships operating in polar waters. A method with a short analysis time, such as a semi-analytical method, is suitable for long-term analysis simulations of fatigue due to contact between level ice and structures such as ships operating in polar waters. However, existing semi-analytical methods still have problems in terms of the accuracy of the results because various assumptions are introduced, as mentioned above. Therefore, we try to solve this problem by using a numerical method with a low computational cost for level ice-structure interaction analysis. The proposed analysis method uses the boundary element method (BEM) as a numerical method. This is the first attempt at using the BEM to analyze level ice-structure interaction, for which the BEM is expected to provide high analytical accuracy and a low computational cost.

The BEM is more advantageous in terms of computational cost than the FEM because elements are divided only at boundaries. Furthermore, when the level ice is broken and a new boundary is created in the conventional FEM, the stiffness matrix must be newly constructed. However, in the case of BEM, the construction time of a new stiffness matrix can also be shortened because only the stiffness matrix components corresponding to the changed boundary elements need to be modified. Furthermore, the third and fourth derivative values of the deflection of the plate should be calculated to determine the stress response of the plate. In the case of FEM, significant accuracy problems occur depending on the type of element. However, the BEM is highly effective at finding the differential values (e.g., stress, strain, moment, shear force) of the response (e.g., deflection) within the domain because the differential value within the domain is directly derived from the Rayleigh-Green identity, which will be discussed later (Katsikadelis, 2002).

A governing equation for the plate bending problem is first established by introducing the plate theory in Section 2.1. In Section 2.2, the BEM for the governing equation is formulated using the BEM. To ensure efficient calculations in this formulation, a constant boundary element was used to lower the computational cost. Analyses using the established BEM methodology were performed for square and triangular models under various boundary conditions and loads. The BEM analysis results were then compared with the FEM analysis results obtained using the commercial finite element structural analysis software Abaqus.

2. Theoretical Background

2.1 Plate Theory

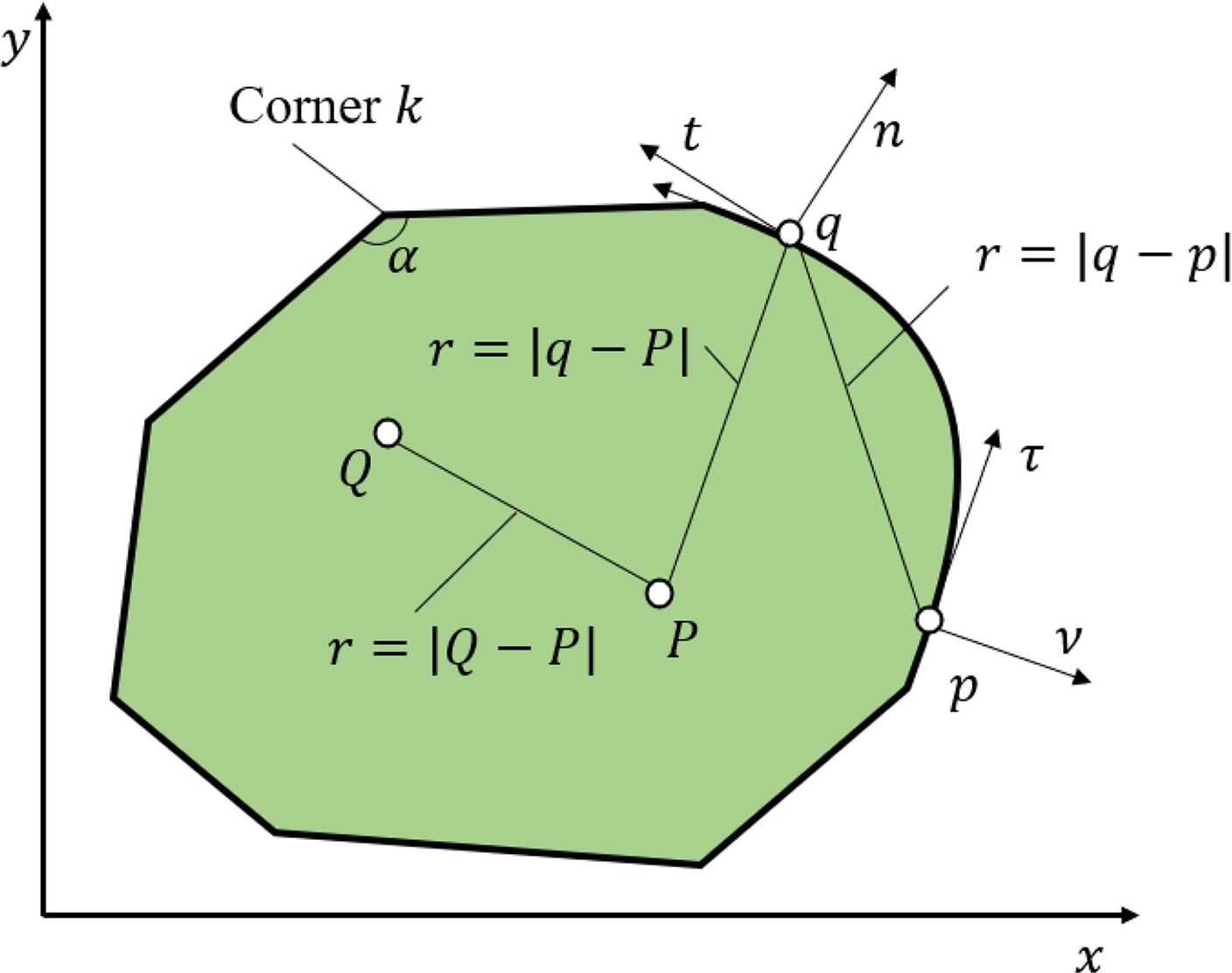
A plate is a flat shape with a relatively small thickness (h) and is defined by the middle plane that bisects the plate thickness, the plate thickness, and the boundary of the plate. In this study, the plate was assumed to be a thin plate. As shown in Fig. 1, the amount of deflection w of an elastic plate subjected to a load perpendicular to the plate can be expressed by the governing equation shown in Eq. (1) (Sillard, 1974).

(1) D∇4w=f in Ω

Fig. 1.

Thin plate

Here, D is the bending stiffness of the plate, which is defined by the modulus of elasticity E, Poisson’s ratio v, and plate thickness h, as follows:

(2) D=Eh312(1−v2)

where ∇⁴ is a biharmonic operator, for which the Laplacian operator is applied consecutively. Using the general Hooke’s law of 3D isotropy, the plate’s bending moment and torsional moments M_x, M_y, and M_xy can be derived from the strain-deflection relationship of the thin plate as follows (Armenakas and Katsikadelis, 1989):

(3) Mx=−D(∂2w∂x2+ν∂2w∂y2)

(4) My=−D(∂2w∂y2+ν∂2w∂x2)

(5) Mxy=D(1−ν)∂2w∂x∂y

The bending moment and effective shear force defined at the boundary are differential operators V and M, which can be expressed as follows:

(6) M=−D[∇2+(ν−1)∂2∂t2]

(7) V=−D[∂∂n∇2−(ν−1)∂∂s(∂2∂n∂t)]

here the n-direction is the normal direction at the boundary point, the t -direction is the tangent direction at the boundary point, and the s -direction is the arc direction at the boundary point on the boundary line with a curvature. The s- and t-directions coincide at the boundary line, which is a straight line.

The boundary conditions of the plate are expressed as Eqs. (8) and (9). The fixed, simply supported, and free boundary conditions are defined in accordance with the values of α_i and β_i (i = 1,2,3).

(8) α1w+α2Vw=α3 onΓ

(9) β1∂w∂n+β2Mw=β3onΓ

Additional boundary conditions are required owing to the discontinuous nature at a corner point where the normal and tangent directions at the boundary change discontinuously. The boundary condition at the kth corner point is given as follows:

(10) c1kw+c2k〚Tw〛k=c3k

where c_ik (i = 1,2,3) is determined by the boundary conditions at both boundaries of the corner point. T is a torsional moment operator that satisfies the relationship of M_nt =Tw and can be expressed as Eq. (11). The torsional moment has discontinuous values owing to the discontinuous changes in the normal and tangent directions at the corner point. It is a fictitious corner force, equal to the difference in 〚Tw〛 values, and can be expressed as Eq. (12). Tw₊ and Tw₋ denote two torsional moments at both boundaries from the corner point.

(11) T=D(1−ν)∂2∂n∂t

(12) 〚Tw〛=Tw+−Tw−

2.2 Boundary Element Method Formulation of Plate Theory

The BEM formulation is performed using a constant boundary element to reduce the computational cost. This formulation starts from the Rayleigh-Green identity based on the Gauss-Green theorem. The Rayleigh-Green identity is an identity that is established for two random functions v and w, where the fourth derivative is continuous within the domain Ω and the third derivative is continuous at the domain boundary Γ. It represents the relationship expressed as follows:

(13) ∫Ω(v∇4w−w∇4v)dΩ =∫Γ(v∂∂n∇2w−w∂∂n∇2v−∂v∂n∇2w+∂w∂n∇2v)dΓ

Eq. (13) can be reorganized as Eq. (14) by using the operator introduced in section 2.1. Eq. (14) is called the generalized Rayleigh-Green identity.

(14) D∫Ω(v∇4w−w∇4v)dΩ =∫Γ(vVw−wVv−∂v∂nMw+∂w∂nMv)dΓ+∑k(v〚Tw〛k−w〚Tv〛k)

The deflection w, which is a response of the plate, is calculated through the relationship with function v using Eq. (14), which is the Rayleigh-Green identity. The function v used here is the fundamental solution of the biharmonic equation, and indicates a particular solution of Eq. (15).

(15) D∇4v=δ(Q−P) in Ω

In Eq. (15), δ(Q −P) is the Dirac delta function. The fundamental solution v = v(Q,P) is also defined by the points P(x,y) and Q(ξ,η). Physically, v(Q,P) denotes the plate deflection at point Q when a concentrated unit load is given at point P. The fundamental solution v can be determined by analytically solving the fourth-order differential equation of Eq. (15) and is expressed as Eq. (16). The integral constant that is generated when is analytically solved is obtained as a result of the physical conditions to be considered (Katsikadelis, 2014).

(16) v(r)=18πDr2lnr, r=|Q−P|=[(ξ−x)2+(η−y)2]0.5

In Fig. 2, v denotes a rotational symmetry function, P denotes the source point at the center of the rotational symmetry of function v in the domain, and Q denotes the field point representing the value of the response field. Furthermore, p and q denote the source point and field point at the boundary, respectively.

Fig. 2.

Source point and filed point on the Plate

Values inside the domain can be calculated using the Rayleigh-Green identity and the fundamental solution. When the source point of v in Eq. (10) is positioned inside the domain, the deflection inside the domain is calculated using the w,〚Tw〛 value at w, ∂w/∂n, Mw, Vw, and the corner point at the boundary, as shown in Eq. (17).

(17) w(P)=∫ΩvfdΩ+∫Γ(vVw−wVu−∂v∂nMw+∂w∂nMv)dΓ −∑k(v〚Tw〛k−w〚Tv〛k)

The term ∫_ΩvfdΩ, which still remains as the domain integral, is calculated by applying the boundary integral and the Rayleigh-Green identity again, and converting to the boundary integral ∫_ΩvfdΩ (Katsikadelis, 2014).

2.2.1 Boundary integral equation

The values inside the domain can be obtained from the boundary values, and the boundary values are calculated from the boundary condition and boundary integral equation. The first boundary integral equation can be obtained by matching the source point in the Rayleigh-Green identity to the boundary and corner points, respectively. This can be expressed as follows (Katsikadelis et al., 1977):

(18) α2πw(p)=∫ΩvfdΩ+∫Γ(vVw−wVv−∂v∂nMw+∂w∂nMv)dΓ −∑k(v〚Tw〛k−w〚Tv〛k)

This α value is different from α_i in Eq. (8). As shown in Fig. 2, α indicates the angle inside the domain at source point p. When the source point p is matched to the corner point at which the n and t directions change discontinuously, α is the inner angle value of the corner. If the source point is positioned at a smooth boundary where the n and t directions are not discontinuous, α is calculated as π.

The second boundary integral equation can be obtained through the ν -direction differentiation of v when point P inside the domain approaches to point p at the boundary, and can be expressed as follows (Bezine, 1978):

(19) 12wn(p)=∫Ωv1fdΩ+∫Γ(v1Vw−wVv1−∂v1∂nMw+∂w∂nMv1)dΓ −∑k(v1〚Tw〛k−w〚Tv1〛k)

where v₁ is a function that has been directionally differentiated in the ν direction, v which is the direction that is normal to the boundary at point p in Fig. 2. It can be expressed as follows:

(20) v1=18πDrrν(1+2lnr)

The linear algebraic equation can be constructed by using both the boundary conditions and boundary integral equations obtained above, and the boundary values can be calculated through this process. The method of calculating detailed boundary elements involving the calculation of singular points of matrix elements and near-singular points is introduced in Katsikadelis (2002).

3. BEM Verification for Plate Problem

3.1 Analysis Model

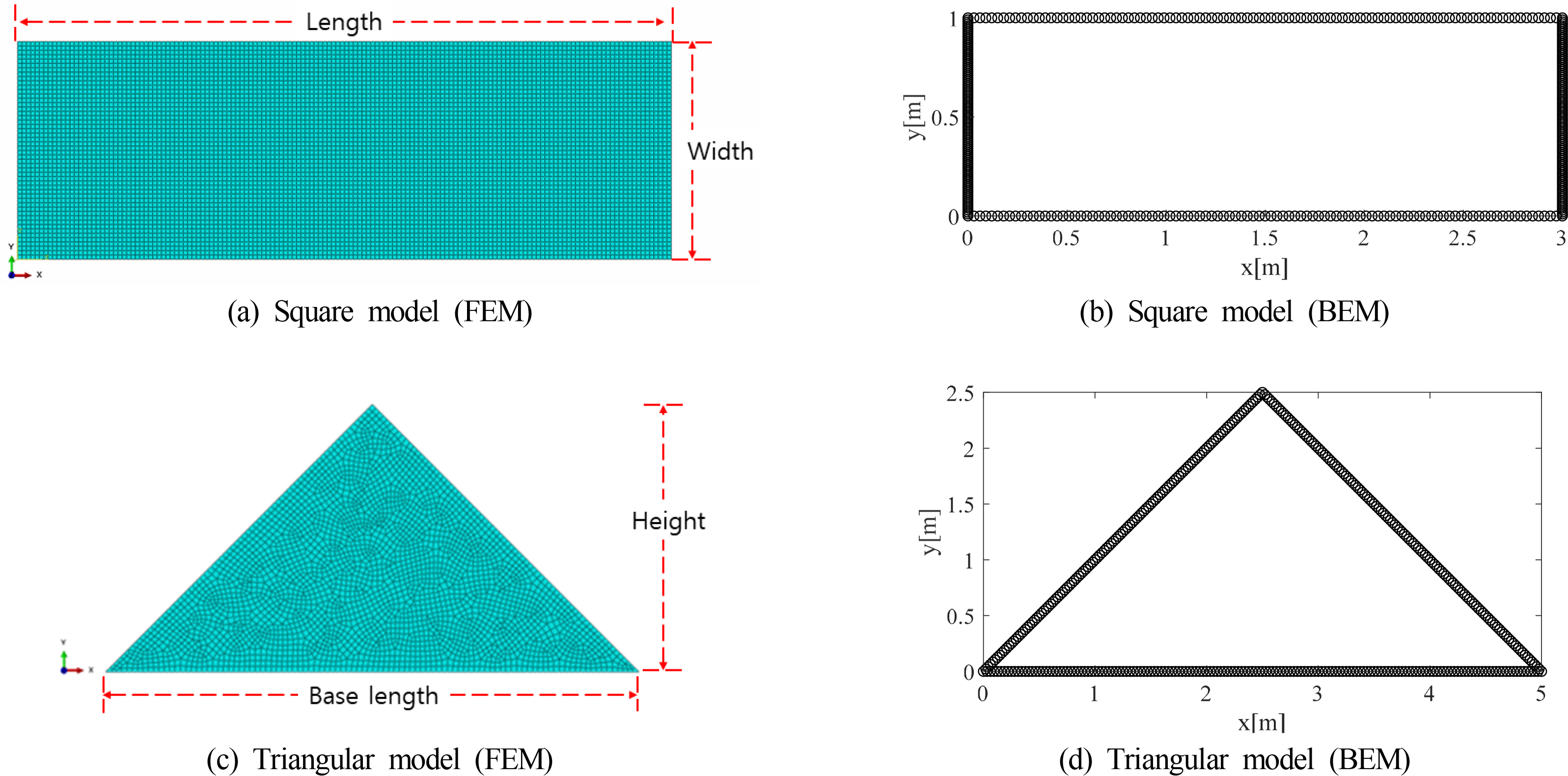
The BEM code of the plate bending problem was verified using two plate models. Square and triangular models were used as simple analysis models. For these two models, the elements were divided into boundary and finite elements, as shown in Fig. 3. The physical properties of the square model are summarized in Table 1, and the material properties of the triangular model are summarized in Table 2.

Fig. 3.

Finite element method (FEM) and BEM models for square and triangular models

Table 1.

Properties of square model

Table 2.

Properties of triangular model

For both triangular and square models, a Poisson’s ratio of 0.3 and a modulus of elasticity of 2×10⁸ N/m² were used. The square model consisted of 7,500 finite elements and 400 boundary elements. The triangular model consisted of 3,043 finite elements and 242 boundary elements.

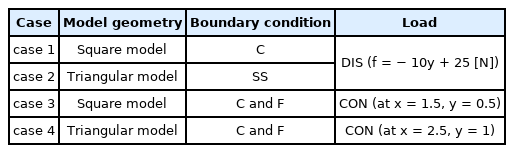
To verify the BEM code for the plate problem, analyses was performed under various boundary and load conditions. Then, the analysis results were compared with the analysis results obtained using the FEM. First, the responses obtained using fixed boundaries and distributed loads were checked. For this purpose, a fixed boundary constraint was given to all boundaries for the square model, and a load of f = − 10y + 25 (N) was applied over the entire domain of the plate. To verify the responses by simply supported and distributed loads, a simply supported constraint was given to the boundary for the triangular model. Then, analysis was performed by applying the load of f = − 10y + 25 (N) over the entire domain of the plate. This corresponds to cases 1 and 2 in Table 3.

Table 3.

Boundary conditions and loads (C: Clamped, SS: Simply supported, F: Free, CON: Concentrated unit load, DIS: Distributed load)

In the case of the boundary condition of a semi-infinite ice sheet such as level ice, It is similar to the situation in which a free boundary is applied at the boundary of the level ice that comes in contact with the ship, and a strong constraint condition is applied at all boundaries except the free boundary. Therefore, the case of exposure to a concentrated unit load in the boundary condition including the free boundary was also analyzed. For the square and triangular models, the free boundary was applied to the boundary at y = 0 m, and the fixed boundary was applied to all boundaries except the free boundary. Then, for the square model, a concentrated unit load of 1 N was applied to the position of x = 0.5 m and y = 1.5 m. For the triangular model, a concentrated unit load of 1 N was applied to the position of x = 2.5 m and y = 1 m. These correspond to cases 3 and 4 in Table 3.

To obtain the responses of the BEM, Eqs. (18) and (19) were concatenated to form a linear algebraic equation. These values were then used to obtain the deflection in the domain and the differential terms of the deflection using Eq. (17). The differential values of the calculated deflection were used to calculate the bending and torsional moments using Eqs. (3) through (5). For comparison, the FEM responses were calculated through an analysis performed using the commercial structural analysis software Abaqus. The finite elements, which are S8R secondary shell elements, were calculated under the same boundary condition and load.

3.2 Analysis Results

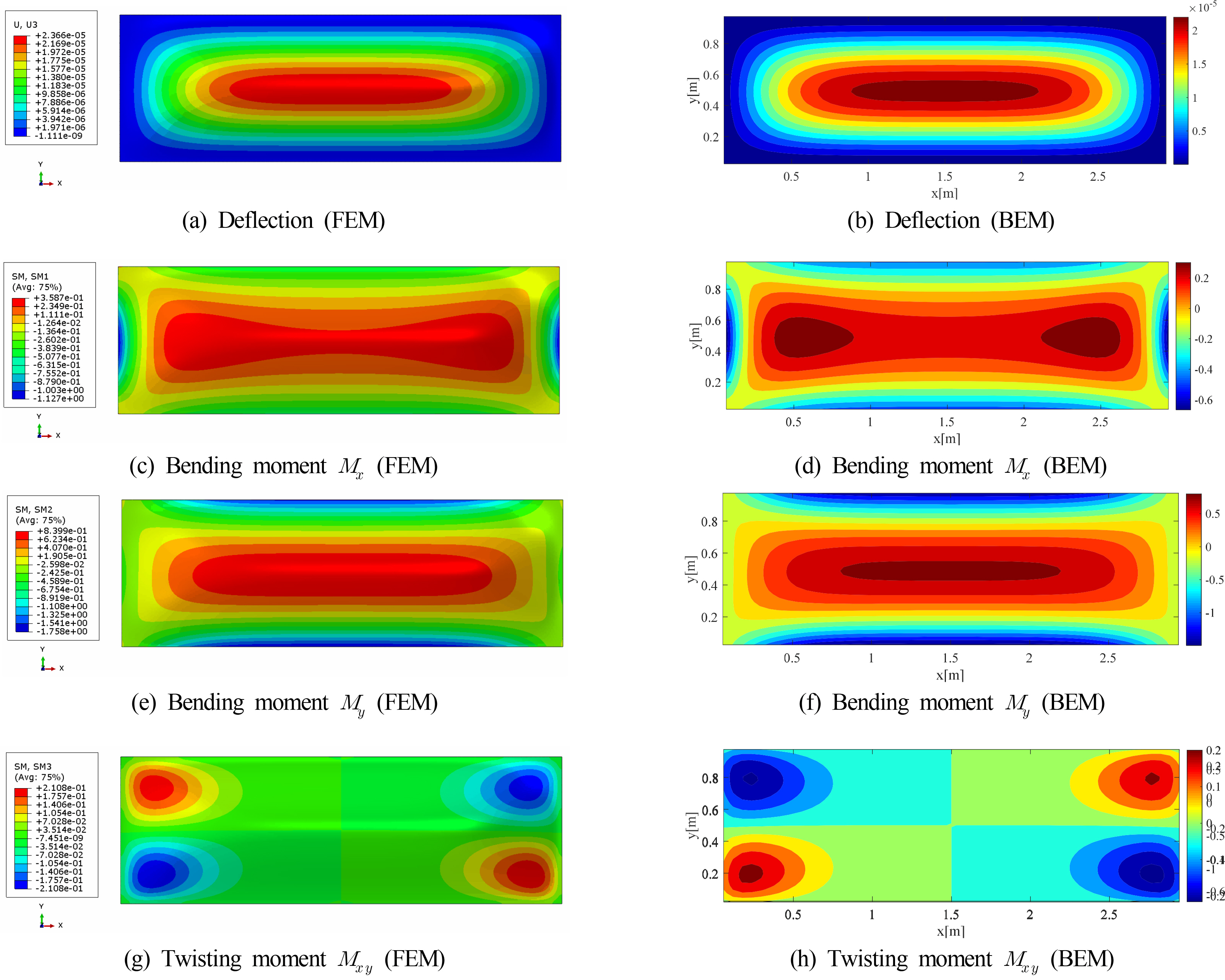
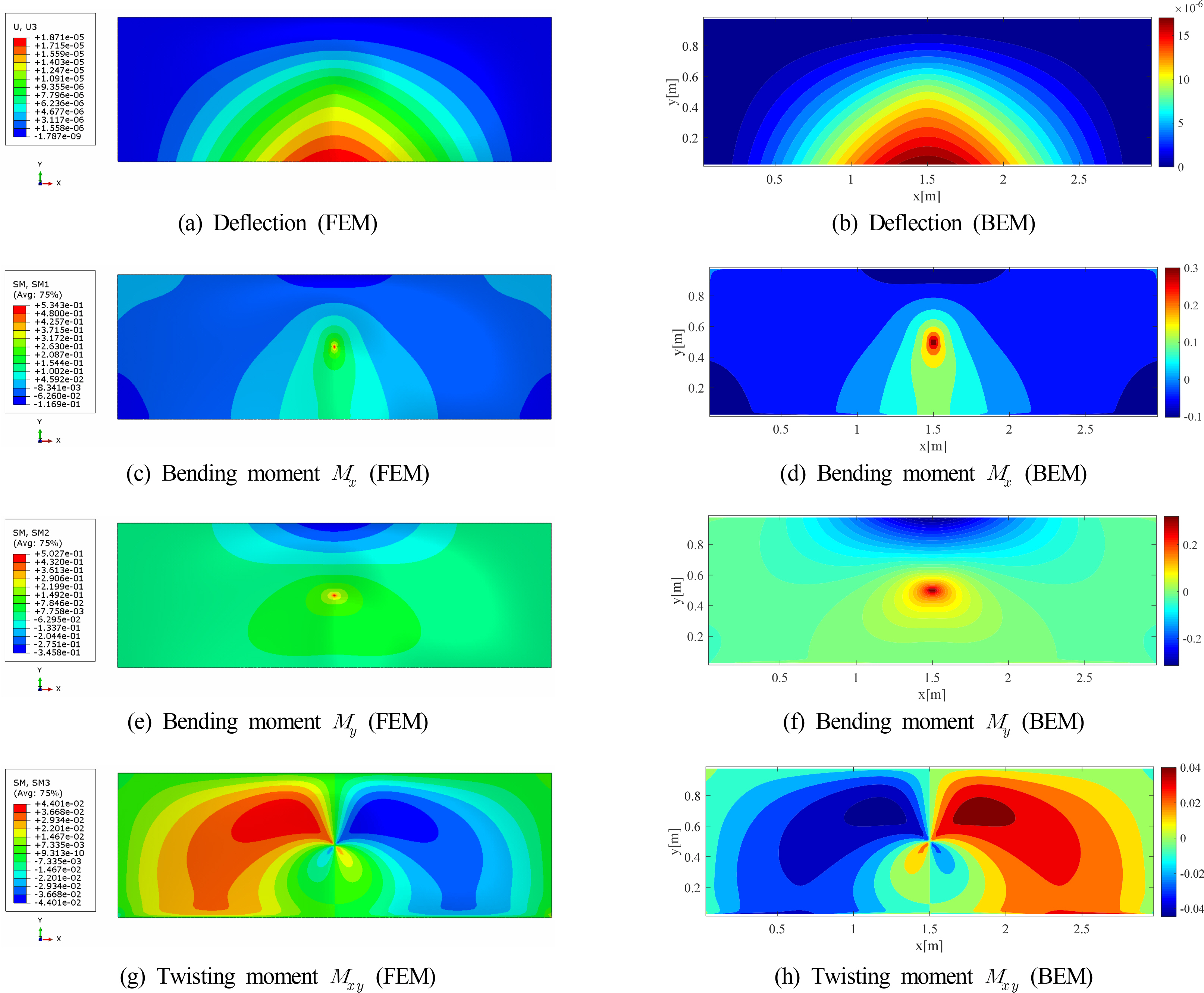
The deflection, bending moment, and torsional moment of the plate were calculated as response results of the BEM and FEM. The response results for cases 1 and 2 are illustrated in Figs. 4 and 5, respectively.

Fig. 4.

Comparison between FEM and BEM results (Case 1)

Fig. 5.

Comparison between FEM and BEM results (Case 2)

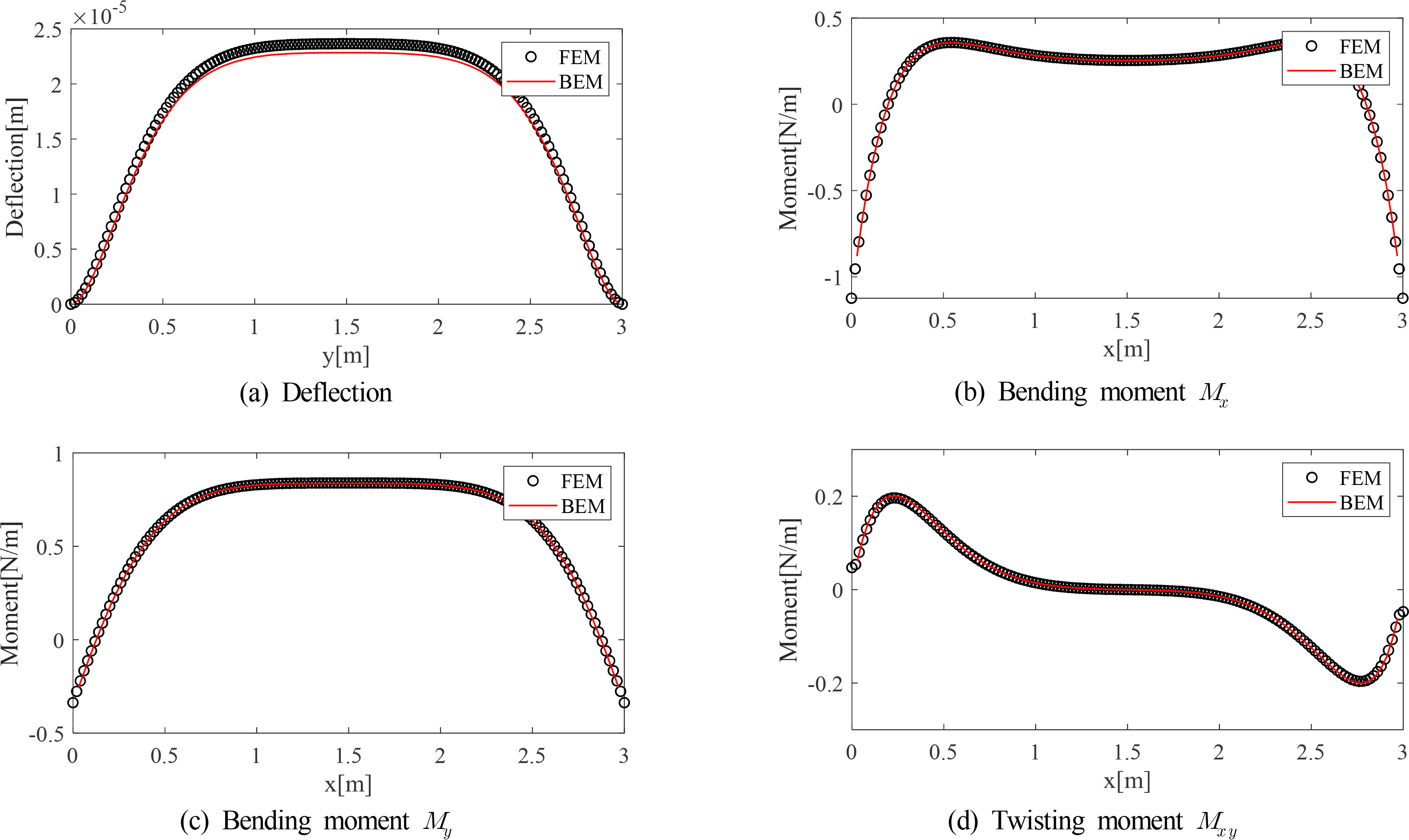
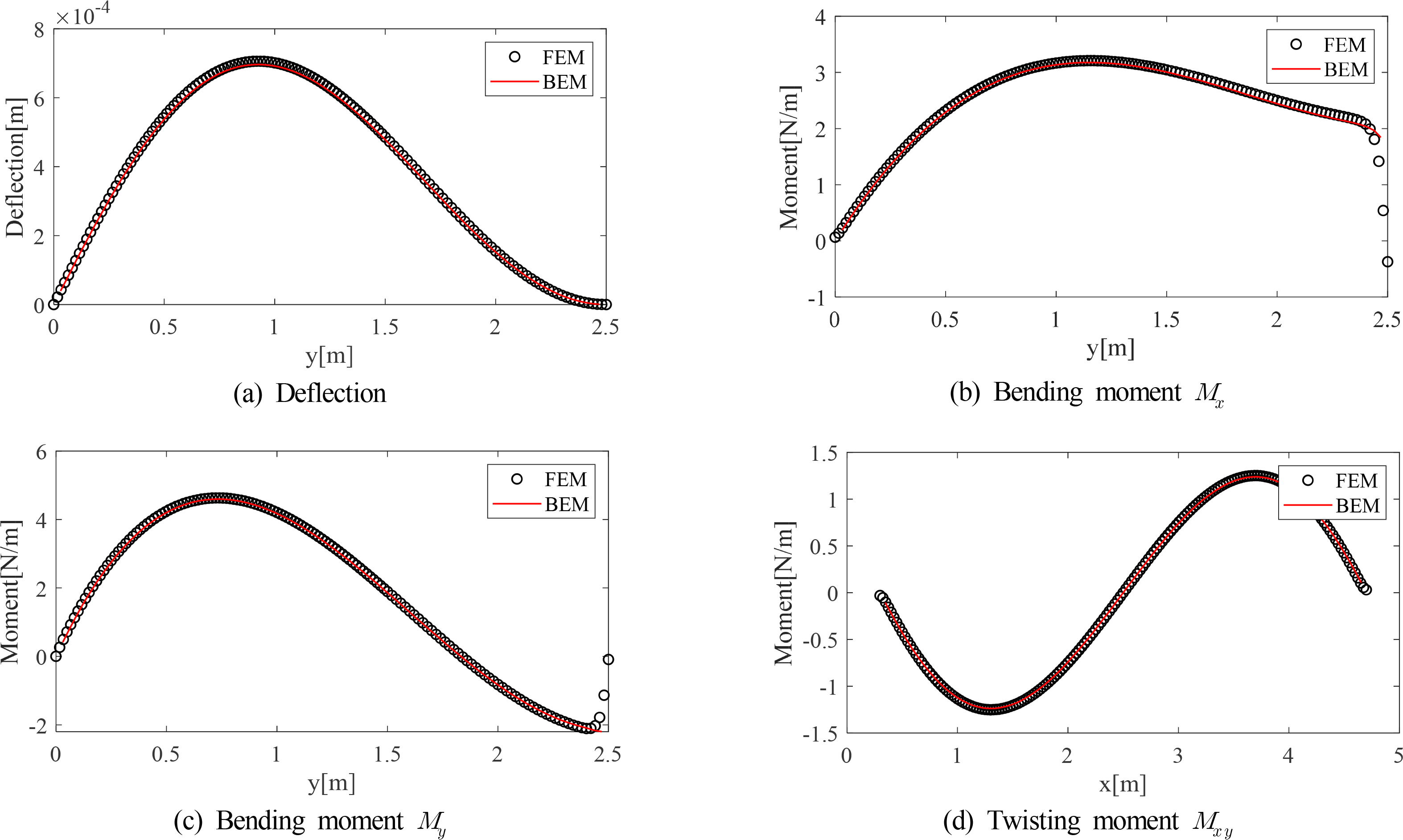
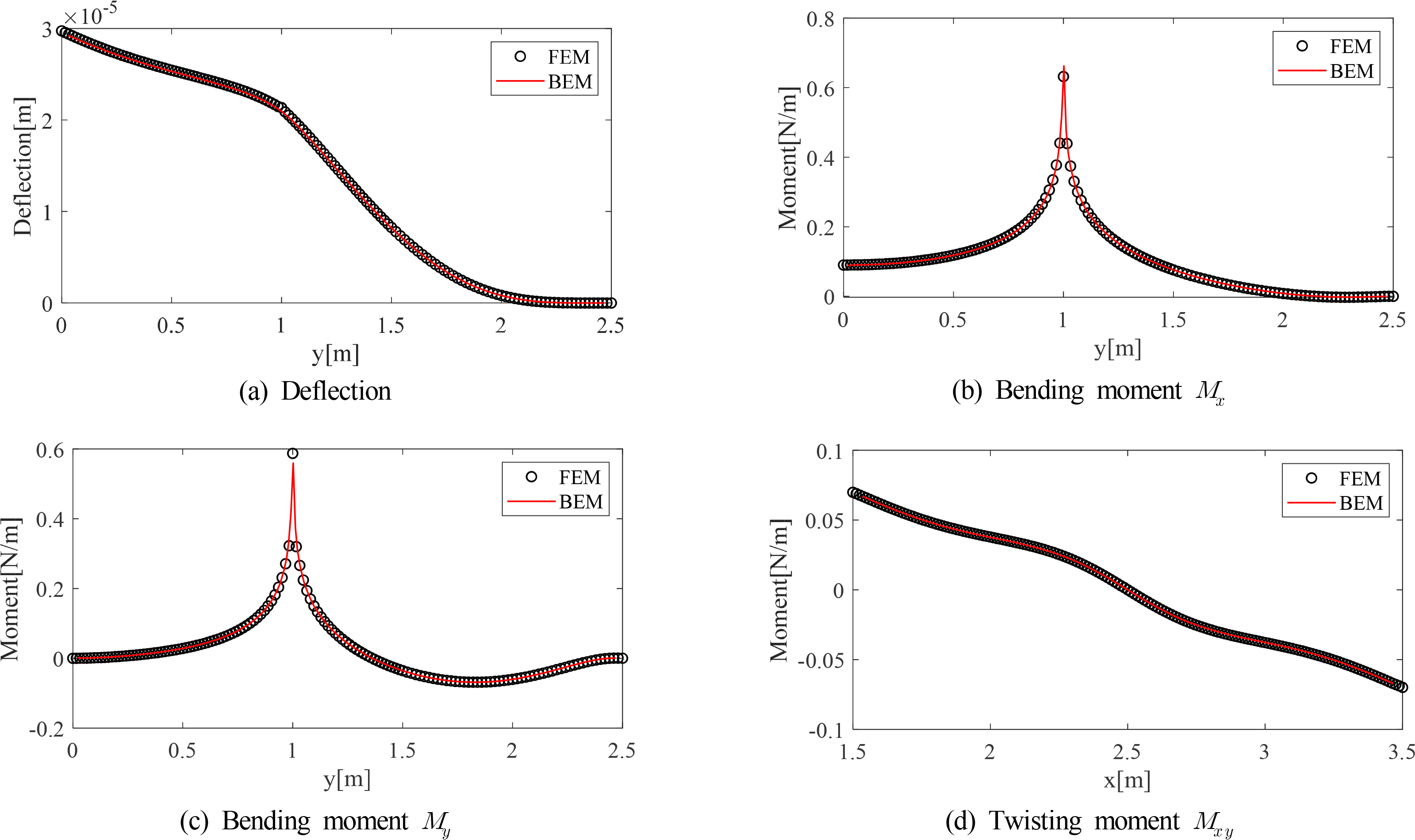
Figs. 4 and 5 show that the FEM results are similar to the BEM results for both bending and torsional moments. In the case of the torsional moment, the signs of the FEM results and the BEM results are different because of the difference in the predetermined sign convention for the torsional moment. To provide a closer comparison in case 1, the results were compared at y = 0.75 m, where the fluctuation of values is large in terms of the deflection and bending moment, and at x = 1.5 m for the torsional moment. The comparison results are shown in Fig. 6. Similarly, in case 2, the results were compared at locations with large fluctuations, and the results are shown in Fig. 7. Here, the deflection and bending moments were compared at x = 2.5 m, and the torsional moment was compared at y =0.3 m.

Fig. 6.

Comparison between FEM and BEM results along the path (Case 1)

Fig. 7.

Comparison between FEM and BEM results along the path (Case 2)

In case 1, the deflection in the BEM result shows slightly smaller responses in general than that in the FEM result. As shown, the bending and torsional moments coincide almost exactly. In case 2, it can be seen that the deflection, bending moment, and torsional moment all coincide almost exactly. Here, torsional moments were compared by matching signs.

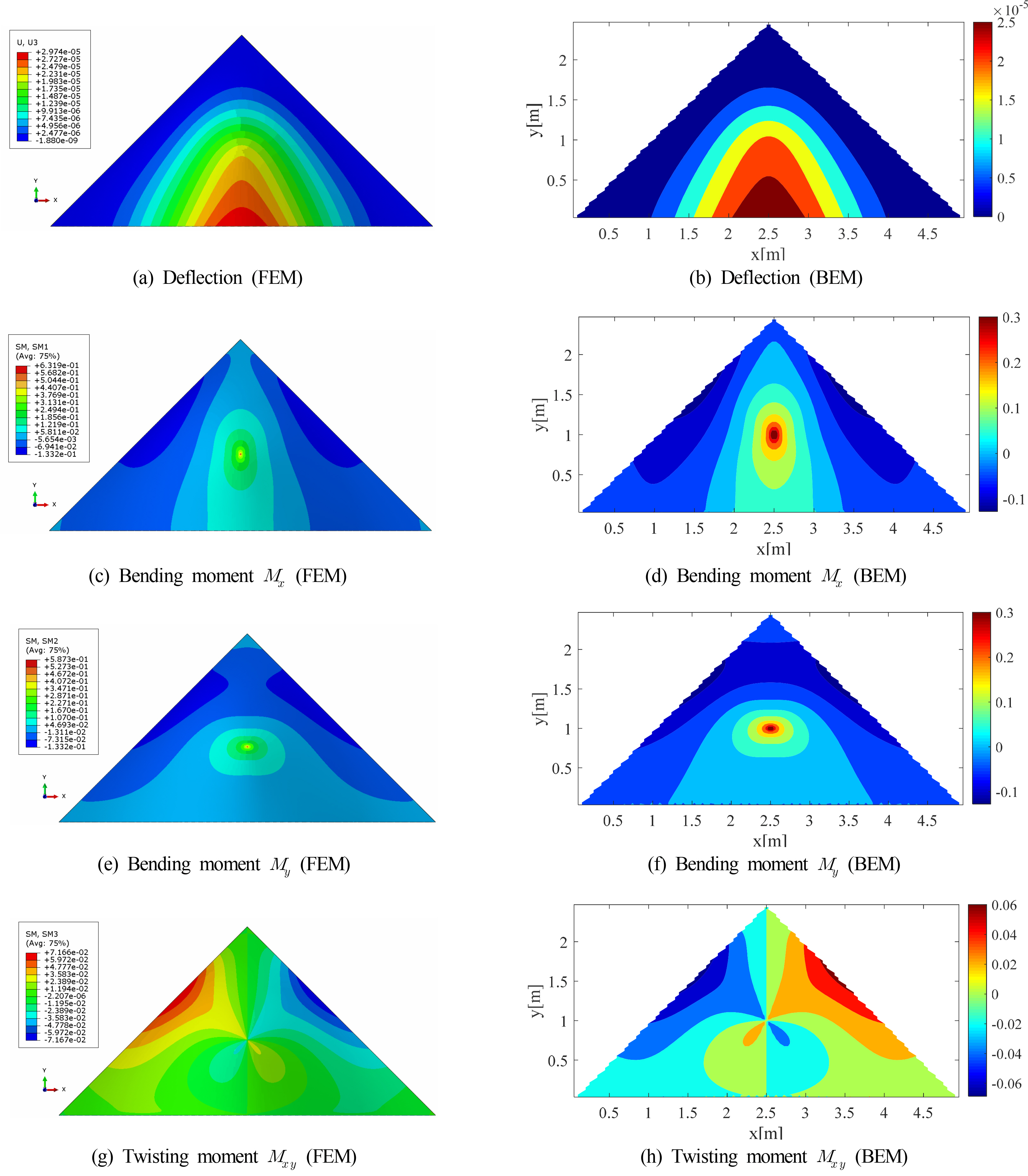
The FEM and BEM response results for cases 3 and 4 are shown in Figs. 8 and 9, respectively.

Fig. 8.

Comparison between FEM and BEM results (Case 3)

Fig. 9.

Comparison between FEM and BEM results (Case 4)

As shown in Figs. 8 and 9, the deflection, bending moment, and torsional moment results obtained using the FEM and BEM are quite similar. Furthermore, comparing the responses of cases 3 and 4 also confirms that the contours of the responses are similar because the bottom edge is a free boundary and the remaining edges have a similar situation involving a fixed support. In case 3, the torsional moment increases to become sufficiently large and then decreases as it approaches the boundaries, except for the lower boundary. However, in case 4, it does not become small enough as it approaches the boundary, and has its maximum and minimum values at the boundary. It seems that this difference appears because the boundaries other than the lower boundary of case 4 are relatively closer, compared to those in case 3, to the point where the concentrated unit load is applied. As in cases 1 and 2, the signs of the torsional moment of the FEM and BEM results are calculated differently owing to the difference in the sign convention.

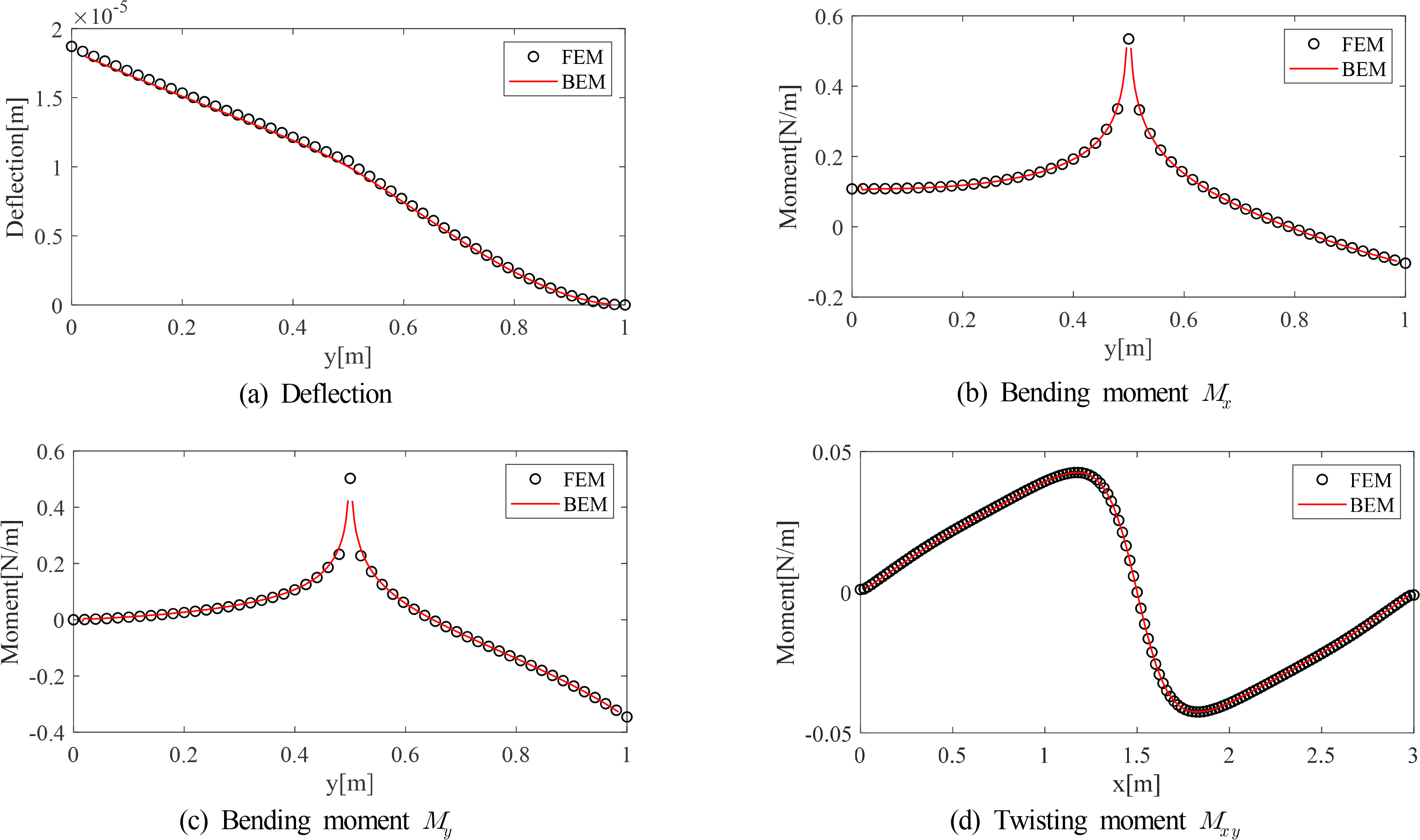
For a more in-depth comparison of cases 3 and 4, a comparison according to the path is shown in Figs. 10 and 11. As in cases 1 and 2, these cases were compared at locations with large fluctuations. In case 3, deflection and bending moments were campared at y = 0.75 m, and the torsional moment was campared at x = 1.5 m. In case 4, deflection and bending moments were campared at x = 2.5 m, and the torsional moment was campared at y =0.3 m.

Fig. 10.

Comparison between FEM and BEM results along the path (Case 3)

Fig. 11.

Comparison between FEM and BEM results along the path (Case 4)

The results for both cases 3 and 4 show that the BEM results are very similar to the FEM results. Moreover, it can be seen that the value of the bending moment changes significantly at the location at which the concentrated unit load is applied.

4. Conclusions

This study proposed a numerical methodology for level ice-structure interaction analysis for application to long-term fatigue analysis of ships operating in polar waters. First, the behavior of level ice was applied to the plate bending problem. In addition, a governing equation for plate behavior was established by introducing plate theory. To solve the governing equation, the BEM, which has high accuracy and a low computational cost, was introduced. The BEM formulation of the governing equation was also performed. BEM and FEM analyses were conducted under various boundary conditions and loads for simple square and triangular models, and the results were compared. Based on the above analysis results, the following conclusions can be drawn.

An analysis method with a low computational cost is needed for long-term fatigue analysis of ships operating in polar waters in contact with level ice. A numerical methodology using the BEM was proposed for this analysis.
The governing equation of the plate theory was formulated using the BEM after applying the behavior of level ice to the plate problem.
The BEM results were compared with the analysis results of Abaqus, a commercial finite element structural analysis program, to verify the accuracy of the BEM methodology.
Both the analysis results performed under distributed load at fixed and simply supported boundaries and the analysis results under concentrated unit load at the boundaries including the free boundary were similar to the analysis results of Abaqus, a commercial finite element structural analysis program.
The proposed method showed results that were sufficiently similar to the finite element results, using very few boundary elements compared to the number of finite elements. Therefore, this method is highly suitable in terms of computational cost and accuracy for application to many flat bending analysis scenarios for fatigue caused by ice load.
It is necessary to assume the condition of an elastic foundation because the level ice at sea is under buoyancy. Therefore, we plan to conduct additional research considering buoyancy.
Furthermore, we will perform fatigue life evaluation by conducting long-term fatigue analysis using the BEM methodology after buoyancy is added.

Notes

No potential conflict of interest relevant to this article was reported.

This work was conducted in 2022 with the support of the Korea Industrial Technology Promotion Agency with funding from the government (Ministry of Trade, Industry and Energy) (P0001968. Industrial Innovation Talent Growth Support Project 2022).

References

Armenakas AE, Katsikadelis JT. 1989;A New Boundary Equation Solution to the Plate Problem. Journal of Applied Mechanics 56(2):364–374. https://doi.org/10.1115/1.3176091 .

Bezine G. 1978;Boundary Integral Formulation for Plate Flexure with Arbitrary Boundary Conditions. Mechanics Research Communications 5(4):197–206. https://doi.org/10.1016/0093-6413(78)90033-2 .

Jeon S, Kim Y. 2021;Numerical Simulation of Level Ice-structure Interaction Using Damage-based Erosion Model. Ocean Engineering 220:108485. https://doi.org/10.1016/j.oceaneng.2020.108485 .

Katsikadelis JT. 2002. Boundary Element: Theory and Applications 1st edth ed. Elsevier.

Katsikadelis JT. 2014. The Boundary Element Method for Plate Analysis 1st edth ed. Elsevier.

Katsikadelis JT, Massalas CV, Tzivanidis GJ. 1977;An Integral Equation Solution of the Plane Problem of the Theory of Elasticity. Mechanics Research Communications 4(3):199–208. https://doi.org/10.1016/0093-6413(77)90083-0 .

Lubbad R, Løset S. 2011;A Numerical Model for Real-time Simulation of Ship-ice Interaction. Cold Regions Science and Technology 65(2):111–127. https://doi.org/10.1016/j.coldregions.2010.09.004 .

Lubbad R, Løset S, Lu W, Tsarau A, van den Berg M. 2018. Simulator for Arctic Marine Structures (SAMS). Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering Madrid. Spain: p. 51296. V008T07A020. https://doi.org/10.1115/OMAE2018-78592 .

Raza N, van der Berg M, Lu W, Lubbad R. 2019. Analysis of Oden Icebreaker Performance in Level Ice Using Simulator for Arctic Marine Structures (SAMS). Proceedings of the 25th International Conference on Port and Ocean Engineering under Arctic Conditions Delft. The Netherlands:

Sillard R. 1974. Theory and Analysis of Plates: Classical and Numerical Methods 1st edth ed. Prentice Hall. New Jersey:

Son JH, Kim Y. 2022. Basic Study on the Boundary Element Method for Ice-structure Interaction Analysis. Proceedings of KAOST 2022 Jeju. Korea: p. 547–551.

Article information Continued

This is an open access article distributed under the terms of the creative commons attribution non-commercial license (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Case	Model geometry	Boundary condition	Load
case 1	Square model	C	DIS (f = − 10y + 25 [N])
case 2	Triangular model	SS	DIS (f = − 10y + 25 [N])
case 3	Square model	C and F	CON (at x = 1.5, y = 0.5)
case 4	Triangular model	C and F	CON (at x = 2.5, y = 1)

Variable	FEM	BEM
Number of elements	7,500	400
Poisson’s ratio	0.3
Young’s modulus	2×10⁸ N/m²
Thickness	0.05 m
Length	3 m
Width	1 m

Variable	FEM	BEM
Number of elements	3,043	242
Poisson’s ratio	0.3
Young’s modulus	2×10⁸ N/m²
Thickness	0.05 m
Base length	5 m
Height	2.5 m