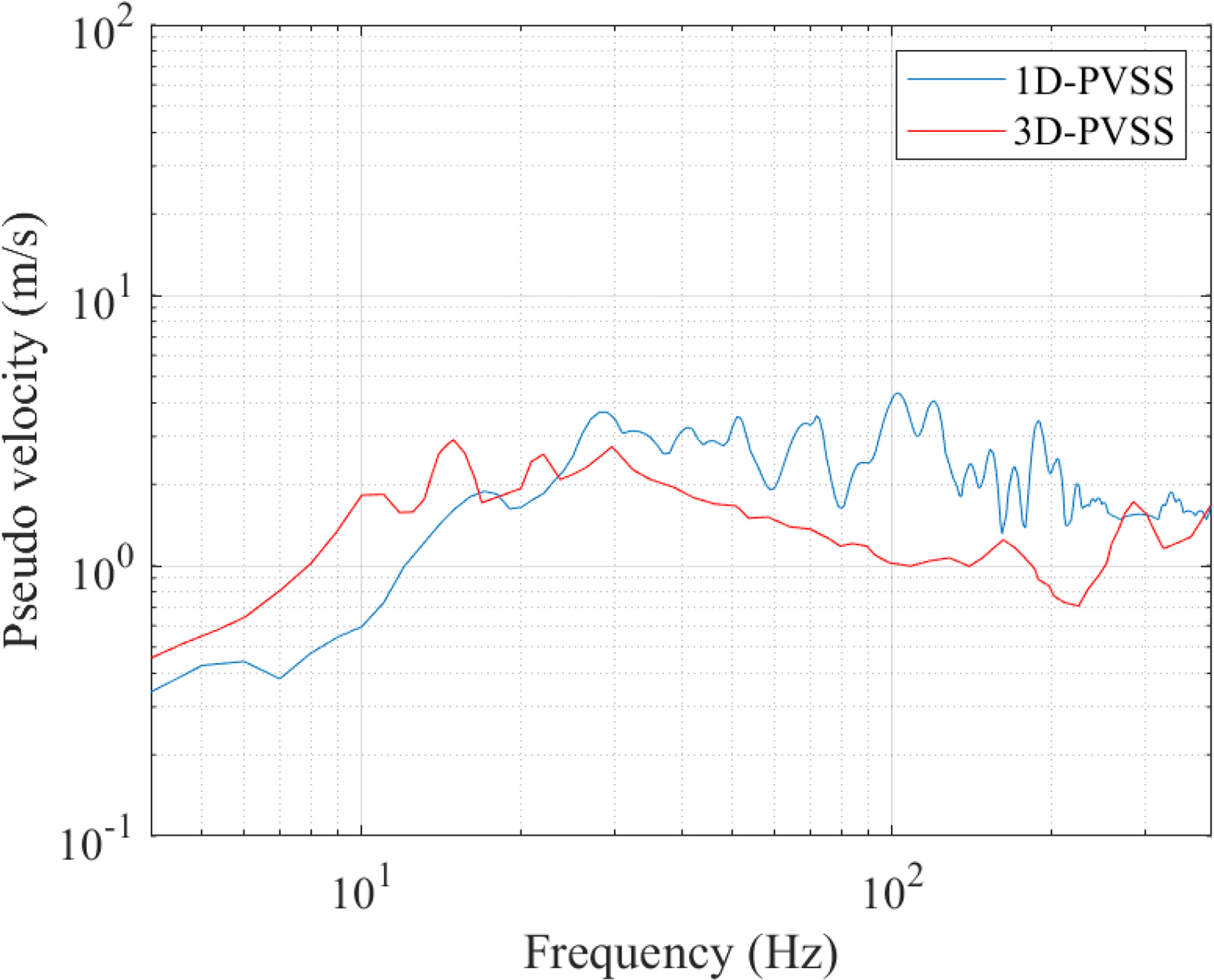
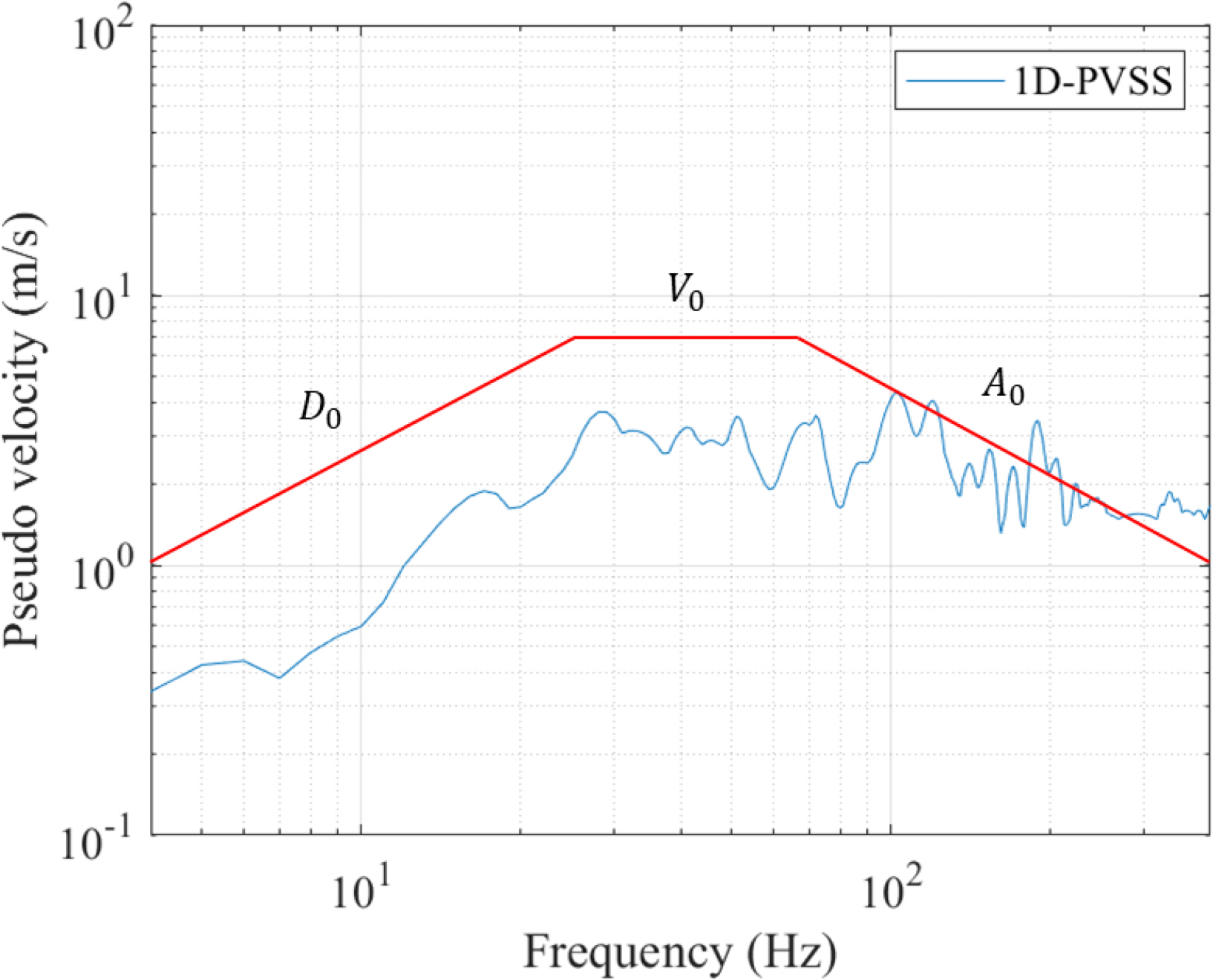
American Bureau of Shipping (ABS). (2021). Guidance Notes on Ship Vibration, New York, USA. ABS.
Building Specification for Ships of the Federal Armed Forces (BV). (1985). Shock Resistance Experimental and Mathematical Proof (BV043).
Bae, SW., Hong, JS., Jeong, WB., & Kim, J. (2009). Structural Safety Analysis of Propulsion Motors by BV043. Proceedings of the Korean Society for Noise and Vibration Engineering Conference, 254-255.
Geers, TL., & Hunter, KS. (2002). An Integrated Wave-Effects Model for an Underwater Explosion Bubble.
Journal of Acoustic Society of America,
111(4), 1584-1601.
https://doi.org/10.1121/1.1458590

Kim, JB., Park, YK., Park, MS., Lee, JH., & An, SC. (2017). Evaluation of the Shock Resistance of a Gas Turbine Package.
Transactions of the Korean Society of Mechanical Engineers A,
41(10), 1005-1009.
https://doi.org/10.3795/KSME-A.2017.41.10.1005

Kim, H., Seo, JH., & Choung, J. (2021). A Study on Inelastic Whipping Responses in a Navy Ship by Underwater Explosion.
Journal of the Society of Naval Architects of Korea,
58(6), 400-406.
https://doi.org/10.3744/SNAK.2021.58.6.400

Lee, SW., Kim, J., & Kong, YK. (2010). A Shock-Proof Evaluation of a Naval Vessel Motor using DDAM and Transient Response Analysis. Journal of the Korean Society of Manufacturing Process Engineers, 9(5), 76-82.
Lee, JB. (2012). A Study on Shock Resistance Evaluation of Steering Units for a War Vessel byUusing Dynamic Design Analysis Method (Master thesis). Changwon National University; Changwon, Korea.
Lee, JB., & Choung, J. (2020). A Study on BEM-Based Numerical Simulation Technique for Underwater Explosions.
Journal of the Society of Naval Architects of Korea,
57(5), 271-277.

Naval Sea System Command (NAVSEA). (1976). Test Plan for Routine Shock Testing of Ships, Washington, DC. NAVSEA.
Naval Sea System Command (NAVSEA). (1995). Shock Design Criteria for Surface Ships, Washington, DC. NAVSEA.
Scavuzzo, RJ., & Pusey, HC. (1996). Principles and Techniques of Shock Data Analysis. Virginia. Booz Allen Hamilton.
Seong, J., Choi, J., Kim, J., & Baek, S. (2015). A Study on Shock Resistance Evaluation of Equipment for a Naval Ship by Using BV-043. The Korean Society of Mechanical Engineers, 1361-1366.
Simulia. (2018). Abaqus User Manual, Providence, RI. Dassault Systemes Simulia Corp.
Smallwood, DO. (1980). An Improved Recursive Formula for Calculating Shock Response Spectra. Shock and Vibration Bulletin, 51(2), 211-217.