수직축 조류 터빈 발전효율 평가를 위한 유동-터빈 연동 CFD 해석 (II)
Flow-Turbine Interaction CFD Analysis for Performance Evaluation of Vertical Axis Tidal Current Turbines (II)
Article information
Trans Abstract
CFD (computational fluid dynamics) analyses that considered the dynamic interaction effects between the flow and a turbine were performed to evaluate the power output characteristics of two representative vertical‐axis tidal‐current turbines: an H‐type Darrieus turbine and Gorlov helical turbine (GHT). For this purpose, a commercial CFD code, Star‐CCM+, was utilized, and the power output characteristic were investigated in relation to the scale ratio using the relation between the Reynolds number and the lift‐to‐drag ratio. It was found that the power coefficients were significantly reduced when the scaled model turbine was used, especially when the Reynolds number was lower than 105. The power output characteristics of GHT in relation to the twisting angle were also investigated using a three‐dimensional CFD analysis, and it was found that the power coefficient was maximized for the case of a Darrieus turbine, i.e., a twisting angle of 0°, and the torque pulsation ratio was minimized when the blade covered 360° for the case of a turbine with a twisting angle of 120°.
1. 서 론
최근 해양 신재생 에너지 개발에 대한 관심이 증가하면서 해수가 가지고 있는 위치 에너지를 이용하는 조력발전과 함께 빠른 유속을 가진 조류의 운동 에너지를 이용하고자 하는 조류발전에 대한 연구개발이 활발히 진행되고 있다. 조류발전에 대한 국내의 연구개발은 조류 에너지 부존량 조사를 비롯하여, 부유식 수평축 조류발전 시스템 개발(Kim et al., 2012), 울돌목 시험조류발전소건설(KORDI, 2011) 등의 주요한 연구개발 사업으로 이어져 왔다. 한편 조류발전과 관련된 연구단계는 우리나라를 비롯하여 영국 등 주요 국가에서도 이미 R&D(연구개발) 단계를 거쳐 R&D&D(연구-개발-실증)의 단계에 있는 것으로 알려져 있다. 앞으로는 경제성 확보를 통한 실용화 및 보급이 가능한 연구를 위하여 시스템 효율 개선 및 실제 적용에 관한 연구가 필요한 시점이라 할 수 있다.
조류발전 시스템은 바람이 가지고 있는 운동 에너지를 이용하는 풍력발전 시스템과 유사하게 구성되며, 가장 기본적인 구성 모듈은 조류의 운동 에너지를 효율적으로 추출하는 조류발전 터빈이다. 조류발전 터빈의 가장 대표적인 형태로 수평축 터빈(Horizontal axis tidal current turbine)이 있으며, 최근 국내에서는 수직축 조류발전 터빈(Vertical axis tidal current turbine)에 대한 연구가 비교적 활발히 진행되고 있다(Jung et al., 2009; Hyun et al., 2012). 터빈의 성능평가와 관련된 연구는 수치 시뮬레이션에 의한 연구와 축소 모형을 이용한 연구를 통하여 수행할 수 있다.
이 연구에서는 축소 모형을 이용한 발전효율 특성 평가와 관련 하여 실제 축소 모형 실험에서 사용되는 규모의 터빈을 수치 시뮬 레이션을 통하여 분석하였다. 즉 상용화 규모의 표준 터빈에 대하 여 이를 1/9과 1/25로 축소한 경우 발전효율 특성이 어떻게 평가 되는지를 분석하였다. 그리고 3차원 수치 시뮬레이션을 통하여 터빈 날개(Blade)가 직선형(Straight)인 H형 다리우스 터빈과 날개 를 일정한 각도로 비틀어 토크의 변동(Ripple 또는 Pulsation) 폭을 개선한 고로프 헬리컬 터빈(Gorlov helical turbine, GHT)의 효율을 비틀림각에 따라 평가하여 H형 다리우스 터빈과 헬리컬 터빈의 성능을 비교 분석하였다.
기존의 수치 시뮬레이션에서는 주로 터빈을 포함한 회전 영역과 나머지 고정 해석 영역을 나누고, 일정한 유입속도로 들어오는 유동 조건 하에 터빈을 강제로 회전시켜 이때 발생하는 토크를 계산하고, 출력계수(Power coefficient)를 산정하고 있다(Jung et al., 2009; Hyun et al., 2012). 그러나 실제 조류발전 터빈의 경우 유입되는 유동의 힘에 의하여 터빈이 회전하기 시작하고, 또한 관성모멘트로 인한 특성이 있으므로 이러한 물리적 현상을 고려하기 위하여 유동과 터빈 간의 상호작용을 고려할 수 있는 STARCCM+코드를 이용하여 조류발전 터빈의 효율특성 곡선을 분석하였다. STAR-CCM+의 기본적인 이론 등은 본 논문의 동반 논문을 참조할 수 있다(Yi et al., 2013).
2. 축소 모형 터빈에 대한 발전효율 특성 평가
2.1 모형 터빈 개요
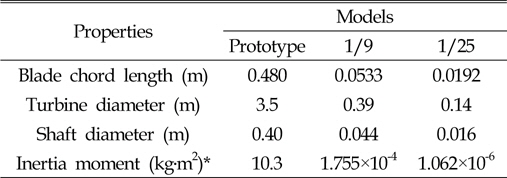
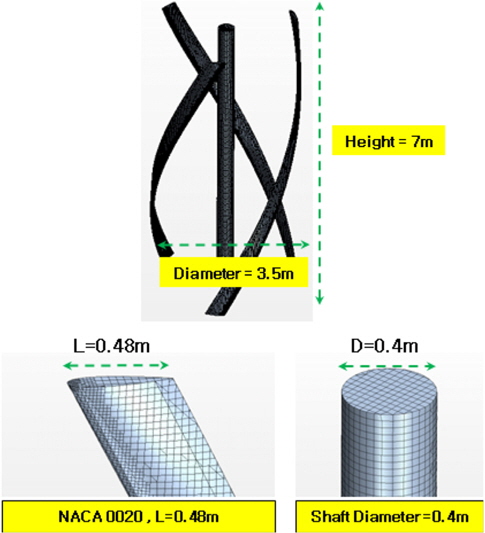
축소 모형 터빈에 대한 발전효율 특성을 분석하기 위하여 고려한 터빈은 수직축 조류발전 터빈의 대표적 형태인 H형 다리우스 터빈으로, 2차원 해석을 통하여 축소 비율에 따른 최적 주속비(Optimal tip speed ratio) 및 출력계수 등을 분석하였다. 이 연구에서 사용된 터빈의 직경은 3.5m이며, 날개 단면의 익형(Airfoil)은 상하대칭의 NACA0020, 그리고 날개의 시위길이(Chord length)는 0.48m, 날개 받음각(Angle of attack)은 0°로 고려하였다. 이러한 조건에서의 터빈 솔리디티(Solidity)는 0.131이다. 표준 모형과 1/9, 1/25 축소 모형에 대한 수치 시뮬레이션을 위한 제원은 Table 1과 같다.
2.2 경계 조건 및 해석 격자
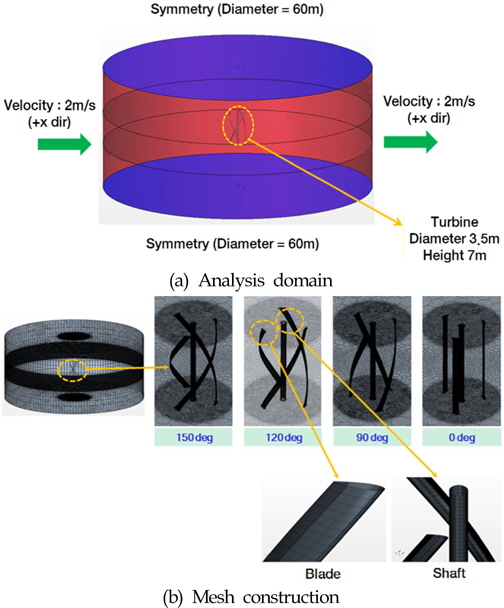
조류발전 터빈의 수치 시뮬레이션을 위한 해석 영역은 동반 논문에서와 동일하게 유동 방향으로는 터빈 직경의 20배 이상으로, 유동 직각방향으로는 터빈 직경의 10배 이상으로 적용하였다. 축소 모형 터빈의 경우 축소비에 따라 해석 영역을 줄여 나갔으며, 표준 터빈과 축소 모형 터빈에 대한 해석 시 사용된 격자는 다면체 격자(Polyhedral mesh)로서 세 가지 경우 모두 약 8만 5천개의 격자가 사용되었다. 즉, 축소 모형의 경우 격자의 크기가 축소비율만큼 줄어든 격자를 사용하였다. 해석 격자의 경우, 날개와 회전축 주위에서는 상대적으로 조밀한 격자를 사용하였으며, 특히 복잡한 유동이 발생할 것으로 예상되는 날개 끝단에서는 더욱 조밀한 격자를 사용하였다. 경계조건은 동반 논문에서와 동일하게 일정 속도를 갖는 유입 조건(Velocity inlet condition), 일정한 압력으로 나가는 출구 조건(Pressure outlet condition), 그리고 좌우면 및 상하면 경계는 대칭(Symmetry) 조건으로 설정하였다.
표준 터빈에 대한 유동 조건(Flow condition)으로는 아래의 Table 2와 같이 조류 유속을 1, 3, 5m/s로 고려하였고, 해석은 전술한 바와 같이 유동에 의한 터빈의 회전을 유발할 수 있도록 유동과 터빈 상호작용을 고려한 CFD 해석을 수행하였다. 표 2에서 r 은 축소비이다. 한편 축소 모형 터빈에 대해서는 레이놀즈 상사(Reynolds similarity)를 만족시키기 위해서는 조류 유속을 축소비의 역수로 더 빠른 유속의 흐름을 적용시켜야 하나 실제 수리모형실험을 고려할 때 펌프 용량 등으로 인하여 이러한 조건을 만족시키기 어려우며, 또한 터빈에 작용하는 하중 측면에서 본다면 프루드(Froude) 상사를 사용하는 것이 가능하므로 조류의 유속은 표준 모형에 적용한 유속에 대하여 축소비의 제곱근에 해당하는 값을 고려하였다. 다만 표준 터빈의 경우에는 조류 유속을 1, 3, 5m/s로 고려하였지만, 축소 모형 터빈의 경우 기본 유속을 2m/s과 3m/s의 두 가지만을 고려하였다.
2.3 해석결과 및 분석
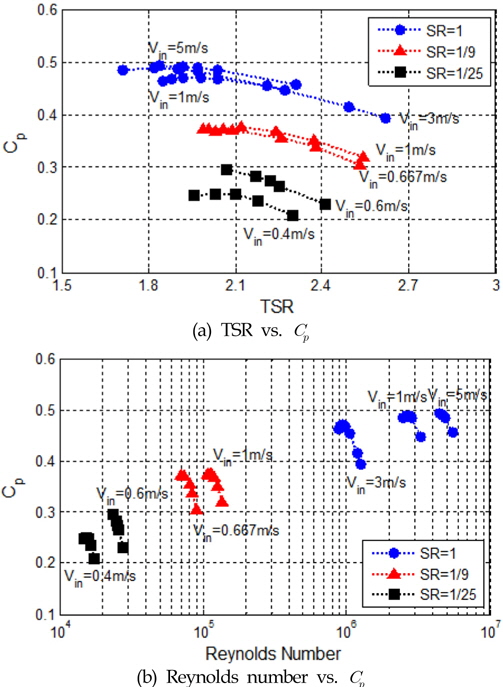
동반 논문에서와 같이 일정한 유입속도와 일정한 외부 토크를 고려하면 해당 조건에서의 토크와 각속도(Angular speed)를 구할 수 있고, 이로부터 출력계수( Cp )를 평가할 수 있다. 일정한 유입속도에서 외부 토크를 변화시켜가면서 여러 주속비(tip speed ratio, TSR)에 따른 Cp 를 구함으로써 터빈의 발전효율 특성곡선(TSR-Cp 곡선)을 구할 수 있다. 이러한 발전효율 특성곡선은 유입속도가 1m/s, 3m/s, 그리고 5m/s인 경우에 대하여 각각 구할 수 있으며, 또한 축소 터빈에 대해서도 동일하게 구할 수 있다. Fig. 1은 표준 모형 및 축소 모형에 대하여 여러 유속 조건에서의 발전효율 특성곡선을 제시한 것으로, 유입속도에 따라, 그리고 축소 비율에 따라 서로 다른 발전 효율곡선이 나타남을 알 수 있다.
Fig. 1을 통하여 표준 모형의 경우 출력계수가 가장 크게 평가됨을 알 수 있고, 또한 표준 모형의 경우에도 유입속도가 증가할수록 최대효율이 증가하는 것을 알 수 있다. 한편 최적 주속비를 살펴보면, 유속 1m/s에서는 1.98, 그리고 유속 3m/s와 5m/s에서는 거의 동일하게 1.84임을 알 수 있었다.
한편 축소 터빈의 경우 최적 주속비가 표준 터빈의 최적 주속비와 달리 평가되며, 특히 효율이 크게 감소되는 것을 알 수 있다. 이는 날개 형상이 일정한 경우 양력과 항력이 레이놀즈 수의 함수로 나타나기 때문이다. 즉, 유속과 날개의 치수가 작은 경우 레이놀즈 수가 작아지고, 양력과 항력의 비, 즉 양항비(Liftto-drag ratio)가 크게 변하게 된다. Fig. 2는 레이놀즈 수에 따른 양항비 및 양력 계수(Lift coefficient)를 나타낸 것으로 조류 터빈과 같은 매끈한 형상을 가진 익형(Smooth airfoil)의 경우 레이놀즈 수가 105 보다 큰 경우 거친 형상을 가진 익형(Rough airfoil)에 비하여 양항비가 큰 것을 알 수 있다. 이는 곧 양력을 이용하여 유체가 가진 에너지를 흡수하는 조류발전 터빈이나 풍력발전 터빈의 경우 레이놀즈 수가 최소한 105 보다 커야 항력을 줄이고, 양력을 증가시켜 에너지 효율을 높일 수 있음을 나타낸다. 그리고 레이놀즈 수가 증가할수록 그 비율이 점차 증가하기 때문에 에너지 효율을 더 높일 수 있는 것이다.
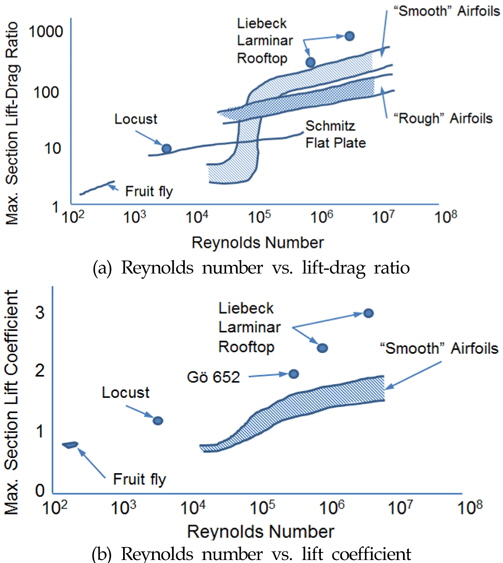
Lift and drag ratio and lift coefficients wih respect to Reynolds number (Kroo, 2007)
일반적인 MW급 풍력발전 터빈의 경우 최적 주속비가 8 부근이며, 발전 시 정격 풍속(Rated wind speed)(V )을 8m/s로, 날개 끝단에서의 시위길이(D )를 0.5m로, 그리고 상온에서 공기 동점성계수(v)를 0.156 ×10- 4m2/s로 고려할 때 레이놀즈 수는 Re = VD/v=2.05×106과 같이 구할 수 있으며, 따라서 레이놀즈 수가 2×106으로 양력이 항력보다 100배 이상 큰 상태임을 알 수 있다. 한편 표준 조류발전 터빈의 경우 최적 주속비가 2 부근임을 고려하여 레이놀즈 수를 계산하면 2.88×106로 풍력발전 터빈의 경우와 마찬가지로 106 보다 커 유체의 에너지를 효과적으로 이용할 수 있음을 알 수 있다. 그러나 동일한 방법으로 1/9 축소 터빈에 대하여 레이놀즈 수를 계산하면, 그 값은 1.07×105이 되며, 1/25 축소 터빈의 경우 레이놀즈 수는 2.3×104이 되어 양항비가 감소되고, 특히 1/25 축소 모형의 경우 그 비율이 급격히 감소된 구간에 있음을 알 수 있다. 이와 같이 레이놀즈 수를 고려하여 축소 터빈의 경우 출력계수가 작게 평가되는 이유을 설명할 수 있다. 한편 1/9 축소 터빈의 경우 양항비가 급격하게 변하는 천이(Transition) 구간에 있기 때문에 실험 조건에 따라서는 발전효율이 표준 터빈과 유사하게 나올 수 있으나 조건에 따라서는 효율이 매우 낮게 나올 수 있는 불안정한 상태임을 알 수 있다.
따라서 축소 모형을 이용하여 터빈의 발전효율 특성을 평가하는 경우 충분한 레이놀즈 수를 갖도록 해야 하는데, 이를 위해서는 (1) 솔리디티를 증가시키거나, (2) 유속을 증가시킬 수 있다. 후자의 경우 회류수조(Circulation water tank)의 펌프 용량 등으로 적용이 어려울 수 있으며 따라서 고속예인수조(High-speed towing tank)를 사용하는 것이 가능할 것이다(Li and Calisala 2010). 그러나 유속을 축소비의 역수로 증가시키는 경우 최적 주속비를 유지하기 위하여 각속도 또한 높게 증가되며, 따라서 기계적인 마찰이나 소음을 비롯하여 다양한 부분을 고려하여야 할 것이다. 한편 솔리디티를 증가시키는 전자의 방법에도 레이놀즈 수를 증가시켜 양력 계수를 높이고, 또 단면을 넓혀 양력 자체가 커져 효과적일 수 있지만 실제 발전에 사용되는 터빈의 경우 발전효율을 높이기 위하여 솔리디티를 어느 정도 수준으로 유지하는 것이 필요하며, 따라서 실제 터빈의 효율을 평가하는 데에는 제한적일 수 있다. Shiono et al.(2000)의 연구에서도 축소 터빈을 이용하여 실험을 하였기 때문에 실제 터빈의 솔리디티로는 사용하기 어려운 솔리디티 0.366의 터빈을 적용한 바 있다. 한편 회류수조를 사용하는 실험의 경우 모형의 크기를 키우기 위하여 축소비를 작게 하는 경우가 있는데, 이러한 경우 유동이 터빈으로 인하여 방해를 받게 되어 차단 효과(Blockage effect)가 발생한다. 따라서 실제 조건과 다른 관유동(Pipe flow)의 효과로 인하여 실제 해역에서의 발전 효율을 평가하는 데에는 어려움이 있고, 단지 다양한 형태의 터빈에 대한 상대적인 효율 비교는 가능할 것이다.
3. 비틀림각에 따른 헬리컬 터빈의 발전효율 특성
3.1 모형 터빈 개요
양력을 이용하는 수직축 조류발전 터빈 중 가장 대표적인 터빈이 H형 다리우스 터빈이며, 이러한 다리우스 터빈의 경우 위상에 따른 토크의 크기가 상대적으로 다르고 또한 특정한 위상에서는 음의 토크가 발생하여 자기 기동(Self-starting) 특성이 불량해질 수 있다. 또한 발전 중에도 토크 변동(Torque ripple 또는 Torque pulsation)이 발생하여 구조적인 피로를 발생시킬 수 있는 단점이 있다. 이러한 다리우스의 단점을 보완하기 위하여 개발된 것이 고로프 헬리컬 터빈(Gorlov helical turbine, GHT)이다(Gorlov, 1995). GHT는 Fig. 3에서와 같이 날개를 일정한 각도로 비틀어 다리우스 터빈이 가지는 토크 변동성과 자가 기동의 문제를 해결한 터빈이다. 이 연구에서는 이러한 GHT의 발전 효율특성과 토크 변동성 등을 평가하기 위하여 3차원 수치 시뮬레이션을 수행하였다. 터빈의 높이와 직경, 날개 형상 등은 2차원 수치 시뮬레이션에서 사용한 표준 터빈과 동일하며, 날개의 비틀림각을 0°, 90°, 120°, 150°로 증가시켜가면서 그 특성을 분석하였다. 이때 터빈의 높이는 7m이며, 관성모멘트는 7269kgm²이다. 비틀림각은 회전축의 중심에서 볼 때 날개의 시작과 끝이 이루는 각도로, 다리우스 터빈의 비틀림각은 0°이다.
3.2 해석 영역 및 해석 격자
3차원 시뮬레이션을 위한 해석영역은 다음 그림과 같이 직경 60m, 높이 27m의 원통형으로 해석영역을 고려하였으며, 유입 속도와 유출 속도가 동일한 것으로 고려하였다. 한편 격자계는 다음과 같이 터빈 주변, 특히 상단과 하단에서의 흐름을 합리적으로 모사하기 위하여 매우 작은 격자를 사용하였으며, 사용된 격자는 다면체 격자로 약 290만개의 격자를 사용하였다. 해석 시 난류 모델로는 Realizable k-𝜖, Two-layer all y+ 모델을 사용하였고, 해석 시 내부 수렴횟수는 10~20번으로 내재적 비정상 상태의 계산을 수행하였다.
3.3 해석 결과 및 분석
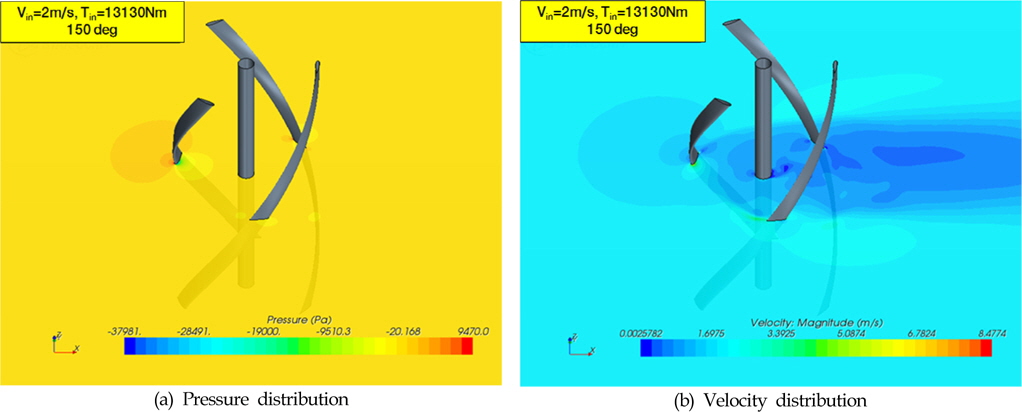
다음의 Fig. 5는 비틀림각이 150°인 경우 터빈 주변에서의 압력과 유속 분포를 나타낸 것이다. 전연부(Leading edge)에서 높은 압력이 발생하고 있으며, 상류측 날개에 의한 후류(Wake)가 발생하는 것을 알 수 있다.
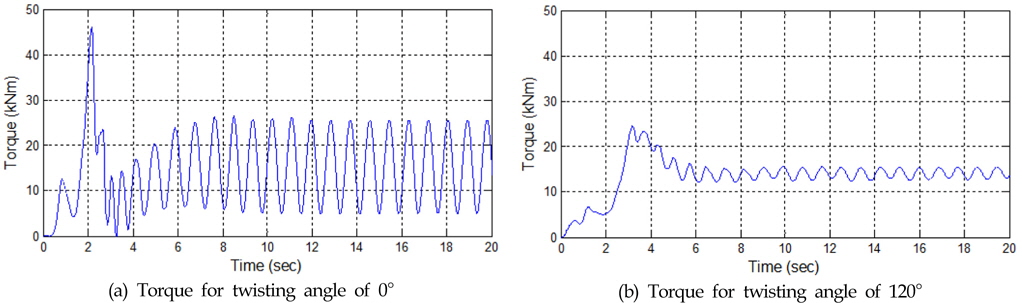
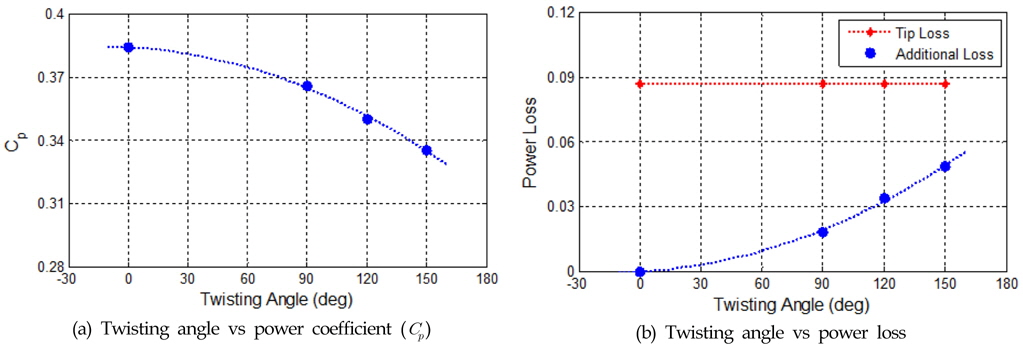
Fig. 6은 비틀림각이 0°와 120°인 터빈에 대하여 발생된 토크를 제시한 것이다. 비틀림각이 큰 경우 토크 변동량이 크게 감소하고, 순간 최대 토크 역시 크게 감소하는 것을 알 수 있다. 한편 Fig. 7은 유속 2m/s, 솔리디티가 0.131에서 최고효율을 나타내는 최적 주속비 부근에서의 비틀림각에 따른 최대 출력계수를 비교한 것이다. 비틀림각이 0°에서 90°, 120°, 150°로 증가할수록 출력계수는 38.4%, 36.5%, 35.0%, 33.5%로 감소하는 것을 알 수 있다. 즉, 다리우스 터빈의 효율이 가장 높은 것을 알 수 있다. 2차원 해석의 경우 날개 끝단에서의 손실(Tip loss)을 고려하지 못하지만 3차원 해석의 경우 이를 고려할 수 있다. 3차원 해석에서 비틀림각에 따른 끝단 손실이 없다고 가정할 때 끝단에서의 손실은 모두 9% 정도이며, 비틀림각이 증가할 때 추가적으로 발생하는 손실은 유체가 날개 방향으로 일부 분산되어 발생하는 효율의 손실이라고 판단할 수 있으며 이는 Fig. 7(b)에서와 같이 비틀림각에 따라 5% 정도까지 발생함을 알 수 있다.
한편 Fig. 8은 터빈의 비틀림각에 따른 터빈 각속도와 토크의 변동율(Ripple ratio 또는 Pulsation ratio)을 정리한 것이다. 각 속도의 경우 비틀림각이 0°인 경우, 변동율이 18 % 내외로 가장 크고, 120°이상인 경우 이러한 변동율이 5 % 내외로 크게 감소하는 것을 볼 수 있다. 또한 토크의 경우에는 비틀림각이 0°인 경우 변동율이 130 %로 매우 큰 토크 변동이 발생하나, 비틀림각이 120° 이상인 경우, 20 % 내로 크게 감소하게 된다. 즉, 터빈 날개가 360°이상의 영역을 모두 포함하게 되는 경우 위상에 따른 영향이 크게 감소하는 것을 알 수 있다. 이와 같은 결과는 발전 효율과 관련된 출력계수는 다리우스 터빈이 더 크게 나오며, 토크의 변동 측면에서는 헬리컬 터빈이 더 우수하다는 기존 Shiono et al.(2000)의 실험 연구결과와 동일하다.
4. 결 론
이 연구에서는 유동과 터빈 사이의 상호작용을 고려한 수치 시뮬레이션을 수행하여, 유동에 의하여 터빈이 회전하기 시작하고, 또한 외부 하중에 의한 발전 상태까지를 모사하여 수직축 조류발전 터빈의 효율특성을 분석하였다. 축소 모형 터빈에 대한 재원을 이용하여 축소 모형을 이용한 경우의 발전효율 특성을 레이놀즈 수 등과 비교하여 분석하였고, 또한 3차원 해석을 수행하여 헬리컬 터빈의 날개 비틀림각에 따른 발전효율을 비교하였다. 이 연구의 결과를 다음과 같이 간략히 정리하였다.
(1) 터빈의 출력계수는 최적 주속비에서 가장 크게 산정되며, 이러한 최적 주속비는 솔리디티 외에 레이놀즈 수에 의하여 큰 영향을 받는다.
(2) 매끈한 익형의 경우 레이놀즈 수가 105 보다 큰 경우 높은 양항비를 갖기 때문에 이러한 조건에서 높은 출력계수를 가질 수 있다. 그러나 축소 터빈에서와 같이 치수가 작은 경우 레이놀즈 수가 감소되고, 그 값이 105 보다 작은 경우에는 출력이 크게 감소되는 것을 알 수 있었다.
(3) 헬리컬 터빈의 비틀림각이 증가할수록 터빈의 최대 출력계수는 5%까지 감소하며, 토크의 변동량 역시 크게 감소하게 된다. 출력계수의 감소는 비틀림각이 증가할수록 유동이 날개 방향으로 분산되는 효과 때문인 것으로 사료되며, 토크의 변동량 감소는 날개가 360°의 모든 위상에서 동일한 조건을 갖는 120°의 비틀림각을 가질 때까지 지속적으로 감소한다.
Acknowledgements
본 연구는 한국해양과학기술원 주요사업(PE98943)과 국토해양부 한국해양과학기술진흥원의 "능동제어형 조류발전 기술 개발" 연구사업 연구결과 중 일부임을 밝히며, 연구비 지원에 감사드립니다.
References
Gorlov, A.M., 1995. The Helical Turbine: a New Idea for Lowhead Hydropower. Hydro Rev., 14(5) 44-50.
Gorlov A.M.. The Helical Turbine: a New Idea for Lowhead Hydropower. Hydro Rev. 1995;14(5):44–50.Hyun, B.S., Choi, D.H., Han, J.S., Jin, J.Y., 2012. Performance Analysis and Design of Vertical Axis Tidal Stream Turbine. Journal of Shipping and Ocean Engineering, 2, 191-200.
Hyun B.S., Choi D.H., Han J.S., Jin J.Y.. Performance Analysis and Design of Vertical Axis Tidal Stream Turbine. Journal of Shipping and Ocean Engineering 2012;2:191–200.Jung, H.J., Rhee, S.H., Song, M., Hyun, B.S., 2009. A Numerical Study of Unsteady Flow around a Vertical Axis Turbine for Tidal Current Energy Conversion. Journal of the Korean Society for Marine Environmental Engineering, 12(1), 9-14.
Jung H.J., Rhee S.H., Song M., Hyun B.S.. A Numerical Study of Unsteady Flow around a Vertical Axis Turbine for Tidal Current Energy Conversion. Journal of the Korean Society for Marine Environmental Engineering 2009;12(1):9–14.Kim, J.M., Han, D.H. Chung, H., 2012, Field test for 100kW floating tidal power system. Proceedings of the Asian Wave and Tidal Energy Conference 2012.
Kim J.M., Han D.H., Chung H.. Field test for 100kW floating tidal power system In : Proceedings of the Asian Wave and Tidal Energy Conference 2012; 2012.Korea Ocean Research and Development Institute (KORDI), 2011. Development of Utilization Technique for Tide and Tidal Current Energy. Final Report Submitted to the Ministry of Land, Transport and Maritime Affairs.
Development of Utilization Technique for Tide and Tidal Current Energy, Final Report Submitted to the Ministry of Land, Transport and Maritime Affairs 2011.Kroo, I., 2007. Applied Aerodynamics:A Digital Textbook. Desktop Aeronautics, Inc.
Kroo I.. Applied Aerodynamics:A Digital Textbook Desktop Aeronautics, Inc.; 2007.Li, Y., Calisala, S.M., 2010. Modeling of Twin-turbine Systems with Vertical Axis Tidal Current Turbines: Part I-Power output. Ocean Engineering, 37(7), 627-637
. Li Y., Calisala S.M.. Modeling of Twin-turbine Systems with Vertical Axis Tidal Current Turbines: Part I-Power output. Ocean Engineering 2010;37(7):627–637. 10.1016/j.oceaneng.2010.01.006.Shiono, M., Suzuki, K., Kiho, S., 2000. An Experimental Study of the Characteristics of a Darrieus Turbine for Tidal Power Generation. Electronic Engineering in Japan, 132(3), 781-787.
Shiono M., Suzuki K., Kiho S.. An Experimental Study of the Characteristics of a Darrieus Turbine for Tidal Power Generation. Electronic Engineering in Japan 2000;132(3):781–787.Yi, J.-H., Oh, S.-H., Park, J.-S., Lee, K.-S., Lee, S.-Y., 2013. Flow- Turbine Interaction CFD Analysis for Performance Evaluation of Vertical Axis Tidal Current Turbines (I). Journal of Ocean Engineering and Technology, 27(3), 67-72.
Yi J.-H., Oh S.-H., Park J.-S., Lee K.-S., Lee S.-Y.. Flow- Turbine Interaction CFD Analysis for Performance Evaluation of Vertical Axis Tidal Current Turbines (I). Journal of Ocean Engineering and Technology 2013;27(3):67–72.