Fault Classification of a Blade Pitch System in a Floating Wind Turbine Based on a Recurrent Neural Network
Article information
Abstract
This paper describes a recurrent neural network (RNN) for the fault classification of a blade pitch system of a spar-type floating wind turbine. An artificial neural network (ANN) can effectively recognize multiple faults of a system and build a training model with training data for decision-making. The ANN comprises an encoder and a decoder. The encoder uses a gated recurrent unit, which is a recurrent neural network, for dimensionality reduction of the input data. The decoder uses a multilayer perceptron (MLP) for diagnosis decision-making. To create data, we use a wind turbine simulator that enables fully coupled nonlinear time-domain numerical simulations of offshore wind turbines considering six fault types including biases and fixed outputs in pitch sensors and excessive friction, slit lock, incorrect voltage, and short circuits in actuators. The input data are time-series data collected by two sensors and two control inputs under the condition that of one fault of the six types occurs. A gated recurrent unit (GRU) that is one of the RNNs classifies the suggested faults of the blade pitch system. The performance of fault classification based on the gate recurrent unit is evaluated by a test procedure, and the results indicate that the proposed scheme works effectively. The proposed ANN shows a 1.4% improvement in its performance compared to an MLP-based approach.
1. Introduction
Offshore wind turbines are prone to unexpected faults as they are often operated in a harsher environments compared to turbines on land. Accordingly, there has been a growing interest toward developing technologies for detecting and diagnosing faults in advance for the effective maintenance and operation of these turbines. Unexpected faults influence system components, actuators, sensors, and controllers, which may result in the inoperability of a turbine in case of serious failures. Moreover, faults can lead to economic losses by inducing changes in the system characteristics, operation safety, and power efficiency of a wind turbine. Maintenance costs account for approximately 25%–30% of the life-cycle cost of an offshore wind power plant (Dinwoodie et al., 2013), and therefore, the reliability of such a wind turbine is critical.
Among the components of an offshore turbine, the blade pitch system has the highest downtime and failure rate (Gayo, 2011; Carroll et al., 2016; NordzeeWind, 2010). A system fault affects the aerodynamic loads of a blade, the power generation output, and the behavior of substructures. Therefore, it is crucial to diagnose faults at the early stage in a blade pitch system to protect a turbine and prevent downtime of the entire system (Cho et al., 2018). Early fault diagnosis can reduce risks and prevent accidents by raising alarms at appropriate times, thus enabling wind power plant operators to effectively operate and maintain a turbine (Isermann, 2006). It can also prevent long-term damage to turbines and provide a reliable technological guarantee for the further development of the wind power generation industry.
Up to recently, classical fault diagnosis methods with statistical classification, approximation methods, and density-based methods has been used. Deep learning methods, which are a type of machine learning algorithm, have emerged in recent years; they have been used for learning or training the complex structures of an actual large-scale dataset continuously collected by sensors in various applications including computer vision, object classification, voice recognition, natural language processing, and robots (Wason, 2018).
A method for diagnosing faults through a series of measurement data can be learned by applying a deep learning algorithm. When diagnosing faults in the components of a wind turbine, a machine learning-based method can detect state changes of a system. Such machine learning methods include wavelet analysis, Support vector machines (SVN), Bayesian networks, and artificial neural networks (ANNs) (Blanke et al., 2006). Faults have been detected and diagnosed using support vector machines (Santos et al., 2015; Zeng et al., 2013; Laouti et al., 2011) and fuzzy clustering methods (Badihi et al., 2014; Simani et al., 2014) based on data collected by various sensors such as force sensors, accelerometers, speed sensors, and tower tops located on the blade route as well as the generator of wind turbine control systems.
In particular, researchers have used use neural network theories based on multilayer perceptron (MLP) (Kusiak and Li, 2011; Wang et al., 2016; Zaher et al., 2009; Kusiak and Verma, 2012; Cho et al., 2021), convolutional neural networks (CNNs) (Bach-Andersen et al., 2015; Bach-Andersen et al., 2018), and autoencoders (AEs) (Dervilis et al., 2014; Jiang et al., 2017) in order to develop reliable fault diagnosis systems for the components of wind turbines including the main bearing, gearbox, and generator. In particular, Cho et al. (2021) used an MLP-based ANN technique to perform fault diagnosis of a blade pitch system. This technique is, however, unsuitable for processing time-series data during training, and therefore, a recurrent neural network (RNN) that is apt for processing time-series data is required. Among various RNNs that have been proposed, long-short term memory (LSTM) and gated recurrent unit (GRU) (Cho et al., 2014) techniques are considered to be suitable for processing time-series data as they are capable of linking previous information with the current task during training. The GRU used in this paper exhibits a level of performance similar to that of LSTM networks but can be trained at a faster speed owing to its simple architecture.
For the effective fault diagnosis of a blade pitch system in a floating wind turbine, this paper proposes a fault classification model that employs a GRU-based ANN, which is suitable for processing time-series data. The modeling and control techniques for a wind turbine are detailed in Section 2; the data collection procedure as well as the steps and structure of the proposed method are described in Section 3. In Section 4, the performance of the proposed algorithm is compared with that of conventional MLP models. Future research directions are discussed in the last section.
2. Modeling and Control Method of a Wind Turbine
2.1 Floating Wind Turbine Model
The floating wind turbine model in this paper is designed based on an NREL 5 MW offshore wind turbine, OC3–Hywind floater (spar-type), and three catenary mooring cables, as illustrated in Fig. 1 (Jonkman et al., 2009; Jonkman, 2010).
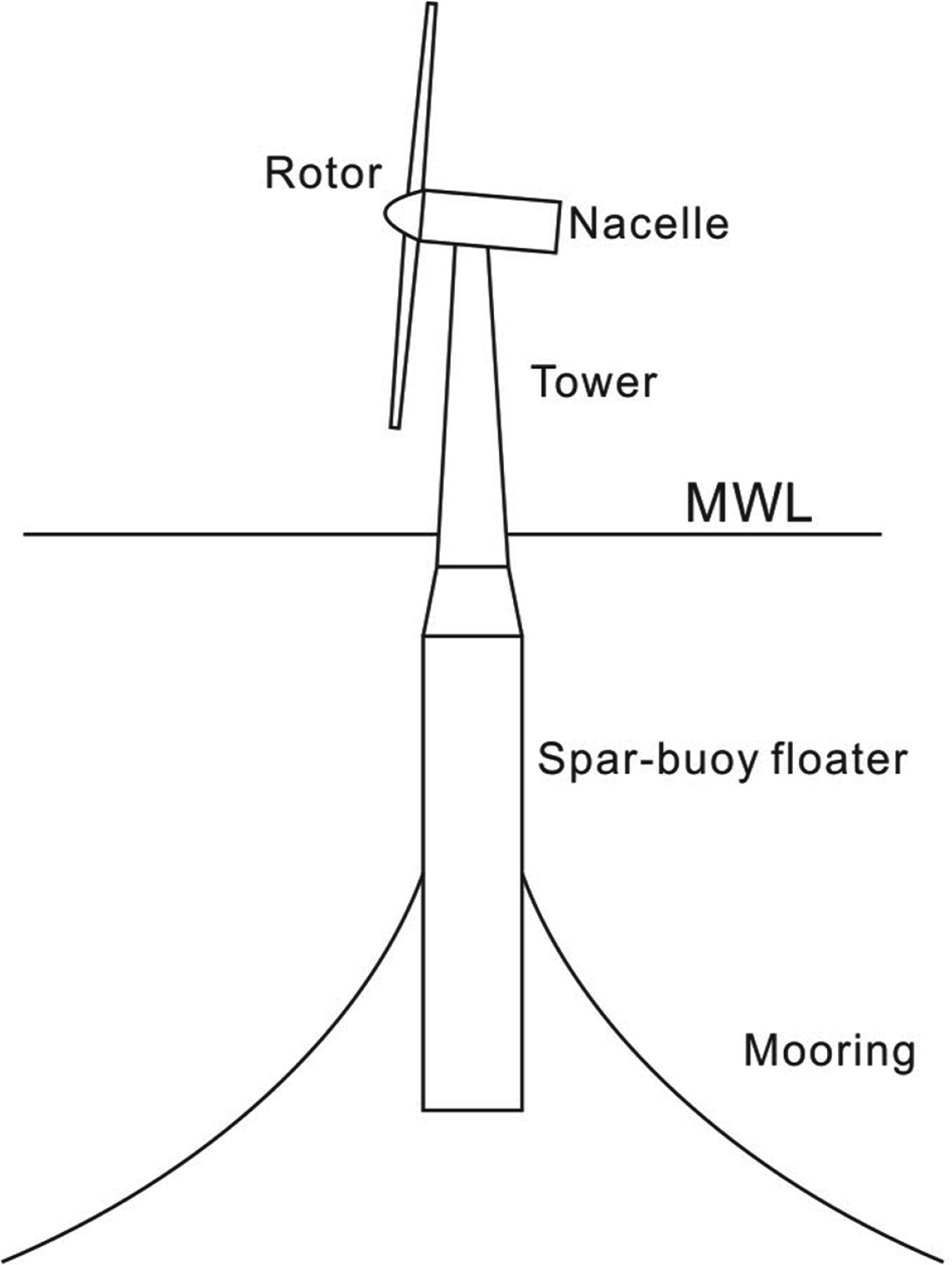
Schematic view of a spar-type floating wind turbine (Cho et al., 2020)
2.2 Hydraulic Blade Pitch System
The hydraulic pitch system has a pump, fluid control valve, fluid reservoir, and a hydraulic cylinder (Cho et al., 2020). The hydraulic cylinder positioned in a turbine hub controls the blade pitch angle. The pump directly operates the cylinder using fluid pressure. The directional control valve effectively adjusts the flow rate and direction of the fluid into the cylinder, thus controlling the blade pitch angle. Fig. 2 shows the blade pitch system that consists of a pump with a certain level of pressure, a hydraulic cylinder, a directional control valve, an accumulator, and a fluid reservoir. In addition, an encoder and a linear variable differential transformer (LVDT) measure the blade pitch angle and valve spool position that are used as input variables of the controller.

Schematic view of a hydraulic blade pitch system (Cho et al., 2020)
2.3 Baseline Control System
The baseline control system comprises a generator torque and blade pitch controller (Cho et al., 2020). In the below-rated wind region, the torque controller regulates the generator torque in order to keep the optimal tip-speed ratio, thus generating the maximum power. The blade pitch controller controls the angle of the blade pitch to lower the aerodynamic forces applied on the blade while generating rated power in the above-rated wind region. A floating wind turbine can improve system response and reduce the motion of a floater by using a wind turbine controller.
The blade pitch angle β is determined by the position of the piston in the hydraulic cylinder xp, based on the geometrical relationship explained in Eq. (1). Fig. 3 shows the geometrical relationship of the blade pitch system.

Geometry of the blade pitch actuator: (a) β = 0° and (b) β = 90° (Cho et al., 2020)
The position of the piston in the cylinder xp is determined by the valve spool position xvs, which is controlled by the control input voltage uvs in Eq. (2). A proportional-integral controller (PI controller) is used in this case, wherein the directional control valve is effectively controlled by calculating the control input voltage uvs after providing feedback on the piston position error e(t), which is expressed using Eq. (3).
Here, kp is the proportional gain and Ti is the integral time. The valve spool position error e(t) is determined by the function of the blade pitch angle β and the blade pitch command βc of the pitch controller, as shown in Fig. 3. Detailed equations of the blade pitch system have been provided in a study by Cho et al. (2020).
2.4 Fully Coupled Numerical Simulation
For the analysis of the dynamic response of a floating wind turbine, Simo-Riflex (SINTEF Ocean, 2018a; SINTEF Ocean, 2018b), an aero-hydro-servo-elastic simulation tool, was used to perform numerical simulations. Simo calculates the fluid dynamic force and moment applied to the substructures based on the potential flow theory and a Morison-type viscous drag force. Riflex performs an structural analysis of the blade, shaft, tower, and mooring system based on the finite element method (FEM). Moreover, Riflex also calculates the aerodynamic force and moment applied to the blade using the blade element momentum (BEM) theory. Thus, Simo-Riflex performs a numerical analysis linking the baseline control system based on structural dynamic, fluid dynamic, and aerodynamic models. Fig. 4 shows the data transmission between Simo-Riflex and the control algorithm.
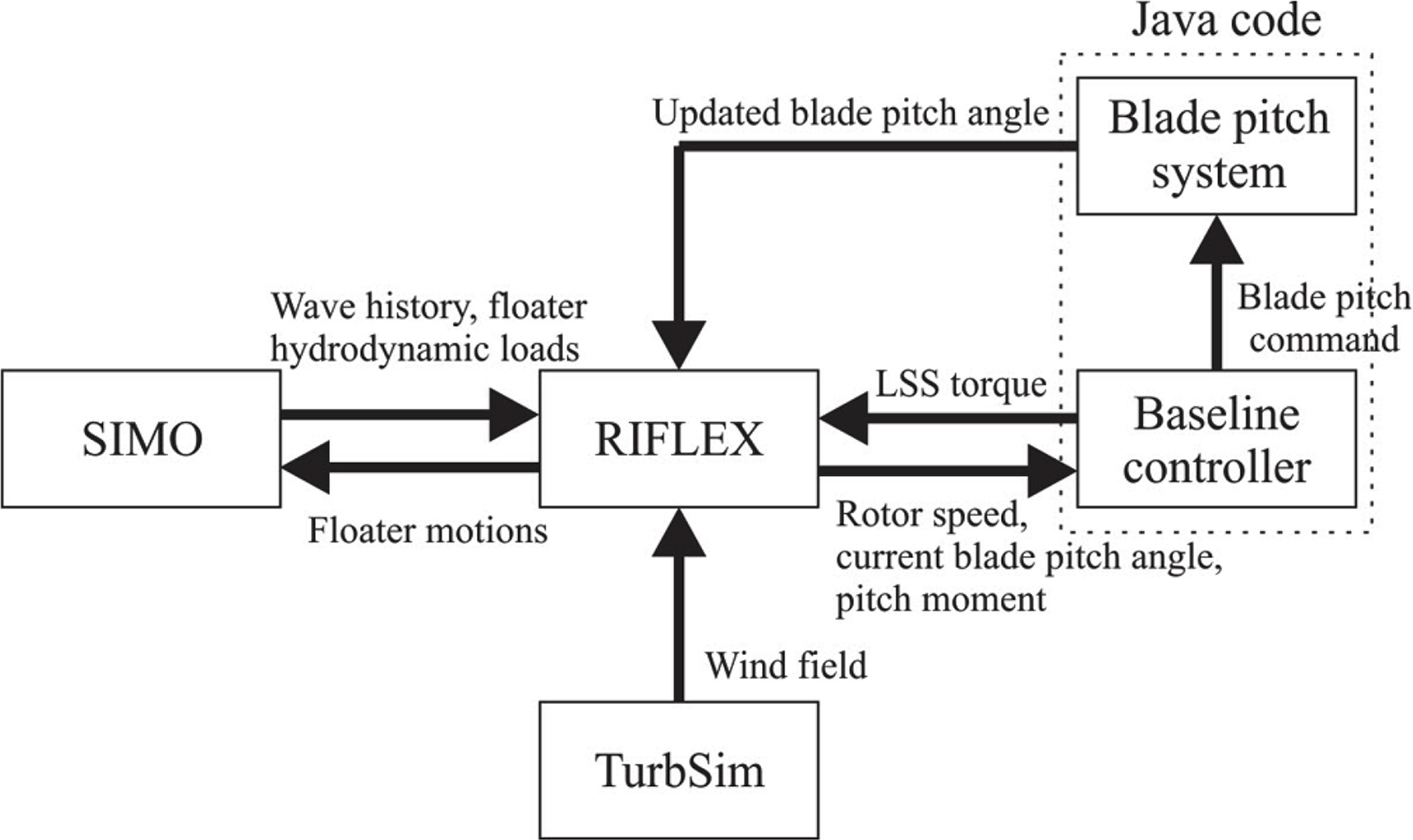
Data transmission between Simo-Riflex and controller (Cho et al., 2020)
Six ocean environmental load cases with related wind and wave conditions for simulations of dynamic responses of a floating wind turbine are presented in Table 1. In terms of wind loads, turbulence modeling was performed using TurbSim (Jonkman and Kilcher, 2012) based on the Kaimal turbulence model according to IEC 61400-1 (IEC, 2005a) and 3 (IEC, 2005b). For irregular wave loads, the JONSWAP spectrum was used (Hasselmann et al., 1973). Peak wave period (Tp) and significant wave height (Hs) were determined based on their correlation with the wind speed of the Statfjord field in the North Sea (Johannessen et al., 2002).
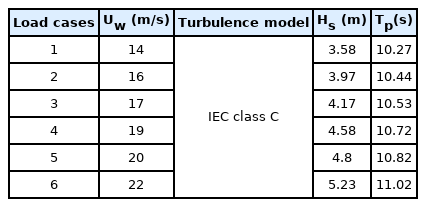
Ocean environmental load cases based on winds and waves (Cho et al., 2021)
3. Fault Classification Method
The first step of fault diagnosis is to discern the actual occurrence of a fault. In general, a model-based or signal-based detection method is used to discern the occurrence of a fault in a system. In particular, a model-based method can detect faults in real time by assessing the system status using a mathematical model. A typical model-based method involves using the Kalman filter often used in various fields such as global positioning systems, computer vision, and computer games. In a study by Cho et al. (2018), the Kalman filter was used to detect sensor and actuator faults of a blade pitch system in a floating wind turbine. If faults are successfully detected, a fault classification technique is required to classify the types of faults. In this paper, fault classification is performed under the assumption that faults are properly detected.
An ANN is used in this paper for classifying the faults of a floating wind turbine. The ANN extracts the features of each fault from the training data and learns their patterns to generate a prediction model, thus accurately classifying six types of faults. The forms of feature extraction for each type of fault are presented in a study by Cho et al. (2021). The proposed ANN consists of an encoder and a decoder and has the structure shown in Fig. 5. The encoder consists of an RNN; it is used to reduce data dimensionality while maintaining the features contained in the information of the input data. The decoder consists of MLPs; it is used to classify faults based on the processed data received from the encoder. More details on the encoder and the decoder are provided in Sections 3.3 and 3.4.
3.1 Fault description of a Hydraulic Blade Pitch System
Faults in a blade pitch system can be classified into sensor and actuator faults. Faults in a sensor or an actuator cause a rotor imbalance and blade asymmetry. With respect to the faults in a pitch actuator, faults related to oil, valve, and sludge constitute a high percent (37.3%) of the total faults of a hydraulic pitch system (Carroll et al., 2016). Furthermore, a fault in the valve of a pitch actuator changes the system characteristics and affect the dynamic responses of a wind turbine in a transient or steady state conditions.
In this paper, six types of faults that occur in a pitch sensor and an actuator of a hydraulic blade pitch system are considered (Cho et al., 2021). Table 2 presents these different types of faults.
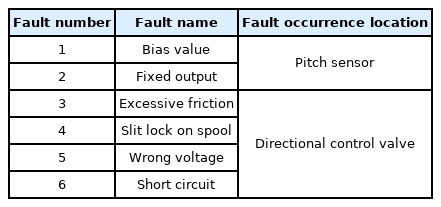
Description of faults (Cho et al., 2021)
Faults in a blade pitch system can be classified into those occurring in a sensor and those occurring in a control valve in an actuator. Among pitch sensor faults, fault 1 refers to the case in which a consistent bias value is observed in a pitch sensor, while fault 2 refers to the case in which one value of a sensor is consistently repeated.
A control valve fault is commonly caused by fluid contamination in a hydraulic actuator or problems in the filter. When excessive sludge is found in a valve spool, the clearance between the valve and spool is reduced, which results in increased frictional force. This is referred to as fault 3. Fault 4 occurs when the valve is locked due to the hardened sludge from fault 3.
Moreover, fault 5 occurs when excessive current is introduced due to a problem in the magnetic field of the valve solenoid, which leads to an incorrect voltage being applied to the solenoid. Fault 6 occurs when the solenoid is burned due to the excessive current. The fault phenomena are explained in detail by Cho et al. (2018) and Cho et al. (2020) using mathematical modeling and figures. The specific characteristics of fault phenomena are reflected in a simulation through mathematical modeling to obtain relevant data, which are then used to train the ANN.
3.2 Data
Fault data are required for training the ANN prior to performing fault classification. Fault data were generated using the Simo-Riflex (SINTEF Ocean, 2018a; SINTEF Ocean, 2018b) simulator. Different fault types (six types as presented in Table 2), ocean environmental load cases (six cases as presented in Table 1), and fault occurrence times (10 values) were combined to perform 360 times of simulations; multiple data were collected during one simulation session by varying the data collection starting time. The fault occurrence time was categorized into 10 values ranging from 75 s to 300 s at intervals of 25 s. A total of 116,330 data points were collected, which were then classified into training data (80,000), validation data (20,000), and test data (16,330). The validation data were used to evaluate the final model recording during training. The test data were used to evaluate the final performance check of the final model. One piece of data consists of data collected during 17 s from a randomly selected observation starting point as shown in Fig. 6. The time step of the simulation Δti was 0.1 s. Four pieces of data were collected per time step; these included including the blade pitch sensor, blade pitch command, valve spool position sensor, and valve control input values, as shown in Fig. 6.
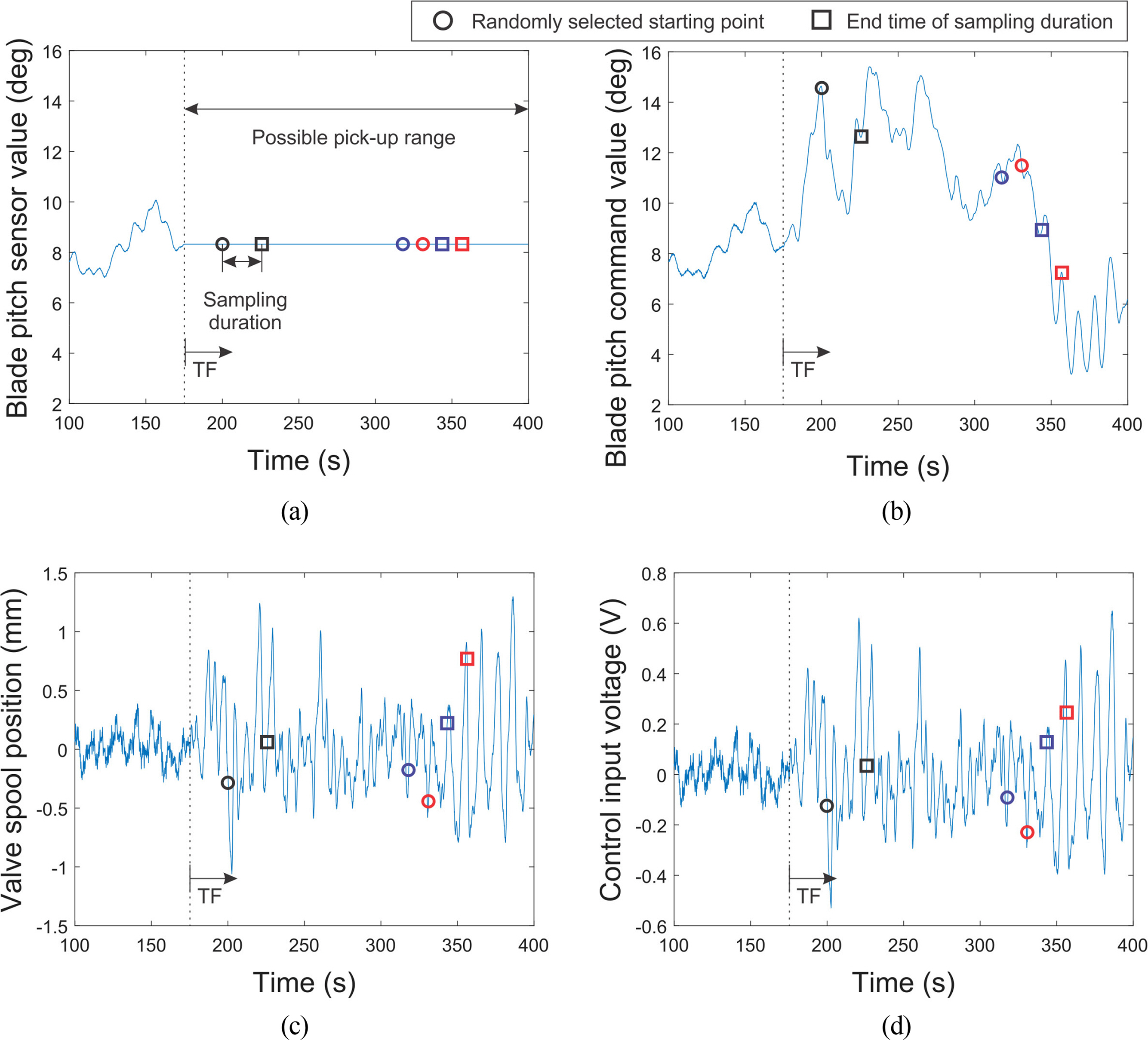
Data sampling processes from simulations: (a) blade pitch sensor value, (b) blade pitch command value, (c) valve spool position, and (d) control input voltage (Cho et al., 2021)
The data were normalized as four different units were included in the data. In this paper, min–max normalization was performed as described in Eq. (4) in which outliers were excluded when determining the minimum and maximum values.
A label was represented with one-hot encoding, where one value is 1 and the remaining values are 0. Considering the labels used in this paper as an example, the data label related to fault type 1 has a vector value of [1 0 0 0 0 0].
One piece of data has a total of 686 values including 680 values collected from four data types ((1) blade pitch sensor value, (2) pitch command value, (3) valve spool position sensor value, and (4) valve control input value) for 17 s at intervals of 0.1 s, and six label values. Fig. 7 shows the constitution of 80,000 pieces of training data set. A GRU was employed by rearranging 680 pieces of data into 4 × 170 arrays.
3.3 Encoder
An encoder uses a GRU having a recursive connection structure and plays a role in reducing data dimensionality while maintaining the major features of time-series data. The GRU responds to the external input value of every time step and gradually updates a hidden state, which is an internal variable. The final hidden state generated preserves only the major features of the continuously input values in a compressed form, thus being capable of representing time-series data effectively. Effective data representation using a GRU reduces the size of the ANN and increases the efficiency of training the model. Eqs. (5)–(8) show the process of updating a hidden state.
Here, ht is the hidden state at time t, whereas xt is the external input value at time t. ht − 1 is the initial hidden state when time t is 0, or the hidden state at time t − 1. Moreover, rt, zt, and nt are the reset, update, and new gates, respectively. σ is the sigmoid function, while * represents the Hadamard product. The above equation can be graphically represented as shown in Fig. 8.
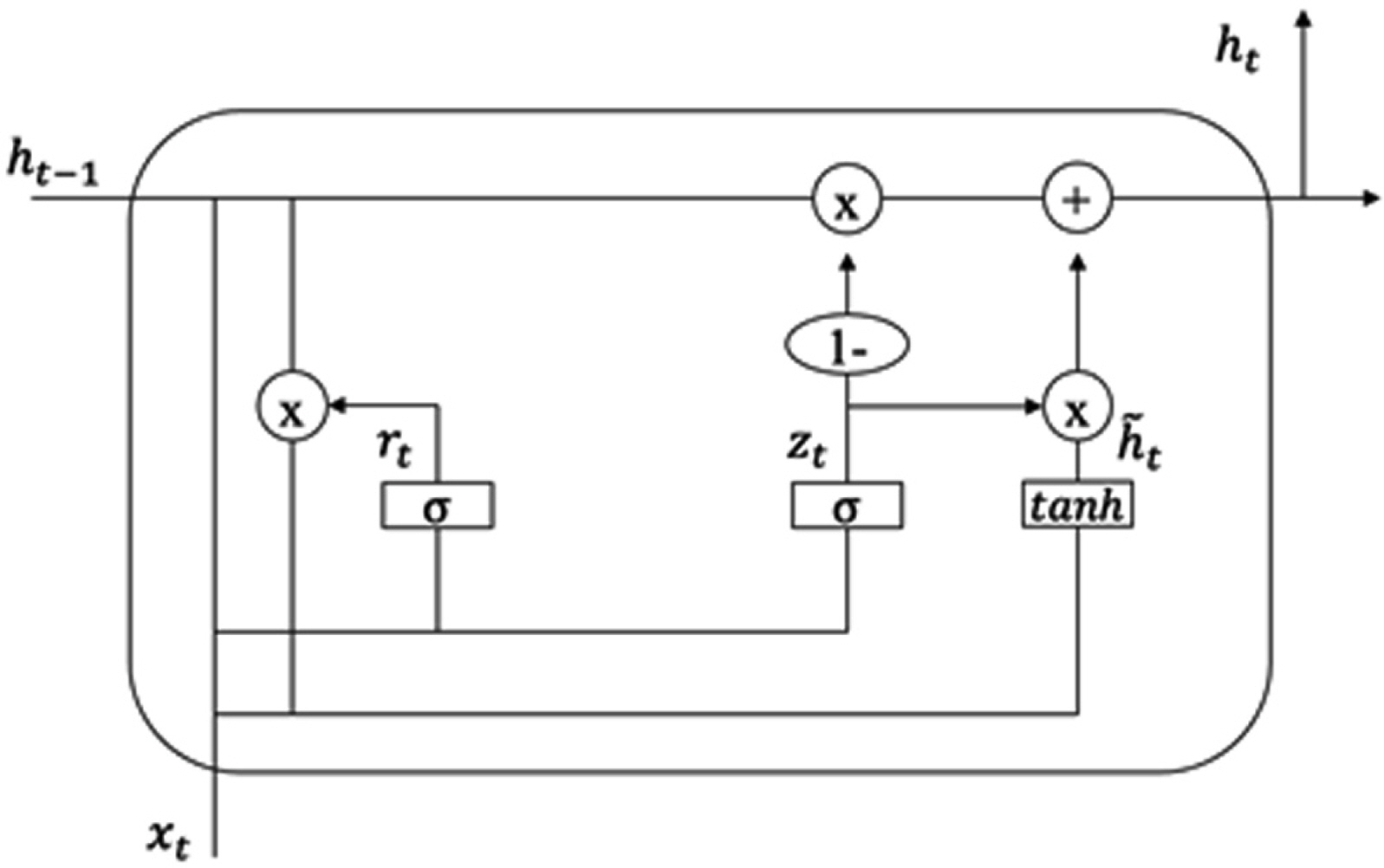
Structure of a gated recurrent unit (Cho et al., 2014)
If the number of data used for training is referred to as batch_size, the dimension of the input value for a decoder is batch_size × 170 × 4. If the size of the hidden state is referred to as hidden_size, the dimension of the output value, which is the set of hidden states generated during 170 time steps, is batch_size × 170 × hidden_size. In general, only the final hidden state, which is the last updated hidden state that best represents the features of all the values, is used. When the batch size is batch_size, the dimension of the final hidden state is batch_size × 1 × hidden_size.
Considering one piece of data, the dimension of the input value for the encoder is 1 × 680 while the dimension of the output value is 1 × 80 if the hidden_size is 80. Specifically, the data size is reduced from 680 to 80. A comparison of the performance with respect to the reduction in dimensions is presented in Section 4.
3.4 Decoder
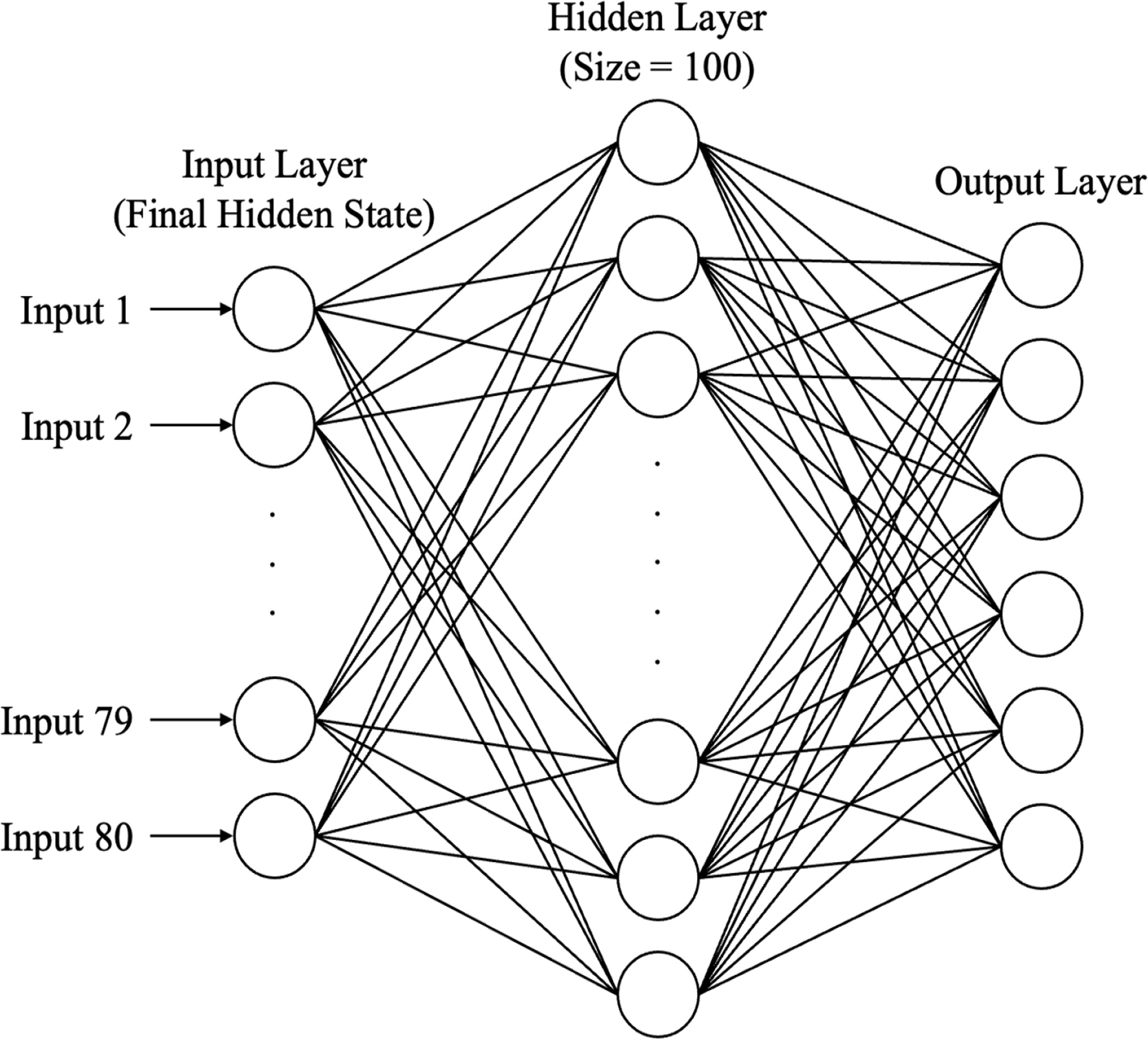
A decoder classifies faults when the final hidden state is input using an MLP. An MLP consists of an input layer, a hidden layer, and an output layer in that order, and output values are deduced through the matrix operations between each layer. In this study, the numbers of hidden layers and neurons (nodes in the hidden layer) were set to 1 and 100, respectively. The MLP used in this study is configured as shown in Fig. 9.
The ANN has a non-linear form between each layer of the MLP, and a rectified linear activation function (ReLU) is used to improve training efficiency. The ReLU returns 0 if the value is 0 or returns the value itself if greater than 0.
The output layer consists of six values, and the softmax function is used as the activation function. The softmax function creates all values to be between 0 and 1 and expresses the probability of their sum being 1. The decoder determines that a fault has occurred in the turn with the highest probability. For example, if the output values are 0.001, 0, 0.997, 0.0005, 0.001, and 0.0005, fault type 3, or excessive friction, is judged to have occurred because the third output is the largest.
The softmax cross-entropy function, often used in classification problems, was used as the loss function. Cross-entropy returns the loss value according to the difference between the predicted value and the answer, based on the value derived by the softmax function. The model was evaluated through the loss function and improved through optimization. The Adam optimizer based on a gradient descent was used as the optimization technique, and the learning rate was set to 0.01.
4. Comparative Test
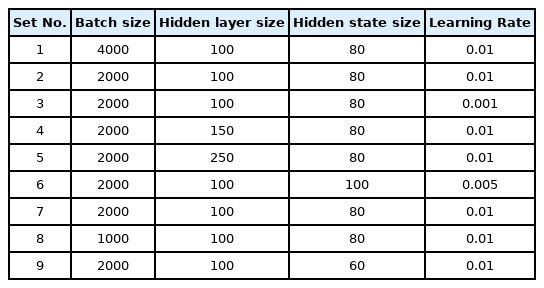
To determine the optimal hyperparameters of the ANN, its performance was compared by combining different hyperparameter values into sets as shown in Table 3. Overfitting occurred when the number of epochs exceeded 100; therefore, the final number of epochs was set to 100 in this study.
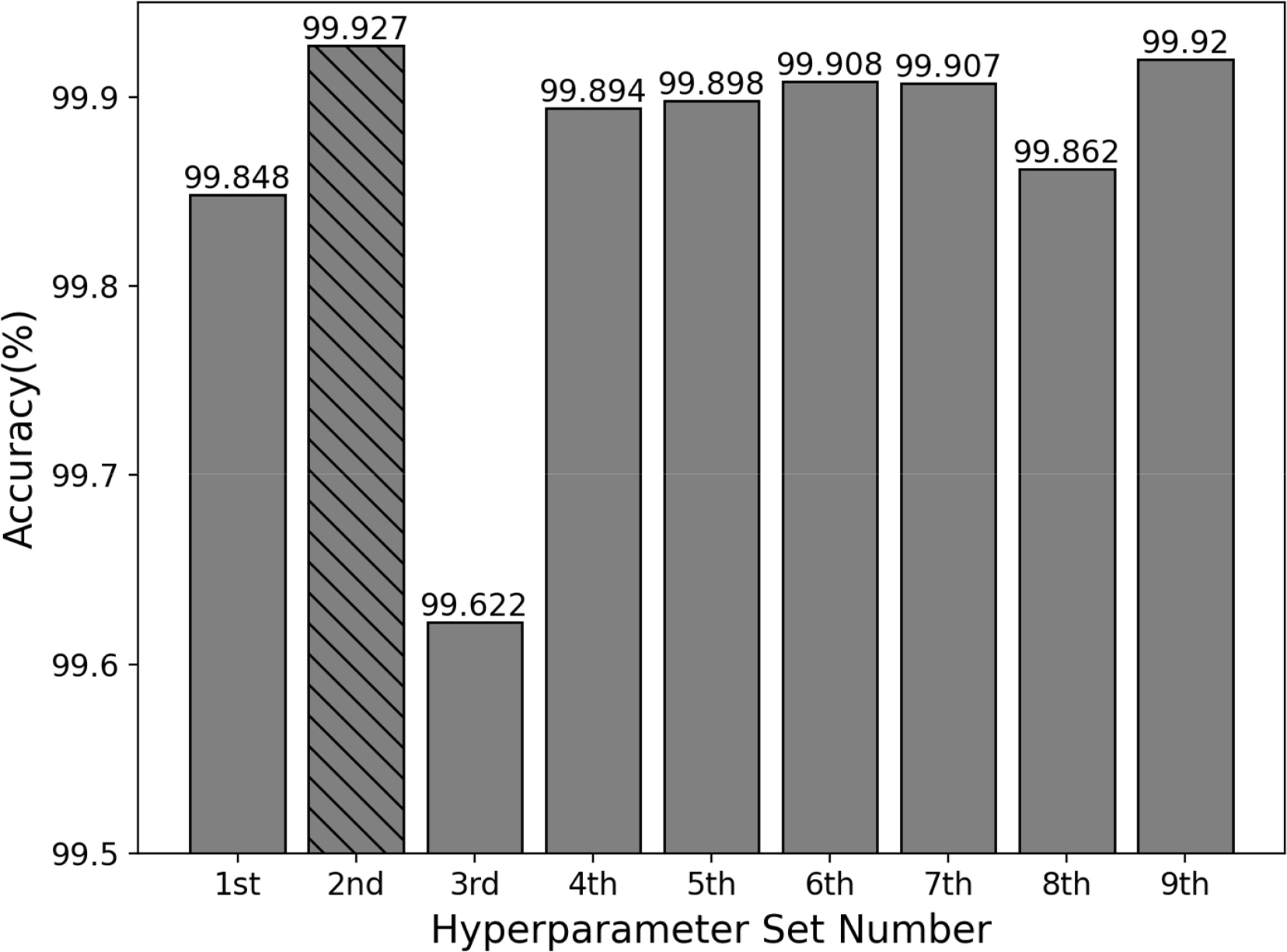
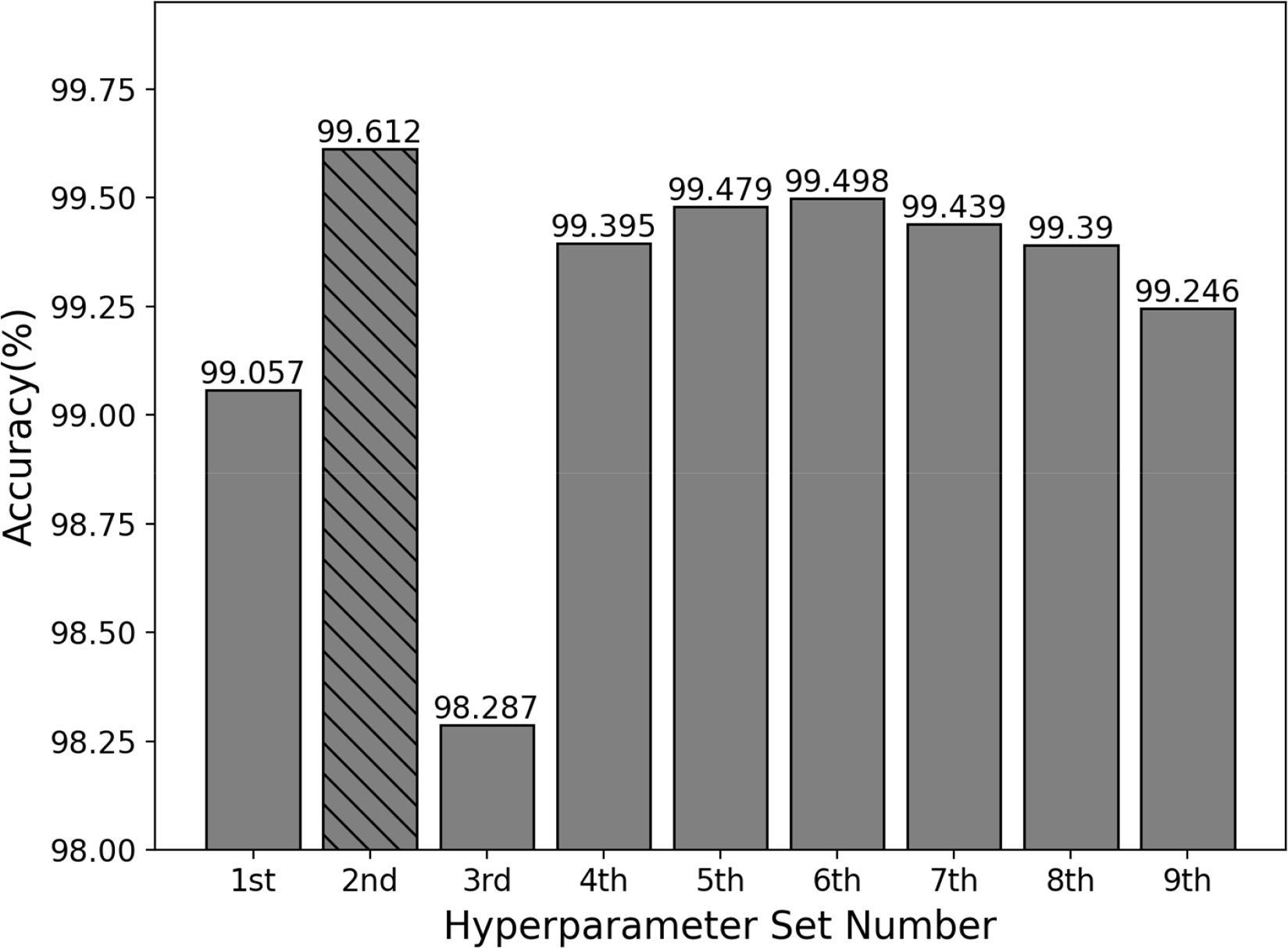
A total of nine hyperparameter sets were considered, and each set was trained 10 times for a total of 90 times. The performance of the ANN considering validation and test data with respect to each hyperparameter set is illustrated in Figs. 10 and 11, respectively. Its overall performance was fairly consistent, but the changes in its performance varied significantly depending on the learning rate and batch size.
Based on the results in Figs. 10–11, the average performance of the network using validation data and test data is presented in Figs. 12–13, respectively. The bar marked with slashes exhibits the best performance among the nine hyperparameter sets. The average success rate using validation data and test data in the second hyperparameter set is 99.927% and 99.612%, respectively; these values are the highest. Thus, the second hyperparameter set was adopted in this study.
The proposed model could reduce the dimension of the input value from 680 to 80 as it used a GRU that could reflect the features of time-series data. Reducing the dimension of the input data facilitates training by reducing the complexity of the ANN. The performance of the proposed model improved by approximately 1.4% in compared to the model proposed by Cho et al. (2021), which consisted only of MLPs using the same test data. The fault classification success rate is directly related to maintenance cost from the perspective of operating wind turbines and thus should be near 100%. Therefore, an increase of 1.4% in the success rate of fault classification using the GRU proposed in this paper implies almost 100% fault classification performance from the perspective of wind turbine operation, which is a significant improvement in fault classification.
5. Conclusion
This paper proposed a GRU based fault classification scheme of a blade pitch system in a floating wind turbine. GRU can quickly train a mathematical model based on previous training models and it processes time-series data by updating new information in real time. Based on various sets of hyperparameters, the proposed model achieved 99.927% and 99.612% successful classification on validation data and test data, respectively. The model also achieved a 1.4% improvement in its classification performance compared to other models that used MLP.
The proposed method only considered one type of fault that occurs independently in a system. In the future, the algorithm needs to be improved to be able to classify multiple faults occurring simultaneously. In addition, the proposed method should be applied to other components such as the generator, gearbox, and yaw system of a wind turbine.
Notes
This work was supported by “The development of a fully electrified car ferry and a removable power supply system (Project No. 20200469-01, PMS4700) funded by a national R&D project of the Ministry of Oceans and Fisheries. The authors gratefully would like to express our sincere gratitude for the research fund granted.