Comparison of Numerical Analyses and Model Test for Evaluation on Hydroelastic and Higher-order Springing Responses of Fixed Cylindrical Structure
Article information
Abstract
Studies on very large offshore structures are increasing owing to the development of deep sea, large-scale energy generation using ocean resources, and so on. The enlargement of offshore structures makes the hydroelastic effect and low natural frequency related responses important. Numerical analyses and model tests for hydroelastic and higher-order springing responses of fixed cylindrical structures are conducted in this study. The panel methods with and without the hydroelastic effect with shell elements, and the Morison analysis method with beam elements are applied. To observe the hydroelastic effect for structural strength, two structures are considered: bottom-fixed cylindrical structures with high and low bending stiffnesses, respectively. The surge motions at the top of the structure and bending stresses on the structure are observed under regular and irregular wave conditions. The regular wave conditions are generated considering the ratios of the cylindrical outer diameter to the wave lengths, and keeping the wave steepness constant. The model tests are performed in the three-dimensional ocean engineering basin in the KRISO (Korea Research Institute of Ships and Ocean Engineering). From the numerical and experimental results, in which the hydroelastic responses are only observed in the case of the structure with a low bending stiffness, it is confirmed that the hydroelastic responses are highly dependent on the structural stiffness. Additionally, the higher-order phenomenon on the specified wave condition is analyzed by observing the higher-order springing responses when the incident wave frequency or its multiples with the high wave height coincides with the natural frequency of the structure.
1. Introduction
Because offshore oil production operations are entering distant waters with increase of water depths, oil production and storage structures are being enlarged to ensure those structural stabilities. Furthermore, as researches and developments on eco-friendly energies, such as offshore wind power generation, wave power generation, floating photovoltaic power generation and so on, are being actively undertaken, the related studies on large structures for large-scale power generation are also increasing. Additionally, the researches and developments for very large structures, including floating LNG (liquefied natural gas) bunkering, floating airports, and so on, are in constant progress. The enlargement of offshore structures increases the relative deformations of the structures, and thus, the hydroelastic effect, which is the interaction between the waves and structural deformation, becomes important. To rigorously estimate the wave-induced and structural responses of large offshore structures, fluid-structure interaction analysis is required, and the hydroelastic effect must be considered. Various numerical analysis methods have been developed and studied based on the aeroelasticity concept in aeronautical engineering to address the need for analysis that considers the hydroelastic effect of offshore structures (Heller and Abramson, 1959). Studies on hydroelastic analysis were conducted by Bett et al. (1977) and Bishop & Price (1977) based on the strip theory, which is the early fluid analysis method for ships, and beam theory. The second-order nonlinear strip theory was applied to the existing method to solve nonlinear problems with large ranges of motion and deformation (Jensen and Pedersen, 1981). Attempts were also made to solve three-dimensional hydroelastic analysis problems by applying the potential theory and the finite element method (Wu, 1984; Price and Wu, 1985; Bishop et al., 1986). Lakshmynarayana et al. (2015) conducted the study on a fluid-structure interaction using the computational fluid dynamics (CFD) method. Additionally, several methods were developed to predict the hydroelastic response of large offshore structures; these hydroelastic analysis methods were applied in studies on hydroelastic problems of various offshore structures, ranging from ships to semi-submersible structures (Andrianov, 2005; Kim et al., 2014). Major studies on very large floating offshore structures include the Mega-Float project (Japan Technical Research Association) and the Mobile Offshore Base (MOB) project (US Navy) (Rognass et al., 2001; Shuku et al., 2001).
Also, as offshore structures become larger, the natural frequency of the structures decreases and becomes close to the wave frequency or its multiples. If the height of the incident wave is large and the multiples of the frequency approach the natural frequency of the structure, the higher-order component of the wave force generates resonance responses, resulting in the springing phenomenon with the occurrence of regular natural frequency responses. Numerical and experimental studies have been conducted on this phenomenon mainly for very large ships (Hong and Kim, 2014; Shin et al., 2015).
Most studies on the hydroelastic responses and higher-order springing phenomenon of offshore structures have focused on floating structures, including ships. In this study, numerical analyses and model tests were performed to consider the hydroelastic and higher-order springing responses of fixed cylindrical structures, and the result of each numerical analysis method was analyzed and compared to the result of the model tests. As numerical analysis methods to study the hydroelastic responses of fixed cylindrical structures, the panel method that considers only wave diffraction but not the hydroelastic effect, the panel method that considers the radiation effect for the bending modes of the structure and applies the hydroelastic effect, and the Morison analysis method with beam elements are applied (Kim et al., 2018). In the panel method, the higher-order boundary element method (HOBEM; Choi et al., 2000; Hong et al., 2005) and the shell elements of the finite element method (FEM) (Bathe, 1996; Kim et al., 2018) are applied. The surge motions at the top of the structure and stress responses acting on the main body are studied, and the response amplifier operator (RAO) characteristics under regular wave conditions and the responses under irregular wave conditions are evaluated. To compare the responses based on the structural strength of the structure, two cases are evaluated: the case where the hydroelastic effect was insignificant owing to high structural strength and the other case where the hydroelastic effect was large owing to low structural strength. The case where the springing phenomenon occurs under certain model test conditions with the case of low structural strength is also considered. From the results of the numerical and experimental studies, it is confirmed that the structural strength has a significant effect on the hydroelastic responses of the structure, and that the higher-order springing responses occur when the wave height is large and the wave frequency or its multiples approaches the natural frequency.
2. Model Tests
2.1 Structures for Model Tests
To compare the hydroelastic responses depending on the structural strength of the fixed cylindrical structures in the numerical analyses and model test, two cases are considered: the stiff-type structure with a small hydroelastic effect and the flexible-type structure with a large hydroelastic effect. The structures are 74 m in height and 6 m (stiff-type) or 4.32 m (flexible-type) in outer diameter on a real scale. The stiff-type structure is made of an aluminum pipe, and the flexible-type structure is made of a PVC pipe.
Model tests are conducted in the three-dimensional ocean engineering basin at the Korea Research Institute of Ships and Ocean Engineering (KRISO). The outer diameters, lengths, and bending stiffnesses of the structures are scaled at the scaling factor of 1/20 to meet the conditions of the model test facility. Fig. 1 and Table 1 show the installed structures for the model tests and their specifications.

Test models installed at ocean engineering basin in KRISO (Kim et al., 2020)

Dimensions of fixed cylindrical models (Kim et al., 2020)
In the case of the flexible-type structure, the hydroelastic effect can be observed more clearly by maintaining the low stiffness of the structure and increasing the weight of the topside structure relatively high to reduce the natural frequency.
The contactless motion-measuring sensor is installed to measure surge motions the top of the structures, and strain gauges are installed on the main bodies to determine the strains and calculate the stresses of the structures. Fig. 2 shows the detailed dimensions of the models and the sensor locations for the tests.
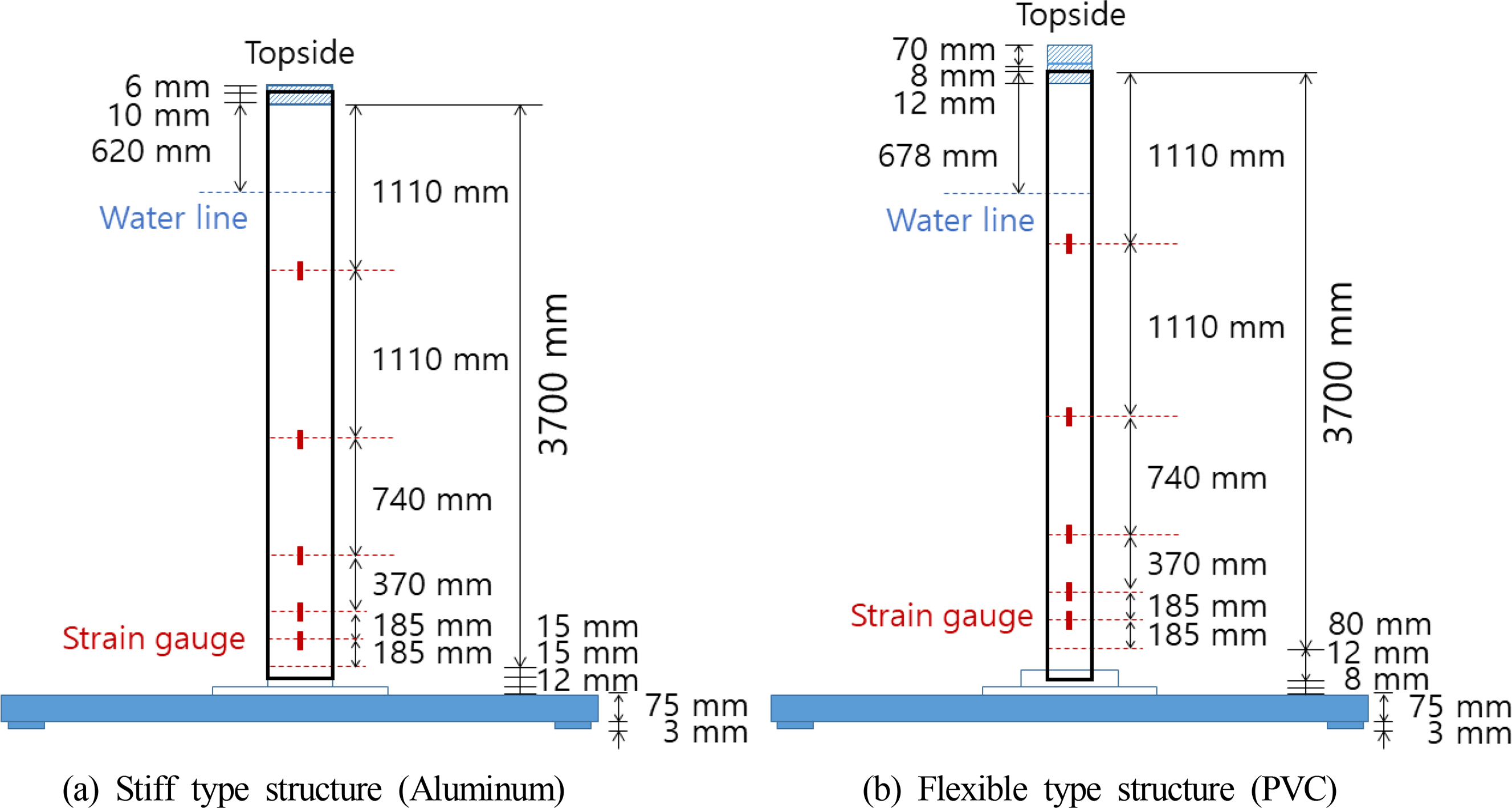
Detailed dimensions and sensor positions of test models (Kim et al., 2020)
2.2 Loading Test
When determining the bending strength (EI ) of cylindrical structures, the second moment of area, I, can be easily obtained through accurate calculations using cross-sectional dimensions; however, Young’s modulus, E, is determined through a loading test owing to the presence of uncertainties. Additionally, the perfect fixed condition could not be implemented at the connection part between the cylindrical structure and bottom plate, which results in slight rotational spring stiffness. It is necessary to consider this point in the numerical analyses and this is calculated through the loading test. Fig. 3 shows the schematic of the loading test.
Fig. 4 shows the loading test results. From the strain distribution results depending on the position, the strain at the bottom part of the cylindrical structure is estimated through regression analysis, and the elastic modulus and bending stiffness can be determined based on the beam theory (Eq. (1)).
The results in Fig. 4 indicate that the regression lines and results of finite element analysis using shell elements are almost identical. The displacement at the top of the structure, denoted as δm, can be measured during the loading test, and this displacement can be expressed as the sum of the displacement by bending deformation (δbend) and the displacement by the rotational spring effect at the bottom connection part (Fig. 3). By applying this relation and the beam theory, the rotational spring constant, Kθ, at the bottom connection part can be derived.
Table 2 shows the results obtained from the above process. The real-scale values for numerical analyses are determined by applying the similarity law to the model test results.
2.3 Hammering Test
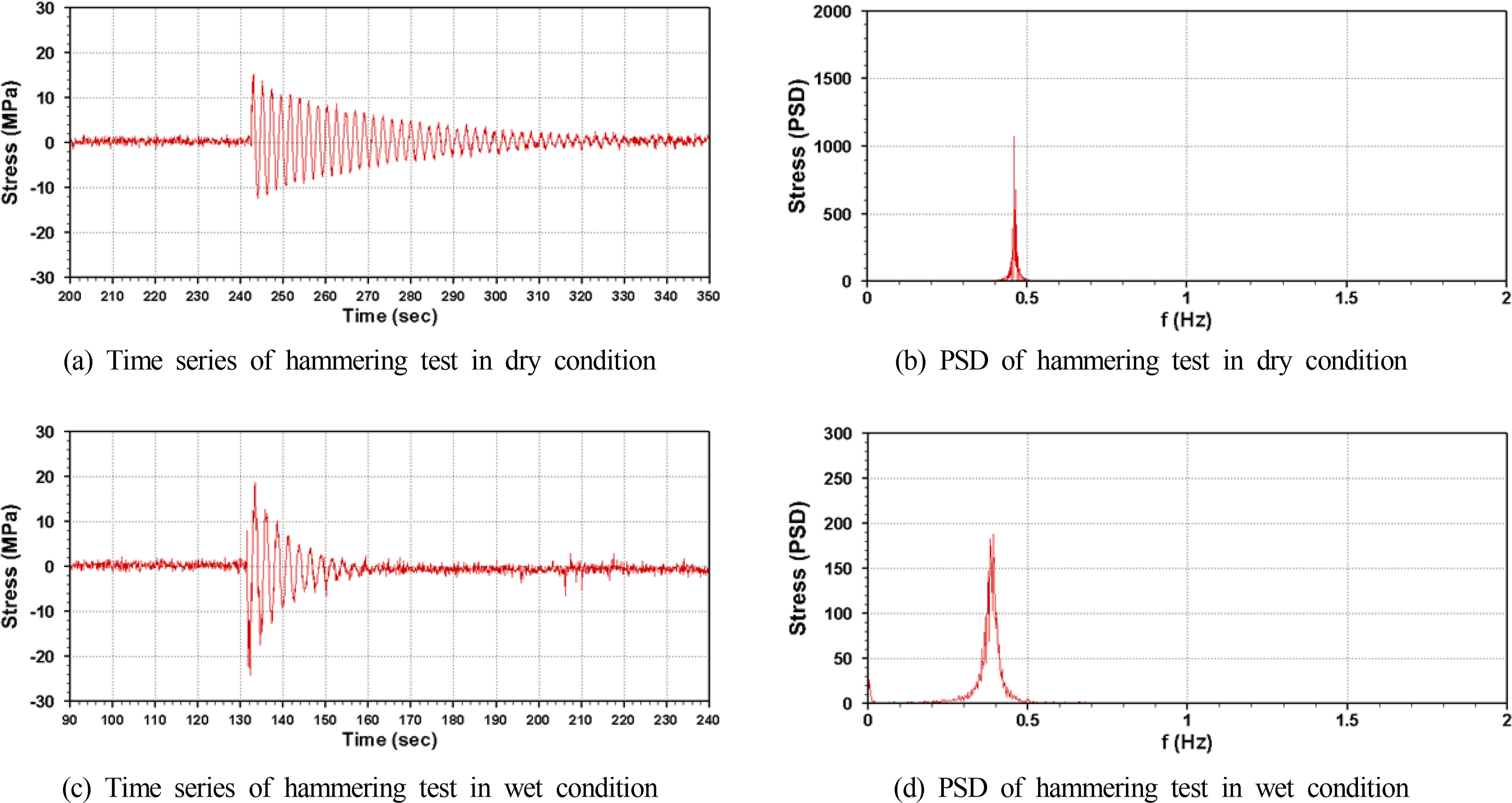
The natural frequency of a structure is one of the most important factors in evaluating hydroelastic responses. In this study, it is numerically evaluated through finite element analysis using shell elements. And the actual natural frequencies of the test models are measured by performing hammering tests. These are performed by applying an impact to the top of the structures under dry and wet conditions. Figs. 5‒6 show the time series and power spectral density (PSD) results on hammering tests, and the overall results are summarized in Table 3. The natural period of the stiff-type structure is 0.838 s in a wet condition, which is slightly different from that in the dry condition. The hydroelastic effect is predicted to be small in both conditions because the results are outside the range of wave period. The natural period of the flexible-type structure is 2.571 s in the wet condition, which is within the range of the wave period under the test condition, and the hydroelastic effect would be confirmed.
2.4 Environmental Conditions
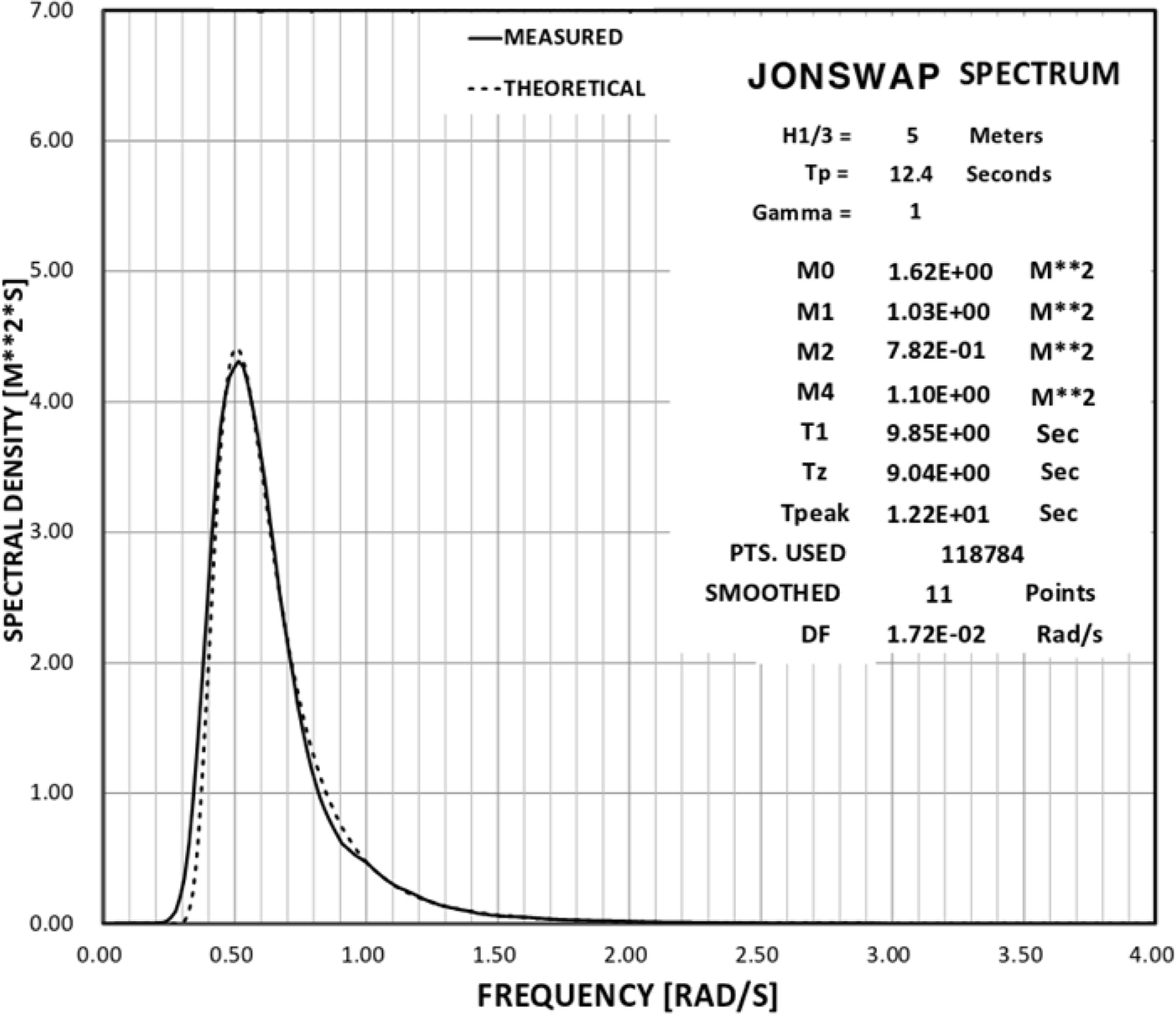
The model tests are conducted by applying a wave load as the only acting environmental load, and varying the ratio of the wavelength (λ) to the outer diameter (D ) of the structure from 1.3 to 34 in the regular wave condition. The wave height (H ) is set such that its ratio to the wavelength (H/λ) is 1/20 (Table 4). For the irregular wave condition, the JONSWAP spectrum is used, and the significant wave height (HS) of 5 m and the modal period (TP ) of 12.4 s are considered. Fig 7 shows the calibration and theoretical results for the irregular wave condition for the model test.
3. Numerical Analysis
3.1 Numerical Analysis Model
For the numerical analysis to study the hydroelastic effect of the fixed cylindrical structures, the panel method using the higher-order boundary element method (HOBEM) and shell elements, and the Morison analysis method using the beam elements are applied. The panel analyses are performed separately for when only diffraction is considered without a hydroelastic effect and when the radiation effect for the bending modes is considered, and the results are compared. Fig. 8 shows the numerical models consisting of the panel and beam elements.
3.2 Numerical Analysis Methods
The higher-order boundary element method (HOBEM) is applied as a fluid analysis method to calculate the hydrodynamic load acting on the fixed cylindrical structures. The higher-order boundary element method is a type of numerical analysis method for calculating the flow field of waves around a structure, which only divides the boundary of the floating structure using the Green function rather than dividing the fluid domain.
This method improves convergence and accuracy by applying 9-node higher-order elements instead of 4-node elements of the existing boundary element method (Choi et al., 2000; Hong et al., 2005). The velocity potential satisfying the governing equation and the boundary conditions is calculated, based on which the hydrodynamic coefficients of the motion equation in the frequency domain can be determined.
Eq. (4) is the governing equation in a fluid domain, and Eqs. (5)–(8) represent the free surface boundary condition, sea bed boundary condition, radiation condition, and body surface boundary condition, respectively. In the above equations, ϕ is the wave-induced velocity potential that consists of three components: incident, scattered, and radiation potentials. For the panel method that does not consider the hydroelastic effect, only the incident potential and scattered potential are considered. In case that the hydroelastic effect is considered, the analysis is performed not only by considering the incident and scattered potentials but also the radiation potential for the bending modes of the structures. ω is the wave frequency, h is the water depth, and r is the radiation boundary.
The pressure RAO (Response Amplitude Operator) of the frequency domain in Eq. (9) can be transformed into the time domain through the inverse Fourier transform and random time series methods, as follows.
S(ω) in Eq. (10) represents the irregular wave spectrum, and the JONSWAP spectrum is applied in the numerical analyses of this study. nW denotes the number of spectrum partitions and ψj is the random phase angle. By applying the time-domain pressure load obtained through Eq. (10) to the motion equation for the structural analysis, the displacements and stresses in the time domain can be determined for structures to which wave load is applied (Eq. (11)).
In the above Eq. (11), [M],[C], and [K] represent the mass, damping, and stiffness matrices, respectively. {u} is the displacement vector, and {f} is the external force vector including the pressure load caused by the wave. [KB ] denotes the buoyancy spring matrix of the structure.
In the Morison analysis method using beam elements, the load acting on the structure is assumed to be the sum of the drag and inertial force, and the velocity of the water particles could be determined using the velocity potential. The Morison equation can be expressed as shown in Eq. (12).
In Eq. (12)D, AM, and SF are the width, projected area, and perimeter length for the beam elements, respectively, ∆s is the length of the beam elements, and ρ is the fluid density. CD, CM, CA, and CF denote the drag, mass, added mass, and friction coefficients, respectively, and corresponding values of 1.2, 2.0, 1.0, and 0.05 are applied in this study.
In Eqs. (13)–(16),
3.3 Comparison of Numerical Analysis and Test Results
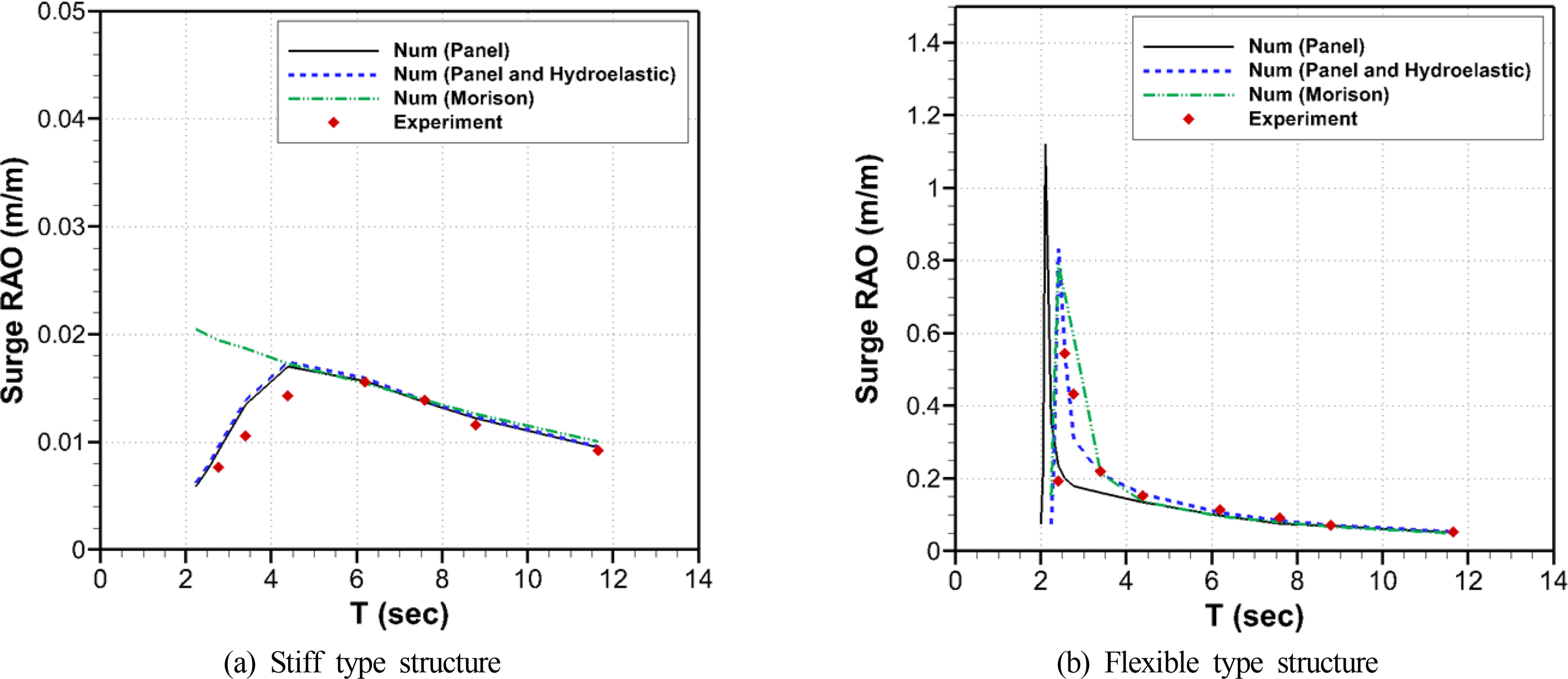
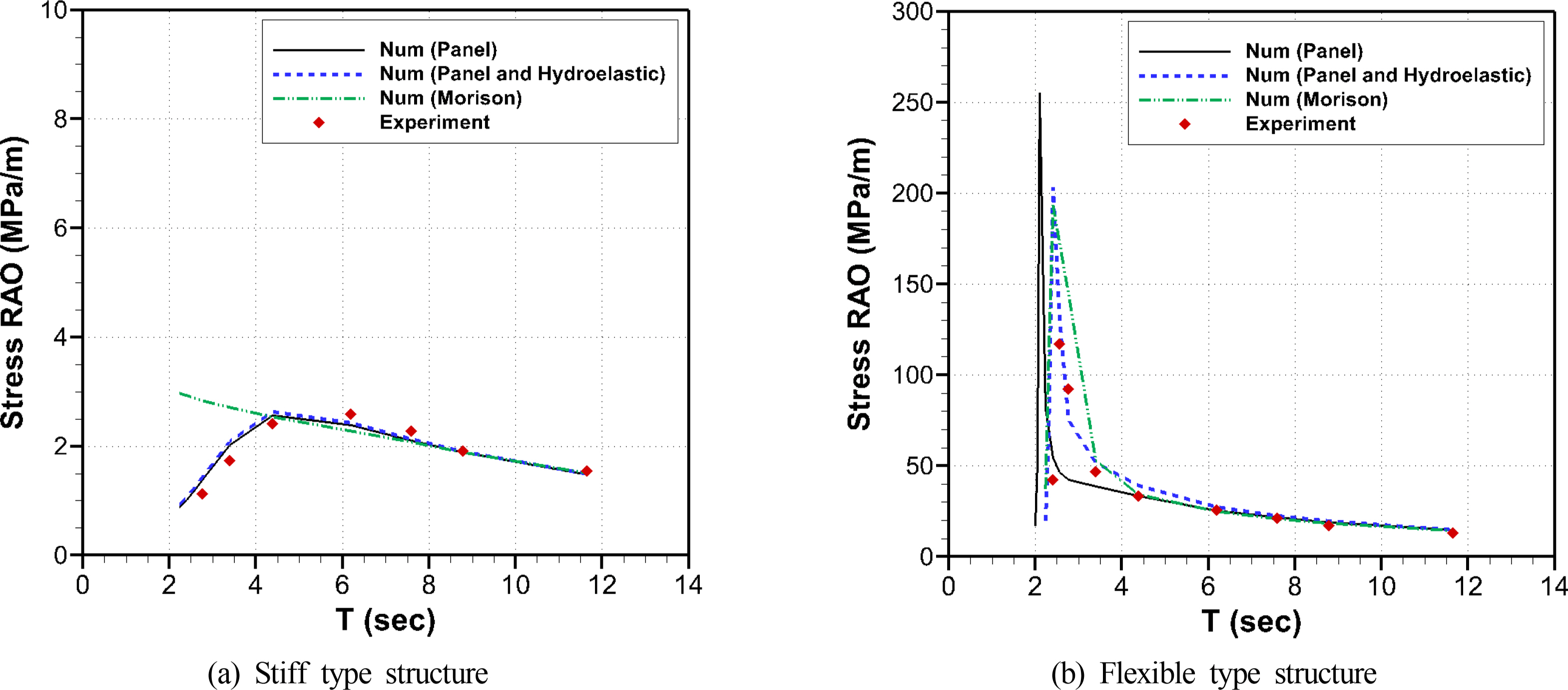
Figs. 9–10 show the results under regular wave conditions. Fig. 9 shows the surge motion results at the top of the structures, and Fig. 10 shows the stress results at the bottom part of the structures. The results on the surge motions at the top and the stresses at the bottom of the stiff type structure confirm that there is no significant difference between considering and not considering the hydroelastic effect, and that the numerical analysis and test results are similar. Based on this, the hydroelastic effect is found to be small when the structural strength is large. However, for the flexible-type structure, the hydroelastic responses occur by the low stiffness of the structure in the model test. Thus, the result of the numerical analysis, which does not consider the hydroelastic effect of the structure, varies from the results of model test for the flexible type structure. This implies that the hydroelastic effect needs to be considered if a structure is flexible. Comparing the Morison analysis and test results, the analysis and test results are similar when the wavelength is long relative to the outer diameter of the structure, but they are different when the wavelength is short relative to the outer diameter of the structure. If the wavelength is relatively short compared to the outer diameter of the structure, the diffraction effect should be considered through the boundary element method, and so on.
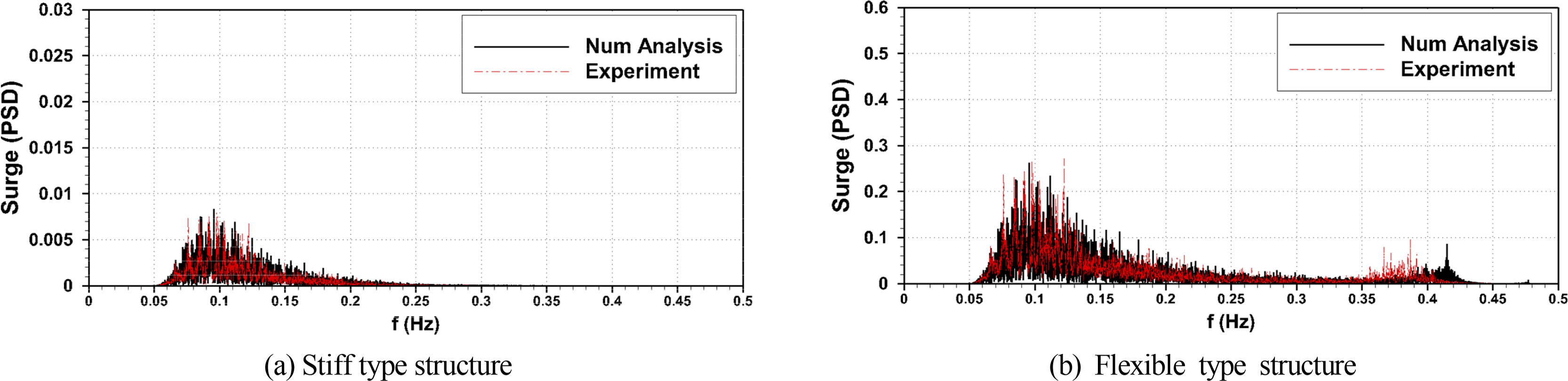
Figs. 11‒12 show the power spectral density (PSD) results on the surge motions at the top and the stresses at the bottom part of the structures under irregular wave conditions. The results of numerical analyses correspond to the ones of the panel analysis, which consider the hydroelastic effect, and are similar to the model test results in all cases. For the flexible type structure, it is confirmed that the wave frequency responses occur near 0.1 Hz, and the natural frequency responses of the structure occur near 0.4 Hz. For the stiff type structure, the natural frequency is rarely measured, and only responses near the wave frequency are observed.
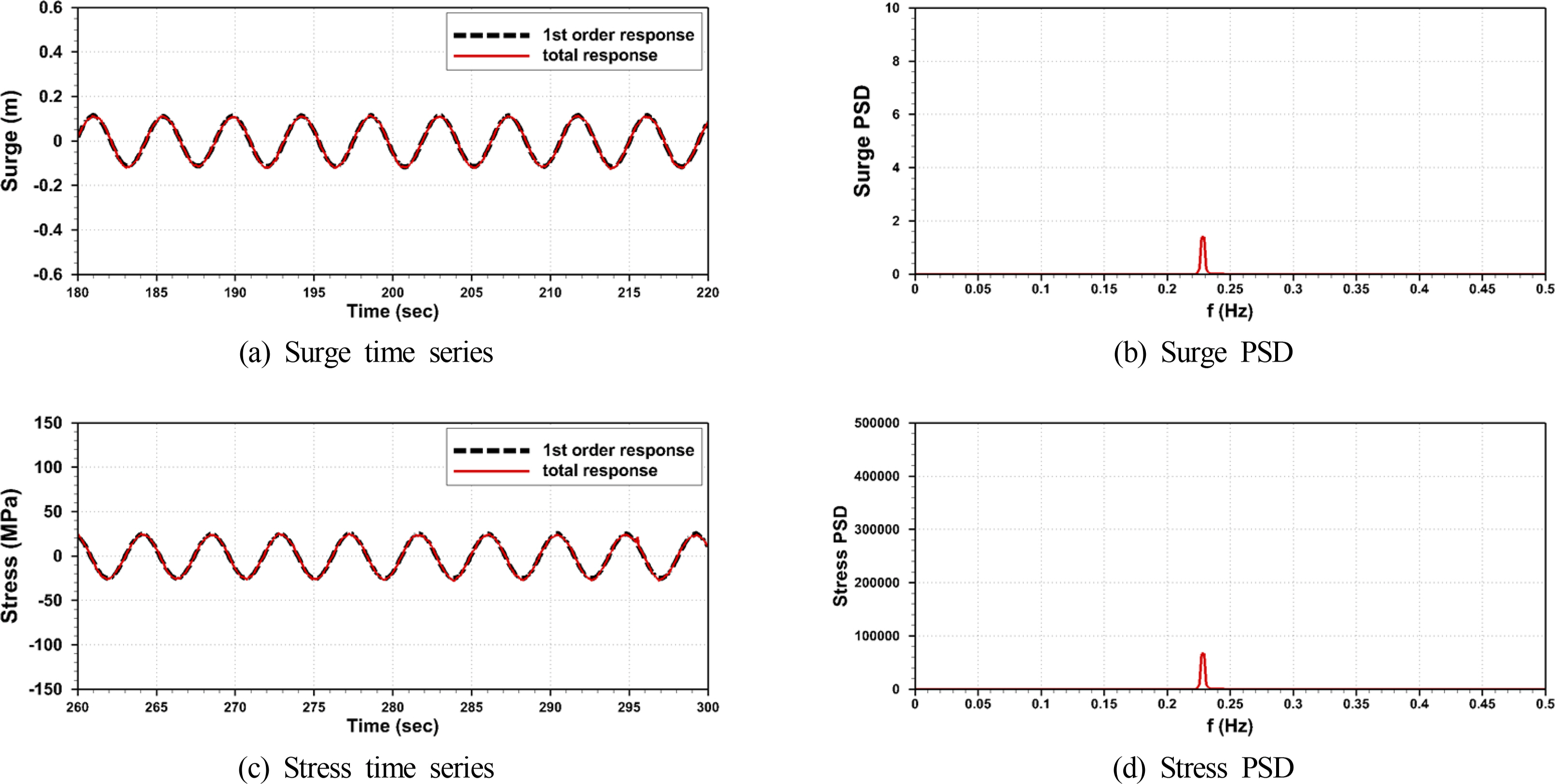
Under regular wave conditions, if the wave height is high, and the multiples of the wave frequency coincide with the natural frequency of the structure, the higher-order components of the wave force may cause a resonance, resulting in the springing phenomenon where the natural frequency responses of the structure occur regularly. This phenomenon is observed under the conditions of the model tests in which the actual phenomenon is embodied. Among the test conditions, the phenomenon is found to occur at the case having a wave height of 4.5 m and a period of 7.595 s (0.13 Hz) as shown in Fig. 13. Under this condition, it is confirmed that the natural frequency response (third-order springing response) also occurs regularly in addition to the wave frequency response (first-order response), because the triple of the wave frequency of 0.13 Hz, 0.39 Hz, almost coincides with the natural frequency of 0.387 Hz. The time-series results in Fig. 13 (a) and (c) show the difference between the first-order response results and the third-order springing response results.
Among the wave conditions, the double of the wave frequency is close to the natural frequency of the structure when the wave period is 4.384 s (0.23 Hz), but there is no springing phenomenon because the wave height is small (Fig. 14). Even when the wave height is large (6 m), no springing phenomenon is observed if the multiples of the wave frequency differ from the natural frequency of the structure (Fig. 15). In these cases, it could be confirmed that there is no difference between the first-order responses and the overall responses in the time series results (Figs. 14–15 (a) and (c)).
4. Conclusion
In this study, the hydroelastic response and higher-order springing one that is a nonlinear response of the waves for fixed cylindrical structures are evaluated numerically and experimentally. Furthermore, the cases where each structural stiffness is high and low are studied to confirm the hydroelastic responses based on the structural stiffness of the structure. For the numerical analysis methods, the panel method with no hydroelastic effect considered but only the scattering effect, the panel method with the hydroelastic effect considered by applying the radiation effect for the bending modes of the structure, and the Morison analysis method using beam elements are reviewed; the corresponding results are compared and analyzed.
Among the waves, the surge motions at the top and stresses at the bottom part of the fixed cylindrical structures are compared and reviewed. When the stiffness of the structures is high, the difference between the panel method with and without hydroelastic effect considered is small, and the results are also found to be similar to the model test results. In case that the structure is flexible, there are differences on the analysis results with and without hydroelastic effect considered, and the results on analysis with hydroelastic effect considered is similar to the ones of model test. Through these results, it is confirmed that the analysis considering the hydroelastic effect is necessary when a structure is flexible. The Morison analysis method using beam elements is found to give different results from the model test when the wavelengths are relatively short compared to the outer diameter of the structure. This indicates that the scattering effect of the wave caused by the structure should be considered if the wave is shorter than the size of the structure, which can be achieved through the boundary element method and so on.
Furthermore, under regular wave conditions in the model tests, when the wave height is large and the multiples of the wave frequency coincide with the natural frequency of the structure, the higher-order components of the wave force result in a higher-order springing phenomenon where the natural frequency response occurs regularly. This phenomenon can be observed in the model tests that realize the actual phenomenon. It is found that the phenomenon does not occur when either of the two conditions of a high wave height and the coincidence of the multiples of the wave frequency with the natural frequency is not satisfied. In the future, nonlinear phenomena such as a higher-order springing phenomenon will be studied through the improvement of numerical fluid analysis methods.
Acknowledgements
We acknowledge that this study is part of the research conducted with support from the Korea Institute of Ships and Ocean Engineering under the project, “Core Technology Development of Hydro-elasticity based Structural Damage Assessment for Offshore Structures considering Uncertainties (Grant No. PES3930)”. We appreciate the support for research funding.