Simulation-Based Prediction of Steady Turning Ability of a Symmetrical Underwater Vehicle Considering Interactions Between Yaw Rate and Drift/Rudder Angle
Article information
Abstract
The prediction of maneuverability is very important in the design process of an underwater vehicle. In this study, we predicted the steady turning ability of a symmetrical underwater vehicle while considering interactions between the yaw rate and drift/rudder angle through a simulation-based methodology. First, the hydrodynamic force and moment, including coupled derivatives, were obtained by computational fluid dynamics (CFD) simulations. The feasibility of CFD results were verified by comparing static drift/rudder simulations to vertical planar motion mechanism (VPMM) tests. Turning motion simulations were then performed by solving 2-degree-of-freedom (DOF) equations with CFD data. The turning radius, drift angle, advance, and tactical diameter were calculated. The results show good agreement with sea trial data and the effects on the turning characteristics of coupled interaction terms, especially between the yaw rate and drift angle.
Nomenclature
ρDensity (kg/m3)
mMass of Underwater Vehicle (kg)
IMoment of Inertia (kg-m2)
X0X Position in Earth-Fixed Frame (m)
Y0Y Position in Earth-Fixed Frame (m)
ψYaw Angle in Earth-Fixed Frame (rad)
uSurge Velocity in Body-Fixed Frame (m/s)
vSway Velocity in Body-Fixed Frame (m/s)
UOverall Speed (m/s)
rYaw Rate in Body-Fixed Frame (rad/s)
βDrift Angle (rad)
δRudder Deflection Angle (rad)
XSurge Force in Body-Fixed Frame (N)
YSway Force in Body-Fixed Frame (N)
NYaw Moment in Body-Fixed Frame (N-m)
LLength of Underwater Vehicle Body (m)
xgX coordinate of Center of Gravity (m)
ygY coordinate of Center of Gravity (m)
1. Introduction
Many kinds of underwater vehicles have been developed for military, commercial, and scientific purposes, such as submarines, torpedoes, autonomous underwater vehicles (AUVs), remotely operated vehicles (ROVs), underwater gliders, etc. Underwater vehicles need to have various types of performance depending on their operating concept and tasks. For example, maneuverability, course-keeping ability, turning ability, and course-changing ability are the most fundamental elements, so their prediction is very important work in the design process of underwater vehicles.
The process of predicting maneuverability consists of constructing equations of motion, obtaining hydrodynamic derivatives, and performing flight simulation. Most equations of motion of an underwater vehicle are based on the submarine dynamic model by Gertler and Hagen (1967). Feldman (1979) proposed a modified dynamic model to describe extreme turning and a high angle of attack accurately based on the model of Gertler and Hagen. Healey and Lienard (1993) proposed a dynamic model for a large AUV for low-speed flight. Many another researchers have also carried out research on equations of motion (Bae et al., 2009; Park et al., 2015).
There are mainly two ways to obtain hydrodynamic derivatives of an underwater vehicle during the design stage. One is by experiments, and the other is by computational fluid dynamics (CFD) simulations. Kim et al. (2012) estimated hydrodynamic derivatives of an underwater vehicle from a captive model test using a computerized planar motion carriage (CPMC). Park et al. (2015) conducted coning motion tests and derived hydrodynamic coefficients for roll motion.
Jeong et al. (2016) predicted hydrodynamic derivatives of a submarine after performing rotating arm tests. Nguyen et al. (2018) estimated hydrodynamic derivatives of a submarine by CFD analysis using a full-scale Reynolds-Averaged Navier-Stokes (RANS) solver. De Barros and Dantas (2012) numerically predicted the effects of a duct on the maneuverability. Kim et al. (2015) estimated the roll derivatives of an underwater vehicle, and Cheon et al. (2018) carried out virtual dynamic tests on an X-form configuration submarine using dynamic mesh methods.
After obtaining hydrodynamic derivatives, equations of motion are generally solved to analyze maneuverability. Bae et al. (2009) performed a simulation of the emergency rising, depth change, and floating of a manta-type AUV. Wang and Liang (2019) performed a maneuverability analysis of a modular underwater vehicle that has four tail thrusters and two tunnel thrusters. Go et al. (2017) conducted a 6-degree-of-freedom (DOF) motion analysis of a tow-fish-type underwater vehicle using hydrodynamic derivatives based on CFD.
Turning ability is also significant and critical to the maneuverability of an underwater vehicle, and many researchers have been trying to predict it in the design phase before sea trials. Seol et al. (2005) performed a simulation of turning and zigzag motion of an underwater vehicle using experiment data from a horizontal planar motion mechanism (HPMM). Jeon et al. (2018) did a sensitivity analysis for the parametric optimization of a hull form by the calculating turning and course changing ability based on a 3-DOF dynamic model. Dubbioso et al. (2017) compared the turning ability of cruciform and X-rudder submarines using unsteady free-running maneuvering simulations.
To predict the maneuverability accurately, research about dynamic model using coupled hydrodynamic effects has been conducted actively. Park et al. (2016) verified the interactions between the angle of attack and elevator angle of underwater vehicles that have fixed fins and movable fins. Dantas and de Barros (2013) numerically analyzed the coupled effects of the control surface deflection and angle of attack in an AUV that has only movable fins. Jeong et al. (2016) carried out a rotating arm test of a submarine for coupled motion, and Nguyen et al. (2018) performed a CFD analysis of a submarine for coupled motion. Thus, we can assume that there is some significant coupling of hydrodynamic derivatives in the turning phase of an underwater vehicle because there is large rudder deflection in turning motion, and most underwater vehicles turn with a drift angle.
In this study, we predicted the steady turning ability of an underwater vehicle while considering interactions between the yaw rate and drift/rudder angle. We did this by applying the hydrodynamic force and moment derived by CFD. In order to find the derivatives by experimental methods, we normally have to perform both vertical planar motion mechanism (VPMM) and rotating arm tests. The reason is that the rotary derivatives obtained by rotating arm tests are more accurate than those from pure yaw in VPMM tests. Performing two tests requires much money and time. Therefore, we carried out only VPMM tests, and rotating arm tests were replaced by numerical simulations.
Static derivatives and control derivatives of fins from CFD were compared to the results of VPMM tests and verified. Based on CFD data, motion simulation of a turning circle test was conducted by solving dynamic equations in a horizontal plane. The turning radius, drift angle, advance, and tactical diameter were calculated and compared to sea trial data.
2. Configuration and Specifications of Underwater Vehicle
The underwater vehicle configuration is shown in Fig. 1. The vehicle is symmetrical in the vertical and lateral directions. There are four fixed fins and movable fins with 90-degree intervals, and the fixed fins are located in front of the movable fins. The four movable fins consist of two elevators that control the attitude and depth in the vertical plane and two rudders that control the attitude and trajectory in the horizontal plane. There is a ducted propeller behind the body. Table 1 shows the specifications of the underwater vehicle in this study.
3. Equations of Motion
3.1 Coordinates
In order to analyze the motion of the underwater vehicle, two coordinate systems were adopted. One is an earth-fixed frame, and the other is a body-fixed frame. The earth-fixed frame can be transformed to the body-fixed frame by the Euler angles, and reverse transformation is also possible. The definition of each coordinate and Euler angle is shown in Fig. 2. In this study, the origin point of the body-fixed frame was set to be the center of buoyancy.
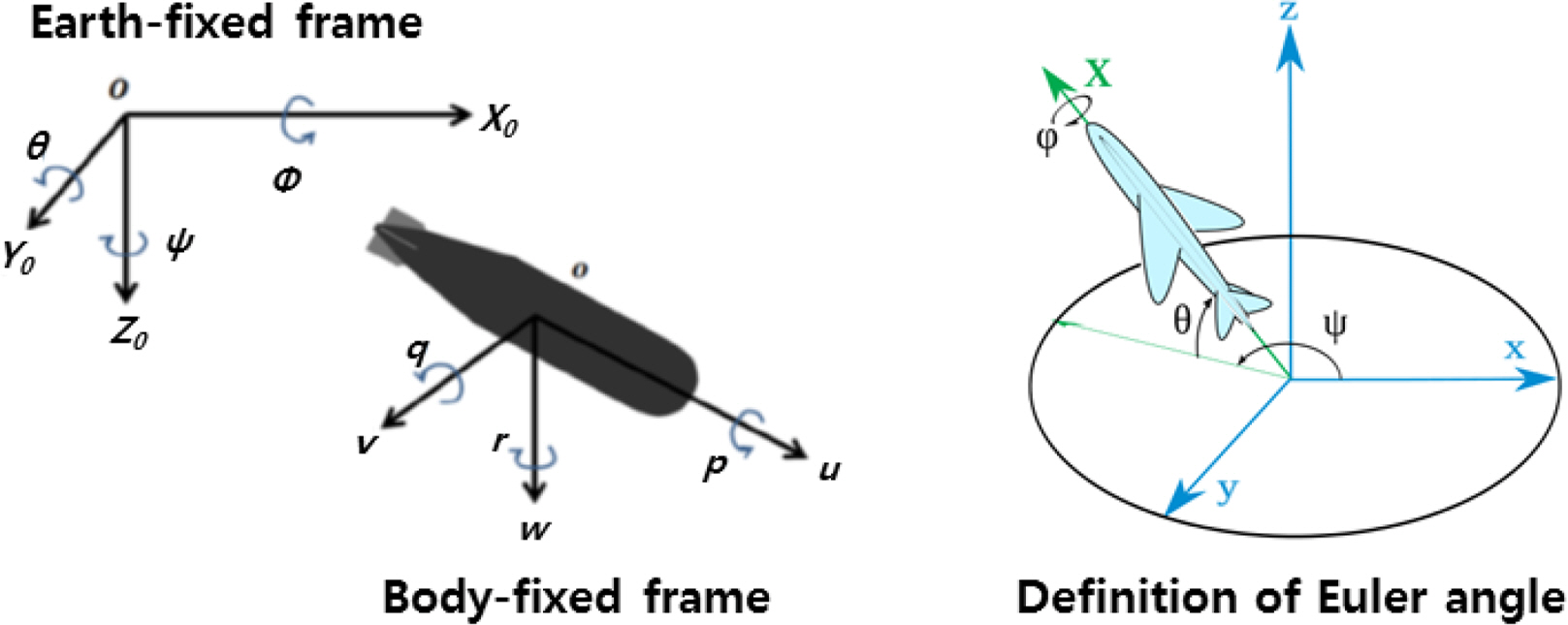
Definition of coordinates (left) and Euler angles (right) (Park et al., 2015)
The equations of motion of the underwater vehicle are generally represented by the body-fixed frame because it is easy to express the hydrodynamic force and moment acting on body. The position and attitude of the body are calculated in the earth-fixed frame, and the translational velocity and angular rate are transformed from the body-fixed frame to the earth-fixed frame using Eq. (1).
Since only horizontal motion is considered in this study, Eq. (1) can be rewritten in the horizontal plane as follows:
3.2 Equations of Motion in Horizontal Plane
The equations of motion of the underwater vehicle to describe steady turning motion are as follows:
X, Y, and N are the external force and moment on the underwater vehicle, including hydrodynamic, hydrostatic (gravity and buoyancy), and thrust terms. Roll motion can be neglected because there is little snap roll angle when the vehicle turns steadily. The roll angle is controlled by the elevators. In addition, a surge equation is not included since it can be considered as constant, and the speed of the vehicle is uniformly controlled in the sea trial of this study when the vehicle goes straight or turns.
Hydrostatic terms can be removed because the roll (ϕ) and pitch angle (θ) are not considered in horizontal plane motion. Hydrodynamic terms (YH and NH) including the interactions between the yaw rate and drift/rudder angle can be expressed as follows:
In Eq. (4)is the sway velocity, r is the yaw rate, and δ is the rudder angle. ṙ is the sway acceleration, v̇ and ṙ is the yaw acceleration. The subscript “coup” means coupled derivatives. i and ṙ are not important in steady motion, so Yv̇,Yṙ and Nv̇, Nṙ can be neglected. In order to solve the equations for steady turning motion, we have to obtain the damping derivatives of the sway and yaw motion, the control derivatives of the rudder, and coupled interaction terms.
4. CFD Analysis
4.1 Simulation Method
In order to obtain the hydrodynamic data for steady turning motion by CFD, we have to perform static drift/rudder and rotating arm simulations. Static drift/rudder simulations calculate the force and moment with respect to the drift/rudder angle when the vehicle goes straight at constant speed (Figs. 3–4). Rotating arm simulations calculate the force and moment with respect to the yaw rate when the vehicle turns just like a circle. Rotating arm simulations can also calculate the interaction terms by combining with the static drift/rudder angle (Fig. 5).

Rotating arm simulations (a) without drift and rudder angle (b) with drift angle (c) with rudder angle
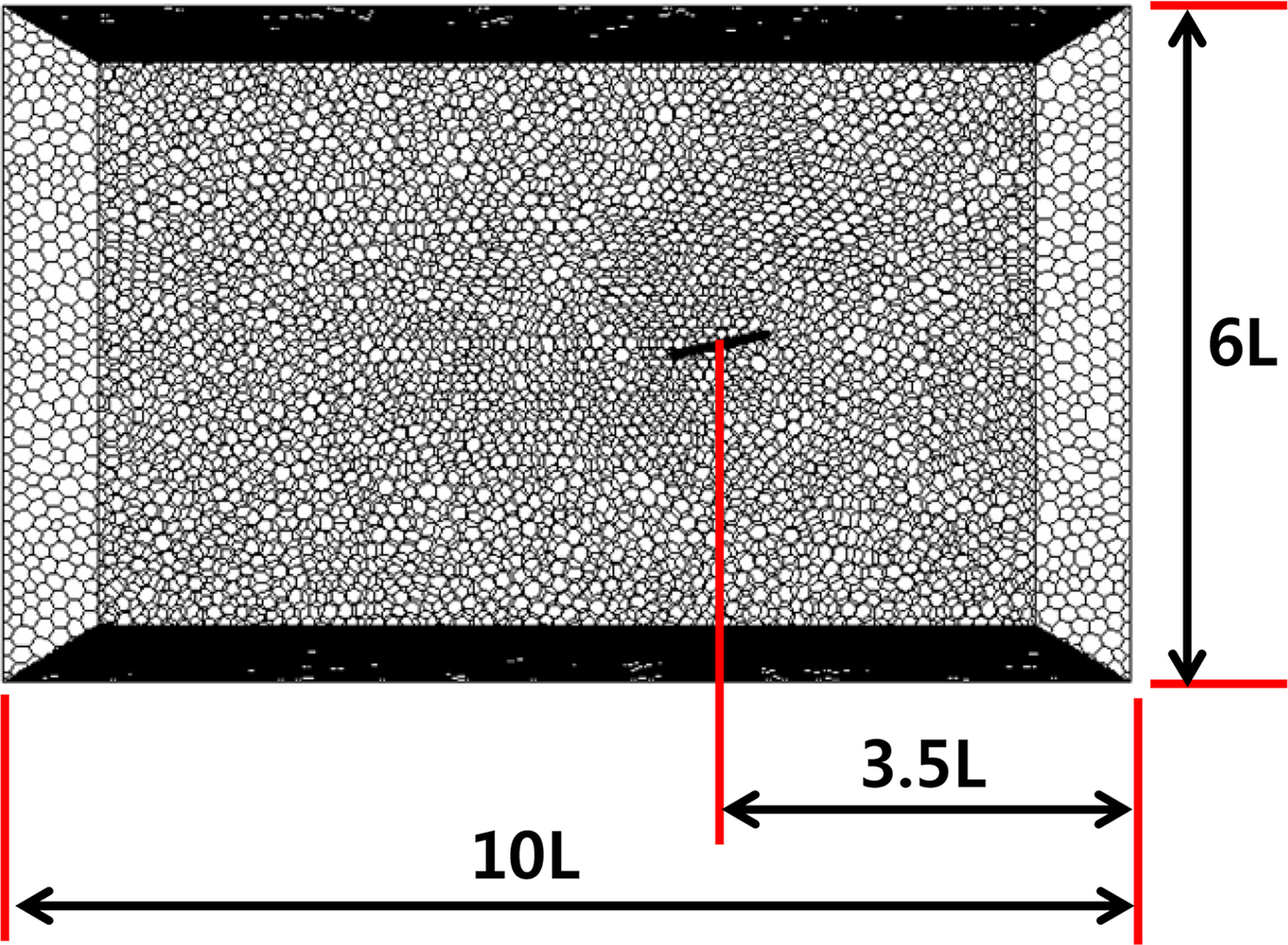
In static drift/rudder simulations, a rectangular domain was adopted, a velocity inlet condition was set at one end, and a pressure outlet condition was set at the other end. This is a very classical method to solve external flow problems. In rotating arm simulations, a cylindrical domain shaped like a donut was used, and the rotation of the vehicle was described by a moving reference frame method (Ansys Inc., 2018; Nguyen et al., 2018). The relative velocity in the moving reference frame is expressed as follows:
vr is the relative velocity in the moving frame, v is the absolute velocity in the stationary frame, ur is the velocity of the moving frame in the stationary frame, vt is the translational frame velocity, and ω is the angular frame velocity.
The domain size is large enough to avoid a blockage effect. A polyhedral mesh based on a tetrahedral mesh was basically adopted, and a prism layer was produced on the surface of the underwater vehicle body to solve the boundary layer flow (Ansys Inc., 2018). The shapes of the domain and mesh are shown in Figs. 6–7.
The propeller thrust affects the hydrodynamic characteristics of the underwater vehicle and changes the flow around it. However, if the detailed propeller configuration is described in the CFD model, the number of mesh elements increases greatly due to the complex geometry. This causes an increase of the computing resources and solution time. Therefore, we adopted the actuator disk theory to simulate propeller thrust. Actuator disk theory represents the thrust force by a pressure jump through a 2D membrane. The pressure jump can be calculated as follows:
T is the thrust, and A is the area of the disk (propeller surface), as shown in Fig. 8. In this study, the input value of thrust is defined as the propeller force in self-propulsion conditions of the vehicle speed and was obtained by self-propulsion tests in the towing tank of the Korea Research Institute of the Ship and Ocean Engineering (KRISO).

Pressure distribution around propeller and relation between thrust and pressure jump (Kim and Chung, 2007)
4.2 Governing Equations and Solver Setting
The governing equations of fluid mechanics are the continuity equation and momentum equations called the Navier-Stokes equations. The equations in the moving reference frame are as follows:
In the case of the stationary frame, ω and vt are 0 and vr equals v.
The k-ω SST turbulence model was applied, and the Semi-Implicit Method for Pressure Linked Equations – Consistent (SIMPLEC) was used as a pressure-velocity coupling scheme. The operating fluid is sea water, of which the density is 1025.87 kg/m3, and the viscosity is 0.00122 kg/m·s. Sea water is considered as an incompressible fluid. All CFD simulations in this study were performed in Ansys Fluent, which is well known and verified commercial CFD software.
4.3 Simulation Conditions
The hydrodynamic derivatives of the underwater vehicle are generally expressed in dimensionless forms. Eq. (4) with non-dimensional coefficients is as follows:
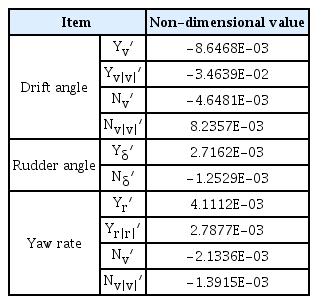
As examples of the notation, the non-dimensional derivative Yv′ means ∂Y′/∂v′, and Nr|r|′ means ∂N′/∂(r ′|r ′|).
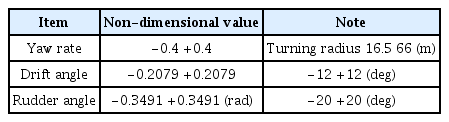
In this study, the ranges of the yaw rate, drift angle, and rudder angle were determined by considering the operating concept and mission of the underwater vehicle, as shown in Table 2. U is the overall speed of the underwater vehicle and is set to 10 kn (≒ 5.1 m/s). In the case of the rotating arm simulations, the turning radius changes as the yaw rate changes, and the overall speed is constant.
5. Results of the CFD Simulations
5.1 Results of the Static Drift/Rudder Simulations
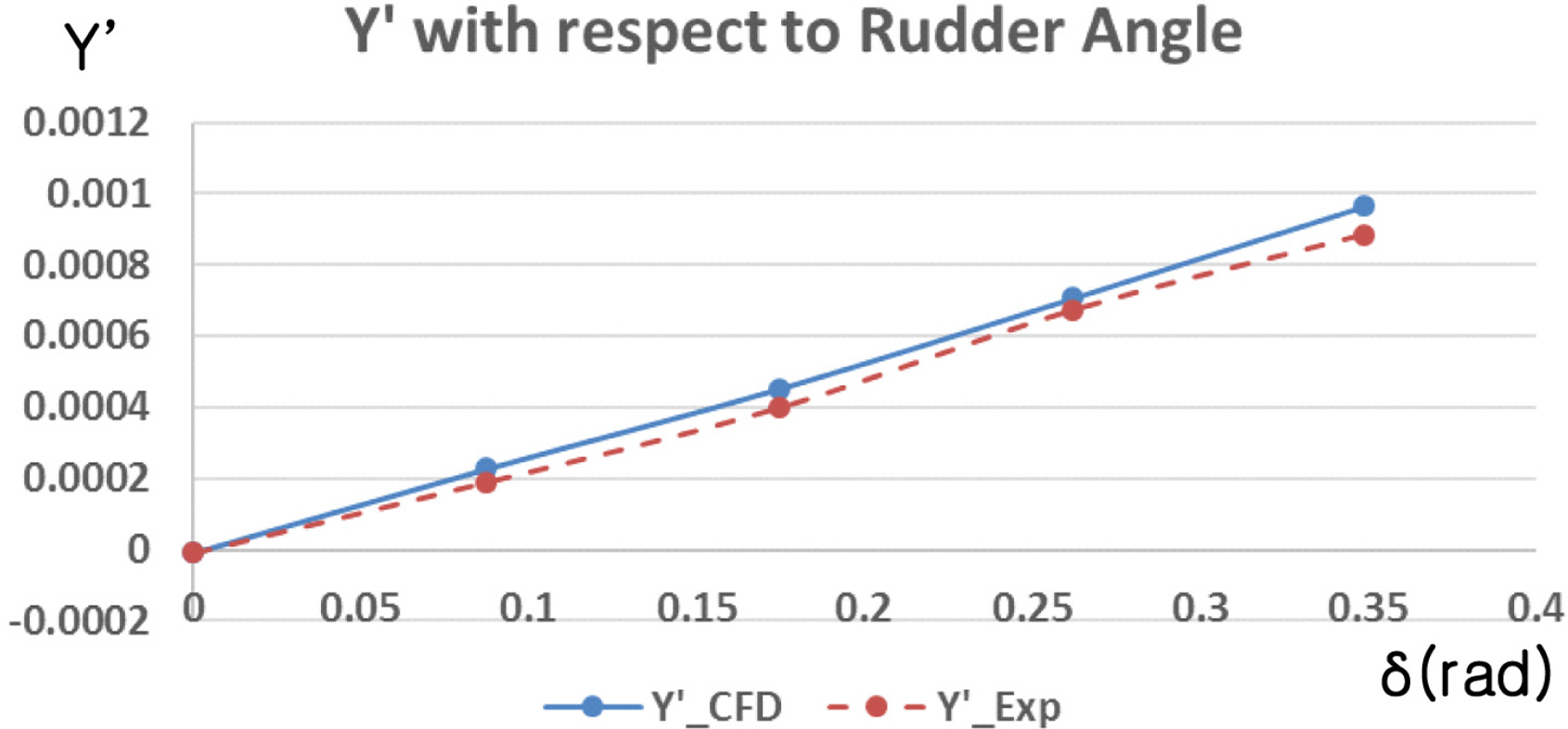
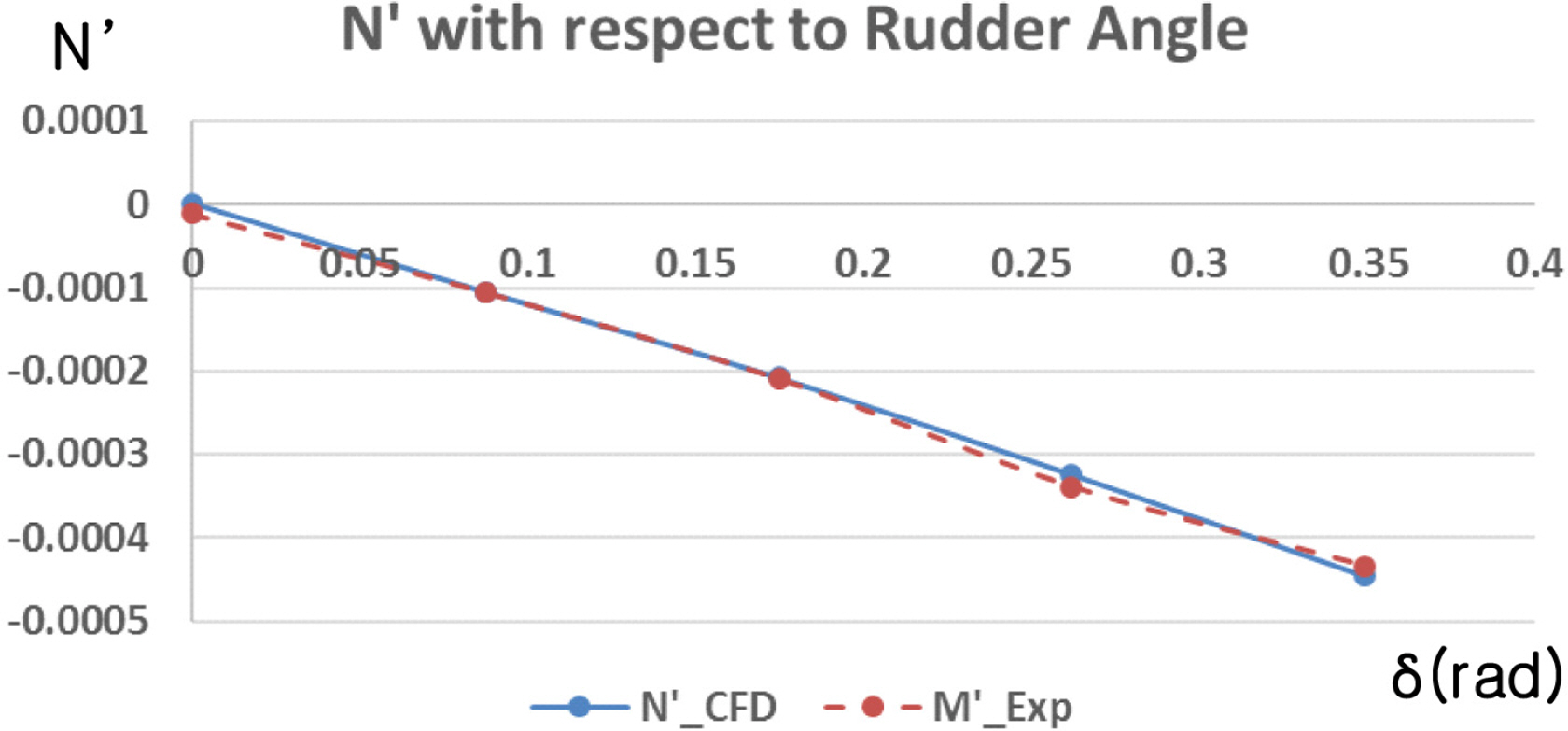
First of the all, static drift and rudder simulations were performed to obtain hydrodynamic data when the vehicle goes straight (r′ = 0). Since the vehicle is symmetrical, simulations for only positive v′ and δ were conducted, and then the simulation results were compared to VPMM test results from the towing tank of KRISO.
Fig. 9 shows the facilities at KRISO and the VPMM tests of the underwater vehicle used in this study. Static rudder simulations and experiments were performed in conditions where two rudders are all actuated with the same value. The towing speed was 2.29 m/s, which is lower than the CFD simulations because a free surface effect can occur at high speed in VPMM tests.
The hydrodynamic force and moment with respect to the drift angle and rudder angle are presented in Figs. 10‒13. Although there are some errors at high drift angle (large v′), the simulation results follow the tendency of the experiments well and have feasibility for predicting to the hydrodynamic derivatives of the underwater vehicle. According to the operating concept of the underwater vehicle, it is very rare that the drift angle is larger than 10 degrees (v′ = 0.1736) during all flight times.
It is still difficult to predict the wake flow characteristics past a body with a high angle of attack using the RANS method. In addition, the gap between the top of the vehicle and free surface is narrow at high drift angle. When the drift angle is 0 degrees, the depth of the vehicle is 2.2 m. As the drift angle changes to 12 degrees, the minimum gap between the vehicle and free surface is reduced to 1.3 m. This may have a slight effect on the results.
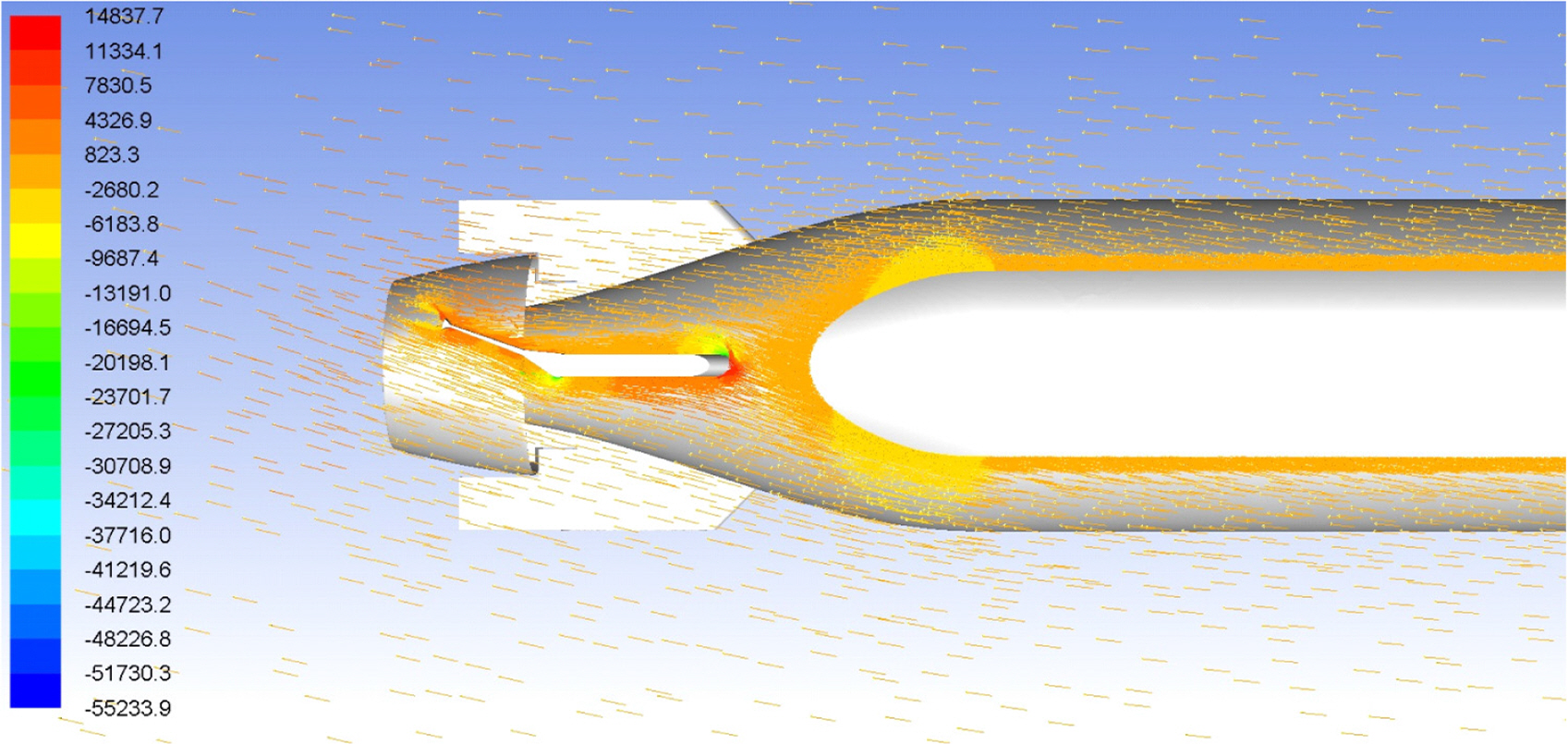
Fig. 14 shows the flow vector field and pressure distribution around the stern body of the underwater vehicle in the case of the static rudder simulations. The change of velocity due to the fin angle makes a pressure distribution on the fin surface, and the pressure distribution makes a force and moment that act on the vehicle (Huang et al., 2015).
5.2 Results of Rotating Arm Simulations with Drift/Rudder Angle
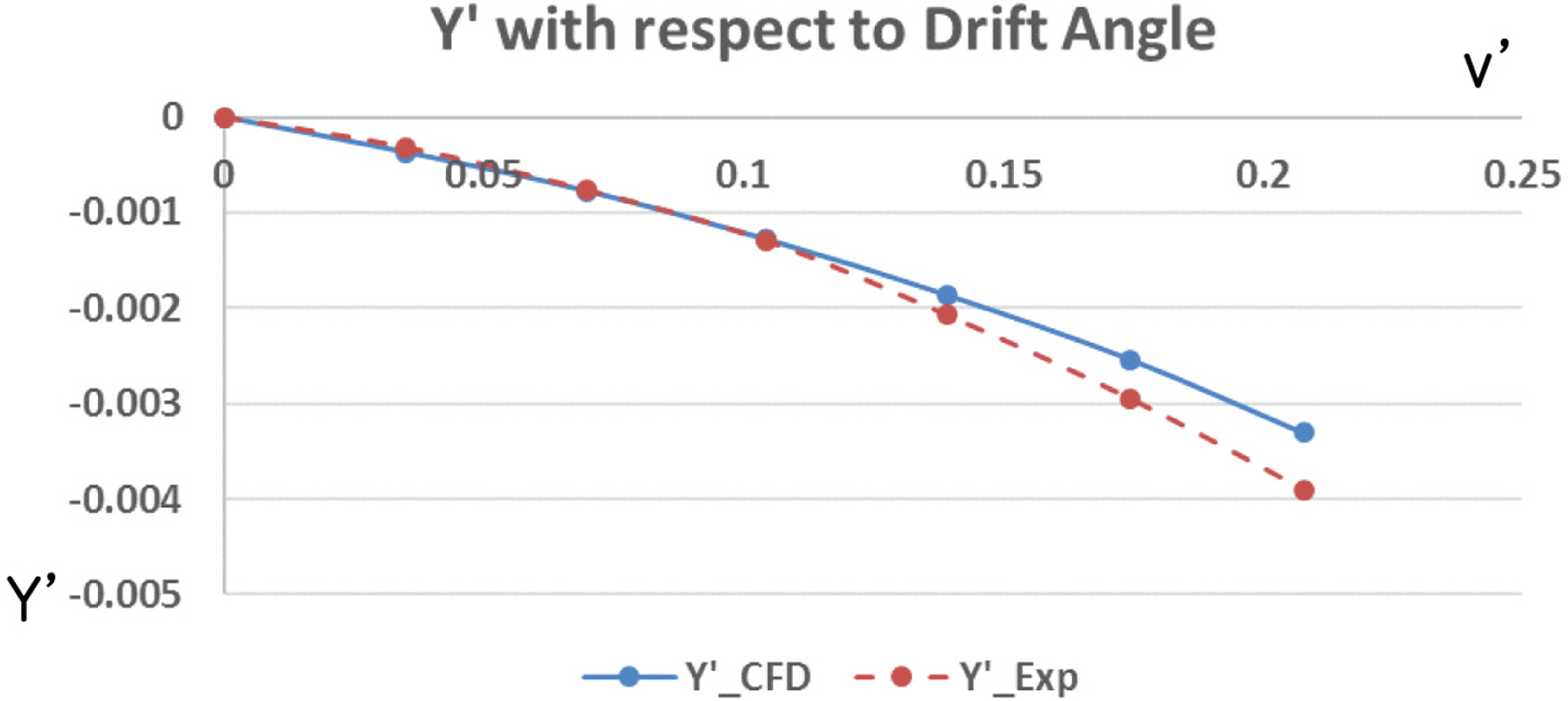
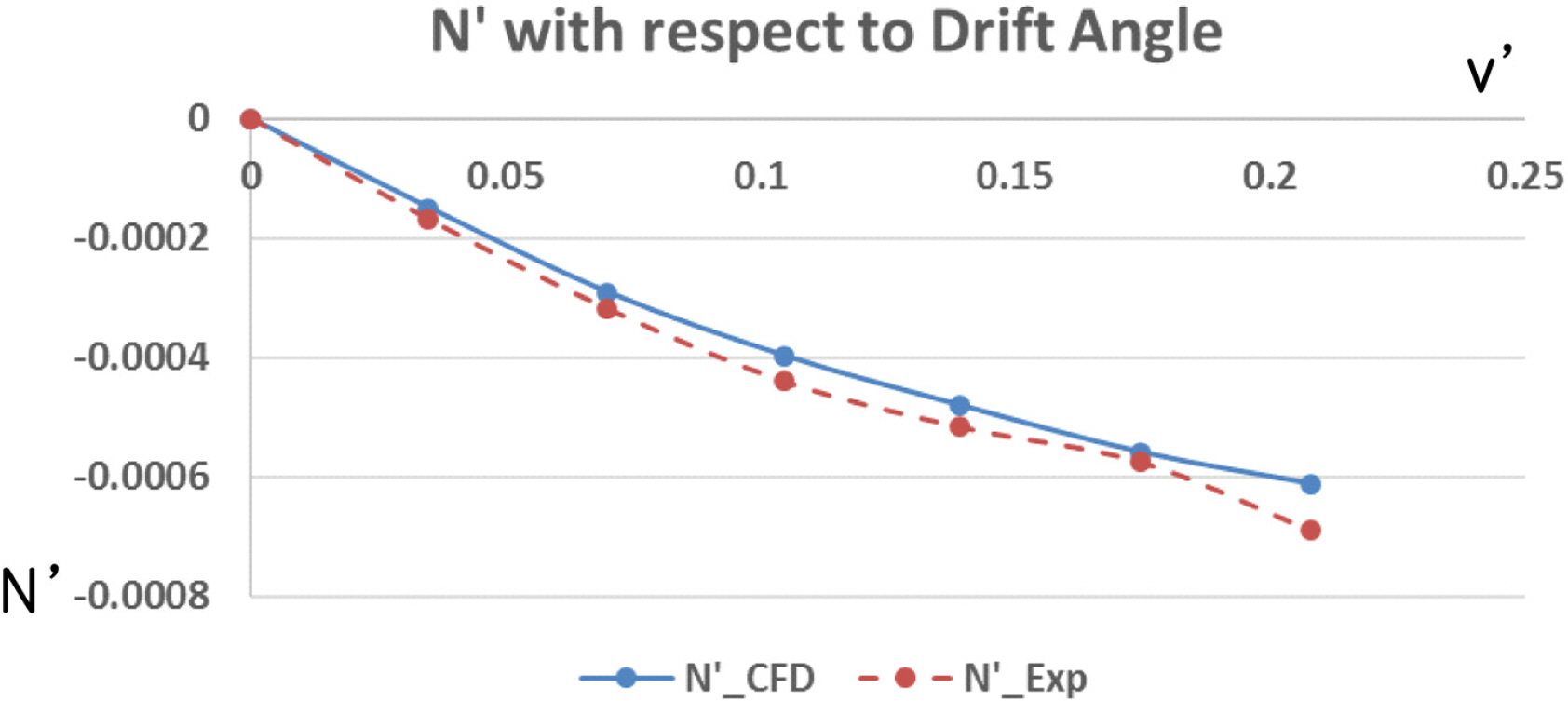
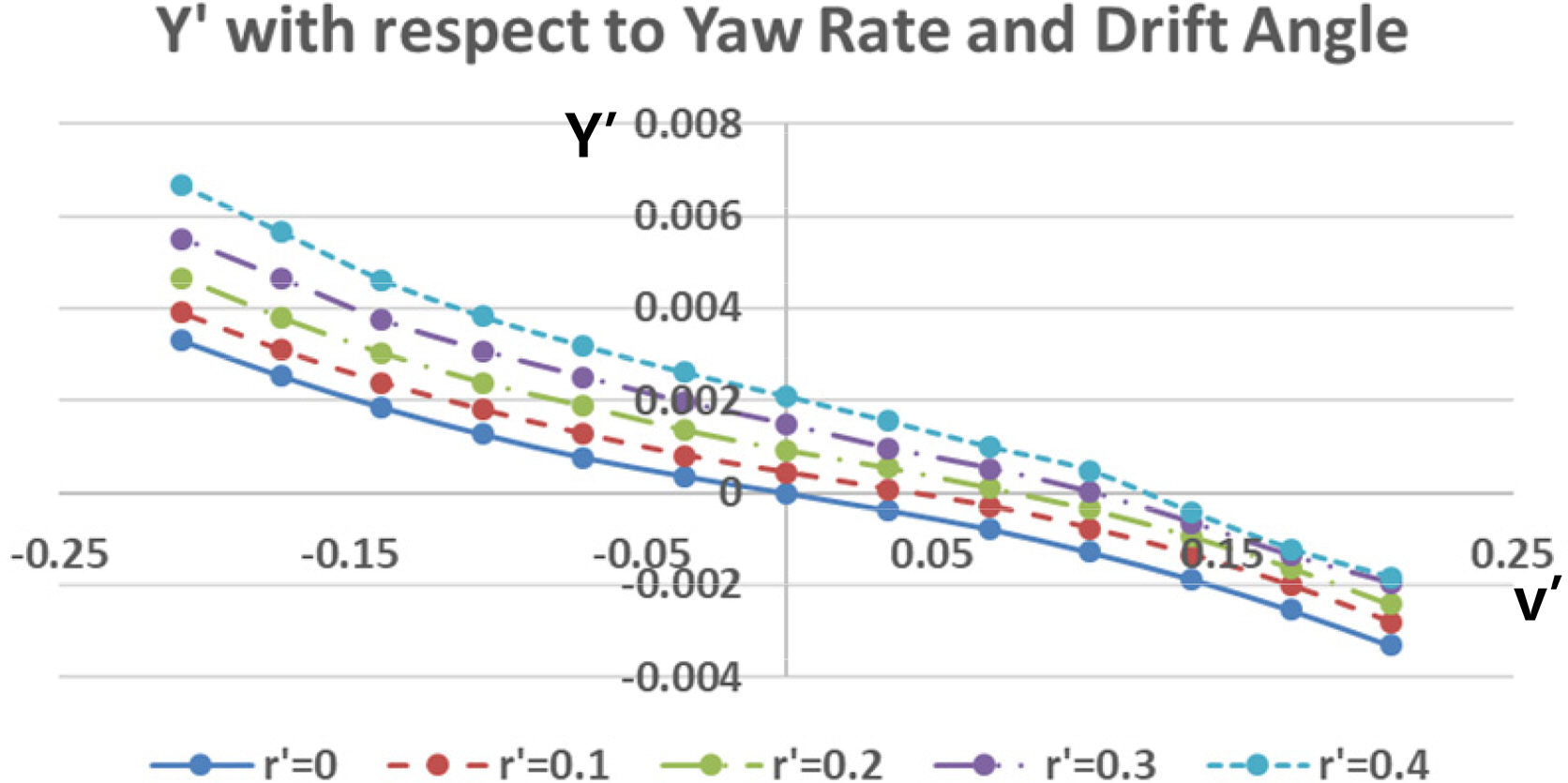
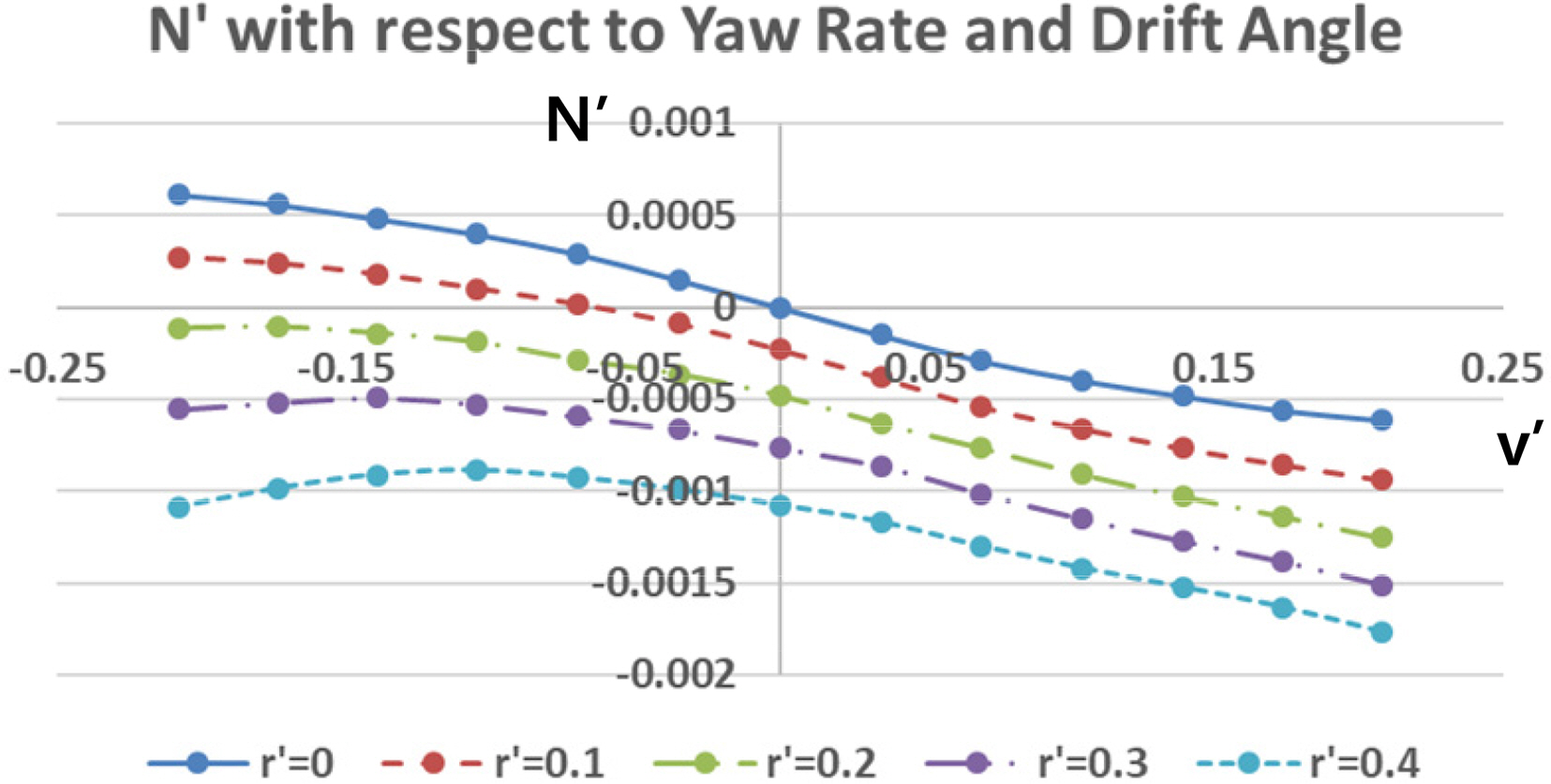
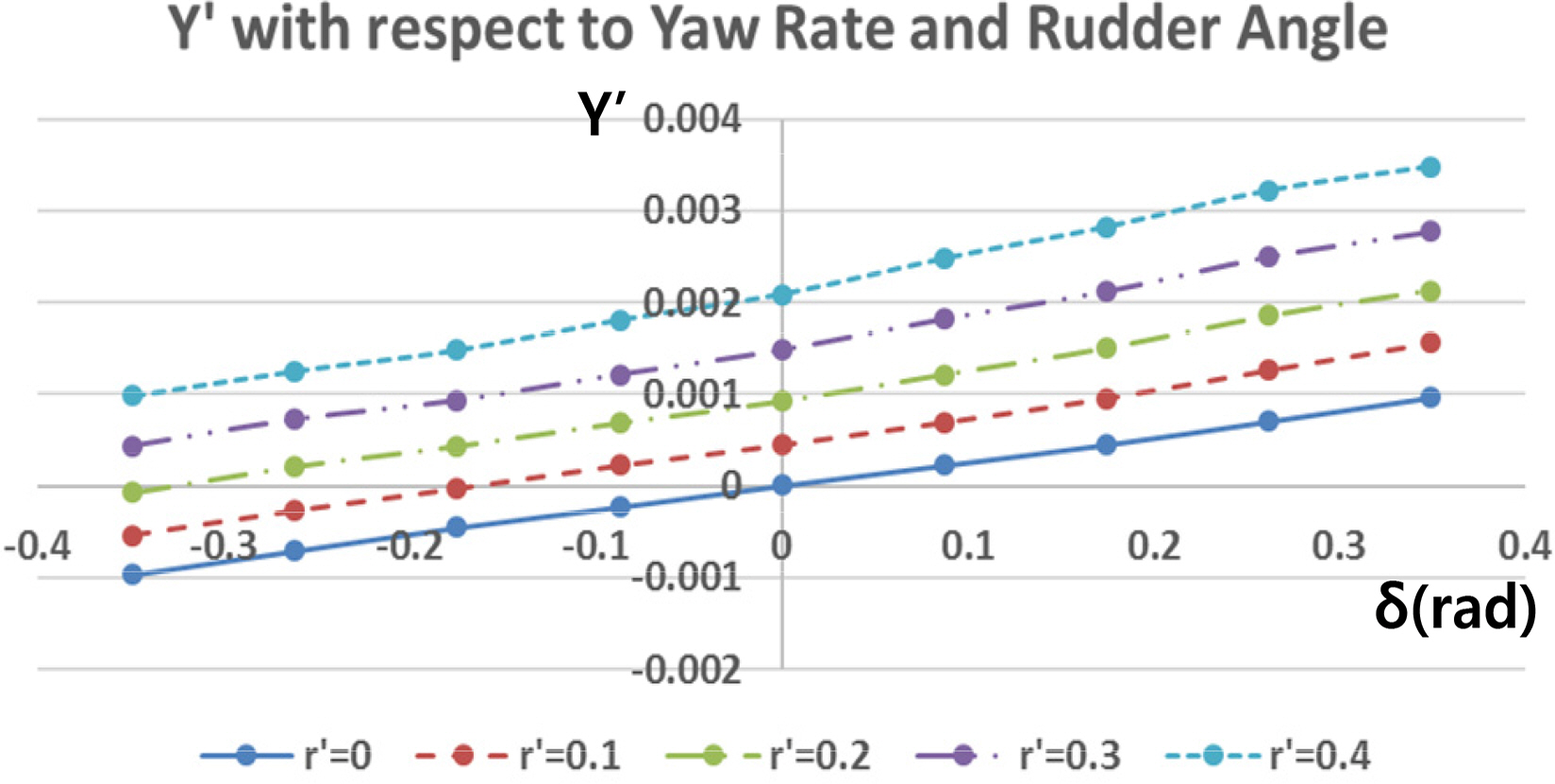
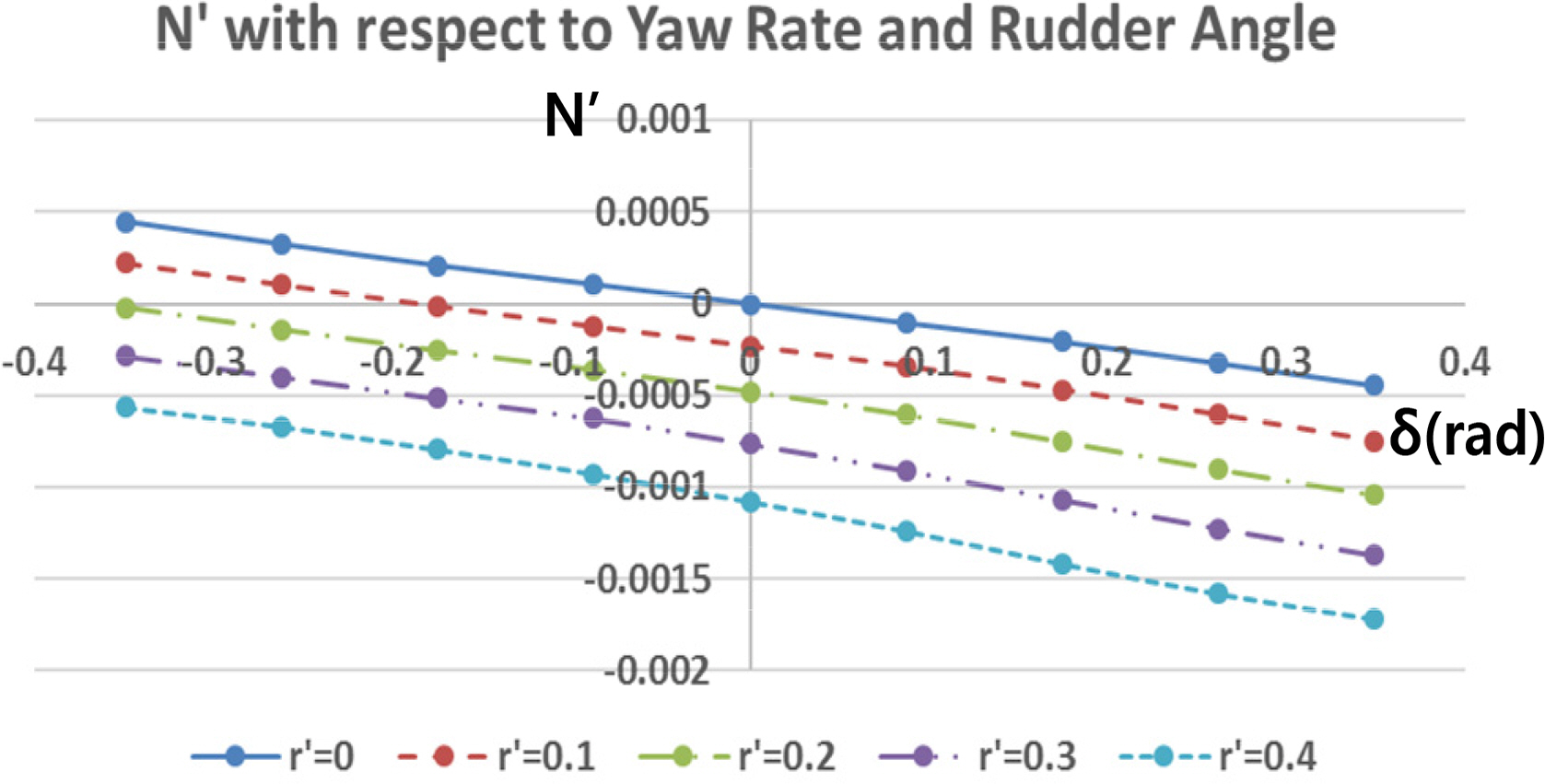
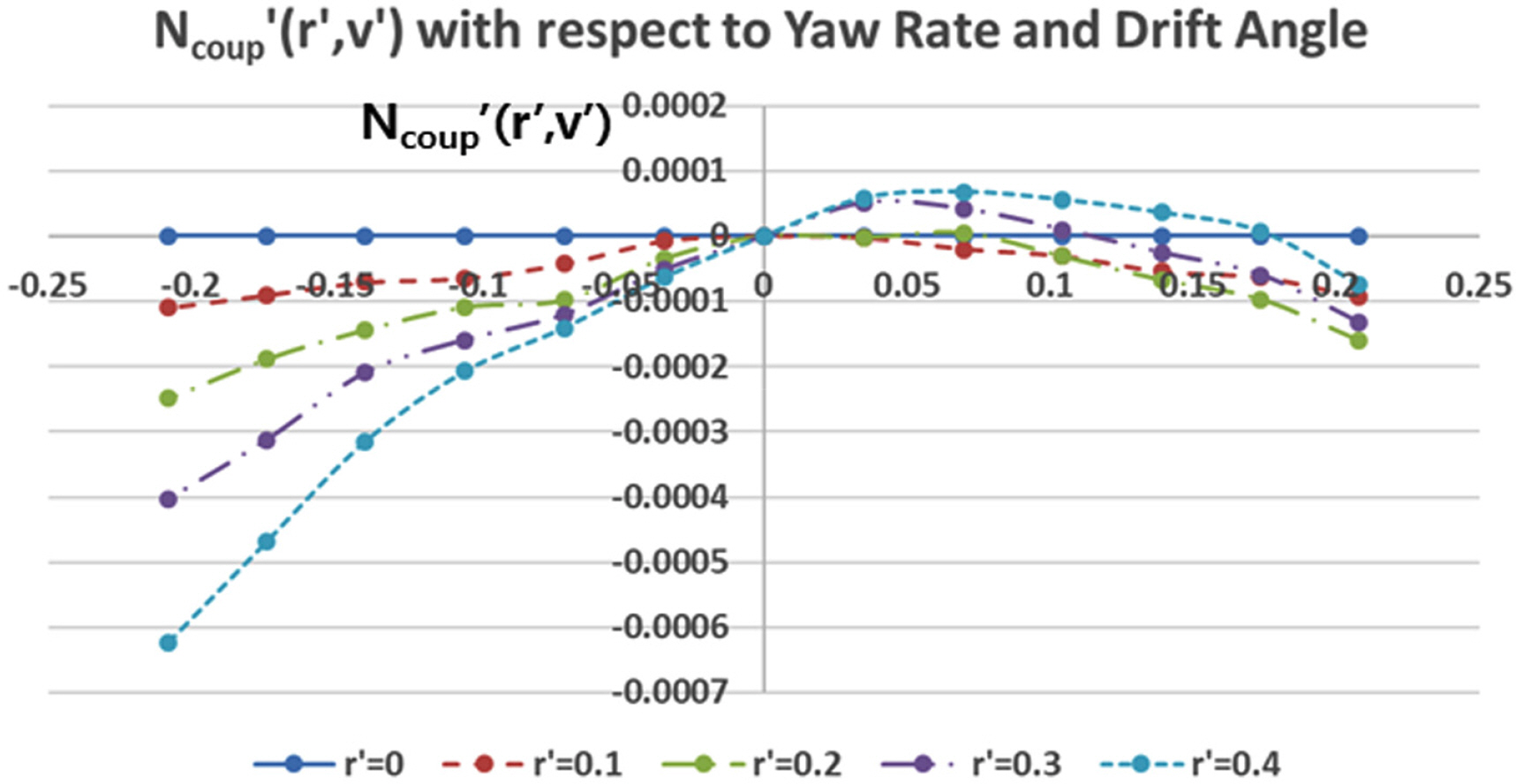
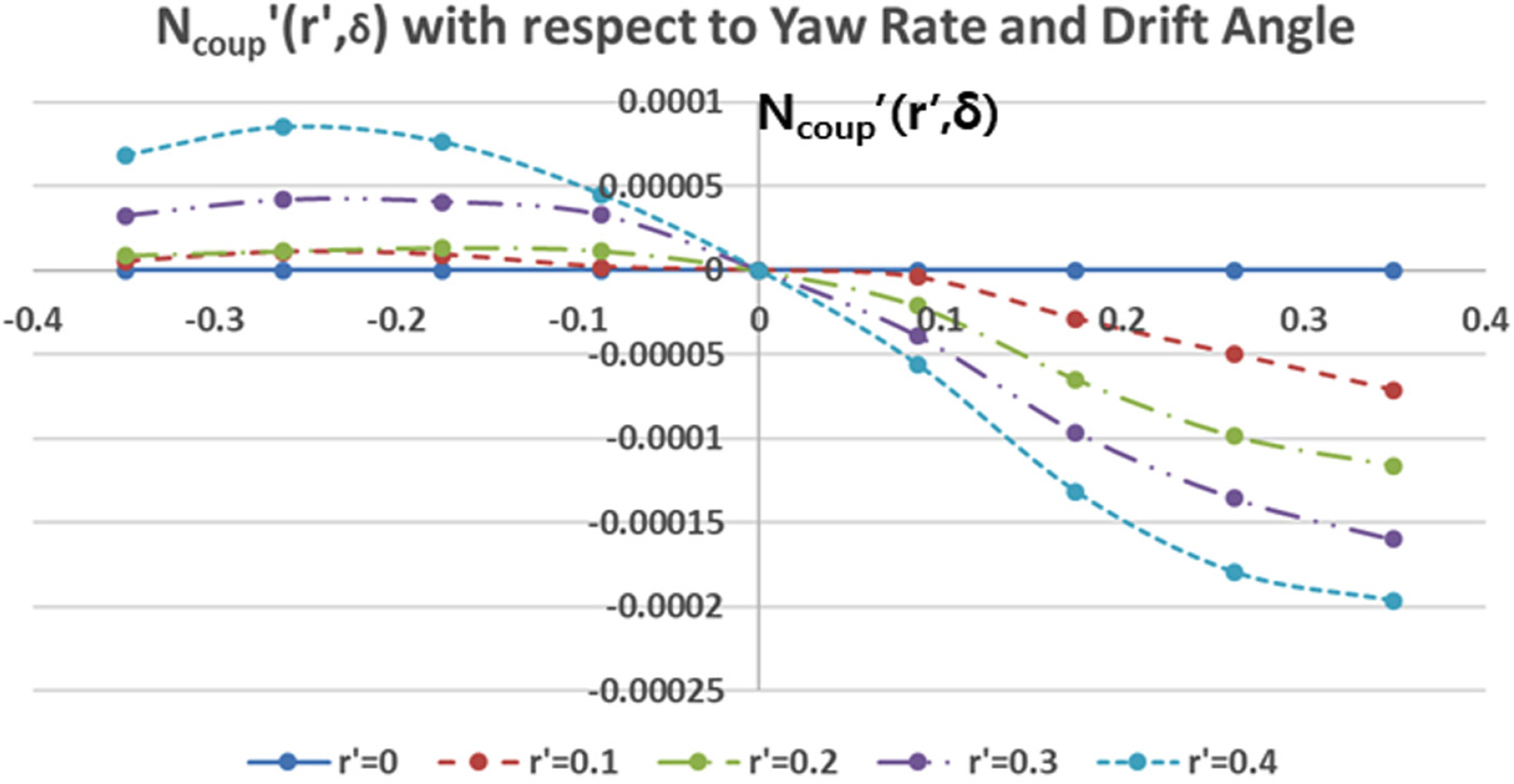
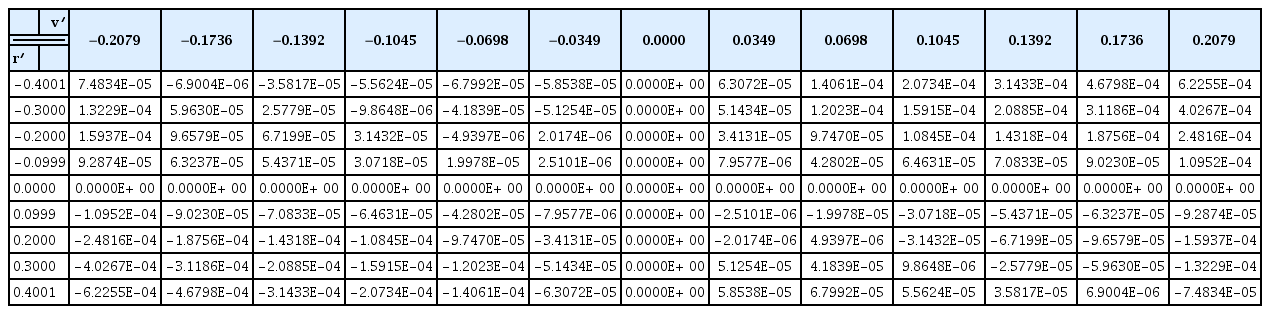
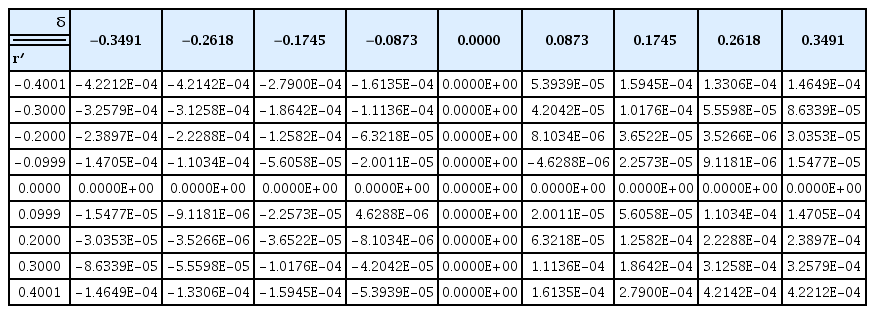
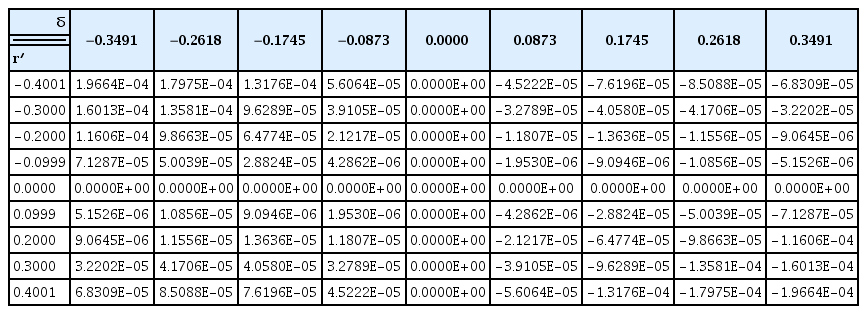
Rotating arm simulations with the drift angle and rudder angle were carried out to estimate the rotary derivatives and coupled hydrodynamic terms. The simulations for only positive r′ and the whole range of v′ and δ were conducted because the vehicle is symmetrical, but the relative direction between yaw rate and drift/rudder angle can affect the tendency of the interactions. Figs. 15–16 show the total non-dimensional force Y′ and moment N’ for the yaw rate and drift angle, and Figs. 17–18 show the results for the yaw rate and rudder angle.
The results when r′ = 0 are the same as in the static drift and rudder simulations, and rotary derivatives for the yaw rate can be estimated from the results when v′ = 0 and δ = 0. If there is no interaction between them, the shape of the force and moment graphs will coincide regardless of the yaw rate. However, the shape of the graphs changes according to the yaw rate.
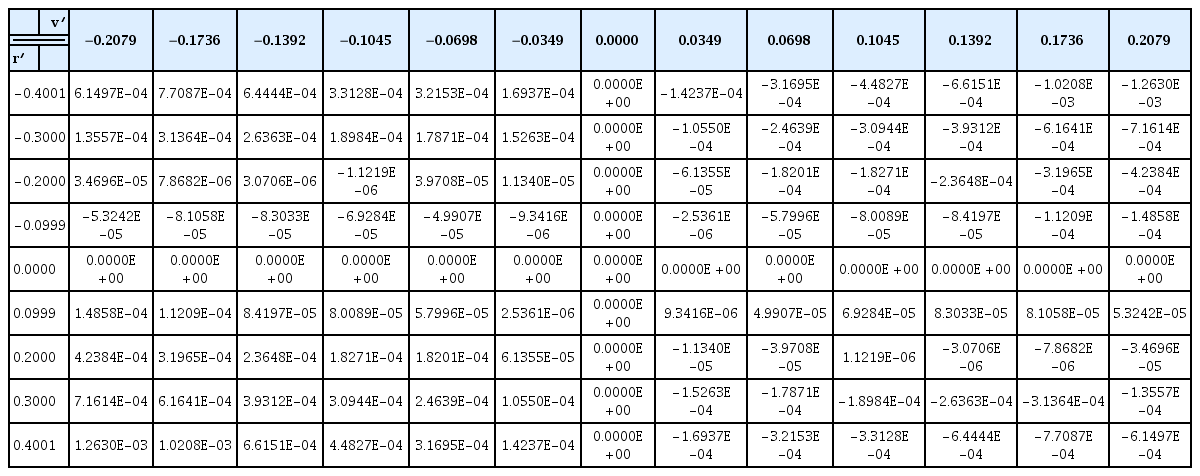
In order to analyze the interactions between the yaw rate and drift/rudder angle, coupled terms were separated from the total force and moment. The total force and moment consist of terms for the yaw rate, drift angle, rudder angle, and coupled terms. The terms of the yaw rate are obtained from rotating arm simulations without the drift and rudder angle, those of the drift angle are obtained from static drift simulations, and those of the rudder angle are obtained from static rudder simulations. The coupled terms can be calculated as follows:
The coupled terms have different tendencies with respect to the relative direction between the yaw rate and drift/rudder angle, as shown in Figs. 19‒22. We predicted that these tendencies would be caused by the change of the flow’s incidence angle and tangential velocity of the partial vehicle body. When the yaw rate (r′) is positive and the drift angle (v′) is negative (in other words, the bow of the vehicle is heading for the inside of the turning circle), the tangential velocity of the bow becomes slower, and that of the stern becomes faster because the partial turning radius changes. In addition, the flow incidence angle of the bow becomes smaller, and that of the stern becomes bigger, as shown in Fig. 23(b). These phenomena become stronger as the yaw rate increases.
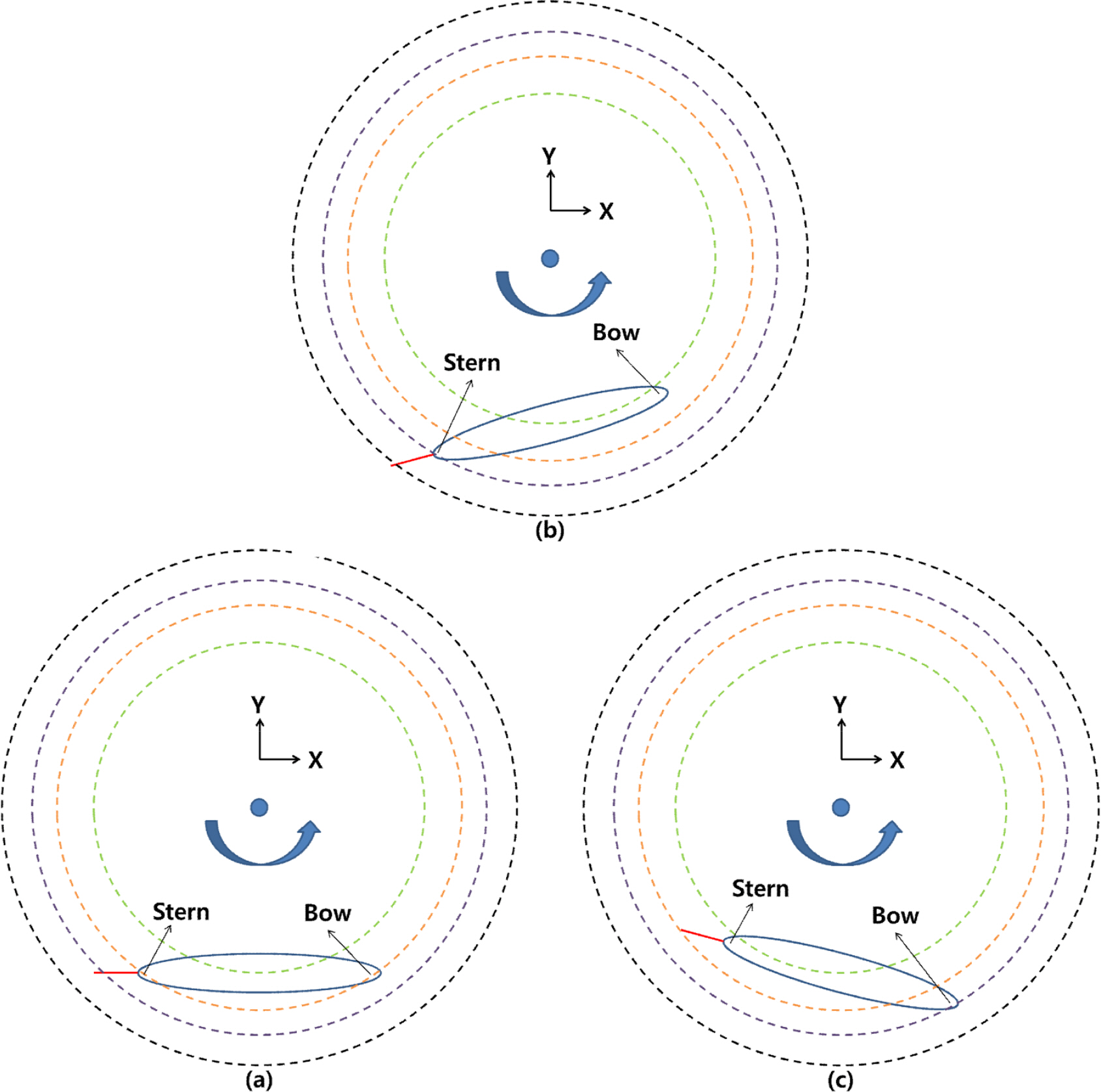
The change of the turning radius and flow incidence angle of the partial vehicle body in turning motion (a) without drift angle (b) when yaw rate is positive and drift angle are negative (c) when yaw rate and drift angle are both positive
In contrast, when the yaw rate (r′) and drift angle (v′) are both positive (in other words, the bow of the vehicle is heading for the outside of the turning circle), the tangential velocity of the bow becomes faster, that of the stern becomes slower, the flow incidence angle of the bow becomes bigger, and that of the stern becomes smaller, as shown in Fig. 23(c). However, in this direction, the interaction force and moments are weak compared to the opposite direction.
In the case of the simulations with a coupled yaw rate and rudder angle, the same analysis can be applied. When the yaw rate (r′) is positive and the rudder angle (δ) is negative, the tangential velocity of the rudder becomes slower, and flow’s incidence angle becomes smaller, as shown in Fig. 24(b). Therefore, reduction of the sway force and yaw moment increases as the yaw rate increases. In contrast, When the yaw rate (r′) and rudder angle (δ) are both positive, the tangential velocity of the rudder becomes faster, and flow’s incidence angle becomes bigger, as shown in Fig. 24(c). Therefore, the additional sway force and yaw moment increase as the yaw rate increases. Fig. 25 shows the velocity distribution of the whole domain in the case of the rotating arm simulations.

Change of turning radius and flow incidence angle of partial vehicle body at turning motion (a) without rudder angle (b) when yaw rate is positive and rudder angle are negative (c) when yaw rate and rudder angle are both positive
5.3 Estimation of Hydrodynamic Derivatives
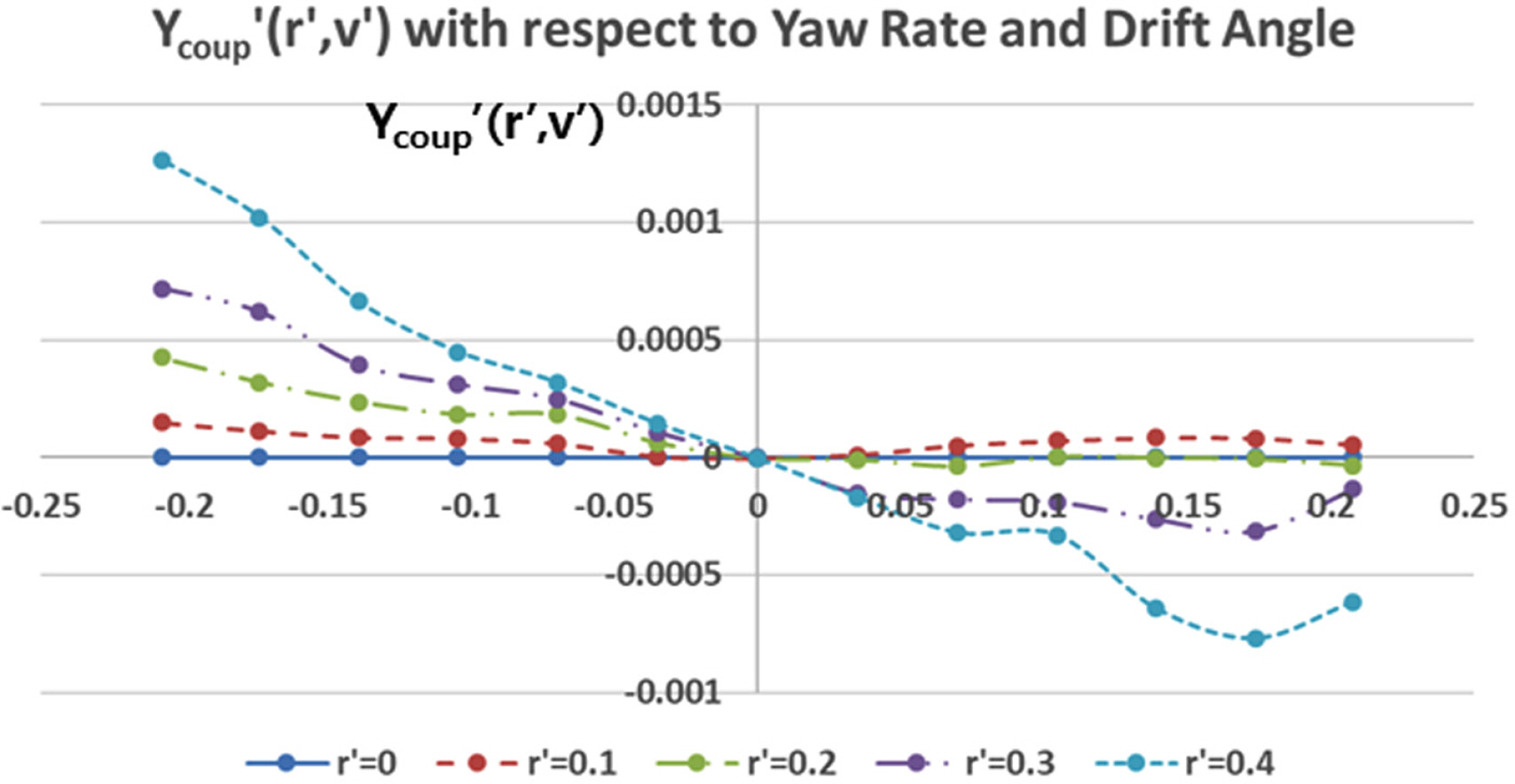
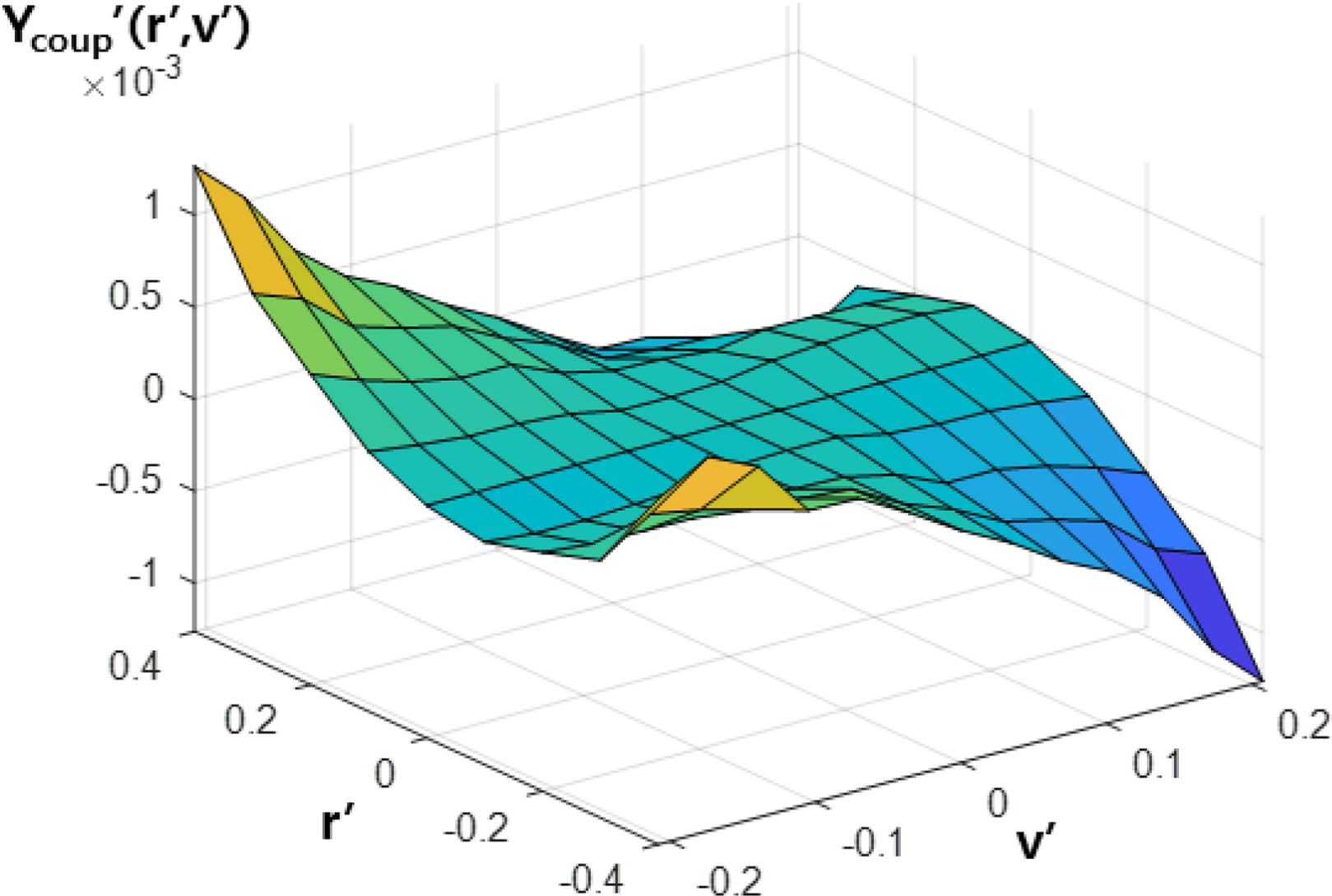
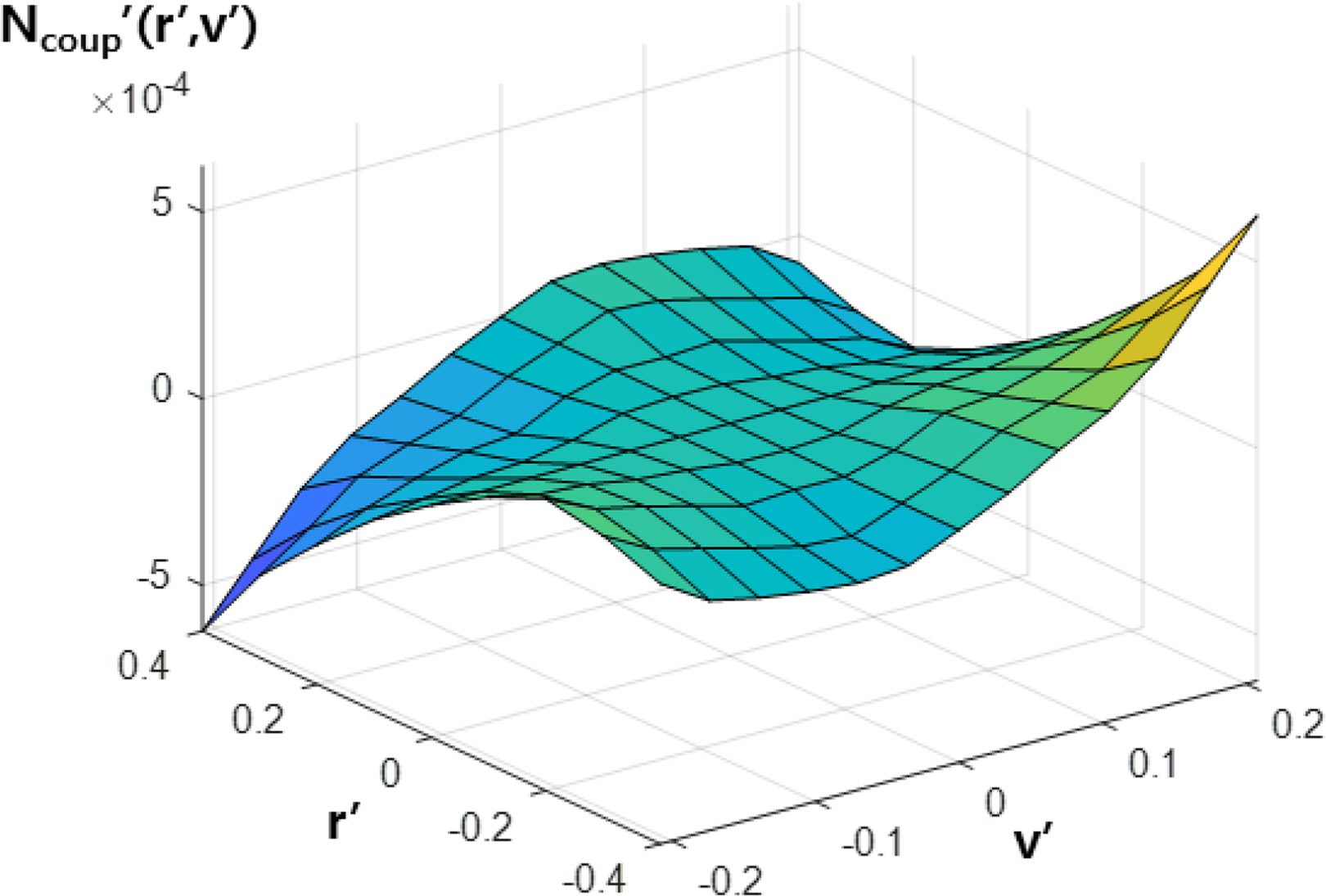
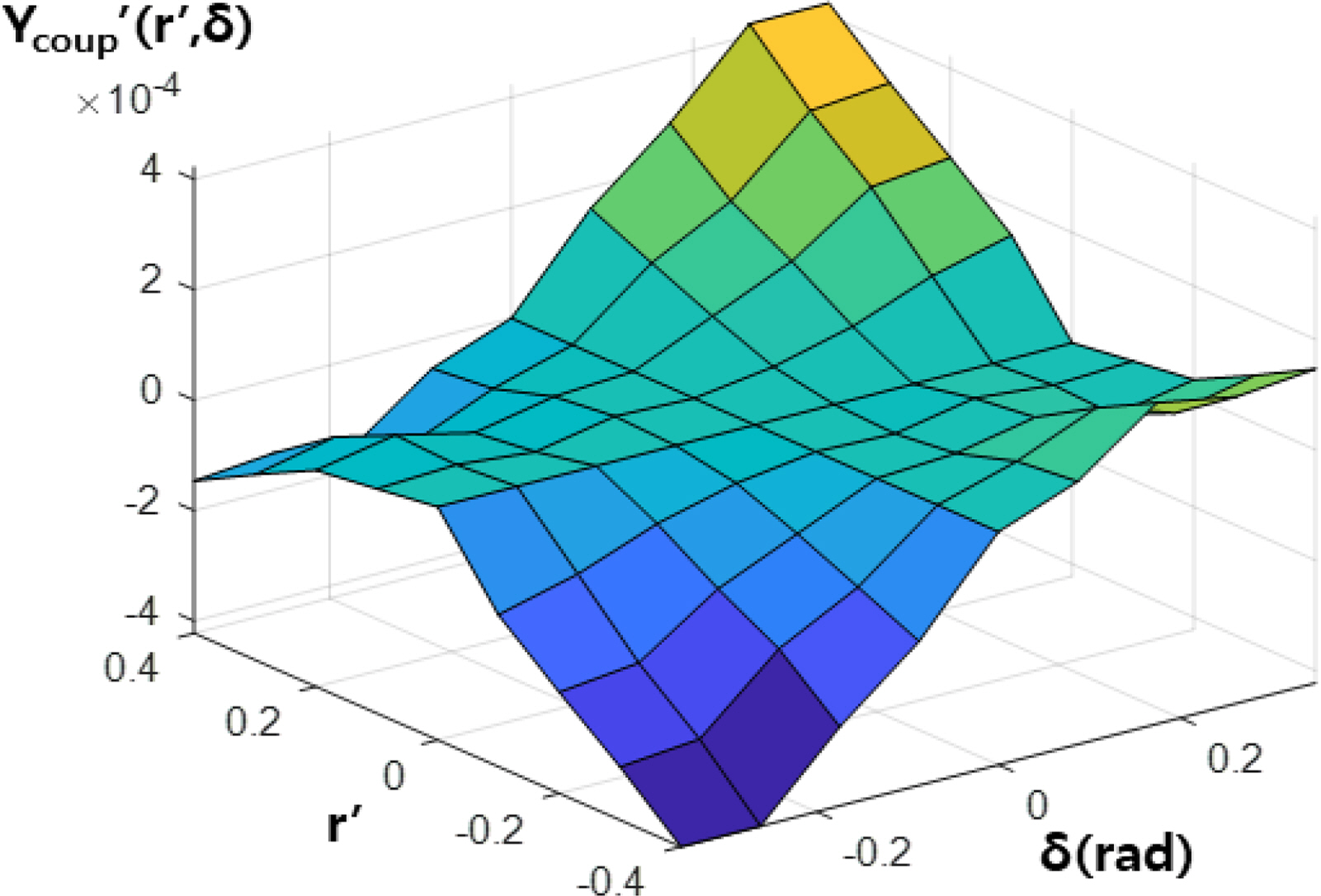
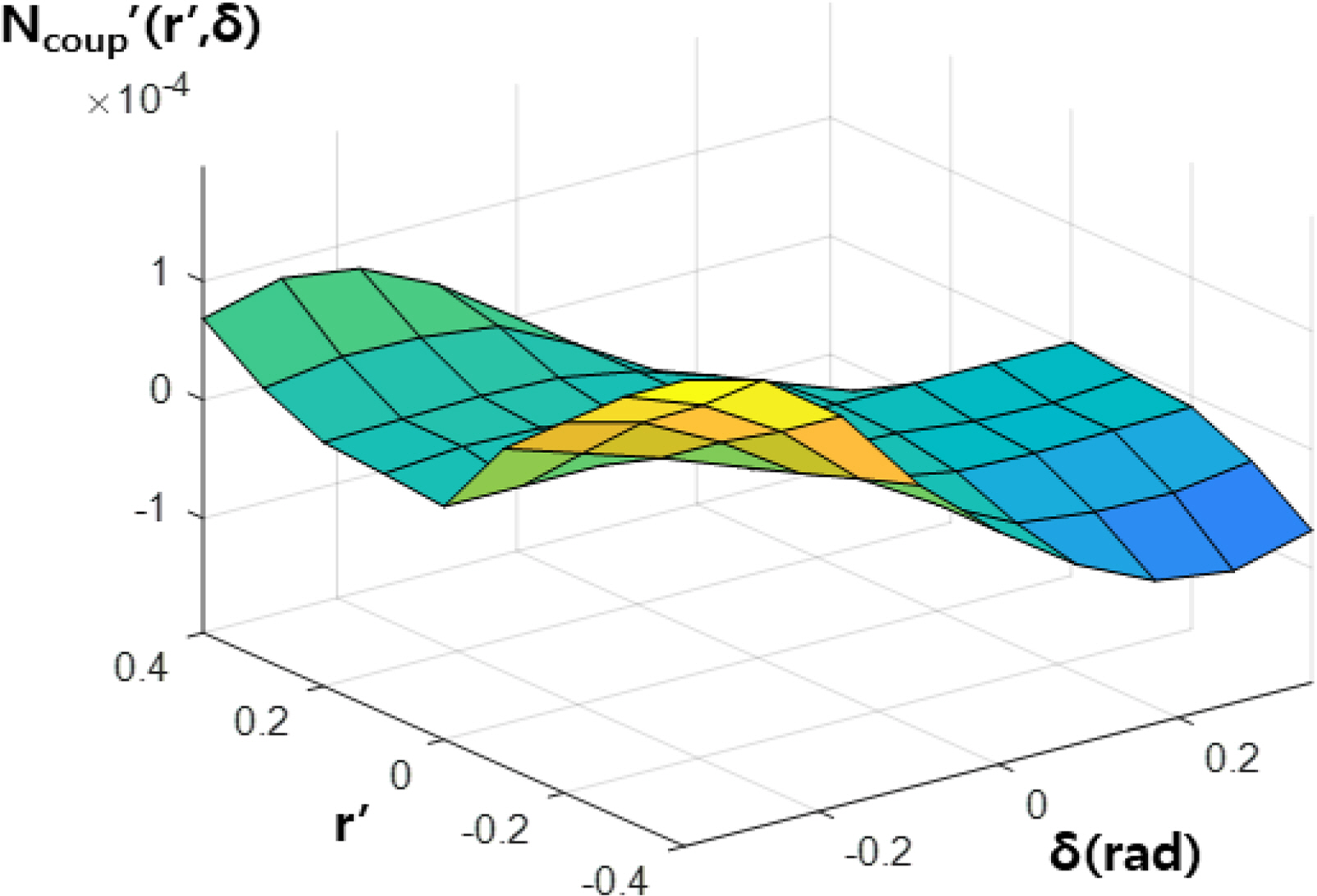
The static coefficients for the drift and rudder angle were obtained from static drift and rudder simulations, and the rotary coefficients for the yaw rate were obtained from rotating arm simulations without the drift and rudder angle. The derivatives were calculated by the least-squares method, as shown in Table 3. Interaction terms are too difficult to define as coefficients because they have strong non-linearities. Therefore, the coupled hydrodynamic force and moment are functions of the yaw rate and drift angle/rudder angle and are calculated by an interpolation method from the data shown in Tables 4–7. These coupled terms are applied to simulate the turning motion of the underwater vehicle. Figs. 26‒29 show 3D contours of the coupled hydrodynamic force and moment from Tables 4–7.
6. Results of Turning Motion Simulations and Sea Trial of Underwater Vehicle
Based on hydrodynamic force and moment data from CFD, motion simulations were performed. Combining Eqs. (3), (4), (8), and (9) and removing high-order terms, 2-DOF equations of motion for the sway and yaw were constructed as follows:
The sway velocity (v) and yaw rate (r) in the body-fixed frame were calculated by solving these equations. The surge velocity (u) was considered as constant. The values in the body-fixed frame were then transformed to the earth-fixed frame using Eq. (3), and the turning radius and drift angle were obtained by deriving the trajectory and attitude of the vehicle. The simulations were carried out using MATLAB.
Three kinds of simulations were performed. In one of them, coupled hydrodynamic forces and moments are not applied (Case A). In another, only coupled terms between the yaw rate and drift angle (Ycoup′(r′,v′) and Ncoup′(r′,v′)) are applied (Case B). In the third one, all coupled terms (Ycoup′(r′,v′), Ncoup′(r′,v′), Ycoup′(r′,δ) and Ncoup′(r′,δ)) are applied (Case C). The initial velocity is 4.15 m/s because this it makes it easy to compare the results with sea trial data. The rudder angle was set to −20 degrees to turn with a positive yaw rate.
Next, we performed a sea trial with a vehicle that has the same geometry as in the simulations. After level flight via way-points, the underwater vehicle steadily turned for 3 minutes with a rudder angle of −20 degrees. An inertial measurement unit (IMU) measured the translational acceleration and angular rate of the underwater vehicle, and a guidance and control unit (GCU) calculated and recorded flight data such as the velocity and Euler angles in the earth-fixed frame and the yaw rate in the body-fixed frame. During the sea trial, the speed and depth of the underwater vehicle were constantly controlled. Fig. 30 shows the scenario of the sea trial in this study.
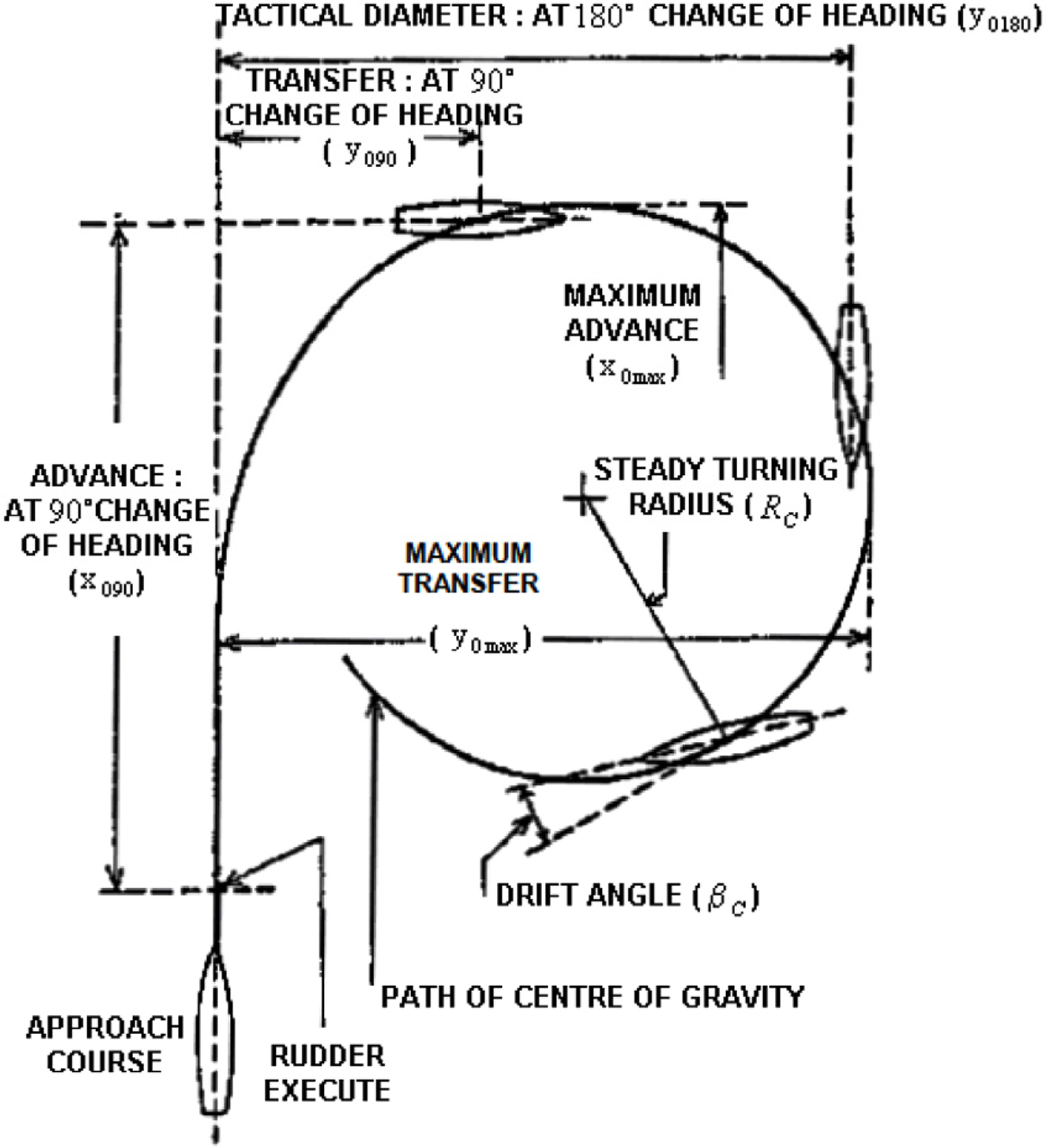
Through the simulation and sea trial, we can obtain the turning performance, turning radius, drift angle, advance, and tactical diameter. These are defined in Fig. 31. In the case of the sea trial, the turning radius can be calculated with the yaw rate and overall speed (R = U/r.), and the drift angle can be calculated with the difference between the Euler angle and the flow’s incidence angle from the X velocity and Y velocity in the earth-fixed frame. The advance and tactical diameter are estimated with the Euler angle, X velocity, and Y velocity in the earth-fixed frame.
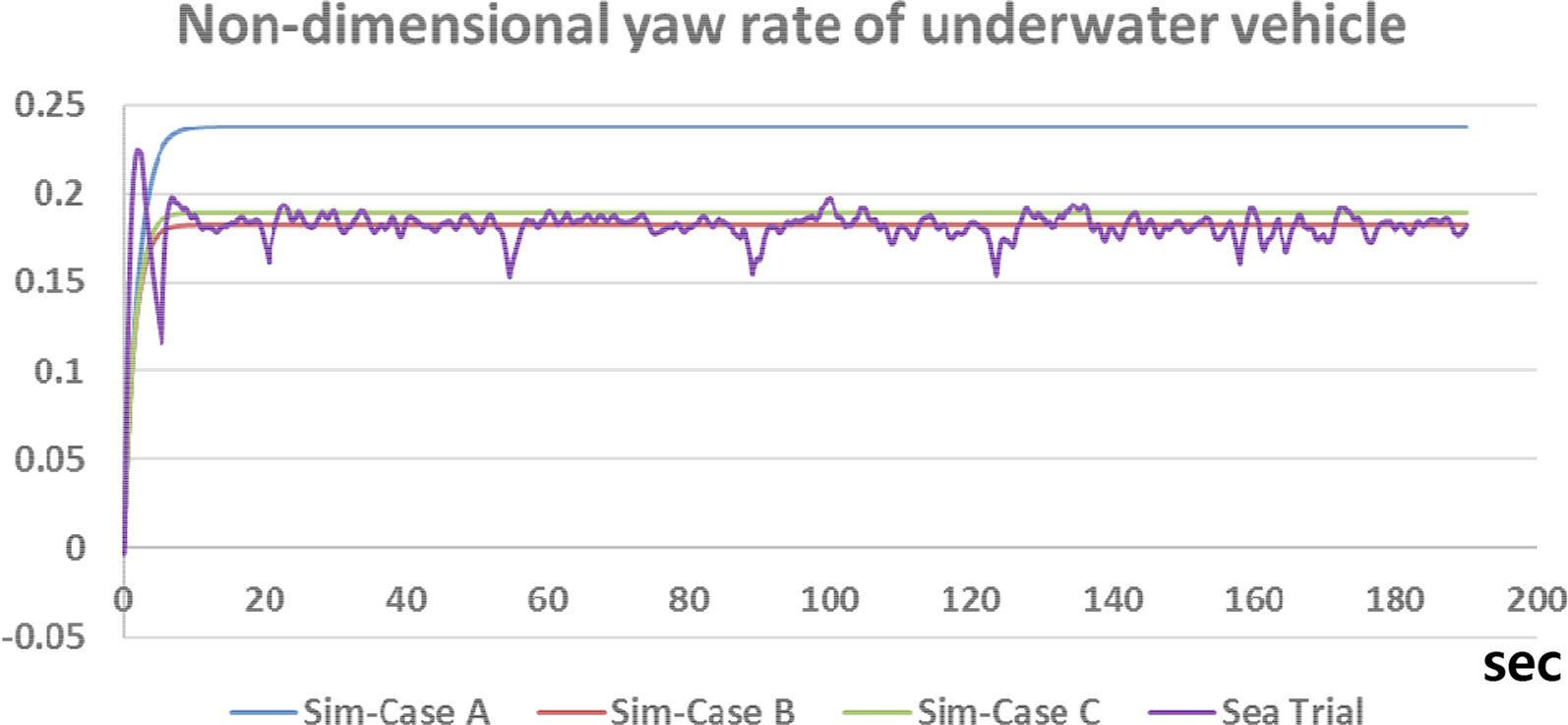
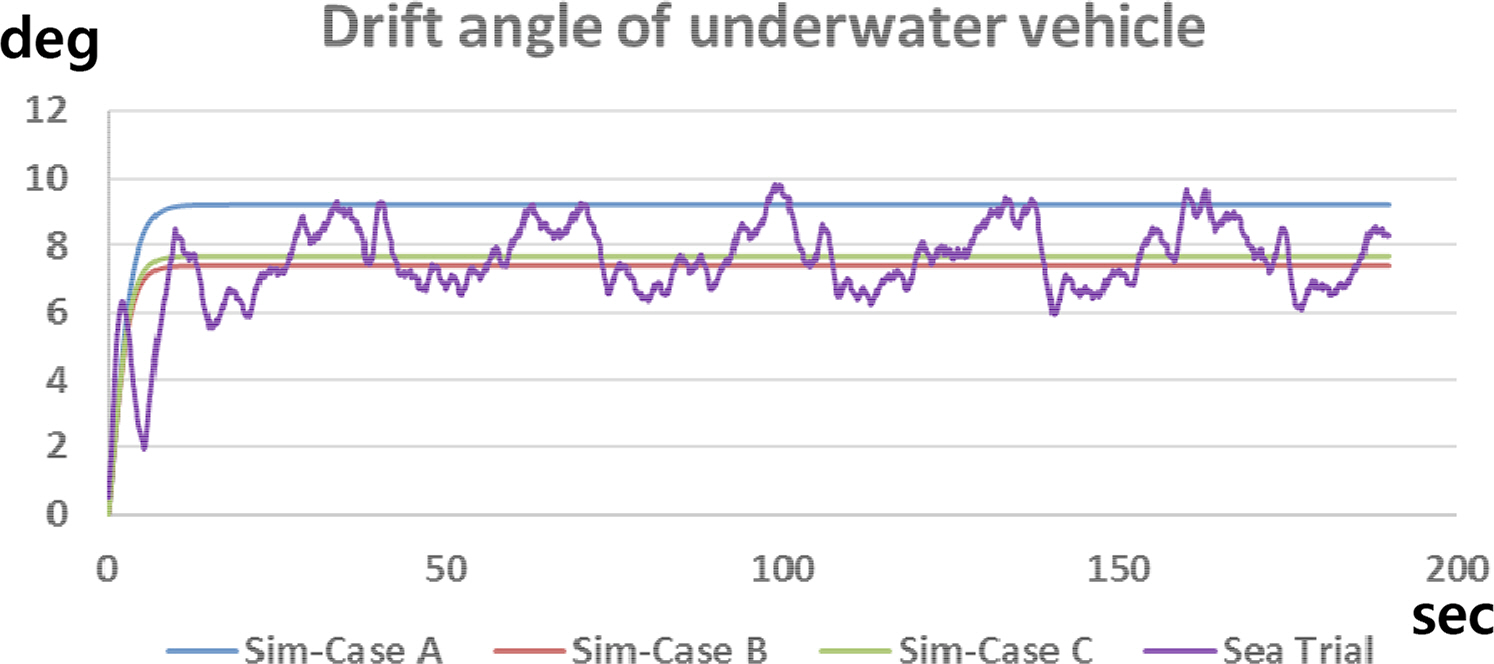
The simulation and sea trial results of the turning motion are shown in Table 8. These values are the average of the steady turning period of the underwater vehicle for 3 minutes. The non-dimensional yaw rates (r′ = rL/U ) are 0.289–0.377, which is in the range of the CFD analysis (0–0.4). When coupled terms are not included, the turning radius, advance, and tactical diameter are smaller, and the drift angle is bigger than the sea trial data.
When coupled terms between the yaw rate and drift angle (Ycoup′(r′,v′) and Ncoup′(r′,v′)) are included, the turning radius, advance, and tactical diameter become bigger, and the drift angle becomes smaller because additional force and moment opposite to the rotational direction are produced by the interaction. When coupled terms between the yaw rate and rudder angle (Ycoup′(r′,δ) and Ncoup′(r′,δ)) are included, the turning radius, advance, and tactical diameter become smaller, and the drift angle becomes bigger because additional force and moment in the rotational direction are produced by the interaction.
The additional force and moment from the coupled terms of the simulation (Case C) are shown in Figs. 32–33. The simulation results considering the coupled hydrodynamic force and moment terms agree well with the sea trial results, and the interactions between the yaw rate and drift/rudder angle affect the turning performance of the underwater vehicle. In particular, the effects of the coupled terms for the yaw rate and drift angle are critical. Based on the difference between the results of the simulations and sea trial, it is estimated that the additional force and moment terms due to the combination of the yaw rate and drift angle are bigger in the real flow.
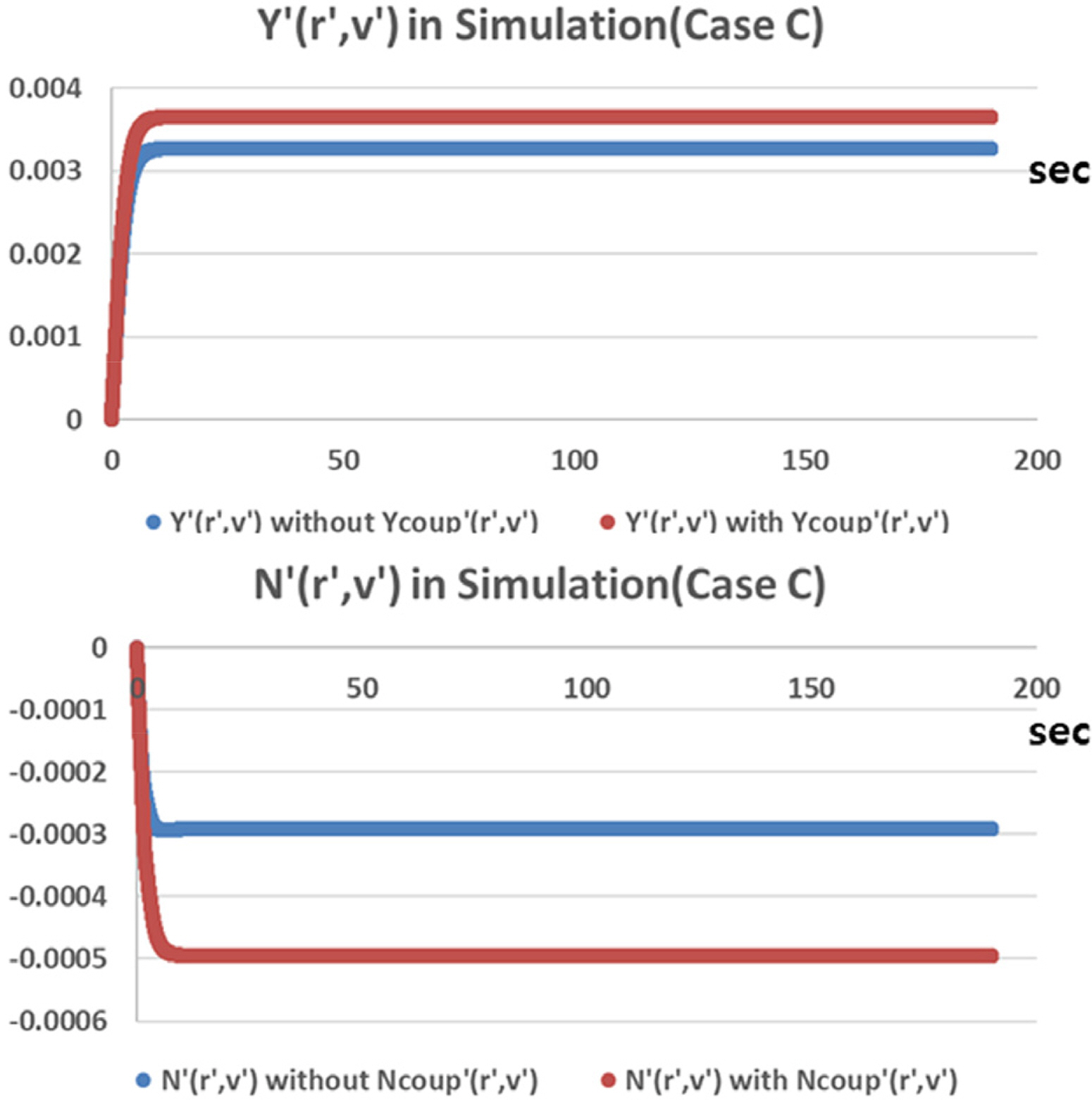
Additional force and moment due to interaction between yaw rate and drift angle in turning motion simulation (Case C)
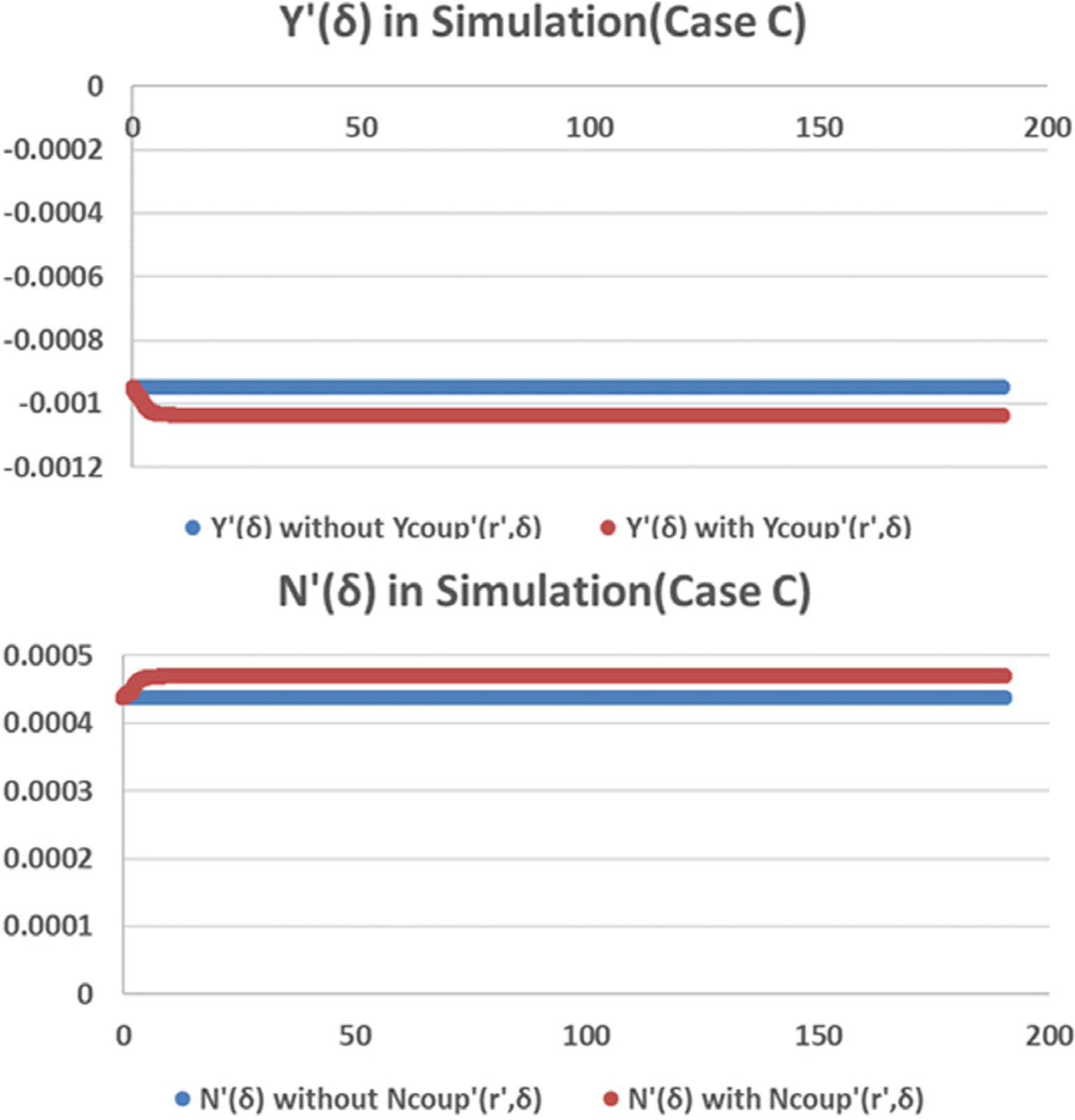
Additional force and moment due to interaction between yaw rate and rudder angle in turning motion simulation (Case C)
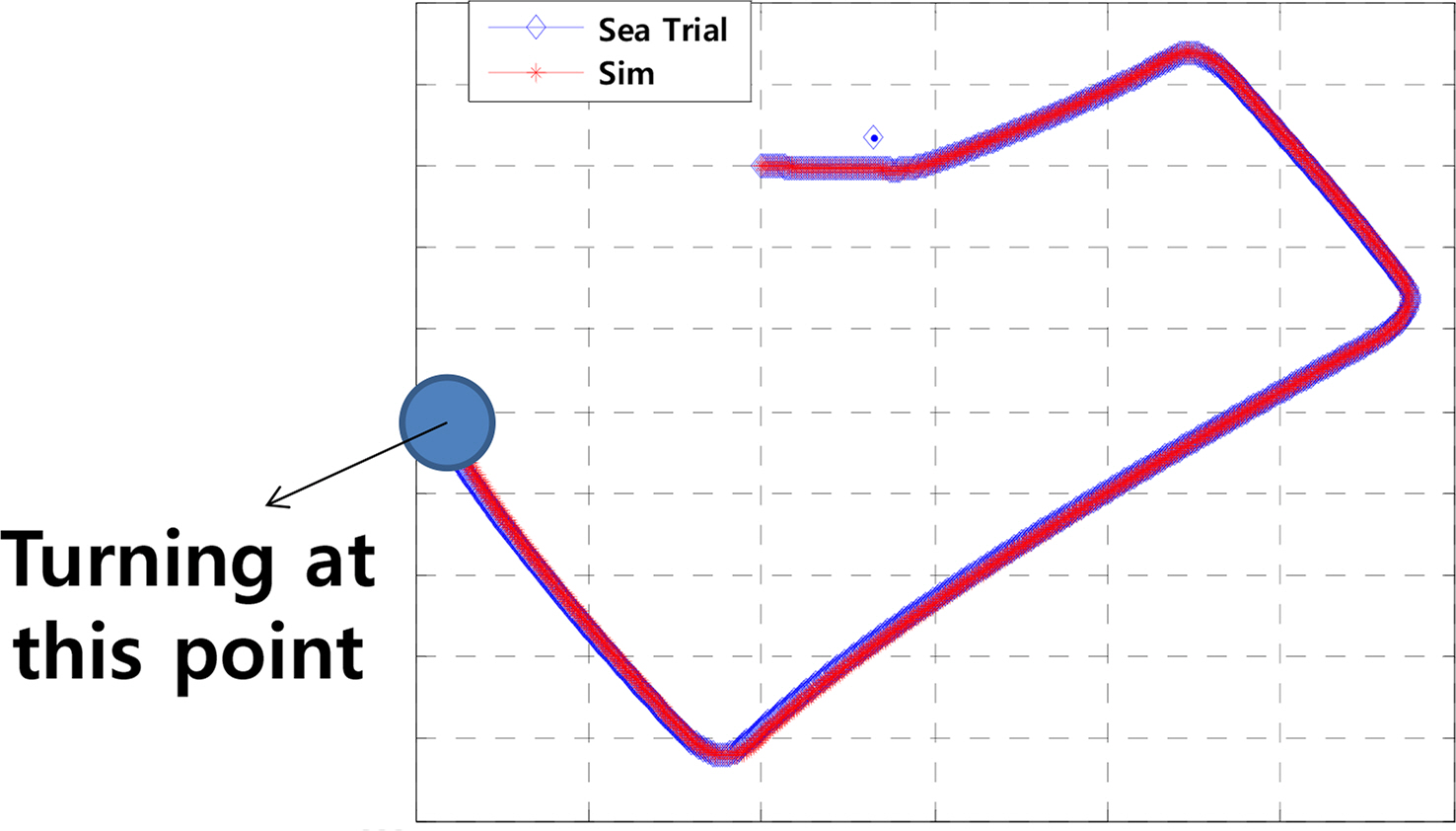
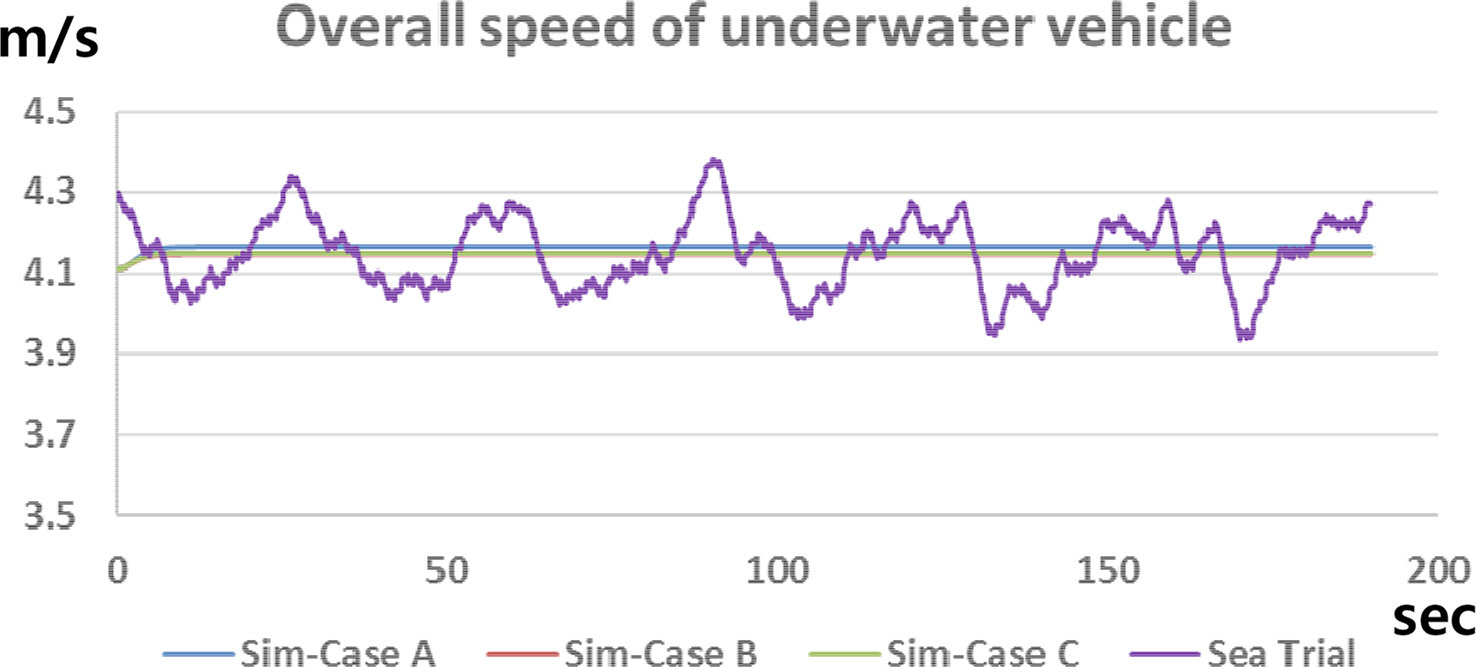
The non-dimensional yaw rate, drift angle, and overall speed are shown in Figs. 34–36. The turning motion starts at 0 s, and the underwater vehicle turns steadily for 3 minutes from 10 s to 190 s. Fig. 37 shows the trajectory of the underwater vehicle. Because there are some disturbances in the sea, the sea trial data have fluctuation, and the trajectory is slightly biased relative to the simulation results.
7. Conclusion
In this study, we predicted the steady turning ability of a symmetrical underwater vehicle while considering interactions between yaw rate and drift/rudder angle through a simulation-based methodology. As a result, we came to the following conclusions:
The feasibility of the hydrodynamic force and moment from the CFD was verified by comparing the results of the static drift/rudder simulations to those of the VPMM tests.
Rotating arm simulations with the drift and rudder angle were performed, and we confirmed the existence of interactions. Coupled terms from the interactions have strong non-linearities and different tendencies according to the relative direction of the yaw rate and drift/rudder angle.
Turning motion simulations were carried out by solving 2-DOF equations based on hydrodynamic data from CFD. The coupled interaction terms should be considered to estimate the turning performance of the underwater vehicle more accurately.
In the future, we will research a transient and detailed analysis of the turning ability of the underwater vehicle by solving full 6-DOF equations that include all hydrodynamic, hydrostatic, added mass, and thrust terms. In addition, other types of maneuverability will be analyzed, such as depth changing and course-changing ability.