1. Introduction
To prevent coastal erosion, several beach and costal structures are actively being developed and constructed. These structures include submerged breakwaters, which are structures that protect beaches by breaking waves that enter from the open sea, thus suppressing wave energy. Submerged breakwaters are mainly used to reduce erosion damage caused by the incursion of high waves, as well as to protect and nourish the sand. Unlike detached breakwaters, submerged breakwaters are installed underwater; therefore they can preserve sea views and minimize environmental pollutants by promoting seawater exchange. However, despite these advantages, the shoreline alteration and coastal erosion prevention functions of submerged breakwaters remain quite unclear, and there have been cases of erosion behind submerged breakwaters (Ranasinghe and Turner, 2006). Therefore, calculating the transmission coefficients of submerged breakwaters is vital to improve the control capacity of wave energy, which is the inherent function of submerged breakwaters.
Several studies have been conducted on analyzing the transmission characteristics of submerged breakwaters according to their shapes and materials. Seelig (1980), Ahrens (1987), Van der Meer and Daemen (1994), and other researchers have conducted hydraulic experiments and proposed empirical equations to determine the reflection and transmission coefficients of submerged breakwaters in single-incident wave conditions. Takayama et al. (1985) proposed the empirical equation of a transmission coefficient based on hydraulic experiments conducted on a tetrapod (TTP) wave-dissipating block body in irregular wave conditions. To analyze transmission characteristics according to the breakwater’s width, Seabrook and Hall (1998) conducted hydraulic experiments on submerged breakwaters that adopt rubble mounds as their body material. Ahrens (1987) and Van der Meer and Daemen (1994) inferred that the empirical equation of the transmission coefficient determined by Seabrook and Hall (1998) differed from that of their hydraulic experiment results when the width of the submerged breakwater was large, and they proposed a novel empirical equation for the transmission coefficient. Later, Van der Meer et al. (2005) concluded that most empirical equations of transmission coefficients are based on limited data. Therefore, they developed a hydraulic experiment database containing 2,337 experiments conducted on several types of submerged breakwaters. On this backdrop, existing transmission- coefficient empirical equations were compared and a novel empirical equation for the transmission coefficient was proposed.
The aforementioned studies on the characteristics of submerged breakwater transmission mainly proposed empirical equations based on the results of hydraulic model experiments, and such equations are limited in recreating actual coastal environments. Furthermore, unlike western countries that adopt breakwaters with high crest heights and rubble mound bodies, South Korea mainly employs TTP-body submerged breakwaters, which possess a low crest height for more effective wave control. Consequently, the practical applications of the aforementioned empirical equations are limited. Therefore, to analyze the transmission characteristics of submerged breakwaters, this study observed waves at the front and back of the submerged breakwater in the Kangwon-do Bongpo Beach during Typhoon Krosa, which directly affected the eastern coast of Korea on August 16, 2019. Hence, this study presents a suitable transmission coefficient empirical equation for Korean coasts, which is compared to existing empirical equations (Takayama et al., 1985; d’Angremond et al., 1996). To compensate for the inability of the pressure-type wave gague to identify wave-direction information, this study adopted a wave-deformation numerical model to analyze the influence of incident wave direction on the transmission coefficient. The applied wave model was implemented using a wave deformation model (WADEM) that performs numerical analysis using the alternating direction implicit (ADI) technique, presented by Lee (1994), on the parabolic mild-slope equation of Radder (1979).
2. Transmission Characteristics Analysis of Submerged Breakwater via Wave Observations
2.1 Analysis of Transmission Coefficient Empirical Equation
Takayama et al. (1985) proposed a transmission-coefficient empirical equation via hydraulic experiments conducted on a TTP wave-dissipating block body in irregular wave conditions, as expressed below:
where, B, Lo, Rc, and H′o represent the crest width of the submerged breakwater, deep-water wavelength, crest height, and equivalent deep-water wave height, respectively.
Van der Meer and Daemen (1994) harnessed the diameter of the rubble mounds to analyze the wave transmission coefficient according to the breakwater crest height, and based on the results obtained from hydraulic experiments, they proposed the following transmission coefficient empirical equation:
Van der Meer and Daemen (1994) verified that when the ratio of the incident wave height Hi to the rubble mound diameter Dn50 is less than one (Hi/Dn50 < 1), the transmission coefficient Kt is dispersed. In addition, a is defined using Hi and Dn50 while b is defined using the waveform wave steepness S, B, Hi, and Dn50, as expressed in Eqs. (3) and (4), respectively.
d’Angremond et al. (1996) stated that breaking the shapes of waves affects the transmission coefficient. They noted that the effect of breaking waves was omitted from the transmission coefficient empirical equation of Van der Meer and Daemen‘s (1994); therefore, they presented a modified equation that can be applied to both impermeable structures and rubble mound breakwaters.
ξ, the surf-similarity parameter (Battjes, 1974), is an index that determines the shape of the breaking waves, as expressed in Eq. (6).
where β and Ho represent the inclination angle of the beach cross section at the breaker zone and deep-water wave height, respectively.
It should be noted that the recreation range of the transmission coefficient presented by the transmission coefficient empirical equation of Van der Meer and Daemen (1994) is limited to a Kt range of 0.75–0.075, whereas that of d’Angremond et al. (1996) is limited to a Kt range of 0.8–0.075. Furthermore, based on the study conducted by Van der Meer et al. (2005), the aforementioned equations were compared to the transmission coefficients observed at actual beaches, and the results showed that the reproducibility of the equations decreased as the ratio of the crest width to the incident wave height (B/Hi) increased. In particular, it was determined that the equation presented by d’Angremond et al. (1996) tends to overestimate the transmission coefficient at B/Hi > 8 when the crest width is larger.
Seabrook and Hall (1998) conducted 2D and 3D hydraulic experiments and inferred that the results of the aforementioned transmission coefficient empirical equations produce inaccurate results with an increase in the crest width of the rubble mound of submerged breakwaters. Consequently, they proposed the following transmission coefficient empirical equation, which exhibits high reproducibility even for very wide submerged breakwaters:
where L is the incident wavelength. However, the empirical equation of the transmission coefficient presented by Seabrook and Hall (1998) can properly recreate results of 2D hydraulic experiments but it cannot recreate that of a 3D hydraulic experiment. Additionally, outside the range expressed in Eqs. (8) and (9), where the crest width B of the submerged breakwater was excessively large or small, the reproducibility of the equation was poor.
Van der Meer et al. (2005) collated results obtained from the hydraulic experiments conducted by Seabrook and Hall (1998), including those of other researchers, and assembled more than 2,300 data to analyze the characteristics of transmission coefficient according to rubble mound protection. In addition, they compared the data with existing empirical equations presented by Van der Meer and Daemen (1994), d’Angremound et al. (1996), etc., then they proposed a transmission-coefficient empirical equation based on the B/Hi range. At B/Hi < 8, the equation presented by d’Angremond et al. (1996) exhibits high reproducibility, when Eq. (4) was applied. At B/Hi > 12 they adopted an empirical equation with high reproducibility, as expressed in Eq. (10). However, at 8 < B/Hi < 12, they performed linear interpolation.
The submerged breakwaters constructed in South Korea are mainly large-scale TTP rather than rubble mounds, as illustrated in Fig. 1. They are very wide submerged breakwaters with low crest heights of approximately 40 m used to increase the wave reducing effect. Consequently, errors can occur when applying the aforementioned transmission coefficient empirical equations of submerged breakwater to Korean structures. Therefore, this study adopted wave data that were observed in the front of and back of a submerged breakwater at the Bongpo Beach on the eastern coast of Korea to propose a transmission coefficient empirical equation of submerged breakwater with high reproducibility in the submerged breakwater environments of Korea.
2.2 Wave Observations Before and After Submerged Breakwater
Wave observations were conducted to analyze the transmission characteristics of the submerged breakwaters installed in the coastal areas of South Korea. The wave observations were carried out at Bongpo Beach, located in Kangwon-do Goseong-gun, from the 6th to 21st of August, 2019, during Krosa, the 10th typhoon of the season, which directly affected Korea’s eastern coast. The length, crest width, and crest height dimensions of the Bongpo Beach submerged breakwater are 150, 40, and 0.5 m, respectively. Three submerged breakwater segments were supposed to be built at 80 m intervals, and 110 m from the shoreline. Section 1 of the submerged breakwater, which is installed at the southern part of Bongpo Beach, has a length, crest width, and crest height of 40, 20, and 0.5 m, respectively. The bodies of the submerged breakwaters at the Bongpo Beach are all TTP 12.5t grade with porosity of 50%. Regarding the wave observations, pressure type wave gagues (WTG-256) were installed in the front and back of the submerged breakwater located at the center of the Bongpo Beach, as shown in Fig. 2.
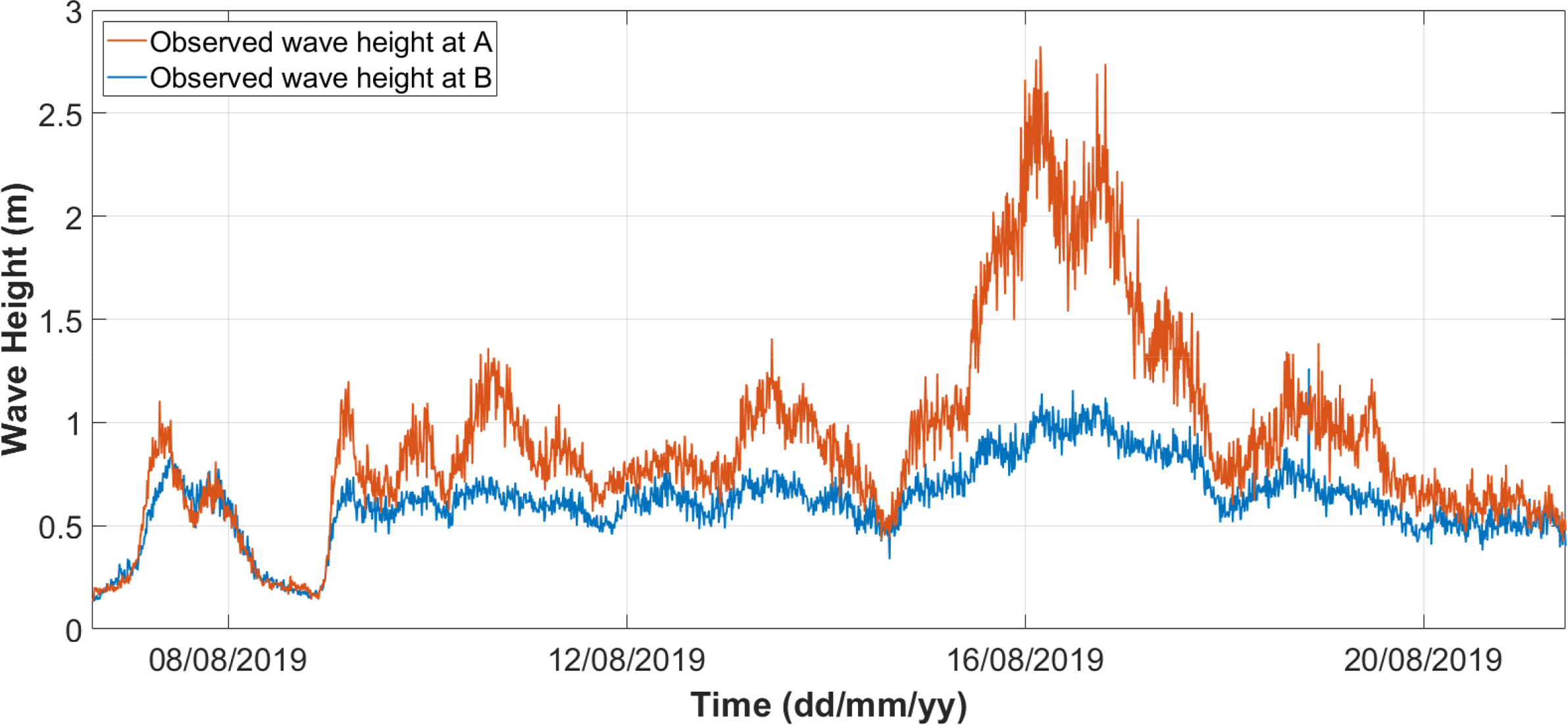
The wave heights at both sides were observed at 10-min intervals to obtain wave observations, as shown in Fig. 3. WTG-256 is a pressure type wave gague that measures wave height and period of time series data installed on the sea floor however, it cannot measure the wave direction. If the water is significantly deep, the accuracy of the measured water pressure may decrease. Therefore, it is recommended that the WTG-256 should only be used in shallow seas with depths of 30 m or less. In short-period wave conditions, WTG-256 tends to underestimate wave height (US Army Corps of Engineers, 1984). In the results obtained from wave observation, the transmission coefficient when Krosa hit on August 16, 2019 remarkably decreased, which means that the design goal of controlling high waves effectively was optimally achieved.
2.3 Analysis of Submerged Breakwater Transmission Coefficient via Wave Observations
This study analyzed transmission characteristics according to incident wave height using the wave data obtained before and after the Bongpo Beach submerged breakwater. In the analysis results of the observation data, it is evident that waves were controlled by breaking mainly at the crest height. Additionally, via the effective crest height Rc and the breaking coefficient γ, changes in the transmission wave height owing to the incident wave height can be easily expressed as the error function below. Here, the effective crest height refers to the crest height, as well as the effects of evaporation, permeability, etc., caused by the porosity of the submerged breakwater porosity.
Therefore, the following transmission coefficient empirical equation can be obtained from Eq. (11).
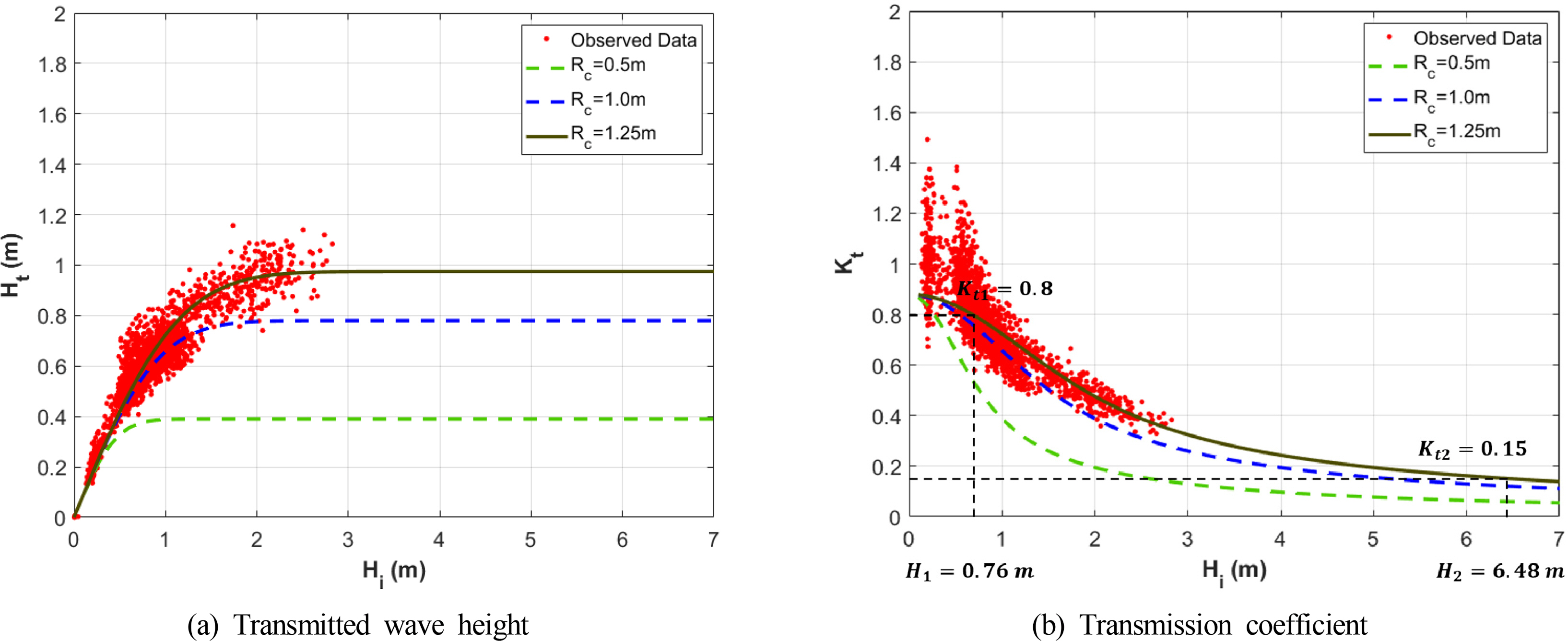
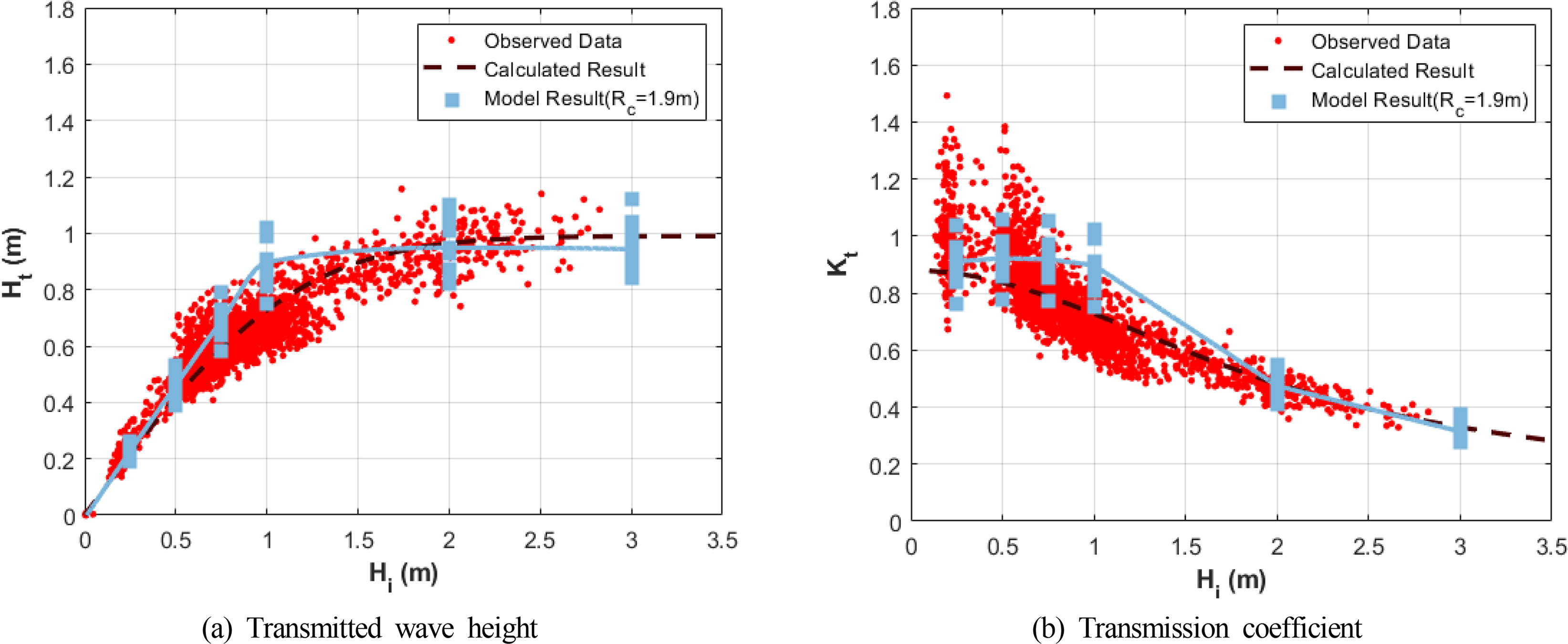
Fig. 4 presents the results obtained from comparing Eqs. (11) and (12) with the wave data observed at the coast. It can be observed that the empirical equations of the transmission coefficient exhibit high reproducibility. Here, 0.78 was taken as the breaking coefficient γ. Based on the observed values presented in Fig. 4, transmission cases where the coefficient Kt was greater than one, owing to reflected waves, were considered to be attributable to reflected waves. The data obtained from the observation of location A were considered to be the incident wave height Hi, which ignores the effect of reflected waves. When the crest heights, 0.5 and 1.0 m, specified in the design diagram of the Bongpo Beach’s submerged breakwater, are used in Eqs. (11) and (12), the results diverge from the observed values, as indicated by the dotted lines in Fig. 4. However, when 1.25 m is used, the results correspond optimally with the observed values, as illustrated by the solid line. This indicates that the effective crest height of the Bongpo Beach is Rc. Therefore, using Eq. (12), the transmission coefficient of the submerged breakwater is estimated to be 0.8 when the incident wave height is equal to Bongpo Beach’s average wave height of 0.76 m, and the transmission coefficient is estimated to be 0.15 at a 30-year wave height of 6.48 m.
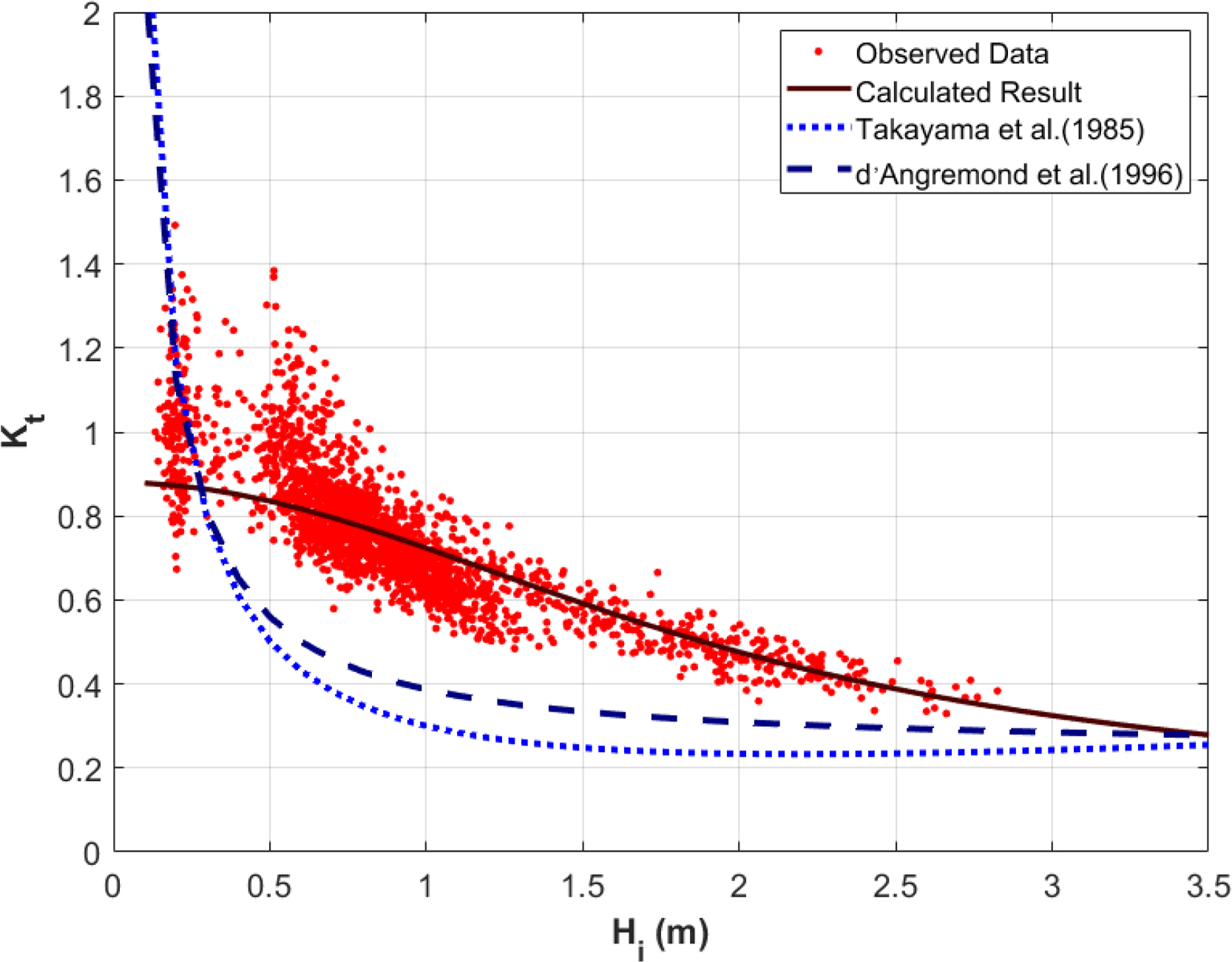
Fig. 5 presents the results obtained from comparing the transmission-coefficient empirical equation proposed in this study with those of Takayama et al. (1985) and d’Angremond et al. (1996). Here, the gradient of the submerged breakwater installed at Bongpo Beach is 3:4, and tanβ = 3/4 is adopted while wave period T is set at 7 s. In the comparison results, when Hi > 2 m, the equations proposed by Takayama et al. (1985) and d’Angremond et al. (1996) both converge in the 0.2 < Kt < 0.4 range as the incident wave height increases, similar to the observed data case. However, at a small wave height of Hi > 2 m, a tendency to underestimate the transmission coefficient was observed.
3. Transmission Coefficient Analysis of Submerged Breakwater via Numerical Modeling
The data observed by the pressure-type wave gague do not include information on wave direction. Therefore, a wave deformation numerical model was used to analyze the effects of wave direction, as well as the wave height and period. This study examined the effects of the direction angles of incident wave, 0°, 10°, and 20°, on the transmission coefficient. For the wave model, this study adopted 2D WADEM, which employs a parabolic mild-slope equation.
3.1 Wave Deformation Numerical Model
The wave deformation phenomena modeled by WADEM include shoaling, refraction, diffraction, and reflection. Excluding non-linearity, most of the phenomena were recreated by the model using the mild-slope equation (Lee and Lee, 2006). The wave model that was used to analyze the transmission characteristics of the submerged breakwater was the WADEM numerical model, which performs numerical analysis on linear and hyperbolic mild-slope equations using the ADI technique introduced by Lee (1994). This model consists of the parabolic equation presented by Radder (1979), which can be used in large areas, and the hyperbolic wave model of Madsen and Larsen (1987), which excels at modeling harbor tranquility after harbor construction. This study adopted Eq. (13) as the governing equation, and it employed a parabolic wave model that provides accurate results on the shoaling, refraction, and wave crossing phenomena in a large area, with significantly stable numerical calculations.
Here,
k c 2 = k 2 + ∇ 2 ( C C g ) 0.5 / ( C C g ) 0.5
3.2 WADEM Application Results
The numerical model used to analyze the transmission characteristics of the submerged breakwater created a regular grid, ∆x = ∆y = 2 m, in a 400 × 400 m area, and submerged breakwater with a width, length, and depth of 40, 200, and 4 m, respectively. Fig. 6(a) presents a contour line of bathymetry at Bongpo Beach where the wave observations were conducted. Fig. 6(b) illustrates the water depth that was created for the numerical model.
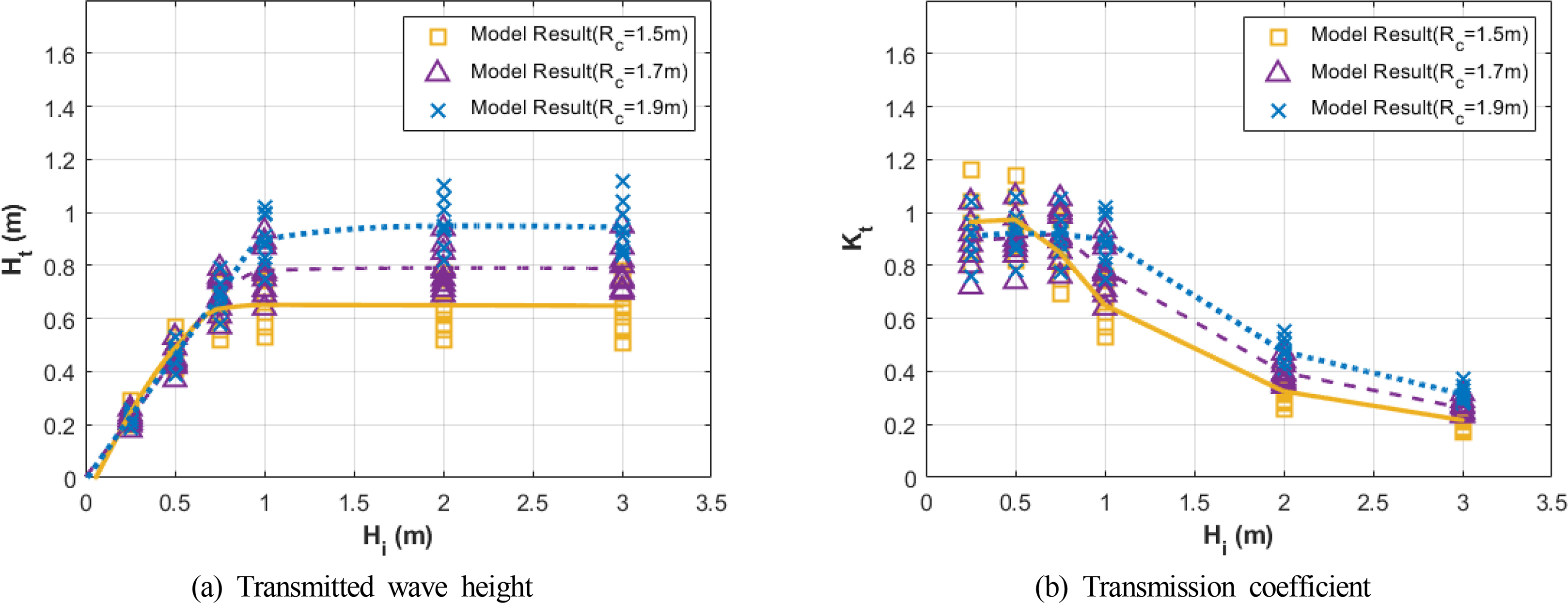
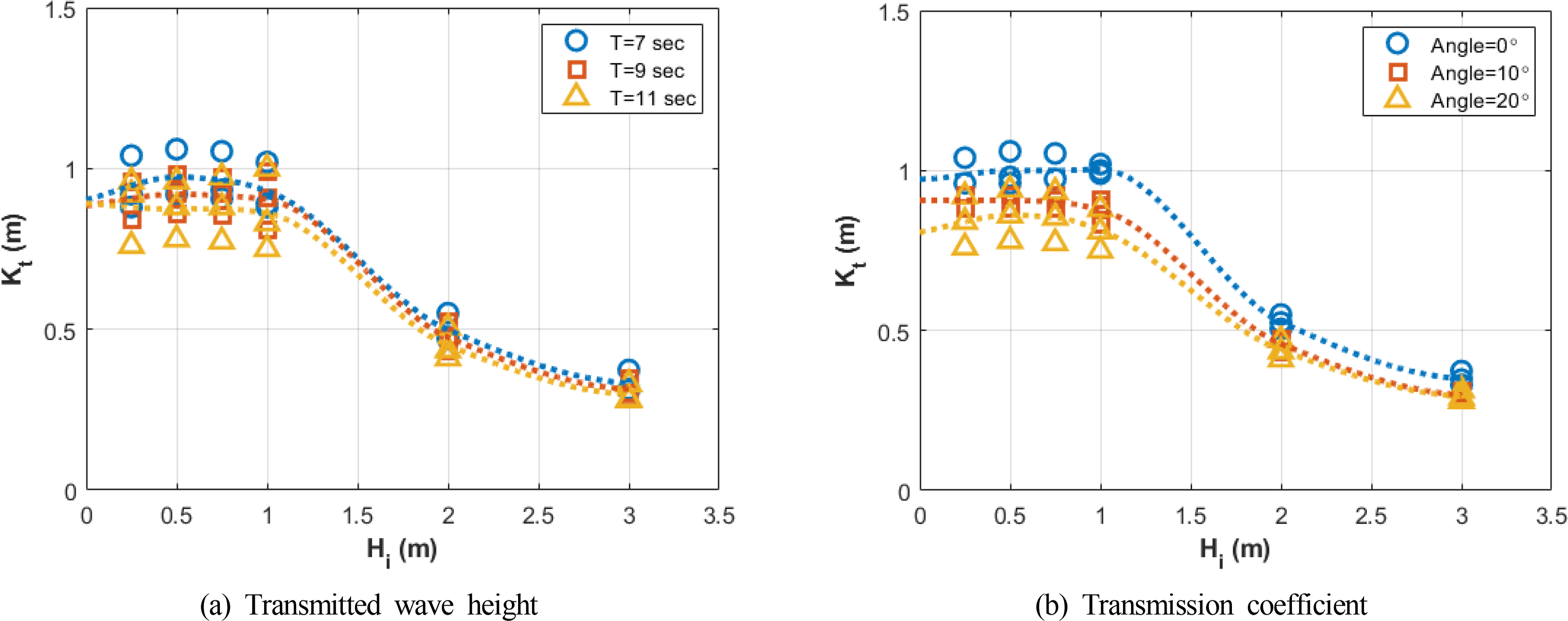
WADEM was utilized to analyze the transmission characteristics of three submerged breakwaters with crest heights of 1.5, 1.7, and 1.9 m, respectively, according to wave height, as presented in Table 1. Fig. 7 presents the results of the numerically modeled transmission wave heights for six incident wave heights from 0.25 to 3 m at wave periods of 7, 9, and 11 s, as well as wave directions of 0°, 10°, and 20°. Here, a wave direction of 0° indicates a wave approaching perpendicularly to the submerged breakwater. Additionally, the wave direction was altered in a clockwise direction. As shown in Fig. 7, at the same incident wave height, the transmitted wave height decreased with the crest height. This indicates that wave control was effectively achieved by a low crest height.
3.3 Transmission Characteristics Analysis of Submerged Breakwater via Numerical Modeling
The three crest height cases modeled in Fig. 7 were compared to the field observation data and Eqs. (11) and (12). As can be observed in Fig. 8, the results show that the characteristics observed in the field were best reflected at a crest height of 1.9 m. Here, the breakwater used in the wave model had a porosity of 0%, whereas TTP, which was adopted as the body of the submerged breakwater installed on the coast, conventionally exhibits a porosity of around 50%, and the results of hydraulic experiment agreed well with this value (Shin et al., 2008). Shin et al. (2008) performed hydraulic experiments that confirmed that the transmission coefficient of breakwater increases with its porosity. This means that submerged breakwaters with low porosity exhibit superior wave dissipating effects. Therefore, it is inferred that the transmission coefficient results of the numerical model’s wave height are greater than those of the observed data owing to the difference in submerged breakwater porosity.
Fig. 9 presents the results of the numerical model for the transmission coefficient according to the wave period and direction when the crest height was 1.9 m. It can be observed that the transmission coefficient appeared to decrease as the wave period and incident wave direction angle increased. It can also be observed that the transmission coefficient exerts a greater effect on the wave period, and the wave control effect of the submerged breakwater is greater when the wave approaches the submerged breakwater perpendicularly compared to when it approaches obliquely.
4. Conclusion
In South Korea, submerged breakwater construction is often used to reduce the energy of incident waves and minimize damage to the landscape, and the transmission coefficient of a submerged breakwater plays a major role in determining the performance of the breakwater. However, research on analyzing the transmission characteristics of submerged breakwaters in South Korea has been insufficient, where the submerged breakwaters usually have low crest heights and large crest widths, and TTP is utilized as the submerged breakwater body. Consequently, it is unavoidable to adopt foreign empirical equations for transmission coefficients of submerged breakwater which leads to inaccurate analysis results when calculating the transmission coefficients. Therefore, this study has proposed an empirical equation for a transmission coefficient that implements wave data observed at actual coastal areas. Additionally, this study has adopted WADEM to analyze the effect of wave direction and compensate for the limitations of the observation data.
When Typhoon Krosa hit in August 2019, two pressure-type wave gagues were installed to conduct wave observations at both sides of a submerged breakwater at Bongpo Beach in Kangwon-do Goseong-gun, where coastal improvement projects are currently taking place. Based on these observations, this study has proposed Eq. (12), an empirical equation with high reproducibility for the transmission coefficient of wave height. This equation was analyzed and compared with the empirical equations of transmission coefficient proposed by Takayama et al. (1985) and d’Angremond et al. (1996). The analysis results demonstrate that the existing equations of transmission coefficient converge on a wave height transmission coefficient range of 0.2–0.4 when the incident wave height is 2 m or greater, similar to that of the observed wave data. However, at an incident wave height of 2 m or less, the equations diverged significantly from the observed wave data. It is inferred that this divergence occurs because of the construction environment in South Korea, where highly porous TTP is preferred to rubble mounds, and low crest heights are used for effective wave control.
The observed data did not include information on wave direction, and 2D WADEM was adopted to analyze the wave period and direction effects. The analysis results showed that the transmission coefficient decreased as the wave period and direction increased, and the wave direction exerted a relatively significant effect on the transmission coefficient. In addition, it was inferred that the transmission coefficient results of the numerical model diverged from the observed data owing to the porosity of the submerged breakwater, and it was concluded that the transmission coefficient of the submerged breakwater increases with its porosity. Therefore, it will be necessary to perform further research to analyze the influence of porosity on the wave height transmission coefficient according to the shape and body of the submerged breakwater.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation
Print
