1. Introduction
The International Maritime Organization (IMO) has mandated a 30% reduction in CO2 emissions by 2025 for ships, which produce 3.3% of global CO2 emissions. To reduce CO2 emissions, it is essential to estimate the ship’s resistance and propulsion accurately and improve performance.
Frictional resistance generally accounts for more than 60% of the total resistance of a ship. An air lubrication system injects air onto the hull surface to form a continuous air layer, reducing frictional resistance on the hull surface and fuel consumption (Bushnell and Hefner, 1990; Ceccio, 2010). The frictional resistance can be reduced in three ways: bubble drag reduction (BDR), air layer drag reduction (ALDR), and partial cavity drag reduction (PCDR). PCDR can increase the form resistance due to remodeling of the air cavity, but it is difficult to apply to a ship. Compared to BDR, ALDR requires high pumping power, but the resistance reduction rate is very high (Ceccio et al., 2012).
Jang et al. (2014) observed air layer formation using ALDR in the lower part of a plate in the cavitation tunnel of the Samsung Ship Model Basin (SSMB). They also measured the decrease in frictional resistance. An air layer was applied to a model 66K DWT Supramax bulk carrier to estimate the power-saving effect by conducting resistance and self-propulsion tests
Mäkiharju et al. (2017) examined the gas pocket morphology with air injection at a single inlet. The formation of a V-type gas pocket and the shape of the gas pocket were observed while changing the inflow rate and air injection rate. Computational fluid dynamics (CFD) simulations and experimental results showed similar tendencies.
Kim et al. (2017) analyzed the air layer pattern and diffusion angle at the bottom of a plate numerically using CFD. The air diffusion angle pattern according to the relationship between the air inflow rate and water inflow velocity was compared with the empirical formulae. They compared the lambda, delta, and transition air-layer patterns through the velocity vectors, velocity contours, and vorticity contours. On the other hand, the practical application of ALDR required multiple complex injections rather than a single injection.
Mäkiharju and Ceccio (2018) observed the shape changes of airflow with complex interactions in a multi-injection experiment. In some cases, multiple injections formed a more stable air layer than a single injection because each of the air layers interacted with each other. Multiple injections generated a larger gas pocket that formed into a liquid cross-flow, but a fortuitous gas pocket formed in some cases. Therefore, additional experiments are needed. In addition, it is necessary to cover a large number of flow parameters and derive clear results through further experiments using models with greater overall lengths.
Estimating the resistance reduction effects of an air lubrication system on a full-scale ship is important before studying the influence of the position, shape, and number of injectors. A more accurate method is also needed to estimate the full-scale ship resistance from the resistance components of a model ship.
The goal of this study was to improve the estimation of the actual resistance of air lubricated ships. A numerical method was developed and verified by comparing with experimental data (Jang et al., 2014). A new extrapolation method was proposed to estimate the full-scale resistance of a ship with an air lubrication system based on the numerical simulations for a model and full-scale ship.
2. Numerical Methods and Models
Incompressible three-dimensional unsteady flow was modeled to analyze the air lubrication performance. The continuity equation and Reynolds averaged Navier-Stokes (RANS) equations were used as the governing equations.
where ui is the velocity tensor, and bi is the tensor of body forces. p and ρ are the pressure and density, respectively. τij is the effective stress of the viscosity and turbulence:
where μe is the effective dynamic viscosity.
The commercial CFD software, STAR-CCM + 12.06, was used for numerical analysis of multiphase flow. The volume of fluid (VOF) method was used for multiphase flow replication, considering the free surface and air layer. The Reynolds stress model (RSM) was used as the turbulence model. Table 1 lists the numerical models.
3. Setup of the Numerical Simulation
A scale model of a 66K DWT Supramax bulk carrier was used in the model test by Jang et al. (2014). Table 2 lists the main specifications of the ship. The model ship was scaled at a factor of 24.0. Therefore, the same factor was applied in numerical analysis.
3.1 Computational Domain and Boundary Conditions
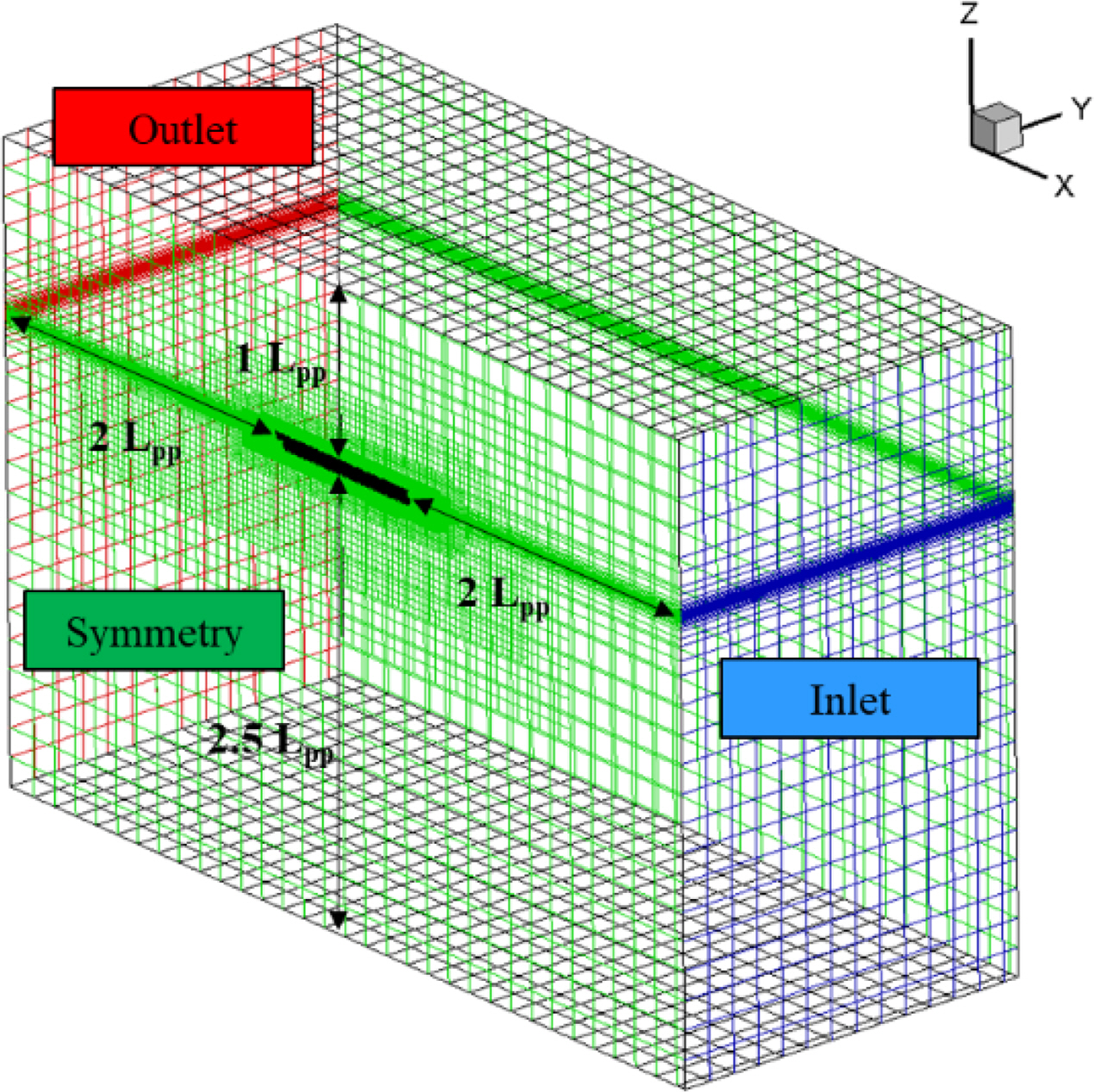
Fig. 1 shows the boundary conditions and the computational domain. A Cartesian coordinate system was used. Based on the center of gravity of the hull, the x-axis was set as the direction from the stern to the bow; the y-axis was set as the portside direction, and the z-axis was set as the opposite direction of gravity. The boundary conditions of the inlet surface, top surface, and bottom surface were set as the velocity inlet, and the outlet surface was set as the pressure outlet. Symmetric conditions were applied across the y-axis interface because the hull is perfectly symmetrical. Symmetric conditions were applied to the side to reduce the distortion of the reflected wave. The distances from the bow to the inlet, the hull to the top, the hull to the bottom, and the stern to the outlet were 2 Lpp, 1 Lpp, 2.5 Lpp, and 2 Lpp, respectively.
3.2 Injector Geometry
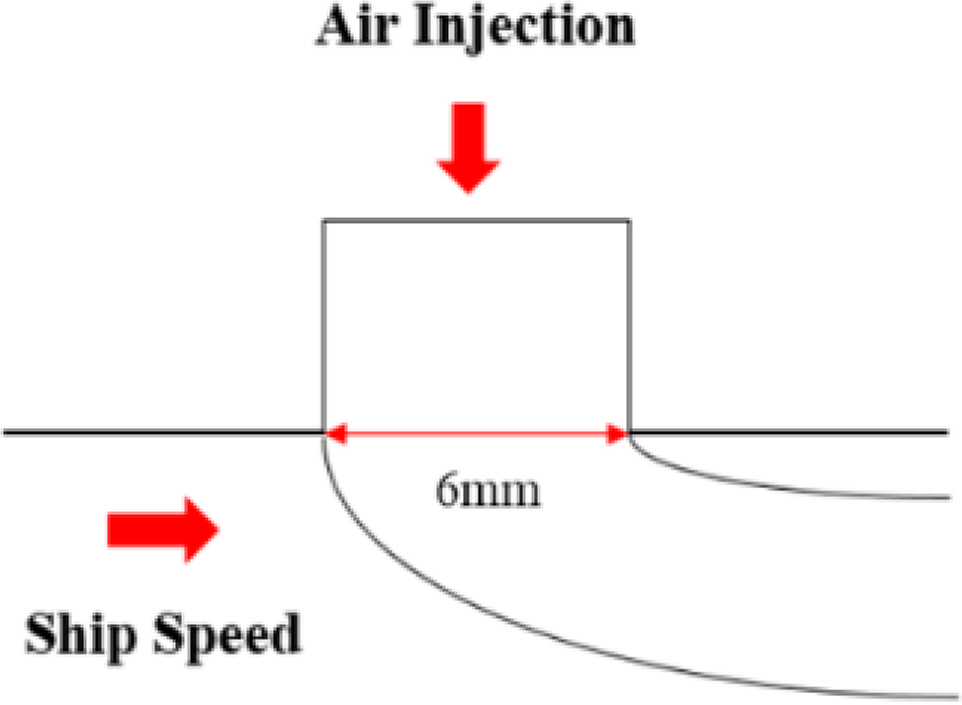
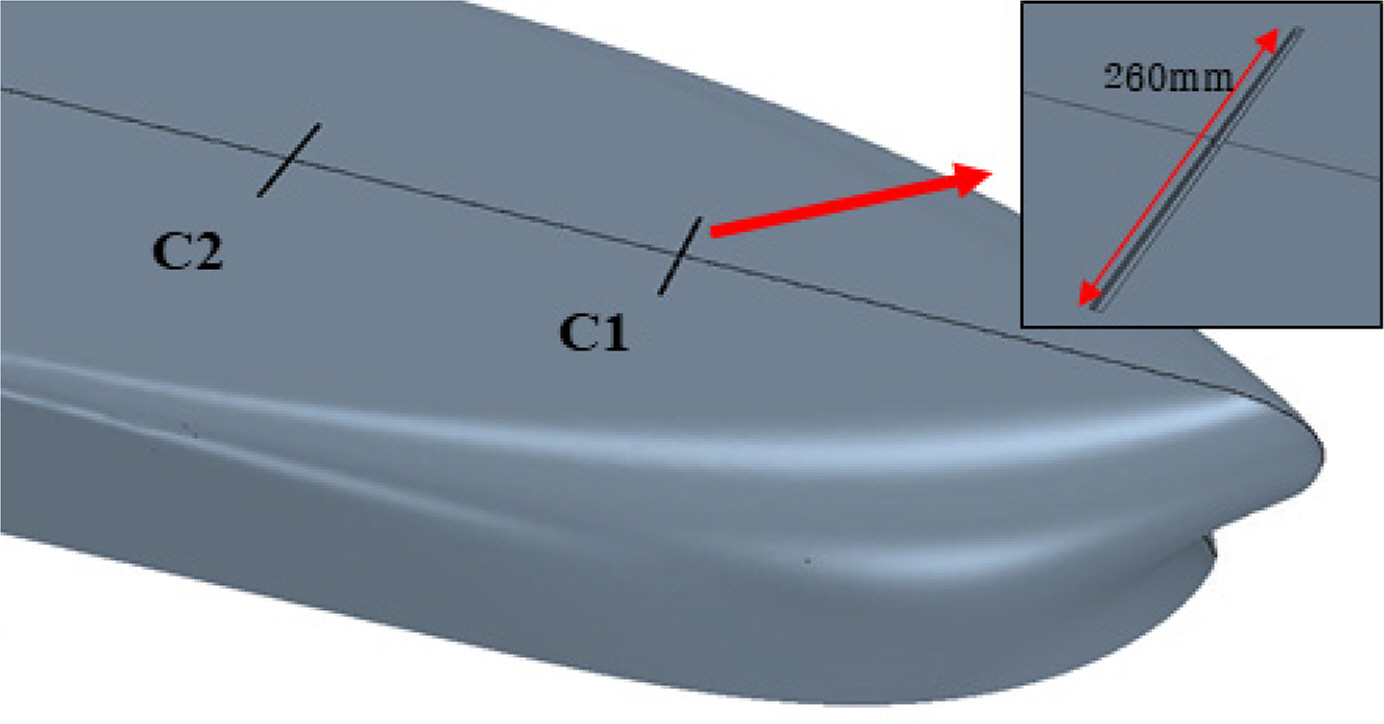
In the model test by Jang et al. (2014), the injector shapes were made with many holes, but they were modeled as a single slit in numerical analysis. Figs. 2 and 3 present the diagrams of the air cavity and the geometry of the air injector. The width and length of the slit were 6 mm and 260 mm, respectively. The air injection slits, C1 and C2, were located at the 17th and 15th, respectively.
3.3 Grid Test
The grid system was verified by measuring the resistance according to the number of grid elements (approximately 1.0 million, 2.5 million, and 6.1 million). Differences of 0.118, 0.092, and 0.013% were observed compared with the model test results performed at SSMB in Fig. 4. The simulation took too much time when there were 6.1 million grid elements. When there were 1.0 million grid elements, realistic phenomena could not be observed when air was injected. Therefore, the medium grid size of 2.5 million was applied for the other simulations.
Table 3 lists the reduction ratio of the resistance due to the air layer under various combinations of the air injection flow rate and injection position. The ship speed was fixed to 1.5226 m/s, which corresponds to the design speed of 14.5 knots for a full-scale ship using Froude scaling. The total amount of air injected from C1 and C2 was set to a wide range of 0 to 400 liters per minute under standard conditions of 1 atm and 25°C (SLPM), as shown in Table 3.
where QAir, BAir, and VInflow are the volume flow rate of the injected air, the width of the air injection slit, and the inflow speed, respectively.
4. Results and Discussion
4.1 Reduction in Resistance
Table 4 presents the trim and sinkage of the ship that occurred when air was injected. A positive value occurs when the ship rises to the top, and the bow is trimmed. The largest change in trim (ΔTrim) was 4.1% in Case 5. The ship was tilted more toward the bow by the buoyancy of air flowing from the bottom to the stern. On the other hand, the change in trim is not proportional to the amount of air. The change in sinkage (ΔSinkage) also increased continuously due to buoyancy as the amount of air injection increased.
Table 5 shows the total resistance reduction of the model ship (ΔRTM), the ratio of the decrease in shear resistance to the decrease in total resistance (ΔRShear), and the ratio of the decrease in pressure resistance to the decrease in total resistance (ΔRPressure). The largest decrease in resistance was 20.7 N in Case 9. The amount of resistance reduction increased with increasing amount of air injected. In addition, as the amount of injected air increased, there was a greater reduction in frictional resistance. Interestingly, the rate of the decrease in the pressure resistance was as large as the rate of the decrease in shear resistance.
In Case 9, the shear resistance and pressure resistance were 52.9% and 47.1%, respectively. Previous research considered only the reduction in frictional resistance. On the other hand, both the frictional resistance and pressure resistance decreased when air lubrication was used. When air is injected, an air layer is generated on the bottom of the hull, which alters the resistance state of the ship. Thus, it is necessary to analyze the various changes due to air at these locations.
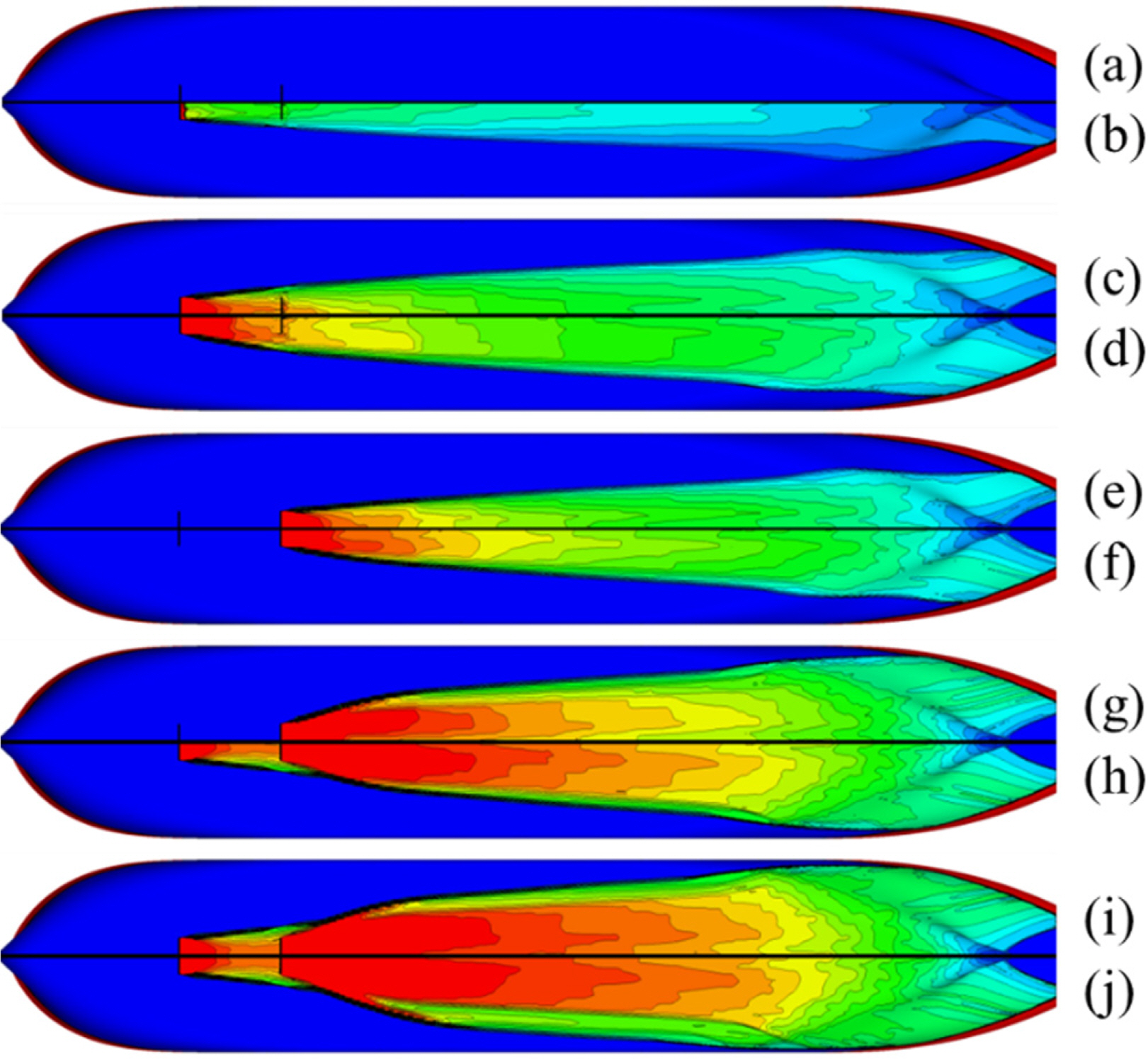
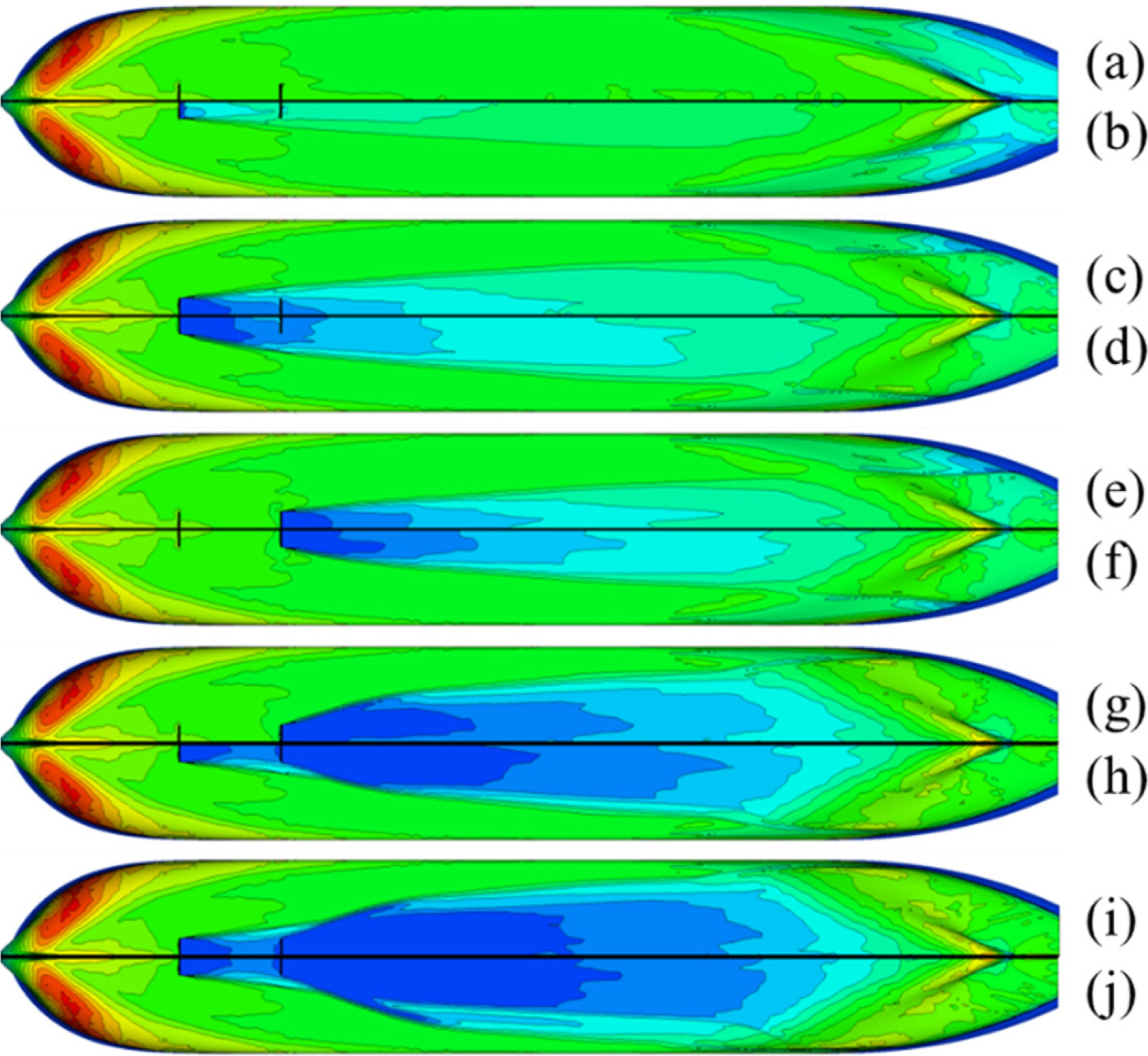
Fig. 5 shows the distribution of the volume fraction on the bottom of the hull. A larger air flow rate resulted in a larger diffusion angle and air layer thickness. The jetted air goes up on the bottom of the hull to the stern.
Fig. 6 shows the wall shear stress distribution on the hull surface, as seen from the bottom of the hull. The rate of decrease in the frictional resistance was the highest in Case 9, which has the highest air injection flow rate. The result appears similar to the shape of the volume fraction on the hull surface.
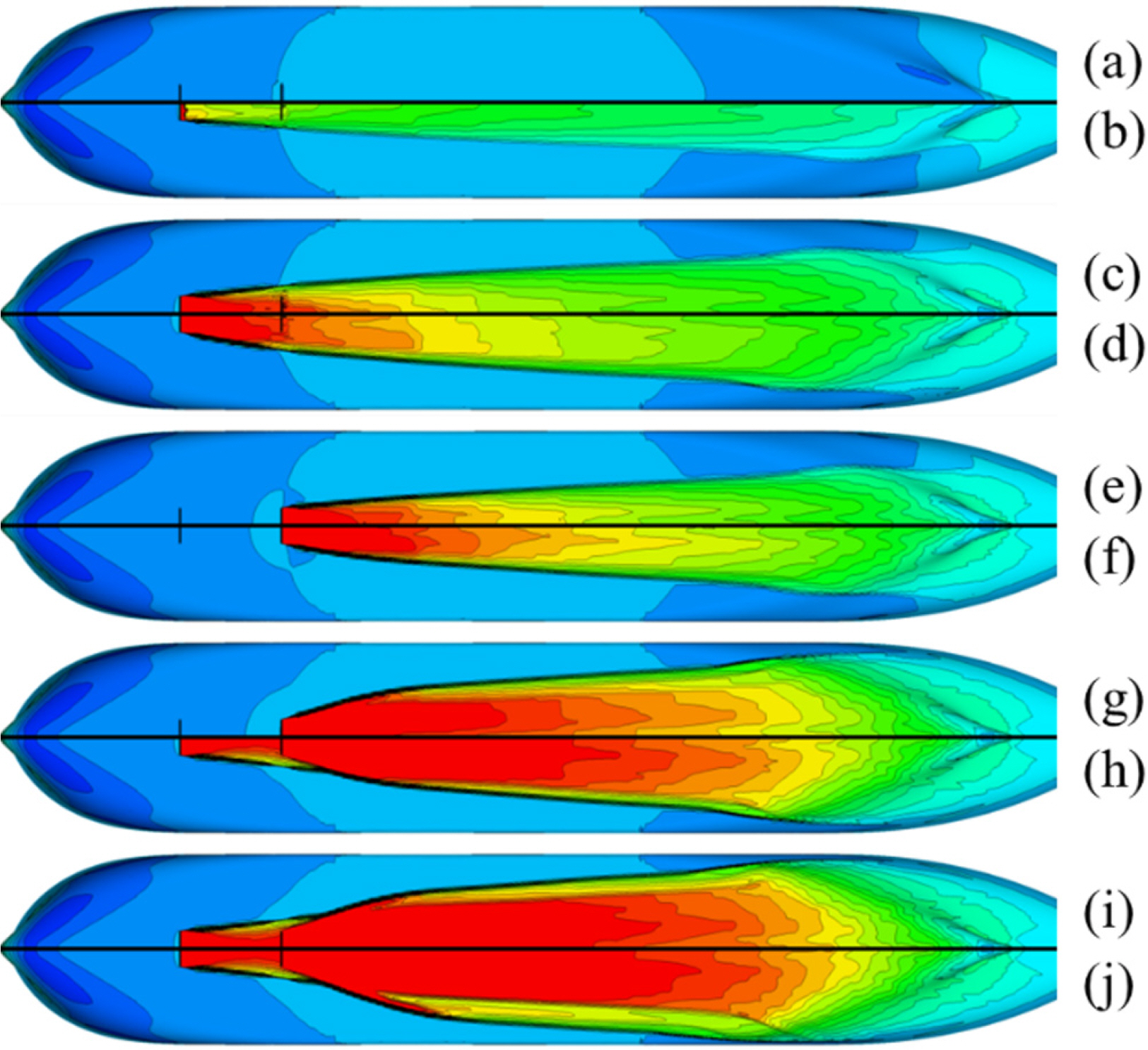
Fig. 7 shows the distribution of the dynamic pressure on the bottom of the hull. When air is injected, the air affects the distribution of the dynamic pressure at the stern. As the quantity of air increases, a high pressure forms, and the affected area increases.
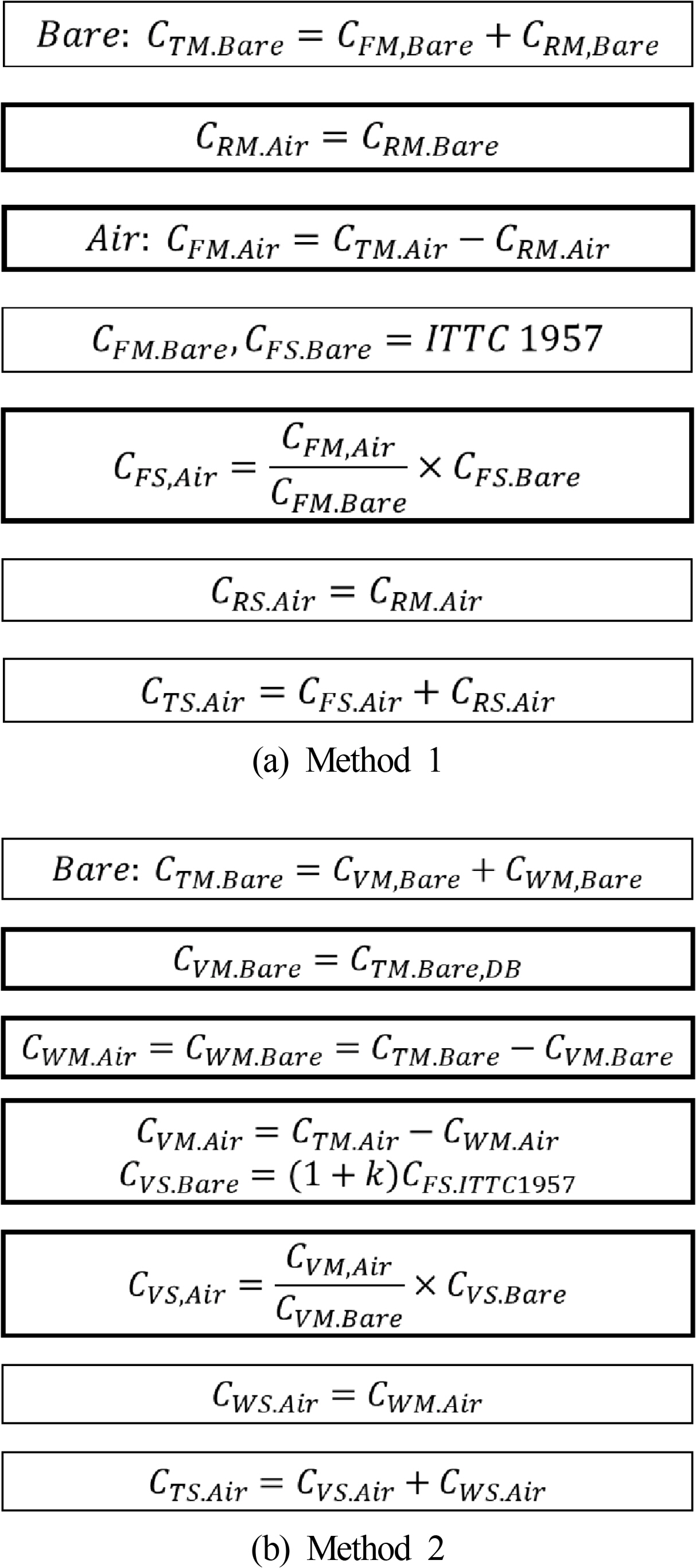
Numerical analysis of the model ship confirmed that the air layer reduces the frictional resistance through the volume fraction of air on the bottom hull surface. In addition, it changes the pressure resistance, as shown in Figs. 7 and 8. Jang et al. (2014) used a modified method based on ITTC 1957 for the estimation (Method 1). On the other hand, they did not consider the change in pressure resistance. Method 2 is proposed in this study, which considers the decrease in pressure resistance.
Fig. 9 shows the extrapolation methods used for an air-lubricated ship. In Method 1, CTM is divided into CFM and CRM, which are the frictional resistance and residual resistance. For CRM, it is assumed that the residual resistance coefficient is the same, regardless of whether air is injected. Furthermore, CRM.Air and CRS.Air are the same. CFM.Air can be obtained from the relationship between CTM.Air and CRM.Air. CFM.Bare and CFS.Bare are estimated using the ITTC 1957 method. In the subscript, Bare and Air refer to the case where the air is not injected and when air is injected, respectively. CFS.Air can be acquired from multiplying CFS.Bare by the ratio of CFM obtained in the air and bare conditions of the model ship. As a result, CTS.Air can be estimated as the sum of CFS.Air and CRS.Air for a full-scale ship.
In Method 2, CTM is divided into the viscous resistance CVM and wave-making resistance CWM to reflect the change in the viscous pressure resistance. The residual resistance of Method 1 is defined as the wave-making resistance in Method 2. CWM.Bare is calculated from the relationship between CTM.Bare and CVM.Bare. CWM.Air is assumed to be the same as CWM.Bare. CVM.Air can be obtained from the relationship between CTM.Air and CWM.Air when the air is injected. CVS.Bare is obtained using the ITTC 1957 method. CVS.Air is obtained by multiplying CVS.Bare by the relationship with CVM of the model ship when air is injected and not injected. The wave-making resistance coefficient is the same for both the full-scale ship and the model ship. This process is used to derive CTS.Air. The largest difference between Methods 1 and 2 is the scaling of the viscous pressure resistance. In Method 2, the effects of the reduction of pressure resistance by the air lubrication are considered in the extrapolation method to predict the full-scale resistance.
To obtain the viscous resistance component, it is necessary to know the component of the wave-making resistance. Accordingly, double- body analysis was performed. The following grid conditions were used: y+ was set to 90, and the number of grids was approximately 1.8 million for the model scale.
Cases 3, 6, and 9 were investigated. A double-body analysis was also carried out for a full-scale numerical analysis. Some cases were validated to set y+ and Method 2 was extrapolated from the result of the model analysis, as shown in Table 6. When air was not injected in y+ (8000), the error rate was less than 3% for a full-scale ship. Yang et al. (2010) compared the wakes between the model and the full-scale ship. When the y+ value was 8000 in numerical analysis using the RSM, the error was 1.5% compared to the full-scale ship. Therefore, y+ was set to 8000, and the number of grid elements was approximately 5.6 million. The air flow rate was analyzed numerically by Froude scaling the quantity of injected air from the model ship.
Table 7 lists the reduction rates of ΔShear, ΔPressure, and ΔCV for the model ship and full-scale ship based on cases, in which air is not injected from the double-body analysis. There was no difference in ΔShear. The overall tendency was similar between the double-body analysis and Method 2. On the other hand, the biggest difference in Δ Pressure between the model and full-scale ship was 4.9%. Consequently, the estimation of ΔCV by Method 2 is consistent with the numerical analysis of the model, but there was a slight difference in the full-scale ship.
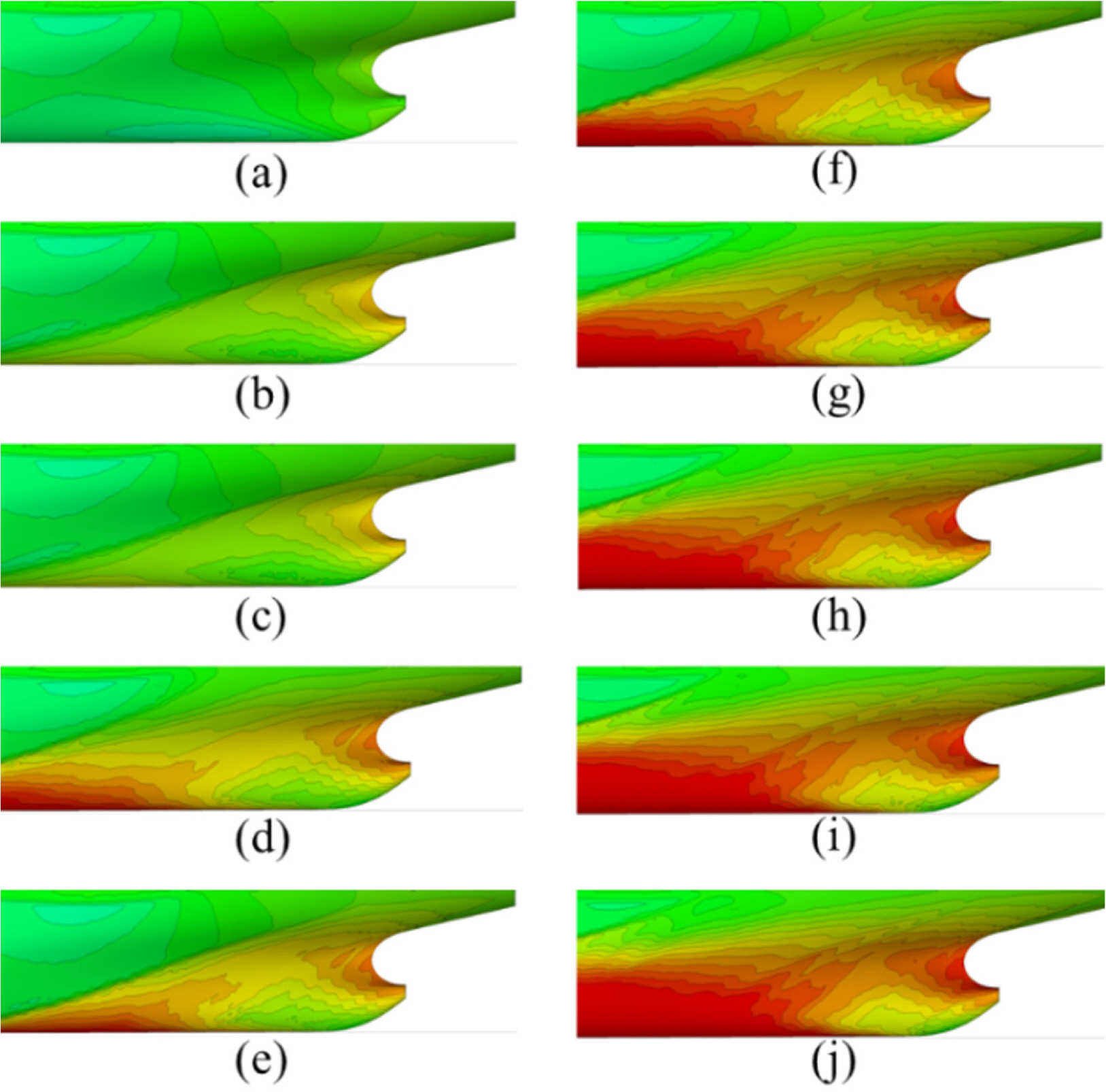
The difference in ΔPressure was attributed to the form factor, which differs between the model and the full-scale ship. The form factor was set to a constant value in Method 2. Therefore, it is believed to result in differences in ΔCV. Fig. 10 shows the volume fraction of the hull surface when using double-body analysis. The branch was stronger at the end of the slit width for the full-scale ship than the model. The overall tendency was similar to that of the model ship.
Table 8 lists the reduction rate of ΔCTS by air injection when using Methods 1 and 2. Method 1 showed a 2 – 5% difference in the numerical analysis results of the model ship; the largest gap was 5.4% in Case 9. Method 2, however, showed a 1 – 2% difference; the largest difference was 1.9% in Case 9. Method 2 was more accurate than Method 1 when the total resistance reduction rate was compared with that of the model ship. Overall, the variation of the pressure resistance should be considered when estimating the resistance of a ship with an air lubrication system.
5. Conclusions
A numerical study was carried out on the effect of air injection on a ship. The mesh was verified, and the reliability of the calculation was confirmed by numerical analysis. The resistance was calculated by double-body analysis, and the estimated resistances of the model and full-scale ship were compared.
Comparisons were made for a bare hull regarding the reduction rate of the total resistance (ΔRTM), the ratio of the decrease in shear resistance to the decrease in total resistance (ΔShear), and the ratio of the decrease in pressure resistance to the decrease in total resistance (ΔPressure). A larger decrease in the total resistance was observed when the air injection flow rate increased. The rate of the decrease in pressure resistance was as large as the rate of the decrease in shear resistance. Bow trim was generated due to the buoyancy by the air, and the heave increased.
Based on the results, a resistance estimation method was proposed to consider reducing the pressure resistance, and the results were compared with those of the modified ITTC 1957 method. The proposed method was more accurate than the modified method. The result of the model scaling showed less than 1% error, whereas the result of the full-scale ship shows a slight difference.
Methods 1 and 2 were compared to find the differences between Δ CTS and ΔCTM. Method 2 was more accurate than Method 1 in estimating the resistance of the full-scale ship from the model ship, and the error rate was less than 2%. The ultimate goal of developing an air lubrication system is to reduce the fuel consumption of a ship by 5% or more and improve the performance at sea. To achieve this goal, it is necessary to estimate the resistance of the model and full-scale ship accurately when air is injected. Future research will be needed to improve the reliability of the results on a full-scale ship.