3D Topology Optimization of Fixed Offshore Structure and Experimental Validation
Article information
Abstract
In this study, we performed a three-dimensional (3D) topology optimization of a fixed offshore structure to enhance its structural stiffness. The proposed topology optimization is based on the solid isotropic material with penalization (SIMP) method, where a volume constraint is applied to utilize an equivalent amount of material as that used for the rule-based scantling design. To investigate the effects of the main legs of the fixed offshore structure on its structural stiffness, the leg region is selectively considered in the design domain of the topology optimization problem. The obtained optimal designs and the rule-based scantling design of the structure are manufactured by 3D metal printing technology to experimentally validate the topology optimization. The behaviors under compressive loading of the obtained optimal designs are compared with those of the rule-based scantling design using a universal testing machine (UTM). Based on the structural experiments, we concluded that by employing the topology optimization method, the structural stiffness of the structure was enhanced compared to that of the rule-based scantling design for an equal amount of the fabrication material. Furthermore, by effectively combining the topology optimization and rule-based scantling methods, we succeeded in enhancing the structural stiffness and improving the breaking load of the fixed offshore structure.
1. Introduction
Fixed-type offshore structures consist of an upper topside and a lower supporting structures to support them. These structures are designed to continuously produce gas and oil at the targeted installation site during the design life. Therefore, it may result in a considerable economic loss when damages or failures of such structures occur. Furthermore, since most of the fixed-type offshore structures are located at a distance from land and isolated, there are significant limitations for its repair. Therefore, designing a fixed offshore structure requires a high level of structural safety, which is strictly governed by the regulations of classification society. Designs based on the regulations of classification society are known to result in a safe fixed-type offshore structures. However, when series of hurricanes struck the Gulf of Mexico in 2005, more than 100 offshore structures were destroyed and over 50 were damaged. Therefore, it is necessary to develop a novel fixed-type offshore structure design beyond the existing regulations of classification society which can improve the structural stiffness.
Topology optimization maximizes the performance of the structure under given constraints. Compared to the size and shape optimizations, topology optimization has an advantage that it can yield a dramatic change in the topology of the resulting optimal design. Therefore, topology optimization has been widely used in various areas since its introduction by Bendsoe and Kikuchi (1988). However, the optimal design obtained through topology optimization was considerably challenging to implement because it has an unclear interface owing to the intermediate material density resulting from the characteristics of the solid isotropic material with penalization (SIMP) method (Bendsoe, 1995). Therefore, efforts have been undertaken to overcome the shortcomings of the stepped boundary obtained through topology optimization using the level-set function. However, due to the development of three-dimensional (3D) printing technology and advancement of computer aided design (CAD) technology, constraints on implementing the optimal design obtained from the topology optimization have been resolved and again topology optimization is attracting attention.
Since most of the obstacles on the implementation of optimal design from topology optimization, the method is gradually applied in the design of offshore structures. Lee et al. (2016) applied the topology optimization method to the design of the transition piece between a fixed-type wind turbine and a jacket-type supporting structure. They developed an optimal design where weight and stress concentration are reduced compared to the original design. Furthermore, the optimal design of transition piece improved the fatigue life of the offshore structure. Also, Kim et al. (2017) applied the topology optimization method to develop a new design of fixed jacket offshore structure panel which maximizes structural stiffness while utilizing the same amount of material of the original design that is based on the rules of classification society and compared there performance numerically. Furthermore, Lee et al. (2018) experimentally verified an optimal design of a two-dimensional (2D) fixed jacket offshore structure panel obtained through topology optimization using a universal testing machine (UTM) and 3D metal printing technology. In addition, although it is slightly different approach that was made in this research, a study was conducted to derive the optimal connectivity of structural members for the helideck of offshore structures, using a genetic algorithm and an attainable design set concept (Sim and Ha, 2019). However, in the previous studies, the topology optimization method was limitedly applied to the substructures or approximate 2D structures of offshore structures. Furthermore, the optimal connectivity of members was derived only for the joints predefined in the formulation process. Therefore, it is necessary to develop a novel offshore structure design by applying topology optimization to the entire structure.
In this study, the optimal design of a 2D fixed jacket offshore structure panel performed by Kim et al. (2017) to examine the applicability of the topology optimization method to offshore structures was expanded to 3D topology optimization of fixed offshore structures to consider the out-of-plane displacement. A 3D fixed offshore structure was designed to be installed at a certain target location using the scantling method and structural strength evaluation method proposed by Lee et al. (2017) and Kim et al. (2018). The 3D topology optimization of the fixed offshore structure was performed by using ANSYS, a commercial structural analysis software, to maximize structural stiffness under the constraint of utilizing the same amount of materials as the original design which is based on classification society rules. Furthermore, to investigate the influence of the legs of fixed-type offshore structures, which are major members to support the entire structure from external loads, they were considered in the design domain selectively and the results were compared. Furthermore, a structural test was carried out for each design by utilizing 3D printing technology, non-contact video extensometer, and UTM under compressive load. Through the experiment, improvement in the performance of the optimal design obtained from topology optimization was experimentally verified by comparing the behavior with the original design based on the classification society rules.
2. Optimal Design of Fixed Offshore Structure
2.1 Design of Fixed Offshore Structure Based on Classification Society Rules
The design of fixed offshore structures based on the classification society rules is performed using cylindrical members. However, since the topology optimization in this study is performed based on 3D solid elements, these were considered with square cross-sections for experimentall validation as shown in Fig. 1(a). A 130m fixed jacket structure (Kim et., 2018), which is designed based on the AISC (American Institute of Steel Construction) Code of Standard Practice for Steel Buildings and Bridges (AISC, 2016) and API(American Institute of Steel Construction) Recommended Practice 2A-WSD (API, 2002), was used as a reference for the original design of 3D fixed offshore structure considered in this research. Here, wind, wave, and current loads at extreme condition were considered as external loads acting on the structure. The applied wind load was 53 m/s. A wave with a height of 16 m was applied as the wave load, and the fifth order stream function theory corresponding to a period of 14 s was applied. A profile which decreases with an increase in the water depth was used for the current load with the surface current velocity of 2.495 m/s. To compare the structural performance of the optimal design derived through topology optimization with that of the design based on the classification society rules, designs of the fixed offshore structure were fabricated utilizing 3D metal printer with the scale ratio of approximately 273:1. Dimensions of each member are shown in Fig. 1(b).
Rule scantling based design of fixed offshore structure
2.2 3D Topology Optimization Formulation of the Fixed Offshore Structure
The 3D topology optimization of the fixed offshore structure based on the solid elements was formulated to minimize the structural compliance of the structure, so that the structural stiffness of the structure could be maximized. The structural compliance is expressed as the product of the external force f and displacement u for the number of elements (NE) in the entire design domain, as shown in Eq. (1). To compare and verify the high effectiveness of the optimal designs derived by topology optimization, a volume constraint using the relative material density ρi and initial volume V0 of each element is introduced as Eq. (2). Thereby, an amount of material (Vc) equal to that in the rule-based scantling design (shown in Fig. 1) could be used in the topology optimization. Based on SIMP, the design variables in the 3D topology optimization problem of the fixed offshore structure can be expressed with ρi and the initial material property E0 of each element as shown in Eq. (3). Here, the penalty parameter n was set as 3. The penalty parameter interpolates the relative material density so that it can be close to the extreme values of 0.0 and 1.0 to reduce the proportion of members with intermediate densities in the topology optimization. It generally exhibits stable convergence at values between 2 and 4. Furthermore, a very small value was selected as the lower limit of the relative material density (as shown in Eq. (4)) to prevent singularity in numerical analysis owing to the void elements generated in the topology optimization process.
2.3 Boundary Conditions and Design Domain for 3D Topology Optimization of the Fixed Offshore Structure
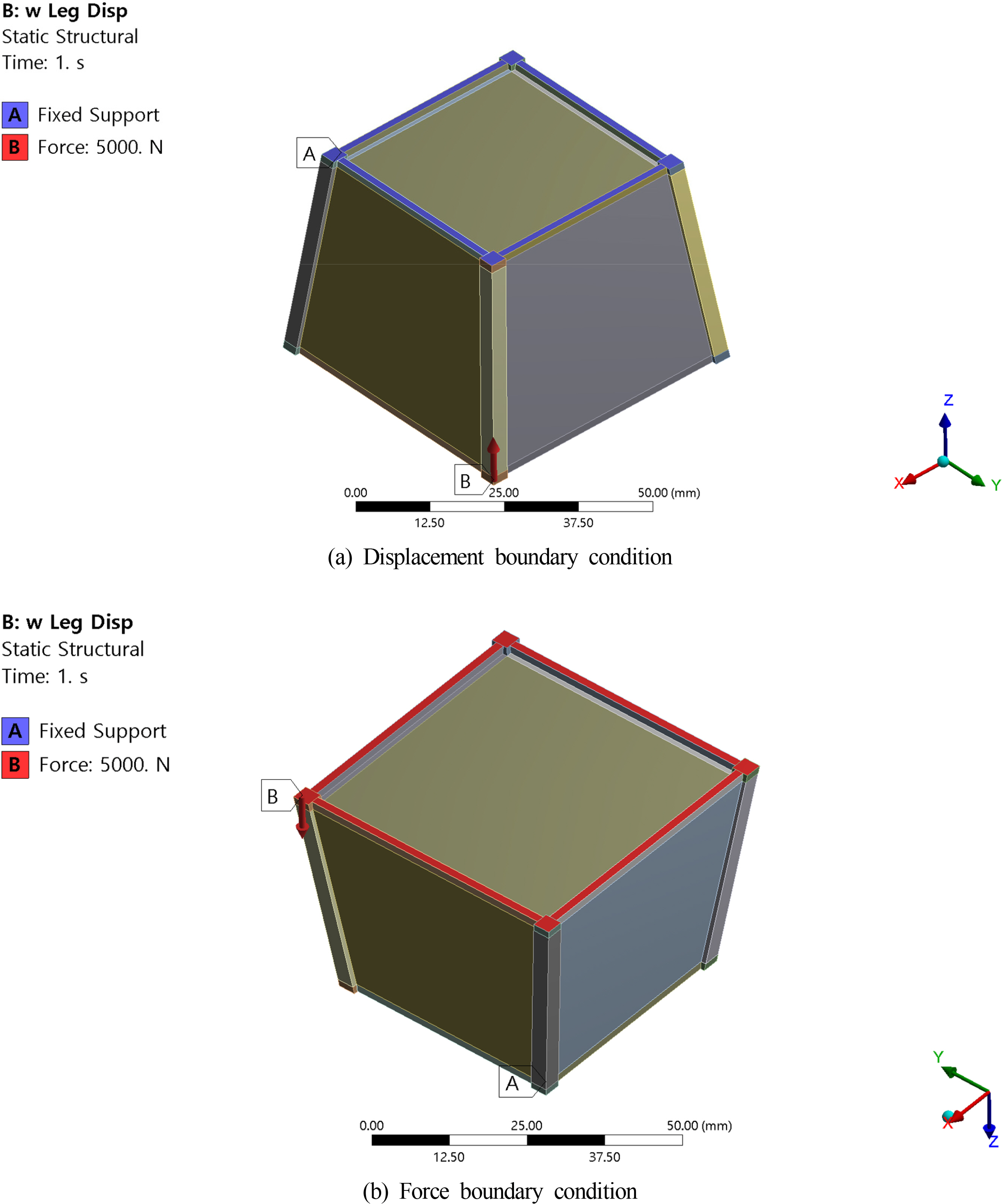
The displacement and force boundary conditions of the fixed offshore structure were assigned to the top and bottom of the structure, respectively, considering connectivity, as shown in Fig. 2. A fixed boundary condition is applied as the displacement boundary condition. A compression load owing to the self-weight of the topside structure was assigned as the force boundary condition. In general, fixed offshore structures experience large loads in the horizontal direction. However, in this study, a compression load of 5 kN caused by the self-weight of the top structure was assumed to seek the applicability of the topology optimization method to the design of fixed offshore structures. Topology optimization problem is a problem of determining the optimal connectivity of members (i.e., the topology), which maximizes the stiffness of the structure under the given force and displacement boundary conditions. However variation in the magnitude of the loads within the elastic region does not significantly affect the result of the topology optimization.
Boundary conditions for 3D topology optimization of fixed offshore structure
The blue colored area in Fig. 3 indicates the design domain considered in the topology optimization of the fixed offshore structure. To investigate the influence of the legs of original fixed offshore structure based on the rules of classification society, design domains with and without considering legs are introduced as Fig. 3(a) and Fig. 3(b), respectively. The red colored areas, expect the legs, in Fig. 3 are the horizontal braces and are excluded from the design domains since the force and displacement boundary conditions are applied. A minimum member thickness constraint was applied to prevent the generation of thin members through the topology optimization. Symmetric conditions and minimum and maximum element sizes were additionally considered for the experimental validation of topology optimization results utilizing 3D metal printing.
Design domains for 3D topology optimization of fixed offshore structure
2.4 3D Topology Optimization of the Fixed Offshore Structure
The 3D topology optimization of the fixed offshore structure was performed using ANSYS Workbench Mechanical Enterprise 2019 R1, a commercial structural analysis software . Here, the static structural module and the topology optimization module were employed for structural analysis and topology optimization, respectively. The 3D optimal designs of the fixed offshore structure that satisfy the given displacement and force boundary conditions as well as the volume constraint were derived as shown in Fig. 4. When the legs of the fixed offshore structure were considered in the design domain under the compression load (Fig. 4(a)), the top sections of the legs were included in the load transfer path and their shapes were maintained. However, the bottom sections were replaced by the Y-shaped braces on both the sides. Meanwhile, when the legs were excluded from the design domain of the topology optimization (Fig. 4(b)), Y-shaped braces similar to the ones in the previous case were generated on both sides of the legs. However, these braces show a relatively thin thickness and wide width compared to the previous optimal design. It was also observed that horizontal braces for reinforcing the space between each plane were freshly generated to increase the stiffness for the out-of-plane displacement under the given load condition. Table 1 compares the volumes of the optimal designs derived through topology optimization (shown in Fig. 4) with that of the rule-based scantling design (shown in Fig. 1). As shown in the table, the optimal designs obtained through topology optimization exhibited volume differences of less than 2%, from the rule-based scantling design.
Optimal designs obtained from 3D topology optimization of fixed offshore structure
Volume comparison of each design
2.5 Conversion of the Topology Optimization Results into CAD Data
The topology optimization of the fixed offshore structure was performed using ANSYS considering the constraints for 3D metal printing. Thus, it cannot stringently satisfy the volume constraint of the use of an amount of material equal to that in the rule-based scantling design, which was applied in this study. Therefore, in this study, the relative material densities of the elements that express the boundaries of the structure in the optimal designs obtained through topology optimization were adjusted so that the results of the topology optimization could match the amount of material in the rule-based scantling design with a maximum error of approximately 3%. In addition, the optimal designs obtained by the topology optimization are derived in the form of mesh data because the topology optimization method is based on the finite element method. Therefore, it is necessary to convert these mesh data into CAD information to fabricate specimens utilizing 3D metal printer to be used in the structural test for experimental validation of the topology optimization results. The mesh data derived through the topology optimization were directly converted into CAD information, i.e., into standard tessellation language (STL) geometry that satisfies the given volume constraint, using SpaceClaim of ANSYS Workbench Mechanical Enterprise 2019 R1. Fig. 5 shows the results of converting each optimal design of the fixed offshore structure into CAD information.
Conversion of topology optimization results to CAD data
3. Experimental Validation of Topology Optimization of Fixed Offshore Structure
3.1 Fabrication of Structural Test Specimens Using a 3D Metal Printer
To experimentally verify the effectiveness of topology optimization, the specimens of the rule-based scantling design and the optimal designs derived through 3D topology optimization were fabricated from Inconel 718 (a nickel–chromium-based alloy) and a 3D metal printer, as shown in Fig. 6. The properties of materials do not significantly affect its results because topology optimization aims to determine the connectivity of materials that maximizes the stiffness of the structure. Inconel 718, one of the commonly used materials for 3D metal printing, was used in this study to examine the applicability of topology optimization to the design of fixed offshore structures. Its mechanical properties are summarized in Table 2.
Manufacturing of fixed offshore structure designs by utilizing 3D metal printer
Mechanical properties of Inconel 718
3.2 Experimental Validation of the Topology Optimization Results
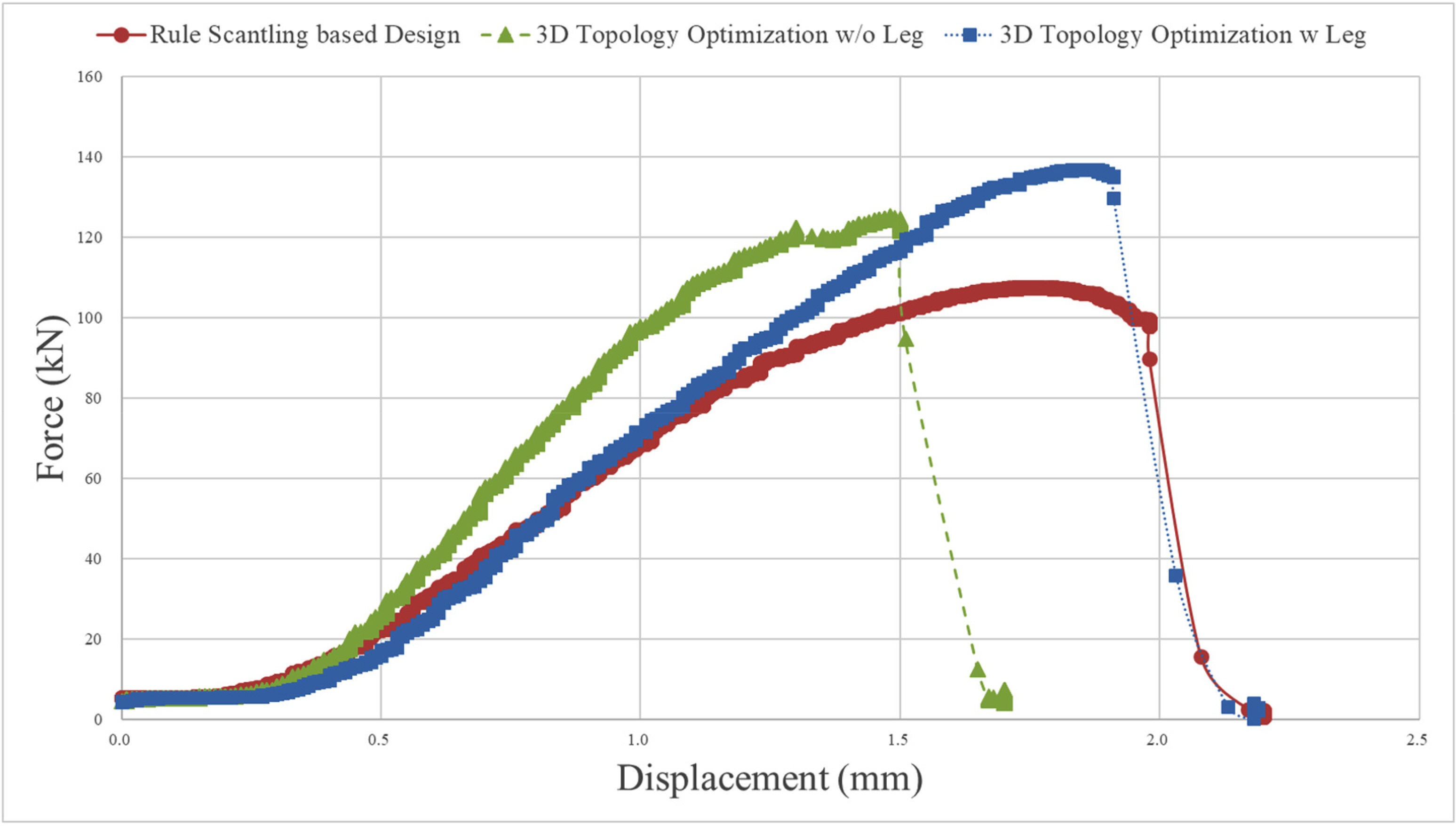
A structural test was conducted under compressive loading using a 100 ton UTM (as shown in Fig. 7) for experimental validation of each optimal design of the fixed offshore structure obtained from 3D topology optimization. The UTM was set to control the maximum displacement of the specimen, and it was operated at the rate of 5 mm/min. The test was conducted until each specimen fractured as shown in Fig. 8. Through the structural test, the displacement and load under compressive loading were derived for the rule-based scantling design, optimal design without legs in the design domain, and optimal design with legs in the design domain. The reaction force of each structure measured by the UTM according to the vertical displacement is expressed through the force–displacement curves in Fig. 9. Since topology optimization is a method for determining the connectivity of members that maximizes the stiffness of the structure in the elastic region, the degree of improvement in the stiffness of the structure because of topology optimization can be obtained by comparing the displacement of the optimal designs derived through topology optimization to that of the existing design under a similar load. The topology optimization of the fixed offshore structure was performed considering a design load of 5 kN, where the structure is assumed to be within the elastic region. However, in this study, we compared the displacement and its ratio when 100 kN load is applied to clearly show the effectiveness of topology optimization, as tabulated in Table 3, since the original rule based offshore jacket design is out of elastic region while optimal designs are still inside or at the end stage of elastic region. As shown in the table, the optimal design that did not consider legs in the design domain during topology optimization and the optimal design that included legs in the design domain exhibited approximately 30% and 12% lower displacement, respectively, compared with the rule-based scantling design under the same load.
Structural experiment of fixed offshore structure designs by utilizing UTM
Last step of the structural experiments of each specimen
Force-displacement curves obtained from structural experiment
Displacement and load comparison
This result is due to the improvement in the structural stiffness of the fixed offshore structure from topology optimization. It was also observed that the optimal design that did not consider the legs of the rule-based scantling design exhibited a higher degree of improvement in structural stiffness than the optimal design that included the legs, under compressive loading. However, the optimal design when legs are considered in the design domain showed a higher fracture load than the optimal design without legs considered in the design domain, although it exhibited relatively lower structural stiffness. This implies that when rule-based scantling method, which has been developed based on long experience and knowledge, and the topology optimization method, which is capable of deriving innovative design and optimal connectivity, are effectively combined, it is possible to improve the structural stiffness as well as their structural performance.
4. Conclusion
In this study, the optimal designs of a fixed offshore structure with improved structural stiffness were derived through 3D topology optimization using the same amount of material as the original rule based design. To examine the influence of the legs of the rule-based scantling design on the structural stiffness of the structure, they were considered selectively in the design domain of the topology optimization problem. For experimental validation, mesh and material data obtained from topology optimization is converted to CAD data utilizing ANSYS SpaceClaim and manufactured employing 3D metal printing technology.
Through the structural experiment utilizing UTM, it is shown that optimal designs obtained from topology optimization show improvement in structural stiffness compared to the original rule-based design. Optimal design which considered legs as design domain showed higher structural stiffness compared to the one not considering legs in the design domain. However, the optimal design derived when the legs were not considered in the design domain of the topology optimization problem showed the highest fracture load, although the degree of improvement in its structural stiffness was relatively lower than that when the legs were considered. This implies that it is possible to improve the stiffness and structural performance of structures by effectively combining the rule-based scantling method with the topology optimization method, which is capable of deriving the connectivity of members that improves the structural stiffness of fixed offshore structures. Although to implement this developed technique to the industry, a method which can consider cylindrical members in topology optimization, as well as consideration of manufacturability, productivity, transportation, and various environmental loadings is necessary. Furthermore, it is also essential to review the structural safety based on the rules of classification society of the proposed optimal designs.
Acknowledgements
This research was supported by a grant from Endowment Project of “Core Technology Development of Hydro-elasticity based Structural Damage Assessment for Offshore Structures considering Uncertainty” funded by Korea Research Institute of Ships and Ocean engineering (PES3490).
