Fatigue Assessment of Very Large Container Ships Considering Springing Effect Based on Stochastic Approach
Article information
Abstract
Evaluation of fatigue strength considering the springing effect of very large container ships is crucial in the design stage. In this study, we established a fatigue strength evaluation method considering a linear springing component in the frequency domain. Based on a three-dimensional global model, a fluid–structure interaction analysis was performed and the modal superposition method was applied to determine the hot spot stress at the hatch corner of very large container ships. Fatigue damage was directly estimated using the stress transfer function with a linear springing response. Furthermore, we proposed a new methodology to apply the springing effect to fatigue damage using hull girder loads. Subsequently, we estimated the fatigue damage contribution due to linear springing components along the ship length. Finally, we discussed the practical application of the proposed methods.
1. Introduction
Hull hydroelastic response, which is represented by springing, has been reported to first occur in low-speed blunt ships constructed with larger hulls, such as ore carriers. Furthermore, owing to the wide openings of high-speed slender ships such as container ships, torsional natural frequency is generated in the low-frequency domain; furthermore, a recent increase in the size and speed of ships causes the natural vibration period of the hull and the wavelength of an incident wave to overlap, thereby increasing the likelihood of resonance between the ship and wave.
Hydroelastic responses, such as springing, which are referred to as vibration-induced waves, have been predicted to cause fatigue failure by increasing the cumulative fatigue damage in structurally discontinuous areas. As such, unexpected fatigue failure may occur if the structural vibration response is not considered in the design stage of very large container ships, which have been constructed recently. Ship owners are demonstrating a steady, increasing demand for the prediction of fatigue damage due to springing response when ordering large ships. However, an efficient numerical methodology applicable to the design stage is still being developed. Research on the springing phenomenon in ships primarily began with numerical approaches. Applying the beam theory of Euler and Timoshenko, Bishop et al. (1985) conducted a dynamic calculation of a cross-section beam and demonstrated that the beam theory produced better results than experimental results. Kim et al. (2009) developed a response analysis method that directly connected a three-dimensional (3D) Rankine panel method with the Vlasov beam model, which considered warping deformation, analyzed the linear and nonlinear responses, and proposed a new method for numerical problems.
In addition to numerical attempts to solve the hydroelasticity problems as described above, studies using the model test and real ship measurement are continuously being conducted. Storhaug et al. (2011) calculated the ultimate load and fatigue damage due to the hydroelastic response of large container ships through model tests. Kim et al. (2018a) and Kim et al. (2018b) analyzed the strain data based on actual ship data measured in a very large container ship, analyzed the vibration mode generated in the ship, and predicted the long-term fatigue damage.
Moreover, Kim et al. (2018c) evaluated the ultimate load considering an increasing vertical bending moment due to slamming–whipping at the center of large container ships. Kim and Song (2019) conducted a study on structural strength using the vertical bending moment in large ore carriers to estimate long-term fatigue damage, while considering nonlinear hydroelastic responses.
This study seeks to establish an efficient methodology based on a statistical fatigue analysis method for springing responses caused by wave loading on a representative weak member of a large container ship. Hence, spectral fatigue analysis based on linear statistical analysis was applied, which is the most widely used technique for evaluating fatigue strength. The stress transfer function including the springing response must be calculated to obtain the fatigue damage by applying a wideband fatigue model. In this context, the stress transfer function considers only the linear component of the unit wave height. To consider the geometric nonlinearity and nonlinearity in a rough sea state with high waves, the nonlinear springing response in each sea state in the time domain must be directly obtained. Although this technique results in a response that is similar to the actual phenomenon, it poses severe time limitations when used in the design stage. Therefore, the spectral fatigue analysis method, which can estimate fatigue damage relatively quickly and accurately, is primarily used in the design stage. In addition, to obtain the springing response, an effective method is presented herein for combining the existing rigid body-based results when estimating fatigue damage in a flexible body-based structural model rather than a rigid-based structural model, which is regarded as the final fatigue design life in ship design evaluations. Finally, the method proposed for 15,000TEU-class very large container ships is applied in this study to analyze its effect on design evaluation.
2. Fatigue analysis procedure
Currently, one of the most extensively used methods in classification and shipyards is a statistical fatigue analysis technique based on the dynamic loading approach, known as spectral fatigue analysis. In this method, fatigue damage is predicted based on an irregular wave sea state, and the cumulative fatigue damage is estimated by applying a probability statistical function to the stress range of a structural member generated by wave loading. As the fatigue damage is subject to the stress range and number of cycles, the statistical fatigue analysis method mentioned above for classification and shipyards utilizes a stress range that follows a narrowband-based Rayleigh distribution calculated by assuming a rigid-body ship (Choung et al. 2013). In the existing fatigue analysis guidelines and hull motion analysis for ship classification, hull motion analysis is conducted based on a rigid body to analyze the fatigue of offshore structures caused by ocean waves. A fatigue analysis program has been developed assuming that the stress range is a Rayleigh distribution. This fatigue analysis methodology calculated from a stress response that assumes a rigid-body-based Rayleigh distribution has been developed and corrected over the decades, in which the results of each ship classification are similar or identical.
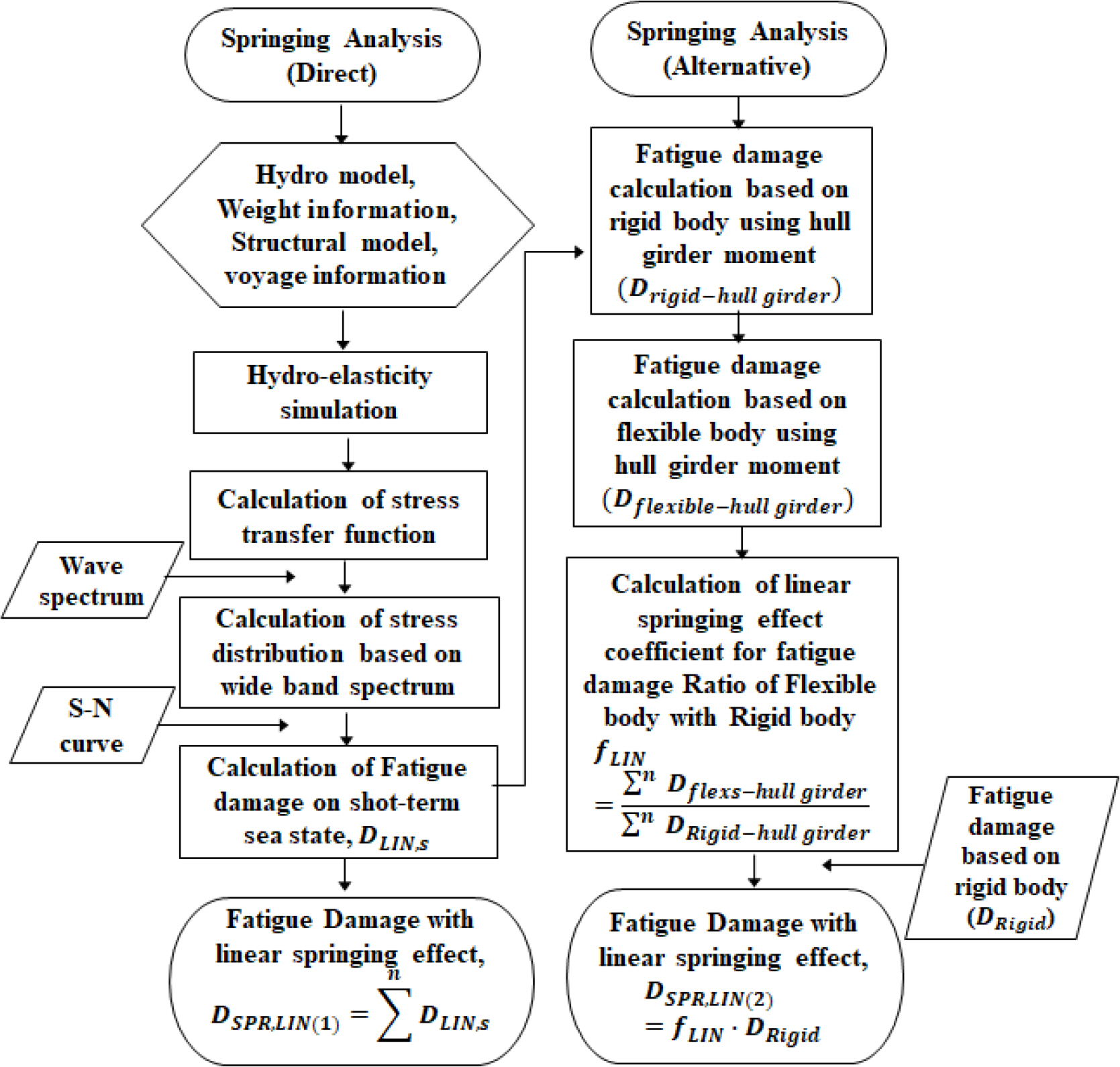
Spectral fatigue analysis based on existing stochastic approach can be also applied to calculation of fatigue damage considering springing responses. To directly estimate the fatigue damage of weak areas, a 3D-model-based analysis of ship motion was conducted to estimate the hydroelastic response, and a structural analysis was performed to calculate the stress transfer function for the unit wave height comprising the springing component. Subsequently, a method for estimating the short-term fatigue damage in each sea state was applied assuming a wideband-based response rather than a narrowband-based response. The wideband model proposed by Benasciutti and Tovo (2005) was applied as it was the most similar to the narrowband-based calculation process. In this method, the fatigue damage based on the narrowband response is first calculated, as in the existing technique. Next, the presented wideband correction coefficient is applied to estimate the fatigue damage considering the springing response (Choung et al., 2012; Park and Jeong, 2014). By considering the expression probability for fatigue damage in each short-term sea state, the long-term fatigue damage (DSPR,LIN) considering the linear springing component can be estimated, as shown in the left of Fig. 1. This method is applicable to design as the fatigue damage is calculated directly considering the springing effect. However, the tendency of results with the fatigue damage estimated in the existing rigid body-based narrowband method, which is regarded as the final fatigue damage in ship design evaluations, may be degraded. Hence, different structural response values can be calculated by applying different theories for structural response calculation and motion analysis to the existing rigid body and flexible body-based structural model theories. Because the fatigue damage is proportional to the inverse slope of the S–N curve, this difference in structural stress responses can result in a substantially greater difference in fatigue damage.
Accordingly, a method is proposed herein that considers the effect of springing response on the fatigue damage estimated from the existing verified rigid-body-based method, as shown in the procedure in the right of Fig. 1. This method can estimate the fatigue damage (DSPR.LIN) by considering the springing effect (fLin) calculated by other motion and structural analysis theory-based programs, based on the fatigue damage (DRigid) estimated in a fully tested rigid body-based program. In this study, the springing effect was calculated by obtaining the stress transfer function from a hull girder load, which has been studied by Jung (2013) and Li et al. (2018). Because the existing rigid-body-based fatigue damage is still regarded as the final fatigue damage in the design evaluation of most ships, the method proposed herein may be an efficient alternative for applying the springing effect, which is estimated in programs that use numerous hydroelasticity theories from academia and the industry, to design evaluation.
3. Numerical theories
3.1 Spectral fatigue analysis
According to the Palmgren–Miner linear cumulative damage rule, the cumulative fatigue damage (D) can be defined as shown in Eq. (1) using the S-N curve
D : Cumulative damage
N : Fatigue life
n : Cycle counting of stress range
a & m : Material factor of S-N curve
When applying the linear wave theory, the height of the wavefront exhibits a normal distribution, whereas the peak of the wave height exhibits a Rayleigh distribution. In this case, as the stress range affecting the fatigue damage is equal to the peak of the wave height, a Rayleigh distribution is applied in the spectral fatigue analysis method, as shown in Eq. (3).
The zero-crossing frequency and peak frequency can be derived using the zero-order moment (m0) and second-order moment (m2) of the response spectrum, as shown in Equations (4) and (5). Furthermore, as shown in Equation (6), if the ratio of the zero-crossing frequency and peak frequency (α) is approximately 1, it can be considered a narrowband; if it is approximately 0, it can be considered a wideband.
3.2 Motion equations for hydroelastic analysis
For hydroelastic analysis, the program WISH-FLEX developed by Kim and Kim (2014) was used, in which 3D global models can be applied. The solution for the fluid domain was obtained by applying the boundary element method, and the 3D finite element method was applied to analyze the rigid body and elastic motion of the hull and directly calculate the stress transfer function at hot spot locations. When using a 3D finite element model to obtain a solution in the time domain, the equation of motion has a large degree of freedom. As such, the method of obtaining the solution at each time interval is not suitable. Hence, a method that divides the solutions of low-order and high-order modes was used. The high-order mode of a flexible body motion possesses strong structural resilience, and therefore exhibits a quasi-static behavior with small displacements and an extremely high natural frequency. As this motion does not disturb the fluid field significantly, the assumption shown in Eq. (7) holds.
In Equation (9), the subscript L indicates the low-order mode and H the high-order mode. u⃗ is the velocity vector; superscripts j and k are the numbers for the low-order and high-order modes indicated in Eq. (7), respectively. Eq. (9) can be separated into two equations, i.e., motion equations for low-order and high-order modes, as follows:
In the motion equation of the low-order mode, all terms on the left hand side are considered, and the solutions on the left hand side are included in the external force term on the right. Hence, the motion of the low-order mode is a dynamic coupled response. Conversely, because the motion equation of the high-order mode assumes a quasi-static decoupled response, both the speed and acceleration components on the left hand side are ignored, and the external force term on the right hand side does not include the motion of the high-order mode. Hence, the motion of the high-order mode is a quasi-static decoupled response. The rigid body motion and low-order mode springing and whipping responses can be obtained from Eq. (10). However, as the local deformation corresponds to the high-order mode, the stress must be calculated from Eq. (11) to the solution of the high-order mode. The motion response of the high-order mode can be calculated from the motion response of the low-order mode.
3.3 Extraction of stress response using hull girder load
In this study, a method using only hull girder loads was used to estimate the ratio of fatigue damage due to springing, as shown in the procedure on the right side of Fig. 1. The hull girder loads include longitudinal bending, transverse bending, and torsional moment due to wave loading; the acceleration component of the hull generated by an external force is considered in these values and can be expressed by superimposing the hull girder mode. The corner parts of the upper deck and hatch top, i.e., the main fatigue strength evaluation locations of the very large container ship used in this study, were barely affected by changes in the local loads, such as the internal and external pressures. Accordingly, a method can be applied to estimate the stress response history of the hot spot locations including the springing response using only the hull girder load. The load distribution in a specific strip can be defined as the load distributed in the longitudinal direction divided into several strips in the longitudinal direction. For longitudinal and transverse bending, the load distribution in the longitudinal direction (x) can be easily calculated using the existing beam theory. The longitudinal distribution (MT) acting on each cross section of the torsional load component can be derived as follows:
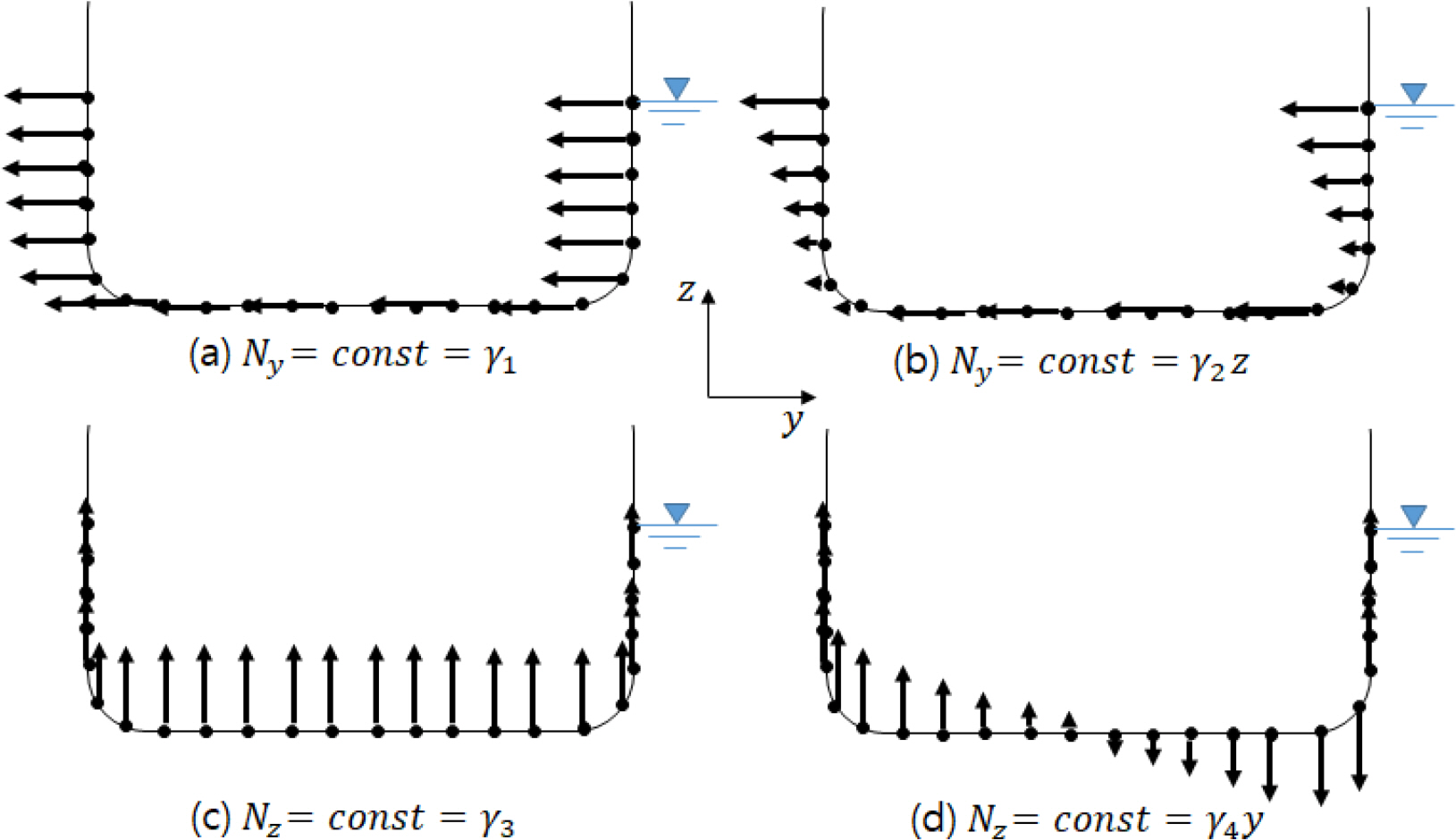
It is assumed that the torsional moment of the ship acts at the shear center (SC) of the transverse section, and because the horizontal shear force does not act at the SC, the horizontal bending moment is always coupled with the torsional moment. The adhesion point where the horizontal shear force acts is assumed to be 65% of the draft (T) used to calculate the strength; based on this assumption, another constraint is created by the horizontal shear force acting at 0.65T of the ship baseline T. Fig. 2 shows the basic shape of the load distribution acting at the points inside each strip, which can be defined as follows. (1) The point load in the horizontal direction acts uniformly on each point (point load Ny = const. = 1); (2) The point load in the horizontal direction is linear in the height direction (point load Ny = const. = r2z); (3) The point load in the vertical direction acts uniformly (point load Ny = const. = r3); (4) The point load in the vertical direction changes linearly in the width direction (point load Nz = const. = r4y). If the number of points in the strip section is n, then the sum of point forces (fH) in the horizontal direction can be expressed as Eq. (13). The moment generated by the horizontal force at the SC satisfies Eq. (14).
Similarly, the sum of the point forces in the vertical direction (fv) can be expressed as Eq. (15), and the torsional load at the SC generated by the sum of vertical direction point forces satisfies Eq. (16).
The following task is required to analyze the correlation between the load distribution calculated from the equation above and the hot spot stress. In the 3D finite element model, the three hull girder load components were assembled for three cases: (i) uniform in the positive direction (+); (ii) uniform in the negative direction (−); and not applied at all. Subsequently, the correlation between load distribution and stress was determined by conducting a structural analysis to examine the stress acting on a specific location. The stress acting on a specific location of the hull (σ) can be obtained using Eq. (18), of which a more detailed theoretical explanation has been provided by Jung (2013).
σVBM : Stress due to vertical bending moment component
σHBM : Stress due to horizontal bending moment component
σTM : Stress due to torsional moment component
4. Fatigue analysis
4.1 Fatigue evaluation model
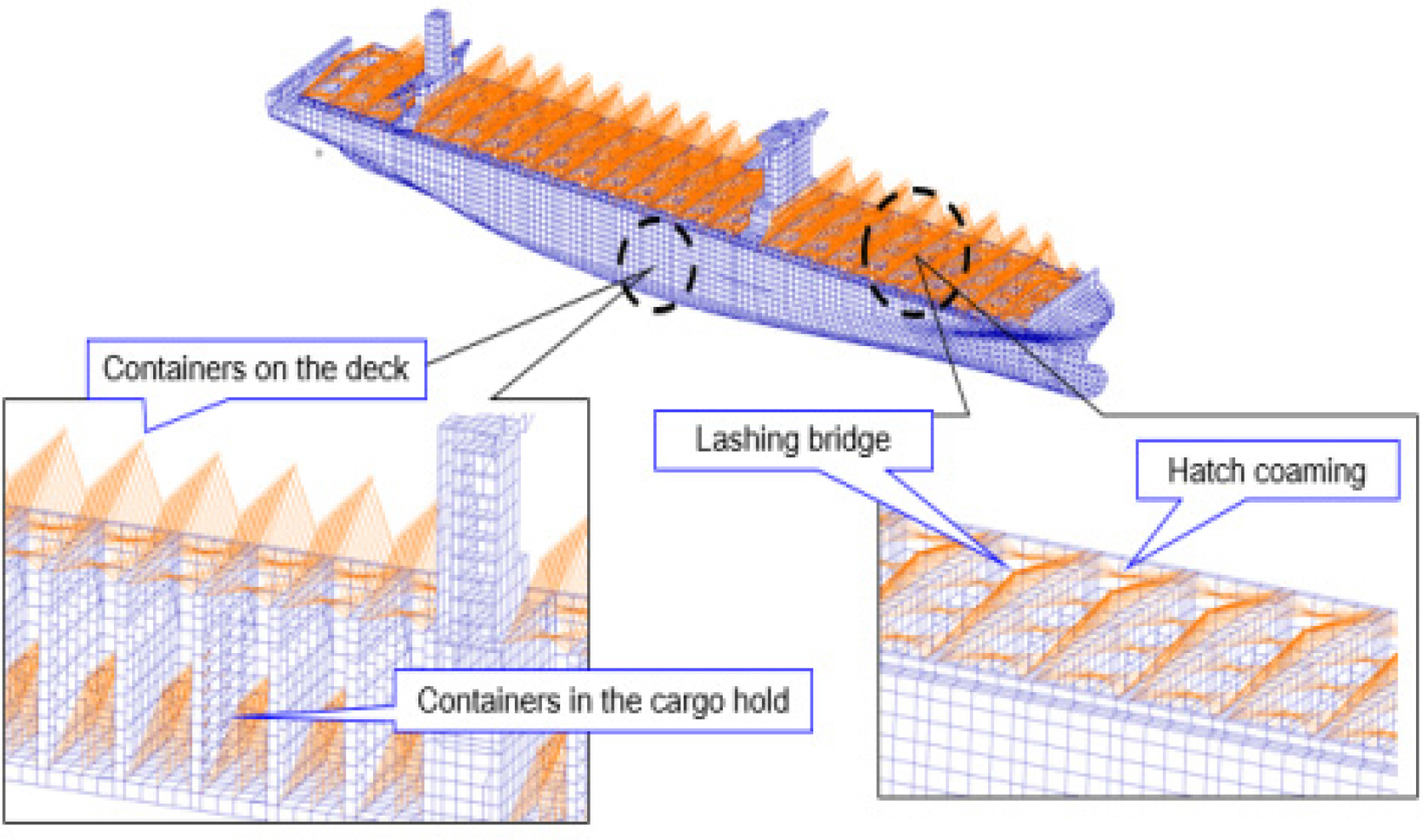
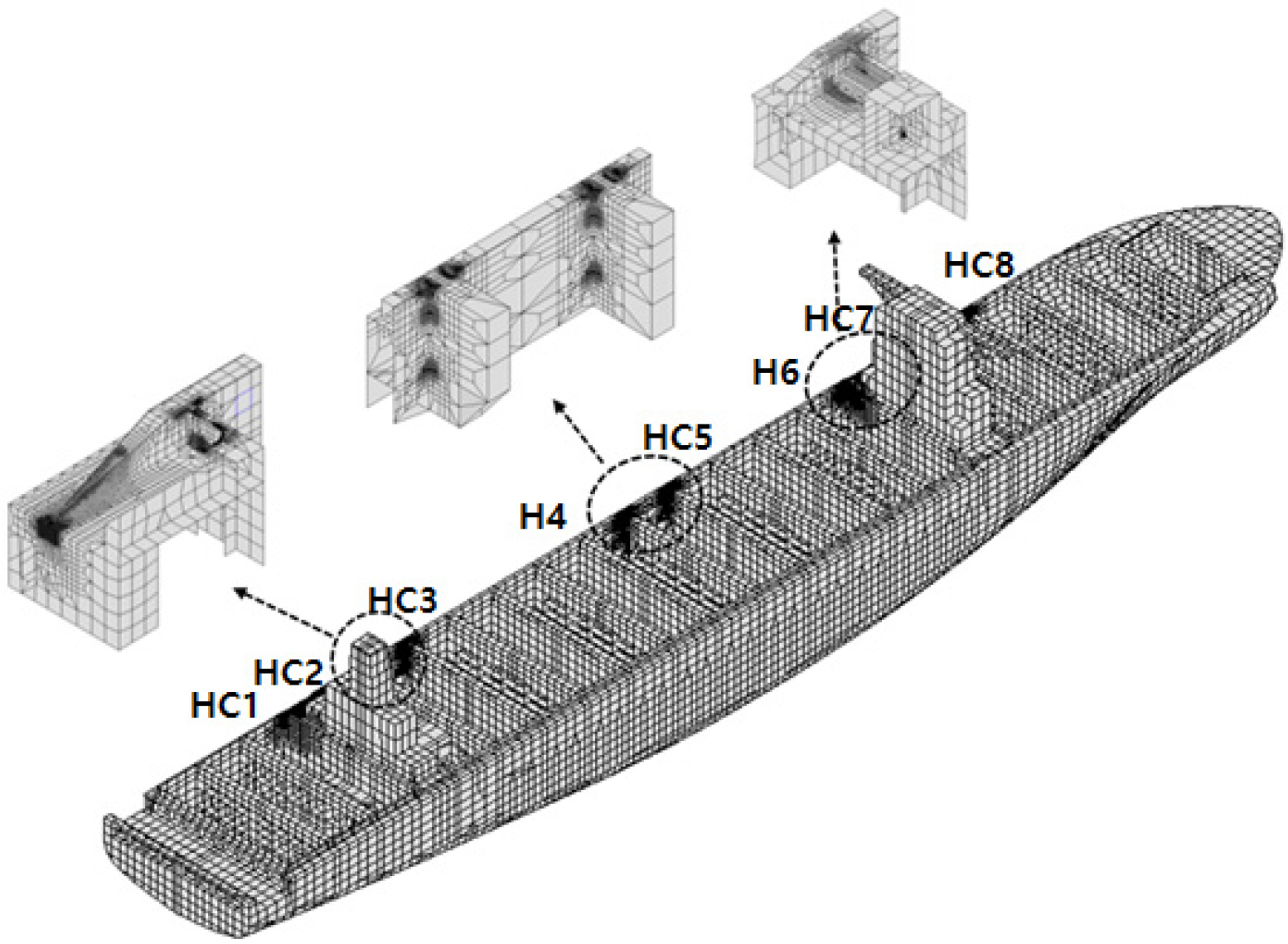
The model used in the analysis was a 15,000 TEU-class very large container ship. Fig. 3 shows the 3D global model considering the mass distribution used in this study. The point mass and rigid body element were used to idealize the mass of the hatch cover, lashing bridge, container, and light weight distribution. Fig. 4 shows the fatigue damage evaluation location. To evaluate the hatch corner in the longitudinal direction, i.e., a representative area weak to fatigue in the container ships, the area was divided into eight sections around the crossing point of the longitudinal and transverse bulkheads.
4.2 Mode analysis
In this study, the stress transfer function was obtained to calculate the fatigue damage through modal superposition. WISH-FLEX, the hydroelastic analysis program introduced in Section 3.2, was used to calculate the modal response to the unit wave height at a specific frequency. By multiplying the stresses corresponding to each mode in the elements of the fatigue strength evaluation locations previously calculated in finite element analysis, the stress corresponding to each modal response can be obtained. Next, by superimposing the stresses corresponding to each modal response and using them for each frequency, the stress transfer function at that location can be obtained. The procedure for evaluating the fatigue strength after calculating the stress transfer function is detailed in Section 3.1. Fig. 5 shows the results of the eigenmode analysis for calculating the structural response. While applying as many eigenmodes as possible to the calculation enables more accurate stress response calculations, when using an entire ship structural model that includes mass, many local modes occur owing to problems arising from the boundary conditions of the structural members and concentrated mass. As shown in Fig. 5, the stress response was obtained using six global modes. For the target ship, after first identifying two low-order torsion modes, a first-order vertical mode occurred; subsequently, four torsion modes and two vertical modes were applied to the analysis.
4.3 Fatigue damage calculation
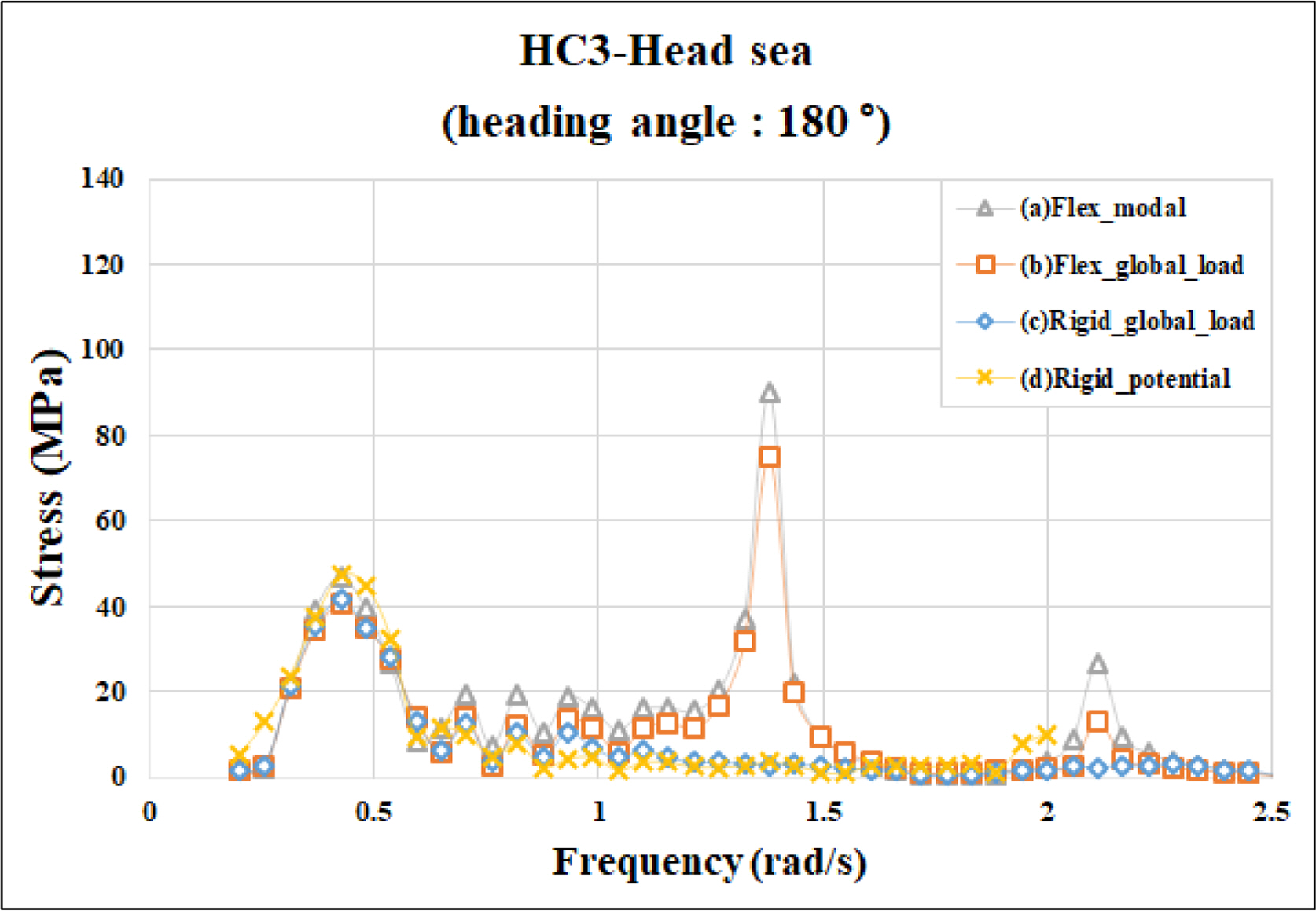
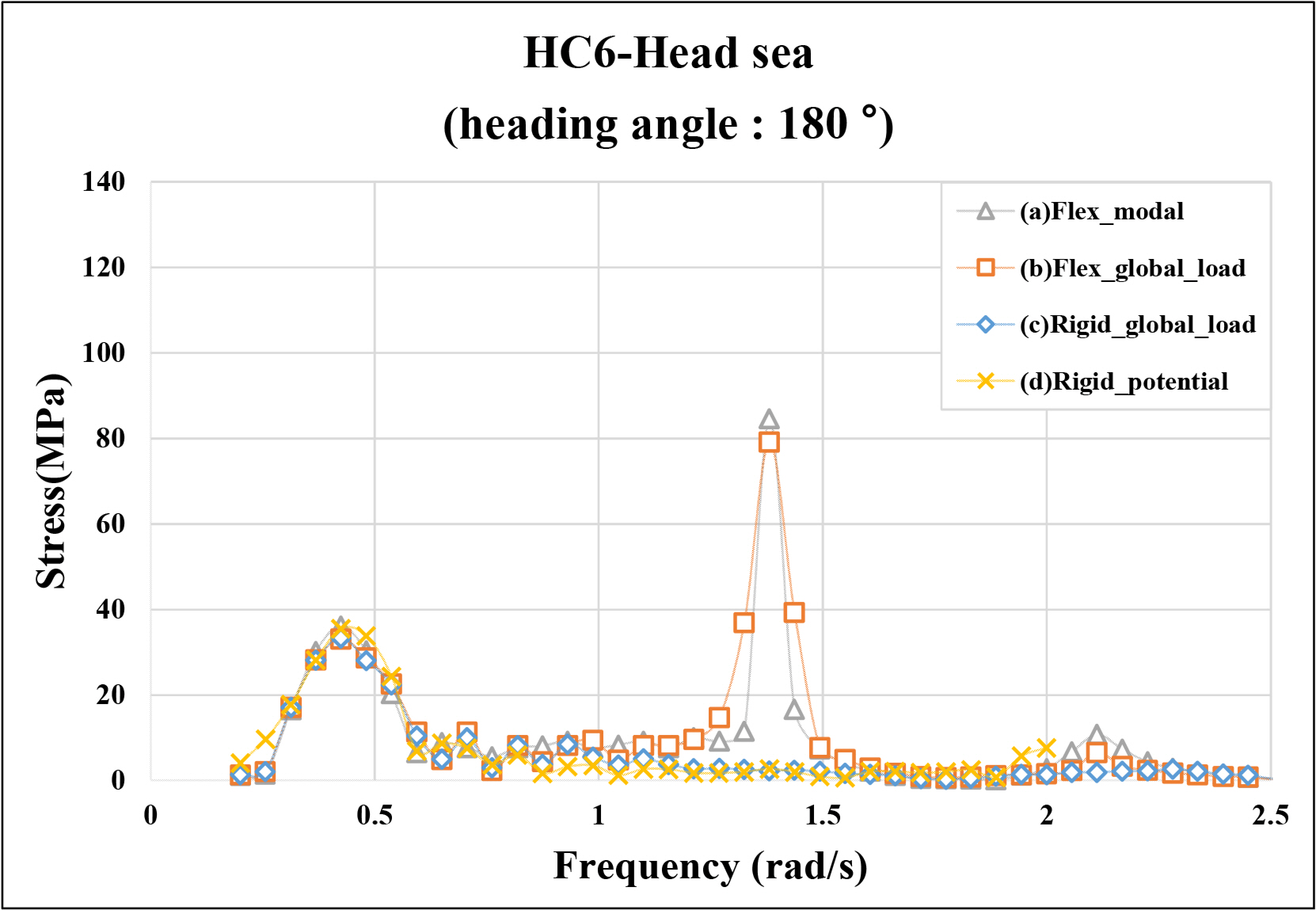
When a ship encounters a wave in the heading direction at a constant speed and advances forward, the resonance frequency generated from the springing vibration response is shortened owing to the effect of the encounter frequency. This creates a cross section involving the wave spectrum with energy in the fatigue analysis calculation based on statistical analysis, which increases the contribution of the springing component in the response spectrum for fatigue damage calculation. By contrast, when the ship encounters a following sea or beam sea and then advances forward, the resonance frequency of the springing vibration response does not lengthen or change. Figs. 6–9 show representative structurally discontinuous areas of container ships for the fatigue evaluation areas shown in Fig. 4. The figures show the stress transfer functions for a bow quartering sea and a head sea in order at HC3 and HC6, which correspond to points 0.25L and 0.75L with weak fatigue strength, respectively, where L is the ship length. Four stress transfer functions were included in the figure, defined as follows:
Stress transfer function considering the springing response obtained by conducting a flexible body analysis using WISH FLEX and applying modal superposition (a coupled analysis was conducted to obtain the modal response, and modal superposition was applied to directly calculate the stress at the hot spot position)
Stress transfer function considering the springing response obtained using only the hull girder load in the flexible body-based structural model (a coupled analysis was conducted to obtain the hull girder moment, and the technique in Section 3.3 was applied to calculate the stress at the hot spot position)
Stress transfer function not considering the springing response obtained using only the hull girder load in the rigid body-based structural model (a decoupled analysis was conducted to obtain the hull girder moment, and the technique in Section 3.3 was applied to calculate the stress at the hot spot position)
Stress transfer function not considering the springing response obtained from the rigid-body-based structural model applying a program (KR 3D) using potential theory, which is currently used in the design evaluation stage (This is the rigid-body-based stress transfer function applied in the existing design stage presented in this study. It is calculated using KR 3D based on potential theory).
First, the figures show that in the head sea, the springing response occurs in a lower frequency domain compared with the following sea, which is attributed to the effect of the encounter frequency described above. In terms of the overall response sizes, the responses of (a) and (b) comprising the hydroelastic response tended to be slightly larger or similar to those of (c) and (d), which comprised only rigid-body responses. As the stress response in the bow quartering sea and head sea occurred at similar levels, it is confirmed that the method introduced in Section 3.2 for estimating the stress response using the hull girder load can efficiently estimate the stress transfer function at any location.
When calculating the response spectrum to estimate fatigue damage, the frequency band with high energy in the wave spectrum is the stress response in the low-frequency domain due to wave loading, instead of a high-frequency response such as springing. As such, a small difference in response due to wave loading compared with the difference in the springing response can result in larger differences in fatigue damage that are proportional to the inverse slope of the S–N curve. Therefore, the difference between the response calculated based on the rigid body-based potential (d) and the response of the low-frequency band caused by wave loading calculated using flexible body-based modal superposition (a) can result in large differences in the final fatigue damage, as well as differences in the trend of the results. Hence, an alternative method is proposed that considers the effect of springing on the existing rigid-body-based value, as shown in the procedure on the right of Fig. 1 in Section 2.
To implement this alternative method, the existing rigid-body-based fatigue damage was calculated from (d), and using the hull girder load, the ratio of fatigue damage calculated from the stress responses containing the springing response (b) and not containing the springing response (c) was calculated as the springing effect. Fig. 10 shows the calculated fatigue damage from HC-1 to HC-8. A worldwide scatter table (DNVGL RP-C205) with a design life of 25 years was applied; for the S–N curves, British Standard “c” curves applicable to welds were applied to all locations. Three fatigue damage levels are shown for each location, and each fatigue damage was calculated as follows:
As the fatigue damage (Drigid) was rigid-body based, it was calculated from the stress transfer function in Fig. 6(d), which is the most widely applied method in actual design stages.
Fatigue damage (Dsprlin.1) was the value at the hot spot location and was calculated directly using modal superposition, as shown in the analysis procedure on the left of Fig. 1. Hence, as shown in Fig. 6(a), the fatigue damage was calculated directly from the stress transfer function containing the springing response.
Fatigue damage (Dsprlin.2) was calculated by applying a method that incorporated the springing effect on the existing rigid-body-based fatigue damage, as shown in the procedure on the right of Fig. 1. Hence, fatigue damages with and without the springing response were calculated using only the hull girder loads calculated based on Figs. 6(b) and 6(c); furthermore, the ratio of the two fatigue damage values was defined as the effect of springing on fatigue damage. This ratio was multiplied by the rigid-body-based damage (Drigid) to obtain Dsprlin.2.
The rigid-body-based fatigue damage showed the smallest value. A comparison between the value calculated directly using modal superposition and the rigid-body-based value calculated considering the springing effect indicated that the fatigue damage estimated in either method was not biased. Moreover, because the fatigue damage was proportional to the inverse slope of the S–N curve as described above, the fatigue damage calculated from the stress transfer function including the springing responses estimated from different methods can be assumed to be similar. This demonstrates that the feasibility of this method for the final design evaluation, even when applying a theory other than the existing rigid body-based theory to estimate the ratio of fatigue damage due to springing.
5. Conclusions
This study aimed to establish a procedure to evaluate fatigue strength based on a linear statistical analysis technique that is widely used in fatigue strength evaluation. Therefore, the springing response of very large container ships was considered, the abovementioned procedure was applied to an actual ship, and its applicability was evaluated. First, a methodology was established for directly calculating the fatigue damage at hot spot locations using a 3D global model. Subsequently, a method was proposed for estimating the final fatigue damage, considering the fatigue damage calculated from the rigid body-based spectral fatigue analysis method, which is currently used as the final fatigue damage in design evaluation, while applying the ratio between the fatigue damage estimated from the theory applied to the design evaluation stage in actual shipbuilding and that due to springing estimated from a different theory. In addition, the proposed method was used to estimate the fatigue damage of a hatch corner along the longitudinal direction of the container ship. To evaluate the applicability of the proposed method, the results and characteristics of the fatigue damage calculated from each method were analyzed.
Some limitations were encountered when evaluating the proposed method’s applicability and efficiency in the design evaluation of actual ships. In the future, the stress transfer functions and stress responses applied to fatigue damage calculation need to be investigated by analyzing the proposed structural theories and analysis procedures. Additionally, studies pertaining to the nonlinear components mentioned in the introduction need to be conducted.