|
 |
- Search
| J. Ocean Eng. Technol. > Volume 33(5); 2019 > Article |
|
Abstract
As exhaust gas systems of ships become more complicated, it is necessary to calculate an accurate pressure loss at their design stage. If the dynamic loss coefficients of non-standard fittings mainly used in exhaust gas pipe (EGP) are well-documented, it would be possible to calculate precise pressure loss more readily than using the conventional method that analyzes the entire system. In the case of a ship's EGP, the flow rates and temperatures of exhaust gas are determined by engine specifications, and the range of the flow rate and temperature is limited according to operating conditions. In addition, as it is possible to define non-standard fittings frequently used in an EGP, a database can be easily constructed and effective. This paper illustrates effective parameters and analysis cases of several types of non-standard fittings mounted in ship EGPs. The analysis procedure proposed in this paper is verified using existing research results on HVAC fittings. The numerical procedure, which is minimally affected by manpower and grid, is established such that it can be applied at the industry level.
The pressure loss in an exhaust gas pipe (EGP) can be broadly divided into two types: friction loss and dynamic loss. Friction loss is determined by surface roughness and is caused by friction between exhaust gas and the internal surface of an EGP. Dynamic loss occurs at the point where fluid flow changes and results from secondary flow due to fittings. Generally, dynamic loss occurs where the fluid flow direction or pipe diameter is changed, such as at elbows or Ts, resulting in an additional pressure loss compared to a straight section of the same length.
Such turbulence at fittings is recognized as a major consideration in the EGP design stage because it affects the downstream conditions and results in significant pressure loss. Dynamic loss coefficients can be measured by conducting actual tests or by using computational fluid dynamics (CFD). Performing actual tests is costly and requires building a test facility. As a result, in recent studies the use of CFD has become more popular to measure dynamic loss coefficients.
Shao and Raffit (1995) carried out numerical simulations to determine the pressure loss of several heating ventilation and air conditioning (HVAC) duct fittings and studied the factors affecting analysis and accuracy. Mumma et al. (1998) calculated the dynamic loss coefficients of several duct fittings, including a 90┬░ elbow, using CFD and proved its applicability. Since then, a number of researchers have attempted to use CFD to calculate dynamic loss coefficients, and more attempts are being made as computer technology evolves. Zmrhal and Schwarzer (2009) performed a comparative analysis of their results in elbow flow analysis with those of Idelchik (Idelchik, 1993) and Recknagel et al. (1995). Kulkarni et al. (2009) provided measurement results from testing several flat oval elbow shapes in accordance with ANSI/ASHRAE Standard 120-1999 to supplement the American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc. (ASHRAE) database (DB). Liu et al. (2012) performed flow analysis, compared the results with those of the ASHRAE DB, and showed the reliability of the CFD method. Santos et al. (2014) analyzed a round elbow using a k-╬Ą model and compared it with that of the ASHRAE DB; they also proposed a formula to estimate dynamic loss coefficients according to the Reynolds number.
In the case of a ship's EGP, the flow rate and temperature of exhaust gas are determined by engine specifications, and the range of the flow rate and temperature is limited according to operating conditions. In addition, as it is possible to define non-standard fittings frequently used in an EGP, constructing a database is more feasible than for an HVAC system. However, dynamic loss coefficients of EGP fittings have not been addressed in existing studies. In this study, we employ the Workbench Meshing (Ver. 18.2) and Fluent (Ver. 18.2) of Ansys Inc. to generate grids and perform a flow analysis on EGP non-standard fittings. The analysis procedure of this study was verified in advance using the results of existing research on HVAC fittings. Effective parameters and analysis cases are determined for five types of non-standard fittings frequently used in a shipŌĆÖs EGP and the dynamic loss coefficients are calculated using CFD.
In the case of a single phase flow, i.e., the exhaust gas flow, an arbitrary scalar ŽĢk is numerically calculated using the following equation (Ansys, 2009).
where ╬ōk is the diffusion coefficient, SŽĢk is the source term supplied for each of the N scalar equations, Žü is the density of the fluid, ui is the velocity component in the i direction, and xi is the coordinate in the i direction.
Grids for flow analysis using the Reynolds-averaged Navier-Stokes (RANS) model can be different depending on the discretization method and selected turbulence model, thus leading to differences in the numerical result. As such, the selection of an appropriate numerical model and grid is a difficulty faced by industrial designers when performing flow analyses. In this study, a realizable k-╬Ą model and Menter-Lechner wall treatment, which is known to be less sensitive to y+, are selected. The numerical method for flow analysis is shown in Table 1.
The dynamic loss coefficient is calculated by taking into account only the dynamic loss in the difference of the total pressure between the inlet and outlet of fittings.
where C is the dimensionless dynamic loss coefficient, ŌłåPt is the total pressure loss, ŌłåPf is the friction loss, and V is the average flow velocity of the pipe section.
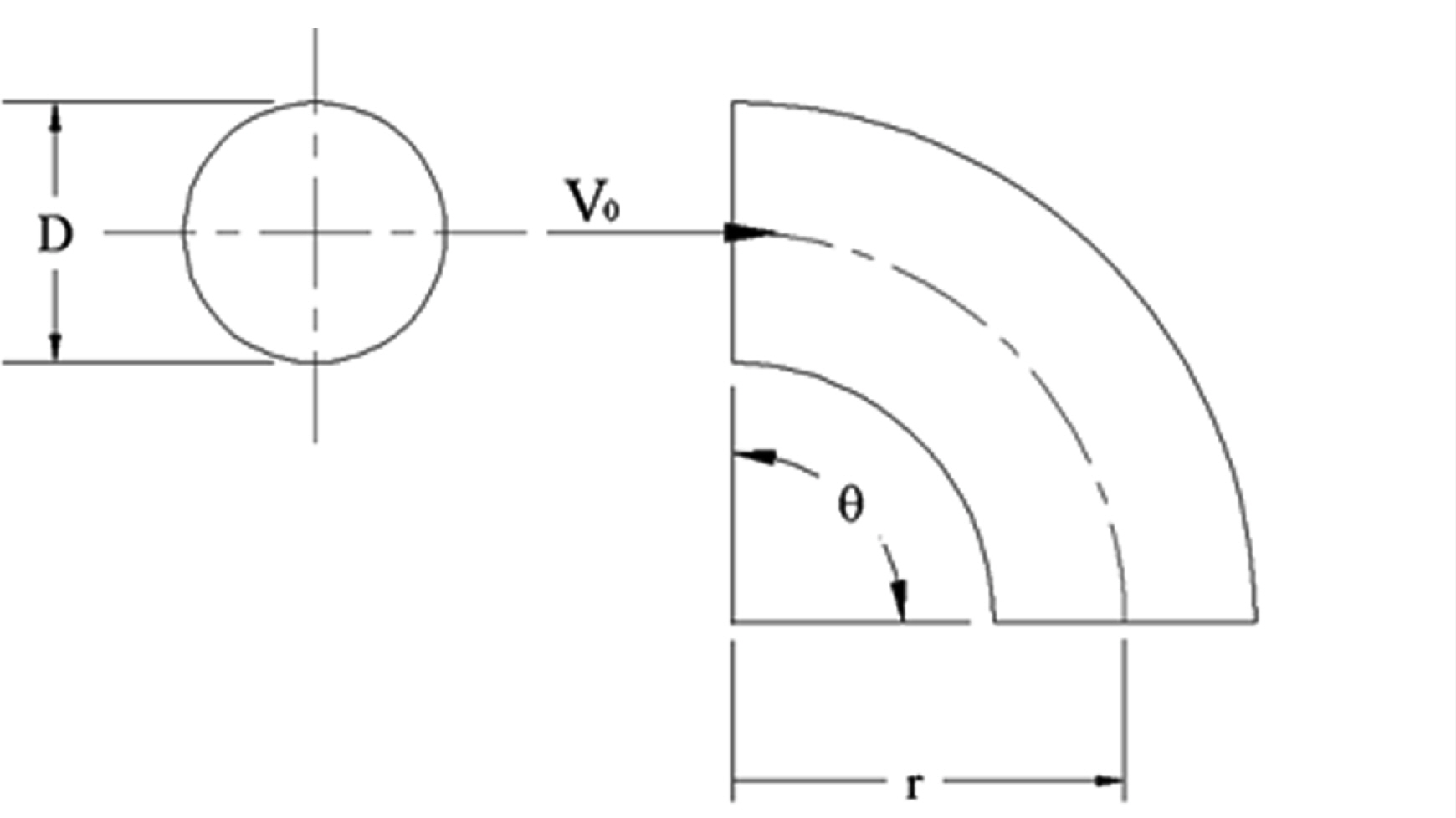
To verify the numerical scheme of this study, a 90┬░ round elbow with a known dynamic loss coefficient is analyzed and compared with the results of Zmrhal and Schwarzer (2009). The schematic of the 90┬░ round elbow to be verified is illustrated in Fig. 1. The pipe diameter is D, the inlet flow velocity is V0,, the elbow radius is r, and the angle is ╬Ė. Each 10D long straight pipe is connected to the upstream and downstream of a round elbow with an angle ╬Ė=90┬░. Inlet velocity and outlet pressure are used as boundary conditions, and the analysis conditions are shown in Table 2. The flow analysis is performed under conditions of Re = 1.0E+04 ~ 1.0E+06 for comparison, and a grid is selected by setting the first spacing such that y+ becomes closer to 30 in each condition according to the Ansys Fluent User's Guide (Ansys, 2009).
The grid for the condition of Re = 1.0E+05 is shown in Fig. 2, and a summary of grids under the conditions of Re = 1.04E+04, 1.04E+05, and 1.04E+06 is provided in Table 3. Fig. 3 shows the results of this study and Zmrhal and Schwarzer (2009). The velocity of the ship exhaust gas is approximately 30~40 m/s, and the Reynolds number corresponds to approximately 2.0E+05. In this study, the verification was performed with Reynolds numbers ranging from 1.0E+04 to 1.0E+06. In the range of Re = 1.0E+05~1.0E+06, which is the operating range of the exhaust gas, this study produced results consistent with Zmrhal and Schwarzer (2009), but with a difference of approximately 10% at Re = 1.0E+04. However, the numerical analysis of non-standard fittings in Section 3 is performed at approximately Re = 2.0E+05.
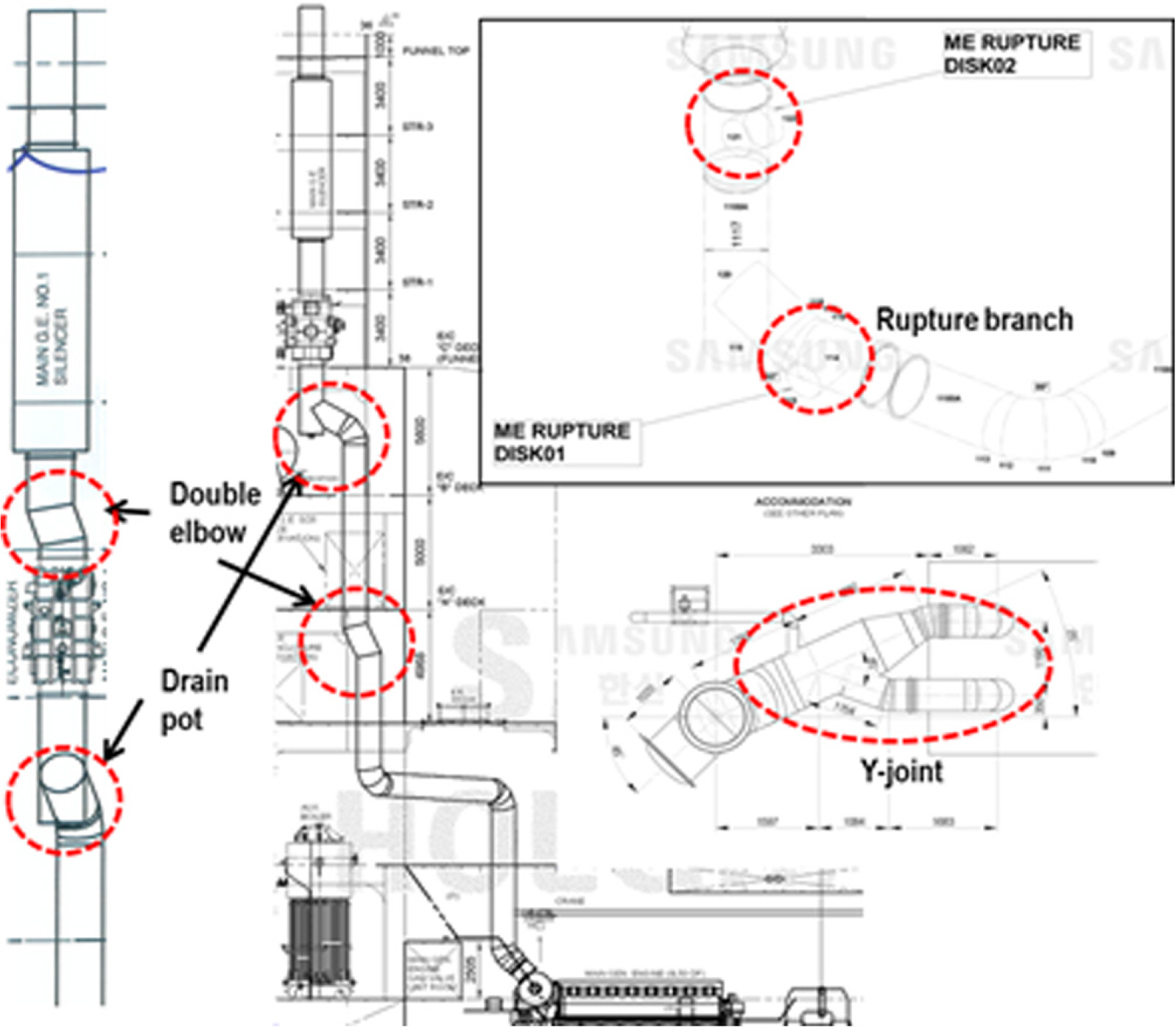
Several types of non-standard fittings are used in the EGP of a ship for improved design layout of an engine casing and for less friction. Fig. 4 and Fig. 5 demonstrate a ship's EGP system and non-standard fittings. In this study, flow analyses are performed on these five fitting shapes. Prior to flow analyses, 23 vessels recently delivered from the shipyard of Samsung Heavy Industries (SHI) were studied in order to understand the flow environment of an EGP. Table 4 shows the basic conditions for the flow analyses of non-standard fittings.
A realizable k-╬Ą model and Menter-Lechner wall treatment are used for flow analyses. Constant velocity is applied as an inlet boundary condition, and for simplicity, the pressure as the outlet boundary condition is assumed to be a gauge pressure measurement.
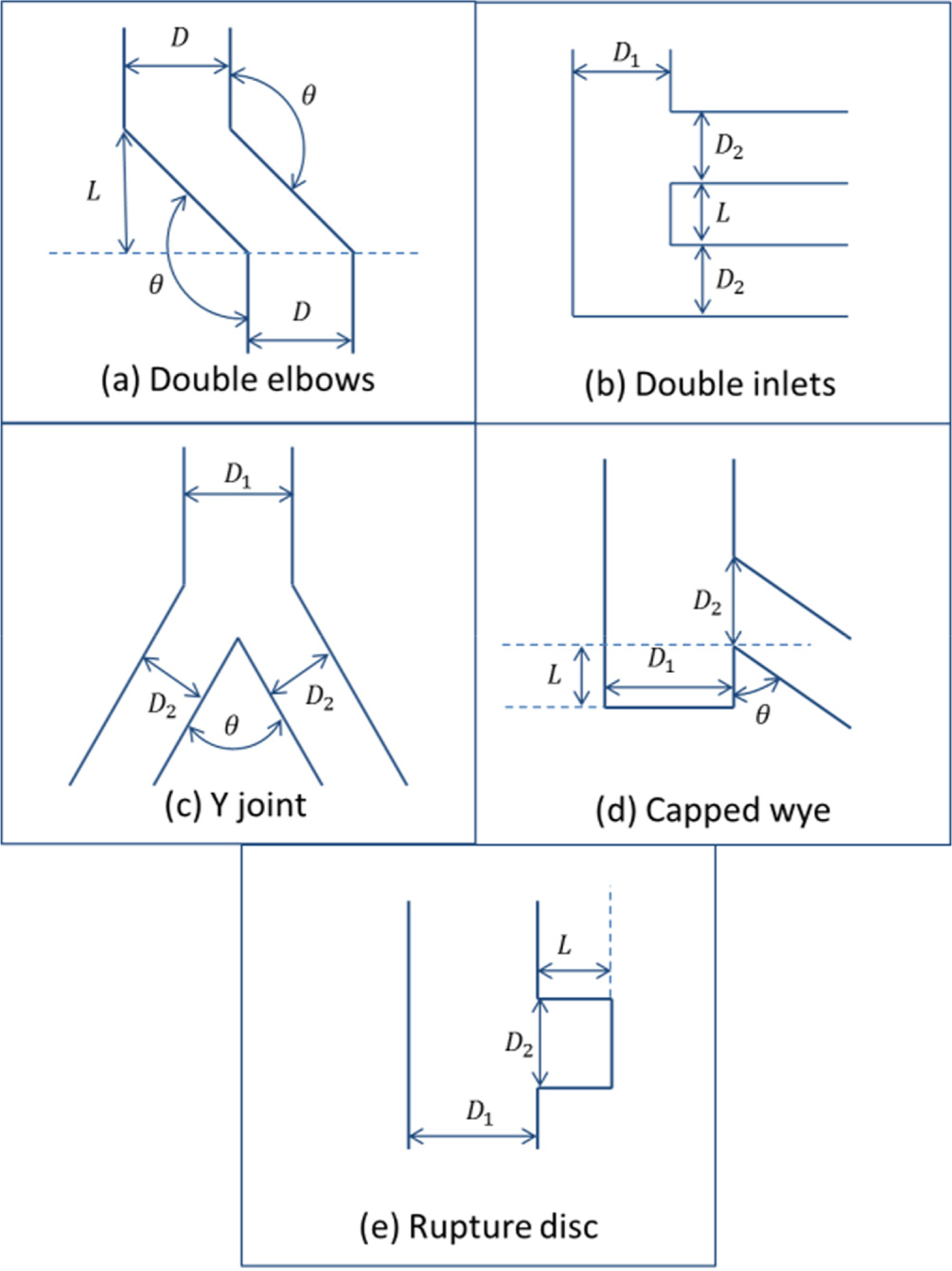
The ŌĆśdouble elbowsŌĆÖ fitting as shown in Fig. 5(a) is often applied to an EGP due to the design layout of an engine casing. In Fig. 5(a), the diameter of the pipe is D, the elbow angles are each ╬Ė, and the distance between two elbows is L. The flow analyses are performed with a variable distance L and a variable angle ╬Ė, and a grid is selected separately for each analysis case. The grid of the condition ╬Ė = 135┬░ and L = 2D is shown in Fig. 6.
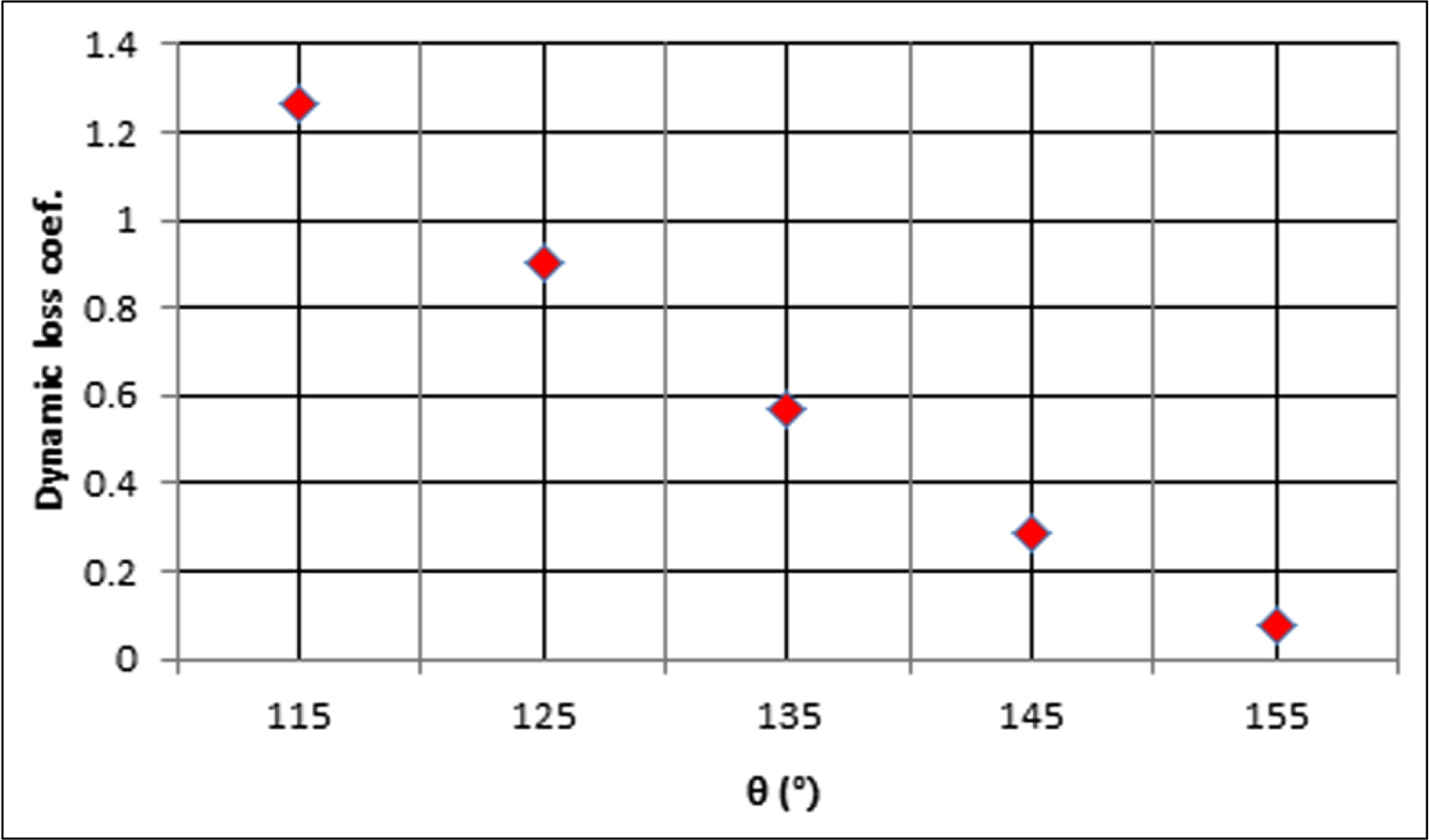
The pipe diameter (D = 0.8 m) and the distance between the two elbows (L = 2D) are fixed to predict the dynamic loss coefficient using the angle ╬Ė as a variable. The analysis is performed by increasing the angle ╬Ė from 115┬░ to 155┬░ in 10┬░ increments. The numerical results of the dynamic loss coefficient are shown in Fig. 7. It can be observed that as the elbow angle ╬Ė increases, the pipe becomes closer to being a straight pipe, thus reducing the pressure loss.
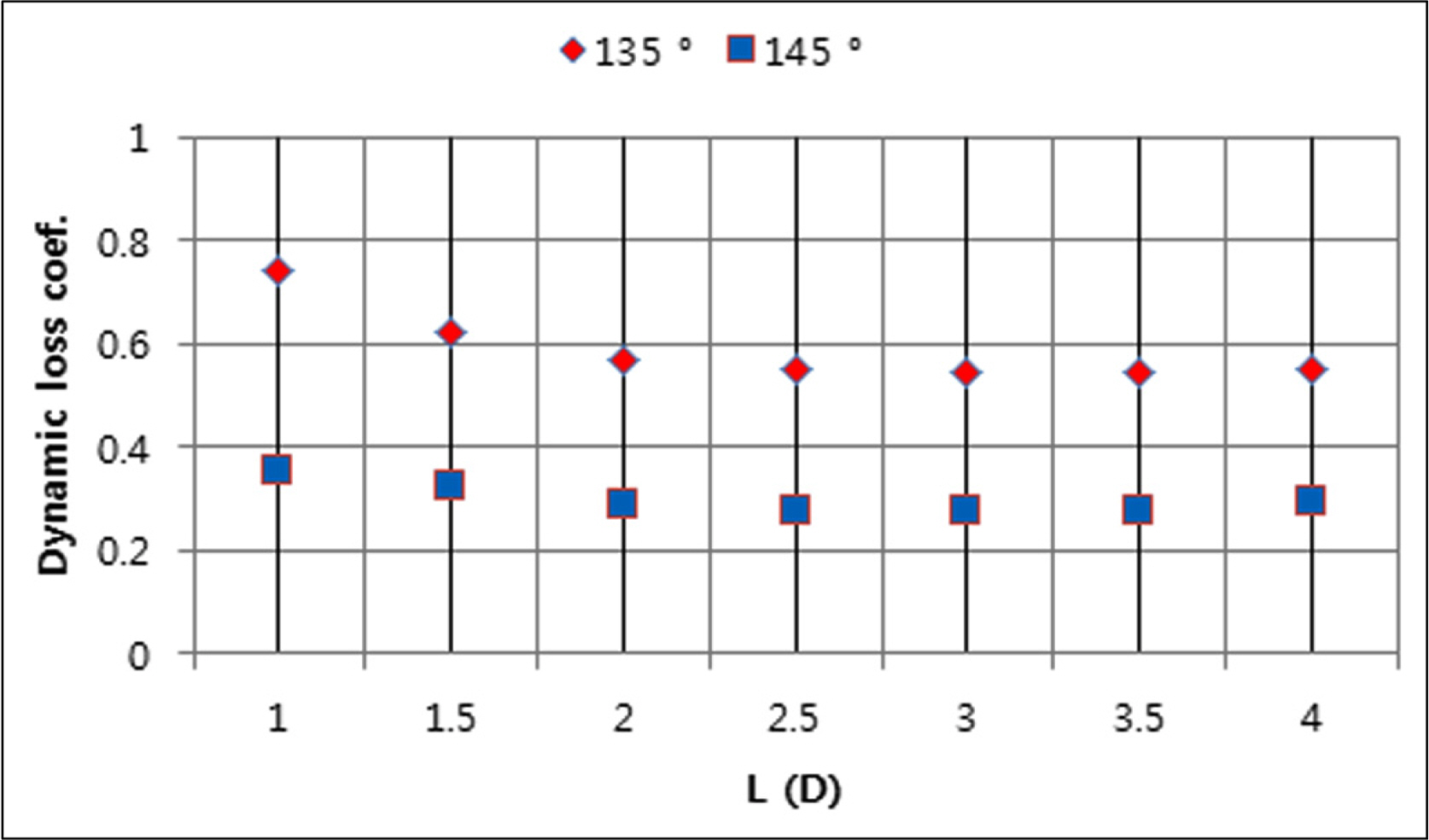
The diameter of the pipe (D = 0.8 m) and the elbow angle (╬Ė = 135┬░ and 145┬░) are fixed to predict the dynamic loss coefficient using the distance L between two elbows as a variable. The distance L is increased from 1D to 4D in increments of 0.5D. The analysis results of the dynamic loss coefficient are shown in Fig. 8. In the condition of elbow angles ╬Ė=135┬░ and 145┬░, it appears that the influence of the distance L on pressure loss is minimized at L = 2D or above. If a double elbow is used in EGP for space allocation, it is recommended to design the elbow with a large angle or with the distance between two elbows greater than 2D if possible.
A scrubber package may be installed in an EGP in order to reduce sulfur oxides (SOx) from exhaust gas, and the ŌĆśdouble inletsŌĆÖ fitting as shown in Fig. 5(b) may be applied. In Fig. 5(b), the diameter of the outlet pipe is Do,, the diameters of the two inlet pipes are each Di,, and the distance between the inlet pipes is L. The flow analysis is performed with the distance L as a variable, and a grid is selected separately for each analysis case. The diameter Do of the outlet pipe is 0.8 m, and the diameters Di of the two inlet pipes are each 0.8/20.5 m. The grid for the case of L = 2D is shown in Fig. 9.
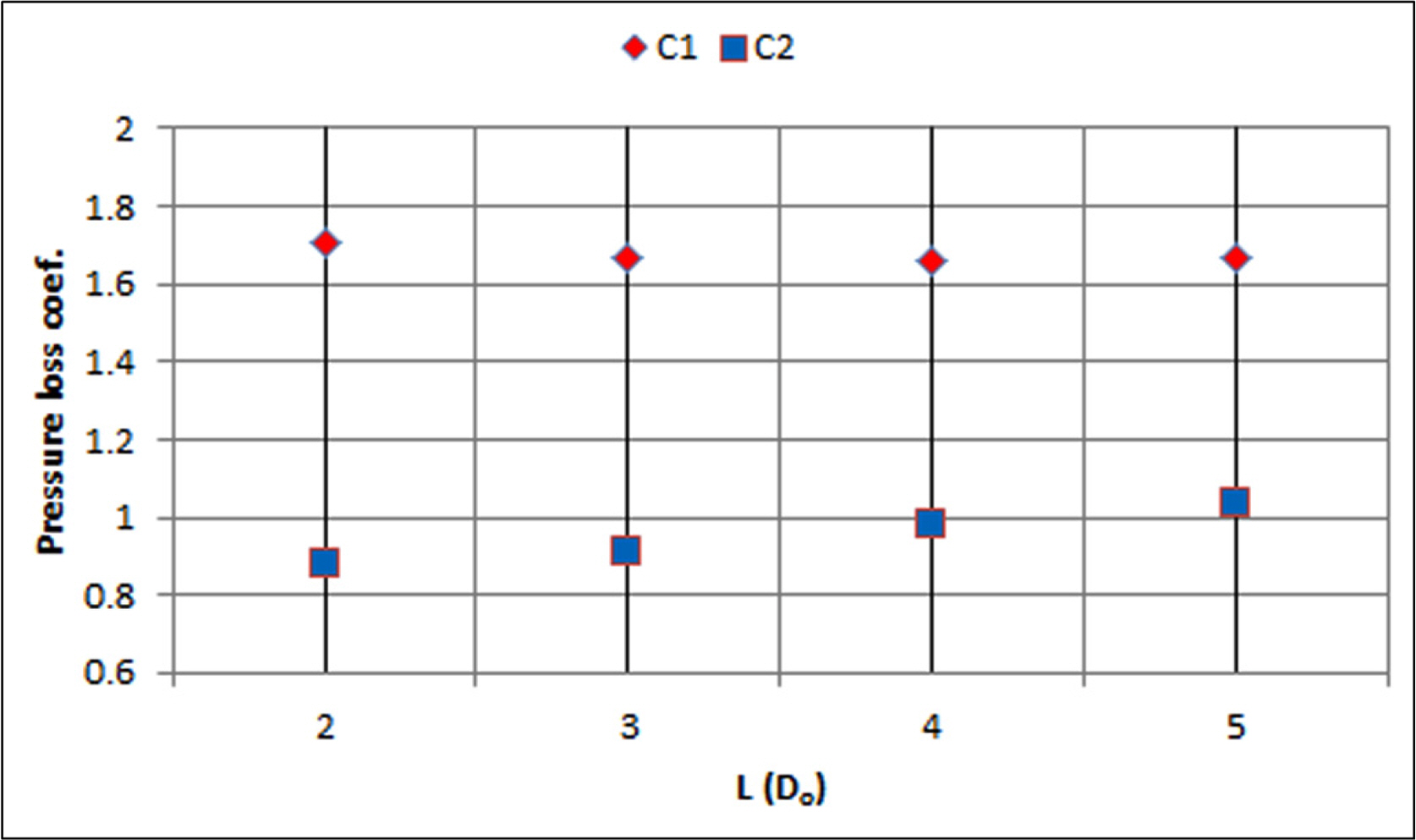
The analysis is performed by increasing the distance L from 2D to 5D in 1D increments. The numerical results of the dynamic loss coefficient are shown in Fig. 10. The dynamic loss coefficient of the inlet located furthest from the outlet is denoted as C1 and the dynamic loss coefficient of the inlet located closest to the outlet is denoted by C2. In the range of the distance L = 2D ~ 5D, the pressure loss of the inlet furthest from the outlet slightly decreased as the distance L increased. The pressure loss of the inlet closest to the outlet gradually increased as the distance L increased.
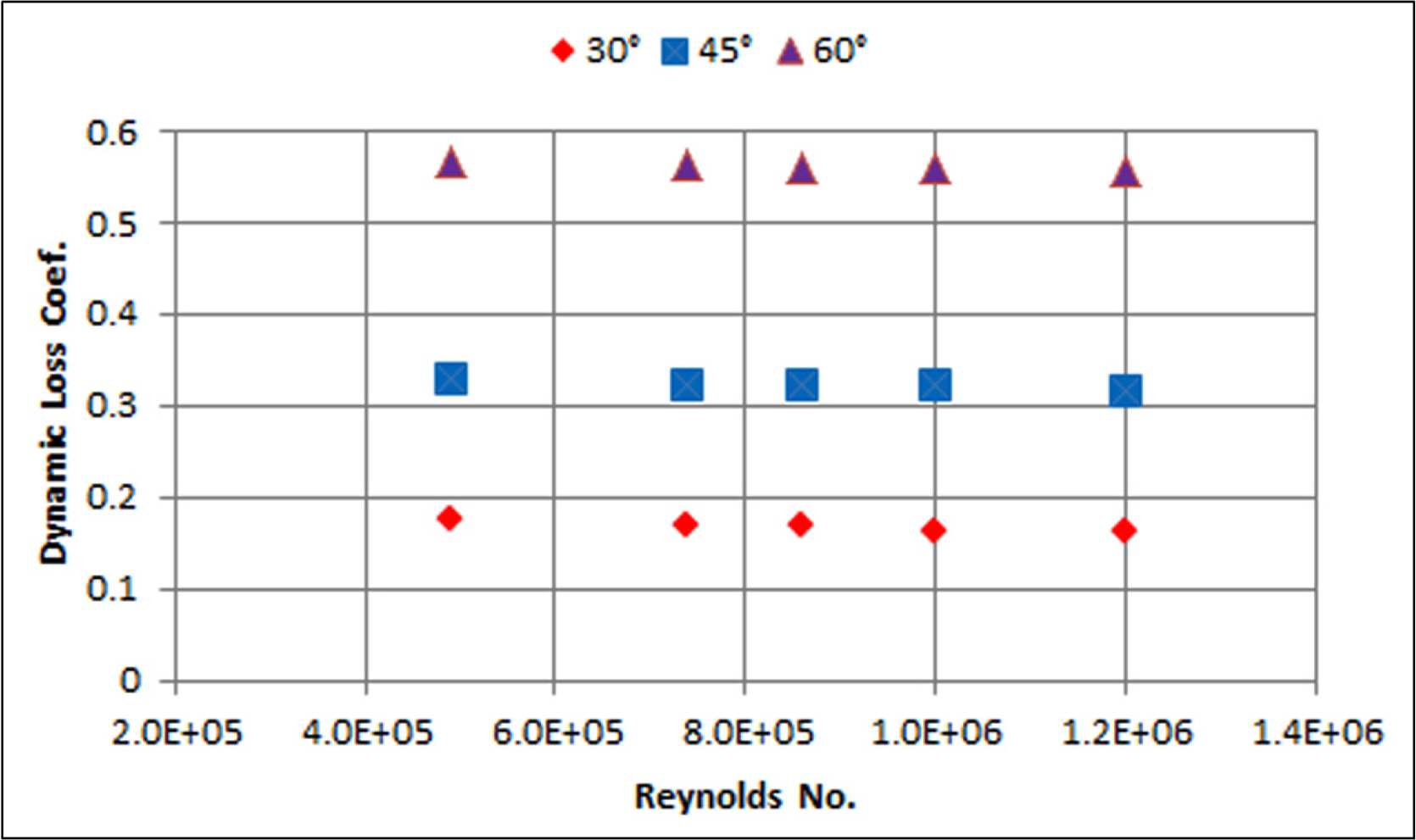
The ŌĆśY jointŌĆÖ fitting can be applied to exhaust pipes connected to two turbochargers merging into one large exhaust gas pipe, as shown in Fig. 5(c). In Fig. 5(c), the diameter of the outlet pipe is Do, the diameters of the two inlet pipes are each Di, and the angle between the inlet pipes is ╬Ė. The flow analysis is performed using the angle ╬Ė as a variable and a grid is separately selected for each analysis case. The diameter Do of the outlet pipe is 0.8 m, and the diameters Di of the two inlet pipes are each 0.8/20.5 m. In order to prevent pressure loss due to reduction of the flow area, the inlet pipe extends its diameter to Do immediately before connection, and the length of the expansion pipe is Do/2. The two inlet pipes are symmetric about the center axis of the outlet pipe. The grid with the angle ╬Ė = 80┬░ is shown in Fig. 11.
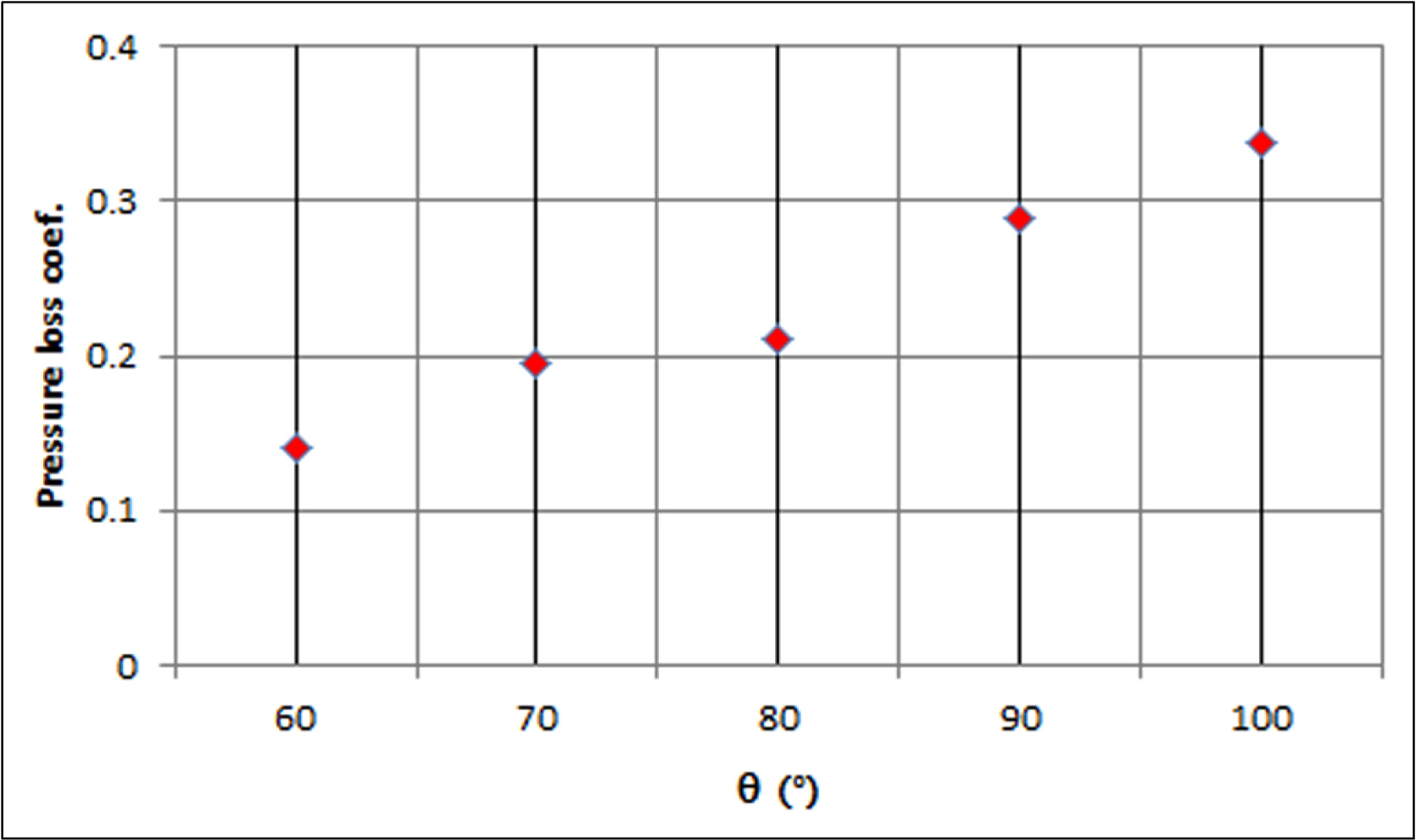
The analysis was performed by increasing the angle ╬Ė from 60┬░ to 100┬░ in increments of 10┬░. The results of the dynamic loss coefficient are illustrated in Fig. 12. In the range of the angle ╬Ė = 60┬░ to 100┬░, as the angle ╬Ė increases, the pressure loss increases almost linearly except for the case of ╬Ė = 80┬░. In general, numerical errors arise from various sources, including selection of grid and numerical methods, which can be cumulative (Mumma et al., 1998). However, even though the same method was applied to the analysis cases in this study, the case of ╬Ė = 80┬░ indicates a slightly different result. Further experiments are required.
The ŌĆścapped wyeŌĆÖ fitting is often used in the EGP of a ship. As shown in Fig. 5(d), when changing the direction of a pipe, a closed pipe with length L is connected downward to be used as a drain pot. In Fig. 5(d), the diameter of the outlet pipe is Do, the diameter of the inlet pipe is Di, and the angle formed between the inlet pipe and the outlet pipe is ╬Ė. The flow analysis is performed with angle ╬Ė and the ratio of diameter Di/Do as the main variables, and a grid is selected separately for each analysis case. Outlet piping diameter Do=0.8 m is applied to the analysis cases. The grid with the angle ╬Ė = 45┬░ and the ratio Di/Do = 1 is shown in Fig. 13.
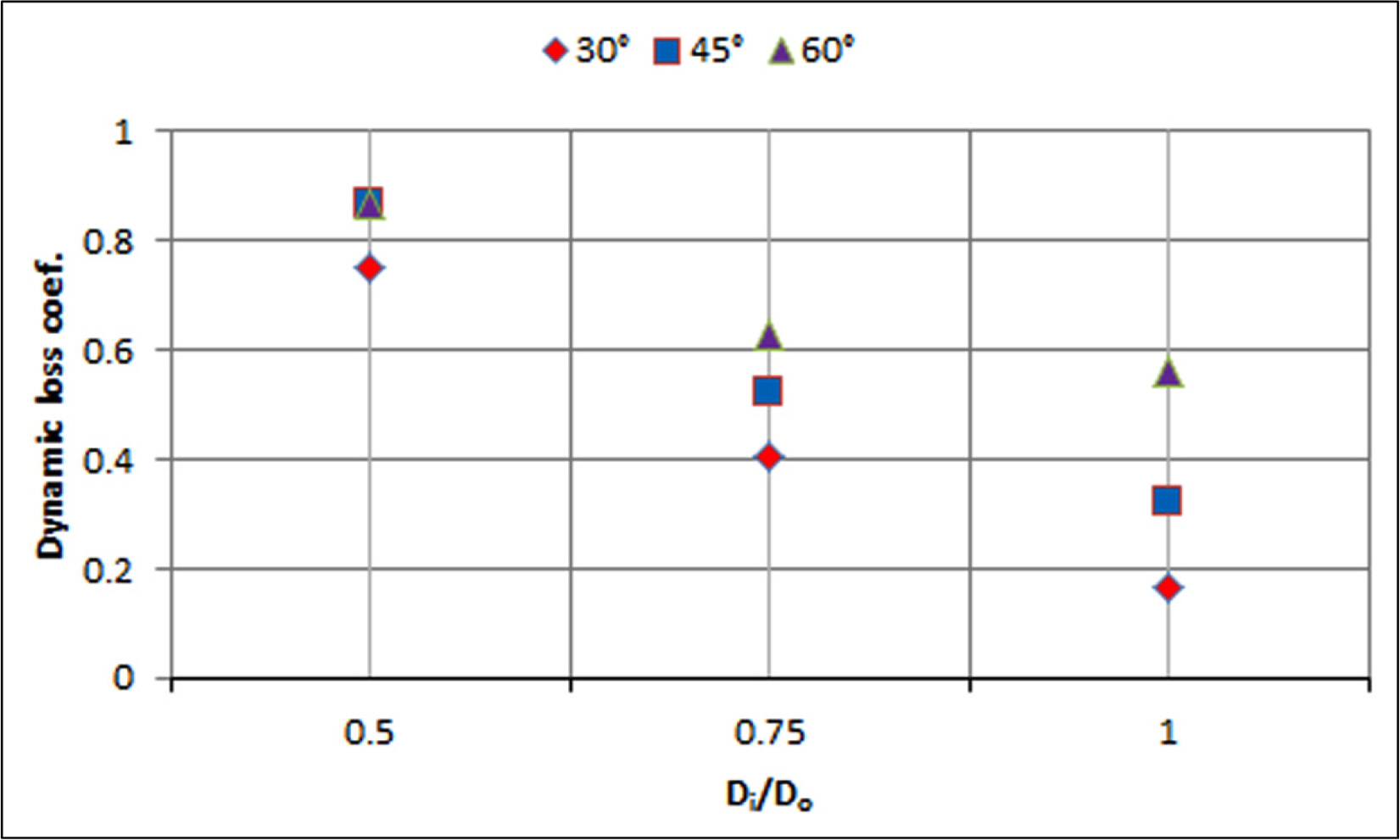
The angle ╬Ė increases from 30┬░ to 60┬░ in increments of 15┬░ and the ratio Di/Do of the diameter increases from 0.5 to 1 in increments of 0.25. The numerical results of the dynamic loss coefficient are shown in Fig. 14. It can be inferred that the pressure loss decreases with diameter ratio Di/Do increasing. Furthermore, in the range of angle ╬Ė = 30┬░~ 60┬░, pressure loss generally increases as the angle ╬Ė increases. The larger the ratio of Di/Do, the greater the effect of angle ╬Ė on the dynamic loss coefficient. However, in the case of the ratio Di/Do = 0.5, the dynamic loss coefficients at angles ╬Ė = 30┬░ and 45┬░ are similar.
In order to investigate the effect of the Reynolds number, the ratio of inlet pipe diameter to outlet pipe diameter (Di/Do = 1) is fixed, and the flow analysis is performed for the inlet flow velocities of 20 m/s, 30 m/s, 35 m/s, 40.7 m/s, and 48.8 m/s. The inlet flow velocities are selected in consideration of safety margin based on the ships delivered from SHI Geoje shipyard. The analysis results of the dynamic loss coefficient with varying Reynolds number are shown in Fig. 15. The influence of the Reynolds number on the dynamic loss coefficient is not observed in the range of Reynolds numbers studied.
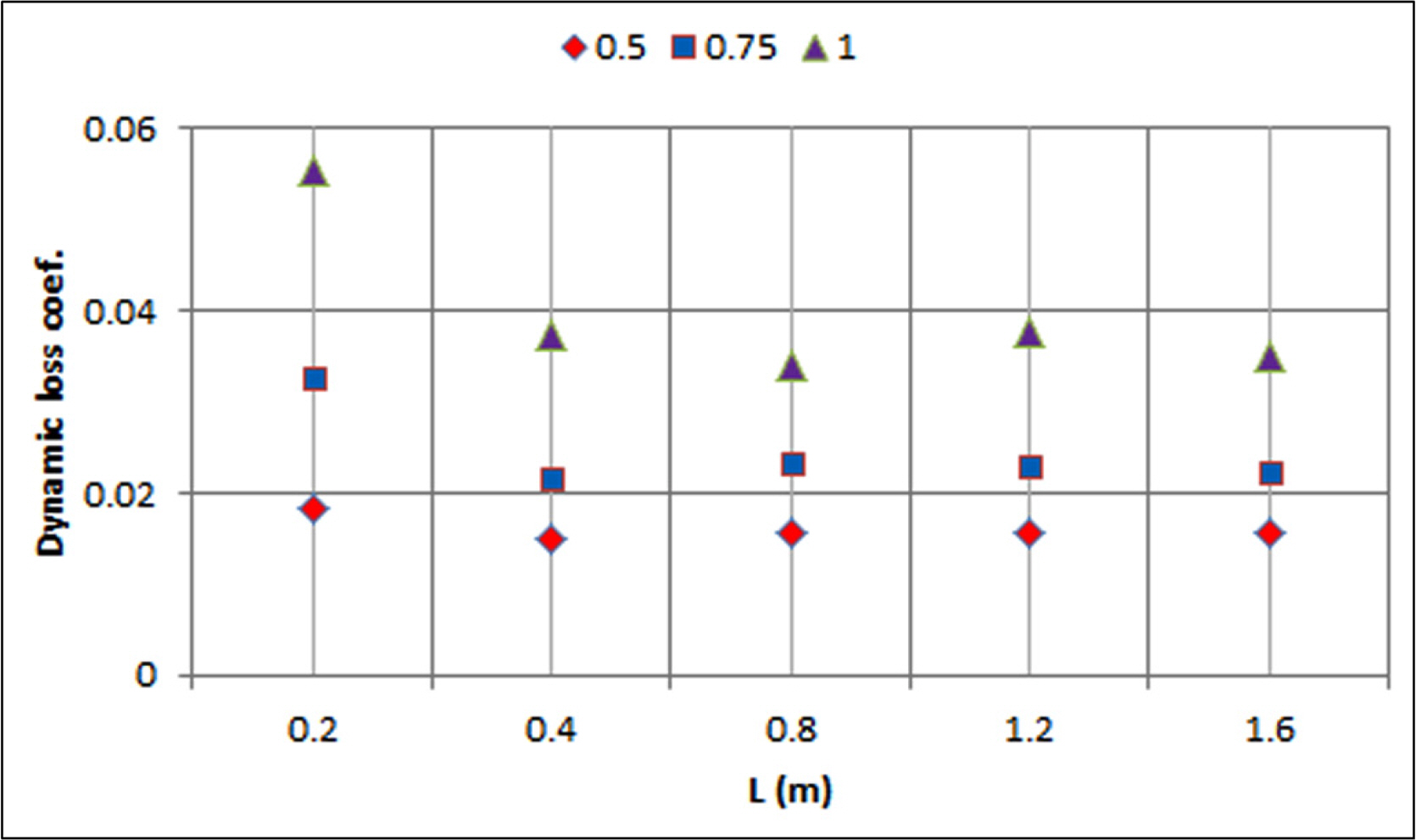
The ŌĆśrupture diskŌĆÖ fitting is installed in the EGP of a ship as a means of pressure relief in case of abnormal explosion. The pipe closed by a rupture disk is connected to the main pipe as shown in Fig. 5(e). In Fig. 5(e), the diameter of the main pipe is denoted by Dm, the diameter of the branch pipe is denoted by Db, and the length of the branch pipe is denoted by L. The flow analysis is performed with the ratio Db/Dm and length L as variables, and a grid is selected separately for each analysis case. The diameter of main pipe Dm = 0.8 m is applied to the analysis cases. A grid with a diameter Db = 0.6 m and a length L = 0.8 m is shown in Fig. 16.
The length L increases from 0.2 m to 1.6 m, and the ratio Db/Dm increases from 0.5 to 1 at intervals of 0.25. The analysis results of the dynamic loss coefficient are described in Fig. 17. As the ratio of Db/Dm increases, so does the dynamic loss coefficient. Larger dynamic loss coefficients are evident in length L = 0.2 m compared to L = 0.4 m ~ 1.6 m. The ŌĆśrupture diskŌĆÖ fitting is one of the major non-standard fittings of exhaust gas pipe. However, the fitting has the shape of clogged pipe, so it does not seem to play a significant role in pressure loss. In this case, the dynamic loss coefficients of the rupture disk fitting are calculated under 0.06, and it appears that the pressure loss due to this shape is not significant.
Depending on operating conditions, the range of velocity and temperature of exhaust gas in EGPs of ships is determined. Furthermore, as a limited number of non-standard fittings are used in EGPs, constructing a database of dynamic loss coefficients is easier than for an HVAC system, and the database can be more extensively utilized. The analysis procedure of this study is verified by using existing research results on HVAC fittings, and the numerical procedure is established so that it can be applied at the industry level. In addition, effective parameters and analysis cases are determined for a ship exhaust system, and flow analyses are performed for five types of fittings (double elbows, double inlets, Y joints, capped wye & rupture disks) commonly used in ship exhaust gas pipes. Based on the CFD results, the dynamic loss coefficients of the fittings are calculated and documented. These dynamic loss coefficients can be employed not only in the shipbuilding industry, but also in other industries. It is expected that this study will lead to a significant increase in the accuracy of a pressure loss calculation and the quality of the design of exhaust gas pipes.
Table┬Ā1.
Solver settings for CFD simulation
| Method | |
|---|---|
| Pressure-velocity coupling | Simple |
| Pressure | Second order |
| Momentum | Second order upwind |
| Turbulent kinetic energy | Second order upwind |
| Turbulent dissipation rate | Second order upwind |
Table┬Ā2.
Inputs for flow analysis of 90┬░ round elbow
| Method | |
|---|---|
| D [m] | 0.076 |
| ╬╝ [kg/ms] | 1.79E-05 |
| Žü [kg/m3] | 1.225 |
References
Ansys. (2009). Fluent 12.0 Documentation. Ansys Inc..
Idelchik, IE. (1993). Handbook of Hydraulic Resistance. 3rd Edition Betelu House Inc..
Kulkarni, D., Khairem, S., & Idem, S. (2009). Measurements of Flat Oval Elbow Loss Coefficients (RP-1319). ASHRAE Transactions, 115(1), 35-47.
Liu, W., Long, Z., & Chen, Q. (2012). A Procedure for Predicting Pressure Loss Coefficients of Duct Fittings Using CFD (RP-1493). HVAC&R Research, 18(6), 1168-1181.

Mumma, SA., Mahank, TA., & Ke, Y. (1998). Analytical Determination of Duct Fitting Loss-coefficients. Applied Energy, 61, 229-247. https://doi.org/10.1016/S0306-2619(98)00041-5

Recknagel, H., Sprenger, E., & Schramek, E. (1995). Taschenbuch fur Heizung und Klima Technik 94/95. Oldenbourg Industrieverla.
Santos, APP., Andrade, CR., & Zaparoli, El. (2014). CFD Prediction of the Round Elbow Fitting Loss Coefficient. International Scholarly Scientific Research & Innovation, 8(4), 743-747.
Shao, L., & Riffat, SB. (1995). Accuracy of CFD for Predicting Pressure Losses in HVAC Duct Fittings. Applied Energy, 51(3), 233-248. https://doi.org/10.1016/0306-2619(95)00002-A

Zmrhal, V., & Schwarzer, J. (2009). Numerical Simulation of Local Loss Coefficients of Ventilation Duct Fittings. Proceedings of 11th International IBPSA Conference Glasgow, Scotland: 1761-1766.
- TOOLS
-
METRICS

-
- 1 Crossref
- Scopus
- 6,141 View
- 111 Download
- Related articles in JOET
-
A Study on the Effect of Filling Ratio on Sloshing Impact Pressure2010 December;24(6)
A Study on the Measuring about the Coefficient of Earth Pressure at Rest 12001 November;15(4)
A Study on the Determination of Wave Load Acting on Offshore Structures2000 February;14(1)