In this study, the numerical code for the 3D nonlinear dynamic analysis of an SLWR (Steel Lazy Wave Riser) was developed using the lumped mass line model in a FORTRAN environment. Because the lumped mass line model is an explicit method, there is no matrix operation. Thus, the numerical algorithm is simple and fast. In the lumped mass line model, the equations of motion for the riser were derived by applying the various forces acting on each node of the line. The applied forces at the node of the riser consisted of the tension, shear force due to the bending moment, gravitational force, buoyancy force, riser/ground contact force, and hydrodynamic force based on the Morison equation. Time integration was carried out using a Runge–Kutta fourth-order method, which is known to be stable and accurate. To validate the accuracy of the developed numerical code, simulations using the commercial software OrcaFlex were carried out simultaneously and compared with the results of the developed numerical code. To understand the nonlinear dynamic characteristics of an SLWR, dynamic simulations of SLWRs excited at the hang-off point and of SLWRs in regular waves were carried out. From the results of these dynamic simulations, the displacements at the maximum bending moments at important points of the design, like the hang-off point, sagging point, hogging points, and touch-down point, were observed and analyzed.

Keywords: : Lumped mass line model; Explicit method; Dynamic simulation; Numerical code; Steel lazy wave riser(SLWR)

Keywords: 집중질량 라인모델; 명시적 방법; 동적 시뮬레이션; 수치코드; 심해 라이저

1. 서 론

천해에서 심해로 해양자원의 개발이 진행됨에 따라 심해 환경에서 효율적으로 활용 가능한 생산시스템의 연구가 주목받고 있다. 특히 유정과 해양 부유생산구조물을 연결하는 장치인 라이저는 해양 석유 및 가스 생산을 위한 필수 시스템으로서 시추 및 생산에 투입되는 대부분의 해양 구조물에 적용된다. 라이저 시스템은 해상 작업 환경에 따라 라이저의 종류 및 설계가 달라질 수 있기 때문에 효율적인 설계가 필수적이다. 심해 석유 및 가스 생산에서는 경제적 효용성이 높은 Steel catenary riser(SCR)가 널리 적용되고 있다. SCR은 상부 해양구조물의 동적운동에 기인한 라이저/지반 접촉 지점의 피로손상과 수심 증가로 인한 과도한 상부 장력 때문에 특정수심 이상에서 적용이 어려운 것으로 알려져 있다.

상기 언급된 SCR의 문제점을 보완하기 위하여 라이저 일정 부분에 부력제(Buoyancy module)를 설치한 Steel lazy wave riser(SLWR)가 개발되었고 적용 가능성이 검토되고 있다. SLWR은 부력제를 통해 라이저 상부장력을 감소시킬 뿐만 아니라 부유 구조물 운동에 기인한 라이저 동적 응답을 완화시켜 라이저/지반 접촉으로 인한 피로손상을 저감시킨다(Wang and Duan, 2015; Kim, 2016).

최근 SLWR의 연구는 설계 관점의 적용성 검토 및 최적화가주를 이루고 있다(Kim, 2016; Yoo and Joo, 2017; Park et al., 2017; Park et al., 2018; Park et al., 2019). 이와 달리 SLWR 해석기법에 대한 연구가 상대적으로 드물다(Ruan et al., 2016). SLWR은 라이저의 유연체 특성에 부력제와 지반의 영향으로 기하학적인 비선형성이 강하며 이를 정확히 고려할 해석 기법은 효율적인 설계를 위해 필수적이다. 최근에 수행된 정적 해석기법에 대한 연구로는 Li(2010)의 현수선 이론을 적용한 추정법, Wang et al.(2013)과 Wang and Duan(2015)이 개발한 유한차분법을 이용한 추정법이 있으며 국내에는 Oh et al.(2018)에 의해 수행된 동적 이완법을 이용한 추정법이 있다. 최근 수행된 동적 해석기법 대한 연구로는 Ruan et al.(2016)에 의해 수행된 유한요소법과 Wang et al.(2018)에 의해 수행된 유한차분법을 이용한 SLWR의 동적해석 기법 연구가 있지만 이 또한 관련된 연구가 드물다.

라이저와 계류삭은 세장체로 유한요소법을 이용한 해석이 주를 이룬다. 계류삭의 동적해석을 위해 Kim et al.(2010)과 Kim et al.(2013)의 비선형 유한요소법에 대한 연구가 지속적으로 진행되고 있다. 동일한 방법론을 통한 SLWR의 동적해석이 Oh et al.(2019)에 의해 수행되었으며 비선형 유한요소법의 수렴성 향상을 위해 동적이완법의 정적형상을 활용하는 기법이 제안되었다. 유한요소법과 마찬가지로 집중질량 라인모델(Lumped mass line model)에 의한 해석 기법도 세장체의 정적/동적해석에 많이 활용되고 있다. van den Boom et al.(1987)과 Hall and Goupee (2015)에 의해 유연 라이저와 계류삭 해석을 위한 집중질량 라인모델 해석기법이 개발되어 활용된 바 있다. 집중질량 라인모델은 명시적 해석법으로 유한요소법과 달리 행렬연산이 없어 알고리즘이 단순하고 계산속도가 빠르다고 알려져 있다(Hall and Goupee, 2015).

본 연구에서는 이러한 장점에 주목하여 포트란 환경에서 집중질량 라인모델을 이용하여 SLWR의 3차원 비선형 동적해석을 위한 코드를 개발하였다. 집중질량 라인모델에서는 라인의각 절점에 작용하는 장력, 굽힘 모멘트에 의한 전단력, 중력, 부력, 라이저/지반 접촉력 그리고 Morison 방정식을 기반한 유체력을 반영하여 라이저의 운동방정식을 구성한다. 시간적분은 안정적이고 정확성이 높은 Runge-Kutta 4차 방법을 이용하였다. 개발된 코드의 정확성을 확인하기 위하여 상용 소프트웨어인 Orcaflex의 결과와 비교 검증하였다. SLWR의 비선형적 동적 특성을 파악하기 위하여 상부 연결부(Hang-off point)의 전후 및 상하가진 해석과 규칙파 중 동적해석을 수행하였다. 수행된 동적해석의 결과에서 SLWR의 설계상 주요지점으로 알려진 상부 연결부, 최대 새깅 및 호깅 지점 그리고 터치다운 영역 굽힌 모멘트 최대 지점의 변위는 물론 장력과 굽힘 모멘트의 시계열을 관찰하고 SLWR의 동적특성을 분석하였다.

2. SLWR 비선형 동적해석을 위한 집중질량 라인모델

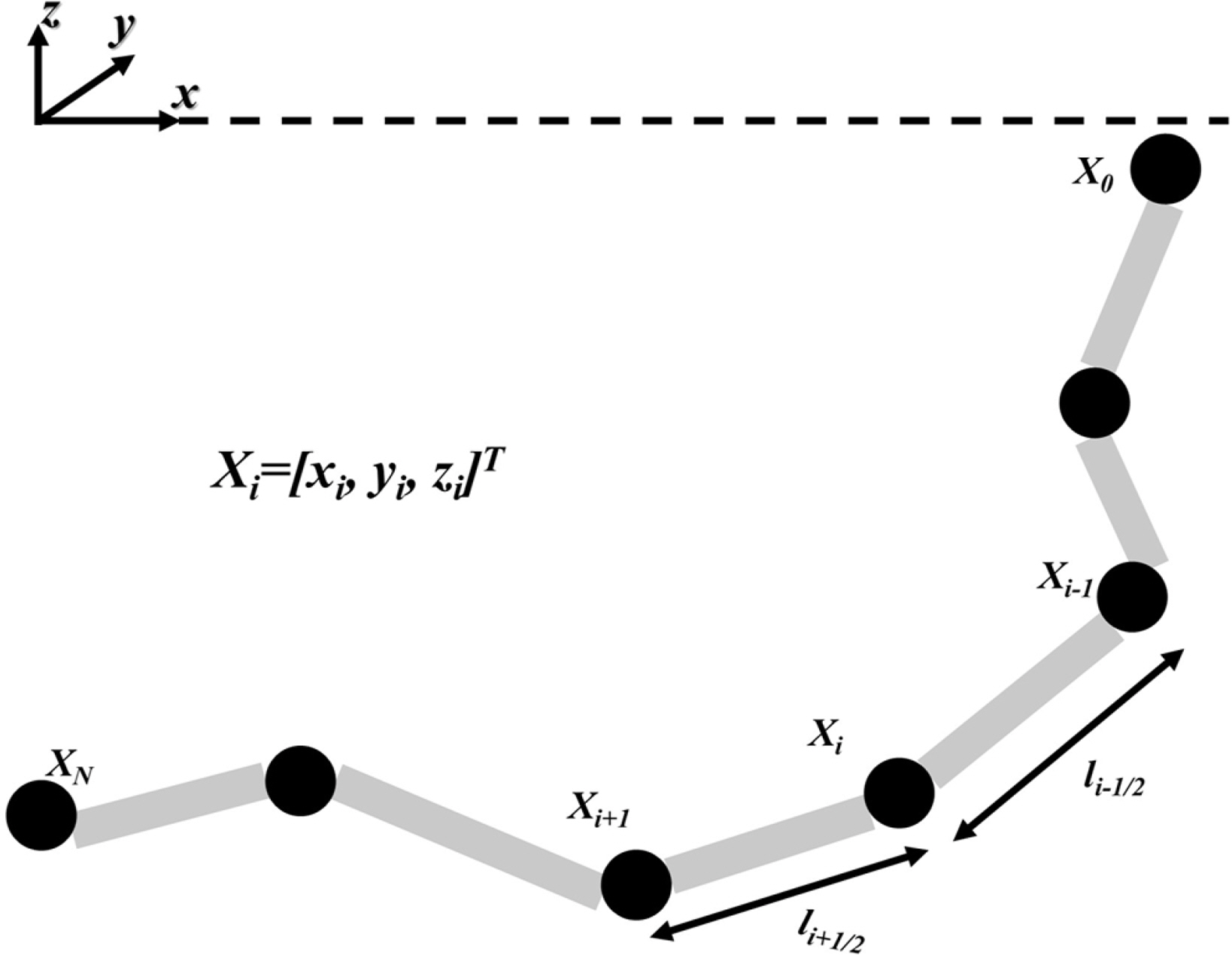
SLWR 비선형 동적해석을 수행하기 위해 집중질량 라인모델을 도입하였다. 집중질량 라인모델에서는 Fig. 1과 같이 N개의 라인과 N+1의 절점으로 이산화 한다(Hall and Goupee, 2015; Oh et al., 2018). 우수좌표계로 z축이 수면의 상방을 향하도록 정의하였다. 각 절점 X_i는 i의 지점에서 [x_i, y_i, z_i]^T와 같은 3차원 벡터로 정의된다. 각 라인은 i+1/2위치에서 정의되며 외경(Outer diameter), 내경(Inner diameter), 건조중량(Dry weight), 굽힘 강성(Bending rigidity), 축 강성(Axial rigidity), 장력의 감쇠계수 및 내부 유체 밀도(Inner fluid density)가 정의된다.

Fig. 1.

Schematic diagram of riser discretization and indexing

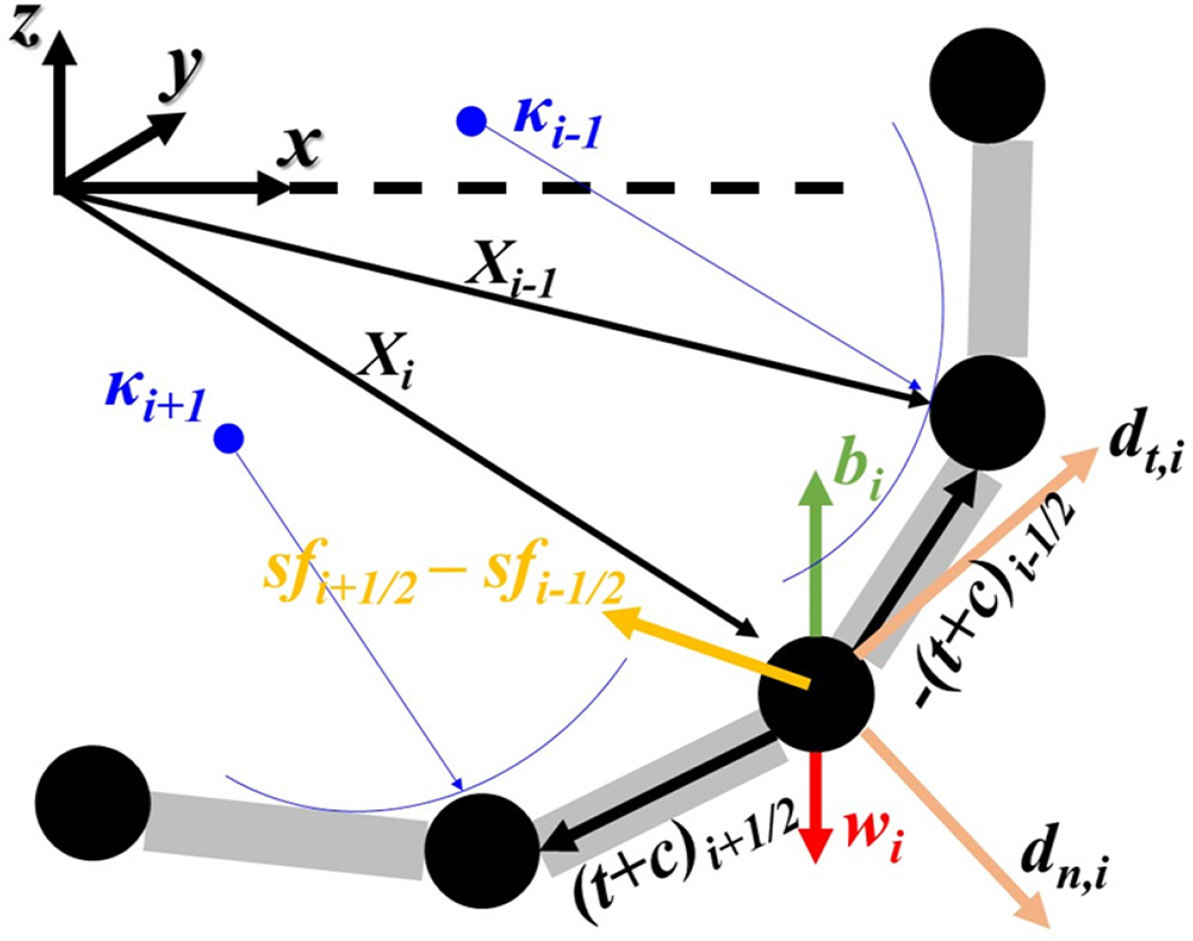
상기 정의된 물성치들을 통해 Fig. 2와 같이 각 라이저 절점에 작용하는 장력과 축 방향에 대한 감쇠력, 굽힘 모멘트에 의한 전단력과 같은 내력과 중력, 부력, 라이저/지반 접촉력 그리고 Morison 방정식을 기반한 유체력과 같은 외력들을 3차원 벡터로 정의할 수 있다.

Fig. 2.

Schematic diagram of internal and external riser force

장력 t_i+1/2는 식 (1)과 같이 정의할 수 있다(Hong and Huh, 2000; Hall and Goupee, 2015; Oh et al., 2018).

(1) ti+1/2=EA(1li+1/2−1‖Xi+1−Xi‖)(Xi+1−Xi) +(pAout−pinAin)i+1/2(Xi+1−Xi)‖Xi+1−Xi‖

여기서 EA는 축 강성, p와 p_in는 라이저 외부와 내부의 정수압 그리고 A_out와 A_in는 라이저 외경을 지름으로 하는 단면적과 내경을 지름으로 하는 단면적을 의미한다. 유연체로 음의 장력(Xi+1-Xi<li+1/2)이 있는 경우에는 축강성의 장력을 0으로 정의하였다. 축방향에 대한 감쇠력 또한 Hall and Goupee(2015)의 정의에 따라 식 (2)와 같이 나타낼 수 있다.

(2) ci+1/2=CintAli+1/2[(Xi+1−Xi)⋅(X˙i+1−X˙i)]‖Xi+1−Xi‖(Xi+1−Xi‖Xi+1−Xi‖)

여기서 C_int는 축방향 감쇠계수이다.

전단력 sf_i+1/2는 van den Boom et al.(1988)의 정의에 따라 식 (3)과 같이 나타낼 수 있다.

(3) sfi+1/2=∂mbd∂s=1li+1/2[G−H]

where

G=mbd,i+1(bv→i+1×(Xi+1-Xi))‖bv→i+1×(Xi+1-Xi)‖

H=mbd,i(bv→i×(Xi+1-Xi))‖bv→i×(Xi+1-Xi)‖

여기서 m_{bd, i+1}는 절점에서 정의된 굽힘 모멘트 그리고 bvi+1→는 굽힘 모멘트의 방향벡터로 식 (4)와 같이 정의된다.

(4) bv→i+1=(Xi+1−Xi)×(Xi+2−Xi+1)

굽힘 모멘트는 식 (5)로 정의되며 각 절점에서 곡률의 계산이 필요하다. 본 연구에서는 효율적인 계산을 위해 Menger 곡률을 사용하였고 식 (6)을 이용하여 계산할 수 있다. 본 연구의 대상인 라이저는 요소 단위의 급격한 곡률 변화가 발생하는 경우가 드물기 때문에 행렬연산 없이 3 point로 계산되는 Menger 곡률의 사용이 타당한 것으로 판단된다(Oh et al., 2018).

(5) mbd,i=EIR=EI⋅κi

(6) κi=4Sa⋅b⋅c

여기서 EI는 라인에서 정의된 굽힘 강성을 의미하며 삼각형의 넓이 S, 절점 간의 거리 a, b, c는 Fig. 3과 같이 정의된다.

Fig. 3.

Schematic diagram of Menger curvature

습윤중량(Wet weight)에 의한 체적력은 Oh et al.(2018)의 정의에 따라 식 (7)과 같이 부력 그리고 라이저의 내부유체의 중량과 건조중량(Dry weight)에 의한 체적력의 상관관계로 표현되며 각 체적력은 라인 i+1/2에서 정의되므로 식 (8)-(10)과 같이 평균을 이용하여 절점 i에서 정의할 수 있다.

(7) wi=wbuoy,i+wdry,i=winner,i

(8) wbuoy,i=12(wbuoy,i+1/2+wbuoy,i−1/2)e^z =12ρwgπ4(Douter,i+1/22+Douter,i−1/22)e^z

(9) winner,i=−12(winner,i+1/2+winner,i−1/2)e^z =−12ρingπ4(Dinner,i+1/22+Dinner,i−1/22)e^z

(10) wdry,i=−12(wdry,i+1/2+wdry,i−1/2)e^z

여기서 ρ_w는 해수 밀도(1,025kg/m³), ρ_in는 내부 유체의 밀도, D_{outer, i+1/2}는 외경, D_{inner, i+1/2}는 외경 그리고 g는 중력가속도(9.807m/s)를 의미하고 ez^는 z방향의 단위벡터이다.

지반에 작용하는 수직 반력은 식 (11)로 정의할 수 있다.

(11) bi=Acon(zbottom−zi)kbe^z

여기서 A_con은 접촉면적 z_bottom은 해저지면 그리고 k_b는 해저의 단위 면적당 강성을 의미한다.

라이저에 작용하는 유체력은 Morison 방정식을 이용하여 계산할 수 있으며 본 연구에서는 Hall and Goupee(2015)의 정의에 따라 유체력을 계산하였다. 유체 입자와 라이저의 상대 수직속도에 의한 항력은 식 (12)와 같이 나타낼 수 있다.

(12) dn,i=ρw2((Cdndl)i−1/2+(Cdndl)i+1/2)2‖Vn,Rel,i‖Vn,Rel,i

where

Vn,Rel,i=(vp,i-X˙i)-((vp,i-X˙i)⋅q^i)q^i

여기서 C_dn은 항력계수를 나타내며 v_p,i는 절점에서의 유체 입자 속도를 나타낸다. qi→ 는 절점의 근사 접선단위벡터로 식 (13)과 같이 정의된다.

(13) q^i=Xi+1−Xi−1‖Xi+1−Xi−1‖

유체 입자와 라이저의 상대 접선속도에 의한 항력 또한 식 (14)와 같이 정의할 수 있다.

(14) dt,i=ρw2π((Cdtdl)i−1/2+(Cdtdl)i+1/2)2‖Vt,Rel,i‖Vt,Rel,i

where

Vt,Rel,i=((vp,i-X˙i)⋅q^i)q^i

여기서 C_dt은 마찰계수를 나타낸다.

유체 입자의 가속도에의 의한 유체력은 식 (15)와 같이 정의할 수 있다.

(15) afn,i=ρwτ4((CMd2l)i−1/2+(CMd2l)i+1/2)‖an,i‖an,i

where

an,i=(ap,i)-(ap,i⋅q^i)q^i

여기서 C_M은 관성력계수를 나타내며 a_p,i는 절점에서의 유체입자 가속도를 나타낸다.

라이저의 절점의 3차원 운동방정식을 구성하기 위하여 절점의 질량을 식 (16)과 같이 3×3 행렬로 정의할 수 있다.

(16) [M]i=(Mdry+ρinlπDinner24)i+1/2+(Mdry+ρinlπDinner24)i−1/22[I]

여기서 I는 3×3 단위행렬(Identity matrix)를 나타낸다.

라이저 가속도에 의한 부가질량은 Hall and Goupee(2015)의 정의에 따라 식 (17)과 같이 3×3 행렬로 나타낼 수 있다.

(17) [m]i=ρw2π((d2l)i−1/2+(d2l)i+1/2)4[[Can,mat]i+[Cat,mat]i]

where

[Can,mat]i=Can,i-1/2+Can,i+1/22([I]-q→q→iT)

[Cat,mat]i=Cat,i-1/2+Cat,i+1/22(q→q→iT)

여기서 C_an과 C_at는 수직방향과 접선방향의 부가질량을 나타낸다.

상기 정의된 질량, 부가질량 및 라이저에 작용하는 내력과 외력을 기반으로 라이저 절점의 3차원 운동방정식을 식 (18)과 같이 구성할 수 있다.

(18) [[M]i+[m]i]X¨i=ti+1/2−ti−1/2+ci+1/2−ci−1/2 +sfi+1/2−sfi−1/2+wi+bi +dn,i+dt,i+afn,i

라이저의 운동방정식은 2계 상미분방정식으로 안정성 및 정확성에서 우수한 Runge-Kutta 4차 시간적분 방법을 적용하였다.

3. 수치계산 및 결과

SLWR은 부력제로 인한 기하학적 비선형성이 강하기 때문에 정확한 정적형상(Static configuration)에서 비선형 동적해석이 수행되는 것이 수치적으로 효율적이다. 본 연구에서는 Oh et al. (2018)의 연구에서 적용한 동적이완법을 3차원으로 확장하여 정적형상을 추정하였다. SLWR의 동적특성을 확인하기 위하여 상부 연결부의 전후 및 상하가진 해석과 규칙파 중 동적해석을 수행하여 상부 연결부, 새깅 및 호깅 최대지점 그리고 터치다운 영역 굽힌 모멘트 최대 지점들의 동적변위들은 물론 장력과 굽힘 모멘트의 시계열들을 면밀히 관찰하였다. 그리고 개발된 수치코드의 정확성을 확인하기 위하여 상용 소프트웨어인 Orcaflex의 해석을 함께 수행하여 비교하였다. 계산에 사용된 SLWR의 제원은 Ruan et al.(2016)에 의해 제시된 Table 1의 제원을 활용하였다. 본 제원에 대하여 Oh et al.(2018)에 의해 정적해석이 수행된 바 있다. Hang off 지점을 (0, 0, -10) 그리고 Anchor 지점을 (-2340, 0, 1255)로 동일하게 선정하였다.

Table 1.

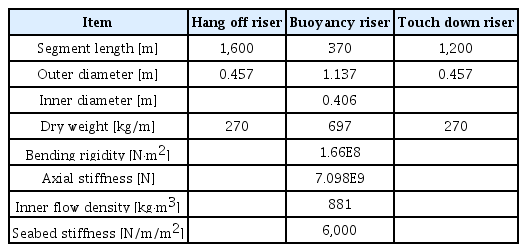
Steel Lazy wave riser parameter (Ruan et al. 2016)

3.1 SLWR의 정적평형

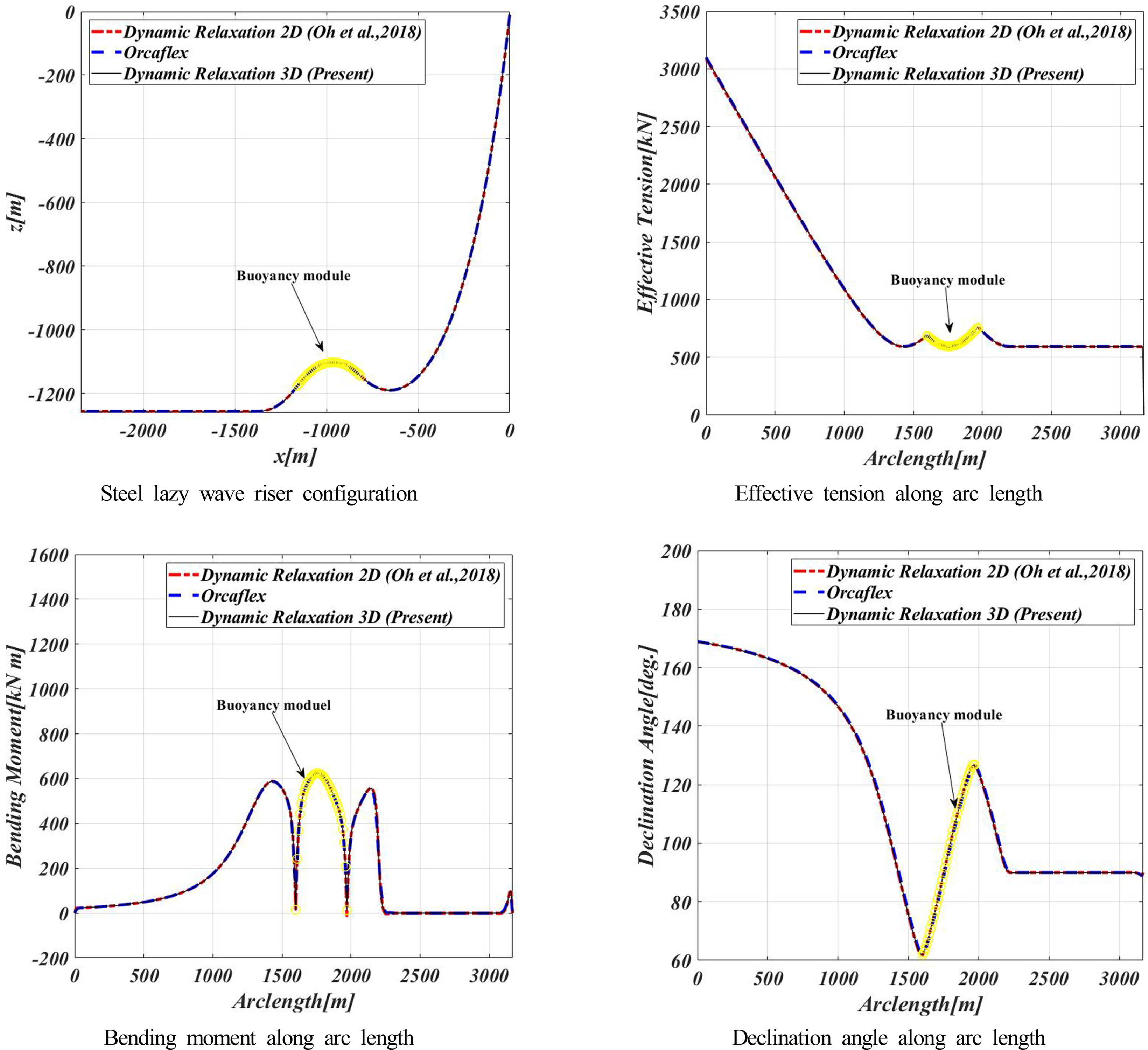
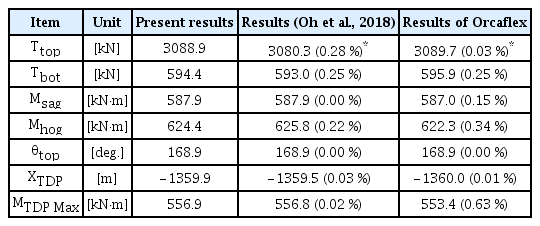
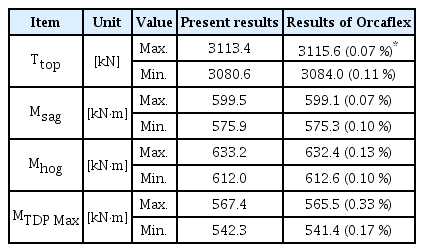
3차원 SLWR의 정적형상을 산정하기 위해 Oh et al.(2018)의 동적이완법을 사용하였다. 해석 절차는 Oh et al.(2018)과 동일하지만 각 요소의 변위와 작용하는 힘은 상기 2 장에서 기술한 바와 같이 3차원으로 확장하였다. 동적이완법에 의한 자세한 정적 해석절차는 Oh et al.(2018)에 기술되어 있다. 해석에 사용된 요소는 Ruan et al.(2016)에 의해 수행된 연구와 같이 총 317개를 사용하였으며 요소의 비인장 길이 10m로 동일하게 모델링하였다. 수행된 계산 결과를 Oh et al.(2018) 그리고 Orcaflex 계산 결과와 함께 비교하였다. 정적 평형의 결과로 형상, 유효장력, 굽힘 모멘트와 경사각을 Fig. 4에 도시하였고 Table 2에 요약하였다. 여기서 T_top는 Hang off에서 유효장력, T_bot는 수면 바닥에서 유효장력, M_sag는 최대 새깅 모멘트의 크기, M_hog는 최대 호깅 모멘트의 크기, θ_top는 Hang off에서 경사각, M_TDP는 해저 접촉영역의 x지점 그리고 M_TDPMax는 터치다운 영역 굽힌 모멘트 최대 지점에서의 최대 굽힘 모멘트의 크기를 나타낸다. 본 논문의 결과가 비교계산의 결과들과 약 0.6% 이내로 잘 일치함을 확인하였다.

Fig. 4.

Static results of steel lazy wave riser

Table 2.

Comparisons for static configuration

3.2 SLWR의 동적해석

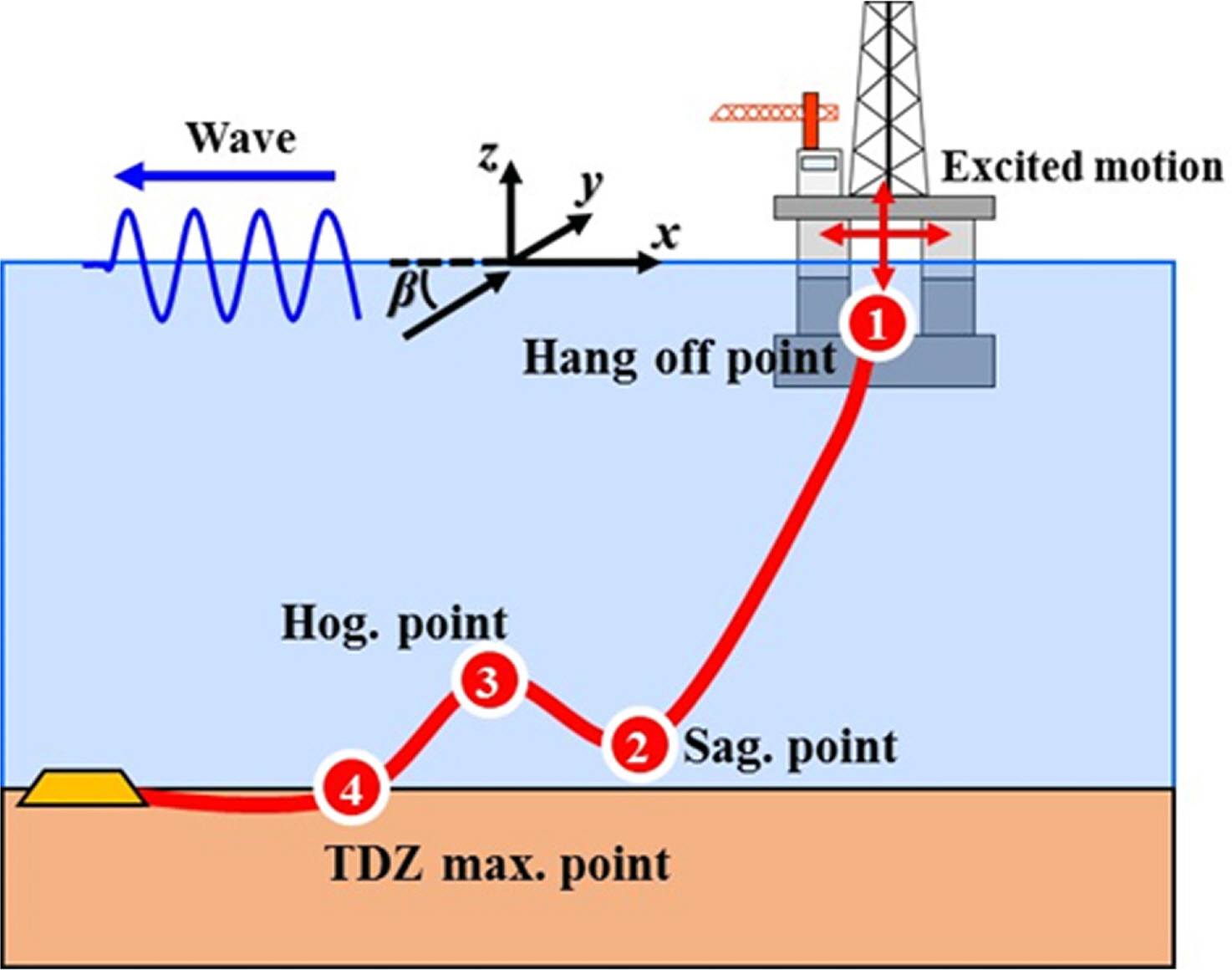
SLWR의 동적 응답은 Fig. 5와 같이 해양구조물의 운동과 유체장의 변화에 주요한 영향을 받는 것으로 알려져 있다. 본 연구에서는 상부 연결부의 규칙적인 강제 가진으로 해양구조물의 운동을 단순화하여 해석을 수행하였다. 그리고 이에 대한 결과를 통해 SLWR의 동적 응답특성을 살펴보았다. 유체장의 변화에 대한 동적특성을 확인하기 위하여 상부 연결부를 고정한 상태에서 규칙파에 대한 해석을 수행하였다.

Fig. 5.

Schematic diagram for dynamic analysis of SLWR

동적 해석은 상기 3.1장에 기술한 정적형상에서 해석이 수행되며 정적해석에서와 동일하게 317개의 요소를 이용하여 해석을 수행하였다. 수치계산은 50초의 Ramp 시간을 포함하여 총 200초 해석을 수행하여 천이구간이 지났다고 판단되는 100초 이후의 값을 사용하였다. 시간간격은 0.002 초로 수치시험을 통해 안정성과 수렴성을 확인하여 결정하였으며 모든 해석에 동일하게 사용하였다. 라이저의 유체력 계산을 위한 유체력 계수는 Table 3에 정리 하였다. 개발된 코드의 정확성을 확인하기 위해 동일한 조건에 대하여 상용 소프트웨어(Orcaflex)를 이용한 계산을 수행하였다.

Table 3.

hydrodynamic coefficient for dynamic analysis

3.2.1 상부 연결부의 가진을 통한 SLWR 동적해석

해양구조물의 운동을 단순화한 SLWR의 상부 연결부 강제가진 동적해석을 수행하였다. 전후 강제가진과 상하 강제가진에 대한 동적해석을 수행하였으며 Table 4에 가진 진폭과 주기를 요약하였다. Fig. 5와 같이 SLWR 설계 상 주요한 지점으로 알려진 상부 연결부, 새깅과 호깅의 굽힘 모멘트 최대지점 그리고 터치다운영역의 굽힘 모멘트 최대지점에서의 동적변위, 장력과 굽힘 모멘트의 변화를 면밀히 살펴보았다.

Table 4.

Dynamic analysis for SLWR excited top-end

전후 강제가진에 대한 SLWR 동적 응답을 Fig. 6에 도시하였다. 상부연결부의 동적변위와 비교하여 호깅과 새깅의 굽힘 모멘트 최대지점과 터치다운 영역 굽힘 모멘트 최대지점의 동적 응답이 작음을 확인할 수 있다. 특히 터치다운 영역 굽힘 모멘트 최대지점의 동적 응답은 상부연결부의 동적 응답의 약 2.3%로 해양구조물의 운동과 라이저의 응답을 분리시키고 있음을 확인할 수 있다. 이는 SLWR의 잘 알려진 특성이다. 비교 계산이 수행된 Orcaflex의 결과와도 매우 잘 일치함을 확인하였다.

Fig. 6.

Dynamic displacements from surge-excited motion

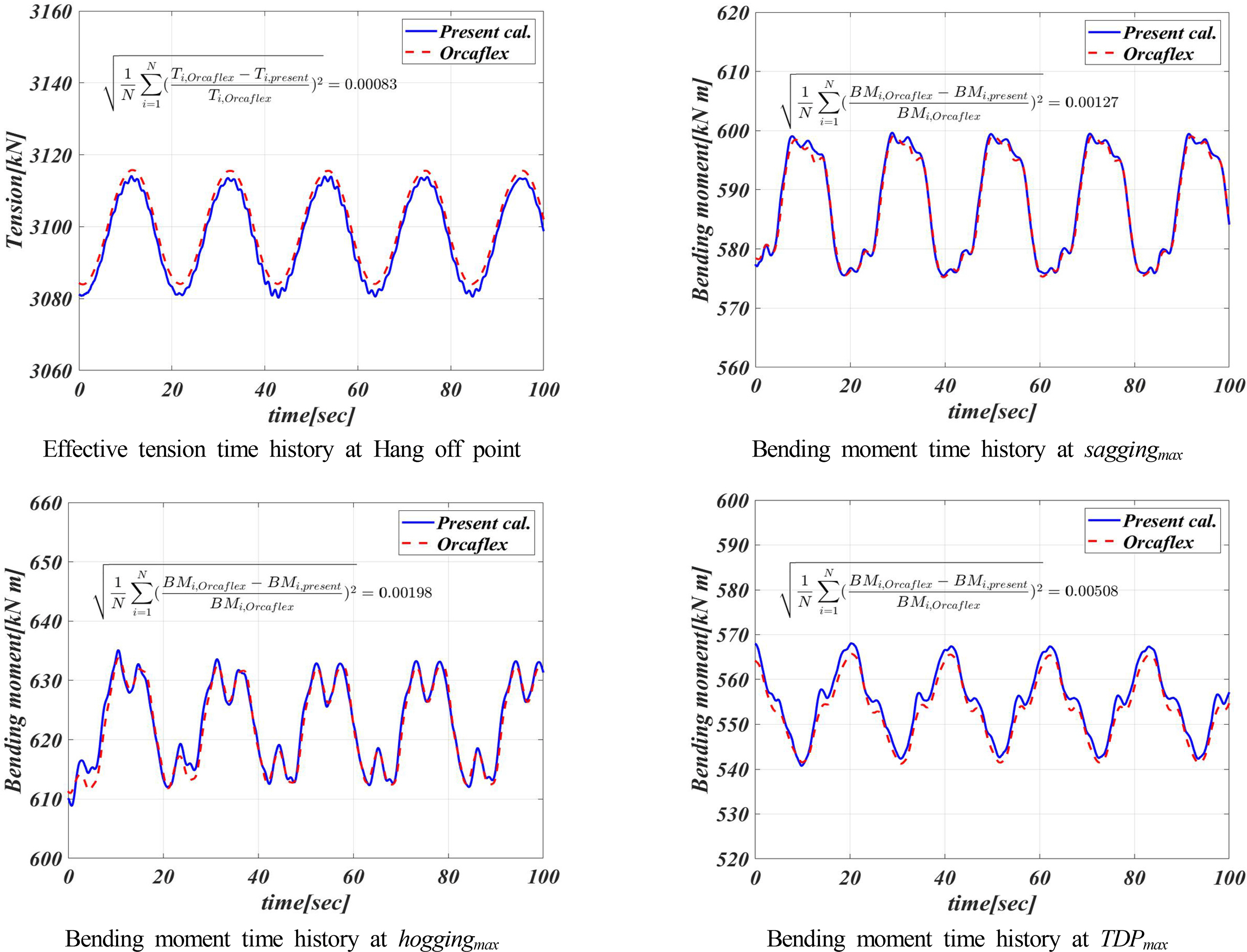
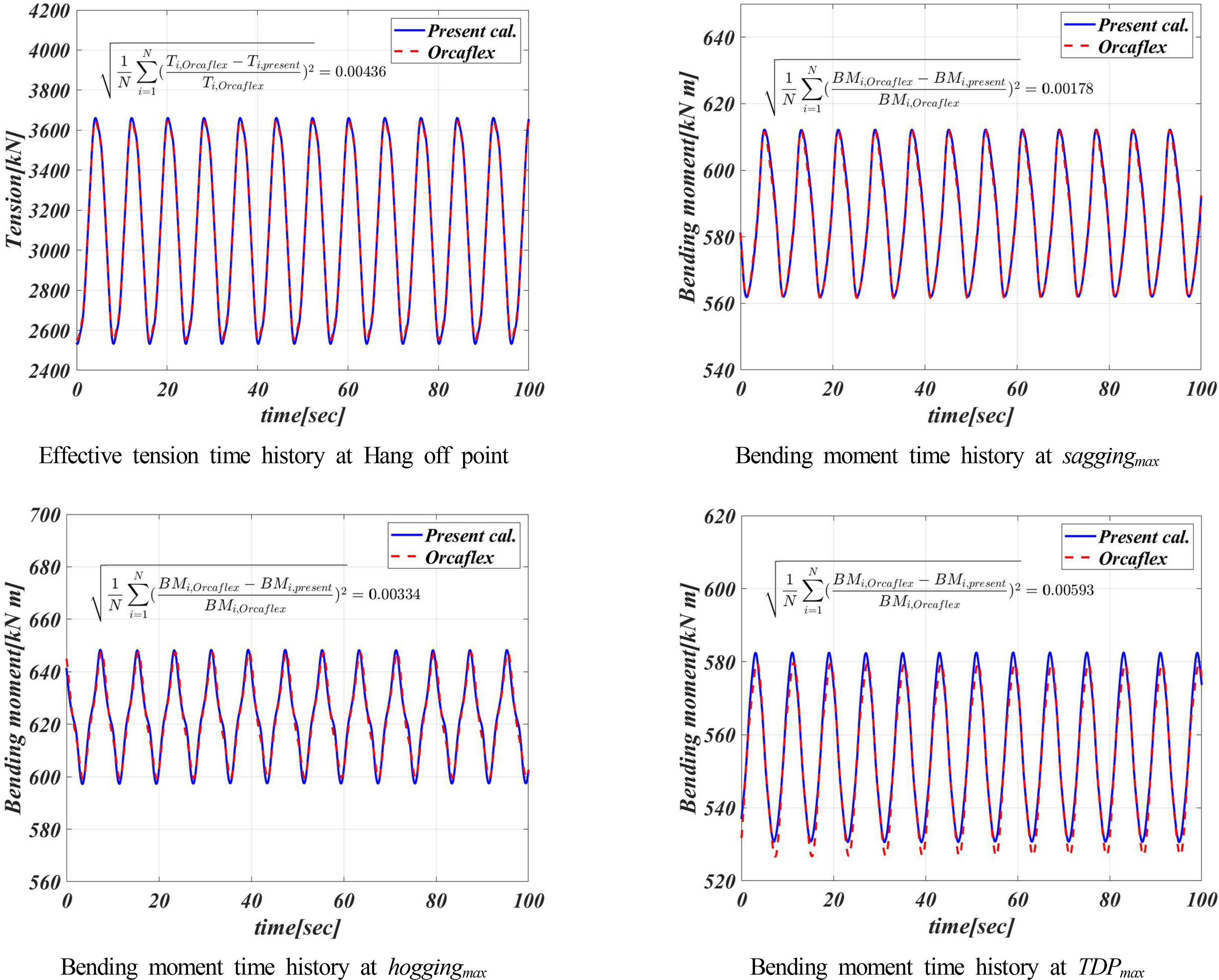
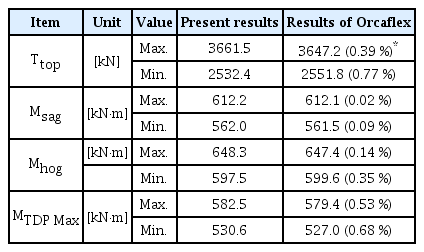
상부 연결부 전후 강제가진에 대한 유효장력과 굽힘 모멘트의 시계열을 평균제곱근 상대오차와 함께 Fig. 7에 도시하였으며 시계열의 최댓값과 최솟값을 Table 5에 정리하였다. 상부 연결부 가진에 의한 유효장력은 약 32.8kN의 동적 진폭을 가지며 상부가진과 동일한 주기로 진동함을 확인하였다. 새깅과 호깅의 굽힘 모멘트 최대지점의 굽힘 모멘트는 각각 약 23.6kNm 그리고 약 21.2kNm의 동적 진폭을 가지며 가진의 주기와 상이한 주기가 혼합된 비선형적인 시계열을 확인하였다. 터치다운 영역 굽힌 모멘트 최대 지점의 굽힘 모멘트는 약 25.1kNm로 절대값은 새깅과 호깅의 굽힘 모멘트 최대지점 보다 적으나 더 큰동적 굽힘 모멘트가 발생하였다. 시계열 또한 지반의 접촉력과 같은 여러요인으로 비선형적인 시계열을 보인다. 비교 계산이 수행된 Orcaflex의 결과와도 최댓값과 최소값 기준 0.33%, 평균 제곱근 상대오차 기준 0.6% 이내에서 잘 일치함을 확인할 수 있다.

Fig. 7.

Dynamic tension and bending moment from surge-excited motion

Table 5.

Comparisons for dynamic results of surge-excited motion at top-end of SLWR

상하 강제가진에 대한 SLWR 동적 응답을 Fig. 8에 도시하였다. 전후 강제가진의 결과와 동일하게 상부연결부의 동적변위와 비교하여 다른 지점의 동적 응답이 상대적으로 감소함을 확인하였다. 터치다운 영역 굽힘 모멘트 최대지점의 동적 응답은 상부연결부의 동적 응답의 약 11.4%로 해양구조물의 운동이 라이저 동적응답에 미치는 영향이 적음을 확인하였다. 상하 강제가진의 해석 또한 비교 계산이 수행된 Orcaflex의 결과와도 매우 잘 일치함을 확인하였다.

Fig. 8.

Dynamic displacements from heave-excited motion

상부 연결부 상하 강제가진에 대한 유효장력과 굽힘 모멘트의 시계열을 평균제곱근 상대오차와 함께 Fig. 9에 도시하였으며 시계열의 최댓값과 최솟값을 Table 6에 정리하였다. 상부 연결부 가진에 의한 유효장력은 전후가진과 비교하여 상대적으로 큰 장력이 발생함을 확인하였다. 유효장력은 약 1129.1kN의 동적 진폭을 가지며 상부가진과 동일한 주기로 진동함을 확인하였다. 새깅과 호깅의 굽힘 모멘트 최대지점의 굽힘 모멘트는 각각 약 50.2kNm 그리고 약 50.8kNm의 동적 진폭을 가지며 비선형적인 시계열 형상을 확인하였다. 터치다운 영역 굽힌 모멘트 최대 지점의 굽힘 모멘트는 약 51.9kNm로 시계열에서 비선형적인 형상이 보인다. 비교 계산이 수행된 Orcaflex의 결과와도 최댓값과 최소값 기준 0.77%, 평균제곱근 상대오차 기준 0.6% 이내에서 잘 일치함을 확인하였다.

Fig. 9.

Dynamic tension and bending moment from heave-excited motion

Table 6.

Comparisons for dynamic results of heave-excited motion at top-end of SLWR

3.2.2 규칙파 중 SLWR 동적특성

규칙파 중 유동장 변화에 따른 SLWR의 동적응답을 관찰하기 위하여 파랑 중 동적해석을 수행하였다. 규칙파의 진폭, 주기 그리고 입사각을 Table 7에 요약하였다. 상부 연결부 가진 동적해석과 마찬가지로 Fig. 5에 도시한 SLWR 설계 상 주요한 지점의 동적변위, 장력과 굽힘 모멘트의 변화를 관찰하였다.

Table 7.

Dynamic analysis for SLWR in a wave

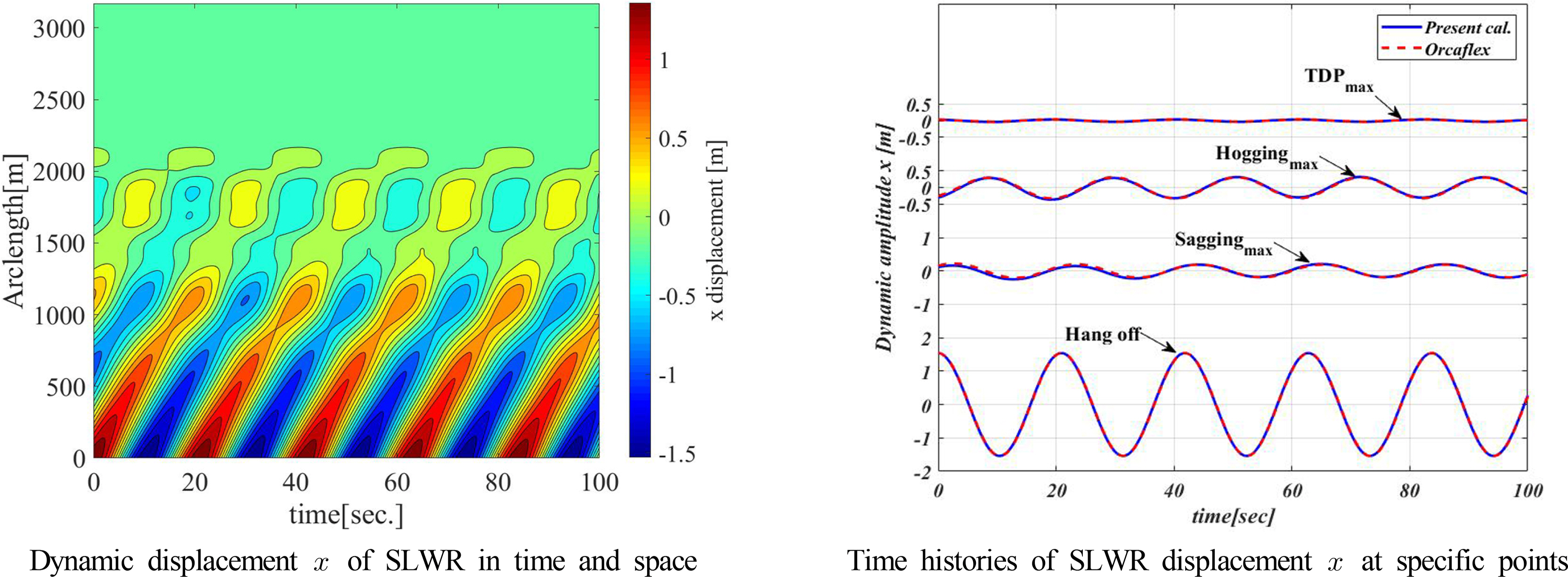
규칙파 중 유동장 변화에 따른 SLWR 동적 응답을 Fig. 10에 도시하였다. Hang off point는 고정된 상태로 해석을 수행하였다. 라이저 상부에는 전후 및 좌우 응답이 두드러지고 하부에는 상하응답이 두드러지는 것을 확인하였다. 이는 SLWR의 형상에 기인한 것으로 라이저 상부는 수직에 가까운 형상이기 때문에 속도장의 저항으로 전후 및 좌우 방향으로 응답이 발생하였고 라이저 하부의 수평에 가까운 형상이기 때문에 속도장의 저항으로 상하방향 응답이 발생함을 유추 할 수 있다. 전체적으로 규칙파의 진폭 대비 라이저의 동적응답은 상대적으로 작은 것으로 확인하였다. 터치다운 영역 굽힘 모멘트 최대지점의 상하동적 응답 진폭은 약 0.20m로 입사파 진폭 5m와 비교하여 상대적으로 크게 감소됨을 확인하였다. 상기 결과를 통해 파도 또는 조류의 기인한 유동장을 고려하여 호깅과 새깅 지점을 적절히 위치하도록 부력제를 배치하는 것이 SLWR 터치다운 영역의 응답진폭 저감에 기여할 것이라 판단된다.

Fig. 10.

Dynamic displacements of SLWR in wave

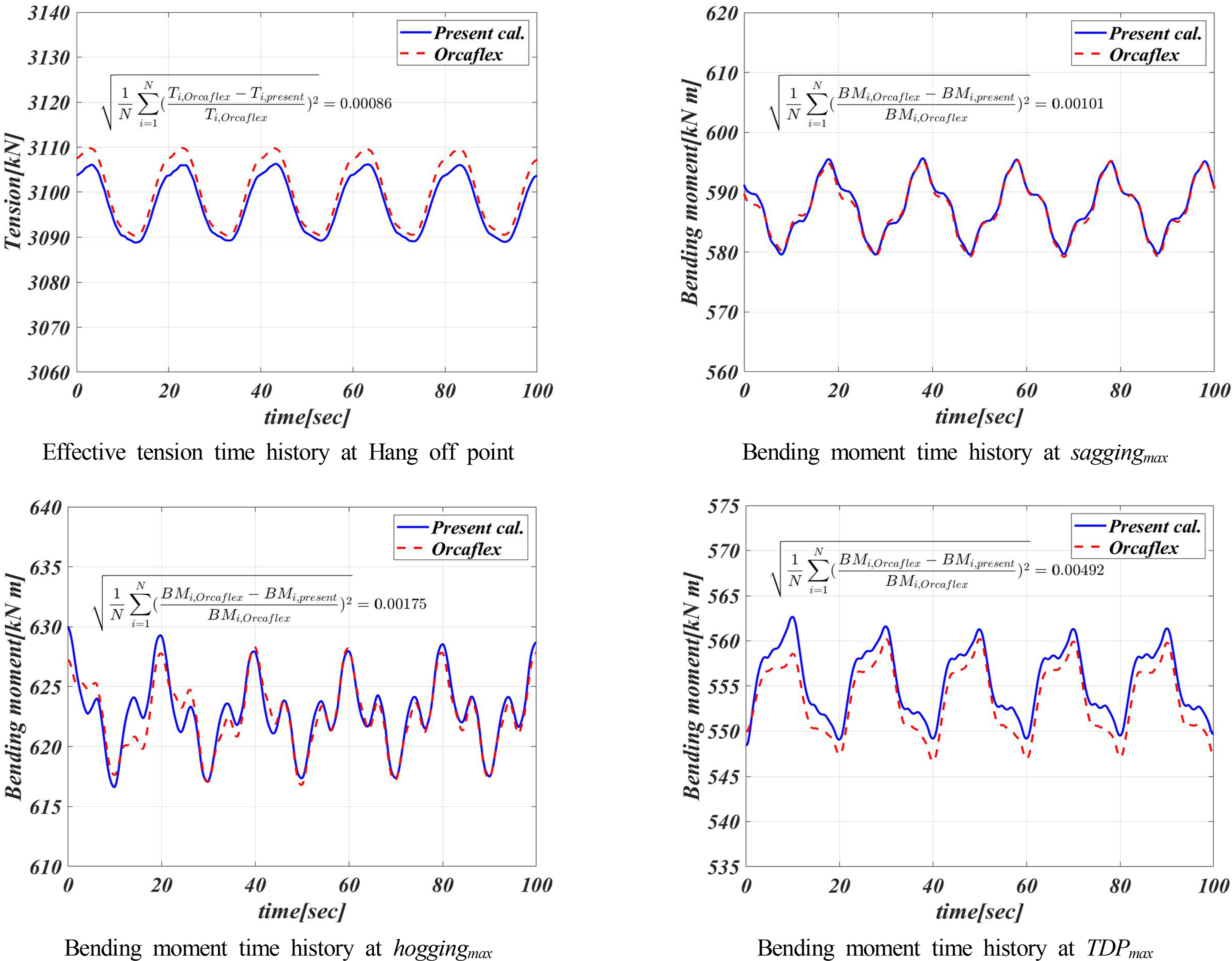
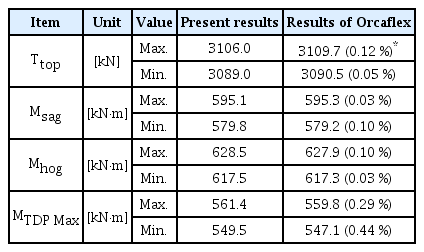
규칙파 중 유동장 변화에 따른 유효장력과 굽힘 모멘트의 시계열을 평균제곱근 상대오차와 함께 Fig. 11에 도시하였으며 시계열의 최댓값과 최솟값을 Table 8에 정리하였다. 규칙파 중 유동장 변화에 따른 유효장력은 약 17.0kN의 동적 진폭을 가지며 입사파와 동일한 주기로 진동함을 확인하였다. 새깅과 호깅의 굽힘 모멘트 최대지점의 굽힘 모멘트는 각각 약 15.3kNm 그리고 약 11.0kNm의 동적 진폭을 가지며 비선형적인 시계열 형상을 확인하였다. 터치다운 영역 굽힌 모멘트 최대 지점의 굽힘 모멘트는 약 11.9kNm로 시계열에서 또한 비선형적인 형상을 확인하였다. 비교 계산이 수행된 Orcaflex의 결과와도 최댓값과 최소값 기준 0.44%, 평균제곱근 상대오차 기준 0.5% 이내에서 잘 일치함을 확인하였다.

Fig. 11.

Dynamic tension and bending moment from wave motion

Table 8.

Comparisons for dynamic results in wave

4. 결 론

본 연구에서는 집중질량 라인모델을 이용한 SLWR의 3차원 비선형 동적해석 코드를 포트란 환경에서 개발하였다. 라이저의 구조적 특성과 유체역학적 특성을 반영하기 위하여 라인의 절점에 장력, 굽힘 모멘트에 의한 전단력, 중력, 부력, 라이저/지반 접촉력 그리고 Morison 방정식에 기반한 유체력을 정식화하여 라이저 운동방정식을 유도하였다. 안정적이고 정확한 시간 적분을 위하여 Runge-Kutta 4차 방법을 적용하였다. SLWR의 비선형 동적특성 파악을 위해 개발된 코드를 활용하여 상부 연결부 강제가진 및 규칙파 중 동적 시뮬레이션을 수행하였다. 수행된 결과를 통하여 아래 결론을 도출하였다.

(1) 상부 연결부의 강제가진의 진폭으로 인한 터치다운 지점의 동적응답이 상대적으로 크게 감소하는것을 계산결과에서 확인하였다. 이는 해양구조물의 운동이 터치다운 지점의 응답에 미치는 영향이 미미함을 의미한다. 이러한 SLWR과 해양구조물의 운동비연성효과에 기인한 동적응답 완화는 라이저의 강도 및 피로수명의 향상을 증가시킬 수 있으며 개발된 코드를 동적응답 완화 최적화에 활용할 수 있을 것이라 기대한다.

(2) 규칙파 중 유동장 변화에 기인한 SLWR의 동적응답에서 라이저 상부에는 전후 및 좌우 응답이 두드러지고 하부에는 상하응답이 두드러지는 것을 확인하였다. 이는 SLWR의 형상에 기인한 것으로 유동장의 저항을 받는 방향으로 SLWR이 응답하는것을 자명하게 알 수 있다. 규칙파의 진폭 대비 SLWR의 전반적인 동적응답은 상대적으로 작으며 터치다운영역에서는 입사파 진폭 5m 대비 약 0.2m 진폭으로 응답하는 것을 확인하였다. 터치다운 영역의 상하 응답 저감을 위해 파도 또는 조류의 기인한 유동장을 고려하여 SLWR의 호깅과 새깅 지점의 위치를 적절히 선정할 수 있을 것이라 판단된다.

(3) SLWR에 작용하는 장력과 굽힘 모멘트는 규칙적으로 가진되는 변위와 규칙파 파형과 비교하여 비선형적인 시계열이 확인되었다. 특히 굽힘 모멘트 시계열에서 강제 가진 또는 규칙파의 주기와 다른 주기의 시계열이 관찰되며 이는 다자유도 물체에서 발생되는 특성이 반영되고 있음을 의미한다.

(4) 본 논문에서 수행된 해석 조건에 대하여 상용소프트웨어 Orcaflex를 이용하여 동일하게 수행하였다. 수행된 결과들이 본 연구에서 개발된 코드의 결과와 잘 일치함을 확인하였고 개발된 코드의 정확성 또한 확인하였다.

개발된 코드를 이용하여 SLWR의 동적응답에 대한 피로해석과 와유기 진동해석에 대한 연구를 이어갈 예정이다. 또한 현재 개발된 코드는 부유체의 연성이 고려되어 있지 않기 때문에 추후 부유체 운동과 연성된 코드로 확장할 예정이다.

Acknowledgements

본 연구는 선박해양프랜트연구소에서 지원하는 ‘초심해역용 라이저(SLWR) 설계엔지니어링 핵심기술 개발(PES3060)’의 결과물임을 밝히는 바입니다.

References

Hall M, Goupee A. 2015;Validation of a Lumped-Mass Mooring Line Model with DeeoCwind Semisubmersible Model Test Data. Ocean Engineering 104:590–603. https://doi.org/10.1016/j.oceaneng.2015.05.035.

Hong N, Huh TN. 2000;Dynamic Analysis of Riser with Vortex Excitation by Coupled Wake Oscillator Model. Journal of Korean Society of Coastal and Ocean Engineers 12(3):109–115.

Kim BW, Sung HG, Hong SY, Jung HJ. 2010;Finite Element Nonlinear Analysis for Catenary Structure Considering Elastic Deformation. Computer Modeling in Engineering and Sciences 63(1):29–45. https://doi.org/10.3970/cmes.2010.063.029.

Kim BW, Sung HG, Kim JH, Hong SY. 2013;Comparison of Linear Spring and Nonlinear FEM Methods in Dynamic Coupled Analysis of Floating Structure and Mooring System. Journal of Fluids and Structures 42:205–227. https://doi.org/10.1016/j.jfluidstructs.2013.07.002.

Kim SJ. 2016;Fatigue Damage of Lazy-Wave SCR for Deepwater Offshore Platforms. Journal of the Institute of Industrial Technology(Daejeon University) 27(1):27–34.

Li SC. 2010. Dynamic Response of Deepwater Lazy-Wave Catenary Riser Deep Offshore Technology International. Amsterdam Netherlands.:

Oh SH, Jung JH, Park BW, Kwon YJ, Jung D. 2018;Numerical Study on the Estimation of Static Configuration of Steel Lazy Wave Riser Using Dynamic Relaxation Method. Journal of Ocean Engineering and Technology 32(6):466–473. https://doi.org/10.26748/KSOE.2018.32.6.466.

Oh SH, Jung JH, Park BW, Kwon YJ, Jung D. 2019. Dynamic Simulation of Steel Lazy Wave Riser Excited at the Top-End. In : International Offshore and Polar Engineering Conference. Honolulu USA. p. 1816–1823.

Park BW, Jung D, Jung JH, Kwon YJ. 2017. Introduction on BOD (Basis of Design) for Concept Design of Steel Lazy Wave Riser. In : Proceedings of the Autum Conference the Korean Society of Ocean Engineers. Geoje Korea.

Park BW, Jung D, Jung JH, Kwon YJ. 2018. A Study on the Initial Configuration of SLWR (Steel Lazy Wave Riser) Considering the Effect of Internal Fluid Density and Buoyancy Arrangement. In : Proceedings of the Joint Conference of the Korean Association of Ocean Science and Technology Societies (KAOSTS). Jeju Korea..

Park BW, Oh SH, Kwon YJ, Jung JH, Jung D. 2019. Dynamic Analysis of SLWR Subjected to Internal Slug Flow Conditions. In : International Offshore and Polar Engineering Conference. Honolulu USA. p. 1861–1867.

Ruan W, Liu S, Li Y, Bai Y, Yuan S. 2016. Nonlinear Dynamic Analysis of Deepwater Steel Lazy Wave Riser Subjected to Imposed Top-End Excitations. In : Proceedings of 35th International Conference on Ocean, Offshore and Arctic Engineering. Busan, South Korea. OMAE2016-54111https://doi.org/10.1115/OMAE2016-54111.

van den Boom HJJ, Dekker JN, van Elsacker AW. 1987. Dynamic Aspects of Offshore Riser and Mooring Concepts. In : Offshore Technology Conference. Houston USA. OTC-5531. p. 405–416. https://doi.org/10.4043/5531-MS.

Wang J, Duan M, Fan J, Liu Y. 2013. Static Equilibrium Configuration of Deepwater Steel Lazy-Wave Riser. In : Proceedings of 23th International Offshore and Polar Engineering Conference. Anchorage, USA; 1; p. 995–998.

Wang J, Duan M. 2015;A Nonlinear Model for Deepwater Steel Lazy-Wave Riser Configuration with Ocean Current and Internal Flow. Ocean Engineering 94:155–162. https://doi.org/10.1016/j.oceaneng.2014.11.025.

Wang J, Duan M, He R. 2018;A Nonlinear Dynamic Model for 2D Deepwater Steel Lazy-Wave Riser Subjected to Top–End Imposed Excitations. Ships and Offshore Structures 13(3):330–342. https://doi.org/10.1080/17445302.2017.1382663.

Yoo KK, Joo Y. 2017;Sensitivity Study on SCR Design for Spread-Moored FPSO in West Africa. Journal of Ocean Engineering and Technology 31(2):111–120. https://doi.org/10.5574/KSOE.2017.31.2.111.

Article information Continued

This is an open access article distributed under the terms of the creative commons attribution non-commercial license (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Item	Hang off riser	Buoyancy riser	Touch down riser
Segment length [m]	1,600	370	1,200
Outer diameter [m]	0.457	1.137	0.457
Inner diameter [m]		0.406
Dry weight [kg/m]	270	697	270
Bending rigidity [N·m²]		1.66E8
Axial stiffness [N]		7.098E9
Inner flow density [kg·m³]		881
Seabed stiffness [N/m/m²]		6,000

Item	Unit	Present results	Results (Oh et al., 2018)	Results of Orcaflex
T_top	[kN]	3088.9	3080.3 (0.28 %)^*	3089.7 (0.03 %)^*
T_bot	[kN]	594.4	593.0 (0.25 %)	595.9 (0.25 %)
M_sag	[kN·m]	587.9	587.9 (0.00 %)	587.0 (0.15 %)
M_hog	[kN·m]	624.4	625.8 (0.22 %)	622.3 (0.34 %)
θ_top	[deg.]	168.9	168.9 (0.00 %)	168.9 (0.00 %)
X_TDP	[m]	−1359.9	−1359.5 (0.03 %)	−1360.0 (0.01 %)
M_TDP _Max	[kN·m]	556.9	556.8 (0.02 %)	553.4 (0.63 %)

Item	Quantity
Drag coefficient C_dn	1.2
Friction coefficient C_dt	0.08
Normal added mass coefficient C_an	1.0
Tangential added mass coefficient C_at	0.08
Inertia coefficient C_M	2.0

Item	Unit	Surge motion	Heave motion
Amplitude	[m]	1.54	1.54
Period	[sec.]	20.94	8.0

Item	Unit	Value	Present results	Results of Orcaflex
T_top	[kN]	Max.	3113.4	3115.6 (0.07 %)^*
T_top	[kN]	Min.	3080.6	3084.0 (0.11 %)
M_sag	[kN·m]	Max.	599.5	599.1 (0.07 %)
M_sag	[kN·m]	Min.	575.9	575.3 (0.10 %)
M_hog	[kN·m]	Max.	633.2	632.4 (0.13 %)
M_hog	[kN·m]	Min.	612.0	612.6 (0.10 %)
M_TDP _Max	[kN·m]	Max.	567.4	565.5 (0.33 %)
M_TDP _Max	[kN·m]	Min.	542.3	541.4 (0.17 %)