조류 중 원형실린더 형상 구조물의 거동감소를 위한 실험적 연구
Experimental Study on Reducing Motion of Circular Cylinder in Currents
Article information
Trans Abstract
The development of marine technology is expected to increase the demand for marine plants because of increasing oil prices. Therefore, there is also expected to be an increase in the demand for cylindrical structures such as URF (umbilical, riser, flowline) structures and spars, which are used operating in various seas. However, a cylindrical structure experiences vortex induced motion (VIM) in a current. In particular, for risers and umbilicals, it is important to identify the characteristics of the VIM because interference between structures can occur. In addition, various studies have been conducted to reduce VIM because it is the cause of fatigue damage to structures. The helical strake, which was developed for VIM reduction, has an excellent VIM reduction performance, but is difficult to install on structures and has a negative effect on heave motion. Therefore, the purpose of this study was to supplement the shortcomings of the helical strake and develop a high-performance reduction device. In the reduction device developed in this study, a string is placed around the structure inside the flow, causing vibration. The vibration of this string causes a small turbulence in the flow field, reducing the VIM effect on the structure. Finally, in this study, the 2-DOF motion characteristics of models without a suppression device, models with a helical strake, and models with a string were investigated, and their reduction performances were compared through model tests.
1. 서 론
최근 지속적인 유가상승으로 인하여 해양플랜트 산업의 회복에 대한 기대감이 높아지고 있고, 이에 따른 다양한 해양구조물들의 수요 또한 증가할 것이라 예상된다. 실제로 해양구조물들은 제작비용이 고가일 뿐만 아니라 유지⋅보수에도 상당한 비용이 필요하다. 하지만 무엇보다 중요한 것은 2010년 GOM(Gulf of Mexico)에서 발생한 Deepwater horizon의 폭발사고와 같은 해양사고가 반복되지 않도록 해양구조물의 신뢰성 있는 설계가 필요하다. 그리고 최근 심해 해양자원 개발의 확대로 인하여 설치해역이 심해로 이동하고 있는 추세이다. 심해에서의 생산과 시추는 더 많은 부하와 스트레스를 유발하기 때문에 추가적인 엔지니어링 기술이 더욱 중요해지고 있다.
일반적으로 부유식 구조물을 대표하는 Spar, 시추를 위한 Riser, 수송을 위해 사용되는 Pipeline 등의 해양구조물은 기본적으로 원형실린더 형상을 지니고 있다. 이러한 원형실린더 형상의 구조물들은 일정한 속도 이상의 조류가 흐르는 경우, 후류에서 급격한 구배 변화로 인한 규칙적인 패턴의 와 흘림 현상(Vortex shedding)이 발생하게 된다. 발생한 와 흘림 현상은 원형실린더 형상 구조물에 주기적인 하중을 발생시키며, 구조물의 움직임과 상호작용에 의해 와 유기 운동(Vortex induced motion, VIM)을 유발하는 원인이 된다. VIM으로 인해 원형실린더 형상 구조물은 흐름에 평행한 방향 응답(In-line response)과 흐름에 직각인 방향 응답(Cross-flow response)이 발생하게 된다. 이러한 VIM 응답은 비선형적인 운동특성을 가지며, Vortex는 원형실린더 형상 구조물에 반복적인 하중을 유발하여 구조적 피로손상을 발생시킨다. 뿐만 아니라 원형실린더 형상 구조물의 와 흘림 진동수(Vortex shedding frequency, fs)와 고유진동수(Natural frequency, fn)의 비가 1에 가까워지면 VIM 응답이 점점 커지게 되고, 두 진동수의 비가 1이 되면 공진현상의 일종인 Lock-in현상이 발생한다. 이러한 이유로 VIM 응답은 원형실린더 형상 구조물의 설계 시 고려해야할 중요한 인자이다.
따라서 구조물에 발생하는 VIM에 의한 영향을 줄이기 위하여 Helical strake와 같은 VIM 저감장치가 사용되고 있다. 그러나 Helical strake는 본체와 따로 제작하여 조립이 어렵고 고가의 시공비가 발생한다(Son, 2010). 뿐만 아니라 구조물의 무게를 증가시키며 Heave motion을 크게 만드는 단점이 존재한다(Oh, 2003). 그래서 기존의 Helical strake의 단점을 보완하고 우수한 저감성능을 가진 저감장치를 개발하기 위한 연구가 진행되어 왔다. 먼저 Son(2010)은 원형실린더 형상 구조물에 필름을 부착함으로 유동장에 위치한 필름이 유선형 형상을 만듦으로써 구조물에 작용하는 수평력을 저감하는 실험적 연구를 진행하였다. 그리고 Jung and Yoon(2015)은 나선형 표면 처리를 한 트위스트 실린더의 VIM 저감성능에 대해서 CFD(Computational fluid dynamics) 해석을 수행하였다.
앞서 진행된 선행연구처럼 VIM 응답과 관련된 연구는 크게 CFD와 실험적 연구 두 가지 방법으로 이루어지고 있다. 먼저 CFD의 경우는 원형실린더 형상 구조물의 경우 길이-직경비(이하 L/D)가 크기 때문에 계산량이 방대해지는 경향이 존재하며, 설치해역의 수심이 깊어짐에 따라 해석의 어려움은 더욱 커지게 된다. 따라서 최근에는 Full scale의 Riser 대신, Riser의 특정 Section을 잘라서 사용하는 방법을 사용한다(Gustafsson, 2012). 하지만 VIM 응답은 점성이 지배적인 동적 응답이기 때문에 주로 실험을 통한 연구가 많이 이루어져 왔다. 그리고 기존의 VIM 응답과 관련한 연구들은 Cross-flow 응답만을 고려한 1-DOF system에 관한 연구가 대다수 이루어졌으나, 최근 연구에서는 In-line 응답과 Cross-flow 응답을 동시에 고려하는 2-DOF system에 대한 실험들이 수행되어지고 있다(Blevins, 2001; Bearman, 2011; Srinil et al., 2013; Kim et al. 2016; Park, 2017).
본 연구에서는 String이 조류환경 속에서 만들어내는 떨림이 유동장의 변화를 주는 메커니즘을 활용하여 VIM 저감을 위한 연구를 수행하였다. 이와 유사한 사전연구로 Silva-Ortega and Assi(2017)는 원형실린더 주변에 직경이 작은 8개의 회전이 가능한 실린더를 배치하여 유동장에 변화를 주는 연구가 진행되었으며, 원형실린더에 작용하는 항력과 양력을 측정하였다. 그리고 Silva-Ortega and Assi(2018)에서는 작은 실린더의 개수, 실린더의 직경비, 설치위치를 파라미터로 설정하여 항력과 양력에 관한 연구를 진행하였다. 마찬가지로 선행연구로 진행되었던, Baek et al. (2018)은 String을 저감장치로 사용하여 String의 떨림을 이용한 항력과 수평력의 저감성능에 대한 실험적 연구를 진행하였다. 앞서 연구경향과 방법들을 종합하여 본 연구는 2-DOF 환경에서 실험을 통해서 진행하였으며, 원형실린더가 조류 중 움직임으로 인한 비선형적인 특성을 파악하기 위해 VIM 응답의 변위에 초점을 두었다. 그리고 실험에 사용된 모델은 크게 네 종류로 저감장치를 부착하지 않은 Bare hull 모델, Helical strake를 부착한 모델, Two string을 부착한 모델과 방사형으로 String이 설치된 모델로 정하였다. 최종적으로 각 모델별 VIM 응답 특성을 파악하면서 VIM의 저감성능을 비교 및 분석하였다.
2. 모형 실험
2.1 실험환경
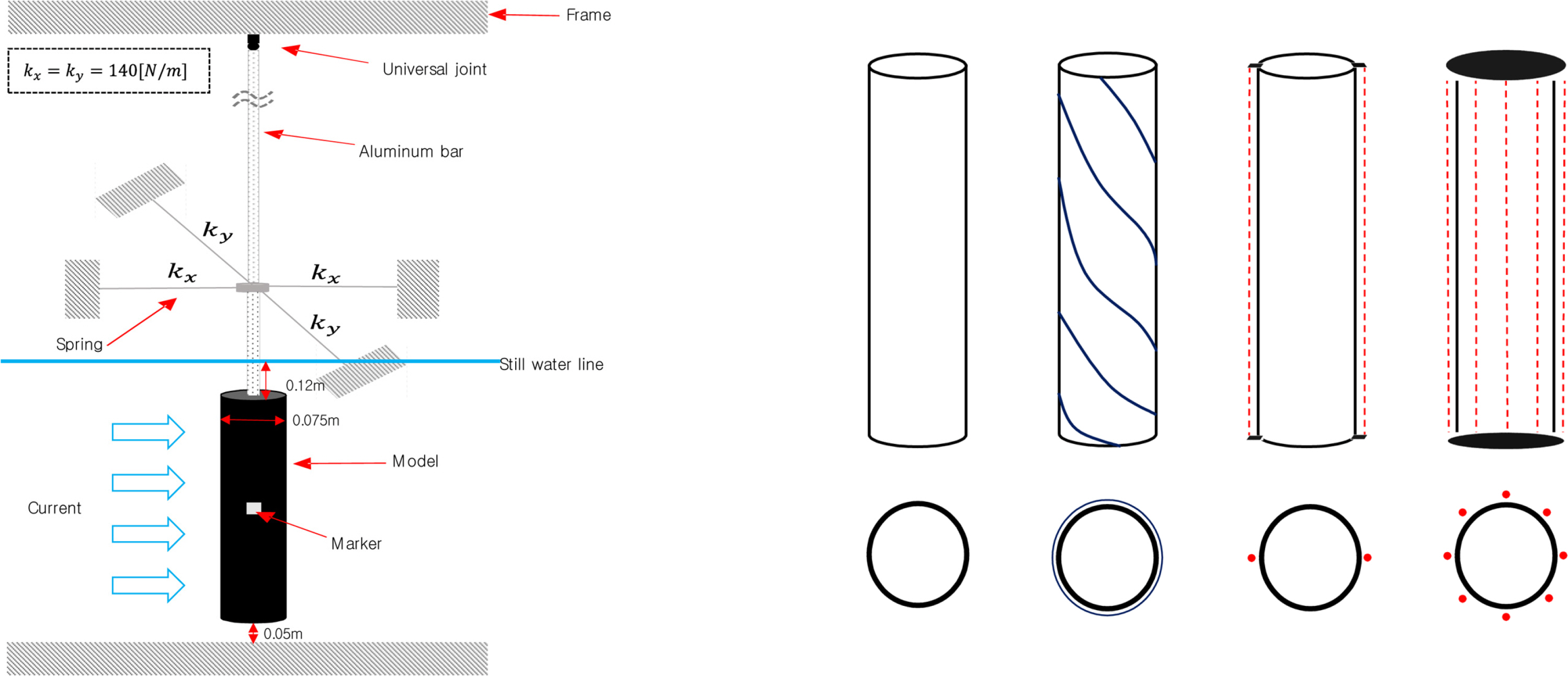
Fig. 1은 연구에서 사용된 실험장비들을 나타내고 있다. 먼저 실험은 한국해양대학교에 있는 회류수조(Circulating water channel, CWC)에서 실시하였다. 그리고 회류수조의 크기는 4.0×1.8×1.2m (Lcwc × Bcwc × Dcwc)이며, 측정수심은 0.915m로 설정하였다. VIM 응답의 측정은 비접촉식 3차원 운동계측기를 사용하였으며, 이는 실험모델이 반사하는 빛을 마커로 인식하는 광학용 계측기이다. 따라서 실험모델에 빛을 반사할 수 있는 마커를 실험모델의 무게중심점에 부착하여 VIM 응답의 변위를 측정하였다.
Fig. 2의 왼쪽 그림은 실험의 전체적인 모식도를 나타내고 있다. 먼저 원형실린더 구조물의 x, y변위를 측정하기 위해 프레임의 상단부에 유니버셜 조인트를 설치하였다. 유니버셜 조인트와 모델을 이어주는 봉은 알루미늄으로 2.6m의 길이로 제작되었으며, 이는 원형 실린더의 회전운동을 최소화하기 위함이다. 여기서 x방향은 회류수조의 길이방향으로 유속은 왼쪽에서 오른쪽으로 진행방향을 가지고 있으며, y방향은 회류수조의 벽면방향이다. 여기에 x, y방향으로 일정한 복원력을 제공하기 위해서 스프링을 설치하였다. 그리고 Fig. 2의 오른쪽 그림은 실험에 사용된 실험모델의 모식도를 나타내었고 Table 1에는 모델별 제원을 나타내었다. 첫 번째로 가장 왼쪽에 있는 실험모델은 저감장치를 부착하지 않은 Bare case(이하 Bare)이며, VIM 저감성능을 비교하기 위한 기준이 되는 구조물이다. Bare는 원형실린더 형상의 구조물이며, 길이는 0.75m로 제작되었고 직경은 벽면효과를 최소화하기 위해 0.075m이며, L/D=10으로 설정하였다. Bare의 바로 오른쪽에 위치한 모식도는 선행기술을 대표할 수 있는 Strake case(이하 Strake)이다. Strake의 경우 Bare에 Helical strake를 부착하였으며, Strake의 제원은 선행자료를 참고하여 제작하였다(Blevins, 2001). 그리고 Strake의 오른쪽에 위한 모델은 선행연구에서 고안된 Two strings case(이하 String)이며, 흐름의 방향에 수직하게 180° 간격으로 String을 설치하였다. 끝으로 가장 오른쪽에 위치한 모델은 이번 연구에서 새롭게 고안한 Radiational string case(이하 Radiation)이며, 원 둘레를 따라서 45° 간격으로 총 8개의 String을 설치하였다. Fig. 3은 본 연구의 실제 실험사진을 나타내었으며, 전체적인 설치사진과 Two string 모델에 대한 실험 광경을 나타내고 있다.
2.2 실험조건 및 방법
본 연구에서 실험유속은 0.3m/s부터 1.2m/s까지 0.1m/s간격으로 설정하였다. 또한 모형실험의 결과를 일반화하기 위하여 무차원 파라미터를 사용하였다. 첫 번째 사용된 파라미터로 구조물의 고유 진동수(fn), 유속, 직경으로 표현되된다. 최종적으로 구조물의 고유 진동속도와 유속의 비로 표현되는 무차원 속도인 Reduced velocity(Vr)를 사용하였으며, 실험유속에 따라 Vr은 4.45~18.0에 형성되었다. Vr은 식 (1)과 같이 나타낼 수 있다.
이때 구조물의 고유 진동수는 식 (2)와 같이 나타낼 수 있다. 본 실험에서 고유 진동수는 자유 감쇠 실험을 통하여 구하였으며, 부가질량의 영향을 최소화하기 위해서 공기 중에서 실시하였다.
ma : Added mass [kg]
k : Stiffness of system [kg/s2]
두 번째 파라미터로 VIM 응답은 점성이 지배적인 현상이므로 관성력과 점성력의 관계를 나타내주는 무차원수인 Reynolds number(Re)를 사용하였고, 식 (3)으로 나타내었다. 본 실험에서는 와류가 활발히 일어나는 아임계 영역인 22,500~90,000 범위에서 형성되었다.
U : Flow velocity [m/s]
D : Diameter [m]
ν : kinematic viscosity [kg/s2]
세 번째는 진동하는 구조물의 응답의 메커니즘을 일반화하기 위하여 Strouhal number(St)를 사용하였으며, Bare에 대해서 전체적으로 약 0.2의 값을 가지고 있었다. St는 와 흘림 진동수(fs)와 구조물의 직경, 유속의 조합으로 식 (4)과 같이 나타낼 수 있다. 이 때 St에 사용되는 와 흘림 진동수(fs)는 실험을 통해서 얻어진 값을 사용하였다.
U : Flow velocity [m/s]
D : Diameter [m]
fs : Vortex shedding frequency [Hz]
끝으로 VIM 응답에 영향을 주는 요인인 Mass ratio(
직립인 상태에서 원형실린더 형상 구조물의 VIM 운동응답특성을 파악하기 위하여 In-line 응답 방향의 용수철의 강성과 Cross-flow 응답 방향의 스프링의 강성은 140[N/m]로 동일하게 설정해주었다. 끝으로 실험 계측 시간은 실험모델의 운동을 안정한 상태에서 계측하기 위하여 각 유속별로 300초로 하였고, 균일류를 얻기 위한 충분한 대기시간을 가졌다. 뿐만 아니라 동일 유속에서 계측의 불확실성을 감소하기 위하여 Case별로 3회 반복 실험을 실시하였다.
3. 실험결과 및 고찰
3.1 In-line amplitude
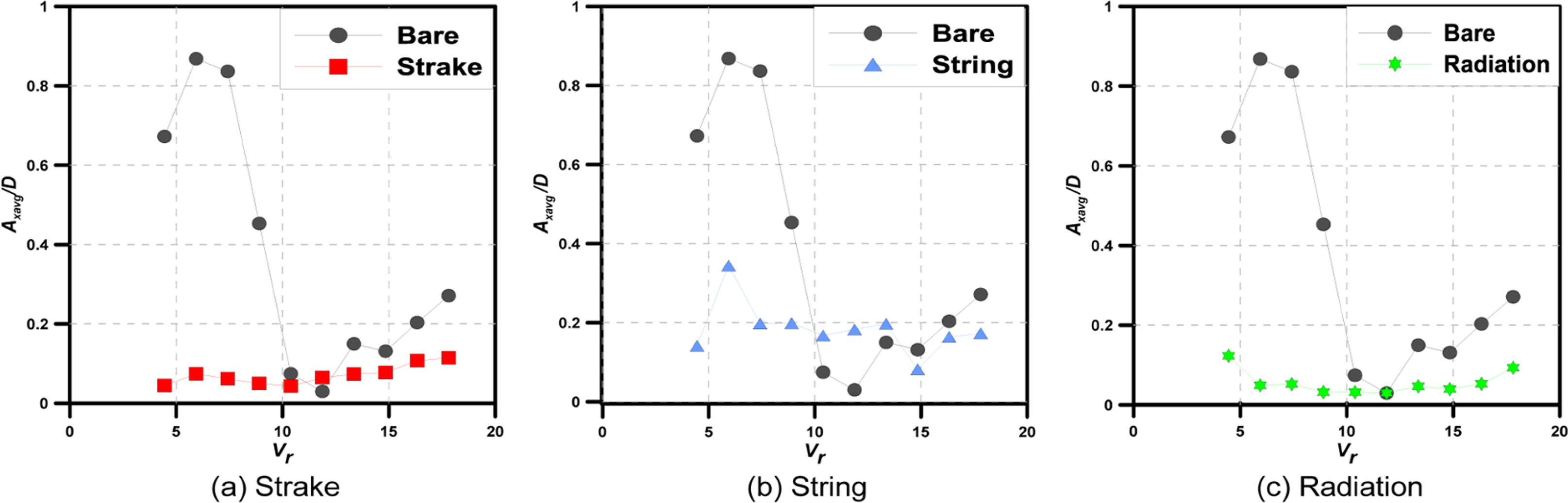
Fig. 4의 그래프는 Vr 변화에 따른 In-line amplitude의 평균값을 실린더의 직경으로 무차원화하여 비교한 그래프이다. Bare는 검은색 원형 표식으로 나타내었고, Strake는 붉은색 사각형 표식, String은 푸른색 삼각형 표식, Radiation은 녹색 다각형 표식으로 나타내었다. Fig. 4(a)에 의하면, 대부분의 유속에 있어서 Strake는 In-line amplitude를 감소시키는 것을 알 수 있다. 그러나 Vr = 12인 유속에서는 Strake의 경우가 Bare보다 미세하게 크게 나타나는 경향을 알 수 있다. 그리고 Fig. 4(b)에 의하면, String의 In-line amplitude는 Strake와 Radiation에 비해 다소 크게 나타나지만, 10.5 ≤ Vr ≤ 13.5인 구간을 제외하면 Bare보다 작은 값을 가지는 것을 알 수 있다. 끝으로 Fig. 4(c)에서는, Radiation은 Bare에 비해 전 유속에서 In-line amplitude의 크기가 감소되었음을 확인 할 수 있다.
3.2 Cross-flow amplitude
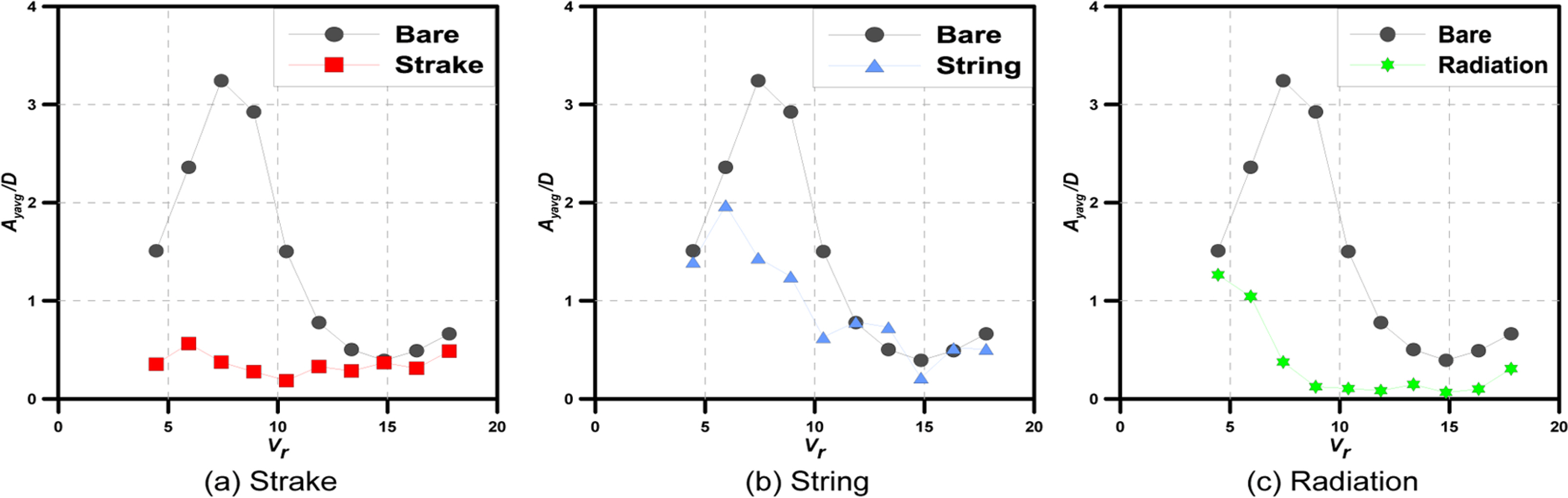
Fig. 5의 그래프는 Vr 변화에 따른 Cross-flow amplitude의 평균값을 실린더의 직경으로 무차원화하여 비교한 그래프이다. Fig. 5(a)에 의하면, Strake는 전체 유속에서 Cross-flow amplitude가 Bare보다 작게 나타나는 것을 알 수 있다. 그리고 Fig. 5(b)를 보면, In-line amplitude의 경향과 마찬가지로 String은 Strake와 Radiation에 비해 Cross-flow amplitude는 크게 나타나는 것을 확인할 수 있다. 하지만 Bare와 비교해보면, Vr이 13.5에서는 미소하게 큰 진폭이 발생하는 구간을 제외한 전반적인 유속에 걸쳐 진폭이 감소되었음을 알 수 있다. Fig. 5(c)에서 Radiation은 Vr이 4.45에서 진폭의 차이는 미소하였으나, 모든 유속에서 진폭이 확실히 저감되었음을 확인할 수 있다.
3.3 In-line & Cross-flow motion response
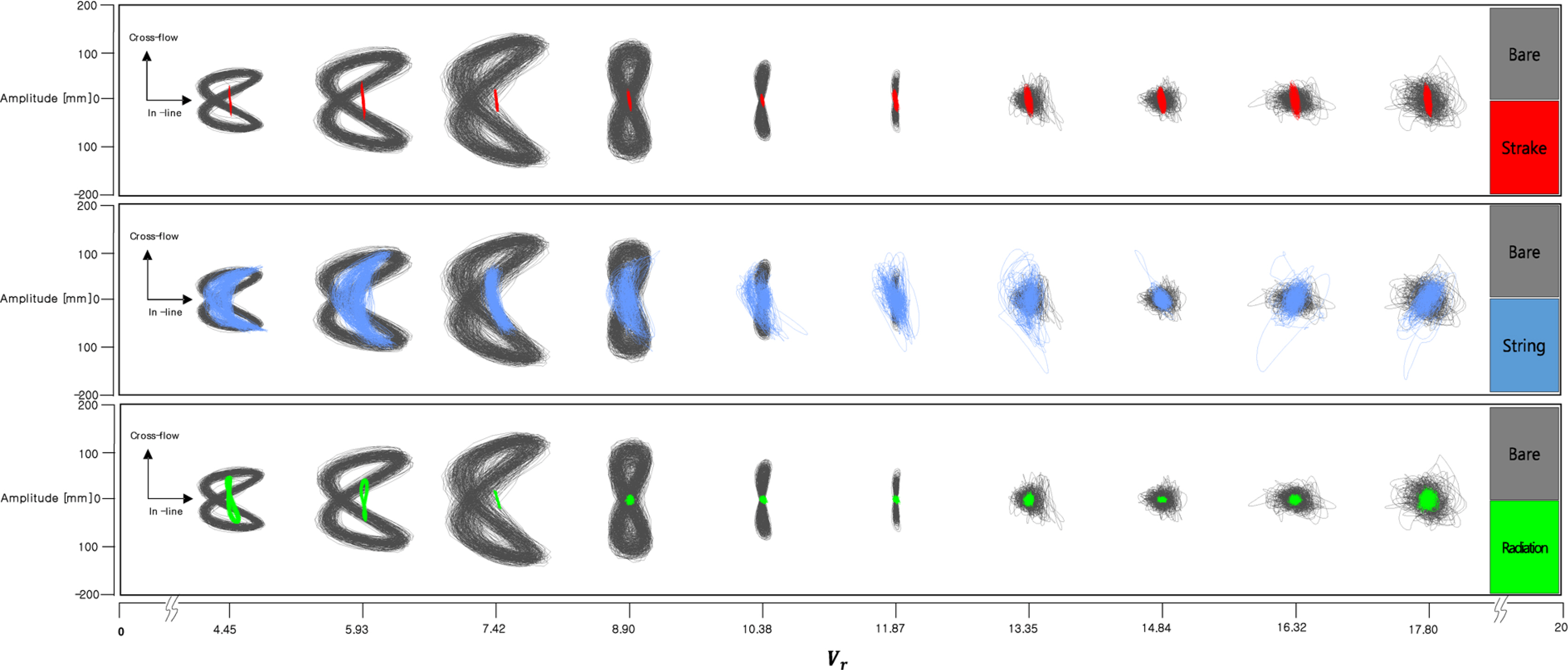
Fig. 6에는 Vr 별로 In-line과 Cross-flow의 응답을 종합하여 나타내었으며, 응답의 형상은 발생하는 진폭의 최대치에 의해 형성된다. 먼저 Bare의 응답은 4.45 ≤Vr ≤ 7.5인 구간에서 기울어진 8자 모양의 운동을 하고 있으며, 7.5 ≤Vr ≤ 12.0까지는 직립 8자 운동을 하고 있다. 그리고 Vr ≥ 13.35인 구간부터 8자 운동의 경향이 사라지고, 점 운동을 하는 것을 관찰할 수 있다. 첫 번째로 Strake의 응답을 보면, Bare의 8자 운동의 경향은 나타나지 않으며 전체 유속에서 In-line 응답이 줄어듦을 관찰할 수 있다. 그리고 Cross-flow 응답의 경우, Vr ≤ 12의 범위에서는 유속별로 응답의 크기가 작음을 확인할 수 있으나, Vr ≥ 12인 구간에서 응답의 크기는 Bare와 유사한 점을 보아 저감성능을 관찰하기 어려웠다. 그리고 String의 응답은 Strake와 마찬가지로 Bare의 8자 운동 경향은 눈에 띄지 않는다. 그러나 String의 In-line 응답은 Bare와 큰 차이를 보이지 않으며, Cross-flow 응답은 Vr이 7.42, 8.9에서만 작음을 알 수 있다. 끝으로 Radiation은 Vr이 4.45, 5.93에서는 약하게 8자 모양의 운동을 가지는 것으로 확인되었고, Bare에 비해 전체 유속에 걸쳐 In-line 응답과 Cross-flow 응답 크기 또한 확연하게 줄어든 모습을 확인할 수 있다.
Fig. 5에 의하면, String은 Strake와 Radiation에 비해 저감성능이 미미하다는 사실을 확인할 수 있다. 따라서 Fig. 7에는 Vr에 따른 Strake와 Radiation의 응답을 비교하였다. Radiation과 Strake의 응답은 Vr이 4.45, 4.5 ≤Vr ≤ 12.0, 12.0 ≤Vr ≤ 17.8 세 구간으로 나누어서 비교를 하였다. 첫 번째 구간인 Vr이 4.45인 유속에서는 Strake가 Radiation보다 In-line 응답과 Cross-flow 응답이 작음을 확인할 수 있다. 그리고 두 번째 구간인 4.5 ≤Vr ≤ 12.0에서 In-line 응답은 큰 차이를 보이지 않지만, Cross-flow 응답은 Radiation이 작은 것으로 관찰되었다. 그리고 세 번째 구간인 12.0 ≤Vr ≤ 17.8에서는 In-line 응답의 크기가 유사하였고, Crossflow 응답의 경우, Radiation이 Strake보다 크기가 작은 것을 확인할 수 있다. 따라서 전체 유속에서 걸쳐서 In-line 응답 측면에서는 Radiation과 Strake가 유사한 응답의 크기를 보이고 있으나, Cross-flow 응답의 측면에서 바라보았을 때에는 Radiation이 Strake보다 작은 응답의 크기를 보여주고 있다. 이는 유속이 증가할수록 Radiation이 Strake에 비해 뚜렷한 VIM 저감성능을 보여주고 있음을 알 수 있다.
3.4 Distribution table of in-line amplitude
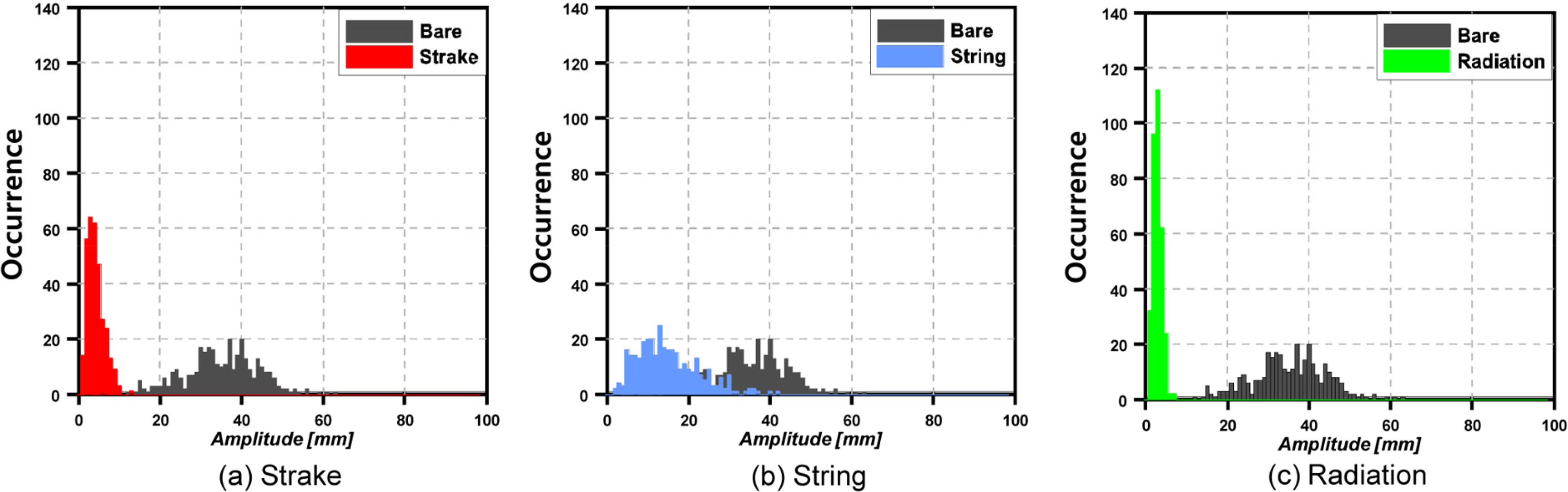
VIM 응답은 항상 일정한 크기의 진폭을 가진 운동이 아니기 때문에 다양한 크기의 진폭이 발생한다. 위의 3.1, 3.2, 3.3에 나타낸 결과들은 VIM 응답의 불규칙한 진폭을 표현하기에는 한계가 존재한다. 따라서 Fig. 7에는 Vr이 8.9인 유속에서 횡축을 In-line amplitude, 종축을 빈도로 한 도수분포표를 이용하여 저감성능을 비교하였다. Bare의 경우, 진폭의 크기가 20~50mm 범위에 형성되어 있었고, Fig. 8(a)를 살펴보면 Strake의 진폭은 0~10mm사이에서 발생하고 있다. Fig. 8(b)에서는 String의 진폭이 0~30mm 범위에서 관찰되었으며, 일정부분 Bare와 겹치는 부분이 발생한 것 또한 확인할 수 있다. 마지막으로 Fig. 8(c)의 Radiation은 Strake와 마찬가지로 0~10mm에서 진폭이 발생하는 것을 확인할 수 있었으며, Strake, String과는 달리 특정 진폭에서 빈도가 집중되어 있음을 알 수 있다.
Fig. 9에는 Fig. 8과 마찬가지로 Vr이 16.32인 유속에서 도수분포표를 이용하여 저감성능을 비교하였다. Fig. 9(a)에 의하면, Bare의 진폭은 0~30mm 범위에서 형성되었으며, Strake는 0~20mm사이의 진폭들이 발생하고 있음을 알 수 있다. 뿐만 아니라 Bare와 Strake의 진폭의 범위가 일정 부분 겹치는 것을 알 수 있다. 그리고 Fig. 9(b)에서는 String이 Bare와 진폭의 범위와 발생빈도가 상당 부분 일치하고 있어, 저감의 정도가 미미하다는 것을 알 수 있다. 끝으로 Fig. 9(c)에서의 Radiation은 0~10mm에서 진폭이 발생하고 있는 점으로 보아 전반적으로 Strake와 Radiation은 진폭의 범위와 빈도수를 바탕으로 저감성능을 파악할 수 있었다. 그리고 0~20mm사이의 범위를 가졌던 Strake에 비해 0~10mm 범위를 가지는 Radiation이 우수한 저감성능을 보여주고 있다고 판단된다. 뿐만 아니라 Radiation의 경우, Vr이 8.9에서 보여주었던 경향과 유사하게 특정 빈도수가 집중되어 있음을 확인할 수 있다.
3.5 Distribution table of Cross-flow amplitude
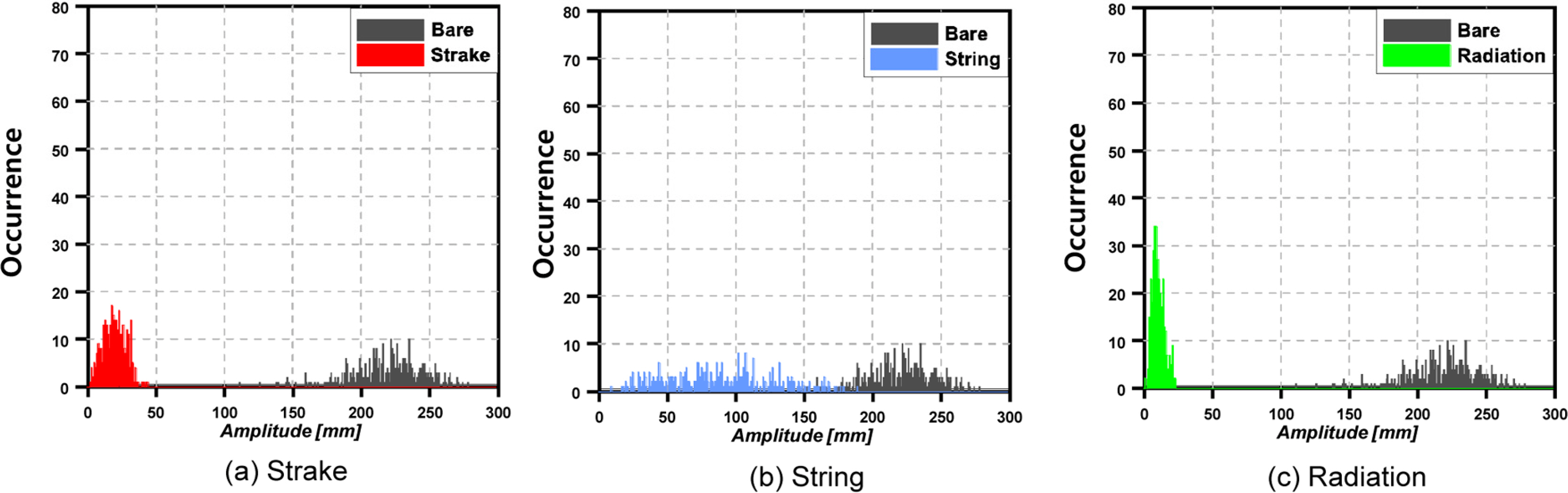
Fig. 10에는 Vr이 8.9인 유속에서 횡축을 Cross-flow amplitude, 종축을 빈도로 한 도수분포표를 이용하여 저감성능을 비교하였다. Bare는 약 170~270mm 사이의 진폭이 발생하였고, 이는 가장 큰 진폭과 가장 작은 진폭의 크기 차이가 100mm정도 발생하였음을 의미한다. Fig. 10(a)의 Strake는 0~50mm 범위에서 진폭이 발생함을 알 수 있다. 그리고 Fig. 10(b)에서 String은 0~170mm의 범위에서 고르게 빈도를 가지고 있음을 알 수 있다. Fig. 10(c)를 살펴보면 Radiation의 경우 0~25mm사이의 진폭이 발생함을 관찰할 수 있으며 In-line 응답의 경향과 마찬가지로 특정 진폭이 집중되어 발생하는 것을 확인할 수 있다. 따라서 Vr이 8.9에서 Strake, String, Radiation은 Cross-flow 응답 감소에 긍정적인 영향을 끼쳤으며, String보다 Strake와 Radiation이 저감성능이 우수하다는 것을 알 수 있다.
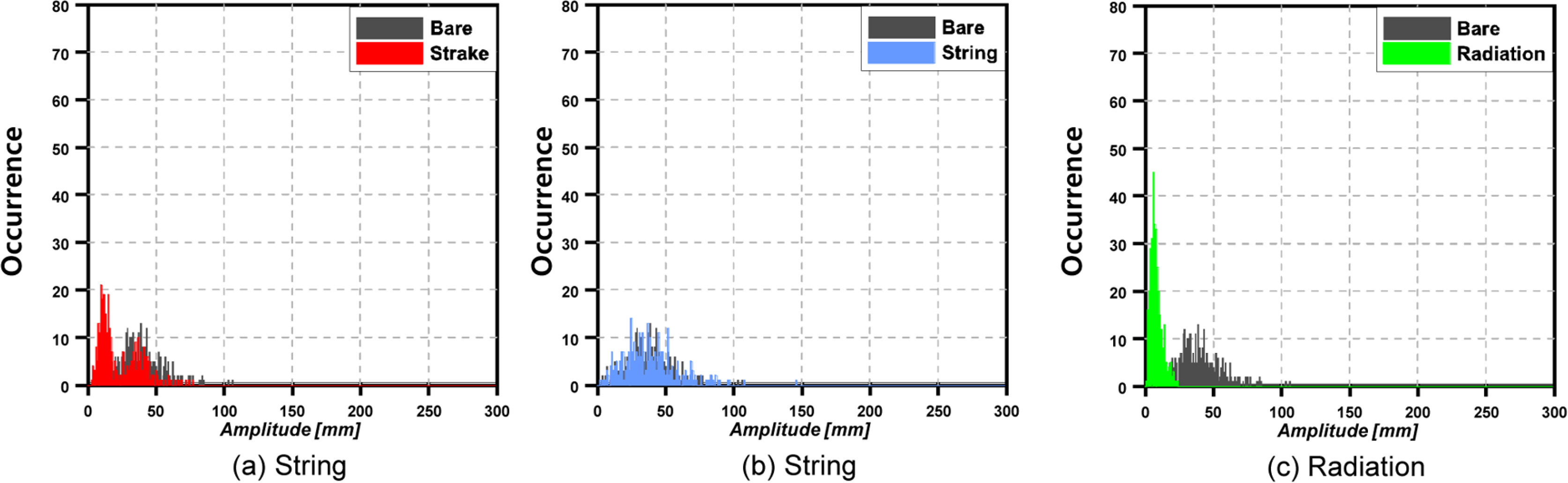
Fig. 11에는 Vr 이 16.32인 유속에서 도수분포표를 바탕으로 저감성능을 비교하였다. Bare는 약 0~70mm 범위에서 진폭이 형성되었다. Fig. 11(a)에 의하면, Strake 경우 진폭의 발생 범위는 0~70mm으로 Bare와 동일하였으나, 보다 낮은 진폭에서 높은 집중도를 가지고 있는 점으로 보아 미미하게 저감성능을 확인할 수 있었다 하지만 Fig. 11(b)의 String은 Bare의 진폭범위와 거의 동일한 범위가 관찰되어 저감성능을 관찰할 수가 없었다. 하지만 Fig. 11(c)의 Radiation을 살펴보면 0~25mm범위의 진폭이 발생하였으며, 마찬가지로 특정 진폭에서 높은 집중도를 보여주고 있다. 따라서 Vr이 8.9에서와 마찬가지로 Vr이 16.32에서 또한 Strake와 String보다 Radiation이 저감성능이 우수하다는 것을 알 수 있다.
4. 결 론
본 논문에서는 모형 실험을 통한 원형실린더 형상 구조물에 작용하는 VIM 응답의 저감에 관한 연구를 진행하였다. 모형 실험모델은 Bare, Strake, String, Radiation로 선정하였고, 동일한 실험조건에서 VIM 응답의 Average amplitude, Response, Distribution table을 활용하여 실험결과를 나타내었고 최종적으로 아래와 같은 결론을 얻을 수 있다.
(1) 저감장치를 부착한 모델에서도 특정 유속에서 8자 운동이 관찰되었으나 Bare보다 운동 응답의 크기가 작음을 확인할 수 있다.
(2) 진폭의 도수분포표를 바탕으로 Radiation의 VIM 응답은 특정 진폭에서 높은 집중도를 보이고 있다. 이는 원형실린더 형상 구조물을 설계 시, 원형실린더 형상 구조물의 간섭에 관련하여 중요한 요인으로 고려될 수 있을 것이라 판단된다.
(3) Strake 모델은 Vr가 4.45과 5.93인 구간에서는 응답의 크기가 작음을 볼 수 있었다. 그러나 Vr이 7.42 이상인 유속 범위부터 17.8까지 유속이 증가할수록 저감효과를 관찰할 수 있었다. 반해 Radiation의 경우 Vr이 4.45와 5.93에서는 Strake에 비해 상대적으로 응답의 크기가 큰 것을 알 수 있었지만 Vr이 증가할수록 뚜렷한 저감효과를 관찰할 수 있다.
(4) Strake는 곡가공 공정과 부착 시 용접 기술이 필요하지만, Radiation의 경우 String을 상하단부에 고정하기 위한 Winch 혹은 고정장치만 필요하다는 점에서 Strake 단점을 보완함과 동시에 우수한 VIM 저감성능을 가진 기술이라 판단된다.
Acknowledgements
본 연구는 한국해양대학교 LINC+사업단의 지원으로 수행된 연구결과 중 일부임을 밝히며, 연구비 지원에 감사드립니다.