1. Вёю вАа
Ж│аВё▒віЦ В╗┤ьЊеьё░ВЮў ВДђВєЇВаЂВЮИ Вё▒віЦ ьќЦВЃЂЖ│╝ вЇћвХѕВќ┤ Вёав░ЋВЮў ВюаВ▓┤ВЌГьЋЎ Вё▒віЦВЮё ВХћВаЋьЋўвіћвЇ░ ВъѕВќ┤Вёю CFD(Computational fluid dynamics)ВЌљ ЖИ░в░ўьЋю вІцВќЉьЋю ьћёвАюЖиИвъеВЮё ВЮ┤ВџЕьЋўвіћ Ж▓ЃВЮ┤ ьЋёВѕўВаЂВЮИ ВѓгьЋГВЮ┤ вљўВЌѕвІц. Жи╝въўВЌљвіћ ВєїВіц ВйћвЊюЖ░ђ Ж│хЖ░ювљю OpenFOAMВЮё ВЮ┤ВџЕьЋўвіћ ВЌ░ЖхгЖ░ђ ВЃѕвАюВџ┤ ВёаьЃЮВю╝вАю ВаюЖ│хвљўЖ│а ВъѕвІц. OpenFOAMьћёвАюЖиИвъеВЮђ ANSYS: Fluent, Star-CCM+ вЊ▒ вїђЖиювфе ВЃЂВЌЁВџЕ ьћёвАюЖиИвъеЖ│╝ вДѕВ░гЖ░ђВДђвАю ВюаьЋюВ▓┤ВаЂв▓Ћ(Finite volume method, FVM)ВЌљ ЖИ░в░ўьЋю ьјИв»ИвХёв░ЕВаЋВІЮ ВѕўВ╣ўьЋ┤ВёЮ ьћёвАюЖиИвъеВЮ┤ВДђвДї ВѓгВџЕВъљЖ░ђ ьі╣ВаЋьЋю ьЋ┤ВёЮЖИ░вЦ╝ ВХћЖ░ђвАю ВаЋВЮўьЋа Вѕў ВъѕвЈёвАЮ ьЋўВЌг Вёав░ЋВЮў ВюаВ▓┤ВЌГьЋЎ Вё▒віЦВХћВаЋВЌљВЮў ВаЂВџЕВЮ┤ ьЎЋвїђвљўЖ│а Въѕвіћ ВХћВёИВЮ┤вІц.
Вёав░ЋВЮў ВюаВ▓┤ВЌГьЋЎВаЂ Вё▒віЦ ВХћВаЋВЌљ ВаёВѓ░ВюаВ▓┤ВЌГьЋЎВЮё ВаЂВџЕьЋю Жи╝въўВЮў ВЌ░ЖхгвАю, Mousavirrad et al.(2015)ВЮђ CFDSHIP-IOWA ьћёвАюЖиИвъеВЮё ьєхьЋўВЌг Fridsma ВёаьўЋВЌљ вїђьЋю ВађьЋГВё▒віЦЖ│╝ Вџ┤вЈЎВё▒віЦВЮё ВХћВаЋьЋўВўђвІц. Islam and Soares(2017)віћ Ropax ВёаьўЋВЌљ вїђьЋю ьїївъЉ ВцЉ ВађьЋГВё▒віЦВЮё ВХћВаЋьЋўВўђЖ│а Go et al.(2016)ВЮђ ВѕўВцЉ ВўѕВЮИВ▓┤ВЌљ вїђьЋўВЌг 6 ВъљВюавЈё Вџ┤вЈЎВЮё ВХћВаЋьЋўВўђвІц. ЖиИвдгЖ│а Bustos and Alvarado(2017)ВЮђ ВїЇвЈЎВёаВЌљ вїђьЋўВЌг ВађьЋГВё▒віЦ ВХћВаЋ ВЌ░ЖхгвЦ╝ ьЋўВўђВДђвДї ьЋГВБ╝ВъљВёИВЌљ вїђьЋю ВЌ░Жхгвіћ ВѕўьќЅьЋўВДђ ВЋіВЋўвІц. ВєїьўЋ Ж│аВєЇВёаВЮў Вџ┤вЈЎВё▒віЦЖ│╝ Ж┤ђваеьЋўВЌг Hassan et al.(2015)ВЮђ вІеВЮ┤ Въѕвіћ ьЎюВБ╝Вёа(Stepped planing hull)ВЌљ вїђьЋўВЌг ВЮ┤вАа в░Ј CFD ьЋ┤ВёЮВЮё ьєхьЋўВЌг ьіИвд╝ в░Ј ВађьЋГВё▒віЦВЮё ВХћВаЋьЋўВўђвІц. Cucinotta and Sfravara(2018)віћ CFD ьЋ┤ВёЮЖ│╝ вфеьўЋВІюьЌўВЮё ьєхьЋўВЌг Ж│аВєЇВёав░ЋВЌљ вїђьЋю ВађьЋГВё▒віЦВЮё ВЌ░ЖхгьЋўВўђВю╝вЕ░ Ж▓ЕВъљЖ│ёВЮў вЈЎВаЂ в│ђьўЋВЌљ вїђьЋўВЌгвіћ ВцЉВ▓ЕЖ▓ЕВъљв░Ев▓Ћ(Overset mesh method)ВЮё ВѓгВџЕьЋўВўђвІц.
ВхюЖи╝ВЌљвіћ Вёав░ЋВЮў ВюаВ▓┤ВЌГьЋЎВаЂ Вё▒віЦ ьЋ┤ВёЮВЌљ Ж│аЖ░ђВЮў вїђЖиювфе ВЃЂВЌЁВџЕ CFD ьћёвАюЖиИвъеВЮё ВѓгВџЕьЋўвіћ Ж▓Ѓ в│┤вІцвіћ ВєїВіцЖ░ђ Ж│хЖ░ювљўВќ┤ ВъѕВќ┤ Ж▓йВаюВаЂВЮ┤вЕ░ ВѓгВџЕВъљЖ░ђ вфЕВаЂВЌљ вДъЖ▓ї ьі╣ВаЋьЋю ьЋ┤ВёЮЖИ░вЊцВЮё ВХћЖ░ђвАю ВаЋВЮўьЋа Вѕў Въѕвіћ OpenFOAMВЮё ВЮ┤ВџЕьЋўвіћ ВЌ░ЖхгЖ░ђ ьЎюв░юьЋўЖ▓ї ВДёьќЅвљўЖ│а ВъѕвІц.
в│И ВЌ░ЖхгВЌљВёювіћ ВўцьћѕВєїВіц CFD ьћёвАюЖиИвъеВЮИ OpenFOAM(OpenCFD Ltd., 2017)ВЮё ВЮ┤ВџЕьЋўВЌг ВБ╝ьўЋВ▓┤ ьЎюВБ╝ВёаВЮИ Fridsma ВёаьўЋ(Fridsma, 1969)ВЌљ вїђьЋўВЌг ВаЋВѕў ВцЉВЌљ ВађьЋГВё▒віЦЖ│╝ ьіИвд╝ в░Ј вХђВЃЂвЪЅ вЊ▒ ьЋГВБ╝ВъљВёИвЦ╝ ВХћВаЋьЋўВўђвІц. ьі╣ьъѕ, ьЎюВБ╝ВёаВЮ┤ Ж│аВєЇВю╝вАю ьЎюВБ╝ьЋа вЋї в░юВЃЮьЋўвіћ ьЋГВБ╝ВъљВёИВЮў ьЂ░ в│ђьЎћВЎђ ВЌ░Ж┤ђвљю ВюаВ▓┤ВЌГьЋЎВаЂ ьўёВЃЂВЮў ВаЋвЈё вєњВЮђ ВХћВаЋВЮё ВюёьЋўВЌг вЈЎВаЂВцЉВ▓ЕЖ▓ЕВъљ ьЋ┤ВёЮЖИ░ВЮИ РђўoverInterDyMFoamРђЎВЮё ВѓгВџЕьЋўВўђвІц. вўљьЋю, в│ИЖ▓ЕВаЂВЮИ CFD ьЋ┤ВёЮВЌљ ВЋъВёю ьЎюВБ╝ВЃЂьЃюВЮў ВёаВєЇВЮИ Fn=1.19ВЌљ вїђьЋўВЌг Ж▓ЕВъљ ьЂгЖИ░ВЎђ Ж│ёВѓ░ ВІюЖ░ё Ж░ёЖ▓Е в│ђьЎћВЌљ вћ░вЦИ вХѕьЎЋВІцВё▒ ьЋ┤ВёЮВЮё ВѕўьќЅьЋўВўђвІц.
вДѕВДђвДЅВю╝вАю OpenFOAMВЮё ВЮ┤ВџЕьЋю в│И ВЌ░ЖхгЖ▓░Ж│╝вЦ╝ FridsmaВЮў ВІцьЌў Ж▓░Ж│╝, ьЃђ CFD ьЋ┤ВёЮ Ж▓░Ж│╝ в░Ј Savitsky Ж▓йьЌўВІЮ(Savitsky, 1964)Ж│╝ВЮў в╣ёЖхљвЦ╝ ьєхьЋўВЌг вХёВёЮьЋўЖ│а ВаЂВџЕ Ж░ђвіЦВё▒ВЮё Ж▓ђВдЮьЋўВўђвІц.
2. ВѕўВ╣ўьЋ┤ВёЮ в░Ев▓Ћ
2.1 OpenFOAMВЮў ЖхгВё▒
OpenFOAMВЮђ ВюаьЋюВ▓┤ВаЂв▓ЋВЮё ЖИ░в░ўВю╝вАю ьЋўвіћ ВўцьћѕВєїВіц ьјИв»ИвХёв░ЕВаЋВІЮ ВѕўВ╣ўьЋ┤ВёЮ ьћёвАюЖиИвъеВЮ┤вІц. OpenFOAMВЮў ЖхгВё▒ВЮђ ьЎћьЋЎ, вѓювЦўВюавЈЎ, ВЌ┤ВЌљвёѕВДђ в░Ј ЖхгВА░ВЌГьЋЎ вЊ▒ Ж┤Љв▓ћВюёьЋю Ж│хьЋЎвХёВЋ╝ВЌљ ВаЂВџЕвљўвіћ вІцВќЉьЋю ьЋ┤ВёЮЖИ░(Solver)вЊцЖ│╝ ВаёьЏёВ▓ўвдг ьѕ┤(Pre-processing & Post-processing tool)ВЮё ьЈгьЋеьЋўЖ│а ВъѕВю╝вЕ░ ьЋ┤ВёЮвфЕВаЂВЌљ вћ░вЮ╝Вёю вІцВѕўВЮў ьЋ┤ВёЮЖИ░вЊцВЮё Ж▓░ьЋЕьЋеВЌљ ВЮўьЋўВЌг ВЏљьЋўвіћ ВѕўВ╣ўьЋ┤ВёЮ ьћёвАюЖиИвъеВЮё ЖхгВё▒ьЋа Вѕў ВъѕвІц.
ьєхВЃЂВаЂВю╝вАю CFD ьћёвАюЖиИвъеВЮђ ВаёВ▓ўвдг, CFD ьЋ┤ВёЮ в░Ј ьЏёВ▓ўвдгВЮў 3Ж░ђВДђ ВаѕВ░еЖ░ђ ВѕюВ░еВаЂВю╝вАю ВДёьќЅвљўвѓў OpenFOAMВЮђ UserРђЎs interfaceЖ░ђ ВЌєВю╝в»ђвАю вфевЊа вІеЖ│ёВЌљВёю Fig. 1ВЌљ в│┤віћ в░ћВЎђ Ж░ЎВЮ┤ Ж▓йЖ│ёВА░Ж▒┤ВЮ┤ ВаЋВЮўвљю Рђў0РђЎ ьїїВЮ╝, Ж▓ЕВъљВЎђ вѓювЦўвфевЇИ вЊ▒ВЮ┤ ВаЋВЮўвљю РђўconstantРђЎ ьїїВЮ╝ в░Ј ВІюЖ░ёВаюВќ┤, ВЮ┤Вѓ░ьЎћВ▓ўвдгв░Ев▓Ћ вЊ▒ВЮ┤ ВаЋВЮўвљю РђўsystemРђЎ ьїїВЮ╝вАю ЖхгВё▒вљювІц. ЖиИвдгЖ│а OpenFOAMВЌљВёю ВаюЖ│хвљўвіћ Ж▓ЕВъљв│ђьЎў ьѕ┤ВЮё ВЮ┤ВџЕьЋўВЌг Fluent, Star-CCM+ в░Ј GAMBIT вЊ▒ВЌљВёю ВЃЮВё▒вљю Ж▓ЕВъљЖ│ёвЦ╝ ВЮйВќ┤ вЊцВЮ╝ Вѕў ВъѕвІц.
2.2 CFD ьЋ┤ВёЮЖИ░
OpenFOAMВЮё ВЮ┤ВџЕьЋю ВюавЈЎьЋ┤ВёЮВЌљВёюВЮў ВДђв░░в░ЕВаЋВІЮВЮђ ВЋёвъўВЮў ВЌ░ВєЇв░ЕВаЋВІЮЖ│╝ RANS(Reynolds averaged navier stokes)в░ЕВаЋВІЮВю╝вАю ЖхгВё▒вљювІц.
ВЌгЖИ░Вёю Uвіћ ВєЇвЈёВЮ┤вЕ░ ¤ЂВЎђ Sвіћ Ж░ЂЖ░Ђ в░ђвЈё в░Ј ВєїВіцьЋГВю╝вАю ВаЋВЮўвљювІц.
ВъљВюаВѕўвЕ┤ в│ђьўЋ ьЋ┤ВёЮВЌљвіћ ВІЮ (3)ВЮў VOF(Volume of fraction)в▓ЋВЮё ВѓгВџЕьЋўВўђвІц.
ВЌгЖИ░Вёю ╬▒(air : ╬▒=0, water : ╬▒=1)віћ VOFВЮ┤вІц.
ВюавЈЎВъЦВЮў ВЋЋваЦЖ│╝ ВєЇвЈё ВЌ░Вё▒ьЋ┤ВёЮВЌљвіћ PISO(Pressure-implicit with splitting of operators)в░Ев▓ЋВЮ┤ ВѓгВџЕвљювІц. ВІЮ (2)ВЌљ вїђьЋю ВЮ┤Вѓ░ьЎћ Ж│╝ВаЋВЮё ьєхьЋўВЌг вІцВЮїВЮў ВІЮВЮ┤ ВюавЈёвљювІц.
ВЌгЖИ░Вёю Apвіћ вїђВѕўв░ЕВаЋВІЮ вДцьіИвдГВіцВЮў вїђЖ░Ђ(Diagonal) ВџћВєїВЮ┤Ж│а H(U), pd в░Ј Sвіћ Ж░ЂЖ░Ђ в╣ёвїђЖ░Ђ(Off-diagonal) ВџћВєї, вЈЎВЋЋваЦ в░Ј ВєїВіцьЋГВЮ┤вІц. вїђВѕўв░ЕВаЋВІЮ ьЋ┤ВёЮЖИ░вЦ╝ ьєхьЋўВЌг Вѓ░ВХюьЋю ВєЇвЈё ВўѕВИАЖ░њ U*вЦ╝ вІцВІю ВІЮ (4)ВЌљ вїђВъЁьЋўЖ│а ВІЮ (5)ВЎђ ВІЮ (6)ВЮў Ж│╝ВаЋВЮё Ж▒░В│љ ВЋЋваЦ ьЈгВЋёВєА в░ЕВаЋВІЮВЮИ ВІЮ (7)ВЮё Вќ╗віћвІц.
2.3 вЈЎВаЂЖ▓ЕВъљЖ│ё(Dynamic mesh)
OpenFOAMВЌљВёю ВѓгВџЕвљўвіћ вЈЎВаЂЖ▓ЕВъљв░Ев▓ЋВЮђ ьЂгЖ▓ї Ж▓ЕВъљв│ђьўЋв░Ев▓Ћ(Mesh deformation method)Ж│╝ ВцЉВ▓ЕЖ▓ЕВъљв░Ев▓Ћ вЊ▒ 2Ж░ђВДђ в░Ев▓ЋВЮ┤ ВъѕвІц.
Ж▓ЕВъљв│ђьўЋв░Ев▓ЋВЮђ Fig. 2В▓ўвЪ╝ Ж▓ЕВъљВЮў в│ђьўЋ Ж│╝ВаЋ ВцЉВЌљ ВаёВ▓┤ Ж▓ЕВъљВѕўЖ░ђ ВюаВДђвљўвЕ░, ВЋЋваЦ-ВєЇвЈё Ж▓░ьЋЕв▓ЋВЮё ьєхьЋўВЌг Ж▓ЕВъљВЮў вЁИвЊю(Node)вЦ╝ ВЮ┤вЈЎВІюьѓцвіћ в░Ев▓ЋВЮ┤вІц. ьЋўВДђвДї Ж│аВєЇ ьЎюВБ╝ВёаВЮў Ж▓йВџ░В▓ўвЪ╝ ВёаВєЇВЌљ вћ░вЮ╝Вёю ьЮўВѕўВЮў в│ђьЎћЖ░ђ ьЂ░ Вёав░ЋВЮђ ВаЋВѕў ВцЉ ВађьЋГ в░Ј ьЋГВБ╝ВъљВёИ ВѕўВ╣ўьЋ┤ВёЮ ВІю вЁИвЊюВЮў ВЮ┤вЈЎЖ▒░вдгЖ░ђ В╗цВДљВЌљ вћ░вЮ╝ ВѕўВ╣ўьЋ┤ВёЮ ВўцВ░еЖ░ђ В╗цВДђЖ▓ї вљўвЕ░, ВІгВДђВќ┤ вХђьћ╝Ж░ђ ВЮїВѕўЖ░ђ вљўвіћ Ж▓ЕВъљЖ░ђ в░юВЃЮьЋўВЌг ВѕўВ╣ў ьЋ┤ВёЮ Ж▓░Ж│╝Ж░ђ в░юВѓ░ьЋўЖ▓ї вљювІц.
ВцЉВ▓ЕЖ▓ЕВъљв░Ев▓ЋВЮђ Fig. 3В▓ўвЪ╝ в░░Ж▓йЖ▓ЕВъљ ВўЂВЌГЖ│╝ Вџ┤вЈЎЖ▓ЕВъљ ВўЂВЌГВЮ┤ вћ░вАю ВъѕВќ┤Вёю ВѕўВ╣ўьЋ┤ВёЮ ВІюВЌљ ВцЉВ▓Евљўвіћ Ж▓йЖ│ёВўЂВЌГвДї Ж│авацьЋўвЕ┤ вљўЖ│а Ж▓ЕВъљВЮў в│ђьўЋВЮ┤ в░юВЃЮьЋўВДђ ВЋіВю╝в»ђвАю Ж▓ЕВъљв│ђьўЋВю╝вАю ВЮИьЋўВЌг ВЋ╝ЖИ░вљўвіћ ВўцВ░еВЮў в░юВЃЮВЮё ВцёВЮ╝ Вѕў ВъѕвІц. ЖиИвдгЖ│а ВцЉВ▓ЕЖ▓ЕВъљвіћ в░░Ж▓йЖ▓ЕВъљ ВўЂВЌГЖ│╝ Вџ┤вЈЎЖ▓ЕВъљ ВўЂВЌГВЌљ в│ёвЈёВЮў Ж▓ЕВъљЖ│ёвЦ╝ ЖхгВё▒ьЋю ьЏёВЌљ Вџ┤вЈЎВўЂВЌГ Ж▓ЕВъљЖ│ёвЦ╝ в░░Ж▓йВўЂВЌГ Ж▓ЕВъљЖ│ёВЌљ ВѓйВъЁьЋўЖ│а DCI(Domain connectivity information)в░Ев▓ЋВЮё ьєхьЋўВЌг Ж░ЂЖ░ЂВЮў Ж▓ЕВъљЖ│ёВЌљ ьЈгьЋевљю ВюавЈЎВъЦ ВаЋв│┤Ж░ђ вѓ┤Вѓйв▓ЋВЌљ ВЮўьЋўВЌг ВаёвІгВЮ┤ вљўвЈёвАЮ ьЋювІц. ВюавЈЎВъЦ ВаЋв│┤Ж░ђ ВаёвІгвљўвіћ Ж│╝ВаЋВЮђ вІцВЮїЖ│╝ Ж░ЎвІц.
ВѓйВъЁвљўвіћ Вџ┤вЈЎВўЂВЌГ Ж▓ЕВъљЖ│ёВЌљВёю РђўcellTypeРђЎ ьЉюВІЮВЮё ьєхьЋўВЌг ВЋёвъўВЎђ Ж░ЎВЮ┤ 0ВЌљВёю 2Ж╣їВДђ Ж▓ЕВъљВЮў ВюаьўЋВЮё ВДђВаЋьЋювІц.
0 РђЊ calculated cell
1 РђЊ interpolated cell
2 РђЊ hole/inactive cell
ВюаьўЋ Рђў2РђЎвАю ВДђВаЋвљю Ж▓ЕВъљВЌљ вїђьЋўВЌгвіћ Cutting hole В▓ўвдгвЦ╝ ьЋўВЌг ВаюЖ▒░ьЋўвЕ░ вѓеВЮђ Ж▓ЕВъљ, ВдЅ ВюаьўЋ Рђў1РђЎвАю ВДђВаЋвљю Ж▓ЕВъљВЌљ вїђьЋўВЌгвіћ вѓ┤ Вѓйв▓ЋВЮё ьєхьЋўВЌг ВюавЈЎВъЦ ВаЋв│┤вЦ╝ ВюаьўЋ Рђў0РђЎ Ж▓ЕВъљВЎђ ВЃЂьўИ ЖхљьЎўьЋювІц.
ВюавЈЎВъЦ ВаЋв│┤ВЮў вѓ┤ВѓйВЮё ВюёьЋўВЌг OpenFOAMВЌљВёю ВѓгВџЕьЋўвіћ в░Ев▓ЋВЌљвіћ InverseDistance, TrackingInverseDistance, CellVolumeWeight в░Ј LeastSquares вЊ▒ 4Ж░ђВДђ в░Ев▓ЋВЮ┤ ВъѕВю╝вЕ░ в│И ВЌ░ЖхгВЌљВёювіћ Inverse Distance в░Ев▓ЋВЮё ВѓгВџЕьЋўВўђвІц.
2.4 вѓювЦў вфевЇИ
OpenFOAMВЌљвіћ вІцВќЉьЋю вѓювЦў вфевЇИВЮё ВаюЖ│хвљўвЕ░, в│И ВЌ░ЖхгВЌљВёювіћ SST k-¤Ѕ вфевЇИВЮё ВѓгВџЕьЋўВўђвІц. SST k-¤Ѕ вѓювЦў вфевЇИВЮђ Wilcox k-¤Ѕ вфевЇИЖ│╝ k-Рѕѕ вфевЇИВЮё Ж▓░ьЋЕьЋю ьЋўВЮ┤вИївдгвЊю вфевЇИвАю ВѕўВєАв░ЕВаЋВІЮВЮў ьўЋьЃювіћ ВІЮ (8)Ж│╝ Ж░ЎвІц.
(8)
ВЌгЖИ░Вёю kвіћ вѓювЦў ВЌљвёѕВДђ, ¤Ѕвіћ вѓювЦў ВЌљвёѕВДђ ВєїВѓ░ в╣ёВюе, G ┬»
ВЌгЖИ░Вёю ¤Ћ1 ВЎђ ¤Ћ2віћ Ж░ЂЖ░Ђ k-¤Ѕв░ЕВаЋВІЮЖ│╝ k-Рѕѕ в░ЕВаЋВІЮВЮў Ж│ёВѕўВЮ┤вІц.
ВёаВ▓┤ьЉювЕ┤ Ж▓йЖ│ёВИхВЌљвіћ в▓й ьЋеВѕўвЦ╝ ВѓгВџЕьЋўВўђВю╝вЕ░ y+ВЮў ьЂгЖИ░вЦ╝ 30~100Вю╝вАю ВюаВДђьЋўВўђвІц.
2.5 ьЋГВБ╝ ВъљВёИ
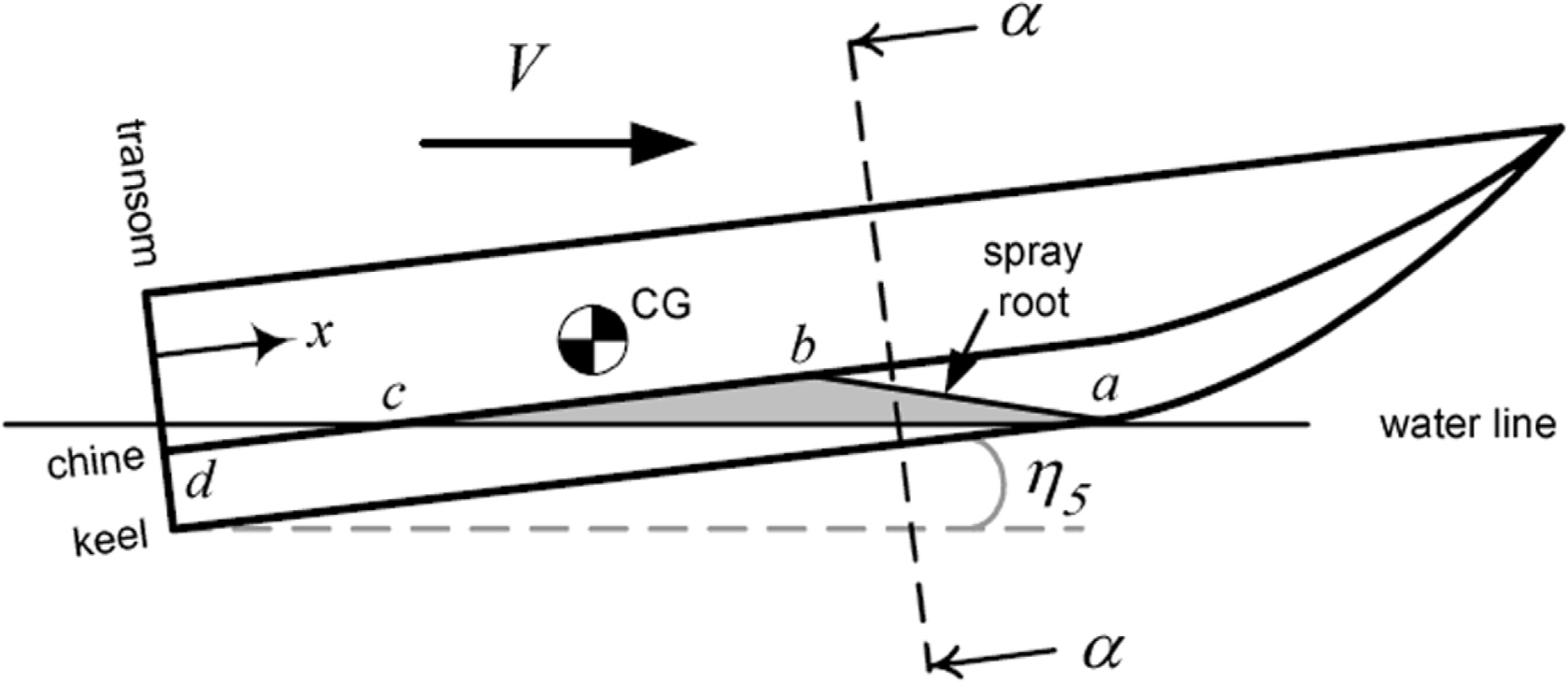
ьЋГВБ╝ ВІюВЌљ ьЮўВѕўВЌљ ьЂ░ в│ђьЎћЖ░ђ ВЌєвіћ в░░ВѕўвЪЅьўЋВёаЖ│╝віћ вІгвдг Ж│аВєЇьЎюВБ╝ВёаВЮђ ВёаьўЋВЮў ьі╣Вё▒ ВЃЂ ВєЇвЈёЖ░ђ ВдЮЖ░ђьЋеВЌљ вћ░вЮ╝ ВѕўВДЂ в░ЕьќЦВЮў ВќЉваЦВЮ┤ в░юВЃЮьЋўВЌг Fig. 4ВЌљ в│┤ВЮ┤віћ в░ћВЎђ Ж░ЎВЮ┤ ьіИвд╝(Trim)Ж│╝ вХђВЃЂвЪЅ(Sinkage)ВЮ┤ в░юВЃЮьЋўВЌг ВєЇвЈёВЌљ вћ░вЮ╝ ьЋГВБ╝ ВъљВёИЖ░ђ ьЂгЖ▓ї в│ђьЎћьЋювІц.
OpenFOAMВЌљВёювіћ '6DOFSolver' ьЋ┤ВёЮЖИ░вЦ╝ ВЮ┤ВџЕьЋўВЌг ьіИвд╝ в░Ј вХђВЃЂвЪЅ вЊ▒ ВёаВ▓┤ ьЋГВБ╝ВъљВёИвЦ╝ ВХћВаЋьЋўвіћвЇ░ ЖИ░в│Ив░ЕВаЋВІЮВЮђ ВІЮ (11)Ж│╝ ВІЮ (12)ВЮў Ж░ЋВ▓┤Вџ┤вЈЎв░ЕВаЋВІЮ(вЅ┤ьё┤ Ваю2в▓ЋВ╣Ў)ВЮ┤вІц.
ВЌгЖИ░Вёю aвіћ ВёаьўЋЖ░ђВєЇвЈёВЮ┤Ж│а ╬▒віћ Ж░ЂЖ░ђВєЇвЈёВЮ┤вІц. вДц ВІюЖ░ё ВІЮ (13)Ж│╝ ВІЮ (14)ВЌљ ВЮўьЋўВЌг Ж│ёВѓ░вљю Ж░ђВєЇвЈё aВЎђ Ж░ЂЖ░ђВєЇвЈё ╬▒вЦ╝ ВЮ┤ВџЕ Newmark в░Ев▓Ћ(Newmark, 1959)ВЮё ВѓгВџЕьЋўВЌг ВІюЖ░ё ВаЂвХёьЋўВЌг ВЃѕвАюВџ┤ ВєЇвЈё vnewВЎђ Ж░ЂВєЇвЈё ¤ЅnewвЦ╝ Ж│ёВѓ░ьЋўвЕ░ ВєЇвЈёЖ▓░Ж│╝вЦ╝ Ж▓ЕВъљвЁИвЊюВЌљ ВаЂВџЕьЋўВЌг Ж▓ЕВъљв│ђьўЋВЮё ВІцьўёьЋўвЕ░, ВёаВ▓┤ВЮў ьіИвд╝Ж│╝ вХђВЃЂвЪЅВЮё ВХћВаЋьЋювІц.
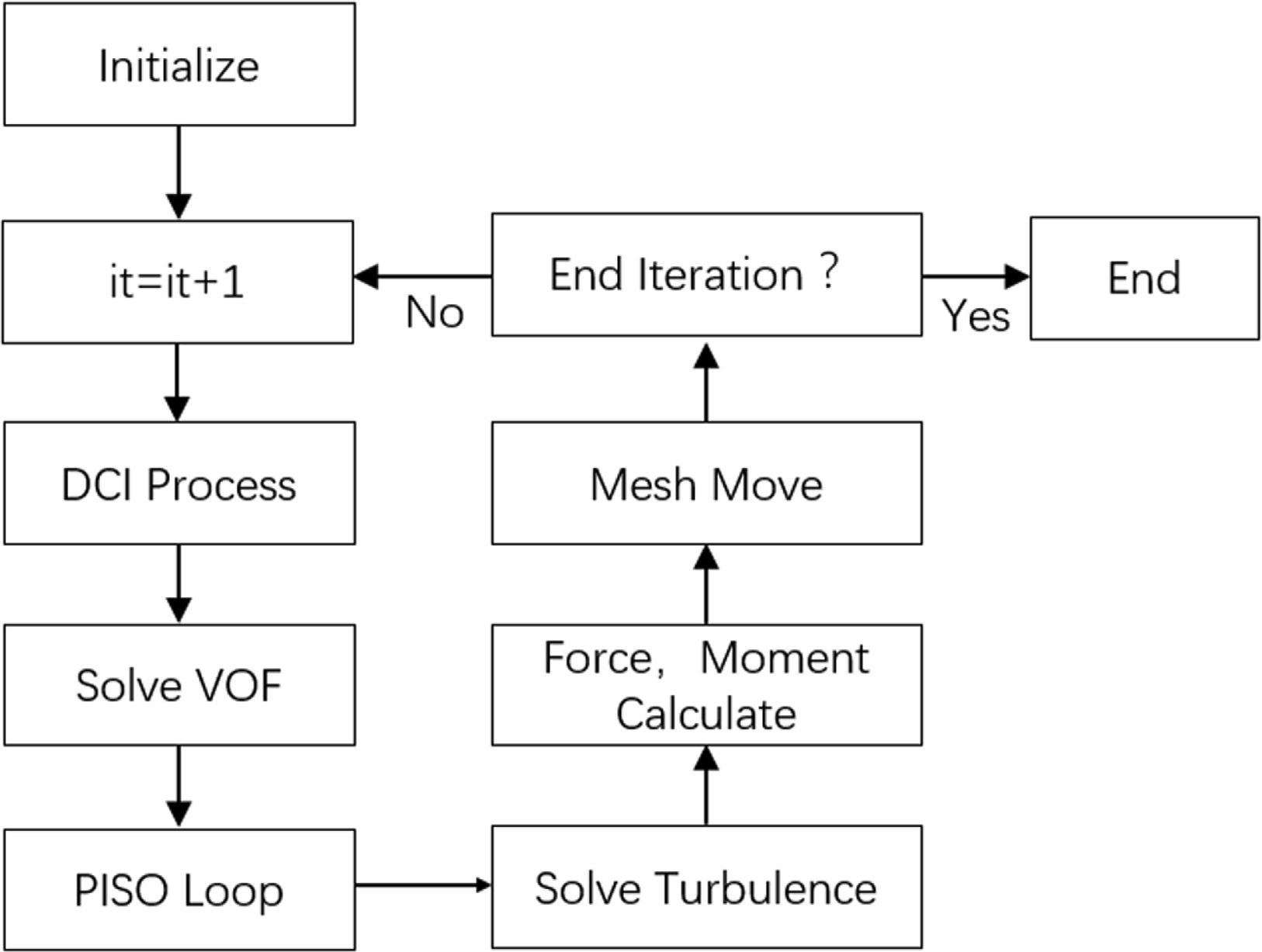
OpenFOAMВЌљВёю ВцЉВ▓ЕЖ▓ЕВъљв░Ев▓ЋВЮё ВЮ┤ВџЕьЋю ВюавЈЎВъЦ в░Ј ьЋГВБ╝ВъљВёИ(ВёаВ▓┤Вџ┤вЈЎ) ьЋ┤ВёЮ Ж│╝ВаЋВЮё Fig. 5ВЌљ Ж░ёвІеьъѕ вЈёВІюьЋўВўђвІц.
3. ВѕўВ╣ўьЋ┤ВёЮ Ж▓░Ж│╝
3.1 Fridsma ьЎюВБ╝Вёа в░Ј ВаёВ▓ўвдг
в│И ВЌ░ЖхгВЌљ ВѓгВџЕвљю ьЎюВБ╝ВёаВЮђ Fridsma(1969)ВЌљ ВЮўьЋ┤ В▓┤Ж│ёВаЂВЮИ вфеьўЋВІюьЌўВЮ┤ ВѕўьќЅвљю ВБ╝ьўЋВ▓┤ ьЎюВБ╝ВёаВю╝вАю Fig. 6ВЌљ L/BЖ░ђ 4ВЮИ ВёаьўЋВЮў ВёавЈё(Lines)вЦ╝ в│┤ВЌгВБ╝Ж│а ВъѕвІц. ВБ╝ВџћвфЕВЮђ Table 1Ж│╝ Ж░ЎвІц.
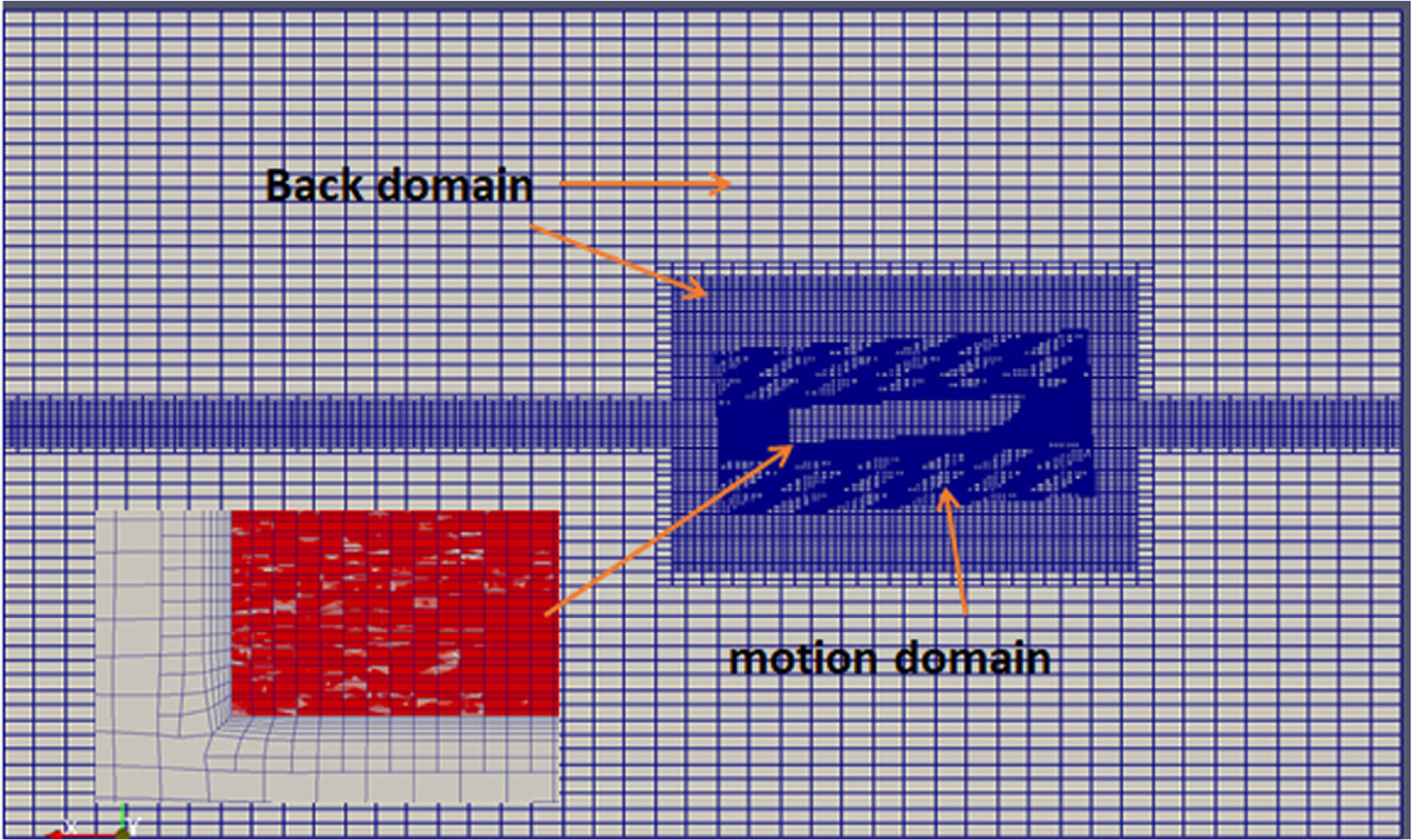
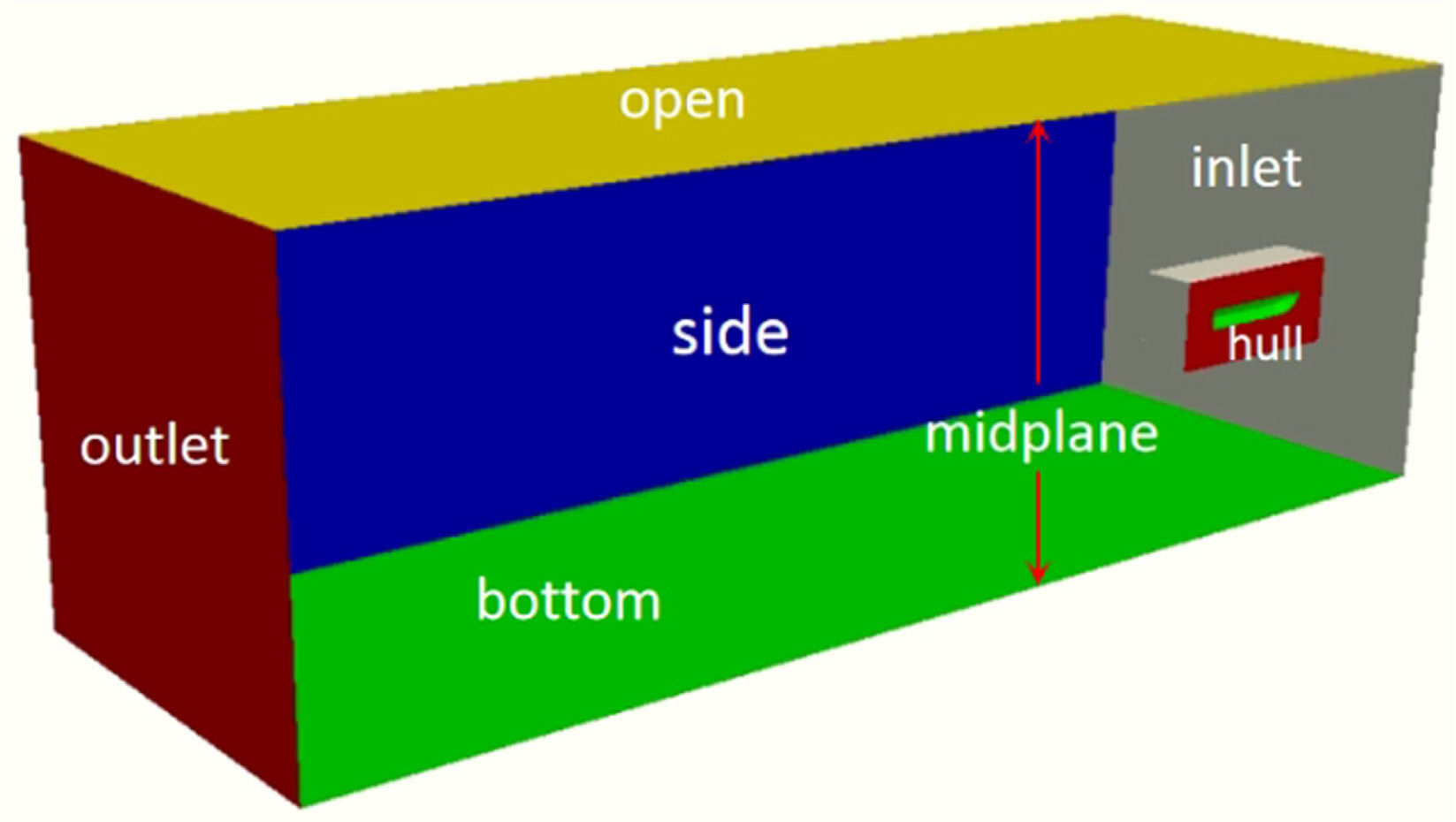
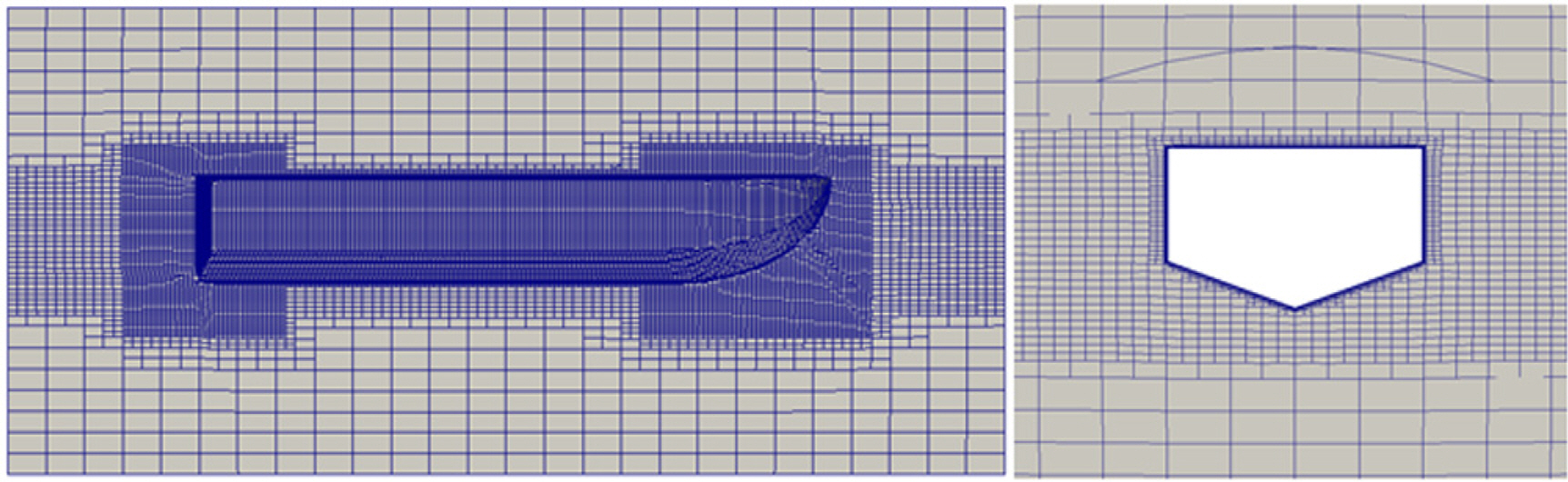
ВаёВ▓┤ ВѕўВ╣ўьЋ┤ВёЮ ВўЂВЌГВЮђ ЖИИВЮ┤ в░ЕьќЦВю╝вАю 8LвАю, ВъЁЖхгВЌљВёю ВёаВѕўЖ╣їВДђ 1L, Вёав»ИвХђьё░ ВХюЖхгЖ╣їВДђ 6LвАю ЖхгВё▒вљўВќ┤ ВъѕвІц. ВюавЈЎВъЦВЮў ьЈГВЮђ 2LвАю ВДђВаЋьЋўВўђвІц. вєњВЮ┤ в░ЕьќЦВю╝вАювіћ ВъљВюаВѕўвЕ┤ ьЋўвХђВЎђ ВЃЂвХђВЌљ Ж░ЂЖ░Ђ LВЮё в░░В╣ўьЋўВўђвІц. Вџ┤вЈЎЖ▓ЕВъљ ВўЂВЌГВЮў ьЂгЖИ░віћ xВХЋ в░ЕьќЦВю╝вАю 1.5L, yВХЋ в░ЕьќЦВю╝вАю 0.4L в░Ј zВХЋ в░ЕьќЦВю╝вАю 0.7LвАю ьЋўВўђвІц(Fig. 7).
Ж▓ЕВъљЖ│ёвіћ SnappyHexMesh ьѕ┤ВЮё ВѓгВџЕьЋўВЌг ВцЉВ▓ЕЖ▓ЕВъљ ВўЂВЌГВЮў Ж▓йЖ│ёвЕ┤ Жи╝В▓ўВЌљвіћ в░░Ж▓йЖ▓ЕВъљ ВўЂВЌГВЮў Ж▓ЕВъљ ьЂгЖИ░ВЎђ Вџ┤вЈЎЖ▓ЕВъљ ВўЂВЌГВЮў Ж▓ЕВъљ ьЂгЖИ░вЦ╝ вЈЎВЮ╝ьЋўЖ▓ї ВЃЮВё▒ьЋўВЌг ВюавЈЎВъЦ ВаЋв│┤ ЖхљьЎў ВІю в░юВЃЮьЋа Вѕў Въѕвіћ ВўцВ░евЦ╝ ВхюВєїьЎћьЋўВўђвІц. ЖиИвдгЖ│а ВюаВєЇЖ│╝ ВЋЋваЦВЮў в│ђьЎћЖ░ђ ьЂ┤ Ж▓ЃВю╝вАю ВўѕВЃЂвљўвіћ ВёаВѕўВЎђ Вёав»И вХђвХёВЌљвіћ Fig. 8Ж│╝ Ж░ЎВЮ┤ ЖхГвХђ ВёИвХёьЋа(Local refinement) ЖИ░віЦВЮё ВЮ┤ВџЕьЋўВЌг ВаЋв░ђьЋю Ж▓ЕВъљвЦ╝ ВЃЮВё▒ьЋўВўђвІц. Fig. 9віћ ВцЉВ▓ЕЖ▓ЕВъљВЮў ЖхгВё▒ВЮё в│┤ВЌгВБ╝Ж│а ВъѕвІц.
ВѕўВ╣ўьЋ┤ВёЮВЌљ ВѓгВџЕвљю Ж░Ђ в│ђВѕўвЊцВЌљ вїђьЋю Ж▓йЖ│ёВА░Ж▒┤ВЮђ Table 2ВЎђ Ж░ЎвІц. ВЌгЖИ░Вёю РђўphaseMeanVelocityРђЎвіћ ВюавЈЎВъЦ ВХюЖхгВЌљВёю ВюавЪЅв│┤ВА┤Вю╝вАю ьЈЅЖиаВєЇвЈёвЦ╝ ВаюВќ┤ьЋўвіћ ВА░Ж▒┤ВЮ┤Ж│а РђўvariableHeightFlowRateРђЎвіћ ВЃЂьЋю(Upper bound)Ж│╝ ьЋўьЋю (Lower bound)ВЮё ьєхьЋўВЌг VOFЖ░њВЮё в│┤ВаЋьЋўвіћ ВА░Ж▒┤ВЮ┤вІц. ВЮ╝в░ўВаЂВю╝вАю ВЃЂьЋюВЮђ Рђў1РђЎвАю ьЋўьЋюВЮђ Рђў0РђЎВю╝вАю ВДђВаЋвљювІц(OpenCFD Ltd., 2017).
ВѕўВ╣ўьЋ┤ВёЮВЌљ ВѓгВџЕвљю вѓювЦўвфевЇИВЮђ SST k-¤ЅВЮ┤вЕ░ ВІюЖ░ёВЮ┤Вѓ░ВЌљ вїђьЋўВЌгвіћ 1В░е ВаЋьЎЋвЈёВЮў Implicit Eulerв▓Ћ, Ж│хЖ░ёВЮ┤Вѓ░ВЮў ьЎЋВѓ░ьЋГВЌљ вїђьЋўВЌгвіћ ВцЉВЋЎ В░евХё ЖИ░в▓ЋВю╝вАю В▓ўвдгьЋўвЕ░, вїђвЦўьЋГВЌљ вїђьЋўВЌгвіћ ВЋЋваЦВЮ┤Вѓ░, ВєЇвЈёВЮ┤Вѓ░, в░Ј вѓювЦўВЮ┤Вѓ░ вЊ▒ВЮђ 2В░е ВаЋьЎЋвЈёВЮИ Linear Upwindв▓ЋВЮё ВѓгВџЕьЋўЖ│а VOFВЮ┤Вѓ░ВЮђ ВЋѕВаЋвљю ВъљВюаВѕўвЕ┤ ВюавЈЎ Ж▓░Ж│╝вЦ╝ Вќ╗ВЮё Вѕў Въѕвіћ Van Leerв▓ЋВЮё ВѓгВџЕьЋўВўђвІц(Chevrier and Galley 1993).
3.2 вХѕьЎЋВІцВё▒ ьЋ┤ВёЮ(Uncertainty analysis)
CFDвЦ╝ ВЮ┤ВџЕьЋю RANS в░ЕВаЋВІЮВЌљ вїђьЋю ВѕўВ╣ўьЋ┤ВёЮ Ж│╝ВаЋВЌљвіћ ВъЁваЦв│ђВѕў ВўцВ░е, в░ўв│х ВўцВ░е, Ж│хЖ░ёВЮ┤Вѓ░ ВўцВ░е, ВІюЖ░ёВЮ┤Вѓ░ ВўцВ░е вЊ▒ вІцВќЉьЋю ВўцВ░еЖ░ђ в░юВЃЮьЋўВЌг ьЋ┤ВЮў вХѕьЎЋВІцВё▒ВЮ┤ ВА┤ВъгьЋювІц. в│И ВЌ░ЖхгВЌљВёювіћ Wilson et al.,(2001)Ж│╝ Stern et al.,(2001)ВЌљ ВаюВІювљю в░Ев▓ЋВЮё ВЮ┤ВџЕьЋўВЌг ВІюЖ░ёВЮ┤Вѓ░ ВўцВ░еВЎђ Ж│хЖ░ёВЮ┤Вѓ░ ВўцВ░еВЮў ВўЂьќЦВЌљ вїђьЋю вХѕьЎЋВІцВё▒ ьЋ┤ВёЮВЮё ВѕўьќЅьЋўВўђвІц.
В▓ФВДИвАю, ВІюЖ░ёВЮ┤Вѓ░ ВўцВ░е ВдЅ, Ж│ёВѓ░ВІюЖ░ё Ж░ёЖ▓ЕВЌљ ВЮўьЋю вХѕьЎЋВІцВё▒ ьЋ┤ВёЮВЮё ВюёьЋўВЌг ВІЮ (15)ВЎђ Ж░ЎВЮ┤ ВаЋВЮўвљю CFL Вѕў(Courant number)вЦ╝ РђўSmall(1)РђЎ, РђўMedium(2)РђЎв░Ј РђўLarge(4)РђЎвЊ▒ ьЂгЖИ░ в│ђьЎћВЮў в╣ёВюеВЮё 2вАю ьЋўВЌг в│ђьЎћВІюьѓцвЕ┤Вёю ВѕўВ╣ўьЋ┤ВёЮВЮё ВѕўьќЅьЋўВўђвІц. Ж░ЂЖ░ЂВЮў ьЋ┤ВёЮВЌљвіћ В┤Ю Ж▓ЕВъљВѕў 93вДїЖ░юВЮў вЈЎВЮ╝ьЋю Ж▓ЕВъљЖ│ёЖ░ђ ВІюВџЕвљўВЌѕвІц. ВёаВєЇВЮђ ьЎюВБ╝ ВєЇвЈёВЮИ Fn=1.19вЦ╝ ВѓгВџЕьЋўВўђвІц.
ВЌгЖИ░Вёю uВЮђ Вхювїђ ВюаВєЇВЮ┤вЕ░, РѕєxВЎђ Рѕєyвіћ Ж░ЂЖ░Ђ ВхюВєїЖ▓ЕВъљ Ж░ёЖ▓ЕЖ│╝ Ж│ёВѓ░ВІюЖ░ё Ж░ёЖ▓ЕВЮ┤вІц.
Table 3ВЌљвіћ CFL Вѕў в│ђьЎћВЌљ вћ░вЦИ Ж│ёВѓ░ ВІюЖ░ё Ж░ёЖ▓ЕЖ│╝ ВѕўВ╣ўьЋ┤ВёЮ Ж▓░Ж│╝ВЮИ В┤Ю ВађьЋГЖ░њВЮё в│┤ВЌгВБ╝Ж│а ВъѕвІц. CFL ВѕўЖ░ђ ВъЉВЋёВДѕВѕўвАЮ Ж│ёВѓ░ВІюЖ░ё Ж░ёЖ▓ЕВЮ┤ ВъЉВЋёВДђЖ│а В┤Ю ВађьЋГЖ░њВЮђ FrismaВІцьЌў Ж▓░Ж│╝ВЌљ ВаЉЖи╝ьЋўвіћ Ж▓░Ж│╝вЦ╝ Вќ╗ВЮїВЮё ВЋї Вѕў ВъѕвІц. Ж▓░вАаВаЂВю╝вАю ВѕўВ╣ўьЋ┤ВёЮВЮў ВІюЖ░ёВЮ┤Вѓ░ ВўцВ░евЦ╝ ВхюВєїьЎћьЋўЖИ░ ВюёьЋ┤Вёювіћ CFL ВѕўЖ░ђ Рђў1РђЎв│┤вІц ВъЉЖ▓ї вљўвЈёвАЮ Ж│ёВѓ░ВІюЖ░ё Ж░ёЖ▓ЕВЮё ВёцВаЋьЋа ьЋёВџћЖ░ђ ВъѕвІц.
вЉўВДИвАю, Ж│хЖ░ёВЮ┤Вѓ░ ВўцВ░е ВдЅ, Ж▓ЕВъљ ьЂгЖИ░ВЌљ ВЮўьЋю вХѕьЎЋВІцВё▒ ьЋ┤ВёЮВЮў ВѕўьќЅВЮё ВюёьЋўВЌг Table 4В▓ўвЪ╝ в░░Ж▓йЖ▓ЕВъљ ВўЂВЌГЖ│╝ Вџ┤вЈЎЖ▓ЕВъљ ВўЂВЌГВЮё ьЈгьЋеьЋю ВаёВ▓┤ ВўЂВЌГВЌљ РђўCoarse MeshРђЎ(В┤Ю Ж▓ЕВъљВѕў 45вДїЖ░ю), РђўMedium MeshРђЎ(В┤Ю Ж▓ЕВъљВѕў 93вДїЖ░ю) в░Ј РђўFine MeshРђЎ(В┤Ю Ж▓ЕВъљВѕў 256вДїЖ░ю) вЊ▒ Ж▓ЕВъљ вХёьЋав╣ё(Refinement ratio)вЦ╝ 2
ВѕўВ╣ўьЋ┤ВёЮВЮђ ьЎюВБ╝ ВєЇвЈёВЮИ Fn=1.19ВЌљВёю ВѕўьќЅьЋўВўђЖ│а ВІюЖ░ёЖ░ёЖ▓ЕВаюВќ┤ЖИ░віЦ(Time step control)ВЮё ВЮ┤ВџЕьЋўВЌг Вхювїђ CFL ВѕўвЦ╝ 1ВЮ┤ьЋўвАю ВюаВДђьЋўВўђвІц.
РђўCoarse MeshРђЎ, РђўMedium MeshРђЎ в░Ј РђўFine MeshРђЎвЦ╝ ВѓгВџЕьЋўВЌг ЖхгьЋю ВѕўВ╣ўьЋ┤ВёЮ Ж▓░Ж│╝вЦ╝ Ж░ЂЖ░Ђ Scoarse, Smedium в░Ј SfineВю╝вАю ьЉюЖИ░ьЋўЖ│а Ж▓░Ж│╝вЦ╝ Table 5ВЌљ ВаЋвдгьЋўВўђвІц.
Ж░ЂЖ░ЂВЮў Ж▓ЕВъљЖ│ёВЌљ вїђьЋю Ж▓░Ж│╝вАювХђьё░ ВІЮ (16)-(18)ВЮё ВЮ┤ВџЕьЋўВЌг ╬х21ВЎђ ╬х32 в░Ј Вѕўва┤в╣ё(Convergence ratio), RВЮё ЖхгьЋа Вѕў ВъѕвІц.
Вѕўва┤в╣ёВЮў ьЂгЖИ░ВЌљ вћ░вЮ╝ ВЋёвъўВЎђ Ж░ЎВЮђ Вѕўва┤ ьі╣Вё▒ВЮё Ж░ђВДёвІц.
(1) вІеВѕю Вѕўва┤(Montonic convergence) : 0 < R < 1
(2) ВДёвЈЎ Вѕўва┤(Oscillatory convergence) : R < 0
(3) в░юВѓ░(Divergence) : R > 1
Table 5ВЌљ ВЮўьЋўвЕ┤ Ж▓ЕВъљВЮў ьЂгЖИ░Ж░ђ ВъЉВЋёВДѕВѕўвАЮ В┤Ю ВађьЋГ, ьіИвд╝ в░Ј вХђВЃЂвЪЅВЮў Вѕўва┤в╣ё RВЮў Ж░њВЮ┤ Ж░ЂЖ░Ђ 0.517. 0.174 в░Ј 0.351вАю ВхюВбЁ Вѕўва┤В╣ўвЦ╝ ьќЦьЋ┤ вІеВѕю Вѕўва┤(Monotonic convergence)ьЋўвіћ Ж▓ЃВЮё ВЋї Вѕў ВъѕВю╝вЕ░ вХѕьЎЋВІцВё▒ ьЋ┤ВёЮВЌљ Richardson ВЎИВѓйв▓ЋВЮё ВѓгВџЕьЋа Вѕў ВъѕвІц.
РђўCoarse MeshРђЎВЎђ РђўMedium MeshРђЎВЮў В┤Ю ВађьЋГЖ░њВЮђ В░еВЮ┤Ж░ђ 5.24%, ьіИвд╝ВЮў В░еВЮ┤віћ 6.5%, вХђВЃЂвЪЅВЮў В░еВЮ┤віћ 12.33%вАю в╣ёЖхљВаЂ ьЂ░ В░еВЮ┤Ж░ђ ВХћВаЋвљўВЌѕвІц. ЖиИвЪгвѓў РђўMedium MeshРђЎВЎђ РђўFine MeshРђЎВЮў Ж▓йВџ░ВЌљ вХђВЃЂвЪЅ В░еВЮ┤Ж░ђ 4.94%вАю вІцВєї ьЂ░ ьјИВЮ┤вѓў В┤Ю ВађьЋГЖ│╝ ьіИвд╝ВЮў В░еВЮ┤віћ Ж░ЂЖ░Ђ 2.58%ВЎђ 1.06%вАю ьЂ░ В░еВЮ┤ ВЌєВЮ┤ Вѕўва┤В╣ўВЌљ ВаЉЖи╝ьЋўвіћ Ж▓йьќЦВЮё в│┤ВЮ┤Ж│а ВъѕВЮїВЮё ВЋї Вѕў ВъѕвІц. вћ░вЮ╝Вёю в│И вХёВёЮ Ж▓░Ж│╝ВЎђ ВѕўВ╣ўьЋ┤ВёЮ ВѕўьќЅВЮў ВџЕВЮ┤Вё▒ВЮё Ж│авацьЋўВЌг вІцВЮї ВаѕВЌљВёю ВѕўьќЅьЋа Fridsma ьЎюВБ╝ВёаВЌљ вїђьЋю ВађьЋГ в░Ј ьЎюВБ╝Вё▒віЦ ьЋ┤ВёЮВЌљвіћ РђўMedium MeshРђЎвЦ╝ ЖИ░в│ИЖ▓ЕВъљЖ│ёвАю ВёаВаЋьЋўВўђвІц.
ВѕўВ╣ўьЋ┤ВёЮ Ж▓░Ж│╝ВЎђ Fridsma ВІцьЌў Ж▓░Ж│╝ВЮў в╣ёЖхљвіћ Ж▓ЕВъљ ьЂгЖИ░Ж░ђ ВъЉВЋёВДѕВѕўвАЮ ьіИвд╝ВЮђ ВІцьЌўВ╣ўВЌљ ВаЉЖи╝ьЋўвіћ Ж▓йьќЦВЮё в│┤ВЮ┤Ж│а ВъѕВю╝вѓў В┤ЮВађьЋГЖ░њЖ│╝ вХђВЃЂвЪЅВЮђ Ж│хьъѕ ВІцьЌўВ╣ўВЎђВЮў В░еВЮ┤Ж░ђ В╗цВДљВЮё ВЋї Вѕў ВъѕвІц. ВдЅ, ВађьЋГЖ│╝ вХђВЃЂвЪЅВЮў ВЃЂьўИ ВЃЂЖ┤ђЖ┤ђЖ│ёЖ░ђ ьіИвд╝в│┤вІцвіћ вДцВџ░ ьЂ╝ВЮё ВЋї Вѕў ВъѕвІц. ВѕўВ╣ўьЋ┤ВёЮ Ж▓░Ж│╝Ж░ђ ВІцьЌў Ж▓░Ж│╝ВЌљ Вѕўва┤ьЋўВДђ ВЋівіћ Ж▓йьќЦВЮђ ьЎюВБ╝Вёа ВађьЋГ в░Ј ьЎюВБ╝Вё▒віЦ Ж┤ђвае ьЃђ CFDьЋ┤ВёЮ ВЌ░Жхг Ж▓░Ж│╝(Fu et al., 2012; Marcello, 2015; Mousavirrad et al., 2015) вЊ▒ВЌљвЈё Ж│хьєхВаЂВю╝вАю вѓўьЃђвѓўвіћ Ж▓░Ж│╝вАю ВЮ┤вЪгьЋю ьўёВЃЂВЮё ЖиювфЁьЋўЖИ░ ВюёьЋ┤Вёювіћ ВѕўВ╣ўьЋ┤ВёЮ Ж│╝ВаЋВЌљ ВА┤ВъгьЋўвіћ вІцвЦИ ВўцВ░е ВџћВєївЊцВЌљ вїђьЋю ВХћЖ░ђВаЂВЮИ вХёВёЮВЮђ вг╝вАа ьЎюВБ╝Вёа вфеьўЋВІюьЌў Ж│╝ВаЋВЌљВёю в░юВЃЮьЋа Вѕў Въѕвіћ ВІцьЌў ВўцВ░е ВџћВєївЊц ьі╣ьъѕ, вг┤Ж▓ївХёьЈг, ВўѕВЮИ в░Ев▓Ћ в░Ј ВўѕВЮИВаљВЌљ вїђьЋю Ж▓ђВдЮВЮ┤ ьЋёВџћьЋа Ж▓ЃВю╝вАю в│ИвІц.
Wilson et al.(2001)Ж│╝ Stern et al.(2001)ВЮў ВаѕВ░еВЌљ вћ░вЮ╝ Richardson ВЎИВѓйв▓ЋВЮё ВЮ┤ВџЕьЋўВЌг Ж▓ЕВъљьЂгЖИ░ВЮў в│ђьЎћВЌљ вћ░вЦИ вХѕьЎЋВІцВё▒ ьЋ┤ВёЮВЮё ВѕўьќЅьЋўВўђвІц. ВІЮ (19)-(23)ВЌљ Ж▒ИВ│љВёю Вѕўва┤В░еВѕў, PG, в│┤ВаЋЖ│ёВѕў, CG, вХѕьЎЋВІцВё▒, UG, ВѕўВаЋвљю ВўцВ░е ╬┤*G, в░Ј ВѕўВаЋвљю ьЋ┤, ScвЦ╝ Ж░ЂЖ░Ђ ЖхгьЋа Вѕў ВъѕвІц. ВЌгЖИ░Вёю ьЋюЖ│ё Вѕўва┤В░еВѕў, P G e s t 2
Ж│хЖ░ёВЮ┤Вѓ░ ВўцВ░е ВдЅ Ж▓ЕВъљьЂгЖИ░ВЮў в│ђьЎћВЌљ вћ░вЦИ вХѕьЎЋВІцВё▒ ьЋ┤ВёЮ Ж▓░Ж│╝вЦ╝ Table 6ВЌљ ВаЋвдгьЋўВўђвІц.
РђўFine meshРђЎВЌљ вїђьЋю В┤Ю ВађьЋГВЮў вХѕьЎЋВІцВё▒ВЮђ 2.7%, ьіИвд╝Ж│╝ вХђВЃЂвЪЅВЮў вХѕьЎЋВІцВё▒ВЮђ Ж░ЂЖ░Ђ 1.9%ВЎђ 8%вАю ВХћВаЋвљўВЌѕвІц. ЖиИвдгЖ│а Ж▓ЕВъљВЮў ьЂгЖИ░Ж░ђ 0Вю╝вАю Вѕўва┤вља Ж▓йВџ░ВЌљ В┤Ю ВађьЋГ, ьіИвд╝ в░Ј вХђВЃЂвЪЅВЮђ Ж░ЂЖ░Ђ 24.08N, 5.77┬░ в░Ј 0.0249mвАю Вѕўва┤ьЋа Ж▓ЃВю╝вАю ВХћВаЋвљювІц.
3.3 ьЎюВБ╝Вё▒віЦ ьЋ┤ВёЮ
ВѕўВ╣ўьЋ┤ВёЮ вїђВЃЂ ьЎюВБ╝ВёаВЮИ Fridsma ВёаьўЋВЮў ВБ╝ВџћвфЕВЮђ Table 1ВЎђ Ж░ЎЖ│а, ВёаВєЇВЮђ ьћёвБевЊю ВѕўЖ░ђ 0.59, 0.89, 1.19, 1.48 в░Ј 1.78ВЮў 5Ж░ђВДђ ВёаВєЇВЮё ВёаьЃЮьЋўВЌг в░░ВѕўвЪЅьўЋ ВађВєЇВЃЂьЃювХђьё░ ьЎюВБ╝ВёаьўЋ Ж│аВєЇВЃЂьЃювЦ╝ ьЈгьЋеьЋўвЈёвАЮ ьЋўВўђвІц.
Ж▓ЕВъљЖхгВё▒ВЮђ вХѕьЎЋВІцВё▒ ьЋ┤ВёЮВЌљВёю вХёВёЮьЋю Ж▓░Ж│╝вЦ╝ в░ћьЃЋВю╝вАю В┤ЮЖ▓ЕВъљвіћ 93вДїЖ░юВЮў РђўMedium meshРђЎвЦ╝ ВѓгВџЕьЋўВўђВю╝вЕ░ Вхювїђ CEL Вѕўвіћ 1вАю ВДђВаЋьЋўВўђвІц.
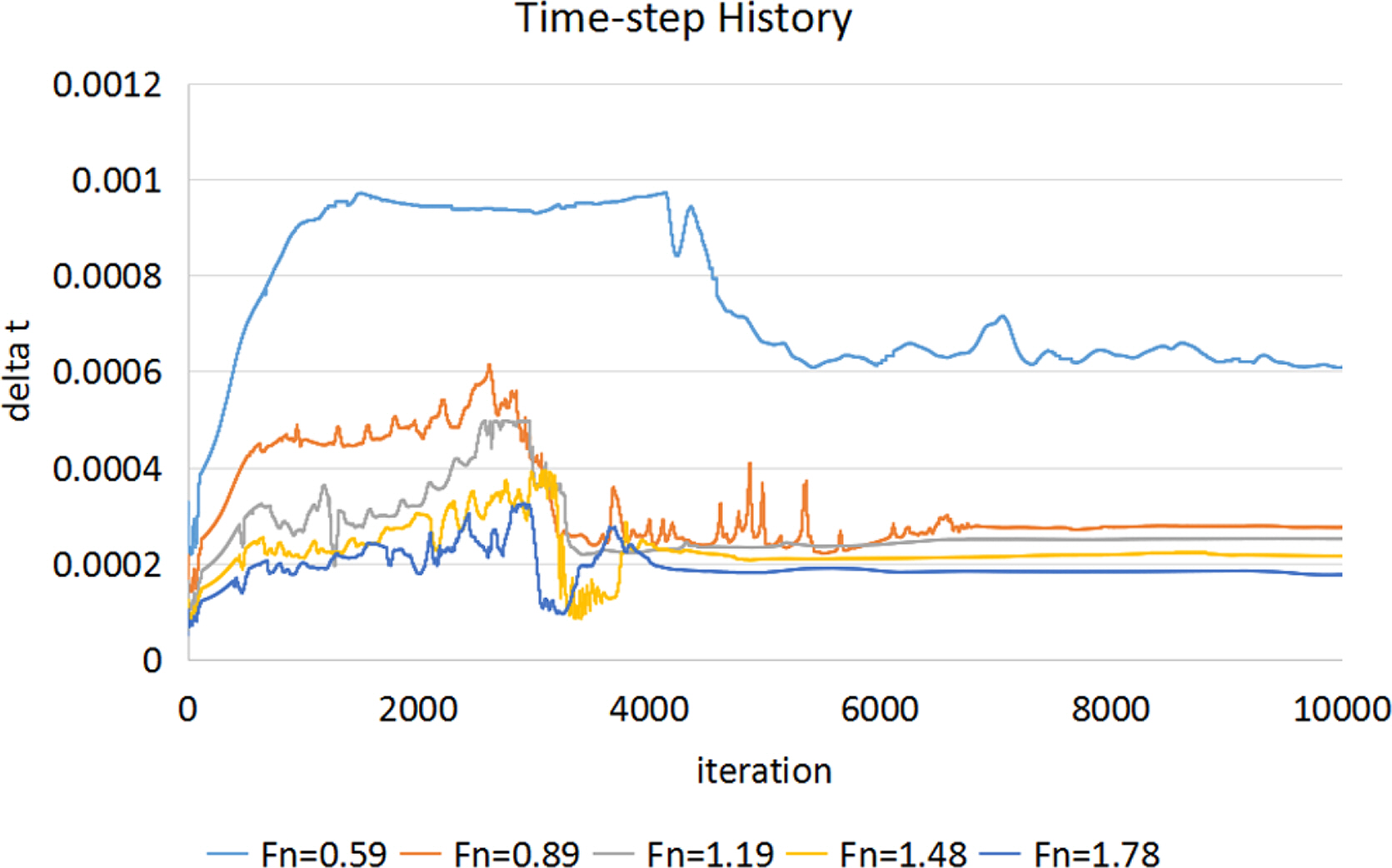
Fig. 10ВЮђ Вхювїђ CFLВѕўЖ░ђ 1вАю ВюаВДђвља вЋї ВєЇвЈёВЌљ вћ░вЦИ Ж│ёВѓ░ ВІюЖ░ё Ж░ёЖ▓Е(Delta t)ВЮё в│┤ВЌгВБ╝Ж│а ВъѕвІц. ВєЇвЈёЖ░ђ в╣евЮ╝ВДѕВѕўвАЮ Ж│ёВѓ░ ВІюЖ░ё Ж░ёЖ▓ЕВЮ┤ 0.0006В┤ѕвХђьё░ 0.0002В┤ѕЖ╣їВДђ ВаљВаљ ВъЉВЋёВДљВЮё ВЋї Вѕў ВъѕвІц. вўљьЋю, Ж│ёВѓ░ ВІюЖ░ё Ж░ёЖ▓ЕВЮў в╣авЦИ Вѕўва┤ВЮђ ВюавЈЎВъЦ ВаёВ▓┤ВЮў ВєЇвЈёВЎђ ВЋЋваЦЖ░њвЊцВЮ┤ в╣авЦ┤Ж▓ї Вѕўва┤ьЋеВЮё ВЮўв»ИьЋювІц.
Fig. 11ВЮђ ьћёвБевЊю Вѕў 1.19ВЮ╝ вЋї ВъљВюаВѕўвЕ┤ВЮў ьїїЖ│а вХёьЈгвЦ╝ в│┤ВЌгВБ╝Ж│а ВъѕвІц. Ваёв░ўВаЂВю╝вАю вфЁьЎЋьЋю В║ўв╣ѕ ьїїьўЋВЮё в│╝ Вѕў ВъѕВю╝вЕ░ Вёав»ИвХђ ьЏёвЦўВЌљ в░юВЃЮьЋўвіћ вБеВіцьё░(Rooster) ьўёВЃЂВЮё ьЎЋВЮИьЋа Вѕў ВъѕвІц.
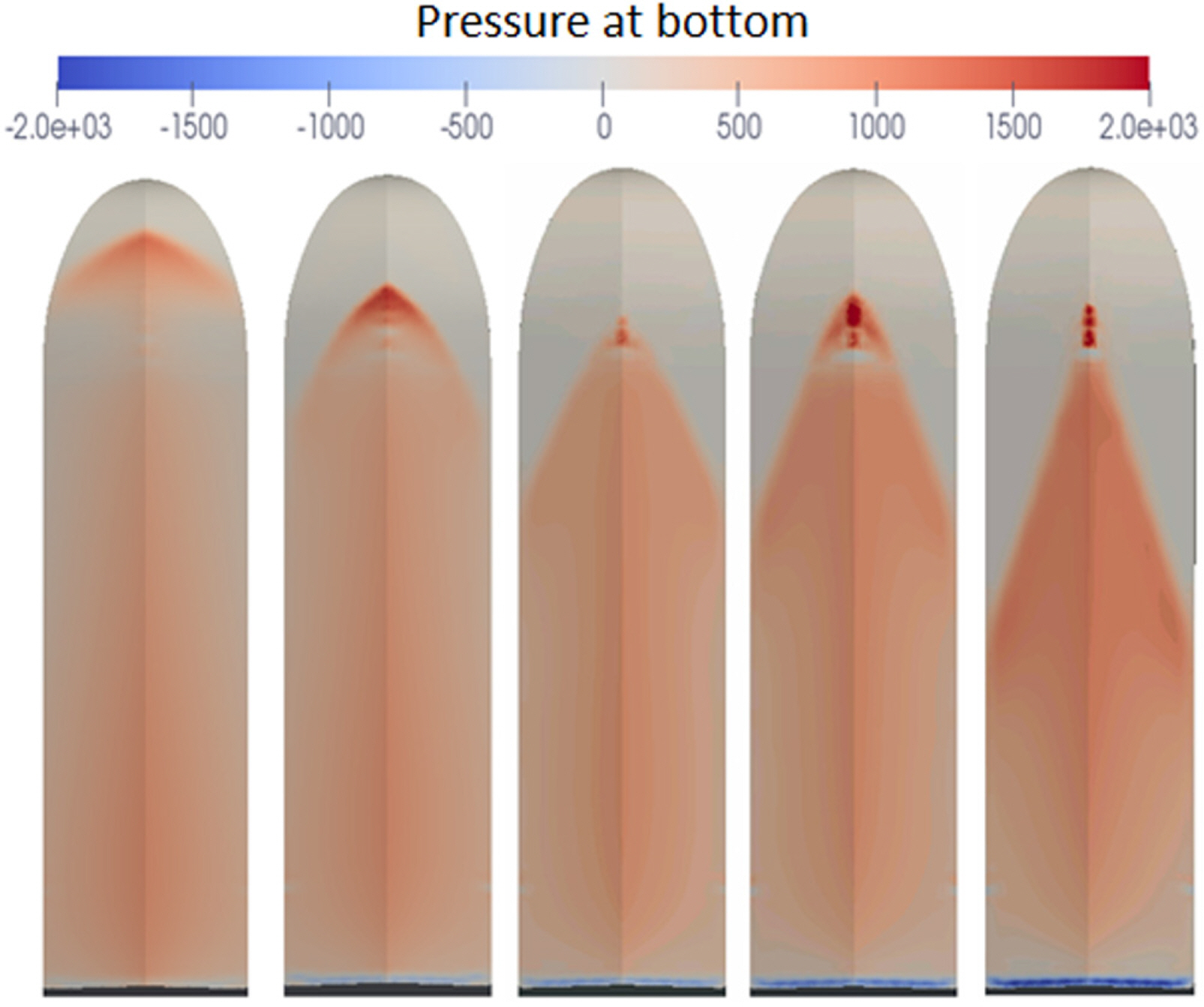
Fig. 12віћ ВађВєЇвХђьё░ Ж│аВєЇЖ╣їВДђ ВёаВєЇВЮў в│ђьЎћВЌљ вћ░вЦИ ВёаВађвЕ┤ВЮў ВЋЋваЦ вХёьЈгвЦ╝ в│┤ВЌгВБ╝Ж│а ВъѕвІц. ВёаВєЇВЮ┤ ВдЮЖ░ђьЋўвЕ┤Вёю вХђВЃЂЖ│╝ ьіИвд╝ВЮ┤ в░юВЃЮьЋеВЌљ вћ░вЮ╝Вёю Ваёв░ўВаЂВю╝вАю В╣еВѕўвЕ┤ВаЂВЮ┤ Ж░љВєїьЋўвіћ Ж▓йьќЦВЮё в│╝ Вѕў ВъѕвІц. ЖиИвЪгвѓў, ьћёвБевЊю ВѕўЖ░ђ 1.19ВЌљВёю 1.48вАю ВдЮЖ░ђьЋа вЋївіћ В╣еВѕўвЕ┤ВаЂВЮ┤ ВдЮЖ░ђьЋеВЮё в│╝ Вѕў ВъѕвіћвЇ░ ЖиИ ВЮ┤Вюавіћ ьћёвБевЊю ВѕўЖ░ђ 1.19в│┤вІц В╗цВДђвЕ┤ вХђВЃЂвЪЅВЮў ВдЮЖ░ђВюеВЮђ вЉћьЎћвљўЖ│а ьіИвд╝ВЮђ ВДђВєЇВаЂВю╝вАю Ж░љВєїьЋўвЕ┤Вёю ВЃЮЖИ░віћ ьўёВЃЂВю╝вАю ВХћВаЋьЋа Вѕў ВъѕвІц. В╣еВѕўвЕ┤ВаЂВЮў в│ђьЎћвіћВ┤Ю ВађьЋГВ╣ўВЌљ ВДЂВаЉВаЂВЮИ ВўЂьќЦВЮё ВБ╝віћ ВџћВєїВЮ┤вІц.
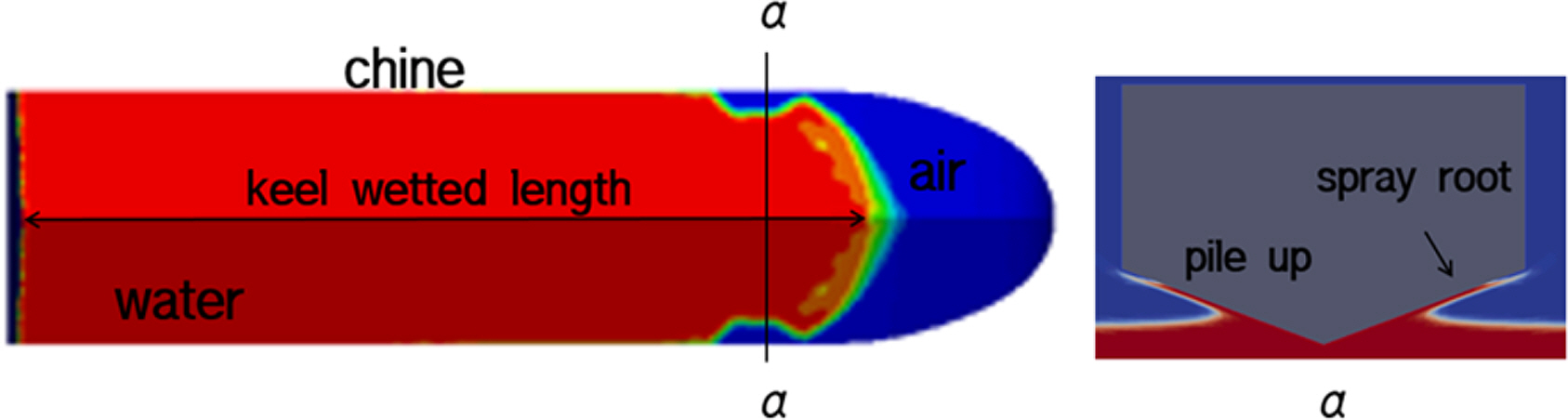
Fig. 13ВЮђ ьћёвБевЊю ВѕўЖ░ђ 1.19ВЮИ Ж▓йВџ░ВЌљ VOFВЮў в│ђьЎћвЦ╝ ьєхьЋўВЌг ВёаВађВаЉВѕўвЕ┤ВЮў ьўЋВЃЂВЮё в│┤ВЌгВБ╝Ж│а ВъѕвІц. вХЅВЮђВЃЅ вХђвХёВЮђ VOFЖ░ђ 1ВЮИ вХђвХёВю╝вАю Ж▓ЕВъљЖ░ђ вг╝вАювДї В▒ёВЏїВаИ Въѕвіћ вХђвХёВЮ┤Ж│а ьЉИвЦИВЃЅ вХђвХёВЮђ VOFЖ░ђ 0Вю╝вАю Ж▓ЕВъљ вѓ┤ВЌљ Ж│хЖИ░вДї Въѕвіћ вХђвХёВЮ┤вІц. вўљьЋю, ВёаВађвЕ┤ ЖИ░Вёа вХђвХёвХђьё░ Chine-dry ВўЂВЌГЖ│╝ Chine-wet ВўЂВЌГВЮё в│╝ Вѕў ВъѕВю╝вЕ░ Chine-dry ВўЂВЌГВЮИ ╬▒-╬▒ вІевЕ┤ВЌљ в░юВЃЮьЋўвіћ ВіцьћёваѕВЮ┤ ьўёВЃЂВЮё ьЎЋВЮИьЋа Вѕў ВъѕвІц.
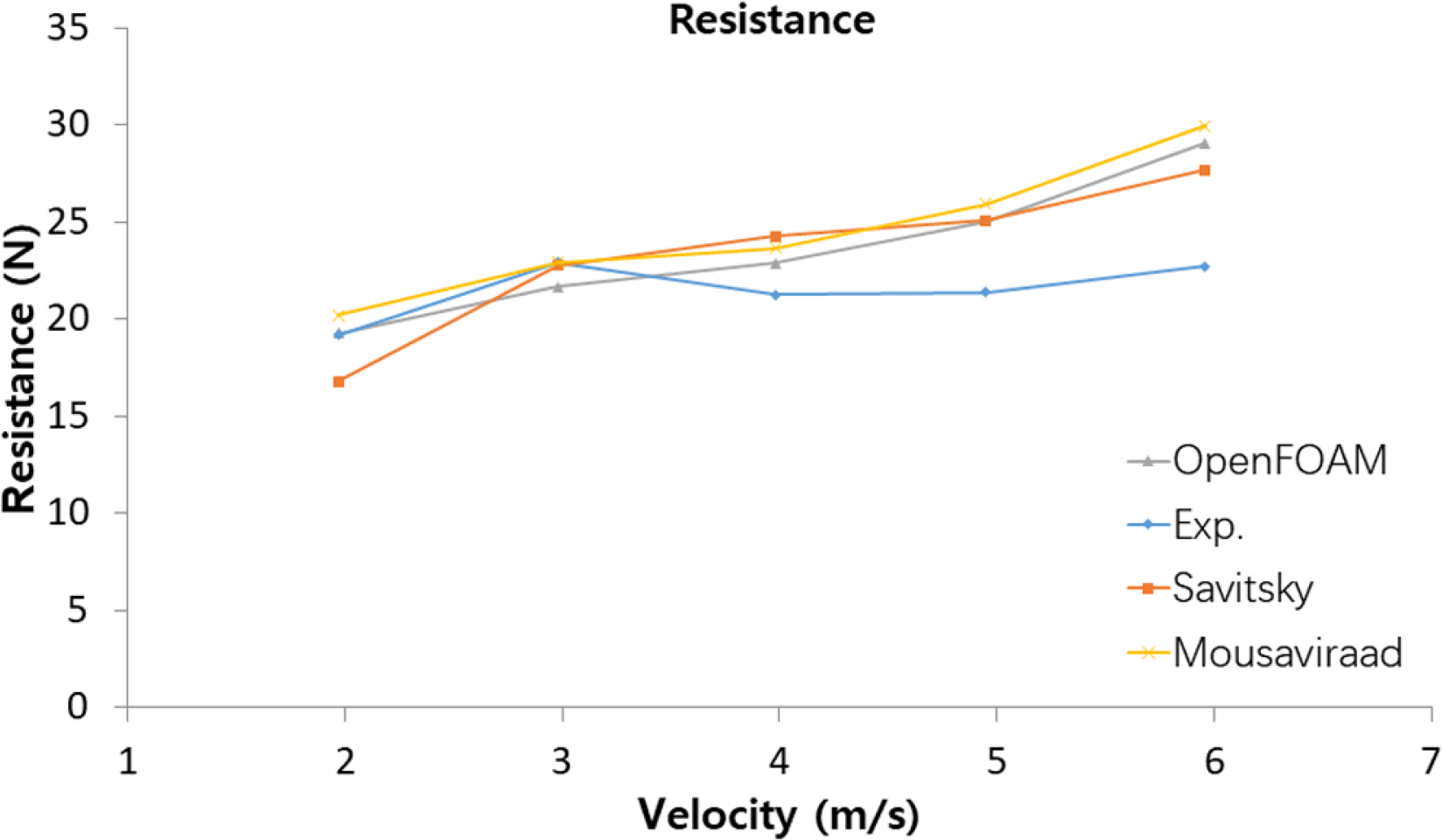
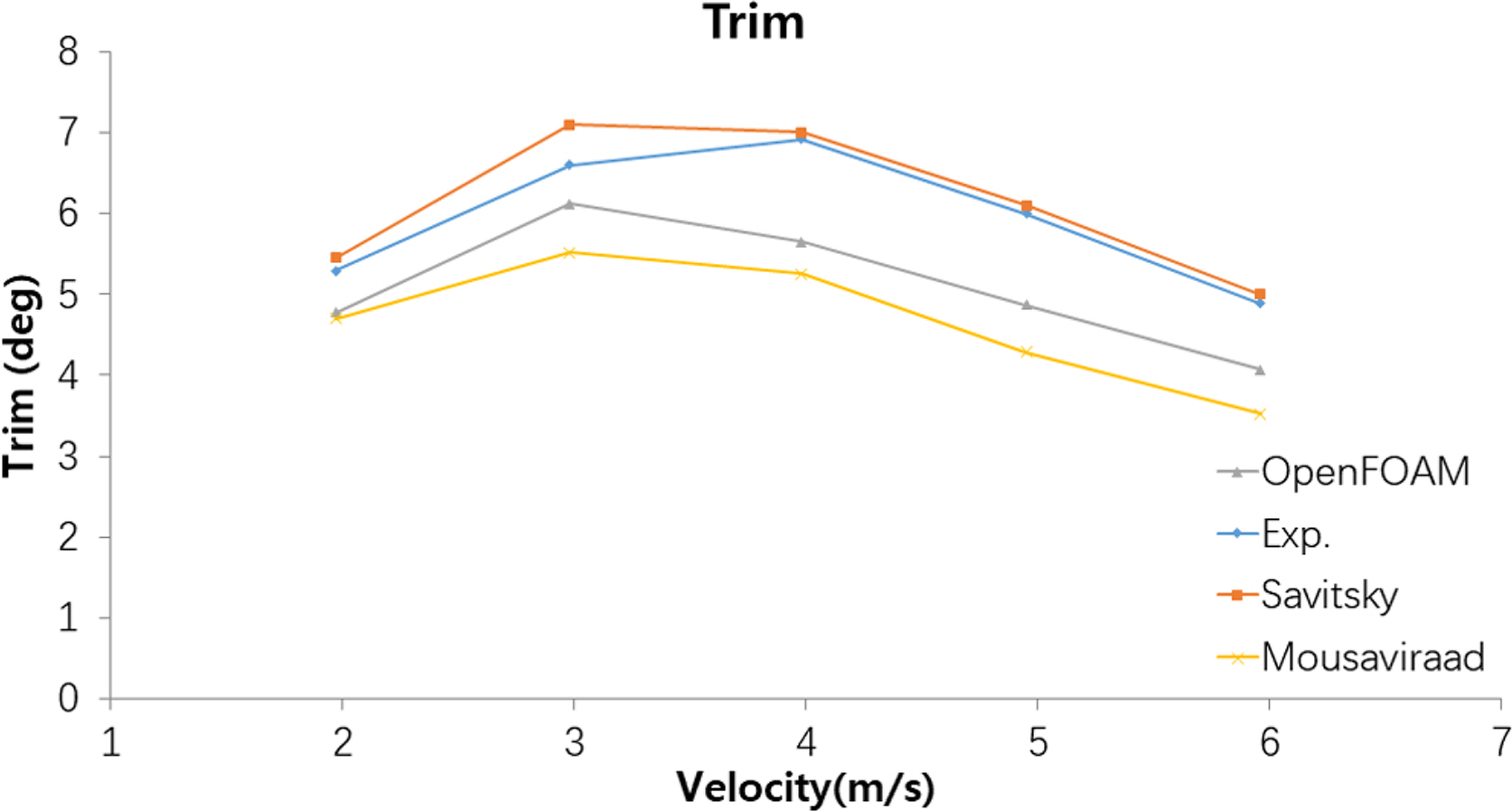
Fig. 14-16ВЮђ Ж░ЂЖ░Ђ ВєЇвЈёВЮў в│ђьЎћВЌљ вћ░вЦИ В┤Ю ВађьЋГ, вХђВЃЂвЪЅ в░Ј ьіИвд╝ВЮў в│ђьЎћвЦ╝ в│┤ВЌгВБ╝Ж│а ВъѕвІц. Вѓ╝Ж░ЂьўЋ(OpenFOAM)ВЮђ в│И ВЌ░ЖхгВЮў Ж▓░Ж│╝ВЮ┤вЕ░ ВІцьЌў Ж▓░Ж│╝, Mousaviraad et al.(2015)ВЮў Ж▓░Ж│╝ в░Ј Savitsky Ж▓йьЌўВІЮЖ│╝ВЮў в╣ёЖхљвЦ╝ ьєхьЋўВЌг ВѕўВ╣ўьЋ┤ВёЮ Ж▓░Ж│╝вЦ╝ Ж▓ђВдЮьЋўВўђвІц.
В┤Ю ВађьЋГВЮў Ж▓йВџ░ВЌљ вХђваЦВЮў ВўЂьќЦВЮ┤ ВДђв░░ВаЂВЮИ ВађВєЇВЌљВёювіћ 4Ж░ђВДђ в░Ев▓ЋВЌљ ьЂ░ В░еВЮ┤ ВЌєВю╝вѓў ВєЇвЈёЖ░ђ ВдЮЖ░ђьЋўЖ│а ВѕўвЈЎВЌГьЋЎВаЂВЮИ ьъўВЮИ ВќЉваЦВЮў ВўЂьќЦВЮ┤ ВдЮЖ░ђьЋўвЕ┤Вёю в│И ВЌ░Жхг Ж▓░Ж│╝ВЎђ MousaviraadВЮў Ж▓░Ж│╝ в░Ј Savitsky Ж▓йьЌўВІЮ Ж▓░Ж│╝віћ в╣ёЖхљВаЂ Въў ВЮ╝В╣ўьЋўвЕ┤Вёю ВдЮЖ░ђьЋўВДђвДї ВІцьЌўЖ░њВЮђ Ваёв░ўВаЂВЮИ в│ђьЎћВЮў Ж▓йьќЦВЮђ ВЮ╝В╣ўьЋўвѓў ьЂгЖИ░Ж░ђ ВъЉЖ│а ВєЇвЈёЖ░ђ ВдЮЖ░ђьЋеВЌљ вћ░вЮ╝ В░еВЮ┤Ж░ђ В╗цВДљВЮё ВЋї Вѕў ВъѕвІц.
вХђВЃЂвЪЅВЮў Ж▓йВџ░ВЌљвЈё ВаЋВё▒ВаЂВЮИ в│ђьЎћВЮў Ж▓йьќЦВЮђ ВЮ╝В╣ўьЋўвѓў ВађВєЇВЮё ВаюВЎИьЋю вїђвХђвХёВЮў ВєЇвЈё ЖхгЖ░ёВЌљ Ж▒ИВ│љВёю ВІцьЌўЖ░њВЮ┤ Ж░ђВъЦ ьЂгЖ│а Savitsky Ж▓йьЌўВІЮВЮђ Ж░ђВъЦ ВъЉВЮђ Ж░њВЮё Ж░ђВДђЖ│а ВъѕВЮїВЮё ВЋї Вѕў ВъѕвІц. в│И ВЌ░ЖхгВЮў Ж▓░Ж│╝ВЎђ MousaviraadВЮў Ж▓░Ж│╝Ж░ђ ВцЉЖ░ёЖ░њВЮё Ж░ђВДђЖ│а ВъѕВю╝вѓў в│И ВЌ░ЖхгВЮў Ж▓░Ж│╝Ж░ђ ВІцьЌўЖ░њВЮў в│ђьЎћ Ж▓йьќЦВЮё вїђВ▓┤вАю вћ░вЮ╝Ж░ђЖ│а ВъѕВЮїВЮё ВЋї Вѕў ВъѕвІц. ВІцьЌў Ж▓░Ж│╝ВЎђ CFD Ж▓░Ж│╝Ж░ђ В┤Ю ВађьЋГЖ│╝ вХђВЃЂвЪЅВЮў ьЂгЖИ░ВЌљВёю ВЌГВаёвљўвіћ Ж▓йьќЦВЮё в│┤ВЌгВБ╝Ж│а Въѕвіћ Ж▓ЃВю╝вАю в│╝ вЋї В┤ЮВађьЋГВЌљ в»ИВ╣ўвіћ вХђВЃЂвЪЅВЮў ВўЂьќЦВЮ┤ вДцВџ░ ьЂ╝ВЮё ВЋї Вѕў ВъѕвІц.
ьіИвд╝ВЮў Ж▓йВџ░віћ ВІцьЌўЖ░њЖ│╝ Savitsky Ж▓йьЌўВІЮ Ж▓░Ж│╝Ж░ђ Ваёв░ўВаЂВю╝вАю Въў ВЮ╝В╣ўьЋўЖ│а ВъѕВю╝вЕ░ в│И ВЌ░ЖхгВЮў Ж▓░Ж│╝віћ ВІцьЌўЖ░њЖ│╝ ьЂ░ В░еВЮ┤вЦ╝ в│┤ВЌгВБ╝Ж│а ВъѕВю╝вѓў MousaviraadВЮў Ж▓░Ж│╝в│┤вІцвіћ ВІцьЌўЖ░њВЌљ Жи╝ВаЉьЋю Ж▓░Ж│╝вЦ╝ в│┤ВЌгВБ╝Ж│а ВъѕвІц.
ВЋъ Ваѕ РђўвХѕьЎЋВІцВё▒ ьЋ┤ВёЮРђЎВЌљВёювЈё ЖИ░ВѕаьЋю в░ћВЎђ Ж░ЎВЮ┤ ьЎюВБ╝ьўЋВёаВЌљ вїђьЋю в│И ВЌ░ЖхгВЮў Ж▓░Ж│╝вЦ╝ ьЈгьЋеьЋю вїђвХђвХёВЮў CFD Ж▓░Ж│╝Ж░ђ FridsmaВЮў ВІцьЌў Ж▓░Ж│╝ВЎђ ьЂгЖ▓ї В░еВЮ┤Ж░ђ вѓеВЮё в│╝ Вѕў ВъѕвіћвЇ░ ЖиИ ВЏљВЮИВЮё ЖиювфЁьЋўЖИ░ ВюёьЋўВЌгвіћ CFD ВѕўВ╣ўьЋ┤ВёЮВЌљВёю в░юВЃЮьЋа Вѕў Въѕвіћ вІцВќЉьЋю ВўцВ░е ВџћВєївЊцВЮђ вг╝вАа вфеьўЋВІцьЌўВЮў Вцђв╣ё в░Ј ВѕўьќЅЖ│╝ВаЋВЌљВёю в░юВЃЮьЋўвіћ вХѕьЎЋВІцВё▒ВЌљ вїђьЋю в│┤вІц Жи╝в│ИВаЂВЮИ ВЌ░ЖхгЖ░ђ ьЋёВџћьЋа Ж▓ЃВю╝вАю в│ИвІц.
4. Ж▓░ вАа
В▓ФВДИ, в│И ВЌ░ЖхгвЦ╝ ьєхьЋ┤Вёю OpenFOAM ьћёвАюЖиИвъеВЮё ВЮ┤ВџЕьЋўВЌг ВБ╝ьўЋВ▓┤ Ж│аВєЇ ьЎюВБ╝ВёаВЌљ вїђьЋю ВађьЋГВё▒віЦ в░Ј ьЋГВБ╝ВъљВёИвЦ╝ ВѕўВ╣ўьЋ┤ВёЮьЋўвіћ в░Ев▓ЋВЮё ВаЋвдйьЋўВўђвІц.
вЉўВДИ, ВБ╝ьўЋВ▓┤ ьЎюВБ╝ВёаВЮў ВађьЋГ в░Ј ьЋГВБ╝ВъљВёИ ВѕўВ╣ўьЋ┤ВёЮВЌљ вїђьЋўВЌг Ж│ёВѓ░ВІюЖ░ё Ж░ёЖ▓ЕЖ│╝ Ж▓ЕВъљьЂгЖИ░ВЮў в│ђьЎћВЌљ вїђьЋю вХѕьЎЋВІцВё▒ ьЋ┤ВёЮВЮё ВѕўьќЅьЋю Ж▓░Ж│╝ Ж░ЂЖ░ЂВЮў вг╝вдгвЪЅВЌљ вїђьЋю вХѕьЎЋВІцВё▒ВЮў ьЂгЖИ░ВЎђ Richardson ВЎИВѓйв▓ЋВЮё ВѓгВџЕьЋўВЌг Ж▓ЕВъљВЮў ьЂгЖИ░Ж░ђ 0Вю╝вАю Вѕўва┤вља Ж▓йВџ░ВЌљ Вѕўва┤Ж░њ(В░ИЖ░њ)ВЮё ВХћВаЋьЋўВўђвІц.
ВЁІВДИ, ьЎюВБ╝Вёа Ж│аВєЇьЋГВБ╝ ВІю ВъљВюаВѕўвЕ┤ВЮў ьїїЖ│а вХёьЈгВЎђ Chine-dry ВўЂВЌГВЌљВёюВЮў ВіцьћёваѕВЮ┤ ьўёВЃЂВЮё ВѕўВ╣ўьЋ┤ВёЮВю╝вАю ьЎЋВЮИьЋўВўђЖ│а ВёаВєЇ в│ђьЎћВЌљ вћ░вЦИ ВёаВађ ВаЉВѕўвЕ┤ВЮў ьўЋВЃЂ в│ђьЎћвЦ╝ ьєхьЋўВЌг ВађВєЇВЃЂьЃювХђьё░ Ж│аВєЇВЃЂьЃюЖ╣їВДђВЮў ьЎюВБ╝ьўёВЃЂВЮё ьЎЋВЮИьЋа Вѕў ВъѕВЌѕвІц.
вёиВДИ, FridsmaВЮў ВБ╝ьўЋВ▓┤ ьЎюВБ╝ВёаВЌљ вїђьЋўВЌг Ж│аВєЇ ьЋГВБ╝ВІю ВађьЋГВё▒віЦЖ│╝ ьЋГВБ╝ВъљВёИвЦ╝ ВХћВаЋьЋўВўђвІц. В┤Ю ВађьЋГ Ж░њЖ│╝ вХђВЃЂвЪЅВЮў Ж▓йВџ░ВЌљ ьЃђ CFD Ж▓░Ж│╝ в░Ј Ж▓йьЌўВІЮ Ж▓░Ж│╝ВЎђ вїђВ▓┤вАю ВЮ╝В╣ўьЋўвіћ Ж▓йьќЦВЮё в│┤ВЌгВБ╝Ж│а ВъѕВДђвДї Ж│аВєЇ ьЎюВБ╝ ВўЂВЌГВю╝вАю Ж░ѕВѕўвАЮ ВІцьЌўЖ░њЖ│╝ВЮў В░еВЮ┤Ж░ђ В╗цВДђвіћ Ж▓░Ж│╝вЦ╝ Вќ╗ВЌѕвІц. ьіИвд╝ Ж▓░Ж│╝віћ Ваё ВєЇвЈё ВўЂВЌГВЌљВёю в│ђьЎћВЮў Ж▓йьќЦВЮђ вїђВ▓┤вАю ВЮ╝В╣ўьЋўвѓў ВІцьЌўЖ░њЖ│╝ в╣ёЖхљВаЂ ьЂ░ В░еВЮ┤вЦ╝ в│┤ВЌгВБ╝Ж│а ВъѕвІц.
вІцВё»ВДИ, ьЎюВБ╝ьўЋВёаВЌљ вїђьЋю в│И ВЌ░ЖхгВЮў Ж▓░Ж│╝вЦ╝ ьЈгьЋеьЋю вїђвХђвХёВЮў CFD Ж▓░Ж│╝Ж░ђ FridsmaВЮў ВІцьЌў Ж▓░Ж│╝ВЎђ ВаЋВё▒ВаЂВЮИ в│ђьЎћВЮў Ж▓йьќЦВЮђ ВЮ╝В╣ўьЋўвѓў ьЂгЖ▓ї В░еВЮ┤Ж░ђ вѓеВЮё в│╝ Вѕў ВъѕвіћвЇ░ ЖиИ ВЏљВЮИВЮё ЖиювфЁьЋўЖИ░ ВюёьЋ┤ CFD ВѕўВ╣ўьЋ┤ВёЮЖ│╝ вфеьўЋВІцьЌўВЌљ ВА┤ВъгьЋўвіћ вІцВќЉьЋю вХѕьЎЋВІцВё▒ВЌљ вїђьЋю ВЌ░ЖхгЖ░ђ ьЋёВџћьЋа Ж▓ЃВю╝вАю в│ИвІц.
в│И ВЌ░Жхг Ж▓░Ж│╝вЦ╝ в░ћьЃЋВю╝вАю ьќЦьЏёВЌљвіћ в╣ёВБ╝ьўЋВ▓┤ ьЎюВБ╝ВёаВЌљ вїђьЋю ВаЋВѕў ВцЉ ВађьЋГВё▒віЦ в░Ј ьЋГВБ╝ВъљВёИ ВХћВаЋ ВЌ░Жхг, ьЎюВБ╝ВёаВЮў ьїївъЉ ВцЉ Вџ┤вЈЎВё▒віЦ ВХћВаЋВЌљ вїђьЋю ВЌ░Жхг в░Ј CFD ВѕўВ╣ўьЋ┤ВёЮЖ│╝ вфеьўЋВІцьЌўВЮў вХѕьЎЋВІцВё▒ВЌљ вїђьЋю ВЌ░ЖхгвЦ╝ ВѕўьќЅьЋа ВўѕВаЋВЮ┤вІц.