Article information

J. Ocean Eng. Technol. 2019;33(3):272-279

Publication date (electronic) : 2019 June 27

doi : https://doi.org/10.26748/KSOE.2018.099

Jae-Hwan Lee^*, Byoungjae Park^,**, Hyuek-Jin Choi^**

^*Naval Architecture and Ocean Engineering, Chungnam National University, Daejon, Korea

^**Korea Research Institute of Ships and Ocean Engineering, KRISO, Daejon, Korea

이재환^*, 박병재^,**, 최혁진^**

^*충남대학교 선박해양공학과

^**한국해양과학기술원 부설 선박해양플랜트연구소

Corresponding author Byoungjae Park: +82-42-866-3736, byoungjae@kriso.re.kr

Received 2019 January 4; Revised 2019 May 27; Accepted 2019 June 13.

Trans Abstract

1. 개 요

해양플랜트의 건설, 해양자원 탐사 및 개발 등 해저 작업의 확대에 따라 다양한 해양장비 및 로봇의 개발되고 운용되고 있다. 일반적으로 해양장비 및 로봇의 전원, 통신 및 제어를 위한 전자장비등은 운용환경의 높은 수압으로부터 보호하기 위하여 내압용기에 탑재된다. 따라서 내압용기 설계는 외압으로부터 내부를 대기압 상태로 유지하기 위하여 다양한 해석과 실험이 필수적으로 요구된다. 내압용기는 주로 원통형이 사용되며 직경과 두께의 비(D/t)를 기준으로 20이하이면 두꺼운 원통형 내압용기로, 20이상이면 얇은 원통형 내압용기로 분류할 수 있다. 국내의 원통형 내압용기 설계 관련 연구는 1991년 소형잠수정(옥포6000)의 개발을 위한 심해용 압력용기 붕괴해석 연구(Shin and Yoo, 1999)를 시작으로 티타늄 Ti-6AI-4V 재료의 심해저 잠수정용 내압용기의 항복응력, 설계압력, 외경과 두께의 확률변수에 대한 신뢰성기반의 최적설계 연구(Jeong et al., 2006)와 동일 내압용기의 고압챔버 실험 관련 연구(Jeong et al., 2007)가 수행되었다. 또한 천해용 얇은 실린더의 설계(Lee et al., 2016) 및 잠수함 내압선체의 좌굴과 관련한 연구(Kim, et al., 2012; Nho, et al., 2017)등의 연구가 수행되었다. 다만, 앞서 언급한 연구들은 대부분 얇은 원통형 내압용기를 대상으로 수행되었다. 한편, 두꺼운 원통형 내압용기와 관련한 연구는 원자로 실린더 설계와 관련한 파손압력 추정(Yoo et al., 2010)이 있으나 주로 육상의 원자력 분야에서 수행되고 있으며 특히 조선⋅해양 분야에서는 수심 2000m급 두꺼운 내압용기 설계를 위하여 ASME(The American Society of Mechanical Engineers) BPVC(Boiler and pressure vessel code) Section VIII 규정을 기초로 하여 초기설계 후 구조해석을 하고, 내압용기를 제작하여 내압시험과의 결과를 비교하는 연구(Choi et al., 2016)를 수행하였으나 두꺼운 원통형 내압용기에 대한 연구는 아직 많이 부족한 실정이다.

본 연구에서는 두꺼운 내압용기의 설계/해석/실험에 필수적으로 요구되어지는 붕괴하중의 예측을 위하여 기 발표된 두꺼운 실린더의 붕괴하중과 관련한 다양한 이론식들을 현상에 따라 정리하고 비선형 좌굴해석을 수행하여 붕괴하중을 산출하고 기발표된 연구 및 이론식과 비교하였다. 또한 추후 계획된 두꺼운 강철 내압용기의 압력챔버 실험을 위하여 설계치수를 검토하고 붕괴하중을 산출하였다.

2. 두꺼운 실린더의 붕괴하중식

외압을 받는 실린더의 손상과정은 좌굴을 거쳐 소성붕괴에 이르게 되므로 좌굴하중과 붕괴하중을 모두 고려해야한다. 특히, 두꺼운 실린더의 좌굴하중은 항복이 발생하기 시작하는 하중으로 정의되는 탄성한계하중보다 큰 경우가 많으므로 좌굴하중, 소성붕괴하중과 함께 탄성한계하중에 대한 검토도 병행되어야 한다. 실린더의 붕괴하중과 관련한 참고문헌들마다 사용기호가 달라 혼동을 줄이고자 본 논문에서는 Fig. 1과 같이 사용 기호를 통일하여 정리하였다.

Fig. 1

Basic geometric variables

2.4 난형도(Ovality)의 영향

Timoshenko and Gere(1961)에서 처음 소개된 실린더의 난형도(Ovality or noncircularity)는 원형의 완벽함을 의미한다. 난형도는 구조의 불안정성이 발생함을 의미하며 정도가 커지면 불안정성이 커지므로 좌굴하중은 작아진다. 즉, 난형도에 비례하여 좌굴에 취약하다는 의미이다. Bickell and Ruiz(1967)은 Fig. 2와 같은 형태의 난형도가 있는 두꺼운 실린더의 좌굴하중식을 식 (14)-(15)와 같이 제시하였다.

Fig. 2

Ovality of cylinder

(14) Pc'=2σ0t/D1+1.5u(1−0.2D/L)100t/D(with D/L<5)

(15) Pc'=2σ0tD(withDL>5)

여기서, σ₀은 항복응력, D는 평균지름을 나타내며u는 Out-of-roundness로 다음 중 큰 값을 사용한다.

(16) u=2(Dmax−Dmin)Dmax+Dmin×100    or  u=4aD×100

3. 두꺼운 원통형 내압용기의 비선형좌굴해석

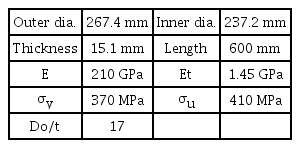
비선형좌굴해석은 Choi et al.(2016)에서 수행한 압력챔버 실험을 참고하여 수행하였다. Choi et al.(2016)의 실험에 사용된 덮개를 갖는 알루미늄 내압용기의 주요 제원은 Table 1과 같으며 직경과 두께의 비(D/t)가 14.75로 두꺼운 실린더로 분류될 수 있다. 실험에서는 Fig. 3과 같이 60MPa까지 가압하고 원주방향 변형량을 측정하였다.

Table 1

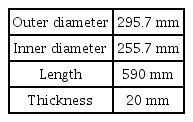
Dimension of cylinder (Choi et al., 2016)

Fig. 3

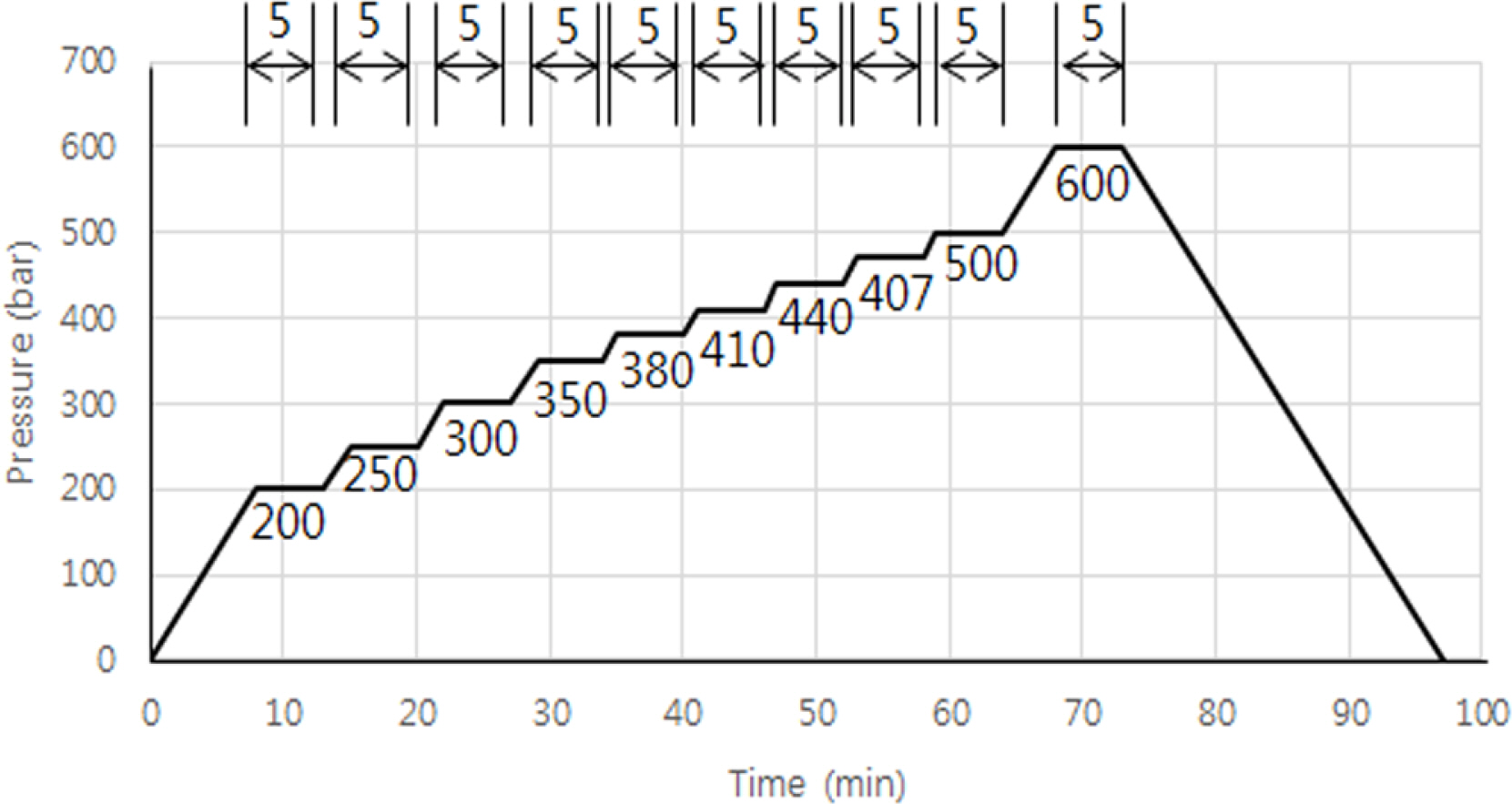
Chamber test Condition (Choi et al., 2016)

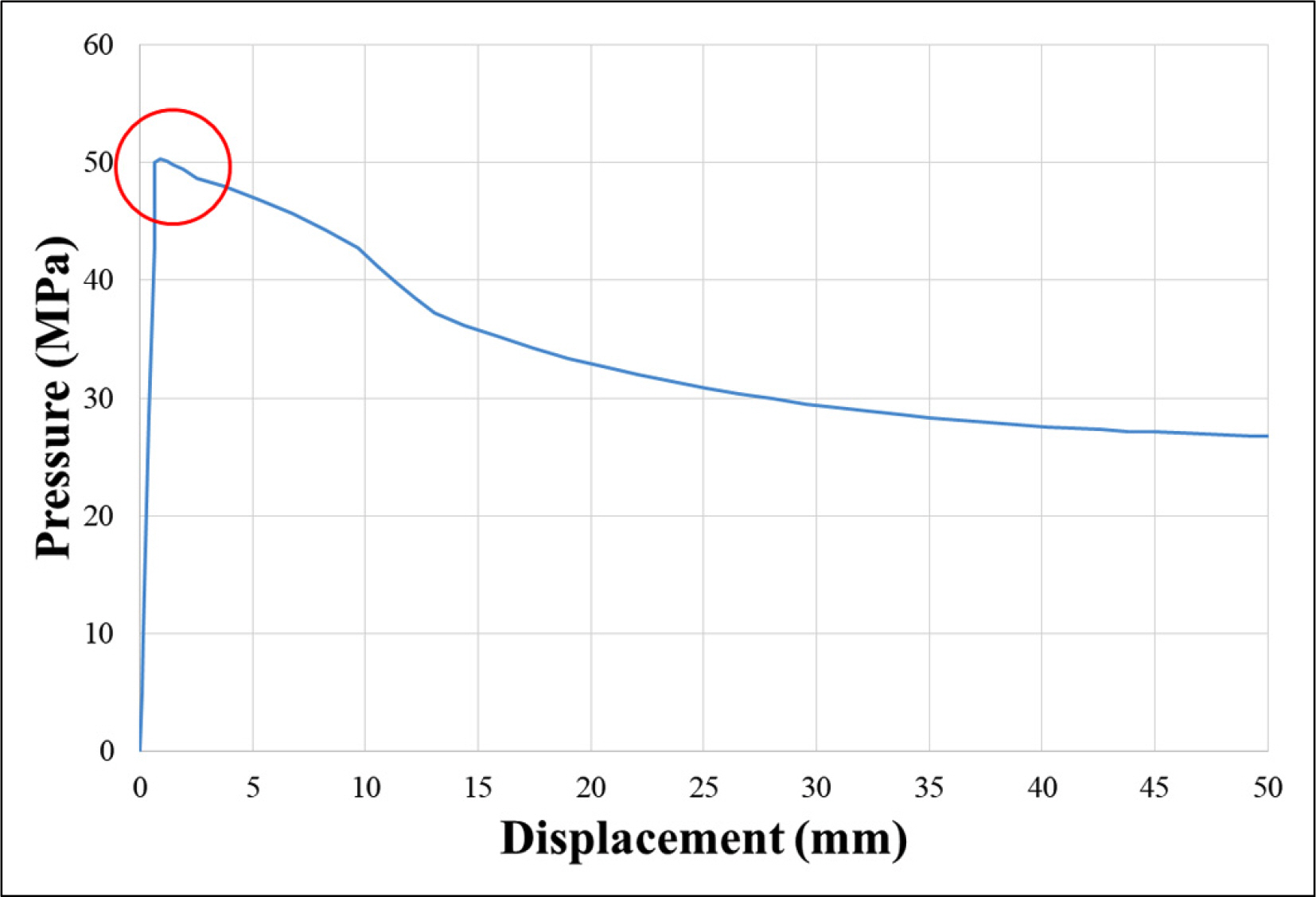
Fig. 4는 Choi et al.(2016)의 압력챔버 실험의 결과로 내압용기 외부 표면에서 측정된 원주방향 변형률은 압력이 45MPa까지 선형적으로 증가하다 이후 급격하게 변화하는 것으로 보아 45MPa에서 항복이 발생하고 소성변형이 발생하여 50.5MPa에서 붕괴되었다. 단, 압력챔버 실험은 덮개와 내압용기의 결합부에 틈이 발생하여 종료되었으므로 실제 붕괴하중은 더 클 것으로 예상되나 정확한 예상이 어려우므로 본 연구에서는 붕괴하중을 50.5MPa로 가정하였다. 또한 Fig. 5와 같이 내압용기의 최종 변형형상은 좌굴차수가 3(Lobe 3)인 형상이다.

Fig. 4

Comparison of test and FEA (Choi et al., 2016)

Fig. 5

Collapse of thick aluminum cylinder (Choi et al., 2016)

3.1 비선형 좌굴해석

비선형 좌굴해석은 완전 원형단면의 내압용기와 제작공차를 가정하여 실제 형상에 난형도를 부여한 내압용기에 대하여 수행하고 붕괴하중을 산출하였다. 비선형 좌굴해석에 사용된 주요 물성조건은 Table 2와 같다. 비선형좌굴해석은 Fig. 6과 같이 탄성좌굴해석과 고유치해석을 통하여 좌굴형상을 결정하고 이를 연계하여 비선형 좌굴해석을 수행하였다. Choi et al.,(2016) 실험의 붕괴하중은 50.5MPa이나 실험이 중단된 것을 감안하여 60MPa의 압력을 부여하였으며 실험조건과 동일하게 바닥면을 고정하였다. 위/아래 덮개와 내압용기의 연결부와 3차 모드에 의한 변형(외부 겉면이 3방향에서 안쪽으로 진행됨)을 고려하여 내압용기 내부에 접촉조건을 적용하였다. 해석은 상용 유한요소해석 프로그램인 ANSYS를 사용하였으며 증분량의 크기를 일정한 값으로 제어하여 안정적인 수렴성을 확보할 수 있는 호장증분법(Arc-Length method)을 사용하였다.

Table 2

Conditions of nonlinear buckling analysis

Fig. 6

Procedure of nonlinear buckling analysis

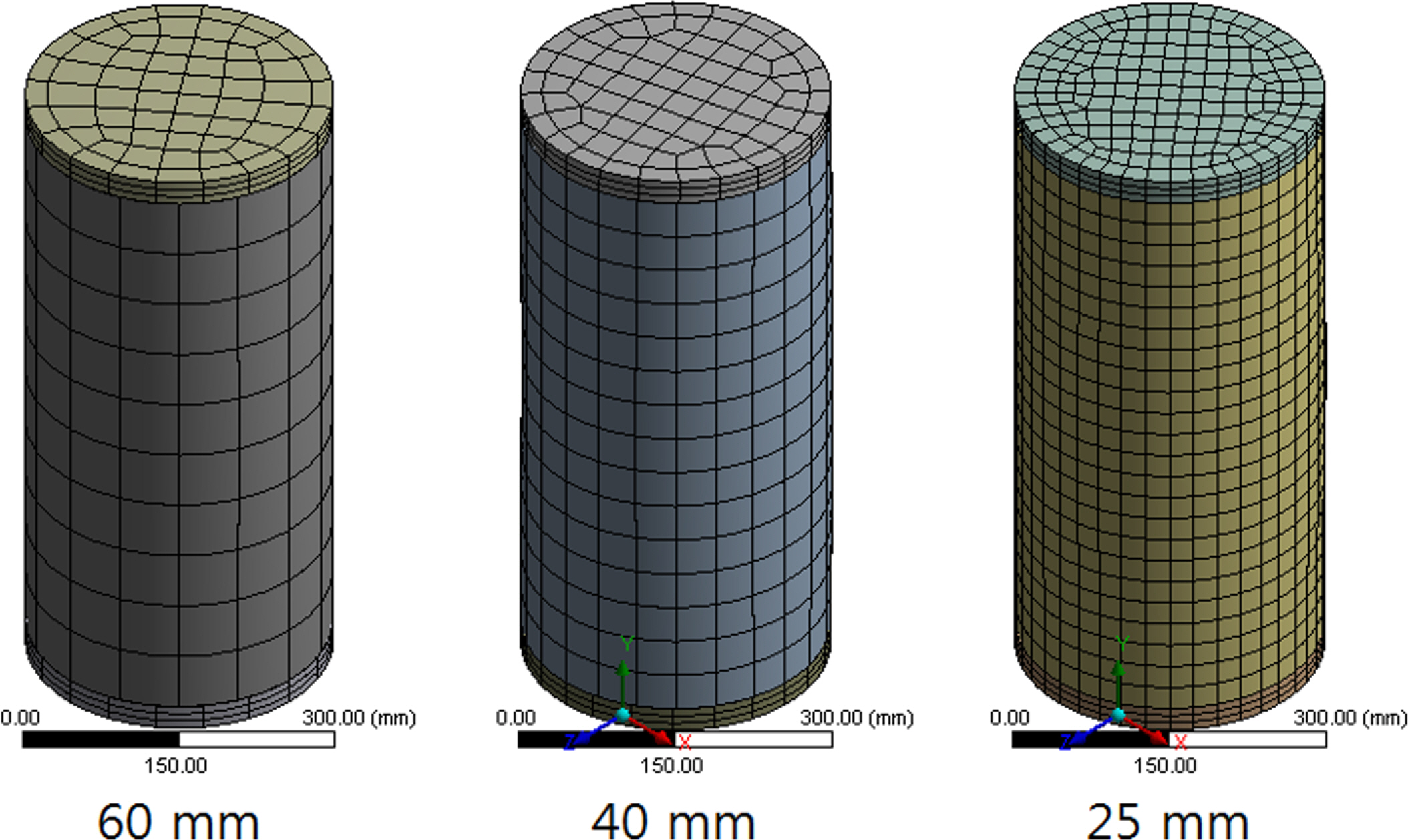
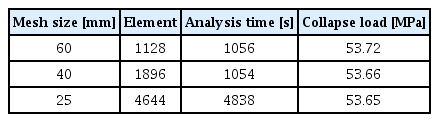
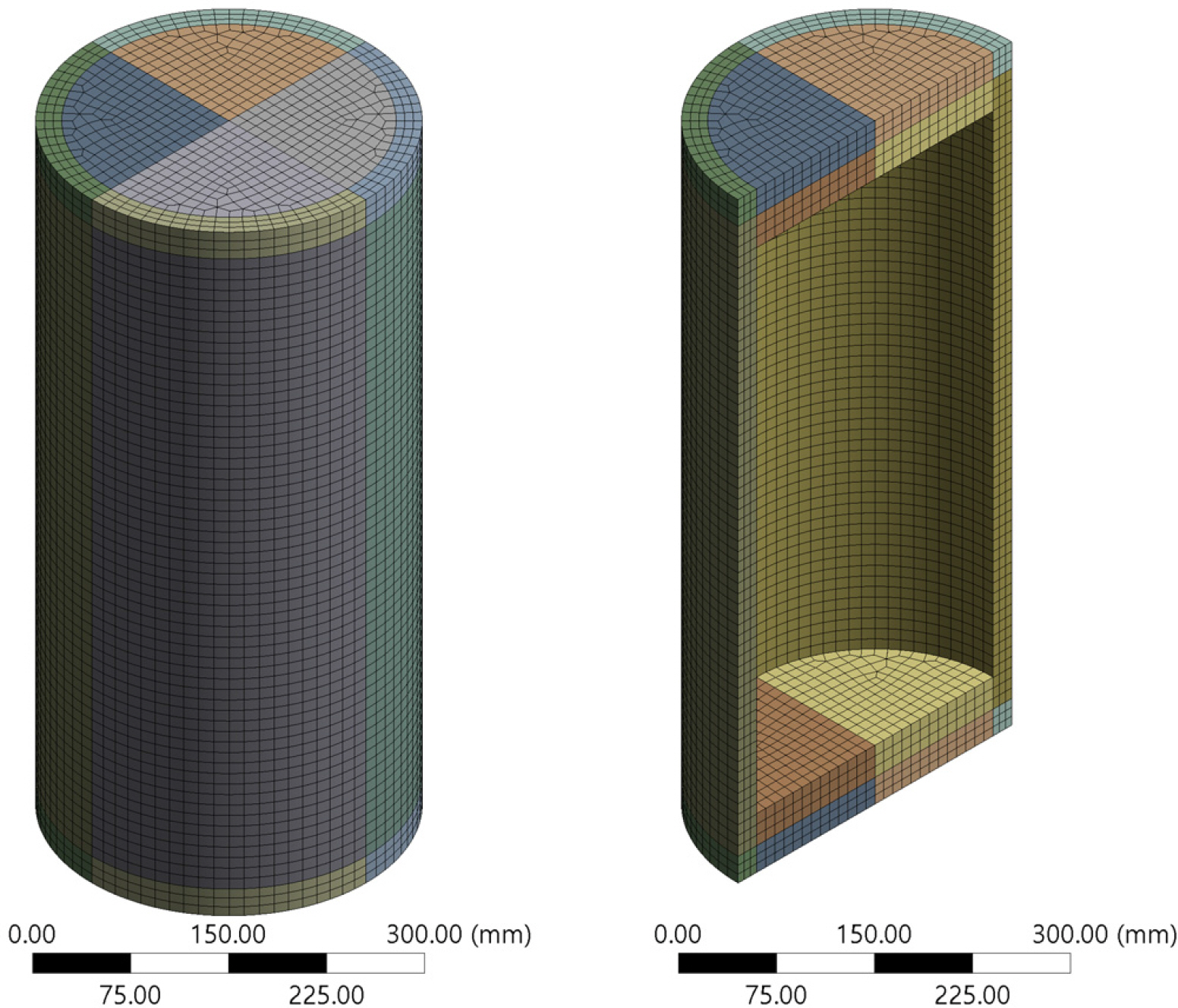
완전 원형단면 내압용기의 경우, Fig. 7 및 Table 3과 같이 요소크기에 관계없이 수렴된다. 반면 1mm의 Imperfection이 있는 단면의 내압용기의 비선형 해석결과는 요소의 대칭성과 크기에 따라 Fig. 8과 같이 변형형상이 달라지므로 대칭성과 요소 크기를 고려해야한다. 이를 고려하여 작성된 유한요소모델은 Fig. 9와 같으며 사용된 절점은 111,295개, 요소는 22,416개이다.

Fig. 7

Elements for mesh test

Table 3

Analysis time

Fig. 8

Comparison of deformation shape according to the number of element

Fig. 9

FEM model

3.2 완전 원형단면 내압용기의 비선형 좌굴해석

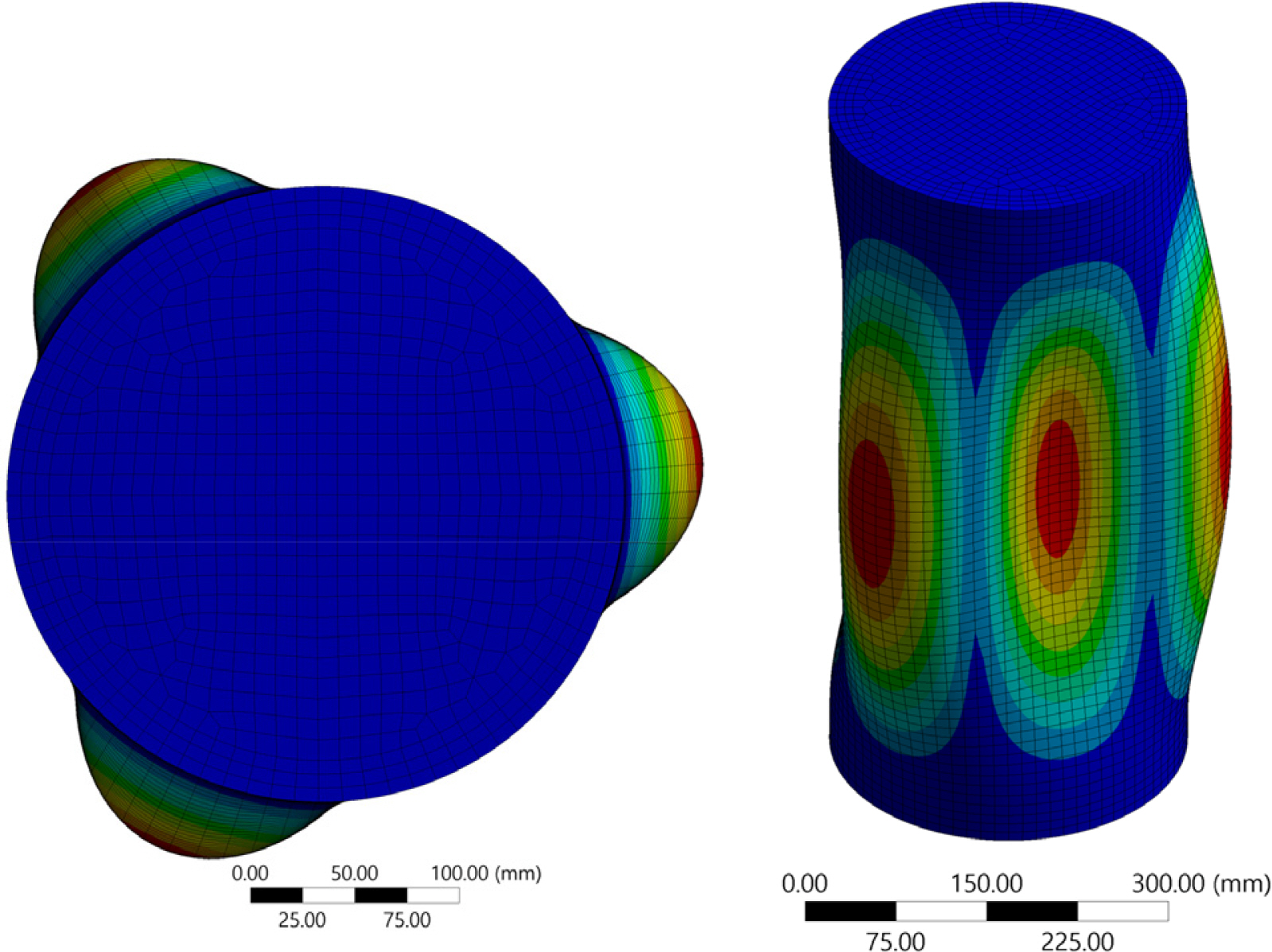
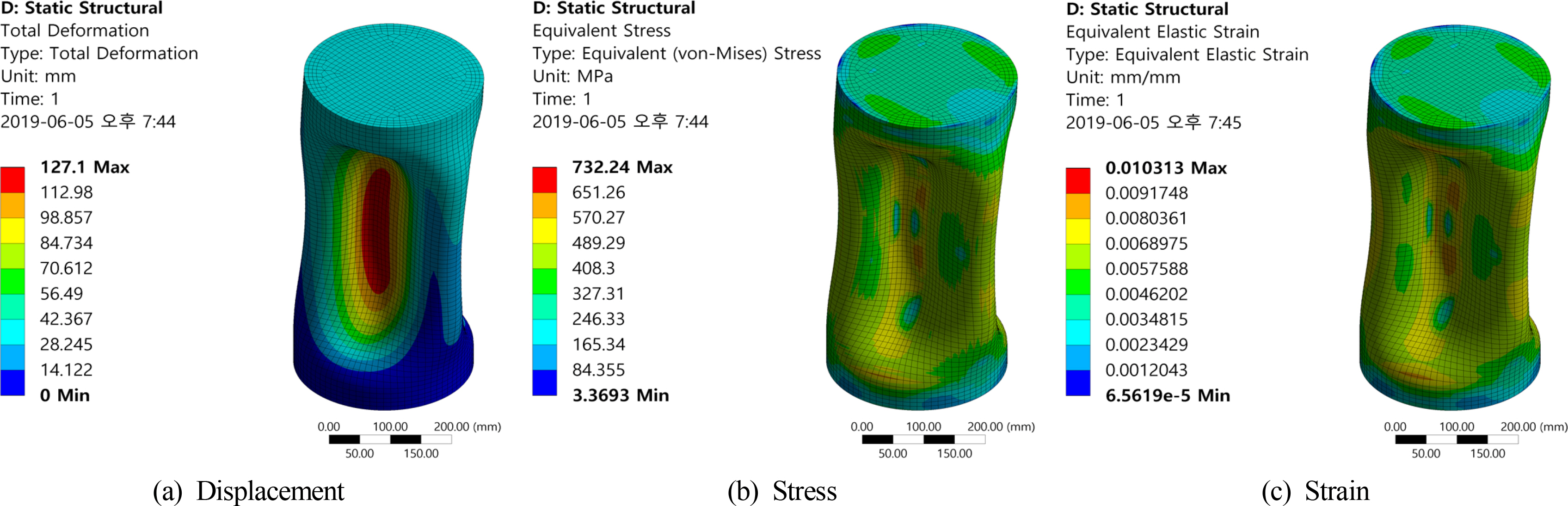
일반적인 구조물에서 좌굴은 1차 모드에서 붕괴가 되면 나머지 모드들은 큰 의미를 갖기 어려운 것으로 알려졌으나 외압을 받는 덮개가 있는 실린더는 3차 모드로 붕괴가 된다(Timoshenko and Gere, 1961; Nho et al., 2017). 완전 원형단면 내압용기의 고유치 해석결과에 따른 3차 모드 형상은 Fig. 10과 같으며 Fig. 11은 해석결과의 변위, 응력, 변형률을 보여주고 있다. Fig. 12는 완전 원형단면 내압용기 비선형 좌굴해석의 변위와 하중 그래프로 하중이 급격히 감소하는 53.25MPa을 붕괴하중으로 산정할 수 있다.

Fig. 10

Eigenvalue buckling analysis (Perfect section)

Fig. 11

Results of nonlinear buckling analysis (Perfect section)

Fig. 12

Displacement-Collapse pressure curve (Perfect section)

3.3 Imperfection이 있는 내압용기의 비선형 좌굴해석

완전 원형이 아닌 즉, 난형에 의한 영향을 검토하기 위하여 Table 3과 Fig. 13과 같이 2가지 경우에 대하여 비선형좌굴 해석을 수행하였다. 일반적으로 기계금속의 제작공차는 0.05로 매우 작아 난형을 발생시키기에 부족할 것으로 판단하여 제작공차에 비해 비교적 큰 1mm와 2.95mm를 대상으로 해석을 수행하였다. 단, 두께는 20mm로 일정하게 유지하였다.

Fig. 13

Variables of imperfection section

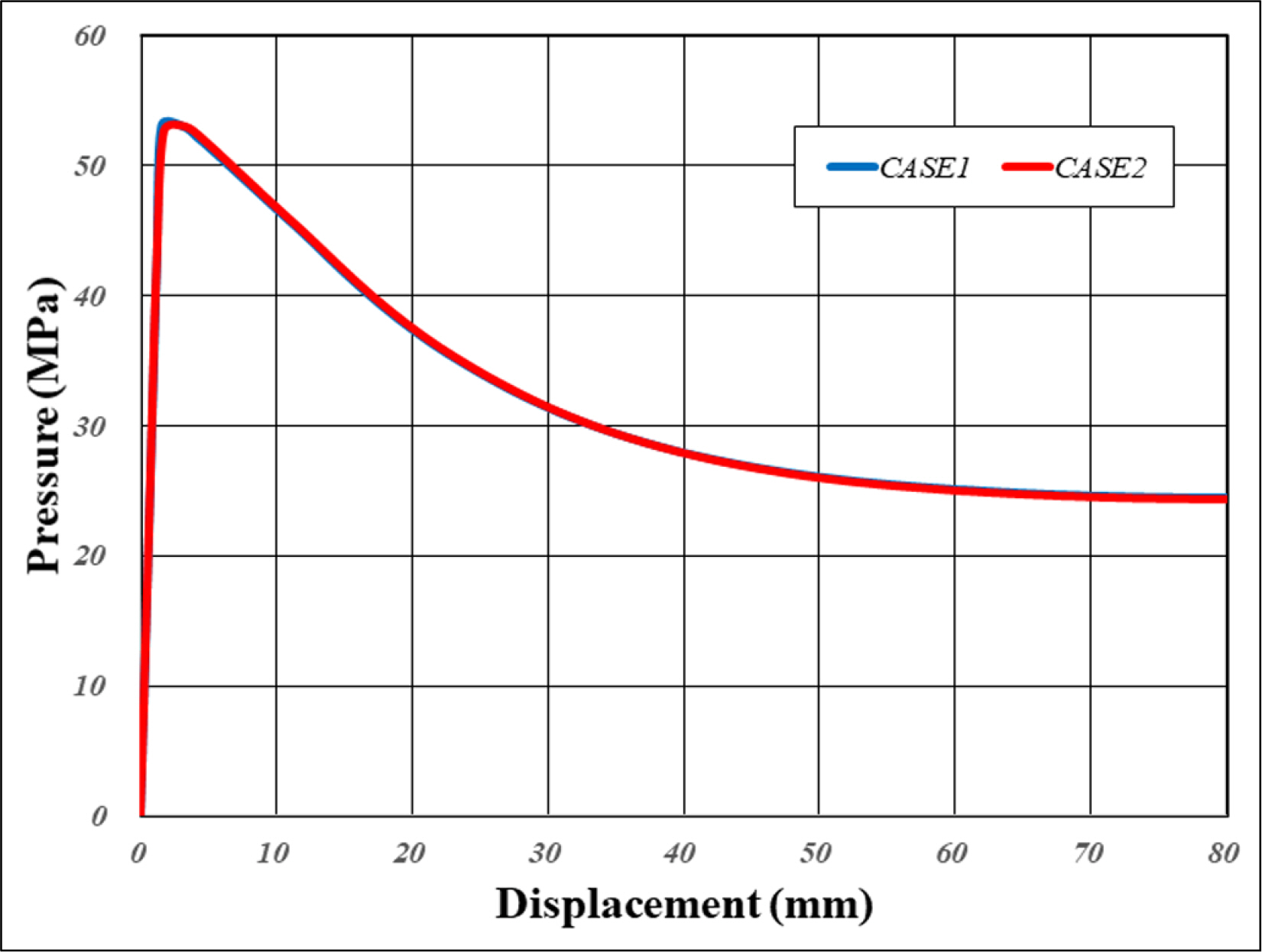
Fig. 14는 Case 1의 비선형 해석결과이며 Fig. 15는 Case 2의 비선형 해석결과이다. 변형형상은 완전 원형단면 내압용기 비선형좌굴해석 결과(Fig. 11)와 유사하나 난형에 의하여 응력 및 변형량의 분포가 다름을 확인할 수 있다. Fig. 16은 Case 1과 Case 2의 변위 하중곡선을 보여주고 있으며 각각의 붕괴하중은 53.12MPa, 52.96MPa로 난형에 의하여 붕괴하중이 감소함을 확인할 수 있다.

Fig. 14

Results of nonlinear buckling analysis (Imperfect section-Case1)

Fig. 15

Results of nonlinear buckling analysis (Imperfect section-Case2)

Fig. 16

Displacement-Collapse pressure curve (Imperfect section)

Table 4

Dimensions of imperfection section

4. 이론식 및 비선형 좌굴해석의 붕괴하중 비교

압력챔버실험으로 도출된 붕괴하중과 이론식 및 비선형좌굴해석의 붕괴하중은 Table 5와 같다.

Table 5

Collapse pressure

Table 5에서와 같이 탄성한계하중(식 (11))은 53.88MPa로 실험의 붕괴하중(50.50MPa)과 비교하여 약 6.69% 크게 예측하고 있으나 완전 원형 단면의 비선형좌굴해석의 붕괴하중(53.25MPa)과는 약 1.18%의 오차를 보인다. 반면 좌굴하중(식 (3))은 55.77MPa로 탄성한계하중(53.88MPa)보다 약 3.51% 크게 예측하고 있으며 이를 통하여 좌굴이 탄성한계를 벗어나 발생하는 것으로 유추할 수 있다. 소성붕괴하중(식 (13))은 62.10MPa로 실험의 붕괴하중과 비교해서는 약 22.97%, 완전 원형 단면의 비선형좌굴해석에 비해서는 16.62% 크게 예측하고 있다. 또한 난형도를 고려한 붕괴하중(식 (15))는 50.05MPa로 실험결과와 가장 유사하나 실험이 중단된 것을 감안하면 실제보다 작게 예측하고 있다고 판단된다. 위의 분석을 통하여 두꺼운 실린더의 붕괴하중 예측을 위해서는 탄성한계하중식을 적용하는 것이 좋을 것으로 판단된다.

Imperfection을 고려한 비선형좌굴해석인 Case 1과 Case 2의 붕괴하중은 각각 53.12MPa과 52.96MPa로, 완전원형 단면 비선형좌굴해석의 붕괴하중에 비하여 0.24%, 0.55% 감소함을 알 수 있다. 즉, Imperfection이 존재하는 경우, 붕괴하중이 감소함을 확인하였다. 하지만 가정한 Imperfection의 크기가 일반적인 제작공차에 비하여 매우 크기 때문에 제작상의 이유로 붕괴하중이 줄어들진 않을 것으로 보인다.

5. 강철 원통 실린더 제원(치수) 산출

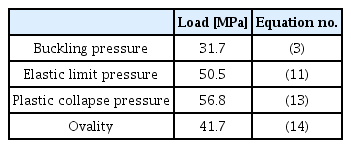
Choi et al.(2016)에 활용된 압력챔버는 최대 60MPa(수심 6,000m)까지 하중을 가할 수 있다. 현재 알루미늄으로 제작된 내압용기의 붕괴하중이 50.5MPa이므로 동일제원의 강철 원통형 내압용기는 실험을 통하여 붕괴 혹은 좌굴의 관측이 불가능하다. 따라서 원통형 내압용기의 제원 결정 시 이를 고려해야한다. Table 6의 강철 실린더 치수는 외경 267.4mm, 내경 237.2mm, 길이 600mm, 두께 15.1mm, 탄성계수 210GPa, 소성접선계수 1.45GPa, 항복강도 370MPa, 최종강도 410MPa이다. 직경/두께 비(D/t=17)로 두꺼운 실린더에 속한다. 이론식에 의해 실린더의 붕괴하중을 예측하면, Table 7과 같이 좌굴하중은 31.86MPa, 탄성한계하중은 45.53MPa이며 소성붕괴하중은 51.20MPa이다. 실린더의 제작공차를 0.1%로 가정할 경우(Dmax와 Dmin의 차가 0.267mm)에는 난형도의 붕괴하중식에 의하여 40.82MPa로 예상된다. 한편 비선형좌굴해석에 의한 붕괴하중 값은 Fig. 17에서와 같이 50.3MPa로 산출되며 본 제원으로 압력챔버 실험을 수행할 경우 붕괴과정을 확인할 수 있을 것으로 보인다.

Table 6

Steel cylinder dimension

Table 7

Estimation of buckling and collapse loads by theory

Fig. 17

Collapse pressure (load) of thick steel cylinder

6. 결 론

본 연구에서는 정수압을 받는 두꺼운 알루미늄 내압용기의 붕괴하중 값을 도출하기 위하여 다양한 이론식을 조사하고 비선형 좌굴해석을 수행하여 기 발표된 압력챔버실험 결과와 비교하였으며 이로부터 다음과 같은 결론을 얻을 수 있다.

(1) 다양한 붕괴하중 이론식 중, 소성붕괴하중식 보다 탄성한계하중 식이 비선형좌굴해석과 가장 유사함을 확인하였으며 두꺼운 원통형 내압용기의 붕괴하중 예측을 위해서는 탄성한계하중식을 사용하는 것이 적정하다고 판단된다.

(2) 난형도가 존재할 경우에는 완전 원형단면의 내압용기의 붕괴하중보다 작아짐을 확인하였다. 하지만 그 영향이 크지 않아 실제 제작공차로 인한 난형도의 영향은 크지 않음을 알 수 있다.

(3) 난형도를 포함한 해석의 경우, 요소의 질에 따라 최종형상이 달라질 수 있으므로 요소의 대칭성과 크기가 매우 중요함을 확인하였다.

(4) 두꺼운 강철 내압용기 실험의 붕괴과정 검토를 위하여 비선형 좌굴해석과 이론식을 통하여 붕괴하중을 산출하여 실험을 위한 제원이 적정함을 확인하였다.

Article information Continued