|
 |
- Search
| J. Ocean Eng. Technol. > Volume 32(6); 2018 > Article |
|
Abstract
Recently, in an effort to reduce the energy efficiency design index (EEDI), studies on energy saving devices (ESDs) have been conducted. In this study, we designed a post-device suitable for a KRISO container ship (KCS) using computational fluid dynamics (CFD). In order to increase the efficiency of the post-device, a twisted rudder was used, which has a proven performance (showing a 1.34% reduction in DHP compared to the bare hull at 24 knots) in previous research at Pusan National University. In addition, an increase in efficiency was expected by the use of a rudder bulb, including the discontinuous section of the twisted rudder and a divergent propeller cap to prevent the contraction of the wake. The optimization criterion was the case where the delivery power was the least compared with the bare hull. We analyzed the cause of the efficiency increase through an analysis of the self-propulsion factor. The case study for optimization was divided into 4 types (1. clearance of the bulb and cap, 2. shape of the bulb, 3. size of the bulb and cap, and 4. asymmetric bulb). Finally, with a clearance of 50 mm from the ship, a spherical bulb with the cap having an angle of 5В°, and an asymmetric rudder bulb with a bulb diameter of 1.2H H/1.4H (horizontal/vertical) showed a 2.05% reduction in DHP compared to the bare hull at 24 knots. We will fabricate a post-device that will be optimized in the future and verify the performance of the post-device through model tests.
м „ м„ёкі„м ҒмңјлЎң нҷҳкІҪмҳӨм—јм—җ лҢҖн•ң кҙҖмӢ¬мқҙ лҶ’м•„м§җм—җ л”°лқј көӯм ңн•ҙмӮ¬кё°кө¬мқё IMO(International Maritime Organization)м—җм„ңлҠ” EEDI (Energy efficiency design index)лқјлҠ” м§Җн‘ңлҘј м ңмӢңн•ҳм—¬ м„ л°•мқҙ лӮҙлҠ” мқҙмӮ°нҷ”нғ„мҶҢ л°°м¶ңмқ„ к·ңм ңн•ҳкі мһҲлӢӨ. мқҙм—җ л”°лқј ESD(Energy saving device, м—җл„Ҳм§Җ м Җк°җ мһҘм№ҳ)м—җ лҢҖн•ң м—°кө¬к°Җ нҷңл°ңнһҲ 진н–үлҗҳкі мһҲлӢӨ. Carlton(1994)мқҖ лӢӨм–‘н•ң ESDлҘј н”„лЎңнҺ лҹ¬ м „л°©(Zoneв… ), н”„лЎңнҺ лҹ¬(Zoneв…Ў), н”„лЎңнҺ лҹ¬ нӣ„л°©(Zoneв…ў)м—җ л¶Җм°©лҗҳлҠ” ESDлЎң лӮҳлҲ„м—ҲлӢӨ(Fig. 1). к·ёлҰ¬кі ліё м—°кө¬м—җм„ңлҠ” мқҙлҘј к°Ғк°Ғ Pre-device, Main-device, Post-deviceлқјкі лӘ…н•ҳкІ лӢӨ.
лҢҖн‘ңм Ғмқё Pre-deviceлЎңлҠ” Pre-swirl stator(PSS), Pre-swirl duct (PSD) л“ұмқҙ мһҲмңјл©°, Main-deviceлЎңлҠ” Tip Rake propeller(TRP), Contra-rotating propeller(CRP), к·ёлҰ¬кі Post-deviceлЎңлҠ” 비лҢҖм№ӯ нғҖ(Twisted rudder), лҹ¬лҚ” лІҢлёҢ(Rudderbulb) л“ұмқҙ м•Ңл Өм ё мһҲлӢӨ.
ліё м—°кө¬лҠ” ESD мӨ‘ Post-deviceм—җ лҢҖн•ң м—°кө¬лЎң лҹ¬лҚ” лІҢлёҢ(Rudder bulb, лІҢлёҢ) л°Ҹ н”„лЎңнҺ лҹ¬ мәЎ(Cap, мәЎ)мқ„ ліөн•©м ҒмңјлЎң м„Өкі„н•ҳм—¬ CFD(Computational fluid dynamics)лҘј нҶөн•ң м„ л°•мқҳ м „лӢ¬лҸҷл Ҙ к°җмҶҢлҘј нҷ•мқён•ҳмҳҖлӢӨ.
лҹ¬лҚ” лІҢлёҢлҠ” м„ л°•мқҳ м—җл„Ҳм§Җ нҡЁмңЁмқ„ мғҒмҠ№мӢңнӮӨкё° мң„н•ҙ л„җлҰ¬ мӮ¬мҡ©лҗҳкі мһҲлҠ” ESDлЎң, мқјл°ҳм ҒмңјлЎң м•Ңл Ө진 лҹ¬лҚ” лІҢлёҢмқҳ мң мІҙлҸҷм—ӯн•ҷм Ғ нҡЁкіјлҠ” лӢӨмқҢкіј к°ҷлӢӨ(Okada et al., 2015).
(1) Hub vortex к°җмҶҢ
(2) н”„лЎңнҺ лҹ¬лЎң мқён•ң нӣ„лҘҳмқҳ мҲҳ축 к°җмҶҢ
(3) л°ҳлҘҳ мқҙл“қмңјлЎң мқён•ң м„ к°ҒнҡЁмңЁ н–ҘмғҒ
мҙҲкё° лҹ¬лҚ” лІҢлёҢлҠ” Costa bulbмҷҖ к°ҷмқҖ кө¬нҳ• лІҢлёҢлЎң м„Өкі„лҗҳм–ҙ мқјл°ҳм Ғмқё кө¬нҳ• н”„лЎңнҺ лҹ¬ мәЎкіј н•Ёк»ҳ мӮ¬мҡ©лҗҳм—ҲлӢӨ(Mewis and Deichmann, 2013). к·ёлҹ¬лӮҳ мң„мҷҖ к°ҷмқҖ лІҢлёҢ нҡЁкіјлҘј лҚ”мҡұ н–ҘмғҒмӢңнӮӨкё° мң„н•ҙ лҹ¬лҚ” лІҢлёҢлҝҗл§Ң м•„лӢҲлқј нғҖ(Rudder) л°Ҹ н”„лЎңнҺ лҹ¬ мәЎмқҙ ліөн•©м ҒмңјлЎң к°ңм„ лҗҳм—Ҳкі , к·ём—җ л”°лқј лӢӨм–‘н•ң Post-deviceк°Җ к°ңл°ңлҗҳм—ҲлӢӨ.
Nielsen et al.(2012)лҠ” м„ мІҙлҘј м ңмҷён•ң Conventional rudderм—җ Kappel propeller л°Ҹ лҹ¬лҚ” лІҢлёҢлҘј мӮ¬мҡ©н•ҳм—¬ м„Өкі„ мҶҚлҸ„ 18.5л…ёнҠё(34.262km/h)м—җм„ң м•Ҫ 9.3%мқҳ Specified MCR(Maximun continuous rating) к°җмҶҢ нҡЁкіјлҘј CFDлҘј нҶөн•ҙ нҷ•мқён•ҳмҳҖлӢӨ. Kim et al.(2014)лҠ” 13,000TEU м»Ён…Ңмқҙл„Ҳм„ мҡ© 비лҢҖм№ӯ нғҖм—җ лІҢлёҢмҷҖ Thrust finмқ„ м Ғмҡ©н•ҳм—¬ м•Ҫ 2% нҡЁмңЁ мҰқк°ҖлҘј мӢӨн—ҳмңјлЎң нҷ•мқё н•ҳмҳҖлӢӨ. Cha(2017)м—җм„ңлҠ” KCS(KRISO container ship)м„ л°•м—җ лҹ¬лҚ” лІҢлёҢмқҳ нҒ¬кё°м—җ л”°лҘё нҡЁмңЁмқ„ 비көҗн•ҳмҳҖлӢӨ. к·ё кІ°кіј лІҢлёҢмқҳ м§ҒкІҪмқҙ н”„лЎңнҺ лҹ¬ н—ҲлёҢ м§ҒкІҪмқҳ 0.9% мқј л•Ң м•Ҫ 1.6% нҡЁмңЁ мҰқк°ҖлҘј CFDлҘј нҶөн•ҙ нҷ•мқён•ҳмҳҖлӢӨ.
к·ёлҹ¬лӮҳ ліҙлӢӨ нҡЁмңЁм Ғмқё ESDк°ңл°ңмқ„ мң„н•ҳм—¬ мәЎкіј лІҢлёҢ мӮ¬мқҙ к°„к·№, лІҢлёҢ нҳ•мғҒ, нҒ¬кё° л“ұ Post-deviceлҘј м„ёл¶Җм ҒмңјлЎң лӮҳлҲ„м–ҙ лӢӨк°Ғм Ғмқё мғҒнҳё мҳҒн–Ҙ 분м„қмқҙ н•„мҡ”н•ҳлӢӨ. мқҙм—җ л”°лқј ліё м—°кө¬м—җм„ңлҠ” лҢҖмғҒм„ мқё 3,600TEUгҖҖKCSмқ„ кё°мӨҖмңјлЎң Post-deviceлҘј 2к°Җм§Җ(лҹ¬лҚ” лІҢлёҢ, мәЎ)лЎң лӮҳлҲ„м–ҙ м„Өкі„н•ҳмҳҖлӢӨ. Post-deviceмқҳ нҡЁмңЁ мҰқлҢҖлҘј мң„н•ҙ нғҖлҠ” м„ н–үм—°кө¬мқё Tae(2017)м—җм„ң мӢӨн—ҳ л°Ҹ CFDлҘј нҶөн•ҙ м „лӢ¬лҸҷл Ҙ к°җмҶҢ нҡЁкіјк°Җ мһ…мҰқлҗң 비лҢҖм№ӯ нғҖлҘј мӮ¬мҡ©н•ҳмҳҖмңјл©°, 추к°Җм ҒмңјлЎң 비лҢҖм№ӯ нғҖмқҳ л¶Ҳм—°мҶҚ лӢЁл©ҙмқ„ нҸ¬н•Ён•ҳлҠ” лҹ¬лҚ” лІҢлёҢ л°Ҹ нӣ„лҘҳмқҳ мҲҳ축мқ„ м–өм ңн•ҳлҠ” л°ңмӮ°нҳ• н”„лЎңнҺ лҹ¬ мәЎмқ„ мӮ¬мҡ©н•ҳм—¬ нҡЁмңЁ мғҒмҠ№мқ„ кё°лҢҖн•ҳмҳҖлӢӨ. Post-deviceмқҳ нҡЁмңЁ 비көҗлҠ” Bare hull лҢҖ비 м „лӢ¬лҸҷл Ҙмқҙ к°ҖмһҘ м ҒмқҖ caseлҘј лӘ©м Ғн•ЁмҲҳлЎң л‘җм—Ҳмңјл©°, мһҗн•ӯмҡ”мҶҢ 분м„қмқ„ нҶөн•ң нҡЁмңЁ мғҒмҠ№ мӣҗмқёмқ„ 분м„қн•ҳмҳҖлӢӨ. 추нӣ„ мөңм Ғ м„Өкі„лҗң Post-deviceлҘј м ңмһ‘н•ҳм—¬ лӘЁнҳ•мӢңн—ҳмқ„ нҶөн•ң мһҗн•ӯ м„ұлҠҘмқ„ кІҖмҰқн• мҳҲм •мқҙлӢӨ.
ліё м—°кө¬м—җ мӮ¬мҡ©лҗң нғҖлҠ” м„ н–үм—°кө¬мқё Tae(2017)м—җм„ң м„Өкі„лҗң Prototype 비лҢҖм№ӯ нғҖмқҙлӢӨ. Tae(2017)м—җм„ңлҠ” CFDн•ҙм„қмқ„ нҶөн•ҙ 비лҢҖм№ӯ нғҖм—җ мң мһ…лҗҳлҠ” мһ…мӮ¬к°Ғмқ„ нҢҢм•…н•ң нӣ„ м„Өкі„н•ҳкі мһҗ н•ҳмҳҖмңјлӮҳ, 비нӢҖлҰј к°Ғмқҙ 30В°мқҙмғҒ кіјлҸ„н•ҳкІҢ кІ°м •лҗҳм–ҙ м°Ём„ мұ…мңјлЎң к°ҖмһҘ мқјл°ҳм ҒмңјлЎң мӮ¬мҡ©н•ҳлҠ” Prototype 5В°мқҳ 비лҢҖм№ӯ нғҖлҘј мӮ¬мҡ©н•ҳмҳҖлӢӨ. Kim et al.(2009)мқҖ мң м „мһҗ м•Ңкі лҰ¬мҰҳмқ„ кё°лІ•мқ„ мӮ¬мҡ©н•ҳм—¬ 12,000TEU м»Ён…Ңмқҙл„Ҳм„ мқ„ лҢҖмғҒмңјлЎң мәҗ비н…Ңмқҙм…ҳмқҙ к°ҖмһҘ м ҒмқҖ 비лҢҖм№ӯ нғҖлҘј м„Өкі„н•ҳмҳҖлӢӨ. м—°кө¬ кІ°кіј 비нӢҖлҰј к°Ғ 7~8лҸ„м—җм„ң к°ҖмһҘ м ҒмқҖ мәҗ비н…Ңмқҙм…ҳмқҙ л°ңмғқлҗҳлӮҳ мқҙ кІҪмҡ° нҡЁмңЁ л°Ҹ м Җн•ӯкҙҖм җм—җм„ң л¶ҲлҰ¬н•ҳм—¬ мқјл°ҳм Ғмқё 비нӢҖлҰј к°Ғмқё 5В°лҘј мӮ¬мҡ©н•ҳмҳҖлӢӨ. Heo(2017)мқҖ 3,600TEU KCS м„ л°•м—җ нҳјнғҖ(Semi-spade rudder)лҢҖ비 мҡ°мҲҳн•ң м „лӢ¬лҸҷл Ҙ к°җмҶҢ л°Ҹ м–‘н•ӯ비лҘј к°Җм§ҖлҠ” 비лҢҖм№ӯ нғҖлҘј м„Өкі„н•ҳмҳҖлӢӨ. 비лҢҖм№ӯ нғҖмқҳ м„Өкі„ мӢң м Җмһҗмқҳ мӢӨм„ л№„лҢҖм№ӯ нғҖ м„Өкі„ мӢңмқҳ кІҪн—ҳмқ„ нҶ лҢҖлЎң н‘ңмӨҖмңјлЎң мӮ¬мҡ©н•ҳлҠ” 비нӢҖлҰј к°Ғ 5В°лҘј мӮ¬мҡ©н•ҳмҳҖлӢӨ.
비лҢҖм№ӯ нғҖлҠ” м „нғҖ(Full-spade rudder)мқҳ мқјмў…мңјлЎңмҚЁ нҳјнғҖмқҳ к°„к·№м—җм„ң л°ңмғқн•ҳлҠ” мәҗ비н…Ңмқҙм…ҳ л¬ём ң л°Ҹ нҳј(Horn) л’·л¶Җ분м—җ л°ңмғқн•ҳлҠ” мҷҖлҘҳлҘј м°ЁлӢЁн•ҙ мЈјлҠ” мһҘм җмқҙ мһҲлӢӨ. ліё м—°кө¬м—җ мӮ¬мҡ©лҗң нҳјнғҖ л°Ҹ 비лҢҖм№ӯ нғҖмқҳ нҳ•мғҒмқҖ Fig. 2мҷҖ к°ҷмңјл©°, мһҗм„ён•ң м ңмӣҗмқҖ Table 1кіј к°ҷлӢӨ.
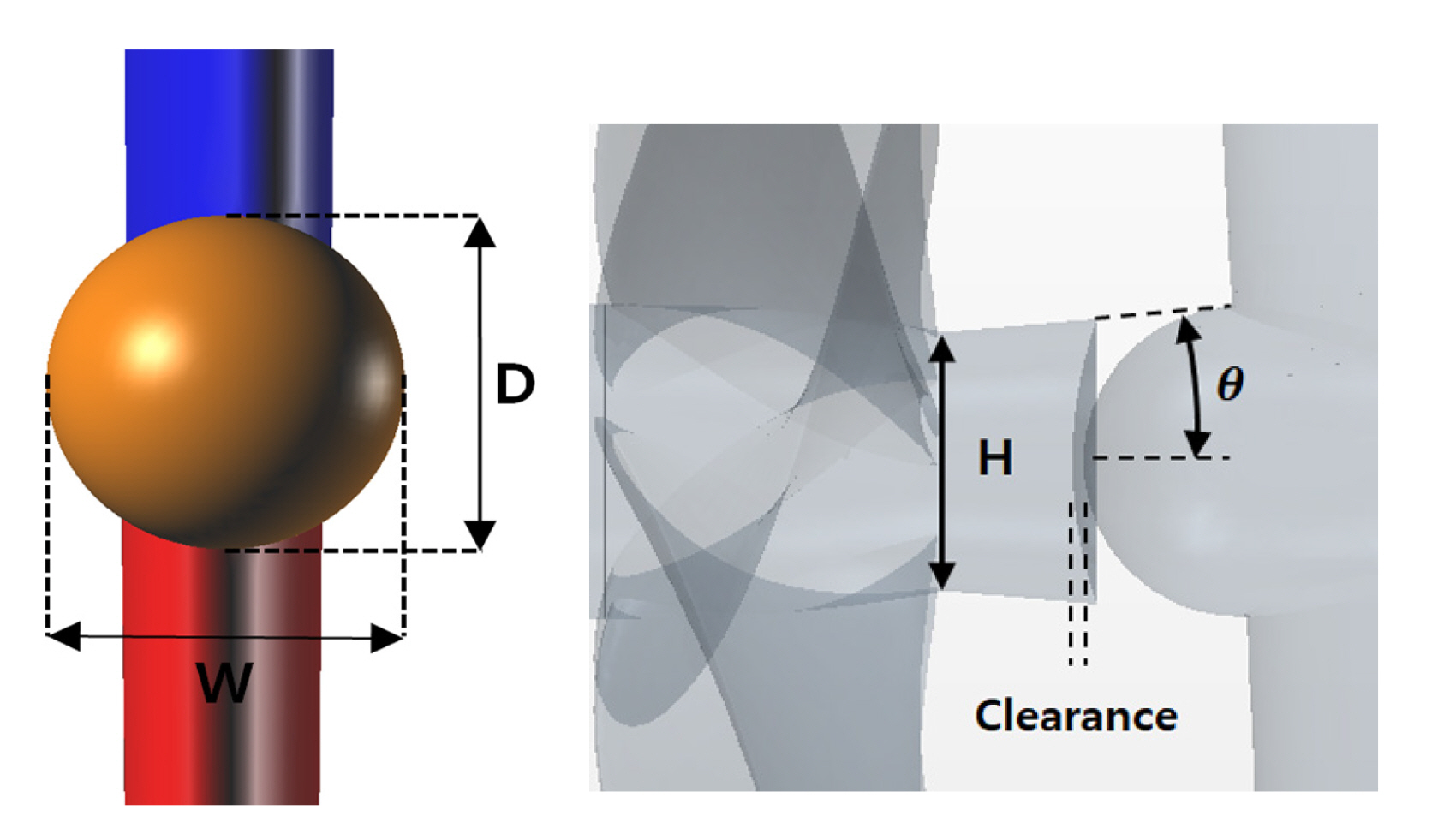
Fig. 3мқҖ лҹ¬лҚ” лІҢлёҢ л°Ҹ мәЎмқҳ кё°нҳём—җ кҙҖн•ң м •мқҳмқҙлӢӨ. WлҠ” лҹ¬лҚ”лІҢлёҢмқҳ к°ҖлЎңл°©н–Ҙ м§ҒкІҪ, DлҠ” лҹ¬лҚ” лІҢлёҢмқҳ м„ёлЎңл°©н–Ҙ м§ҒкІҪ, HлҠ” н•ҳлҘҳл°©н–Ҙмқҳ н—ҲлёҢ м§ҒкІҪ, ОёлҠ” мәЎмқҳ к°ҒлҸ„мқҙлӢӨ. лҹ¬лҚ” лІҢлёҢмҷҖ мәЎмқҖ н”„лЎңнҺ лҹ¬ нӣ„лҘҳмқҳ мҲҳ축мқ„ м–өм ңн•ңлӢӨлҠ” кҙҖм җм—җм„ң лҸҷмқјн•ң лӘ©м Ғмқ„ к°Җм§җмңјлЎң н•ҳлӮҳмқҳ ESDмІҳлҹј м„Өкі„н•ҳмҳҖлӢӨ. мҰү, мәЎмқ„ л”°лқј л°ңмӮ°лҗң нқҗлҰ„мқҙ лҹ¬лҚ” лІҢлёҢм—җ мң м„ нҳ•мңјлЎң мқҙм–ҙм§Ҳ мҲҳ мһҲлҸ„лЎқ мәЎмқҳ к°ҒлҸ„мҷҖ лІҢлёҢмқҳ м§ҒкІҪмқ„ н•ҳлӮҳмқҳ ліҖмҲҳлЎң м„Өкі„н•ҳмҳҖлӢӨ. лҹ¬лҚ” лІҢлёҢмқҳ нӣ„лҘҳл°©н–Ҙ кёёмқҙлҠ” 비лҢҖм№ӯ нғҖмқҳ мөңлҢҖ л‘җк»ҳ м§Җм җк№Ңм§Җ м„Өкі„н•ҳм—¬ 비лҢҖм№ӯ нғҖмқҳ мғҒл¶ҖмҷҖ н•ҳл¶Җ л¶Ҳм—°мҶҚл©ҙмқ„ нҸ¬н•Ён•ҳмҳҖлӢӨ. лҳҗн•ң н”„лЎңнҺ лҹ¬лЎң мқён•ҙ мҲҳ축лҗҳлҠ” нӣ„лҘҳлҘј ліҙмҷ„н•ҙ мЈјкё° мң„н•ҙ мәЎмқҖ л°ңмӮ°нҳ•мңјлЎң(Оё>0), лҹ¬лҚ” лІҢлёҢмқҳ м§ҒкІҪмқҖ н—ҲлёҢліҙлӢӨ нҒ¬кІҢ(W, D>1H) м„Өкі„н•ҳмҳҖлӢӨ. к·ё нӣ„ Table 2мҷҖ к°ҷмқҙ 4к°Җм§Җ CaseлҘј м„ м •н•ҙ мәЎкіј лІҢлёҢмқҳ м„ұлҠҘмқ„ 비көҗн•ҳмҳҖмңјл©°, 2.2.1~2.2.4м Ҳм—җлҠ” Caseм—җ лҢҖн•ң м„Өкі„ л°©лІ•мқ„, 4.2.1~4.2.4м Ҳм—җлҠ” Caseм—җ лҢҖн•ң м „лӢ¬лҸҷл Ҙ 비көҗ л°Ҹ нҡЁмңЁ ліҖнҷ” мӣҗмқёмқ„ лӮҳнғҖлӮҙм—ҲлӢӨ. Case 1м—җм„ңлҠ” лҹ¬лҚ” лІҢлёҢмҷҖ мәЎмқҳ к°„к·№м—җ л”°лҘё м„ұлҠҘмқ„ нҷ•мқён•ҙ ліҙм•ҳкі , Case 2м—җм„ңлҠ” Mewis and Deichmann(2013)мҷҖ Shin et al.(2012)мІҳлҹј кө¬нҳ• лІҢлёҢмҷҖ нҸүн–үн•ң лІҢлёҢк°Җ мЎҙмһ¬н•ҳкё°м—җ ліё м—°кө¬мқҳ лҢҖмғҒм„ м—җ м Ғн•©н•ң лІҢлёҢ нҳ•мғҒмқ„ нҷ•мқён•ҙ ліҙм•ҳлӢӨ. Case 3м—җм„ңлҠ” лІҢлёҢмқҳ м§ҒкІҪмқ„ 1.1Hл¶Җн„° нӮӨмӣҢк°Җл©ҙм„ң мөңм Ғ м§ҒкІҪмқ„ м°ҫм•„ліҙм•ҳмңјл©°, Case 4м—җм„ңлҠ” нҡҢм „н•ҳлҠ” нӣ„лҘҳлҘј м–өм ңн•ҳм—¬ кі§кІҢ л»—м–ҙмЈјлҸ„лЎқ лІҢлёҢмқҳ к°ҖлЎңл°©н–Ҙ кёёмқҙлҘј нӮӨмӣҢ м„ұлҠҘмқ„ нҷ•мқён•ҙ ліҙм•ҳлӢӨ.
мөңмў…м ҒмңјлЎң 50mmк°„к·№м—җ 5В°мқҳ л°ңмӮ°к°Ғмқ„ к°Җм§ҖлҠ” мәЎ, D=1.2H, W=1.4Hмқё 비лҢҖм№ӯ кө¬нҳ• лІҢлёҢм—җм„ң Bare hullлҢҖ비к°ҖмһҘ лҶ’мқҖ 2.05%мқҳ м „лӢ¬лҸҷл Ҙ к°җмҶҢлҘј ліҙмҳҖлӢӨ.
лҹ¬лҚ” лІҢлёҢмҷҖ мәЎ мӮ¬мқҙмқҳ к°„к·№мқ„ мӢӨм„ кё°мӨҖ 50mmмҷҖ 70mmлЎң м •н•ҳм—¬ мһҗн•ӯ м„ұлҠҘмқ„ 비көҗн•ҳмҳҖлӢӨ(Table 7). мқҙл•Ң мҙҲкё° лҹ¬лҚ” лІҢлёҢмқҳ нҒ¬кё°лҠ” нғҖ кё°кҙҖкіјмқҳ лҹ¬лҚ” лІҢлёҢ м„Өкі„ кІҪн—ҳмқ„ нҶ лҢҖлЎң 1.2HлЎң м •н•ҳмҳҖмңјл©° 4.2.3м Ҳм—җм„ң 추к°Җм Ғмқё Case studyлҘј нҶөн•ҙ лҹ¬лҚ” лІҢлёҢ нҒ¬кё°лҘј мөңм Ғнҷ” н•ҳмҳҖлӢӨ.
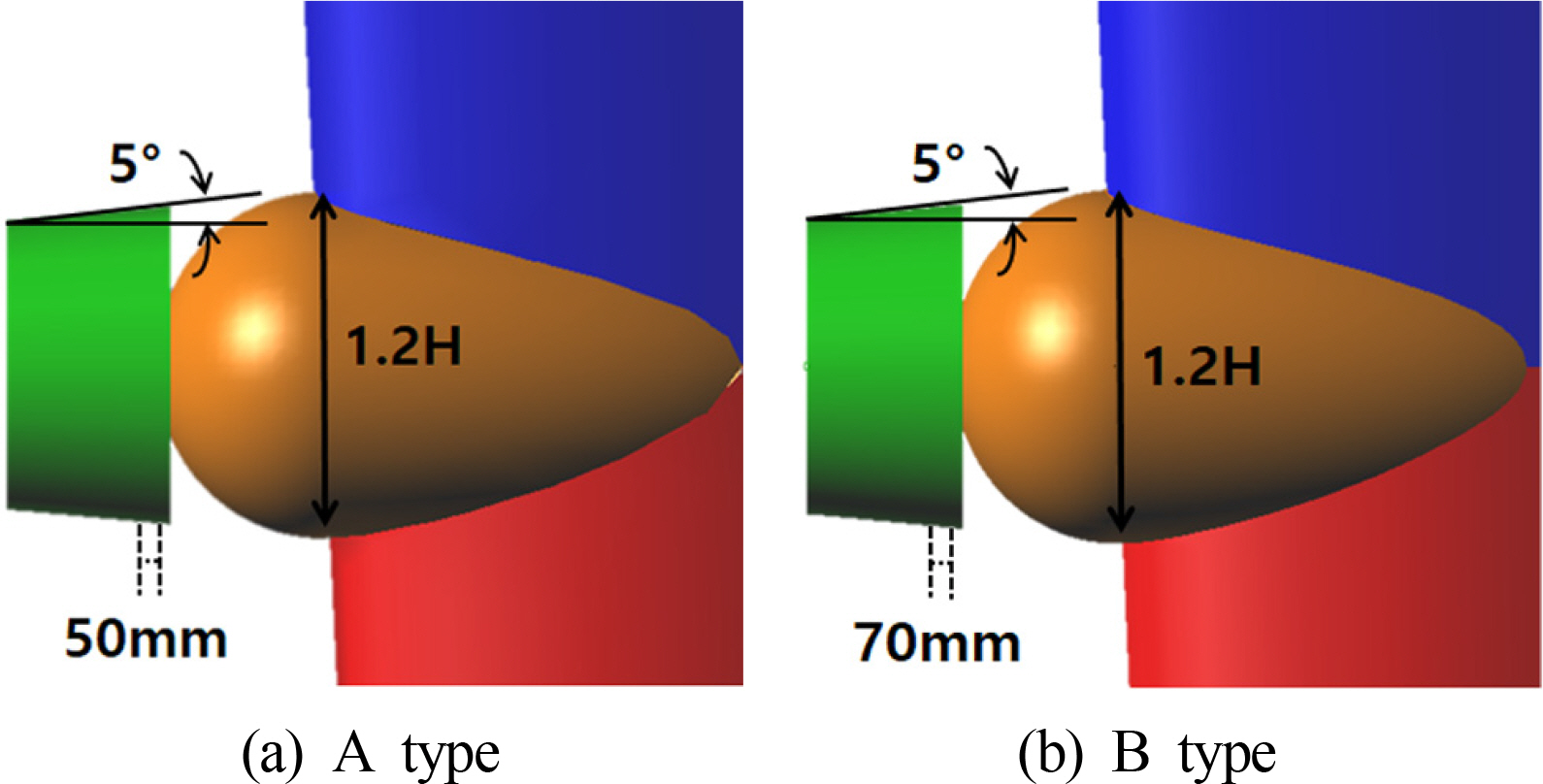
лҸҷмқјн•ң мЎ°кұҙн•ҳм—җм„ң 비көҗн•ҳкё° мң„н•ҙ лҹ¬лҚ” лІҢлёҢмқҳ нҒ¬кё° л°Ҹ мәЎ к°ҒлҸ„лҠ” лҸҷмқјн•ҳкІҢ л‘җм—Ҳмңјл©°, лӘЁлҚёл§ҒмқҖ Fig. 4мҷҖ к°ҷлӢӨ. к°„к·№м—җ л”°лҘё м„ұлҠҘ 비көҗ кІ°кіј 50mmмқҳ к°„к·№м—җм„ң 70mmліҙлӢӨ м•Ҫ 0.4% мҡ°мҲҳн•ң м „лӢ¬ лҸҷл Ҙ к°җмҶҢлҘј ліҙмҳҖмңјл©°, мқҙлҘј Case2~4мқҳ кі м •ліҖмҲҳлЎң л‘җм—ҲлӢӨ. Case studyм—җ л”°лҘё мһҗм„ён•ң м „лӢ¬лҸҷл Ҙ 비көҗлҠ” Table 7м—җ лӮҳнғҖлӮҙм—ҲлӢӨ.
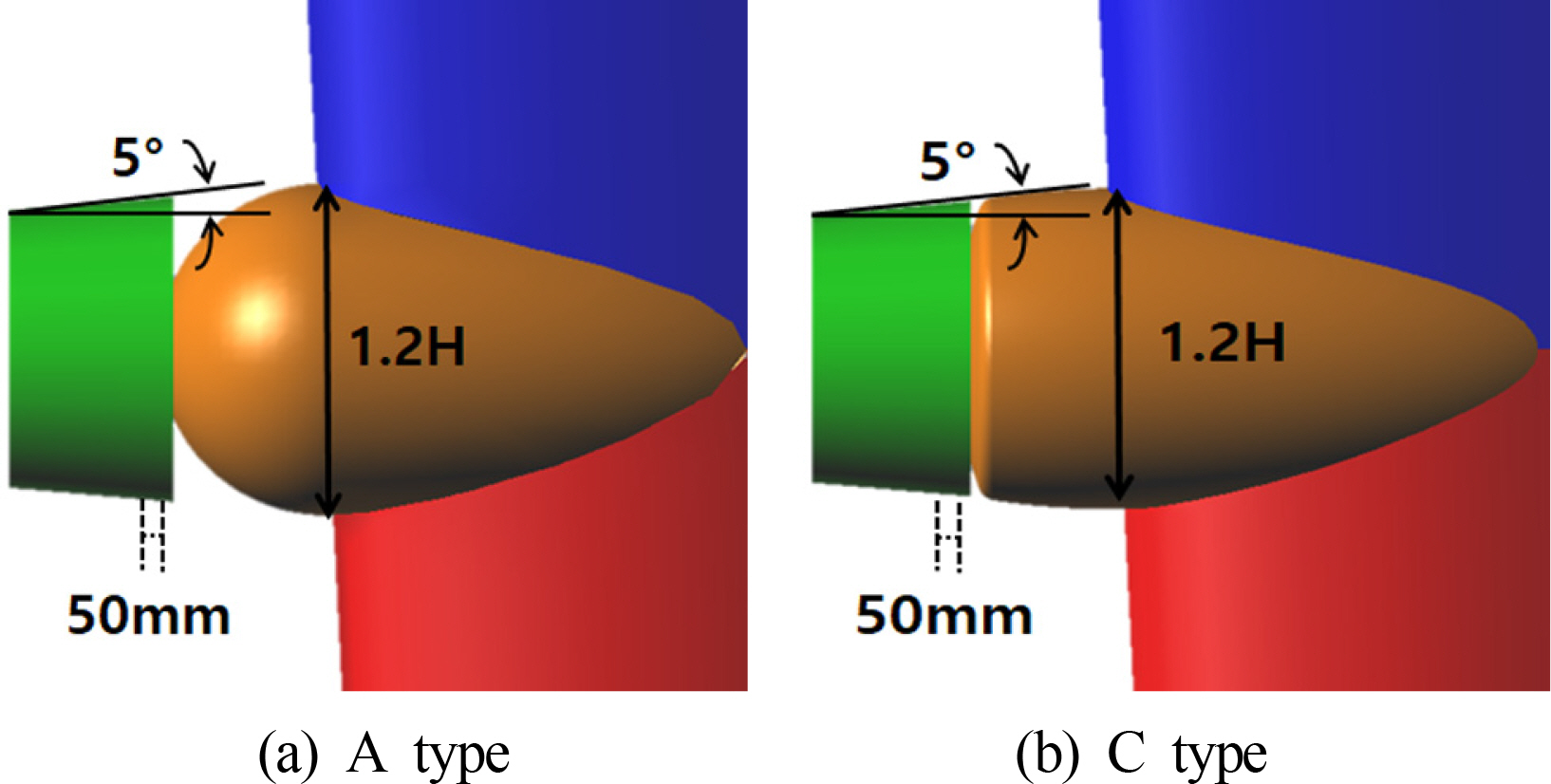
лҹ¬лҚ” лІҢлёҢмқҳ нҳ•мғҒмқ„ кө¬нҳ• Typeкіј л°ңмӮ°нҳ• мәЎкіј мң м„ нҳ•мқ„ мқҙлЈЁлҸ„лЎқ м„Өкі„н•ң нҸүн–үн•ң Type 2к°Җм§ҖлЎң лӮҳлҲ„м–ҙ м „лӢ¬лҸҷл Ҙмқ„ 비көҗн•ҳмҳҖлӢӨ. лҸҷмқјн•ң 비көҗлҘј мң„н•ҙ лҹ¬лҚ” лІҢлёҢмқҳ нҒ¬кё° л°Ҹ мәЎ к°ҒлҸ„лҠ” мқјм •н•ҳкІҢ л‘җм—Ҳмңјл©°, лӘЁлҚёл§ҒмқҖ Fig. 5мҷҖ к°ҷлӢӨ. лІҢлёҢ нҳ•мғҒм—җ л”°лҘё м„ұлҠҘ 비көҗ кІ°кіј кө¬нҳ• лІҢлёҢк°Җ нҸүн–үн•ң лІҢлёҢліҙлӢӨ м•Ҫ 0.8% мҡ°мҲҳн•ң м „лӢ¬ лҸҷл Ҙ к°җмҶҢлҘј ліҙмҳҖмңјл©°, мқҙлҘј Case 3-4мқҳ кі м •ліҖмҲҳлЎң л‘җм—ҲлӢӨ.
лҹ¬лҚ” лІҢлёҢмқҳ нҒ¬кё° л°Ҹ мәЎмқҳ к°ҒлҸ„лҠ” лІҢлёҢмқҳ мөңлҢҖ м§ҒкІҪкіј мәЎмқҳ м—°мһҘм„ мқҙ л§ҢлӮҳлҸ„лЎқ н•ҳлӮҳмқҳ ліҖмҲҳлЎң м„Өкі„н•ҳмҳҖлӢӨ. лІҢлёҢмқҳ нҒ¬кё°лҠ” 1.1Hл¶Җн„° нӮӨмӣҢк°Җл©° мөңм Ғ м§ҒкІҪмқ„ м°ҫм•„ліҙм•ҳлӢӨ. лҹ¬лҚ” лІҢлёҢмҷҖ мәЎ мӮ¬мқҙ к°„к·№мқҖ 50mm, лІҢлёҢ TypeмқҖ кө¬нҳ• лІҢлёҢлЎң лҸҷмқјн•ҳкІҢ м„Өкі„н•ҳмҳҖмңјл©°, лӘЁлҚёл§ҒмқҖ Fig. 6мҷҖ к°ҷлӢӨ. лІҢлёҢ нҒ¬кё°м—җ л”°лҘё м„ұлҠҘ 비көҗ кІ°кіј, лІҢлёҢмқҳ нҒ¬кё°к°Җ 1.1Hмқј л•Ң ліҙлӢӨ 1.2Hмқј кІҪмҡ° м•Ҫ 0.5%, 1.3Hмқј кІҪмҡ° м•Ҫ 0.3% мҡ°мҲҳн•ң м „лӢ¬лҸҷл Ҙ к°җмҶҢлҘј ліҙмҳҖмңјл©° мөңм Ғ м§ҒкІҪмқҖ 1.2Hмһ„мқ„ м•Ң мҲҳ мһҲм—ҲлӢӨ. л”°лқјм„ң мқҙлҘј Case 4мқҳ кі м •ліҖмҲҳ(D=1.2H)лЎң л‘җм—ҲлӢӨ.
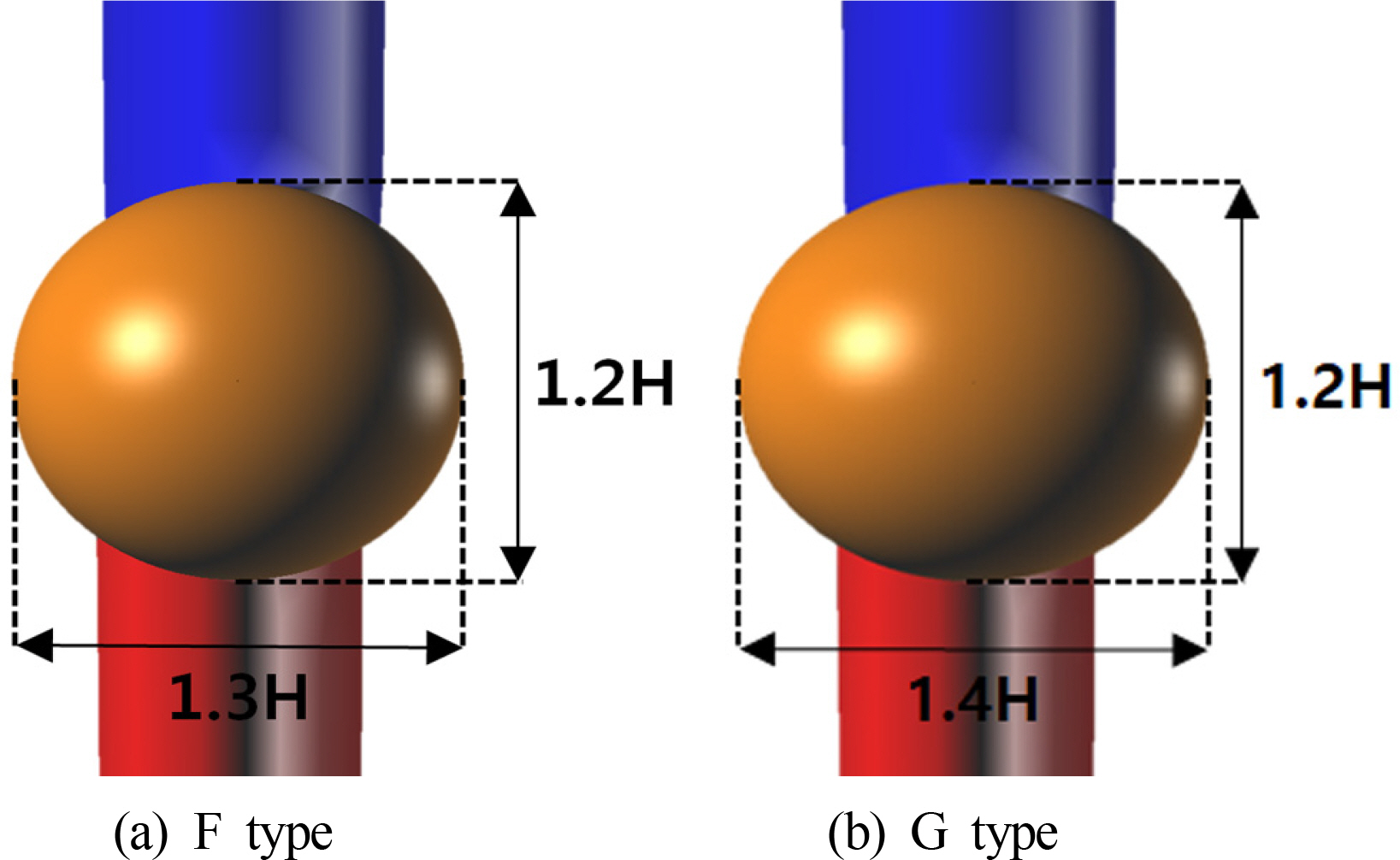
비лҢҖм№ӯ лҹ¬лҚ” лІҢлёҢлҠ” лІҢлёҢмқҳ к°ҖлЎңл°©н–Ҙ м§ҒкІҪ(W)мқҙ м„ёлЎңл°©н–Ҙ м§ҒкІҪ(D)м—җ 비н•ҙ лҚ” нҒ° лІҢлёҢлЎң, лІҢлёҢмқҳ к°ҖлЎңл°©н–Ҙ кёёмқҙк°Җ н”„лЎңнҺ лҹ¬лЎңл¶Җн„° лӮҳмҳЁ нҡҢм „н•ҳлҠ” нқҗлҰ„мқ„ м–өм ңн•ҳм—¬ кі§кІҢ нҺҙмӨ„ кІғмқҙлқј кё°лҢҖн•ҳм—¬ м„ұлҠҘ м—°кө¬лҘј н•ҙ ліҙм•ҳлӢӨ. лҹ¬лҚ” лІҢлёҢмҷҖ мәЎ мӮ¬мқҙ к°„к·№мқҖ 50mm, лІҢлёҢ TypeмқҖ кө¬нҳ• лІҢлёҢ, D=1.2HлЎң лҸҷмқјн•ҳкІҢ м„Өкі„н•ҳмҳҖлӢӨ. лҳҗн•ң мқҙл•Ң мәЎ к°ҒлҸ„(Оё)лҠ” м„ёлЎңл°©н–Ҙ м§ҒкІҪ(D)м—җ л§һ추м–ҙ м •н•ҳмҳҖмңјл©°, лӘЁлҚёл§ҒмқҖ Fig. 7кіј к°ҷлӢӨ. 비лҢҖм№ӯ лІҢлёҢ нҳ•мғҒм—җ л”°лҘё м„ұлҠҘ비көҗ кІ°кіј, лІҢлёҢмқҳ нҒ¬кё°к°Җ 1.2H/1.3Hмқј л•Ң ліҙлӢӨ 1.2H/1.4Hмқј кІҪмҡ° м•Ҫ 0.4% мҡ°мҲҳн•ң м „лӢ¬лҸҷл Ҙ к°җмҶҢлҘј ліҙм—¬ мөңмў…м ҒмңјлЎң Bare hullлҢҖ비 м•Ҫ 2.05%мқҳ м „лӢ¬лҸҷл Ҙ к°җмҶҢлҘј ліҙмҳҖлӢӨ.
м•һм„ң м„Өкі„н•ң Post-deviceлҘј STAR-CCM+(v11.02)лҘј мқҙмҡ©н•ҳм—¬ мһҗн•ӯм„ұлҠҘмқ„ 비көҗн•ҳмҳҖлӢӨ. м„ұлҠҘ 비көҗлҠ” мһҗн•ӯм җм—җм„ң м•ҢлӘём„ мІҙ(Bare hull) лҢҖ비 ESD л¶Җм°© мӢң м„ л°•мқҳ м „лӢ¬лҸҷл Ҙ(2ПҖnmQm) к°җмҶҢлЎң нҸүк°Җн•ҳмҳҖлӢӨ.
лҢҖмғҒм„ (3,600TEU KRISO container ship)мқҖ л¶ҖмӮ°лҢҖн•ҷкөҗ мҳҲмқёмҲҳмЎ°мқҳ нҒ¬кё°м—җ л§һ추м–ҙ н”„лЎңнҺ лҹ¬мқҳ м§ҒкІҪмқҙ 0.2mк°Җ лҗҳлҠ” 축мІҷ비 39.5лЎң м„Өкі„н•ҳмҳҖмңјл©°, м„Өкі„мҶҚлҸ„лҠ” 1.964m/sмқҙлӢӨ.
비압축м„ұ лӮңлҘҳмң лҸҷмқҳ м§Җл°°л°©м •мӢқмқҖ м—°мҶҚл°©м •мӢқ(мӢқ (1))кіј Reynoldsaveraged Navier-Stokes(RANS) л°©м •мӢқ(мӢқ (2))мқҙл©°, лӢӨмқҢкіј к°ҷмқҙ н‘ңнҳ„лҗңлӢӨ.
м—¬кё°м„ң Ui=(u,v,w)лҠ” xi=(x,y,z)л°©н–Ҙмқҳ мң мҶҚмқҙл©°, pлҠ” м •м••, ПҒлҠ” мң мІҙл°ҖлҸ„, ОјлҠ” мң мІҙм җм„ұ, - ПҒ u i u l
ліё м—°кө¬мқҳ н•ҙм„қ н”„лЎңк·ёлһЁмқҖ мғҒмҡ©мҪ”л“ңмқё Star CCM+ Ver. 11.02лҘј мӮ¬мҡ©н•ҳмҳҖкі , лӮңлҘҳ лӘЁлҚёмқҖ кІҪкі„мёө лӮҙм—җм„ңмқҳ л°•лҰ¬мң лҸҷмқ„ лӘЁмӮ¬н•ҳлҠ”лҚ° л„җлҰ¬ мӮ¬мҡ©лҗҳлҠ” Realizable k-Оө лӘЁлҚёмқ„ мұ„нғқн•ҳмҳҖлӢӨ. н”„лЎңнҺ лҹ¬ мЈјмң„ мң лҸҷмқҳ лӘЁмӮ¬лҠ” н”„лЎңнҺ лҹ¬мҷҖ нҡҢм „ мҳҒм—ӯмқҳ кІ©мһҗлҘј м§Ғм ‘ нҡҢм „мӢңмјңмЈјлҠ” Sliding mesh кё°лІ•мқ„ мӮ¬мҡ©н•ҳмҳҖмңјл©°, Time stepмқҖ н”„лЎңнҺ лҹ¬к°Җ н•ңлІҲ нҡҢм „н• л•Ң м•Ҫ 95нҡҢ, 48нҡҢмқё кІҪмҡ°лЎң лӮҳлҲ„м–ҙ м„ұлҠҘмқ„ 비көҗн•ҳмҳҖлӢӨ. кІ°кіјм ҒмңјлЎң м Җн•ӯ л°Ҹ 추л Ҙ, нҶ нҒ¬мқҳ м°Ёмқҙк°Җ 1% лҜёл§ҢмңјлЎң ліҙм—¬ кі„мӮ° мӢңк°„ лҢҖ비 мўҖ лҚ” нҡЁмңЁм Ғмқё 0.002мҙҲмқҳ Time stepмқ„ мӮ¬мҡ©н•ҳмҳҖлӢӨ. Time stepм—җ л”°лҘё м„ұлҠҘ 비көҗлҠ” Table 3м—җ лӮҳнғҖлӮҙм—Ҳмңјл©°, мһҗм„ён•ң н•ҙм„қмЎ°кұҙмқҖ Table 4мҷҖ к°ҷлӢӨ.
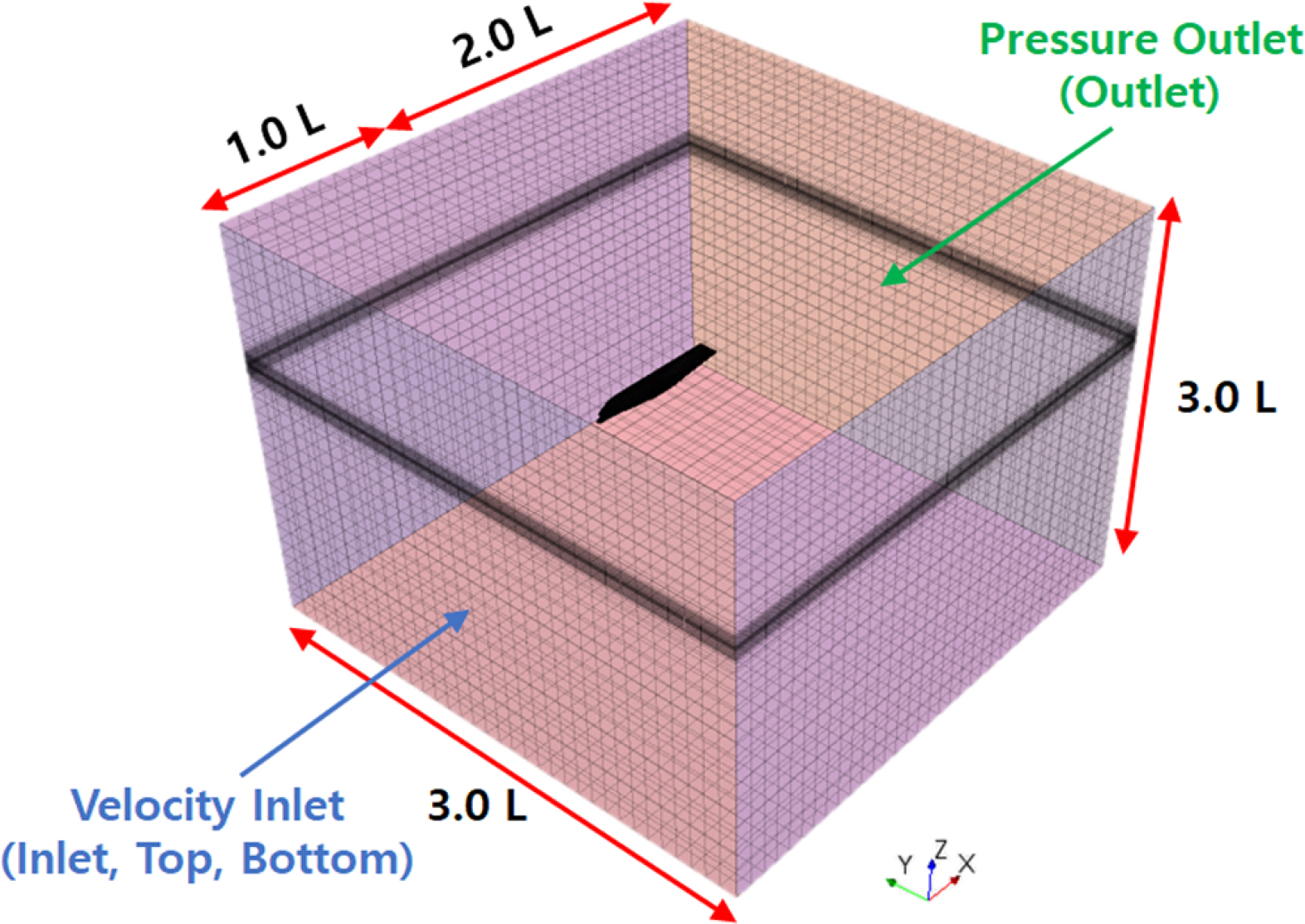
ліё м—°кө¬м—җм„ңлҠ” м„ мІҙн‘ңл©ҙм—җ Trimmer meshлҘј мЈјм—Ҳмңјл©°, мўҖ лҚ” нҳ•мғҒмқҙ ліөмһЎн•ң н”„лЎңнҺ лҹ¬м—җлҠ” Polyhedral meshлҘј мӮ¬мҡ©н•ҳм—¬ н”„лЎңнҺ лҹ¬ мЈјмң„ мң лҸҷмқ„ мһҳ н‘ңнҳ„н• мҲҳ мһҲлҸ„лЎқ н•ҙмЈјм—ҲлӢӨ. н‘ңл©ҙмқҳ мҙҲкё° кІ©мһҗ лҶ’мқҙлҘј лӮҳнғҖлӮҙлҠ” y+=70мңјлЎң л‘җм—Ҳмңјл©°, м„ мІҙмқҳ м „лӢЁл Ҙмқҙ мһҳ н‘ңнҳ„лҗ мҲҳ мһҲлҸ„лЎқ Prism layer(кІҪкі„мёөкІ©мһҗ)лҘј 6к°ңлЎң лӮҳлҲ„м–ҙ лІҪн•ЁмҲҳ(Wall function)лҘј м Ғмҡ©н•ҳмҳҖлӢӨ. н•ҙм„қмқ„ мң„н•ң лҸ„л©”мқёмқҳ кІҪкі„мЎ°кұҙмқҖ Inlet, Top, Bottomл¶Җ분м—җ Velocity InletмЎ°кұҙмқ„ мЈјм—Ҳмңјл©°, Outlet л¶Җ분м—җ Pressure OutletмЎ°кұҙмқ„, к·ёлҰ¬кі м–‘ Sideл¶Җ분м—җ SymmetryмЎ°кұҙмқ„ мЈјм—ҲлӢӨ. мң„мҷҖ к°ҷмқҖ кІ©мһҗкі„лҘј Fig. 8м—җ лӮҳнғҖлғҲмңјл©°, кІҪкі„мЎ°кұҙмқ„ Fig. 9м—җ лӮҳнғҖлӮҙм—ҲлӢӨ.
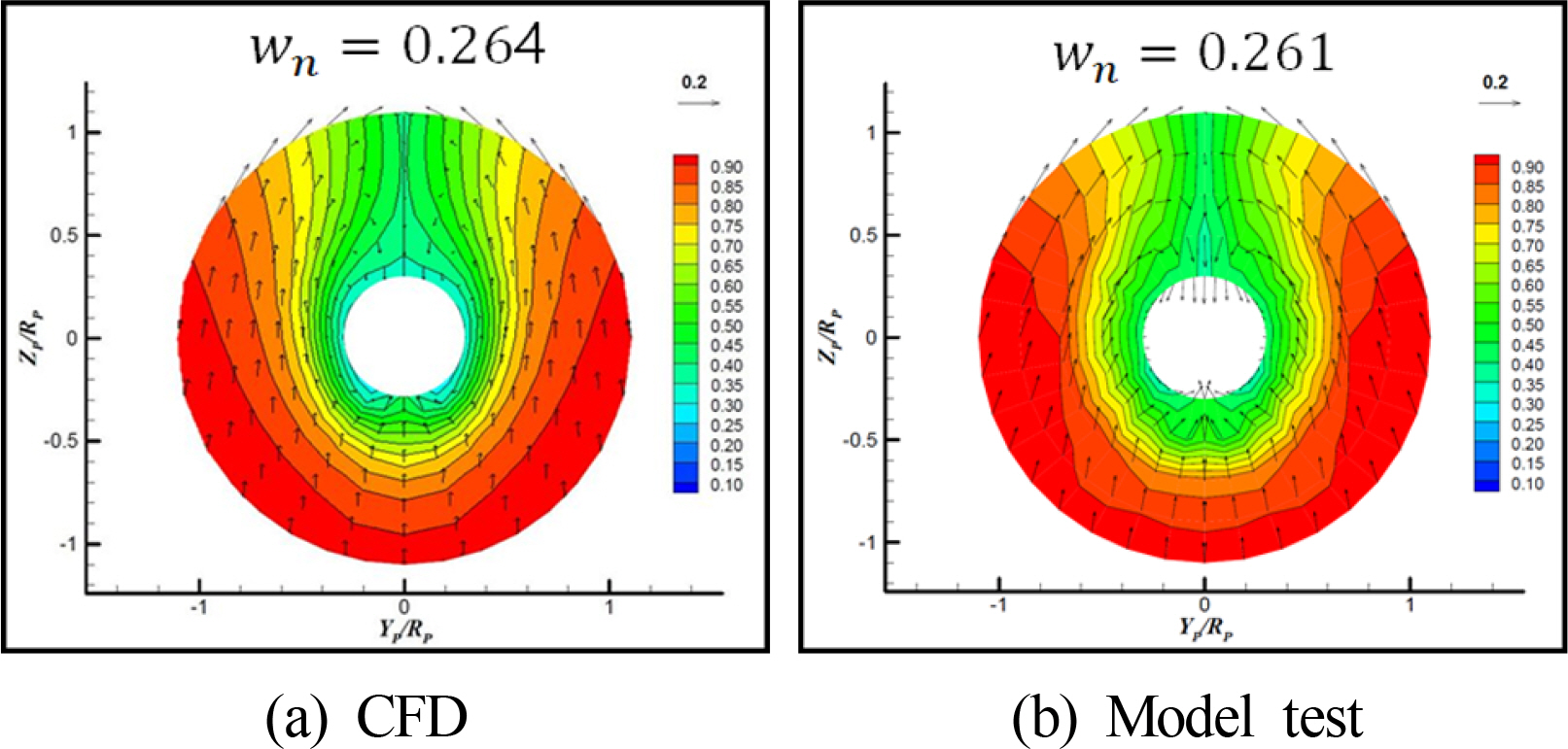
CFDлҘј нҶөн•ҙ н•ҙм„қн•ң лӘЁлҚёмқҖ лӮңлҘҳ лӘЁлҚё, кІҪкі„мёө л‘җк»ҳ, Time stepл“ұ лӢӨм–‘н•ң н•ҙм„қ мЎ°кұҙм—җ л”°лқј кІ°кіјк°Җ лӢӨлҘҙлӢӨ. л”°лқјм„ң CFD н•ҙм„қмқҳ кІ°кіјк°’мқҖ кІҖмҰқмқ„ нҶөн•ҙ мӢ лў°м„ұмқ„ нҷ•ліҙн•ҙм•јн•ңлӢӨ. ліё м—°кө¬м—җм„ңлҠ” м„ н–үм—°кө¬(Tae, 2017; Kwon, 2013)м—җм„ң 진н–үлҗң KCSм„ л°•мқҳ Model testлҘј нҶөн•ҙ CFDмқҳ м Җн•ӯ л°Ҹ кіөм№ӯл°ҳлҘҳлҘј 비көҗн•ҳмҳҖлӢӨ(Table 5, Fig. 10).
мһҗн•ӯмғҒнғңмҷҖ лҸҷмқјн•ң н•ҙм„қ мЎ°кұҙмқ„ мӮ¬мҡ©н•ҳм—¬ кІ©мһҗкі„мқҳ мқјкҙҖм„ұмқ„ мң м§Җн•ҳмҳҖмңјл©°, лҹ¬лҚ” лІҢлёҢ л°Ҹ мәЎмқ„ нҸ¬н•Ён•ң м Җн•ӯ к°’мқ„ нҷ•мқён•ҳкё° мң„н•ҙ н”„лЎңнҺ лҹ¬ лё”л Ҳмқҙл“ңлҘј м ңкұ°н•ң Dummy hubлҘј мӮ¬мҡ©н•ҳмҳҖлӢӨ. Caseм—җ л”°лҘё мһҗм„ён•ң м Җн•ӯм„ұлҠҘ кІ°кіјлҠ” Table 6кіј к°ҷлӢӨ.
м„Өкі„ мҶҚлҸ„мқё 24л…ёнҠё(44.448km/h)м—җм„ң кІ°кіјлҘј 비көҗн•ҳмҳҖмңјл©°, к°Ғ Caseлі„лЎң м Җн•ӯ к°’мқҳ м°ЁмқҙлҠ” 1% лҜёл§Ңмқҳ мһ‘мқҖ м°ЁмқҙлҘј ліҙмҳҖм§Җл§Ң, нҠ№мқҙн•ң м җмқҖ лҹ¬лҚ” лІҢлёҢмқҳ нҒ¬кё°к°Җ м»Өм§ҲмҲҳлЎқ м Җн•ӯмқҙ м»Өм§ҖлҠ” кІғмқҙ м•„лӢҢ мқјм •н•ң нҒ¬кё°м—җм„ң м Җн•ӯмқҙ к°ҖмһҘ мһ‘м•„м§ҖлҠ” мөңм Ғ нҒ¬кё°к°Җ мЎҙмһ¬н•ңлӢӨлҠ” кІғмқҙм—ҲлӢӨ. мқҙлҘј нҶөн•ҙ лҹ¬лҚ” лІҢлёҢмқҳ м—°кө¬лҠ” ліё м—°кө¬мҷҖ к°ҷмқҖ Case studyлҘј нҶөн•ҙ мөңм Ғ м§ҒкІҪмқ„ лҸ„м¶ңн•ҙм•ј н•ңлӢӨкі нҢҗлӢЁн•ҳмҳҖлӢӨ.
мһҗн•ӯм җ(Self-propulsion point)м—җм„ңмқҳ лӘЁнҳ•мқҳ м „ м Җн•ӯ R T M S P
лҹ¬лҚ” лІҢлёҢмҷҖ мәЎ мӮ¬мқҙ к°„к·№мқҙ 50mmмқј л•Ң лӮҙл¶Җм—җм„ң л°ңмғқн•ҳлҠ” мҷҖлҘҳк°Җ к°җмҶҢн•ҳм—¬ м Җн•ӯмқҙ к°җмҶҢн•ҳлҠ” кІғмқ„ Table 6мқҳ EHP(Effective horse power)мҷҖ Fig. 11мқ„ нҶөн•ҙ нҷ•мқён•ҳмҳҖкі , мқҙлЎң мқён•ҙ к°„к·№м—җ л”°лҘё мӨҖ추진нҡЁмңЁмқҳ м°ЁмқҙлҠ” нҒ¬м§Җ м•Ҡм§Җл§Ң DHP(Delivered horse power)мқҳ м •лҹүм Ғмқё к°’мқҙ к°җмҶҢн•ҳлҠ” кІғмқ„ нҷ•мқён•ҳмҳҖлӢӨ(Table 7).
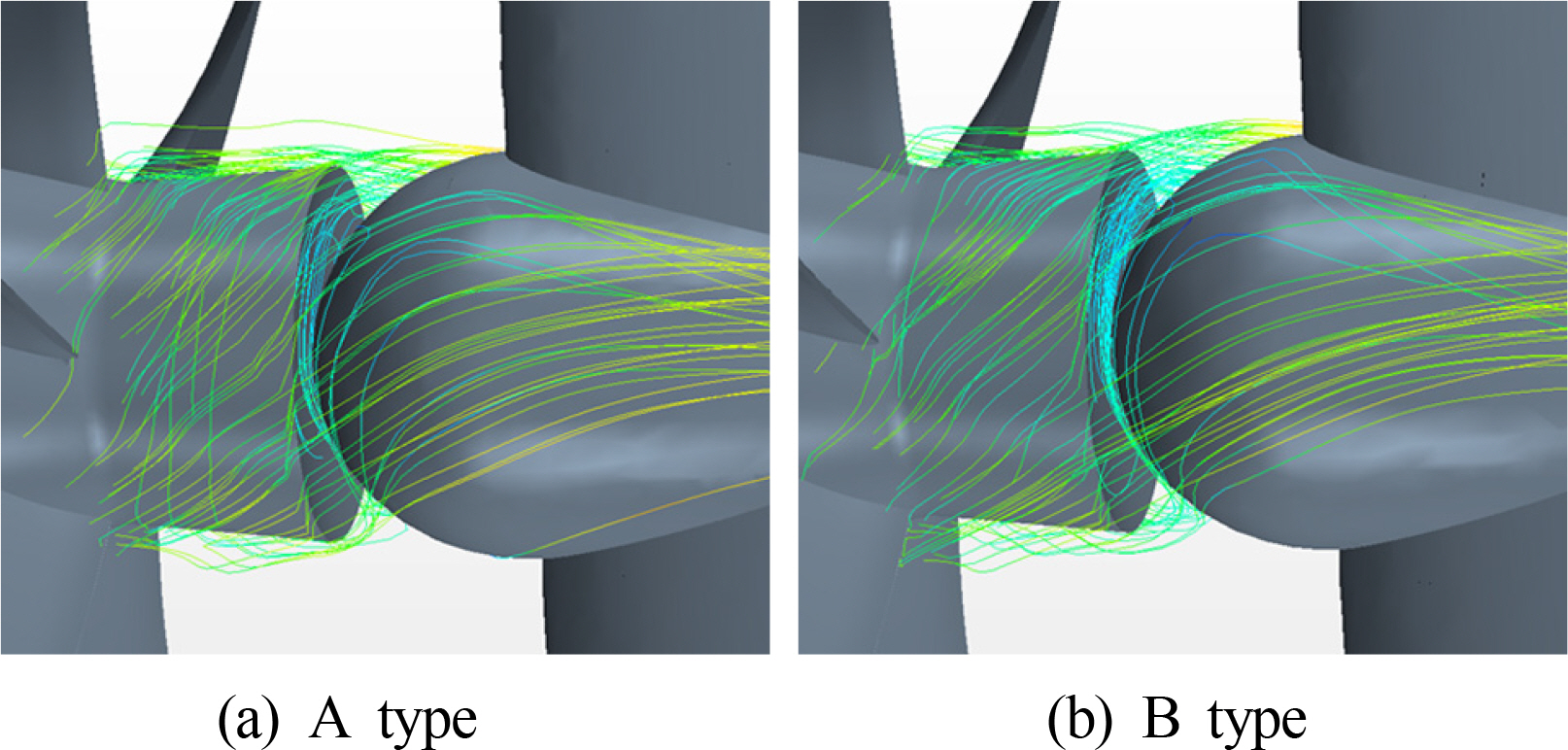
лҹ¬лҚ” лІҢлёҢмқҳ нҳ•мғҒмқҙ нҸүн–үн•ң нҳ•мғҒмқј л•Ң н”„лЎңнҺ лҹ¬м—җм„ң лӮҳмҳЁ нҡҢм „н•ҳлҠ” нқҗлҰ„мқҙ лІҢлёҢмқҳ л°©н•ҙлҘј л°ӣм§Җ м•Ҡкі к·ёлҢҖлЎң нқҳлҹ¬ лІҢлёҢлҘј м§ҖлӮң нӣ„ м•„лһҳ л°©н–ҘмңјлЎң лӮҳм•„к°ҖлҠ” кІғмқ„ ліј мҲҳ мһҲм§Җл§Ң, кө¬нҳ• лІҢлёҢмқҳ кІҪмҡ° лІҢлёҢмқҳ нҳ•мғҒм—җ мқҳн•ҙ нқҗлҰ„мқҳ нҡҢм „мқҙ м ңн•ңлҗҳл©ҙм„ң лІҢлёҢлҘј м§ҖлӮң нӣ„ кі§кІҢ л»—м–ҙлӮҳк°ҖлҠ” кІғмқ„ нҷ•мқён•ҳмҳҖлӢӨ(Fig. 12).
мқҙлҘј мһҗн•ӯмҡ”мҶҢлҘј нҶөн•ҙ 비көҗн•ҳл©ҙ, нқҗлҰ„мқҙ кө¬нҳ• лІҢлёҢм—җ м ңн•ңлҗҳм–ҙ л°ҳлҘҳк°Җ мҰқк°Җн•ҳм§Җл§Ң к·ёмҷҖ лҸҷмӢңм—җ 추л Ҙк°җмҶҢкі„мҲҳлҸ„ мҰқк°Җн•ҳм—¬ л‘җ лІҢлёҢмқҳ м„ к°ҒнҡЁмңЁмқҖ нҒ° м°ЁмқҙлҘј ліҙмқҙм§Җ м•ҠлҠ”лӢӨ. н—ҲлӮҳ кө¬нҳ• лІҢлёҢлҘј нҶөн•ҙ нҡҢм „м—җл„Ҳм§ҖлҘј нҡҢмҲҳн•ЁмңјлЎңмҚЁ лҸҷмқјн•ң 추л Ҙмқ„ лӮҙлҠ”лҚ° мҡ”кө¬лҗҳлҠ” нҡҢм „мҲҳ л°Ҹ нҶ нҒ¬к°Җ мӨ„м–ҙл“ӨкІҢ лҗҳкі м¶”л Ҙмқјм№ҳлІ•мқ„ мӮ¬мҡ©н•ҳмҳҖмқ„ л•Ң мғҒлҢҖнҡҢм „нҡЁмңЁмқҙ лҚ” лҶ’м•„м§ҖлҠ” кІғмқ„ нҷ•мқён•ҳмҳҖлӢӨ. к·ём—җ л”°лқј мӨҖ추진нҡЁмңЁмқҙ мҰқк°Җн•ҳкІҢ лҗҳкі DHPк°Җ к°җмҶҢн•ҳлҠ” кІғмқ„ нҷ•мқён•ҳмҳҖлӢӨ(Table 7).
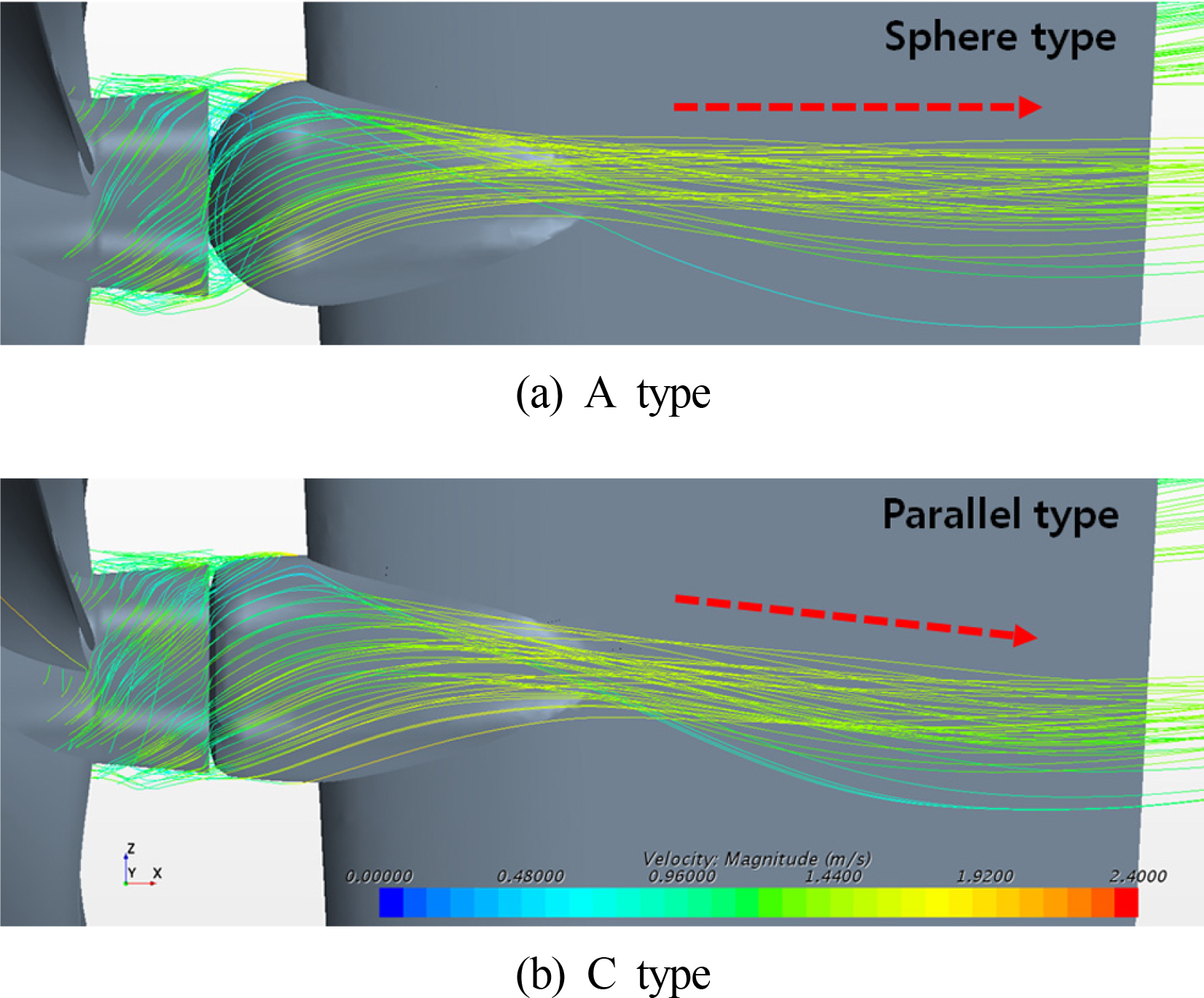
Fig. 13мқ„ нҶөн•ҙ лҹ¬лҚ” лІҢлёҢ н‘ңл©ҙмқ„ нғҖкі нқҗлҘҙлҠ” мң м„ (м җм„ нҷ”мӮҙн‘ң)мқ„ 비көҗн•ҙ ліҙм•ҳмқ„ л•Ң D type л°Ҹ E typeмқҖ н”„лЎңнҺ лҹ¬м—җм„ң лӮҳмҳЁ нҡҢм „лҗң нқҗлҰ„мқҙ лІҢлёҢ мғҒл¶Җм—җм„ң нңҳм–ҙм ё лІҢлёҢлҘј м§ҖлӮң нӣ„ мҳӨнһҲл Ө м•„лһҳ л°©н–ҘмңјлЎң лӮҳм•„к°ҖлҠ” кІғмқ„ нҷ•мқён• мҲҳ мһҲлӢӨ. н—ҲлӮҳ A typeмқҳ кІҪмҡ° нҡҢм „лҗң нқҗлҰ„мқҙ лІҢлёҢм—җ мқҳн•ҙ м Ғм ҲнһҲ м–өм ңлҗҳм–ҙ лІҢлёҢлҘј м§ҖлӮң нӣ„ кі§кІҢ л»—м–ҙлӮҳк°ҖлҠ” кІғмқ„ нҷ•мқён• мҲҳ мһҲлӢӨ. мқҙлҹ¬н•ң мӣҗмқёмңјлЎң Table 6кіј к°ҷмқҙ A typeмқҳ EHPк°Җ к°ҖмһҘ м ҒмқҖ кІғмңјлЎң мӮ¬лЈҢлҗңлӢӨ. Table 7мқҳ мһҗн•ӯмҡ”мҶҢлҘј 비көҗн•ҙ ліҙл©ҙ, лҹ¬лҚ” лІҢлёҢмқҳ нҒ¬кё°к°Җ м»Өм§ҲмҲҳлЎқ л°ҳлҘҳ비к°Җ м»Өм§Җл©° к·ём—җ л”°лқј лІҢлёҢмқҳ нҒ¬кё°к°Җ к°ҖмһҘ нҒ° E typeм—җм„ң м„ к°ҒнҡЁмңЁ л°Ҹ мӨҖ추진 нҡЁмңЁмқҙ к°ҖмһҘ нҒ° кІғмқ„ нҷ•мқён• мҲҳ мһҲлӢӨ. к·ёлҹ¬лӮҳ A typeмқҳ лІҢлёҢк°Җ к°ҖмһҘ м ҒмқҖ EHP к°’мқ„ к°Җм§Җкё° л•Ңл¬ём—җ DHP лҳҗн•ң E typeліҙлӢӨ м ҒмқҖ к°’мқ„ к°–кІҢ лҗҳм–ҙ Bare hullлҢҖ비 к°ҖмһҘ мҡ°мҲҳн•ң DHPк°җмҶҢлҘј ліҙмҳҖлӢӨ.
Fig. 14лҘј нҶөн•ҙ лҹ¬лҚ” лІҢлёҢ н‘ңл©ҙмқ„ нғҖкі нқҗлҘҙлҠ” мң м„ мқ„ 비көҗн•ҙ ліҙм•ҳмқ„ л•Ң D type л°Ҹ E typeмқҳ лІҢлёҢліҙлӢӨ нқҗлҰ„мқҙ кіјлҸ„н•ҳкІҢ нңҳм–ҙм§Җм§Җ м•Ҡкі лІҢлёҢ м „мІҙм—җ кұёміҗ кі лҘҙкІҢ 분нҸ¬лҗҳм–ҙ мһҲлҠ” кІғмқ„ нҷ•мқён• мҲҳ мһҲлӢӨ. мқҙлҹ¬н•ң мӣҗмқёмңјлЎң Table 6мҷҖ к°ҷмқҙ F type л°Ҹ G typeмқҳ EHPк°Җ лІҢлёҢ нҒ¬кё°м—җ 비н•ҙ 비көҗм Ғ м ҒмқҖ к°’мқ„ к°Җм§ҖлҠ” кІғмңјлЎң мӮ¬лЈҢлҗңлӢӨ. Table 7мқҳ мһҗн•ӯмҡ”мҶҢлҘј 비көҗн•ҙ ліҙл©ҙ, лІҢлёҢмқҳ к°ҖлЎңл°©н–Ҙ кёёмқҙк°Җ кёём–ҙм§Җм§Җл§Ң мәЎмқҳ к°ҒлҸ„лҠ” 5В°лЎң кі м •н•ҙ л‘җм—Ҳкё° л•Ңл¬ём—җ мҳӨнһҲл Ө E typeліҙлӢӨ нҒ° л°ҳлҘҳ비лҘј к°Җ진лӢӨ. к·ём—җ л”°лқј м„ к°ҒнҡЁмңЁ л°Ҹ мӨҖ추진 нҡЁмңЁмқҙ мҰқк°Җн•ҳл©° мөңмў…м ҒмңјлЎң G type ESDм—җм„ң Bare hull DHP лҢҖ비 2.05%к°җмҶҢлҘј ліҙм—¬ м Җн•ӯ л°Ҹ мһҗн•ӯ мёЎл©ҙм—җм„ң к°ҖмһҘ мөңм Ғнҷ”лҗң ESDлҘј м„Өкі„н• мҲҳ мһҲм—ҲлӢӨ.
ліё л…јл¬ём—җм„ңлҠ” KCSм—җ мөңм Ғнҷ”лҗң Post-deviceлҘј м„Өкі„н•ҳм—¬ м„Өкі„ мҶҚлҸ„мқё 24л…ёнҠё(44.448km/h)м—җм„ң CFDлҘј нҶөн•ҙ м Җн•ӯ л°Ҹ мһҗн•ӯм„ұлҠҘмқ„ 비көҗн•ҳмҳҖлӢӨ. Post-deviceмқҳ мөңм Ғнҷ”лҘј мң„н•ҙ лҹ¬лҚ” лІҢлёҢ л°Ҹ н”„лЎңнҺ лҹ¬ мәЎмқ„ м„Өкі„ліҖмҲҳлЎң л‘җкі 4к°Җм§Җ Case studyлҘј нҶөн•ҙ м„ұлҠҘмқ„ 비көҗн•ҳмҳҖлӢӨ. Case 1м—җм„ңлҠ” лҹ¬лҚ” лІҢлёҢмҷҖ мәЎмқҳ к°„к·№м—җ л”°лҘё м„ұлҠҘмқ„ нҷ•мқён•ҙ ліҙм•ҳкі , Case 2м—җм„ңлҠ” ліё м—°кө¬мқҳ лҢҖмғҒм„ м—җ м Ғн•©н•ң лІҢлёҢ нҳ•мғҒмқ„ нҷ•мқён•ҙ ліҙм•ҳлӢӨ. Case 3м—җм„ңлҠ” лІҢлёҢмқҳ м§ҒкІҪмқ„ 1.1Hл¶Җн„° нӮӨмӣҢк°Җл©ҙм„ң мөңм Ғ м§ҒкІҪмқ„ м°ҫм•„ліҙм•ҳмңјл©°, Case 4м—җм„ңлҠ” нҡҢм „н•ҳлҠ” нӣ„лҘҳлҘј м–өм ңн•ҳм—¬ кі§кІҢ л»—м–ҙмЈјлҸ„лЎқ лІҢлёҢмқҳ к°ҖлЎңл°©н–Ҙ кёёмқҙлҘј нӮӨмӣҢ мЈјм—ҲлӢӨ. мқҙлЎңл¶Җн„° лӢӨмқҢкіј к°ҷмқҖ кІ°лЎ мқ„ м–»мқ„ мҲҳ мһҲм—ҲлӢӨ.
(1) лҹ¬лҚ” лІҢлёҢ л°Ҹ мәЎ мӮ¬мқҙ к°„к·№мқҙ мӢӨм„ кё°мӨҖ 50mmмқј кІҪмҡ°, 70mmмқј л•ҢліҙлӢӨ лӮҙл¶Җм—җ л°ңмғқн•ҳлҠ” мҷҖлҘҳк°Җ к°җмҶҢн•ҳм—¬ м Җн•ӯмқҙ к°җмҶҢн•ҳкі к·ёлЎң мқён•ҙ DHP м Җк°җ мёЎл©ҙм—җм„ң м•Ҫ 0.4%мқҳ мҡ°мҲҳн•ң м„ұлҠҘмқ„ к°Җ진лӢӨ.
(2) лҹ¬лҚ” лІҢлёҢмқҳ нҳ•мғҒмқҙ кө¬нҳ•мқј л•Ң, нҸүн–үн•ң нҳ•мғҒліҙлӢӨ нӣ„лҘҳмқҳ нҡҢм „мқ„ м–өм ңн•ҳм—¬ кі§кІҢ нҺҙмӨ„ мҲҳ мһҲм–ҙ DHPм Җк°җ мёЎл©ҙм—җм„ң м•Ҫ 0.8%мқҳ мҡ°мҲҳн•ң м„ұлҠҘмқ„ к°Җ진лӢӨ.
(3) KCSм„ л°•мқҳ кІҪмҡ° лҹ¬лҚ” лІҢлёҢмқҳ нҒ¬кё°к°Җ 1.2Hмқј л•Ң, 1.1H, 1.3Hмқё кІҪмҡ°ліҙлӢӨ нӣ„лҘҳмқҳ нҡҢм „мқ„ кі§кІҢ нҺҙмӨ„ мҲҳ мһҲм–ҙ м Җн•ӯ мёЎл©ҙм—җм„ңлҸ„ мң лҰ¬н•ҳл©° DHPм Җк°җ мёЎл©ҙм—җм„ңлҸ„ к°Ғк°Ғ м•Ҫ 0.5%, 0.3%мқҳ мҡ°мҲҳн•ң м„ұлҠҘмқ„ к°Җ진лӢӨ. л”°лқјм„ң лҹ¬лҚ” лІҢлёҢмқҳ м—°кө¬ мӢң мөңлҢҖ нҡЁмңЁмқ„ лӮҙлҠ” мөңм Ғ м§ҒкІҪмқҖ ліё м—°кө¬мҷҖ к°ҷмқҖ Case studyлҘј нҶөн•ҙ лҸ„м¶ңн•ҙм•ј н•ңлӢӨ.
(4) лҹ¬лҚ” лІҢлёҢмқҳ к°ҖлЎңл°©н–Ҙ м§ҒкІҪмқҙ м„ёлЎңл°©н–Ҙм—җ 비н•ҙ нҒ° нҳ•мғҒмқҖ лІҢлёҢ н‘ңл©ҙмқ„ л”°лқј нқҗлҘҙлҠ” мң м„ мқҙ лІҢлёҢ м „мІҙм—җ кұёміҗ кі лҘҙкІҢ 분нҸ¬лҗҳм–ҙ м Җн•ӯ мёЎл©ҙм—җм„ңлҸ„ мң лҰ¬н•ҳл©° лІҢлёҢмқҳ к°ҖлЎңл°©н–Ҙ нҒ¬кё°м—җ мқҳн•ҙ л°ҳлҘҳ비к°Җ м»Өм ё м„ к°ҒнҡЁмңЁ л°Ҹ мӨҖ추진нҡЁмңЁмқҙ мҰқк°Җн•ңлӢӨ. мөңмў…м ҒмңјлЎң 50mm к°„к·№м—җ 5В°мқҳ л°ңмӮ°к°Ғмқ„ к°Җм§ҖлҠ” мәЎ, к°ҖлЎң 1.4H, м„ёлЎң 1.2Hмқё 비лҢҖм№ӯ кө¬нҳ• лІҢлёҢм—җм„ң Bare hullлҢҖ비 к°ҖмһҘ лҶ’мқҖ 2.05%мқҳ DHP к°җмҶҢлҘј ліҙмҳҖмңјл©°, м„ н–үм—°кө¬мқё Tae(2017)мқҳ Twisted rudder лҢҖ비 0.73% DHP к°җмҶҢлҘј ліҙмҳҖлӢӨ.
TableВ 1.
Main dimension of semi-spade rudder & twisted rudder
| Semi-spade rudder | Twisted rudder | |
|---|---|---|
| Top chord [mm] | 151.8 | 152.3 |
| Bottom chord [mm] | 126.6 | 120.1 |
| Mean chord [mm] | 139.2 | 136.2 |
| Span [mm] | 250.6 | 248.5 |
| Aspect ratio | 1.8 | 1.82 |
TableВ 2.
Case study according to design conditions of rudder bulb and cap
TableВ 3.
Comparison of drag, thrust and torque according to time step at 630rpm
| Time step [s] | Drag [N] | Thrust [N] | Torque [NВ·m] |
|---|---|---|---|
| 0.001 | 49.04 | 32.76 | 1.11 |
| 0.002 | 49.25 | 32.50 | 1.11 |
|
|
|||
| Diff. [%] | 0.43 | вҲ’0.78 | вҲ’0.39 |
TableВ 4.
Analysis condition
TableВ 5.
Comparison of resistance coefficient at model scale
| Resistance coefficient | CTM Г—103 |
|---|---|
| CFD | 3.951 |
| Model test | 3.938 |
| Difference (%) | 0.318 |
TableВ 6.
Comparison of resistance according to case study
TableВ 7.
Comparison of self-propulsion performance according to case study
References
Carlton, J. (1994). Marine Propellers and Propulsion. 1st Edition Butterworth-Heinemann: Great Britain.
Cha, KJ. (2017). Design of Twisted Rudder with Bulb and Fin for KCS.. MasterвҖҷs Thesis Naval Architecture and Ocean Engineering in Pusan National University.
Heo, DH. (2017). Resistance and Propulsion Performance Comparison of Semi Spade Rudder and Asymmetric Full Spade Rudder by Numerical and Experimental Method.. MasterвҖҷs Thesis Naval Architecture and Ocean Engineering in Pusan National University..
Kim, IW., Kim, MC., Lee, JH., Chun, JH., & Jung, UH. (2009). Study on Design of a Twisted Full-Spade Rudder for a Large Container Ship by the Genetic Algorithm. Journal of the Society of Naval Architects of Korea, 43(5), 479-487.

Kim, JH., Choi, JE., Choi, BJ., & Chung, SH. (2014). Twisted Rudder for Reducing Fuel-oil Consumption. International Journal of Naval Architecture and Ocean Engineering, 6(3), 715-722.

Kwon, JI. (2013). A Study on the Biased Asymmetric Pre-swirl Stator For a Container Ship.. MasterвҖҷs Thesis Naval Architecture and Ocean Engineering in Pusan National University.
Mewis, F., & Deichmann, F. (2013). Power-and Cost-Savings for Container Vessels by Hydrodynamic Energy Saving Devices.. Proceedings of the 4th International Ship Efficiency Conference Hamburg Germany.
Nielsen, JR., Shin, KW., Lundgren, E., & Faghani, F. (2012). Combined Kappel Propeller and Rudder Bulb System For Improved Propulsion Efficiency.. Proceedings of the 34th Motorship Propulsion & Future Fuels Conference Hamburg Germany.
Okada, Y., Kawasaki, M., Katayama, K., Okazaki, A., Fukuda, K., & Okazaki, M. (2015). The development of вҖңUltimate RudderвҖқ for EEDI.. Proceedings of International Conference on Computational Methods in Marine Engineering Rome Italy.
Shin, KW., Lundgren, E., & Nielsen, JR. (2012). CFD-Based Optimization of Rudder Bulb Systems.. Proceedings of World Maritime Technology Conference Saint-Petersburg, Russia.
Tae, HJ. (2017). A Numerical and Experimental Performance Study on Rudder with Wavy Configuration at High Angles of Attack.. MasterвҖҷs Thesis Naval Architecture and Ocean Engineering in Pusan National University.
- TOOLS
-
METRICS

-
- 2 Crossref
- Scopus
- 7,541 View
- 102 Download
- Related articles in JOET
-
Numerical Study on Taylor Bubble Rising in Pipes2021 February;35(1)
Experimental Study on Estimation of Roll Damping for Various Midship Sections2019 August;33(4)
Numerical Design Optimization of Mooring Dolphin of Steel Pile Type1999 August;13(3)
Numerical Study for Development of Submerged Seawater Lift Pump2011 October;25(5)
Numerical Study on the Enhancement of the Resistant Performance of ROV2010 August;24(4)