1. 서 론
1980년대에 최초의 광섬유 형식 해저케이블이 부설된 이후 해저케이블은 국⋅내외에서 해외통신 연결의 중요한 인프라 시설로 사용되고 있으며, 통신 시간 지연이 발생하는 위성통신을 대체할 수 있어 그 수요가 급격하게 늘어나는 추세이다. 특히 국내에서는 도서 지역의 전력 및 통신 설비용 해저 케이블이 다수 설치되어 있으며, 제주도의 경우 소비전력의 대부분을 해저케이블을 통해 육지로부터 송전 받고 있다(Ahn and Kim, 2009).
해저케이블 설치의 증가에 따른 파손사례 또한 증가하고 있으며, 특히 선박의 계류시 사용되는 앵커(Anchor)에 의한 해저케이블의 파손사고는 2007년 이후로 약 40% 가량 증가하였다. 이러한 현상은 연안 해역의 산업 시설과 생활 기반 시설 등이 지속적으로 증가되어 해상과 육지 간의 물동량의 증가로 이어졌고, 그에 따른 선박 통행량의 증가가 원인이었다(ICPC, 2009). 국내의 경우 2006년 제주 정전사태의 원인이 선박의 투묘에 의한 앵커와의 충돌로 인해 육지에서 제주로 연결된 해저케이블이 파손되어 발생된 것으로 보고되었다(KEPCO, 2006). 해저케이블 파손사고가 발생하게 되면 통신 및 데이터 전송 기능의 손실과 전력공급의 중단 상황이 발생할 수 있고, 해저케이블이 매설된 해역의 해양환경 조건에 따라 복구에 대한 높은 비용이 소요된다. 해저케이블의 파손사고의 주요 위해인자로는 스톡 앵커(Stock anchor)나 스톡리스 앵커(Stockless anchor)와 같은 선박용 앵커의 투묘에 의한 낙하충돌, 앵커의 주묘에 의한 끌림, 로켓포(Rocket pile)와 같은 양식어업용 조업도구의 낙하충돌 등이 보고되고 있다(KEPCO, 2006).
이와 같은 해저케이블 파손사고의 위험성을 낮추기 위해 다양한 형태의 해저케이블 보호설비가 고안되어 오고 있다. 그러나 국⋅내외의 해저케이블 보호설비의 설계 및 시공에 관한 규정이 미비하기 때문에 해저케이블 보호설비의 설계 안전도를 확보하기 위해서는 위해인자로 인한 수중 낙하충격에 대한 극한상태 평가가 선행되어야 한다. 해저케이블 보호설비의 낙하충격과 관련하여 여러 연구가 수행되어 오고 있다. Woo and Na(2010)는 수중 낙하하는 스톡 앵커의 속도를 뉴턴의 제2법칙을 이용한 이론식을 토대로 산출하여 강체로 모델링된 스톡 앵커 상에 초기속도로 적용하고 육상조건에서 보호구조물에 충돌시키는 수치해석 연구를 수행하였다. 매장형태의 해저케이블 보호설비에 대한 스톡 앵커 충돌 수치 시뮬레이션(Cho et al., 2012), 유연 콘크리트 매트리스(Flexible concrete mattress, FCM) 형태의 해저케이블 보호구조물에 대한 스톡 앵커와의 충돌해석과 콘크리트 재료모델 및 낙하 높이에 따른 FCM 보호구조물의 충돌강도 특성 평가(Ryu et al., 2015), 해저케이블 보호용 FCM 구조물의 스톡 앵커 충돌에 의한 손상 영향도 평가를 위한 철근 모델링과 앵커 충돌각도에 따른 비선형 동적해석 (Ryu et al., 2016) 등의 연구에서도 앞서 언급된 뉴턴의 제2법칙을 이용한 이론식을 기반으로 충돌체의 낙하속도를 산정하여 육상조건에서 충돌현상을 수치적으로 모사하였다. 이와 같이 기존의 연구현황을 살펴보면 이론식 기반의 위해인자 낙하속도를 이용하여 육상조건 기준으로 해저케이블 보호설비의 역학적 특성을 평가하였으며, 실제 해양환경을 고려하여 충돌성능을 평가한 사례가 미비한 것으로 파악되었다.
본 연구에서는 다양한 해저케이블 위해인자에 대한 실증시험의 현상을 실제 해양환경과 유사하게 모사하기 위한 기초연구 중에 하나로 3차원 CEL(Coupled euler-lagrange) 방법 기반의 유체-구조 연성(Fluid-structure interaction, FSI)해석을 이용하여 다양한 위해인자의 수중낙하 현상에 대한 수치 시뮬레이션을 수행하고, 위해인자의 종류에 따른 낙하특성을 비교하였다. 이를 통해 본 연구는 해저케이블 보호설비의 극한강도 평가를 위한 FSI 해석기법의 확립과 위해인자에 의한 극한하중 산정 연구의 기초자료로 활용하는 것을 주요 목적으로 하였다. 본 연구에서 사용한 FSI 해석방법의 정확도를 검증하기 위해 기존에 수행되었던 베어링 강재 구체(Bearing steel ball)의 수중낙하시험과 동일한 수치 시뮬레이션을 수행하여 결과를 비교하였다. 다양한 해저케이블 위해인자의 수치 시뮬레이션에서 고려한 위해인자의 종류는 실제 국내 서남해안에 설치된 해저케이블 보호설비의 파손사례보고에서 사고 발생빈도가 높았던 스톡 앵커, 스톡리스 앵커, 양식장 로켓포이다. 각각의 위해인자는 라그랑지안 모델(Lagrangian rigid model)로 생성하였고, 오일러 방정식(Eulerian equation)으로 생성된 수중 유체영역과 연성하여 3차원 전체 규모의 FSI 해석모델을 구성하였다. 위해인자 별로 수중낙하 FSI 해석의 낙하속도 결과를 이론식의 결과와 비교하여 수치 시뮬레이션의 타당성을 검증하고 위해인자의 종류에 따른 수중 낙하특성을 비교하였다.
2. 유체-구조 연성(FSI) 해석 방법
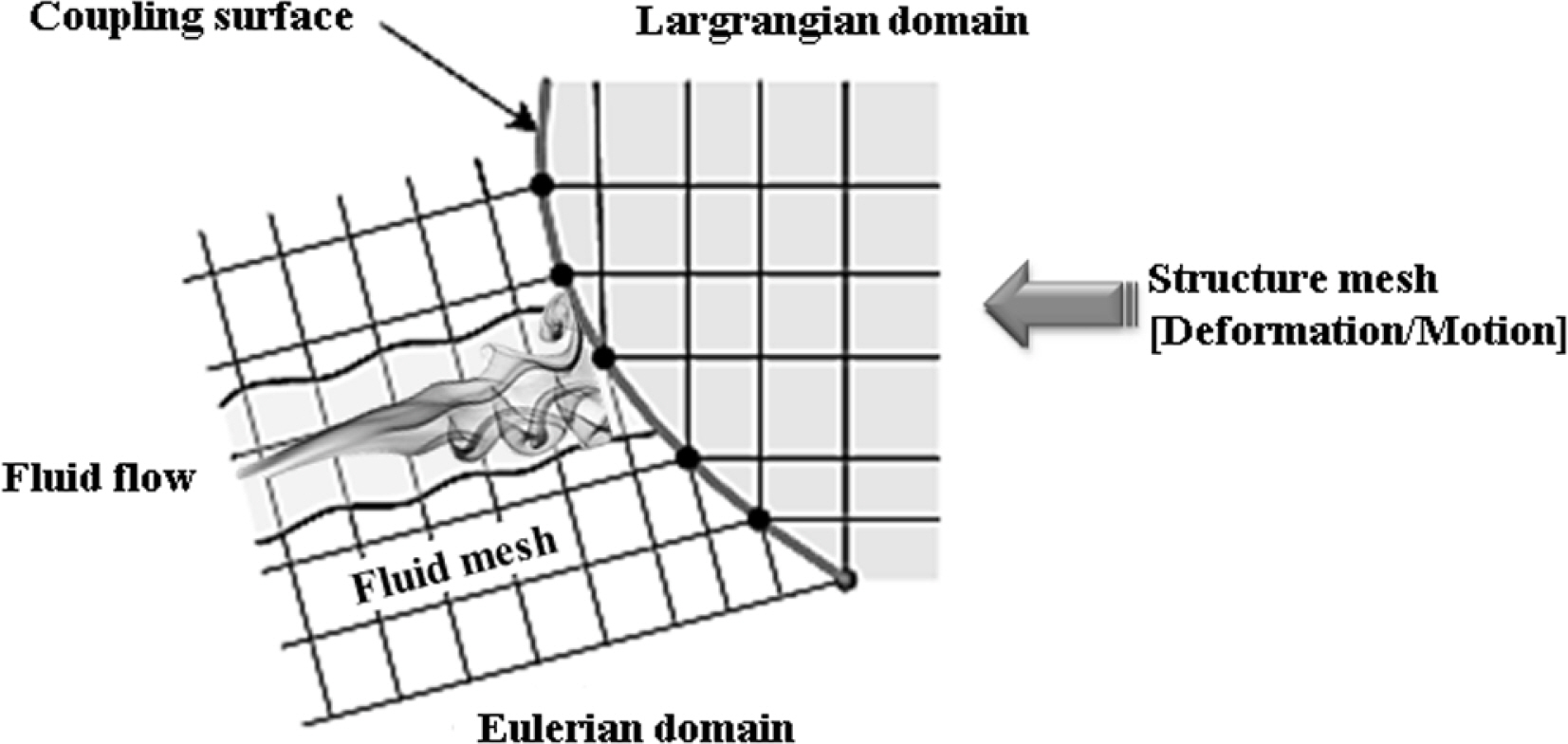
본 연구에서 적용한 FSI 해석 방법은 유체영역을 유한체적법(Finite volume method, FVM)으로 구현하는 오일러리안(Eulerian) 방법과 구조영역을 유한요소법(Finite element method, FEM)으로 표현하는 라그랑지안(Largrangian) 방법을 연성하여 유체와 구조체의 상호작용을 모사하는 해석방법이다. 다양한 해저케이블 위해인자에 대해 수중낙하 특성을 분석하기 위한 FSI 해석방법에서 수중 유체영역은 오일러 요소로 고려하고, 위해인자는 라그랑지 요소로 고려하였다. FSI 해석의 수치계산은 외연 시간 적분법(Explicit time integral method) 기반의 범용 비선형 유한요소해석 코드인 MSC.Nastran SOL700을 이용하였다(MSC Software, 2017). FSI 해석방법에서 유체-구조 접촉면은 유체-구조 연성 알고리즘(Fluid-structure coupled algorithm)으로 정의된다. FSI 해석방법의 유체-구조 상호작용에 대한 개념은 Fig. 1에 나타나 있다.
Fig. 1에 나타난 바와 같이 라그랑지 구조 영역의 변형이나 운동은 유체-구조 연성 영역의 경계에 영향을 미치게 되고 오일러 유체 영역에서 발생된 압력은 구조 영역의 외력으로 작용한다. 유체-구조 매질의 상호작용을 반영하기 위해 두 매질이 접하는 공통 경계표면을 연성표면(Coupling surface)으로 설정하여 이 표면을 통해 두 매질간의 상호작용이 연성된다.
3. 베어링 강재 구체의 수중 낙하해석
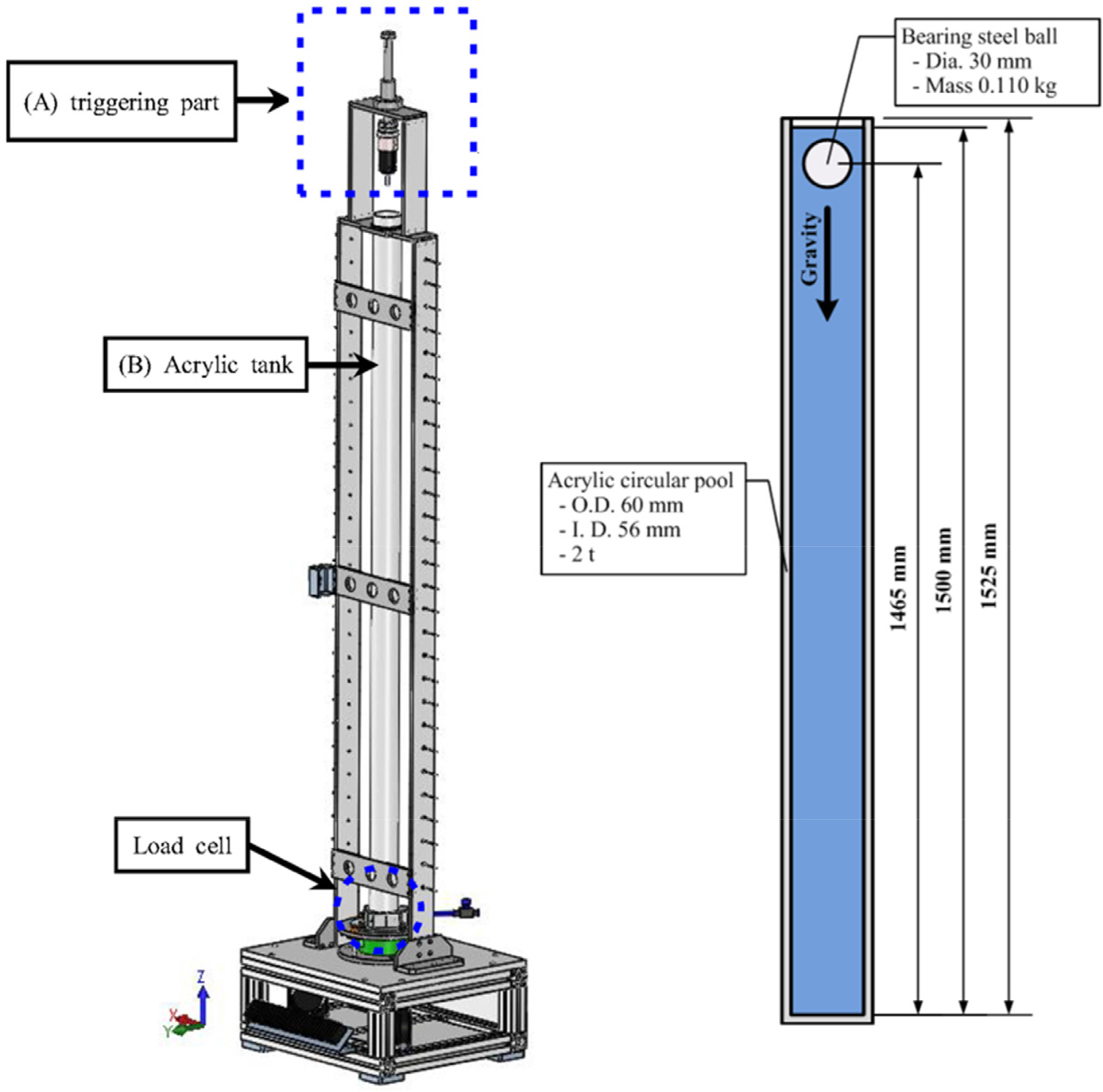
다양한 해저케이블 위해인자의 수중낙하 특성을 검토하기 위한 수치 시뮬레이션 기법의 타당성을 사전에 검증하기 위해 기존에 수행되었던 베어링 강재 구체의 수중낙하시험의 연구결과(Kim, 2015)에 대해 본 연구에서 적용한 FSI 해석방법을 동일하게 모사하여 비교하였다. Fig. 2에는 베어링 강재 구체의 수중낙하시험을 위한 시험장치 형상과 상세 치수가 나타나있다.
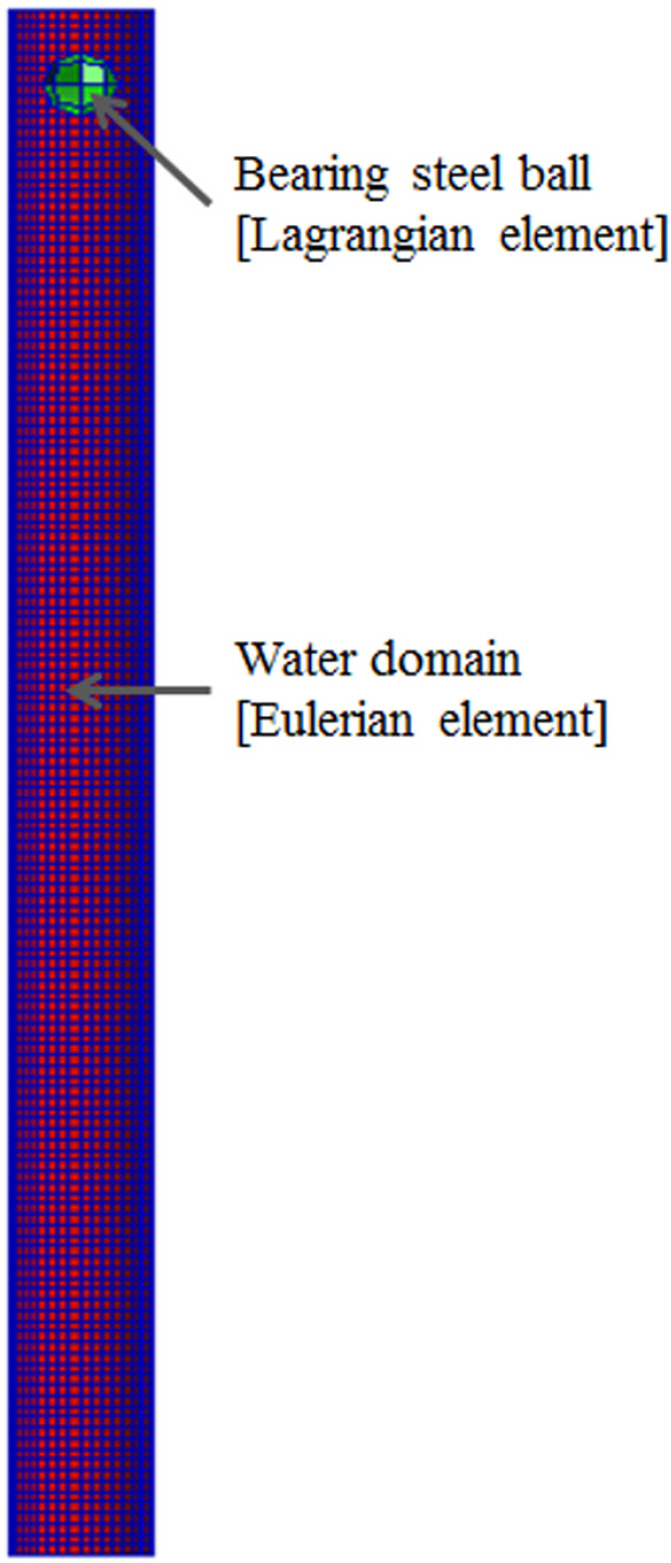
Fig. 2에 나타난 바와 같이 베어링 강재 구체의 수중낙하시험에서는 수위가 1,500mm인 수조에 밀도가 7,795kg/m3, 직경이 30mm, 무게가 0.11kg인 구체를 자유낙하 시켜 시간에 따른 구체의 위치변화를 1초 동안 중력방향에서 측정하였다. 본 연구에서 적용한 CEL 방법 기반의 FSI 해석의 정확도를 기존의 연구결과와 비교하기 위해 Fig. 3과 같이 수치해석 모델을 생성하였다. Fig. 3에 나타난 바와 같이 베어링 강재 구체는 8절점 솔리드(Solid) 형태의 라그랑지 요소를 사용하였으며, 124개의 절점과 24개의 요소로 구성하였다. 수조 내의 물의 오일러 격자는 정육면체 요소를 사용하였으며, 77,959개의 절점과 42,140개의 요소로 구성하였고, 밀도와 체적탄성계수는 1,000kg/m3, 2.1GPa를 각각 적용하였다. 유체-구조 매질의 상호작용을 반영하기 위해 두 매질이 접하는 공통 경계표면인 베어링 강재 구체의 표면을 연성표면으로 설정하였다. FSI 해석기법에서는 오일러 영역의 재료거동을 수치적으로 구현하기 위해 상태방정식(Equation of state, EOS)이 필요하게 되는데, 본 연구에서는 선형 다항 상태방정식(Linear polynomial EOS)을 사용하였다(Shin et al., 1998). 수치 시뮬레이션 모델의 격자수는 격자수에 따른 수치해석 결과의 정확도와 수치계산 시간에 관한 기존의 연구결과를 근거로 하여 오일러 모델의 격자크기를 라그랑지 모델의 요소크기 대비 25% 정도 세밀하게 적용하였다(Kim et al., 2017).
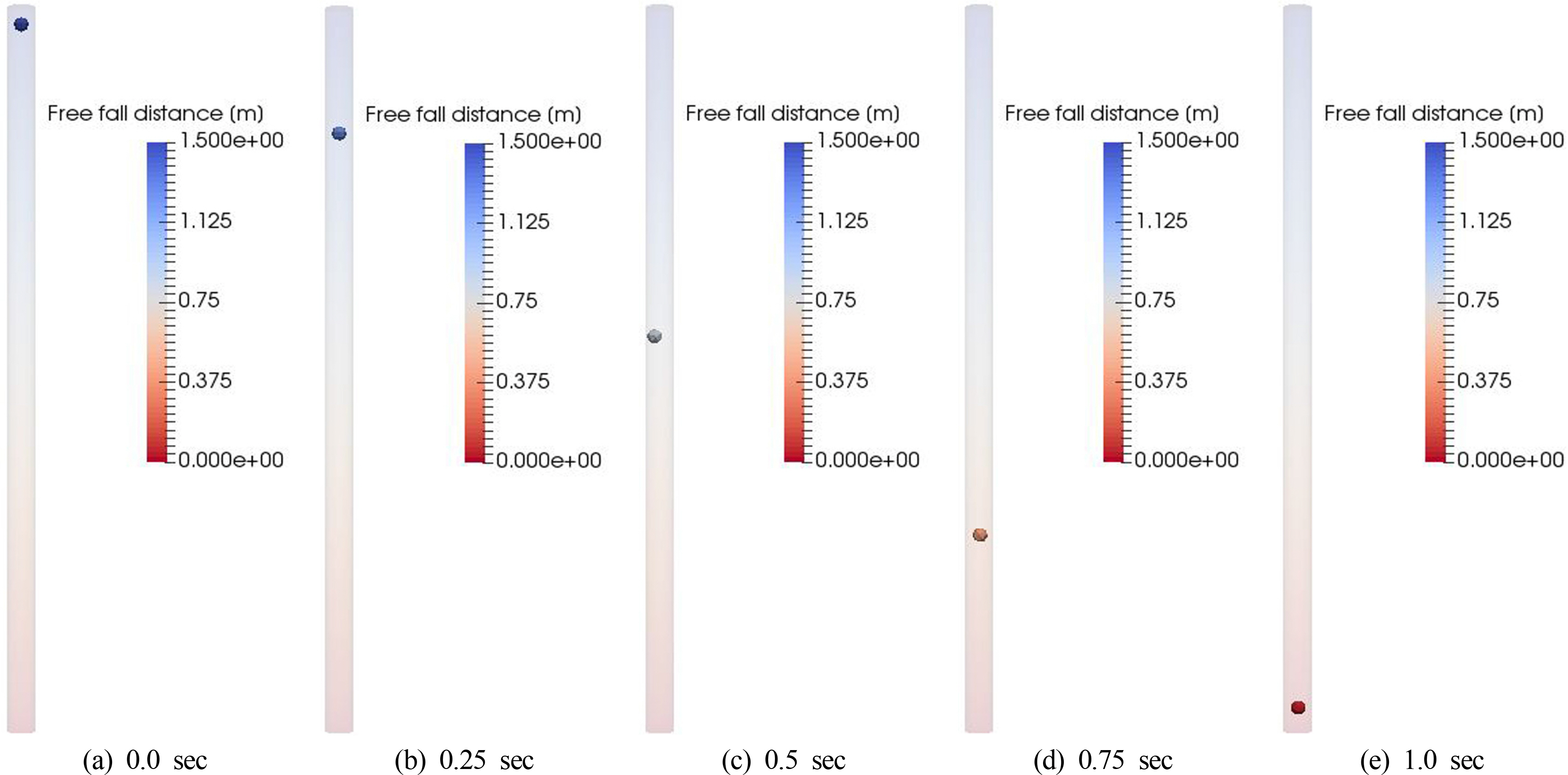
Fig. 4에는 FSI 해석을 통한 베어링 강재 구체의 낙하시간에 따른 구체의 수중낙하 이동거리에 대한 대표적인 결과를 나타내었다.
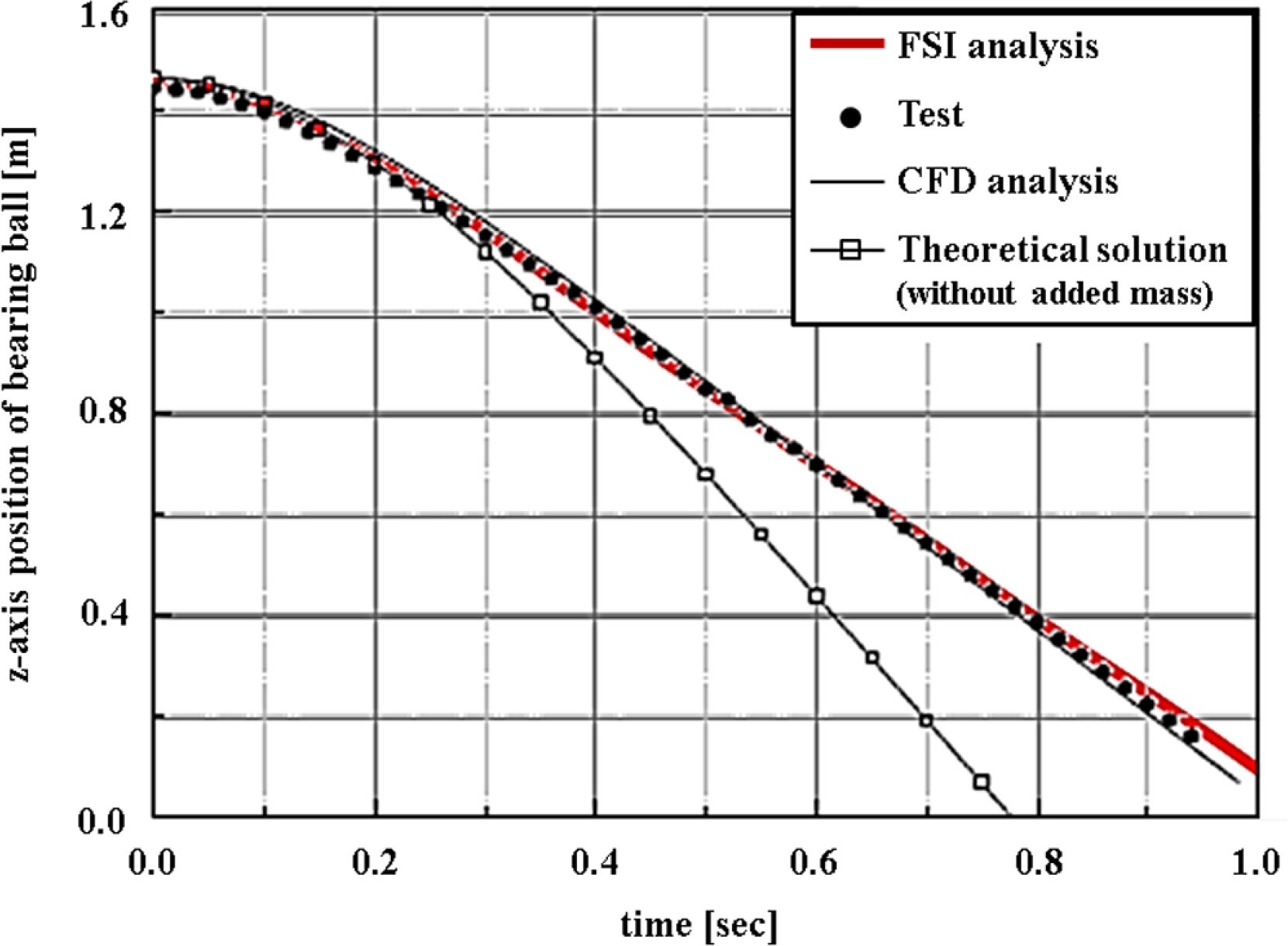
Fig. 4에 나타난 바와 같이 베어링 강재 구체의 수중낙하 이동거리는 유체와의 연성에 의한 운동에너지 손실로 인해 시간에 따라 불규칙하게 나타나는 것을 확인할 수 있다. Fig. 5에는 베어링 강재 구체의 낙하시간에 따른 구체의 수중낙하 이동거리에 대한 FSI 해석결과를 기존 연구문헌(Kim, 2015)의 수중낙하시험 연구결과, CFD(Computational fluid dynamics) 결과 및 이론해의 결과와 비교하여 나타내었다.
Fig. 5에 나타난 바와 같이 이론해의 결과를 제외한 FSI 해석결과, 시험결과 및 CFD 해석결과는 높은 일치도를 나타내었다. 수중낙하에 대한 이론해는 정상상태에서 항력계수를 고려한 자유낙하 운동식으로부터 산출되었는데, 부가질량(Added mass) 및 에너지감쇠를 고려하지 못하였기 때문에 전체적인 수중낙하운동의 거동은 유사하지만 수심이 깊어질수록 FSI 해석, 시험 및 CFD 해석결과보다 수중낙하속도가 빨라지는 경향을 나타내는 것을 확인할 수 있다. 이와 같이 베어링 강재 구체에 대한 비교 검토를 통해 본 연구에서 사용한 CEL 방법 기반의 FSI 해석방법을 수중낙하 시뮬레이션에 적용할 경우 유의한 결과를 도출할 수 있음을 검증하였다.
4. 해저케이블 위해인자의 수중 낙하특성
4.1 수치해석 모델
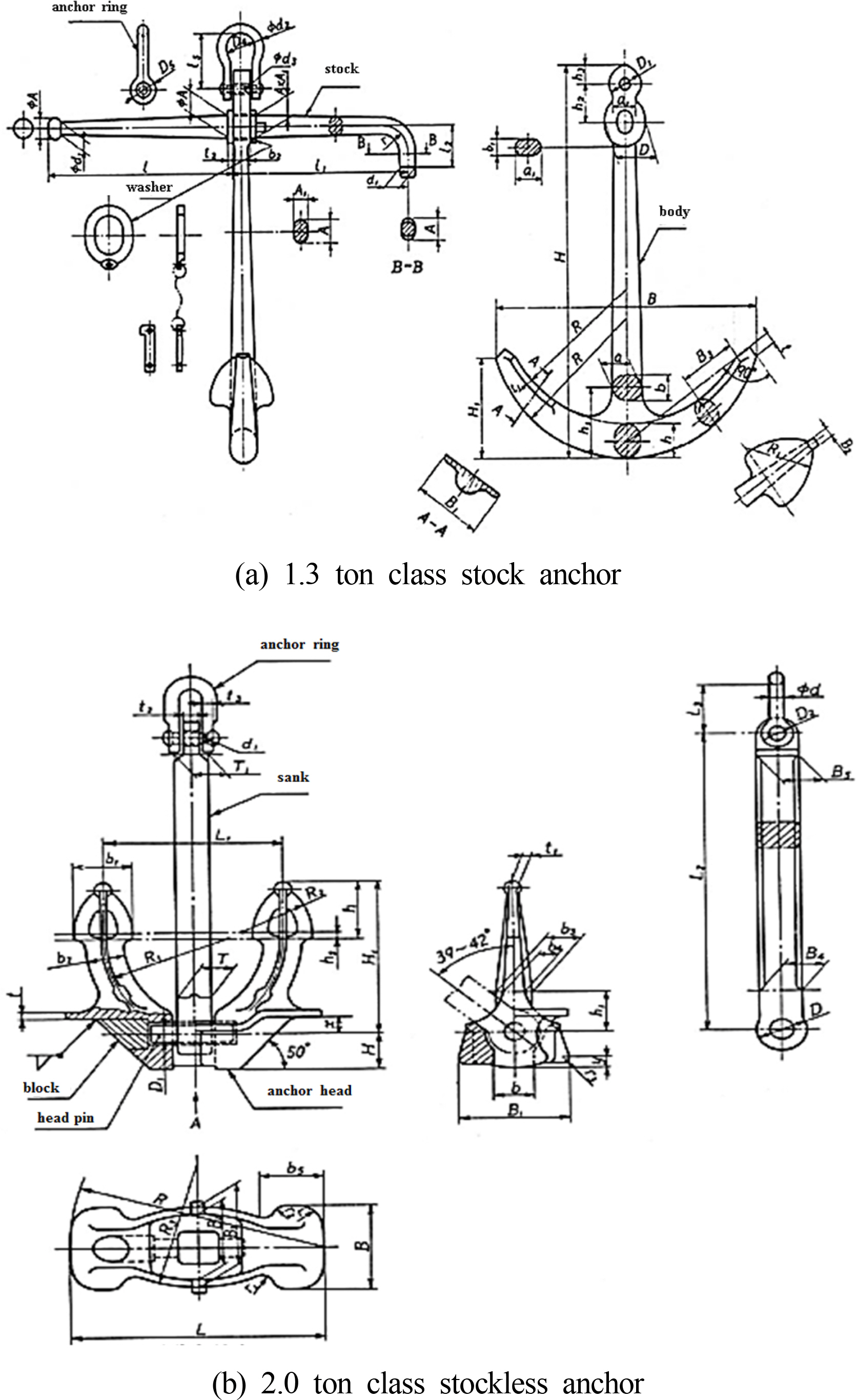
국내에서 해저케이블 매설이 가장 많이 이루어지고 있는 해역은 전남해안과 제주도 사이의 서남해역이며, 본 연구에서는 이 해역에 설치된 해저케이블 보호설비의 파손사례보고에서 사고 발생빈도가 높았던 스톡 앵커, 스톡리스 앵커, 양식장 로켓포의 수중낙하 특성을 분석하기 위해 FSI 해석 기반의 수치 시뮬레이션을 수행하였다. 스톡 앵커와 스톡리스 앵커의 사양은 서남해 해역을 주로 운항하는 선박 중 최대 선박 총 톤수를 기준으로 1.3톤급과 2.0톤급을 각각 고려하였다(Woo et al., 2017). Fig. 6에 나타낸 바와 같이 1.3톤급 스톡 앵커와 2.0톤급 스톡리스 앵커의 형상은 한국 산업 규격(KS, Korean industrial standard)상에 설계제원이 표준화되어 있다(KS, 2013).
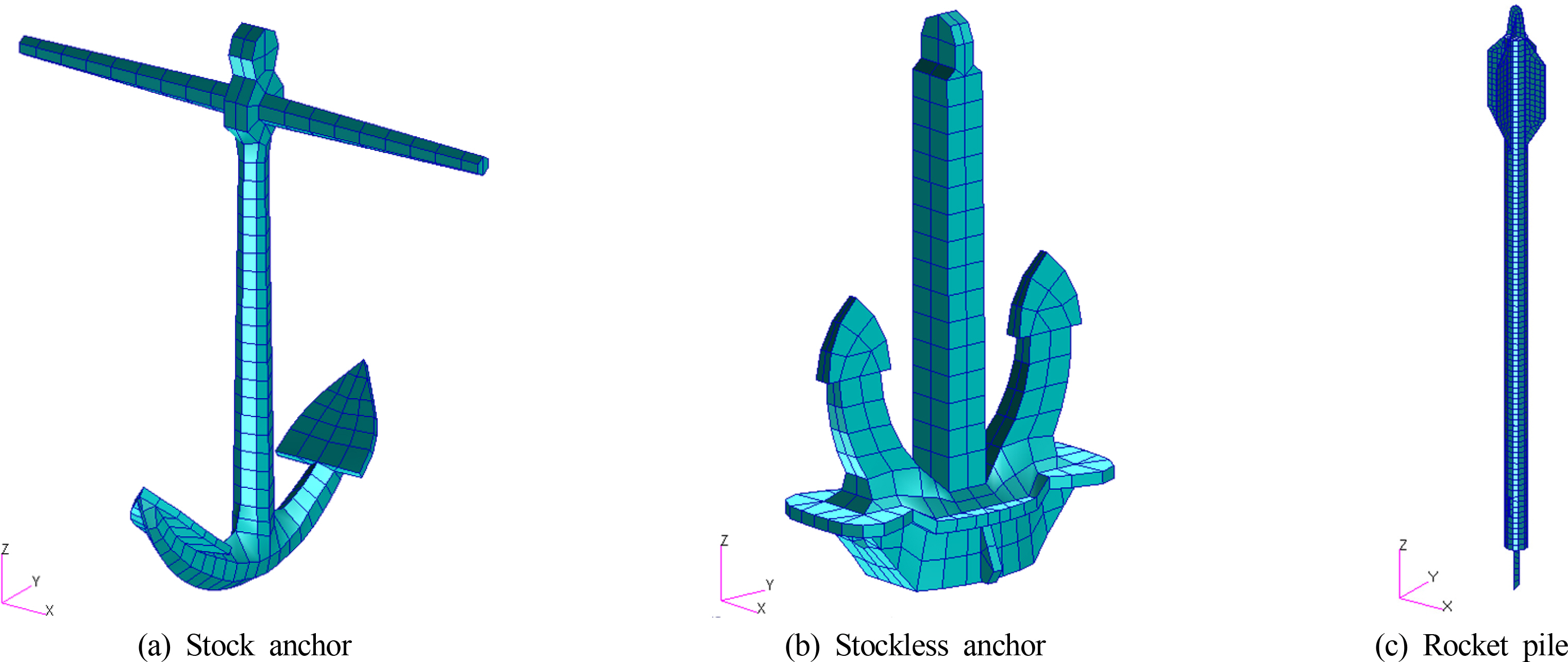
로켓포는 양식장용 지지대의 설치 깊이를 확보하기 위해 약 20m 수심의 해저지반에 자유낙하 시키는 어업 도구이며, 설계제원은 표준화되어 있지 않다. 서남해안에 주로 사용되는 로켓포의 제원은 길이 7.5m, 외경 ϕ190, 두께 20mm의 강관 내에 50×50×4mm의 L 형강을 관입하여 구성하는 형태이며, 중량은 600kg이다(Woo et al., 2017). 수치해석모델은 Fig. 7에 나타나 있는 바와 같이 스톡 앵커와 스톡리스 앵커는 KS에서 규정된 설계제원을 토대로 3차원 캐드 데이터를 생성하고 이를 이용하여 라그랑지 유한요소 모델을 구성하였고, 로켓포는 서남해안에서 주로 사용되는 600kg 중량의 제원을 반영하여 구성하였다. 3가지 해저케이블 위해인자의 유한요소 모델은 모두 8절점 솔리드(Solid) 요소를 사용하였다. 스톡 앵커 모델은 550개의 절점과 560개의 요소로 구성하였고, 스톡리스 앵커 모델은 628개의 절점과 652개의 요소로 구성하였으며, 로켓포 모델은 2,399개의 절점과 2,420개의 요소로 구성하였다. 해저케이블 위해인자의 재질은 밀도 7,850kg/m3, 탄성계수 210GPa, 프와송 비(Poisson's ratio) 0.3인 일반강재를 적용하였다. 또한 위해인자의 유한요소 모델의 중량을 확인하여 각각의 실제 중량과 동일하도록 구성하였다. 스톡 앵커의 경우 Fig. 6(a)와 같이 스톡의 형상이 비대칭으로 고려되면 수중낙하 시 스톡 앵커가 회전운동을 발생시킬 수 있는데, 수직방향으로 해저면에 낙하하는 운동체의 이론적 수직 낙하속도와 수치해석 결과와의 비교를 위해 유한요소 모델의 스톡 형상을 대칭으로 구성하였다.
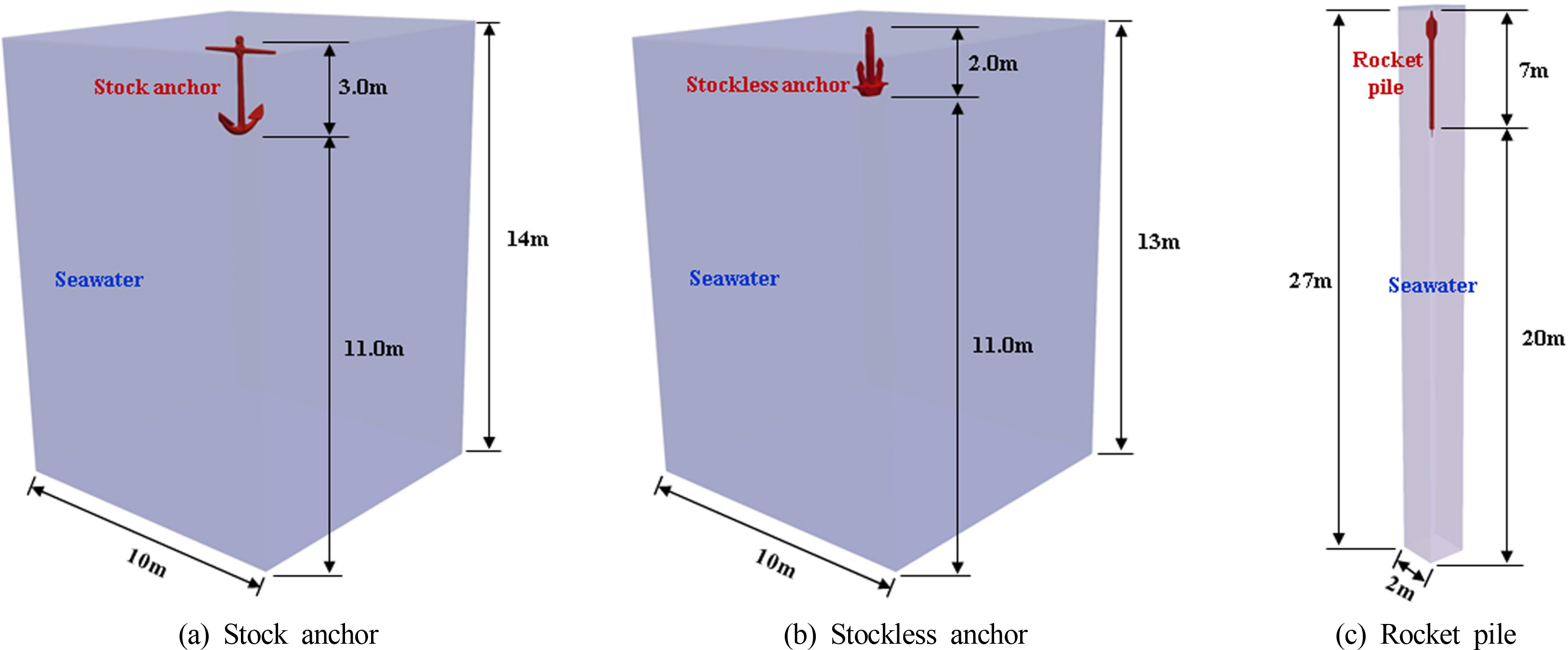
3가지 해저케이블 위해인자의 수중낙하 특성을 분석하기 위해 FSI 해석모델은 Fig. 8에 나타내었다.
Fig. 8에 나타난 바와 같이 스톡앵커와 스톡리스 앵커 및 로켓포에 대한 수치해석 모델의 수심은 실제 전남해안과 제주도 사이의 서남해역에서 사고빈도가 높았던 것으로 보고된(KEPCO, 2006) 10m 및 20m 전후의 수심으로 각각 고려하였다. Fig. 8의 FSI 해석모델에서 오일러 영역의 격자는 정육면체 요소를 사용하였으며, 스톡 앵커 모델에서는 6,139,259개의 절점과 3,318,519개의 요소로 구성하였고, 스톡리스 앵커 모델에서는 5,700,741개의 절점과 3,081,481개의 요소로 구성하였으며, 로켓포 모델에서는 473,600개의 절점과 256,000개의 요소로 구성하였고, 해수의 밀도와 체적탄성계수는 1,020kg/m3, 2.2GPa을 각각 적용하였다. 유체-구조 매질의 상호작용을 반영하기 위해 두 매질이 접하는 공통 경계표면인 각각의 위해인자의 표면을 연성표면으로 설정하였다. 오일러 영역의 상태방정식은 앞서의 베어링 강재 구체의 수중낙하해석과 동일하게 선형 다항 상태방정식을 사용하였다. 오일러 영역의 모델링 범위와 격자크기는 기존의 연구결과(Kim et al., 2017)를 근거로 하여 오일러 모델의 범위를 라그랑지 모델의 최대 폭의 약 5배 이상으로 설정하고, 오일러 모델의 격자크기는 라그랑지 모델의 요소크기 대비 25% 정도 세밀하게 적용하였다.
4.2. FSI 해석 결과 및 수중낙하 특성 고찰
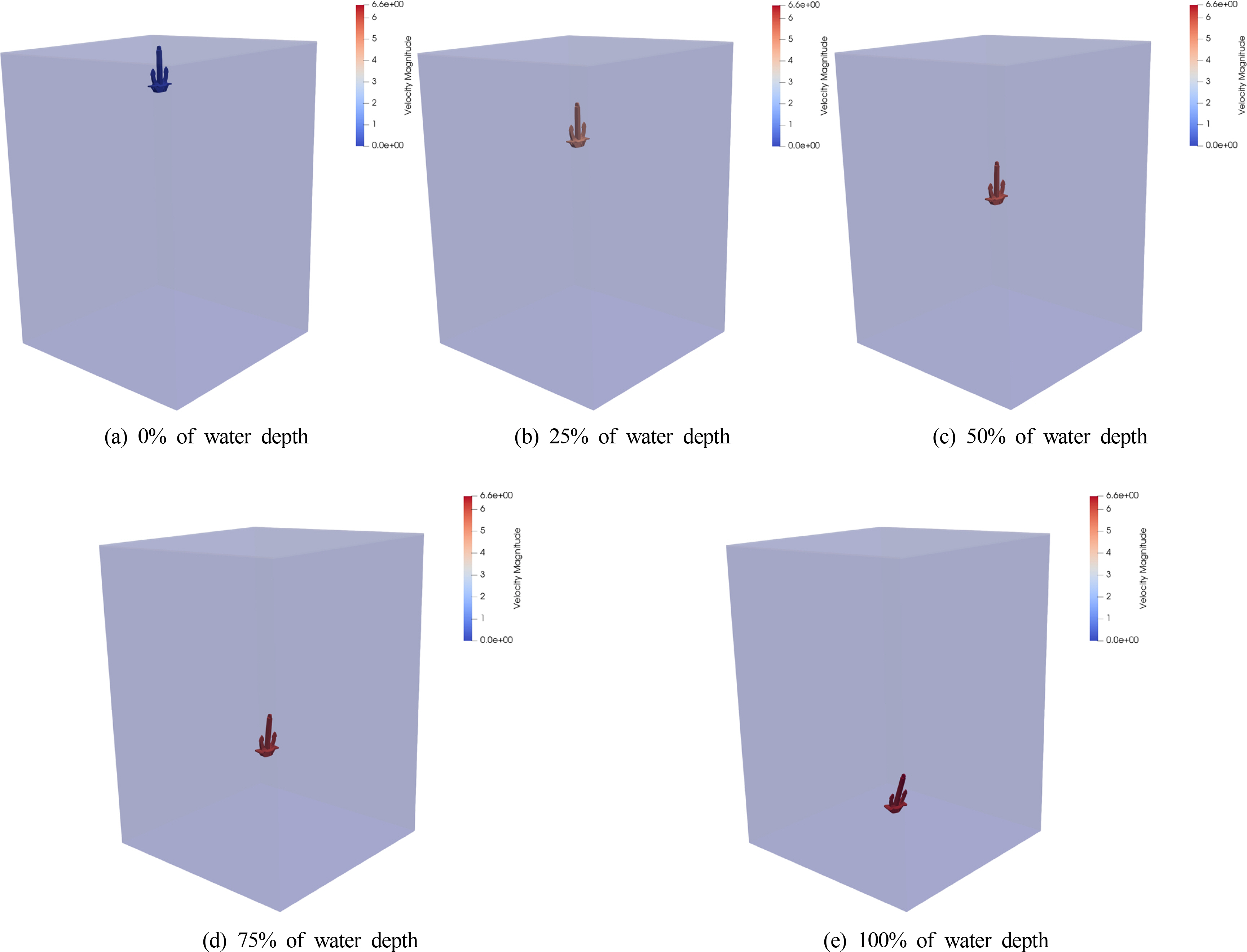
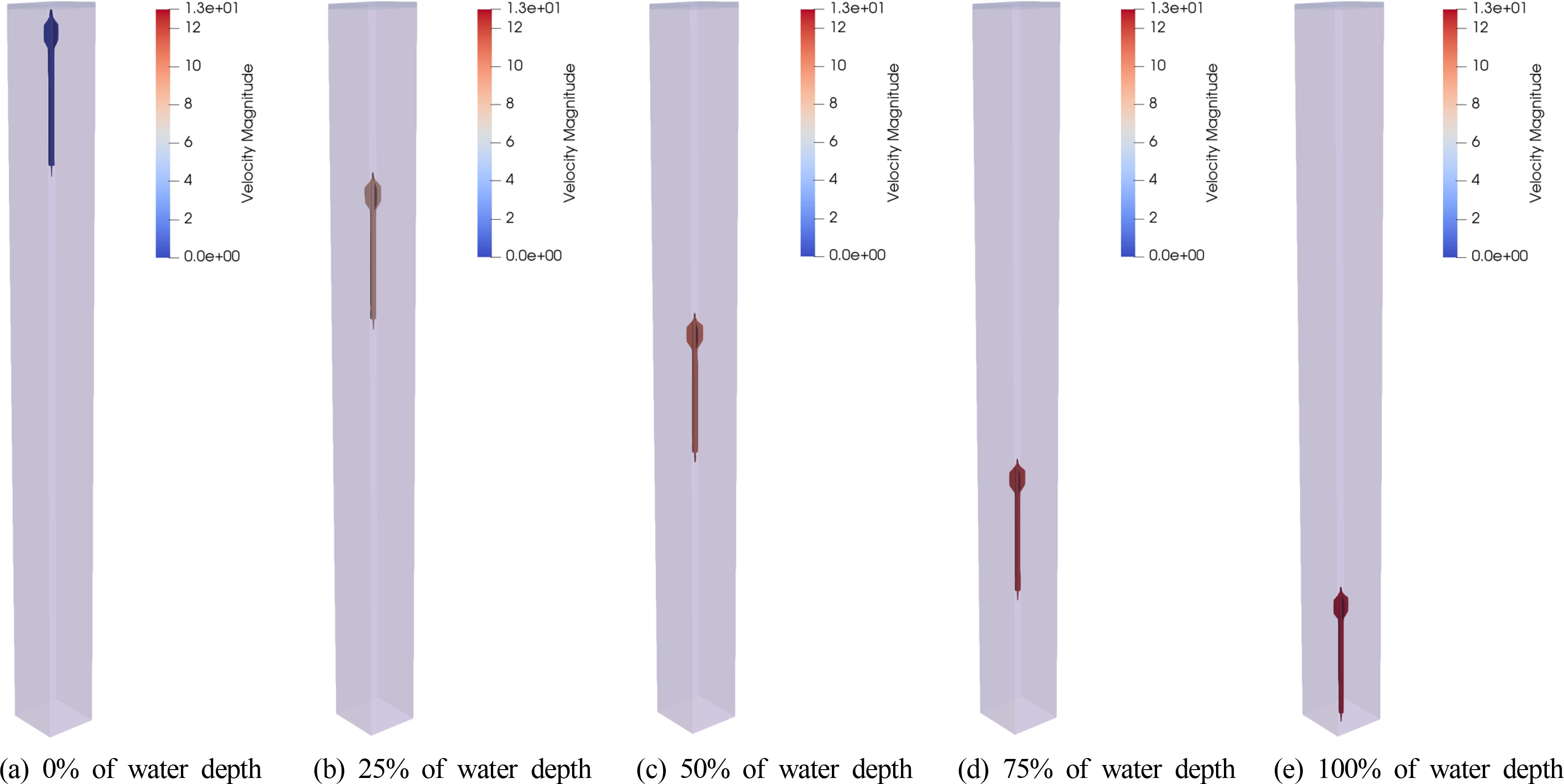
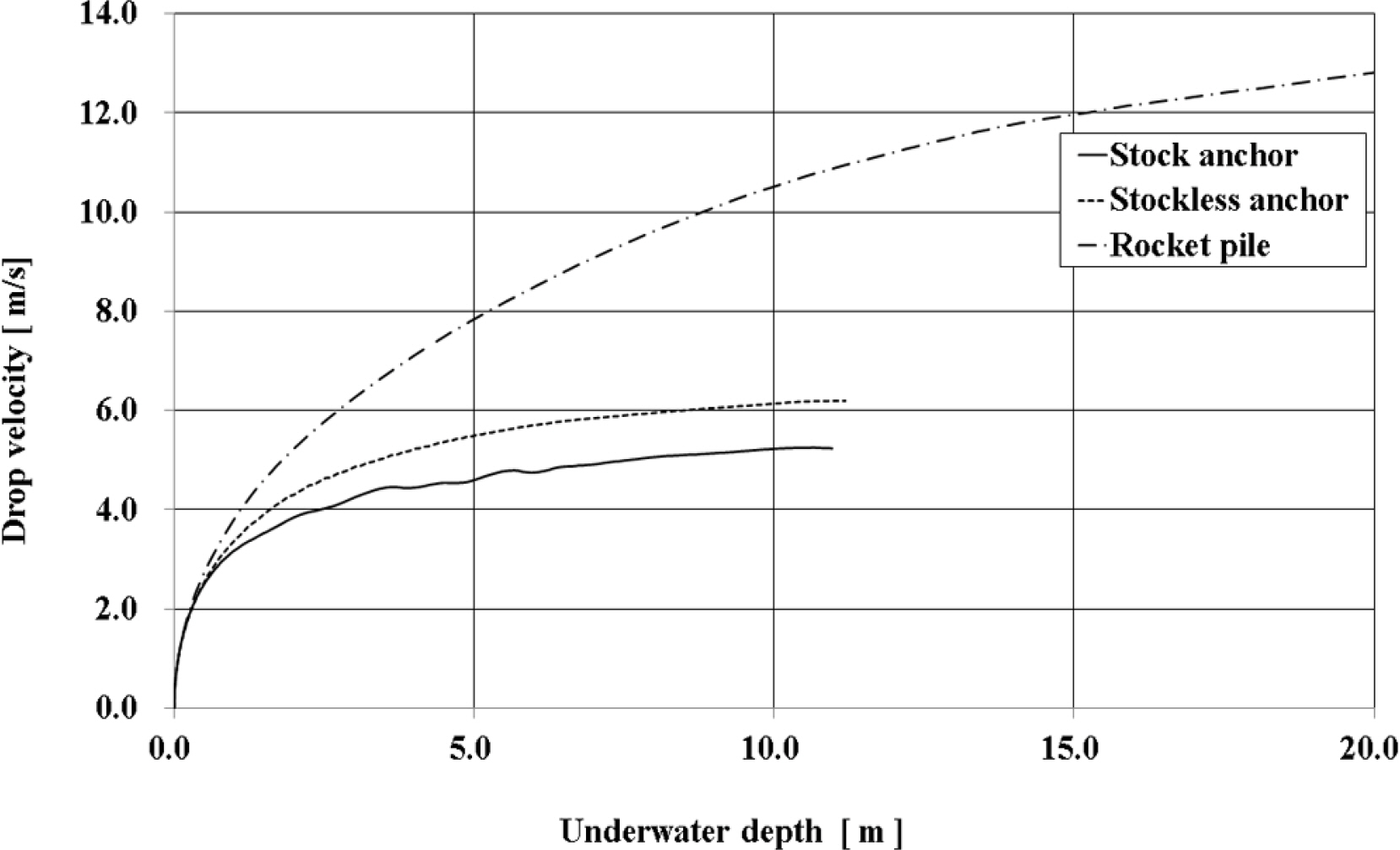
해저케이블 위해인자의 수중낙하 해석에서 스톡앵커, 스톡리스 앵커, 로켓포가 각각 수심 14m, 13m, 27m의 해수로 자유낙하 되는 상태에 대해 Fig. 8의 수치해석모델을 이용하여 FSI 시뮬레이션을 수행하였다. Figs. 9-11에는 해저케이블 위해인자의 수중낙하 깊이에 따른 위해인자 별 낙하속도에 대한 대표적인 결과를 나타내었다. 또한 Fig. 12에는 수중낙하 깊이에 따른 위해인자의 낙하속도 특성을 비교하여 도식적으로 나타내었다.
Figs. 9-11에서 나타나 있는 것처럼 해저케이블 위해인자의 수중 투묘 시 낙하속도의 변화율은 점성에 의한 운동에너지 손실로 수심이 깊어질수록 줄어드는 것을 확인할 수 있다. 스톡앵커와 스톡리스 앵커의 수중낙하 속도 변화의 경향성이 유사하게 나타난 반면, 로켓포의 경우 형상적 특성으로 인해 다른 경향성을 보였다. 스톡앵커와 스톡리스 앵커는 수심 5미터 전후로 낙하속도의 변화율의 변화가 매우 적어지는 특성을 나타내었고, 중량이 더 무겁고 형상이 작은 스톡리스 앵커의 수중낙하속도가 상대적으로 빠르게 나타났다. 로켓포의 경우 수심이 깊어질수록 낙하속도의 변화율이 줄어들기는 하지만 지속적으로 증가하는 경향성을 나타내었다. 이러한 로켓포의 수중낙하 특성은 투묘 완료 후 해저면에서 파지력을 유지해야하는 앵커와 달리 투묘 완료 후에도 해저면을 깊이 관통하도록 설계된 로켓포의 형상적인 특성 때문인 것으로 파악된다. 해저케이블용 보호설비의 급격한 파손사고 현상은 해저의 수압이나 환경적인 영향보다는 중량물인 해저케이블 위해인자의 투묘 시 수중낙하 운동으로부터의 동적 외력, 즉 충격력에 의한 것이기 때문에 위해인자의 최종낙하 상태의 충격량에 대한 정량적 평가가 중요하다고 할 수 있다. 운동역학 이론으로부터 충격량(I)과 운동량(p)의 관계는 다음의 식과 같이 나타낼 수 있다(Halliday et al., 2011).
여기서 p1, p0는 t1, t0에서의 운동량이고, m은 운동물체의 질량, v는 운동물체의 속도이다. 식 (1)과 식 (2)로부터 해저케이블 위해인자와 같은 중량물체의 수중낙하로 인한 충격의 문제는 낙하운동 속도의 정량적 평가가 핵심적인 사항임을 알 수 있다. 따라서 본 연구에서 수행한 위해인자 별로 수중낙하 FSI 해석 결과의 타당성을 평가하기 위해 수중낙하속도의 이론식 결과와 비교를 수행한다.
해저케이블 위해인자와 같은 중량체의 수직방향 수중낙하운동에 대한 속도와 운동거리는 다음과 같은 식을 통하여 이론적으로 산출할 수 있다(Woo and Na, 2010).
여기서 ρh와 ρw는 각각 해저케이블 위해인자와 해수의 밀도, V는 위해인자의 부피, g는 중력가속도, Cd는 항력계수, A는 위해인자의 투영면적(Projected area), v는 위해인자의 낙하운동속도이다. 낙하운동거리 x는 다음의 식을 통하여 이론적으로 산출할 수 있다(Woo and Na, 2010).
여기서 mh와 mw는 각각 해저케이블 위해인자와 해수의 질량, t는 시간이다. 식 (3)에 나타난 바와 같이 수중낙하운동에 대한 속도의 추정은 항력계수 산정의 정확도에 영향을 받게 된다. 수중낙하운동체의 형상에 따른 시험이나 CFD 기법과 같은 수치 해석을 이용하여 항력계수를 산정하게 되고, 항력계수의 정확도가 확보된 경우 식 (3)의 정확도는 높아진다(Fox et al., 2003; Hasanloo et al., 2012). 식 (3)과 (4)를 이용하여 해저케이블 위해인자의 수중낙하속도와 낙하거리를 이론적으로 산출하기 위해 FSI 해석에서 사용된 것과 동일한 위해인자의 제원과 재질을 적용하였으며, 이론해의 계산에 사용된 위해인자의 형상 특성치는 Table 1과 같다.
Table 1에서 해저케이블 위해인자의 체적과 투영면적은 FSI 해석모델로부터 산출하였으며, 항력계수는 유사한 형상과 제원의 위해인자에 대한 기존의 항력계수 산정 연구문헌의 결과를 참조하였다(Woo, 2014). Table 2에는 해저케이블 위해인자가 최저수심에 도달하는 낙하거리를 기준으로 FSI 해석과 이론식으로부터 산출된 위해인자의 수중낙하 종단속도 결과를 비교하여 나타내었다.
Table 2에 나타난 바와 같이 FSI 해석과 이론식의 해저케이블 위해인자의 수중낙하 종단속도 결과의 편차는 스톡리스 앵커가 가장 적게 나타났고, 로켓포의 경우가 상대적으로 높게 나타났다. 이러한 편차는 이론식의 항력계수 추정에 따라 발생된 것으로 볼 수 있다. 또한 이론식으로부터 산출된 해저케이블 위해인자의 종단속도는 베어링 강재 구체의 결과와 유사하게 FSI 해석으로부터 산출된 종단속도보다 전체적으로 높게 나타났다. 따라서 이론식을 통해 산출된 수중낙하 종단속도를 이용할 경우 낙하체의 특성에 따른 보정계수가 필요할 수 있다. Table 2에서와 같이 본 연구에서 수행한 FSI 해석과 이론식의 결과 차이가 적기 때문에 FSI 해석 기반의 수치시뮬레이션 방법의 타당성이 확보된 것으로 판단할 수 있다. 이와 같이 FSI 해석을 통해 해저케이블 위해인자의 수중낙하 특성이 구현될 수 있으면 실제 해양환경 상태를 고려하여 극한상태에서 해저케이블 보호설비의 구조강도에 대한 실제적인 성능평가가 수행될 수 있다. FSI해석의 수치 모델링과 시뮬레이션에 소요되는 비용은 높지만, 항력계수의 산정에 추가적인 노력이 필요한 이론식 보다 좀 더 직관적이고 높은 정확도가 보장되기 때문에 FSI 해석 기법은 해저케이블 보호설비의 실질적인 성능평가에 유용하게 적용될 수 있다. 또한 추후 연구에서 앵커 체인(Chain)의 거동을 수치 모델링에 고려할 예정이며, 이 경우 체인의 기구학적인 거동을 고려하면 FSI 해석의 유용성이 더 높아질 것으로 판단된다.
5. 결 론
본 연구에서는 3차원 CEL 방법 기반의 FSI 해석을 이용하여 다양한 해저케이블 위해인자의 수중낙하에 대한 수치 시뮬레이션을 수행하고, 위해인자의 종류에 따른 수중낙하 특성을 비교하였다. 본 연구에서 사용한 FSI 해석방법의 정확도를 검증하기 위해 기존에 수행되었던 베어링 강재 구체의 수중낙하시험 및 CFD 해석과 동일한 조건으로 FSI 해석을 수행하여 높은 일치도의 결과를 확인하였다. 검증된 FSI 해석방법을 기반으로 다양한 해저케이블 위해인자의 수중낙하 현상에 대한 수치 시뮬레이션을 수행하였다. 수치 시뮬레이션에서 고려한 해저케이블 위해인자의 종류는 실제 국내 서남해안에 설치된 해저케이블 보호설비의 파손사례보고에서 사고 발생빈도가 높았던 스톡 앵커, 스톡리스 앵커, 양식장 로켓포를 대상으로 하였다. 각각의 위해인자는 라그랑지안 모델로 생성하였고, 오일러 방정식으로 생성된 수중 유체영역과 연성하여 3차원 전체 규모의 FSI 해석모델을 구성하였다. 위해인자 별로 FSI 해석을 통해 수중낙하 속도 결과를 이론식의 결과와 비교하여 수치 시뮬레이션의 타당성을 검증하고 위해인자의 종류에 따른 수중 낙하특성을 비교하였다. 스톡앵커와 스톡리스 앵커는 일정 수심 이후로 낙하속도의 변화율의 변화가 매우 적어지는 유사한 특성을 나타내었고, 중량이 더 무겁고 형상이 작은 스톡리스 앵커의 수중낙하속도가 상대적으로 빠르게 나타났다. 로켓포의 경우 수심이 깊어질수록 낙하속도의 변화율이 줄어들기는 하지만 지속적으로 증가하는 경향성을 나타내었다. FSI 해석과 이론식의 수중낙하 종단속도의 결과 차이는 적게 나타났으며, FSI 해석 기반의 해저케이블 위해인자의 수중낙하 수치시뮬레이션 방법의 타당성이 확보된 것으로 판단할 수 있었다. 따라서 FSI 해석을 통해 해저케이블 위해인자의 수중낙하 특성의 구현을 통해 실제 해양환경 상태를 고려하여 극한상태에서 해저케이블 보호설비의 구조강도에 대한 실제적인 성능평가가 수행될 수 있다. FSI해석의 수치 모델링과 시뮬레이션에 소요되는 비용은 높지만, 항력계수의 산정에 추가적인 노력이 필요한 이론식 보다 좀 더 직관적이고 높은 정확도가 보장되기 때문에 FSI 해석 기법은 해저케이블 보호설비의 실질적인 성능평가에 유용하게 적용될 수 있다고 판단되었다. 또한 CFD 해석 기법 대비 FSI 해석은 라그랑지안 구조체의 변형이나 응력 등의 구조강도 특성을 유체 연성효과와 함께 모사할 수 있기 때문에 해저케이블 보호설비의 구조성능 평가에 있어서 유효성이 더 높다고 할 수 있다. 향후 저자들은 본 연구의 결과를 확장하여 3차원 FSI 해석 기반의 해저케이블 위해인자의 투묘상황과 해저케이블 보호구조물의 수중 충돌 파손현상의 연계에 관한 연구를 수행할 예정이다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation
Print
