정수 중 바지선의 예인안정성에 관한 수치 시뮬레이션
Numerical Simulation of Towing Stability of Barges in Calm Water
Article information
Trans Abstract
This paper presents the results of a numerical study on the towing stability of barges. Towing simulations were carried out by using two different numerical models (MMG model and cross-flow model). Stability criteria are also suggested based on the analysis of the linearized governing equations for towed vessel motion. In order to validate the present numerical models, the experimental data of Yasukawa et al. (2006) were used. Simulations were conducted for single and double barges under constant towing speed and direction conditions. The time histories of the heading angle, yaw rate, and towline tension were compared between the numerical results and experiments. The effects of the towline length on the slewing frequency and maximum heading angle were also observed. In addition, a series of numerical simulations using variable hydrodynamic coefficients were performed to investigate the effects of the hydrodynamic forces on the towing stability.
1. 서 론
해양플랜트 산업의 신장세와 함께 예인(Towing)에 의한 해양구조물의 운송작업이 점차 증가하고 있다. 통상적으로 예인작업에서는 예인줄(Towline)에 연결된 부선(Towed ship)을 끌고 가는 형태로 이뤄지며, 이 경우 부선의 형상 및 예인방법에 따라 예인안정성(Towing stability)은 매우 달라질 수 있다. 부선의 불안정한 거동은 과도한 평면 운동을 야기하여 다른 선박 또는 해양구조물과의 충돌사고가 발생할 수 있기 때문에, 예인작업에 앞서 예인안정성에 대한 선행 검토가 매우 중요하다.
예인안정성에 관한 대표적인 기존 연구로는 Bernitsas and Kekerdis(1985)에 의해 예인선박의 안정성에 대한 조건식을 특성 방정식을 이용하여 제시한 바 있다. Latorre(1988)은 모형선을 이용한 예인 바지선의 안정성 판별 시 축척비에 따른 효과를 지적한 바 있다. Yasukawa et al.(2006)은 2가지 바지선의 예인안정성에 대한 일련의 모형시험을 수행하고, 조종운동방식을 이용하여 수치해석 연구를 병행한 바 있다. Fitriadhy and Yasukawa(2010) 은 풍하중 하에서의 예인안정성에 대한 수치해석 연구를 수행하였다.
본 연구에서는 Yasukawa의 MMG(Manoeuvring mathematical modeling group)기반 조종 운동방정식과 Wichers(1988)이 제안한 Cross-flow모델 기반의 저주파수 평면 운동 방정식을 이용하여 바지선의 예인 시뮬레이션을 수행 하였다. Yasukawa et al.(2006)가 수행한 모형시험 데이터를 활용하여 예인해석을 수행하였으며, 예인줄 길이에 따른 선수각 동요주기 및 최대 선수각을 비교 분석하였다. 또한 일련의 수치계산을 수행하여 유체력 계수들의 변화에 따른 바지선의 거동변화를 관찰하였다. 이를 통해 두 수치 모델의 예인안정성 해석의 적용 가능성을 확인하고, 예인안정성에 중요하게 영향을 주는 유체력을 파악하고자 하였다.
2. 운동 방정식
본 연구에서는 바지선의 예인안정성에 관한 수치해석 연구를 수행하기 위하여 두 가지 운동 모델을 고려하였다. 하나는 MMG모델 기반의 조종 운동방정식이며, 다른 하나는 Crossflow모델을 고려한 저주파수 평면 운동 방정식이다.
2.1 Yasukawa's MMG model
Yasukawa et al.(2006)은 MMG 모델에 근간하여 예인 선박의 거동에 대한 운동 방정식을 식 (1)~(3)과 같이 표현하였다.
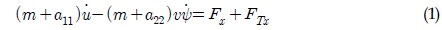
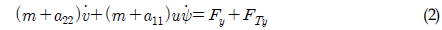

여기서 m과 Iz는 예인바지선의 질량 및 선수동요 관성 모멘트이다. a11, a22, a66는 각각 전후, 좌우, 선수동요 방향의 부가질량 계수이며, u, v, ψ는 선박의 전후속도, 좌우속도, 선수각 운동을 나타내며, 윗첨자 점은 시간미분을 의미한다. FTx, FTy, MTz는 예인줄의 장력에 의해 선체에 작용하는 분력들을 의미한다. Fx, Fy, Mz는 선체에 작용하는 유체하중이고, 식 (4)~(6)과 같이 표현된다.

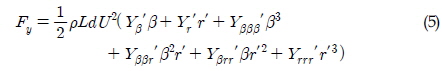
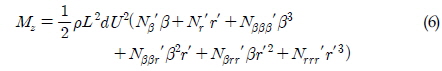
여기서 ρ는 유체 밀도이고, L과 d는 각각 선체의 길이와 흘수에 해당한다. U=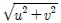 는 선박의 속도이며, r′ 는 무차원화된 선수 각속도(r′=rU/L, r=
는 선박의 속도이며, r′ 는 무차원화된 선수 각속도(r′=rU/L, r=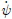 이다. β는 표류각(Drift angle)이며, β=tan−1(−v/U)으로 계산될 수 있다.
이다. β는 표류각(Drift angle)이며, β=tan−1(−v/U)으로 계산될 수 있다. 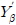 ,
, 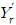 ,
, 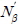 ,
,  등은 유체력 미계수들이며, 이에 대한 자세한 정의는 Yasukawa et al. (2006)에서 발견할 수 있다. 본 연구에서는 타 및 프로펠러에 대한 모델링은 고려하지 않았다. 예인줄은 단순 스프링 모델을 이용 하여 모사하였으며, 스프링 상수와 감쇠 계수는 각각 50N/m와 10N․s/m의 값을 이용하였다.
등은 유체력 미계수들이며, 이에 대한 자세한 정의는 Yasukawa et al. (2006)에서 발견할 수 있다. 본 연구에서는 타 및 프로펠러에 대한 모델링은 고려하지 않았다. 예인줄은 단순 스프링 모델을 이용 하여 모사하였으며, 스프링 상수와 감쇠 계수는 각각 50N/m와 10N․s/m의 값을 이용하였다.
2.2 Wichers' Cross-flow model
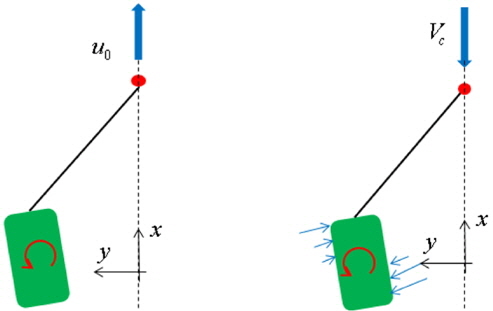
저속 운동 가정아래 Wichers(1988)이 제안한 Cross-flow model 을 이용하면, 예인 바지선에 대한 저주파수 평면 운동방정식은 식 (7)~(11)과 같이 표현될 수 있다. 이 경우 Fig. 1에서 보인 것처럼 전진속도는 입사하는 조류로 대체되어 고려되며, 선체에 작용하는 유체력은 항력계수에 의한 준정상 조류력(Quasi-steady current force)과 Cross-flow에 의한 동적 조류력(Dynamic current force)의 합으로 표현된다(Wichers, 1988).
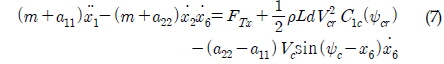
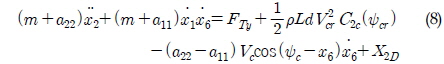

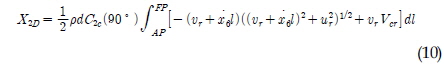
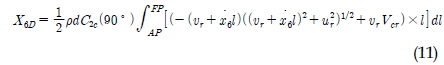
여기서 C1C, C2C, C6C는 무차원화된 조류력 계수이며, Vc와 ψc는 각각 조류 속도와 방향에 해당한다. x1, x2, x6는 각각 전후, 좌우, 선수동요이며, 이때 전후동요는 MMG모델과 다르게 예인속도에 의한 변위가 제외된 성분이다. X2D와 X6D는 Cross-flow에 의한 동적 조류력 성분이며, 이에 대한 좀 더 자세한 설명은 Wichers(1988)에서 발견할 수 있다. Vcr와 ψcr은 선체의 운동을 고려한 상대 조류 속도와 방향에 해당하며, 식 (12)~(15)와 같이 정의 된다. ur과 vr은 선체의 상대속도에 해당한다.




2.3 선형 안정성 판별식
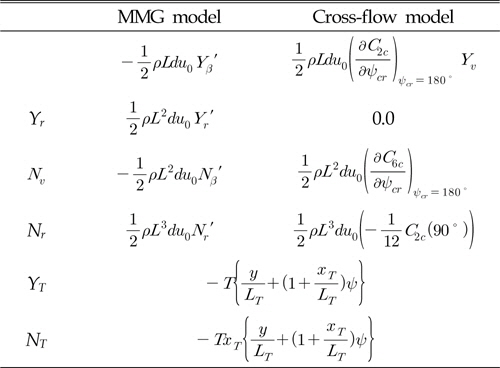
일정한 속도로 진행선을 따라 바지선이 예인되는 경우(u=u0, v=0), 상기의 두 운동방정식은 식 (16)와 (17)과 같이 선형화하여 표현할 수 있다. 두 수치모델에서 선형 동유체력 계수간의 관계는 Table 1에 요약하여 정리하였다. 이 때 선형 동유체력 선형계수는 Taylor 전개를 이용하여 유도되었다.
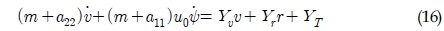

이 모델을 이용할 경우 선형 안정성 판별식은 Bernitsas and Kekerdis(1985)의 방법으로 유도될 수 있으며, Latorre(1988)과 Lee(2012)도 동일한 예인 안정성 조건식을 유도한 바 있다.

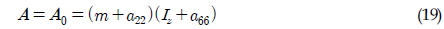

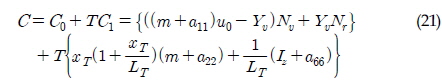
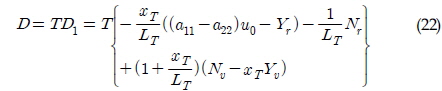
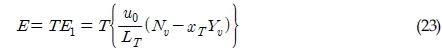
여기서 LT는 예인줄의 길이이며, xT는 무게중심과 예인점 사이 거리이다. 상기의 특성방정식(Characteristic equation)에 대한 해의 실수부가 음의 값을 갖기 위해서는 다음 조건이 만족 되어야 한다(Abkowitz, 1972).
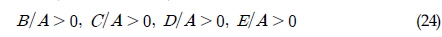
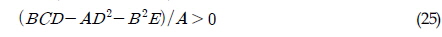
최종적으로 예인 안정성 조건으로 식 (26)과 (27)이 도출 될 수 있다. 식 (26)은 예인점의 위치가 횡방향 압력중심점 보다 앞쪽에 위치해야 한다는 제약조건이며, 식 (27)은 안정적인 예인을 위한 최소 장력을 지시해준다.


3. 수치 모델 검증
본 논문에서 고려된 두 가지 모델을 이용하여 Yasukawa et al.(2006)의 모형 시험 조건에 대해 수치 해석을 수행하고, 검증을 수행하였다. 바지선의 주요 형상인자 및 유체력 계수는 Table 2와 같다. 시뮬레이션에서 고려한 예인속도는 실험 결과와의 비교를 위해 0.509m/s만을 고려하였으며, 이는 실선 기준 7 knots에 해당한다. 수치 시뮬레이션에서 초기조건은 모형 실험결과에서 계측된 선수각, 선수각속도가 근사하게 발생하도록 수치적 조정을 통하여 결정하였다.
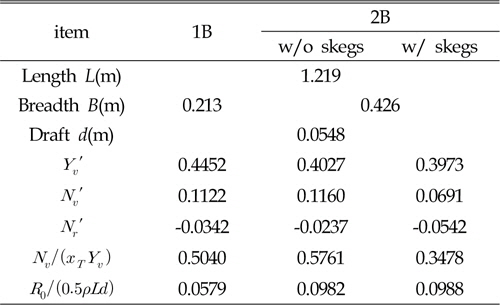
Principle dimensions and main hydrodynamic derivatives for barges (Yasukawa et al., 2006)
MMG 모델의 유체력 계수는 Yasukawa et al.(2006)의 값을 그대로 이용했으며, Cross-flow모델에서의 항력계수는 별도의 값이 존재하지 않기 때문에, 식 (28)~(30)과 같은 형태로 항력계수를 가정하였다.

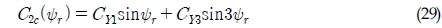

단, MMG 모델과 Cross-flow 모델 간의 Table 1의 선형 동유체력 계수가 동일할 수 있도록 계수들은 식(31)~(33) 관계식에 따라 추정하였다.

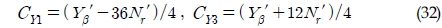

3.1 단일 바지선(1B)
단일 바지선에 대한 예인 해석 결과에 대해 Fig. 2에서 비교하여 보여 주고 있다. 여기서 'Exp'는 Yasukawa et al.(2006)의 모형시험결과이며, 'MMG'와 'Cross-Flow'는 각각 MMG모델과 Cross-flow 모델을 이용한 수치 시뮬레이션 결과를 지시한다. 수치 시뮬레이션에서는 초기조건으로 선수각을 −30도로 주고 수행되었다. 선수각의 변화에 대해서 수치계산은 실험에 비해 다소 큰 진폭을 보여주고 있지만, 동요주기는 오히려 약간 작게 예측해주고 있다. 두 수치모델 중 Cross-flow 모델이 MMG 모델보다 더 큰 선수각 변화가 발생하였다. 이는 두 수치모델 사이의 선수각이 클 때 중요한 영향을 미치는 고차 유체력 계수가 서로 상이하기 때문에 발생한다. 선수각 변화 속도와 예인줄에 걸리는 장력을 보면, 전체적인 경향은 수치계산을 통해 유사하게 확인할 수 있으나, 최대값에 있어서는 약간의 차이를 보여주고 있다. 특히, Cross-flow 모델을 이용한 경우에, 모형시험보다 다소 큰 선수각 변화와 예인선 장력이 발생하였다.

Comparison of time histories of heading angle, yaw rate and towline tension for 1B (LT/L=1, u0=0.509m/s)
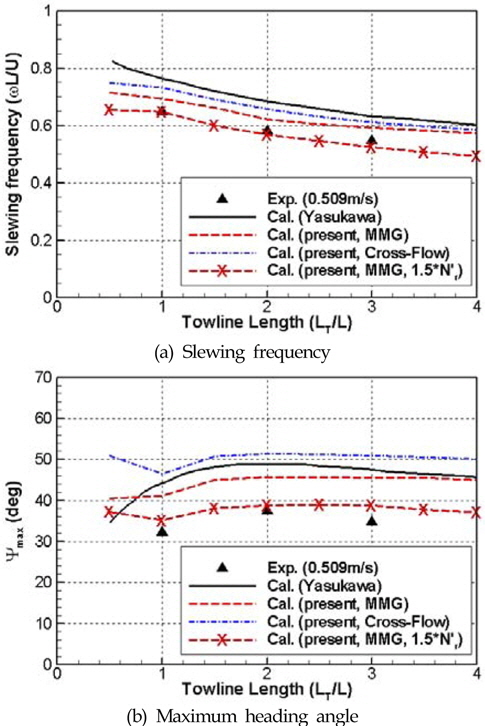
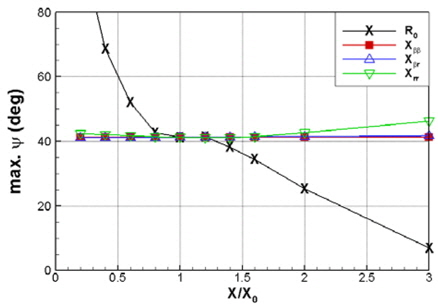
다양한 길이의 예인줄에 대해 선수각의 동요주파수(Slewing frequency)와 최대 선수각에 대한 모형시험 및 수치계산 결과를 Fig. 3에 비교하여 보여 주고 있다. 현재 고려한 두 가지 수치모델 모두 선수각 동요주파수에 있어서는 정도 높게 예측해줄 수 있음을 알 수 있다. 하지만 최대 선수각에 대해서는 수치계산이 약 10도 정도 크게 예측해주고 있으며, 특히 Cross-flow모델을 이용한 결과는 모형시험과 약 15도 가량의 차이를 보여주고 있다. 이는 선수각이 클 때 모형시험의 감쇠력이 현 수치모델에서 고려한 것 보다 더 크게 작용했다고 유추할 수 있다. 수치적으로  계수를 1.5배하여 선수각 동요에 대한 감쇠력을 증가시켰을때, Fig. 3에서 볼 수 있는 것처럼, 최대 선수각에 대한 수치 해석 값이 모형시험 결과에 좀 더 근접해짐을 알 수 있다. 선수각 운동에 대한 정도 높은 수치해석을 위해서는 과대 선수각 상황에서의 감쇠력을 정확히 구현할 필요가 있음을 지시해준다.
계수를 1.5배하여 선수각 동요에 대한 감쇠력을 증가시켰을때, Fig. 3에서 볼 수 있는 것처럼, 최대 선수각에 대한 수치 해석 값이 모형시험 결과에 좀 더 근접해짐을 알 수 있다. 선수각 운동에 대한 정도 높은 수치해석을 위해서는 과대 선수각 상황에서의 감쇠력을 정확히 구현할 필요가 있음을 지시해준다.
3.2 쌍동 바지선 (2B)
쌍동 바지선에 대한 예인 해석 결과에 대해 Fig. 4에서 비교하여 보여 주고 있다. 초기조건으로 선수각을 −20로, 선수각속도 5 deg/s를 주고 수치 시뮬레이션이 수행되었으며, 초기 천이거동을 제외하기 위해 −30초부터 계산을 수행하였다. 단일 바지선의 경우와 유사하게 선수각 변화에 대한 경향 및 동요주기는 모형시험과 수치계산이 유사한 결과를 보여 주고 있지만, 선수각 운동과 예인줄 장력은 수치해석이 다소 크게 계산되었다. 특히 Cross-flow 모델을 이용할 경우 선수각 40도 근처에서의 선수 각속도 및 장력이 과도하게 발생하였다. 이는 현재 항력계수를 식(29), (30)과 같이 단순하게 모델링함에 따라 과대 선수각 운동이 발생했을 시 중요하게 영향을 미치는 고차의 유체력계수가 정도 높게 모델링 되지 않았기 때문으로 생각된다.

Comparison of time histories of heading angle, yaw rate and towline tension for 2B without skegs (LT/L=1, u0=0.509m/s)
Fig. 5는 Skeg의 유무에 따른 선수각의 변화를 보여주고 있으며, 초기 천이구간은 제외하고 제시하고 있다. Skeg가 있을 경우 선수각의 변화는 크게 줄어듦을 알 수 있다. 이러한 경향은 Table 2에서 보인 것처럼 Skeg가 있는 경우N′v값이 크게 줄면서 좌우운동 시 선수동요 모멘트가 작게 발생하게 되고,  이 증가함에 따라 선수동요 시 감쇠력이 증가하게 되기 때문이다.
이 증가함에 따라 선수동요 시 감쇠력이 증가하게 되기 때문이다.
4. 예인 안정성 수치 해석
예인안정성에 중요하게 영향을 주는 인자는 식 (26), (27)에서 보인 것처럼, 측면력과 선수동요 모멘트의 비, 예인줄 장력(저항)으로 구분될 수 있다. 본 연구에서는 두 가지 인자에 대해 유체력 계수들을 변화시켜 가면서, 바지선의 거동 및 예인안정성에 중요하게 영향을 주는 유체력 성분을 검토하고자 하였다.
4.1 Sway Force vs. Yawing Moment
Y′v값을 변화시켜, 식 (26)에 의한 예인안정성 판별식의 값을 조정하였을 때 바지선의 거동을 Fig. 6에 도시하고 있다. 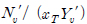 =0.4일 때는 선형 예인안정성이 확보되며, 두 수치계산 결과는 매우 잘 일치하는 것을 볼 수 있다.
=0.4일 때는 선형 예인안정성이 확보되며, 두 수치계산 결과는 매우 잘 일치하는 것을 볼 수 있다. 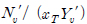 =1.2 일 때는 선형 예인안정성이 확보되지 않은 상황으로, 두 수치계산 에서 바지선은 모두 일정한 선수각을 유지하면서 예인되는 상황이 발생하였다. 다만 최종 선수각은 두 모델 간에 차이가 있었다.
=1.2 일 때는 선형 예인안정성이 확보되지 않은 상황으로, 두 수치계산 에서 바지선은 모두 일정한 선수각을 유지하면서 예인되는 상황이 발생하였다. 다만 최종 선수각은 두 모델 간에 차이가 있었다. 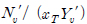 =0.7에서는 수치계산 간 다소 차이는 발생하 였지만, 선수각의 진폭 및 주기는 대체로 일치하였다.
=0.7에서는 수치계산 간 다소 차이는 발생하 였지만, 선수각의 진폭 및 주기는 대체로 일치하였다.
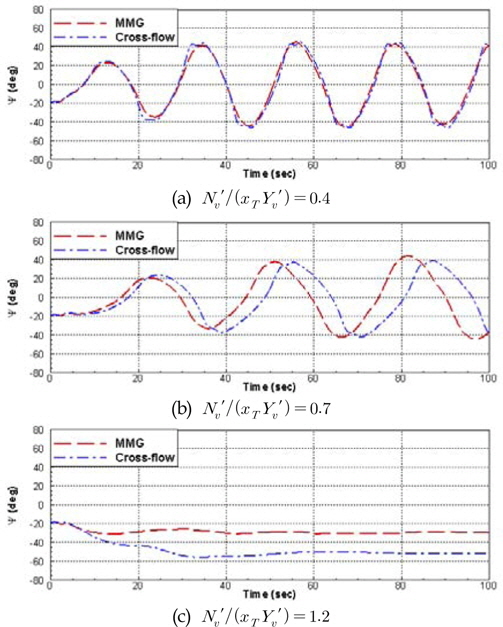
Comparison of time histories of heading angle with different sway hydrodynamic derivative for 2B (LT/L=1, u0=0.509m/s)
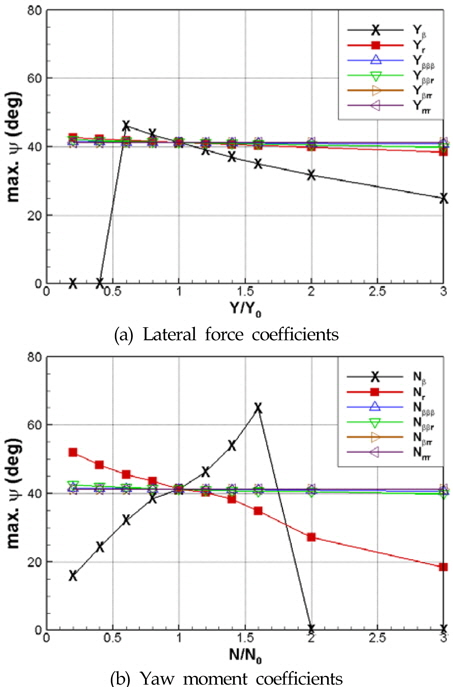
Fig. 7은 유체력 미계수를 기존 실험 계측치(아래첨자 0) 대비 변화시켰을 때 예인 바지선의 최대 선수각이 어떻게 변화하는지를 보여주고 있다. 측면 힘과 관련해서는 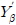 을 제외하고는 바지선의 거동에 큰 영향을 주지 않음을 알 수 있다. 선수동요 모멘트와 관련해서는
을 제외하고는 바지선의 거동에 큰 영향을 주지 않음을 알 수 있다. 선수동요 모멘트와 관련해서는 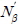 와
와  이 바지선의 거동에 중요한 영향을 줌을 확인할 수 있다.
이 바지선의 거동에 중요한 영향을 줌을 확인할 수 있다.
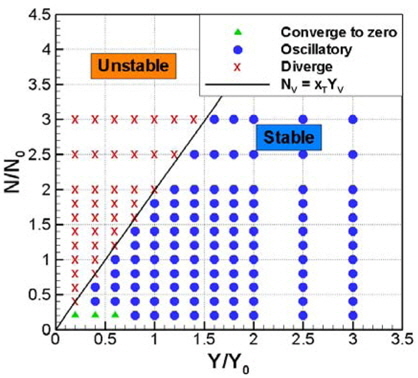
Fig. 8은 식 (26)에 의한 예인안정성 영역에 대해 MMG모델을 이용하여 시간영역 시뮬레이션을 통해 확인할 결과를 같이 보여주고 있다. 수치 결과는 해석적인 안정성 판별식에 의한 안정 및 불안정 경향을 동일하게 보여줌을 알 수 있다.
4.2 저항 변화
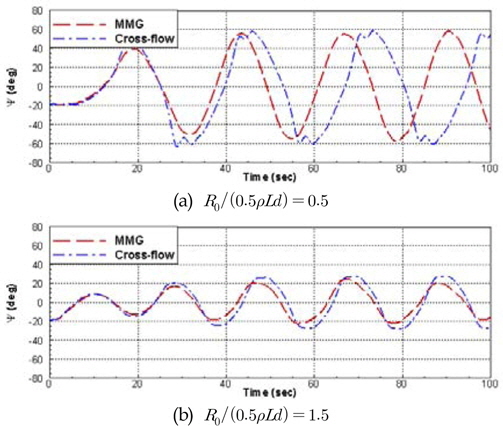
예인 안정성에 영향을 미치는 또 하나의 중요한 인자인 저항에 대한 수치해석을 수행하였다. Fig. 9는 전후동요 방향의 힘의 계수를 조정했을 때 바지선의 선수각 변화에 어떠한 영향을 미치는지를 보여주는 그래프이다. 바지선의 예인안정성에 영향을 주는 중요한 계수는 R0 이며, 이는 바지선의 예인속도에 의해서 결정되는 저항에 해당한다. 저항의 변화는 예인줄의 장력에 변화를 주어 예인 시 바지선의 거동에 중요한 영향을 주게 된다.
Fig. 10은 전후방향의 힘을 변화시켰을 때 시간영역 수치해석 결과를 비교하여 보여주고 있다. R0/(0.5pLd)=0.5일 때 선수각 응답이 약 60도까지 커진 반면, R0/(0.5pLd)=1.5에서는 최대 선수각이 약 20도까지 낮아졌다. 전체적으로 두 수치모델 모두 예인안정성을 판별하는데 잘 적용될 수 있음을 확인할 수 있었으며, 예인안정성이 높은 경우에 두 수치 모델 사이의 계산 결과가 보다 잘 일치하였다.
5. 결 론
본 논문에서는 예인안정성에 관한 수치해석 연구를 위해 MMG모델과 Cross-flow모델을 도입하였다. 두 수치 모델을 이용하여 Yasukawa의 바지선 모델에 대한 예인 시뮬레이션을 수행하였으며, 모형시험 결과와 비교 검증을 수행하였다. 또한 바지선에 작용하는 유체력 계수들을 체계적으로 변화시켜가며 예인안정성에 미치는 영향을 검토하였다. 이상의 연구를 통해 다음과 같은 결론을 얻을 수 있었다.
(1) MMG모델과 Cross-Flow 모델은 모두 예인 시 거동특성 즉, 선수각 운동의 크기 및 동요주기를 비교적 정확히 예측해 줄 수 있었다. 반면 선수각 변화 속도와 예인줄에 걸리는 장력은 선수동요에 작용하는 감쇠력의 크기와 유체력 모델링의 정확도, 예인줄의 수치모델에 따라 다소 차이를 보일 수 있었다.
(2) 상대적으로 Cross-Flow모델이 좀 더 과장된 운동을 계산해 주었으며, 이는 본 연구에서는 항력계수에 대한 단순화된 모델을 이용했기 때문이다. 보다 정확한 항력계수 정보가 주어질 경우 부선의 거동을 좀 더 정확히 예측해 줄 것으로 기대된다.
(3) 예인안정성은 부선에 작용하는 좌우방향 힘과 선수동요 모멘트의 비에 의해서 중요하게 영향을 받으며, 이러한 사실은 해석적인 선형 안정성 판별식과 시간영역 수치 시뮬레이션 결과에서 모두 확인되었다.
(4) 바지선의 선수각 운동에 중요하게 영향을 미치는 MMG모델의 유체력 계수는 R0, 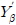 ,
, 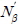 ,
,  이며, 이외의 유체력 계수들은 바지선의 거동에 주는 영향이 상대적으로 작았다.
이며, 이외의 유체력 계수들은 바지선의 거동에 주는 영향이 상대적으로 작았다.
향후 예인안정성을 판별하는데 있어서 두 수치 모델이 모두 적용될 수 있을 것으로 판단되며, 다양한 예인 해석 및 검증을 통해 예인안정성 해석을 위한 정도 높은 수치모델을 확립해 나갈 필요가 있다.
Notes
It is noted that this paper is revised edition based on proceedings of KAOST 2012 in Daegu.
Acknowledgements
본 연구는 해양과학기술원에서 수행중인 지식경제부 과제 "해저 및 해상생산플랜트 설치설계 핵심기술 개발"과 해양과학기술원 주요사업인 "해양구조물의 이송·설치를 위한 작업성능 평가기술 개발" 과제의 지원으로 수행된 연구결과 중 일부임을 밝히며, 연구비 지원에 감사드립니다.
References
Abkowitz, M.A., 1972. Stability and motion control of ocean vehicles. The M.I.T. Press, Cambridge.
Abkowitz M.A.. Stability and motion control of ocean vehicles The M.I.T. Press. Cambridge: 1972.Bernitsas, M.M., Kekerdis, N.S., 1985. Simulation and stability of ship towing. Int. Shipbldg Prog., 32(369), 112-123.
Bernitsas M.M., Kekerdis N.S.. Simulation and stability of ship towing. Int. Shipbldg Prog. 1985;32(369):112–123.Latorre, R., 1988. Scale Effect in Towed Barge Course Stability Tests. Ocean Engineering, 15(4), 305-317.
Latorre R.. Scale Effect in Towed Barge Course Stability Tests. Ocean Engineering 1988;15(4):305–317. 10.1016/0029-8018(88)90048-0.Lee, J.H., 2012. Multi-body and stability analysis of the towed ship system. Master's thesis.
Lee J.H.. Multi-body and stability analysis of the towed ship system. Seoul National University, Master's thesis Seoul National University; 2012.Fitriadhy, A., Yasukawa, H., 2010. Slewing Motion Characteristics of a Towed Ship in Steady Wind. Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2010-20673).
Fitriadhy A., Yasukawa H.. Slewing Motion Characteristics of a Towed Ship in Steady Wind, (OMAE2010-20673) In : Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering; 2010.Wichers, J.E.W., 1988. A Simulation Model for a Single Point Moored Tanker. Marine Publication, No. 797.
Wichers J.E.W.. A Simulation Model for a Single Point Moored Tanker. Marine Publication, No. 797 1988.Yasukawa, H., Hiritaka, H., Nakamura, N., Matsumoto, Y., 2006. Simulation of Slewing Motion of a Towed Ship. Journal of the Japan Society of Naval Architects and Ocean Engineers, 4, 137-146 (in Japanese).
Yasukawa H., Hiritaka H., Nakamura N., Matsumoto Y.. Simulation of Slewing Motion of a Towed Ship. Journal of the Japan Society of Naval Architects and Ocean Engineers 2006;4:137–146.